Κεφάλαιο 10Βασικά Στοιχεία Πολυπλοκότητας
10.1 Εισαγωγή
Σε αυτό το κεφάλαιο θα ασχοληθούμε με τα όρια της αποδοτικότητας των αλγορίθμων. Τι σημαίνει όμως αποδοτικός αλγόριθμος (πάντοτε ως προς τη χρονική διάρκεια εκτέλεσης); Διαισθητικά θα λέμε ότι ένας αλγόριθμος είναι αποδοτικός, αν ο χρόνος εκτέλεσής του είναι λογικός σε συνάρτηση με το μέγεθος του γράφου που χειριζόμαστε. Αυτός ο ορισμός είναι βεβαιώς ανεπαρκής μιας και δεν έχουμε ορίσει τι σημαίνει ”λογικός”. Θα λέμε ότι ένας αλγοριθμος είναι αποδοτικός, αν η χρονική του πολυπλοκότητα είναι πολυωνυμική22της μορφής , όπου είναι το μέγεθος της εισόδου και μία θετική σταθερά. Στην περίπτωση των γράφων το μέγεθος της εισόδου καθορίζεται από το πλήθος των κορυφών και των ακμών .
Από την άλλη πλευρά, υπάρχουν προβλήματα όπως αυτό της εύρεσης ενός Hamiltonian κυκλώματος33Ένα Hamiltonian κύκλωμα σε ένα γράφημα είναι ένας κύκλος που διέρχεται μία και μόνο μία φορά από κάθε κορυφή του γραφήματος . που δεν έχει βρεθεί αποδοτικός αλγόριθμος μέχρι σήμερα (εν έτει 2015) παρόλη την μεγάλη προσπάθεια που έχει γίνει. Όλοι οι αλγόριθμοι για αυτό το πρόβλημα που έχουμε μέχρι τώρα δεν είναι αποδοτικοί, με την έννοια ότι ο χρόνος εκτέλεσης τους είναι εκθετικός44της μορφής , όπου είναι το μέγεθος της εισόδου και μία σταθερά. σε σχέση με το μέγεθος του γράφου εισόδου. Υπάρχουν πάρα πολλά προβλήματα που φαίνεται να μην επιδέχονται αποδοτικής λύσης. Σε αυτό το κεφάλαιο θα αναφερθούμε συνοπτικά στη θεωρία που καταπιάνεται με την ταξινόμηση αλγοριθμικών προβλημάτων με βάση τη σχετική δυσκολία τους, την Πολυπλοκότητα.
Μία από τις βασικές επιδιώξεις της θεωρίας πολυπλοκότητας είναι η ταξινόμηση των προβλημάτων σε κλάσεις πολυπλοκότητας ανάλογα με την φαινομενική δυσκολία τους. Αυτό που μας ενδιαφέρει δεν είναι μόνο η ταξινόμηση των προβλημάτων σε κλάσεις αλλά και η σχέση που υπάρχει μεταξύ διαφορετικών κλάσεων πολυπλοκότητας. Οι σχέσεις αυτές μας φανερώνουν βαθύτερες σχέσεις μεταξύ διαφορετικών μέσων υπολογισμού (π.χ. τυχαίοι αλγόριθμοι σε σχέση με αιτιοκρατικούς αλγόριθμους), ενώ αντίστοιχα προσφέρουν ένα μέτρο δυσκολίας των προβλημάτων που ανήκουν σε αυτές τις κλάσεις. Εμείς θα εστιάσουμε μόνο σε δύο κλάσεις - ίσως τις πιο γνωστές - την κλάση αιτιοκρατικού πολυωνυμικού χρόνου (Polynomial) και την κλάση μη αιτιοκρατικού πολυωνυμικού χρόνου (Non-deterministic Polynomial). Η πρώτη κλάση περιέχει όλα τα προβλήματα που μπορούν να επιλυθούν από έναν αιτιοκρατικό (deterministic) υπολογιστή σε πολυωνυμικό χρόνο. Ένα τέτοιο παράδειγμα προβλήματος είναι η εύρεση Eulerian κυκλωμάτων55Ένα γράφημα έχει Eulerian κύκλωμα αν υπάρχει κύκλος που να διέρχεται από όλες τις ακμές μία και μόνο μία φορά. σε γραφήματα. Η δεύτερη κλάση περιέχει όλα εκείνα τα προβλήματα τα οποία μπορούν να λυθούν σε έναν μη αιτιοκρατικό (non-deterministic) υπολογιστή σε πολυωνυμικό χρόνο. Ένα τέτοιο παράδειγμα αποτελεί η εύρεση Hamiltonian κυκλωμάτων σε γραφήματα. Θα δούμε παρακάτω έναν πιο διαισθητικό ορισμό της κλάσης .
Ένα από τα μεγαλύτερα ανοικτά προβλήματα στην Επιστήμη των Υπολογιστών και στα Μαθηματικά είναι αν . Η πιο σημαντική προσπάθεια που έχει γίνει προς την κατεύθυνση επίλυσης αυτού του προβλήματος είναι η θεωρία -πληρότητας και πιο γενικά η θεωρία ύπαρξης χαρακτηριστικών προβλημάτων για αρκετές κλάσεις πολυπλοκότητας. Κατ’ αυτόν τον τρόπο, για μία κλάση πολυπλοκότητας θα λέμε ότι ένα πρόβλημα είναι -πλήρες αν η πολυπλοκότητά τους καθορίζει και τη θέση της στην ιεραρχία των κλάσεων πολυπλοκότητας.
Στη συνέχεια, θα δούμε πιο αναλυτικά τις βασικές κλάσεις πολυπλοκότητας και θα προσπαθήσουμε να αιτιολογήσουμε διαισθητικά τη σημασία τους ενώ ταυτόχρονα θα αναφερθούμε στην έννοια της πληρότητας. Πριν όμως μιλήσουμε για κλάσεις πολυπλοκότητας θα αναφερθούμε συνοπτικά σε ένα εξαιρετικό εργαλείο επίλυσης προβλημάτων, την αναγωγή.
10.2 Μετασχηματισμοί και Αναγωγές
Η θεωρία πολυπλοκότητας ασχολείται ως επί το πλείστον με συγκεκριμένο τύπο προβλημάτων. Ένα πολύ γνωστό πρόβλημα είναι το πρόβλημα του περιοδεύοντος πωλητή (Travelling Salesman Problem - TSP), το οποίο ορίζεται ως εξής:
Ορισμός 10.1.
Δοθέντος ενός πλήρους μη-κατευθυνόμενου γραφήματος , και ενός βάρους για κάθε ακμή , να βρεθεί το Hamiltonian κύκλωμα στο που να ελαχιστοποιεί το άθροισμα των βαρών πάνω στο κύκλωμα .
Αυτό είναι ένα πρόβλημα βελτιστοποίησης, δηλαδή ένα πρόβλημα όπου μας ζητείται να βρούμε μία δομή (το Hamiltonian κύκλωμα στη συγκεκριμένη περιπτωση) που να μεγιστοποιεί (ή ελαχιστοποιεί) μία συγκεκριμένη ποσότητα (το άθροισμα των βαρών). Από την άλλη πλευρά, το πρόβλημα του Hamiltonian κυκλώματος είναι ένα πρόβλημα αναζήτησης μιας και μας ζητείται μία δομή (ένα κύκλωμα) που έχει μία συγκεκριμένη ιδιότητα (να είναι Hamiltonian). Η θεωρία πολυπλοκότητας από την άλλη ασχολείται κυρίως με προβλήματα απόφασης. Σε ένα πρόβλημα απόφασης η έξοδος της λύσης είναι δυαδική (ΝΑΙ/ΟΧΙ). Ο κυριότερος λόγος για αυτή την επιλογή είναι η απλότητα, χωρίς να σημαίνει βέβαια ότι δεν έχουν οριστεί και ερευνηθεί κλάσεις πολυπλοκότητας που να επιστρέφουν τιμή. Η μετατροπή ενός προβλήματος βελτιστοποίησης σε πρόβλημα απόφασης γίνεται εισάγοντας μία καινούργια μεταβλητή στο πρόβλημα απόφασης, που να αποτελεί άνω ή κάτω φράγμα για την ποσότητα που ελαχιστοποιείται ή μεγιστοποιειται αντίστοιχα στο πρόβλημα βελτιστοποίησης. Το πρόβλημα απόφασης του TSP ορίζεται ως εξής:
Ορισμός 10.2.
Δοθέντος ενός πλήρους μη-κατευθυνόμενου γραφήματος , ενός βάρους για κάθε ακμή και ενός αριθμού , να βρεθεί αν υπάρχει Hamiltonian κύκλωμα στο , έτσι ώστε .
Προσέξτε ότι για αυτόν τον ορισμό αρκεί να σχεδιάσουμε ένα αλγόριθμο που να επιστρέφει ΝΑΙ, αν υπάρχει τέτοιο κύκλωμα αλλιώς θα επιστρέφει ΟΧΙ. Στη δεύτερη περίπτωση μπορεί να υπάρχει Hamiltonian κύκλωμα αλλά το συνολικό του βάρος να είναι μεγαλύτερο από . Το γεγονός οτι από εδώ και στο εξής θα ασχοληθούμε με προβλήματα απόφασης αντί για τα αντίστοιχα βελτιστοποίησης δεν είναι καθόλου περιοριστικό όσον αφορά την απόδοσή τους. Πράγματι, αν έχουμε έναν αλγόριθμο για το πρόβλημα βελτιστοποίησης του TSP τότε για να λύσουμε το αντίστοιχο πρόβλημα απόφασης αρκεί να βρούμε την βέλτιστη λύση και να ελέγξουμε αν ισχύει . Η άλλη κατεύθυνση είναι λίγο πιο πολύπλοκη αλλά βασίζεται στην ιδέα της δυαδικής αναζήτησης πάνω στην τιμή . Πιο συγκεκριμένα, έστω ότι έχουμε έναν αλγόριθμο για το πρόβλημα απόφασης TSP. Έστω ότι είναι το μέγιστο βάρος στις ακμές του . Τότε εφαρμόζουμε δυαδική αναζήτηση για την τιμή στο διάστημα και για κάθε τέτοια τιμή εφαρμόζουμε τον . Αν επιστρέψει ο ΝΑΙ, τότε συνεχίζουμε στο πάνω μισό του διαστήματος αναδρομικά, αλλιώς στο κάτω μισό. Αυτός ο αλγόριθμος θα καλέσει συνολικά φορές τον . Άρα, αν ο ήταν πολυωνυμικός αλγόριθμος τότε και ο θα ήταν επίσης πολυωνυμικός. Αυτή η διαδικασία, δηλαδή, δείχνει ότι η απόδοση του προβλήματος βελτιστοποίησης θα είναι αρκετά κοντά στην απόδοση του αντίστοιχου προβλήματος απόφασης. Από αυτό το σημείο και στο εξής θα αναφερόμαστε μόνο σε προβλήματα απόφασης.
Το κυριότερο εργαλείο για να αποδείξουμε ότι ένα πρόβλημα ανήκει σε μία κλάση πολυπλοκότητας είναι η αναγωγή. Η ιδέα της αναγωγής είναι εξαιρετικά απλή και αναφέρεται στην μετατροπή του στιγμιοτύπου ενός προβλήματος σε ένα στιγμιότυπο του προβλήματος με τέτοιο τρόπο, ώστε η λύση στο να δίνει την λύση και στο . Εμείς θα ασχοληθούμε με αναγωγές που υλοποιούνται σε έναν αιτιοκρατικό υπολογιστή σε πολυωνυμικό χρόνο. Αν το είναι ένα ΝΑΙ στιγμιότυπο του προβλήματος ,66Θα μπορούσαμε να γράψουμε αφού το είναι ένα σύνολο τέτοιων στιγμιοτύπων που έχουν τη συγκεκριμένη ιδιότητα. τότε η αναγωγή θα δώσει ένα ΝΑΙ στιγμιότυπο του προβλήματος . Αντίστοιχα, αν το είναι ένα ΟΧΙ στιγμιότυπο του , τότε και το θα είναι ένα ΟΧΙ στιγμιότυπο του . Δηλαδή, χρησιμοποιώντας σημειογραφία συνόλων θα πρέπει να δειξουμε ότι η αναγωγή είναι πολυωνυμικού χρόνου και ότι .
Σε αυτή την περίπτωση θα λέμε ότι το πρόβλημα ανάγεται στο πρόβλημα και συμβολίζουμε ως , το οποίο σημαίνει ότι μπορεί να χρησιμοποιηθεί η λύση του , ώστε να λύσουμε το . Το παρακάτω λήμμα δίνει μία πρώτη γεύση για την χρησιμότητα της αναγωγής.
Λήμμα 10.1.
Αν το πρόβλημα λύνεται σε πολυωνυμικό χρόνο και το πρόβλημα ανάγεται στο σε πολυωνυμικό χρόνο, τότε και το λύνεται σε πολυωνυμικό χρόνο.
Proof.
Η απόδειξη αναφέρεται ουσιαστικά στο Σχήμα 10.1. Συγκεκριμένα, μετασχηματίζουμε την είσοδο του προβλήματος σε είσοδο για το πρόβλημα σε πολυωνυμικό χρόνο μέσω της αναγωγής. Προσέξτε ότι, αφού η εκτελείται σε πολυωνυμικό χρόνο, το μήκος του στιγμιοτύπου δεν μπορεί παρά να είναι πολυωνυμικά μεγαλύτερο από το . Έπειτα, χρησιμοποιώντας τον πολυωνυμικό αλγόριθμο για το απαντάμε ΝΑΙ/ΟΧΙ σε πολυωνυμικό συνολικά χρόνο για το πρόβλημα . ∎
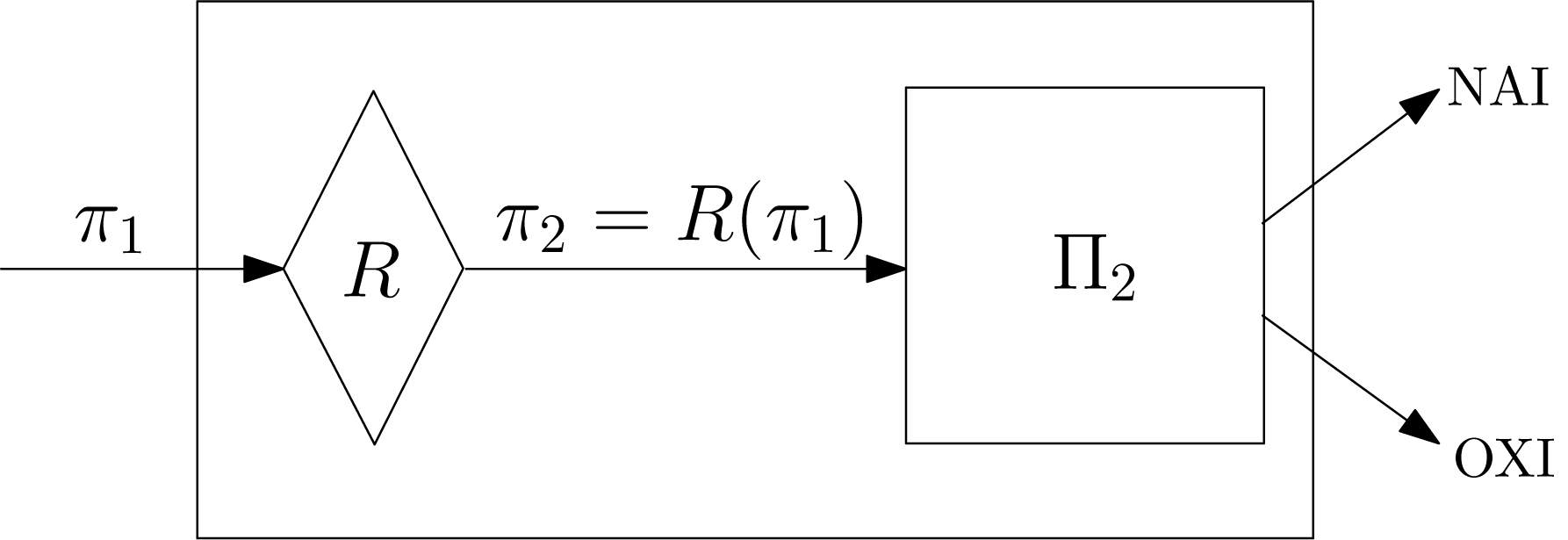
Με βάση αυτό το λήμμα μπορούμε να επιλύουμε προβλήματα σε πολυωνυμικό χρόνο ανάγοντάς τα σε πολυωνυμικό χρόνο σε άλλα γνωστά προβλήματα που επίσης επιλύονται σε πολυωνυμικό χρόνο. Για παράδειγμα, το πρόβλημα της μεγαλύτερης μέγιστης αντιστοίχησης σε διμερές γράφημα ανάγεται στο πρόβλημα μέγιστης ροής σε ένα απλό γράφημα.
Η έννοια της αναγωγής μπορεί να χρησιμοποιηθεί και με έναν αντίστροφο τρόπο. Προσέξτε ότι όταν ανάγουμε το πρόβλημα στο πρόβλημα χρησιμοποιούμε το σαν διαδικασία για να λύσουμε το . Με αυτή την έννοια και λαμβάνοντας υπ’όψιν ότι αναφερόμαστε σε προβλήματα τουλάχιστον πολυωνυμικής πολυπλοκότητας, μπορούμε να βγάλουμε το συμπέρασμα ότι το είναι ίσης ή και μεγαλύτερης δυσκολίας από το . Για παράδειγμα, το θα μπορούσε να είναι πρόβλημα που λύνεται σε εκθετικό χρόνο, ενώ το να λύνεται σε πολυωνυμκό χρόνο αλλά ποτέ το αντίστροφο, αν υπήρχε αναγωγή πολυωνυμικού χρόνου από το στο .
Αναφερόμενοι στην αντιθετοαντίστροφη μορφή του Λήμματος 10.1, αν το ανάγεται σε πολυωνυμικό χρόνο στο και το είναι εκθετικού χρόνου, τότε και το θα πρέπει να είναι εκθετικού χρόνου. Ακριβώς αυτή τη μορφή της αναγωγής χρησιμοποιούμε για να δείξουμε ότι πολλά προβλήματα της Θεωρίας Γράφων είναι δύσκολα ως προς τη πολυπλοκότητά τους προβλήματα.
10.3 Kλάσεις Πολυπλοκότητας
Σε αυτό το κεφάλαιο θα αναφερθούμε σε κάποιες θεμελιώδεις κλάσεις πολυπλοκότητας που περιλαμβάνουν τις κλάσεις , και την . Αν ο αναγνώστης επιθυμεί περισσότερη πληροφορία σε σχέση με τις κλάσεις πολυπλοκότητας, μπορεί να χρησιμοποιήσει σαν αναφορές τα βιβλία [8, 143].
10.3.1 Η Κλάση
Η κλάση περιλαμβάνει όλα τα προβλήματα που μπορούν να λυθούν σε πολυωνυμικό χρόνο. Στην ουσία έχουμε συνδέσει την έννοια της αποδοτικότητας με την κλάση . Η σύνδεση αυτή βασίζεται στην παρατήρηση ότι ένας πολυωνυμικός αλγόριθμος για ένα πρόβλημα βασίζεται σε κάποια βαθύτερη ιδιότητα του προβλήματος που επιτρέπει τη γρήγορη επίλυσή του αποφεύγοντας την λύση της εξαντλητικής αναζήτησης (brute force) που για τυπικά προβλήματα είναι εκθετικής πολυπλοκότητας. Για παράδειγμα, η εύρεση ενός ελάχιστου ζευγνύοντος δένδρου γίνεται σε πολυωνυμικό χρόνο, αφού μπορεί να εφαρμοσθεί η μέθοδος της απληστίας.
Βέβαια, κάποιος μπορεί να ισχυρισθεί ότι ένας αλγόριθμος με πολυπλοκότητα μόνο αποδοτικός δεν είναι. Αυτές οι περιπτώσεις όμως είναι σπάνιες, αν όχι ανύπαρκτες, και συνήθως όταν σχεδιάζεται ένας πολυωνυμικός αλγόριθμος για ένα πρόβλημα, τότε σχεδιάζονται διαδοχικά ολοένα και καλύτεροι αλγόριθμοι. Τέλος, η κλάση είναι πολύ σημαντική γιατι φαίνεται ότι αντιστοιχεί στα όρια που θέτει η φύση ως προς την απόδοση επίλυσης προβλημάτων77Αυτή η παρατήρηση αντιστοιχεί στην Θέση των Church-Turing για την πολυπλοκότητα αν και δεν είναι εντελώς σωστή με την έννοια ότι θα πρέπει να αναφερθούμε σε έναν υπολογιστή που χρησιμοποιεί τυχαιότητα ή ακόμα και σε έναν κβαντικό υπολογιστή..
10.3.2 Η Κλάση
Η κλάση πολυπλοκότητας αντιστοιχεί σε όλα τα προβλήματα για τα οποία υπάρχει πολυωνυμικός ανταιτιοκρατικός (non-deterministic) αλγόριθμος. Υπάρχει όμως ένας ισοδύναμος ορισμός που είναι εξαιρετικά πιο διαισθητικός και δείχνει ακριβώς τη σημασία αυτής της κλάσης πολυπλοκότητας. Ένα πρόβλημα ανήκει στην κλάση αν έχει την ιδιότητα της πολυωνυμικής επαληθευσιμότητας. Για παράδειγμα, το πρόβλημα της ύπαρξης Hamiltonian κυκλώματος (HAMiltonian Circle - HAMC) ορίζεται ως εξής:
Ορισμός 10.3.
Δοθέντος ενός μη-κατευθυνόμενου γραφήματος , να βρεθεί αν υπάρχει Hamiltonian κύκλωμα στο .
Το HAMC έχει αυτή την ιδιότητα αφού, αν μας δοθεί μία υποψήφια λύση (ένα υποψήφιο Hamiltonian κύκλωμα), μπορούμε να ελέγξουμε σε πολυωνυμικό χρόνο ότι όντως το είναι Hamiltonian κύκλωμα του ελέγχοντας τους κόμβους και τις ακμές του . Επομένως, με βάση αυτό τον ορισμό το πρόβλημα HAMC ανήκει στη κλάση .
Πιο τυπικά, θα λέμε ότι ένα πρόβλημα ανήκει στη κλάση όταν υπάρχει αιτιοκρατικός πολυωνυμικός επαληθευτής για το . Ένας πολυωνυμικός επαληθευτής έχει ώς είσοδο ένα στιγμιότυπο του (μπορεί να είναι ΝΑΙ/ΟΧΙ στιγμιότυπο) καθώς και ένα πιστοποιητικό πολυωνυμικού μεγέθους που αποδεικνύει ότι το είναι ΝΑΙ στιγμιότυπο του (). Συνήθως το πιστοποιητικό είναι η λύση στο πρόβλημα χωρίς όμως να σημαίνει ότι δεν υπάρχουν πολλές εξαιρέσεις. Στο παρακάτω λήμμα κατασκευάζεται ένας τέτοιος πολυωνυμικός επαληθευτής.
Λήμμα 10.2.
Το πρόβλημα TSP ανήκει στην κλάση .
Proof.
Θα κατασκευάσουμε έναν πολυωνυμικό επαληθευτή. Αυτός ο αλγόριθμος (ο επαληθευτής δηλαδή) έχει ως είσοδο ένα γράφημα με βάρη και έναν αριθμό ενώ το πιστοποιητικό είναι ένα κύκλωμα . Αρχικά, ελέγχουμε ότι το όντως είναι ένα Hamiltonian κύκλωμα του . Αν δεν είναι, επιστρέφουμε ΟΧΙ και τερματίζουμε αλλιώς συνεχίζουμε ελέγχοντας αν το άθροισμα των βαρών στο είναι . Αν δεν ισχύει, επιστρέφουμε ΟΧΙ και τερματίζουμε αλλιώς έχουμε δείξει ότι το είναι πράγματι μία έγκυρη λύση σε σχέση με το πρόβλημα TSP στο γράφημα και, επομένως, επιστρέφουμε ΝΑΙ. Όλα τα παραπάνω βήματα μπορούν να υλοποιηθούν σε πολυωνυμικό χρόνο σε έναν αιτιοκρατικό υπολογιστή και, άρα, το λήμμα αποδείχθηκε. ∎
Διαισθητικά λοιπόν η κλάση περιέχει όλα τα προβλήματα που λύνονται αποδοτικά, ενώ η κλάση περιέχει όλα τα προβλήματα των οποίων η λύση μπορεί να επαληθευτεί αποδοτικά. Το μεγαλύτερο πρόβλημα στην Επιστήμη των Υπολογιστών αφορά το ερώτημα αν , αν δηλαδή η κλάση των προβλημάτων που λύνονται αποδοτικά συμπίπτει ή όχι με την κλάση των προβλημάτων των οποίων η λύση επαληθεύεται αποδοτικά. Προφανώς, αφού αν η λύση υπολογίζεται αποδοτικά, τότε επαληθεύεται και αποδοτικά από τον ίδιο τον αλγόριθμο που βρίσκει τη λύση.
Υπάρχουν προβλήματα που δεν ανήκουν στην κλάση και, άρα, δεν επαληθεύονται αποδοτικά υποψήφιες λύσεις τους. Ένα τέτοιο πρόβλημα είναι το εξής:
Ορισμός 10.4.
Δοθέντος ενός μη-κατευθυνόμενου γραφήματος να βρεθεί αν δεν υπάρχει Hamiltonian κύκλωμα στο .
Δεν έχουμε ακόμα ανακαλύψει ένα πολυωνυμικού μεγέθους πιστοποιητικό για αυτό το πρόβλημα και, άρα, υποπτευόμαστε ότι δεν ανήκει στην κλάση . Διαισθητικά φαίνεται ότι είναι πιο εύκολο να επαληθεύσει κάποιος ύπαρξη μίας ιδιότητας σε ένα γράφο παρά ανυπαρξία της ιδιότητας από το γράφο. Όλα αυτά τα προβλήματα που κατά κάποιο τρόπο αποτελούν συμπληρωματικά της κλάσης σχηματίζουν την κλάση co- για την οποία υποπτευόμαστε (αλλά δεν έχουμε αποδείξει) ότι διαφέρει από την κλάση .
10.3.3 -πληρότητα
Σε αυτό το σημείο θα ορίσουμε την κλάση (-Complete) που είναι υποσύνολο της κλάσης . Αυτή περιλαμβάνει όλα τα -πλήρη προβλήματα που υπό μία έννοια είναι τα πιο δύσκολα της κλάσης . Ένα πρόβλημα λέγεται -πλήρες, όταν ισχύουν τα εξής:
-
1.
-
2.
Για να δείξουμε, λοιπόν, ότι ένα πρόβλημα είναι -πλήρες θα πρέπει να δείξουμε ότι ανήκει στην κλάση κατασκευάζοντας έναν πολυωνυμικό επαληθευτή και έπειτα να δείξουμε ότι κάθε πρόβλημα στην κλάση ανάγεται στο . Το δεύτερο μέρος, όμως, είναι αρκετά πολύπλοκο και για αυτό το λόγο αν αποδείξουμε ότι ισχύει για ένα πρόβλημα, έπειτα κάνοντας αναγωγές από αυτό θα αποδεικνύουμε ότι και άλλα προβλήματα είναι -πλήρη. Το γνωστό θεώρημα των Cook-Levin δίνει το πρώτο τέτοιο πρόβλημα που είναι -πλήρες.
Θεώρημα 10.1.
Το πρόβλημα SAT είναι -πλήρες.
Το πρόβλημα SAT είναι το πρόβλημα της ικανοποιησιμότητας τύπων. Ένας λογικός τύπος σε κανονική συζευκτική μορφή (CNF) αποτελείται από σύζευξη () φράσεων, όπου κάθε φράση είναι μία διάζευξη () λεξιγραμμάτων και κάθε λεξίγραμμα είναι μία μεταβλητή ή η αντίθετή της (). Ένα παράδειγμα είναι ο λογικός τύπος .
Με βάση το Θεώρημα 10.1 μπορούμε εφεξής να αποδεικνύουμε ότι ένα πρόβλημα είναι -πλήρες δείχνοντας πρώτα ότι ανήκει στην κλάση και έπειτα κάνοντας αναγωγή από ένα ήδη γνωστό -πλήρες πρόβλημα. Σε αυτό το σημείο θα δείξουμε ότι το TSP είναι -πλήρες θεωρώντας ως γνωστό ότι το πρόβλημα ύπαρξης Hamiltonian κυκλώματος HAMC είναι -πλήρες.
Θεώρημα 10.2.
Το TSP είναι -πλήρες.
Proof.
Από το Λήμμα 10.2 προκύπτει ότι το TSP ανήκει στην κλάση . Με δεδομένο ότι το πρόβλημα ύπαρξης Hamiltonian κυκλώματος είναι -πλήρες θα το ανάγουμε στο πρόβλημα του TSP. Έστω ένα στιγμιότυπο του προβλήματος HAMC που αποτελείται από το γράφημα . Κατασκευάζουμε νέο γράφο , όπου και το περιλαμβάνει όλες τις δυνατές ακμές στο (δηλαδή το είναι πλήρες). Επίσης, ορίζουμε μία συνάρτηση βάρους , έτσι ώστε:
Τέλος, θέτουμε . Για να ολοκληρώσουμε την αναγωγή θα πρέπει να δείξουμε ότι ο έχει Hamiltonian κύκλωμα αν και μόνο αν ο έχει Hamiltonian κύκλωμα βάρους το πολύ .
Έστω ότι ο έχει Hamiltonian κύκλωμα . Τότε και ο έχει ως Hamiltonian κύκλωμα το αφού έχει το ίδιο σύνολο κορυφών με τον , ενώ ταυτόχρονα . Μάλιστα, αφού όλες οι ακμές του στον έχουν βάρος σημαίνει ότι ο έχει συνολικό βάρος στον ίσο με και, επομένως, αποδείχτηκε η μία κατεύθυνση.
Έστω ότι ο έχει Hamiltonian κύκλωμα με βάρος το πολύ . Σε αυτή την περίπτωση, το κύκλωμα δεν μπορεί να περιλαμβάνει καμία από τις ακμές του που δεν ανήκουν στο , μιας και αυτές εχουν βάρος και επομένως οι ακμές του δεν μπορούν να έχουν συνολικό βάρος . Επομένως, ο αρχικός γράφος έχει ένα Hamiltonian κύκλωμα .
Αποδείξαμε την ορθότητα της αναγωγής και το μόνο που απομένει είναι να δειξουμε ότι η πολυπλοκότητά της είναι πολυωνυμική. Πράγματι, η κατασκευή του μπορεί να γίνει σαρώνοντας το γράφημα και έπειτα προσθέτοντας τις ακμές που λείπουν, ενώ ταυτόχρονα ενημερώνουμε και τα βάρη τους με βάση την παραπάνω συνάρτηση. Επομένως, αφού το TSP ανήκει στην κλάση και το -πλήρες πρόβλημα HAMC ανάγεται σε αυτό προκύπτει ότι και το TSP είναι -πλήρες. ∎
Ένα πρόβλημα θα λέγεται -δυσχερές (-hard), αν όλα τα προβλήματα που ανήκουν στην κλάση ανάγονται σε αυτό σε πολυωνυμικό χρόνο. Με αυτή την έννοια το πρόβλημα θα είναι είτε -πλήρες, αν δείχναμε ότι ανήκει στην κλάση ή θα ήταν πιο δύσκολο πρόβλημα και θα άνηκε σε μία άλλη μεγαλύτερη κλάση.
10.3.4 Το Πρόβλημα TSP
Το γεγονός ότι ένα πρόβλημα, όπως το TSP, είναι -δυσχερές σημαίνει ότι είναι πολύ πιθανό να μην υπάρχει πολυωνυμικός αλγόριθμος που να λύνει το συγκεκριμένο πρόβλημα για κάθε είσοδο. Σε αυτό το σημείο θα αναφερθούμε συνοπτικά σε κάποιες μεθόδους αντιμετώπισης αυτών των δύσκολων προβλημάτων βελτιστοποίησης (και όχι απλά απόφασης) - που εμφανίζονται συχνά στην πράξη: α) με προσεγγιστικές τεχνικές (approximation), όπου ο στόχος είναι να βρεθεί μία λύση που εγγυημένα είναι κοντά στην βέλτιστη λύση, β) κάνοντας χρήση τυχαιότητας (randomization), όπου πετυχαίνουμε σε μερικές περιπτώσεις καλή αναμενόμενη απόδοση, γ) με ευρετικές μεθόδους (heuristics), όπου προσπαθούμε με μεθόδους που δεν δίνουν κάποια εγγύηση να βρούμε μία σχετικά καλή λύση, δ) με μεθόδους χαλάρωσης (relaxations) που χαλαρώνουν τους περιορισμούς του προβλήματος, έτσι ώστε το νέο πρόβλημα να είναι πιο εύκολο να λυθεί αλλά ταυτόχρονα η λύση αυτή να είναι αρκετά κοντά στη λύση που ψάχνουμε, ε) με τοπική αναζήτηση (local search), όπου μέσα από μία διαδικασίας μετα-βελτιστοποίησης προσπαθούμε να βελτιώσουμε μία λύση που έχουμε ήδη επιλέξει (τυχαία ή με κάποια ευρετική μέθοδο) και στ) με πλήρης απαρίθμηση (complete enumeration), όπου προσπαθούμε να απαριθμήσουμε όλες τις λύσεις και να επιλέξουμε τη βέλτιστη χρησιμοποιώντας διάφορες τεχνικές που επιταχύνουν την όλη διαδικασία. Παρακάτω θα αναφερθούμε ονομαστικά μόνο σε κάποια γνωστά αποτελέσματα σχετικά με το TSP που αφορούν προσεγγιστικές λύσεις.
Αν στην απόδειξη του Θεωρήματος 10.2 αντί για στην συνάρτηση βάρους βάλουμε την τιμή , για αυθαίρετη σταθερά , τότε προκύπτει το εξής αποτέλεσμα:
Λήμμα 10.3.
Αν , τότε για οποιαδήποτε σταθερά δεν υπάρχει πολυωνυμικός αλγόριθμος που να παράγει ένα Hamiltonian κύκλωμα συνολικού βάρους μικρότερου από φορές το βάρος του βέλτιστου Hamiltonian κυκλώματος.
Proof.
Έστω ότι και ότι υπάρχει πολυωνυμικός αλγόριθμος που προσεγγίζει το TSP κατά έναν παράγοντα . Τότε, αν αλλάξουμε τη συνάρτηση βάρους στην απόδειξη του Θεωρήματος 10.2 σε
μπορούμε να χρησιμοποιήσουμε τον , για να λύσουμε σε πολυωνυμικό χρόνο το πρόβλημα της ύπαρξης Hamiltonian κυκλώματος που με δεδομένο, όμως, ότι είναι -πλήρες και αυτό είναι αδύνατο. Πράγματι, ο είτε θα έχει Hamiltonian κύκλωμα με συνολικό βάρος που θα αντιστοιχεί σε πραγματικό Hamiltonian κύκλωμα στο αρχικό γράφημα ή θα έχει Hamiltonian κύκλωμα με συνολικό βάρος που σημαίνει ότι χρησιμοποιείται μία τουλάχιστον ακμή που δεν υπάρχει στον και άρα ο δεν έχει Hamiltonian κύκλωμα. Εφαρμόζοντας τον στον γράφο με τα νέα βάρη που ορίσαμε παραπάνω, αν επιστρέψει ένα μονοπάτι μήκους λόγω της προσέγγισης, τότε σίγουρα υπάρχει κύκλωμα με βάρος το πολύ αφού θα υπάρχει Hamiltonian κύκλωμα και καμία από τις ακμές του δεν θα είναι μία ακμή με βάρος , που σημαίνει ότι αυτή η ακμή δεν υπάρχει στον αρχικό γράφο . Αν το κύκλωμα που επιστρέφει ο έχει συνολικό βάρος τότε αποκλείεται το εν λόγω μονοπάτι να περιέχει ακμές μόνο του αφού αυτό θα σήμαινε ότι η προσέγγιση του θα ήταν χειρότερη του που είναι άτοπο λόγω υπόθεσης. Άρα, αν τότε αποκλείεται να υπάρχει ο αλγόριθμος . ∎
Αυτό σημαίνει ότι μάλλον (θα πρέπει να ισχύει ) για το πρόβλημα TSP είναι αδύνατο να έχουμε μία καλή προσέγγιση σε αποδοτικό χρόνο. Μπορούμε όμως να έχουμε μία πολύ καλή προσέγγιση για μία παραλλαγη του TSP:
Ορισμός 10.5.
Το Ευκλείδειο TSP, ΔTSP, είναι το πρόβλημα TSP με τον περιορισμό ότι οι κόμβοι ειναι σημεία του Ευκλείδειου χώρου και τα βάρη στις ακμές είναι οι Ευκλείδειες αποστάσεις μεταξύ των σημείων.
Για το πρόβλημα ΔTSP υπάρχει αλγόριθμος που επιστρέφει ένα Hamiltonian κύκλωμα του οποίου το βάρος να είναι το πολύ μεγαλύτερο από το βάρος της βέλτιστης λύσης σε χρόνο 88Το είναι μία πολυωνυμική συνάρτηση του ..
10.4 -πλήρη Προβλήματα
Οι Garey και Johnson στο βιβλίο τους ”Computers and Intractability: a Guide to the Theory of -completeness” [52] (σελίδες 187-288), συγκέντρωσαν όλα τα μέχρι το 1979 γνωστά -πλήρη προβλήματα. Τα προβλήματα αυτά ομαδοποιήθηκαν στις εξής 12 κατηγορίες:
-
•
Θεωρία γράφων (65)
-
•
Σχεδιασμός δικτύων (51)
-
•
Σύνολα και διαμερισμοί (21)
-
•
Αποθήκευση και ανάκτηση (36)
-
•
Σειριοποίηση και δρομολόγηση (22)
-
•
Μαθηματικός προγραμματισμός (13)
-
•
Άλγεβρα και Θεωρία αριθμών (18)
-
•
Παίγνια και σπαζοκεφαλιές (15)
-
•
Λογική (19)
-
•
Αυτόματα και γλώσσες (21)
-
•
Βελτιστοποίηση προγραμμάτων (20)
-
•
Διάφορα (19)
Ο αριθμός στην παρένθεση δηλώνει τον αντίστοιχο αριθμό προβλημάτων. Έτσι, το σύνολο των καταγραμμένων -πλήρων προβλημάτων το 1979 ανέρχονταν στα 320 από πολλές περιοχές της Πληροφορικής. Ταυτόχρονα, υπήρχε και μία λίστα 12 ανοικτών προβλημάτων για τα οποία δεν είχε αποδειχθεί αν ανήκουν ή όχι στην κατηγορία των -πλήρων προβλημάτων. Στην επανεκτύπωση του βιβλίου το 1991 υπάρχει ένα νέο σχόλιο των συγγραφέων, όπου καταγράφεται ότι έχουν επιλυθεί τα 8 από τα 12 ανοικτά προβλήματα της έκδοσης του 1979. Από αυτά τα 8 προβλήματα, για 4 αποδείχθηκε ότι ανήκουν στην κλάση , ενώ για άλλα αποδείχθηκε ότι ανήκουν στην κλάση .
Από τότε, όμως, η θεωρία της -πληρότητας έχει εφαρμοσθεί και σε άλλες περιοχές με αποτέλεσμα πολλά προβλήματα που δεν προκύπτουν μέσα από την Επιστήμη της Πληροφορικής να έχουν χαρακτηρισθεί ως -πλήρη. Αναφέρουμε στη συνέχεια ενδεικτικά μερικές περιπτώσεις:
-
•
Βιολογία: πως διπλώνεται μία πρωτεΐνη στον -διάστατο χώρο
-
•
Θεωρία Παιγνίων: εύρεση ισορροπιών Nash που μεγιστοποιούν την ωφέλεια του συνόλου
-
•
Μηχανική Περιβάλλοντος: βέλτιστη τοποθέτηση αισθητήρων μόλυνσης
-
•
Στατιστική Φυσική: εύρεση συνάρτησης διαμέρισης για το -διάστατο Ising μοντέλο
-
•
Πολιτική Επιστήμη: Υπολογισμός του δείκτη Shapley-Shubik ισχύος σε ψηφοφορία
-
•
Pop κουλτούρα: υπολογισμός λύσης από μία συγκεκριμένη θέση για το παιχνίδι Ναρκαλιευτής
10.5 Βιβλιογραφική Συζήτηση
Σε αυτό το κεφάλαιο συζητήσαμε αρκετά συνοπτικά βασικά στοιχεία της πολυπλοκότητας. Γενικά, η θεωρία γράφων είναι μία πλούσια πηγή -πλήρων προβλημάτων λόγω και της εκτεταμένης χρήσης των γράφων ως εργαλείο μοντελοποίησης προβλημάτων. Το βιβλίο των Garey και Johnson [52] παραμένει ακόμα η βασική αναφορά για την θεωρία της -πληρότητας και τα περισσότερα προβλήματα που αναφέρονται στην Ενότητα 10.4 είναι από αυτό το βιβλίο. Από το 1979, όμως, η περιοχή έχει προχωρήσει πολύ. Στο βιβλίο του Παπαδημητρίου [143] υπάρχει μία πιο σύγχρονη αντιμετώπιση του θέματος, ενώ αναλύονται και άλλες υποπεριοχές της Πολυπλοκότητας. Για μία όμως σύγχρονη αντιμετώπιση του θέματος όπου πολλά θέματα στην Πολυπλοκότητα που έχουν αναπτυχθεί την δεκαετία (2000-2009) αναφέρονται αναλυτικά θα πρέπει κάποιος να διαβάσει το βιβλίο των Arora και Barak [8].
10.6 Ασκήσεις
-
1.
Από τη λίστα των -πλήρων προβλημάτων της Ενότητας 10.4 να επιλεγεί ένα πρόβλημα και να αποδειχθεί ότι κάποιο άλλο από τη λίστα είναι επίσης -πλήρες. Προσοχή, η επιλογή του ζεύγους πρέπει να γίνει με τρόπο, ώστε τα προβλήματα να έχουν κάποια συγγένεια και η αναγωγή να είναι εύκολη.
-
2.
Να αποδειχθεί ότι αν ένα -πλήρες πρόβλημα μπορεί να λυθεί σε πολυωνυμικό χρόνο, τότε .
-
3.
Έστω ο τύπος γραφήματος όπου οι κορυφές είναι σημεία ενός πλέγματος σε ένα -διάστατο κύβο, όπου κάθε ακμή έχει κορυφές. Αυτό σημαίνει ότι οι κορυφές μπορούν να αναπαρασταθούν από διανύσματα όπου . Υπάρχει μία ακμή μεταξύ δύο κόμβων μόνο αν διαφέρουν τα διανύσματά τους σε μία διάσταση ακριβώς. Για παράδειγμα, η περίπτωση και αντιστοιχεί σε ένα τετράγωνο, ενώ η περίπτωση αντιστοιχεί σε κύβο. Μερικά από αυτά τα γραφήματα έχουν Hamiltonian κύκλωμα, ενώ κάποια άλλα δεν έχουν. Για παράδειγμα, το τετράγωνο και ο κύβος έχουν Hamiltonian κύκλωμα, αλλά το γράφημα για και δεν έχει.
-
(a)
Να αποδείχθεί ότι το γράφημα για και δεν έχει Hamiltonian κύκλωμα. Υπόδειξη: Σκεφτείτε τι γίνεται αν ένα υποθετικό Hamiltonian κύκλωμα περάσει από τον κεντρικό κόμβο. Από πού έρχεται και που μπορεί να μεταβεί χωρίς να αποκόψει κάποιο κομμάτι από το Hamiltonian κύκλωμα;
-
(b)
Για ποιες τιμές του και υπάρχει Hamiltonian κύκλωμα; Το πρόβλημα ύπαρξης Hamiltonian κυκλώματος σε αυτά τα γραφήματα παραμένει -πλήρες;
-
(a)
-
4.
Ένας γράφος δεν χρειάζεται να είναι εξαιρετικά μεγάλος πριν οι ερωτήσεις σχετικά με -πλήρη προβλήματα γίνουν αρκετά δυσκολες για να λυθούν με το χέρι. Έστω το γράφημα του Σχήματος 10.2.
-
(a)
Έχει ο γράφος Hamiltonian κύκλωμα;
-
(b)
Ποιό είναι το μέγιστο ανεξάρτητο σύνολο;
-
(c)
Ποιό είναι το ελάχιστο σύνολο κάλυψης;
-
(d)
Ποιο είναι το ελάχιστο συνολο κάλυψης ακμών;
-
(e)
Είναι ο γράφος 2-χρωματίσιμος;
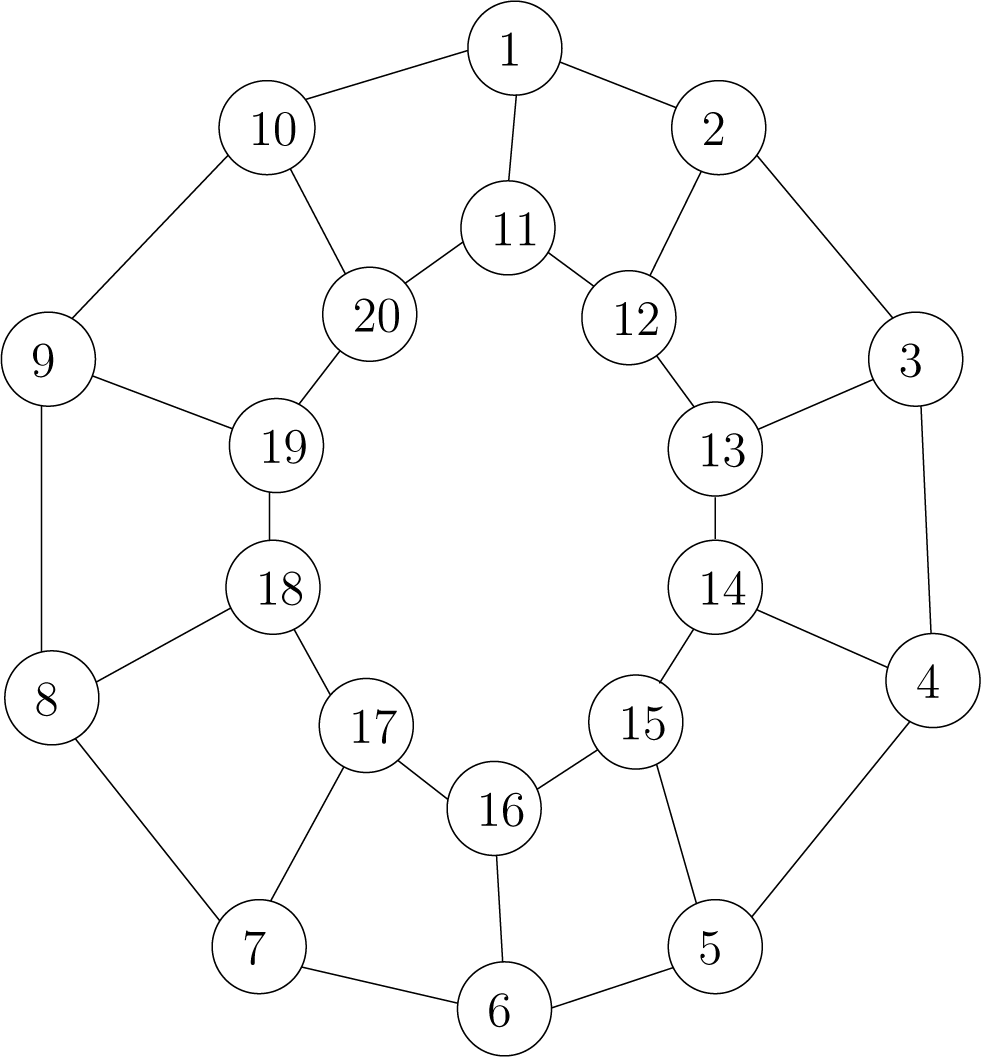
Σχήμα 10.2: Γράφος για την Άσκηση 4. -
(a)
-
5.
Να αποδειχθεί ότι το πρόβλημα της διαπίστωσης, αν ένας γράφος είναι Hamiltonian, ανήκει στην κλάση .
-
6.
Να αποδειχθεί ότι το πρόβλημα της διαπίστωσης, αν ένας γράφος μπορεί να χρωματισθεί με 3 μόνο χρώματα, είναι -πλήρες.