6.4 Μονοπάτια και κυκλώματα Euler και Hamilton

6.4.1 Γενικά

Ορισμός 6.6   (Μονοπάτι Euler, Μονοπάτι Hamilton) Μονοπάτι Euler (αντ. κύκλωμα Euler) ονομάζεται ένα μονοπάτι (αντ. κύκλωμα) που περνάει ακριβώς μία φορά από κάθε ακμή του γραφήματος.

Μονοπάτι Hamilton (αντ. κύκλωμα Hamilton) ονομάζεται ένα μονοπάτι (αντ. κύκλωμα) που περνάει ακριβώς μία φορά από κάθε κορυφή του γραφήματος.

Δεν έχει κάθε γράφημα $G$ κύκλωμα ή μονοπάτι Euler ή Hamilton. Εν γένει είναι πολύ δύσκολο να δώσει κανείς χρήσιμες αναγκαίες και ικανές συνθήκες για την ύπαρξη μονοπατιού ή κυκλώματος Hamilton. Επίσης από υπολογιστική άποψη η εύρεση μονοπατιού ή κυκλώματος Hamilton είναι ένα πολύ δύσκολο πρόβλημα. Ανήκει στην κλάση των λεγομένων NP-πλήρων (Nondeterministic Polynomial Time, NP) προβλημάτων για τα οποία πιστεύται ότι δεν επιδέχονται λύση σε πολυωνυμικό χρόνο. Για το συγκεκριμένο πρόβλημα, της ύπαρξης ή όχι μονοπατιού Hamilton σε ένα γράφημα $G$ με $n$ κορυφές πιστεύεται ισχυρά ότι δεν υπάρχει αλγόριθμος που, παίρνοντας σαν είσοδο το τυχόν γράφημα $G$, μας απαντάει ΝΑΙ αν το γράφημα έχει μονοπάτι Hamilton και ΟΧΙ αλλιώς, και, επιπλέον ο χρόνος που παίρνει (ο αριθμός των «βημάτων») είναι φραγμένος άνω από μια συνάρτηση της μορφής $n^C$ όπου $C$ είναι μια, ενδεχομένως μεγάλη, σταθερά (δεν εξαρτάται δηλ. από το $n$).

Αλλά, παρά τις ισχυρές ενδείξεις ότι αυτό συμβαίνει, αυτό δεν έχει αποδειχθεί ακόμη. Ενα άλλο αξιοσημείωτο που αφορά τα NP-πλήρη προβλήματα είναι ότι αυτά είναι αλληλένδετα με την εξής έννοια: αν ένα από αυτά δειχθεί ότι λύνεται σε πολυωνυμικό χρόνο, τότε όλα λύνονται. Αυτό βεβαίως συνεπάγεται ότι και αν ένα από αυτά δειχθεί ότι δεν λύνεται σε πολυωνυμικό χρόνο τότε κανένα δε λύνεται. Επίσης, η κλάση αυτή προβλημάτων περιλαμβάνει εκατοντάδες προβλήματα τα οποία έχουν προκύψει πολύ φυσιολογικά.

6.4.2 Συνθήκες για κύκλωμα/μονοπάτι Euler

Η κατάσταση είναι τελείως διαφορετική για μονοπάτια και κυκλώματα Euler. Εχουμε το εξής απλό (και στη διατύπωση, και στην απόδειξη) θεώρημα.

Θεώρημα 6.6  

(α)

Ενα συνεκτικό γράφημα $G$ έχει κύκλωμα Euler αν και μόνο αν όλες οι κορυφές του $G$ έχουν άρτιο βαθμό.

(β)

Ενα συνεκτικό γράφημα $G$ έχει μονοπάτι Euler αν και μόνο αν όλες οι κορυφές του $G$ έχουν άρτιο βαθμό ή όλες οι κορυφές του $G$ εκτός από ακριβώς $2$ έχουν άρτιο βαθμό.

Απόδειξη. Αποδεικνύουμε το (α).

Αν το $G$ έχει κύκλωμα Euler

$$\pi: v_1 \longrightarrow \cdots \longrightarrow v_n = v_1,$$

τότε κάθε φορά που κάποια κορυφή $v$ εμφανίζεται στο $\pi$ «μπαίνουμε» στο $v$ κινούμενοι πάνω στο $\pi$ και μετά «<βγαίνουμε» από το $v$, χρησιμοποιώντας έτσι συνολικά $2$ από τις ακμές που καταλήγουν στο $v$, οι οποίες δεν πρόκειται να ξαναχρησιμοποιηθούν, αφού το $\pi$ περνάει από κάθε ακμή ακριβώς μια φορά. Με τον τρόπο αυτό (δηλ. σε ζεύγη πάντα) χρησιμοποιούνται όλες οι ακμές του $v$, άρα το $v$ έχει άρτιο βαθμό.

Για το αντίστροφο, θα δείξουμε με επαγωγή ως προς τον αριθμό ακμών $k$ ότι κάθε συνεκτικό γράφημα με $k$ ακμές και όλες τις κορυφές με άρτιο βαθμό έχει κύκλωμα Euler.

Η μικρότερη τιμή του $k$ με την οποία πρέπει να ασχοληθούμε είναι η τιμή $k=3$, αφού δεν υπάρχει συνεκτικό γράφημα με λιγότερες από 3 ακμές και με όλες τις κορυφές να είναι άρτιου βαθμού. Το μόνο γράφημα που πληρεί τις προϋποθέσεις μας και έχει 3 ακμές είναι το τρίγωνο, το οποίο προφανώς και έχει κύκλωμα Euler.

Για την απόδειξη του επαγωγικού βήματος τώρα, υποθέτουμε ότι η πρόταση ισχύει για αριθμό ακμών $\le k$ και έστω ότι έχουμε ένα γράφημα $G$ με $k+1$ ακμές, συνεκτικό και με όλες τις κορυφές του να έχουν άρτιο βαθμό. Θα δείξουμε ότι έχει κύκλωμα Euler.

Αφού το $G$ δεν έχει κορυφές περιττού βαθμού δε μπορεί να είναι δέντρο (κάθε δέντρο έχει φύλλα, δηλ. κορυφές βαθμού 1) άρα το $G$ έχει κάποιο κύκλο, έστω $C$. Αν αφαιρέσουμε τον κύκλο αυτό από το γράφημα προκύπτει ένα νέο γράφημα $G'$ του οποίου οι κορυφές εξακολουθούν να έχουν άρτιο βαθμό, αφού αφαιρώντας τον κύκλο από το γράφημα αφαιρούμε άρτιο πλήθος ακμών κάθε κορυφής. Αν το $G'$ είναι κενό (δεν έχει ακμές) τότε έχουμε τελειώσει αφού ο κύκλος $C$ περιέχει όλες τις ακμές του $G$ και είναι συνεπώς κύκλωμα Euler. Ας υποθέσουμε από δω και πέρα ότι το $G'$ δεν είναι το κενό γράφημα.

Το $G'$ δεν είναι κατ' ανάγκη συνεκτικό. Ας είναι $G_1, G_2, \ldots, G_r$ οι συνεκτικές του συνιστώσες. Για κάθε ένα από το $G_1, G_2, \ldots, G_r$ ισχύουν οι υποθέσεις του Θεωρήματος (συνεκτικό, άρτιοι βαθμοί κορυφών) και κάθε ένα από αυτά έχει το πολύ $k$ ακμές. Άρα, από την επαγωγική μας υπόθεση κάθε ένα από τα $G_1, G_2, \ldots, G_r$ έχει ένα κύκλωμα Euler, έστω $C_i$.

Παρατηρούμε τώρα ότι κάθε κύκλωμα $C_i$ έχει κάποια κοινή κορυφή με τον κύκλο $C$. (Αν αυτό δε συνέβαινε το αρχικό μας γράφημα $G$ θα ήταν ασύνδετο.) Ας είναι $u_i$ μια κοινή κορυφή του $C$ με το $C_i$. Ένα κύκλωμα Euler στο γράφημα $G$ είναι τότε αυτό που προκύπτει αν διανύουμε τον κύκλο $C$ και όποτε συναντήσουμε την κορυφή $u_i$ αντί να συνεχίσουμε να διανύουμε τον κύκλο $C$ παρεμβάλλουμε τον κύκλο $C_i$. Δείτε το Σχήμα 6.8.

Σχήμα 6.8: Εδώ δείχνουμε πώς, στην απόδειξη του Θεωρήματος 6.6, ενώνουμε τα κυκλώματα $C_i$ και $C$ (πράσινο χρώμα) σε ένα μεγάλο κύκλωμα (κόκκινο χρώμα).

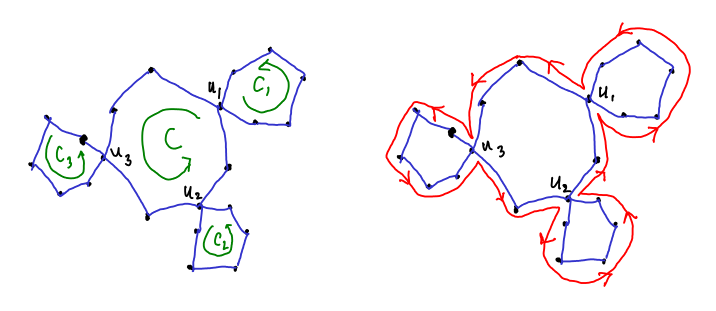
Η απόδειξη του (β) είναι ανάγεται εύκολα στο (α) (δείτε την Άσκηση 6.18).

$\qedsymbol$

Άσκηση 6.18   Αποδείξτε το (β) του Θεωρήματος 6.6.

Υπόδειξη: Προσθέστε έξυπνα μια ακμή και χρησιμοποιήστε το (α) του Θεωρήματος.