Next: 7. Τυπικές γλώσσες και Up: 6. Διμερή γραφήματα και Previous: 6.4 Μονοπάτια και κυκλώματα Contents Index
Ομοίως χρωματισμός ακμών του ![]() με
με ![]() χρώματα είναι
συνάρτηση
χρώματα είναι
συνάρτηση
![]() τ.ώ.
τ.ώ.
Προφανώς μπορούμε πάντα να χρωματίσουμε τις κορυφές ενός γραφήματος
με ![]() κορυφές χρησιμοποιώντας
κορυφές χρησιμοποιώντας ![]() χρώματα, ένα για κάθε κορυφή.
Το ζητούμενο είναι αν μπορούμε να κάνουμε το ίδιο με λίγα χρώματα.
χρώματα, ένα για κάθε κορυφή.
Το ζητούμενο είναι αν μπορούμε να κάνουμε το ίδιο με λίγα χρώματα.
Θα δώσουμε ένα άνω φράγμα για το ![]() σε σχέση με το μέγιστο
βαθμό των κορυφών του και ένα κάτω φράγμα σε σχέση με το πόσο μεγάλα
πλήρη υπογραφήματα έχει.
Αρχίζουμε με το κάτω φράγμα που είναι προφανές.
σε σχέση με το μέγιστο
βαθμό των κορυφών του και ένα κάτω φράγμα σε σχέση με το πόσο μεγάλα
πλήρη υπογραφήματα έχει.
Αρχίζουμε με το κάτω φράγμα που είναι προφανές.
Το άνω φράγμα είναι πιο ενδιαφέρον.
Εστω ![]() ένα γράφημα με
ένα γράφημα με ![]() κορυφές και μέγιστο βαθμό
κορυφές και μέγιστο βαθμό ![]() και έστω
και έστω ![]() οποιαδήποτε κορυφή του
οποιαδήποτε κορυφή του ![]() .
Ορίζουμε
.
Ορίζουμε ![]() να είναι το υπογράφημα του
να είναι το υπογράφημα του ![]() που προκύπτει αν
διαγράψουμε την κορυφή
που προκύπτει αν
διαγράψουμε την κορυφή ![]() και όλες τις ακμές της.
Αυτό έχει
και όλες τις ακμές της.
Αυτό έχει ![]() κορυφές και μέγιστο βαθμό όχι μεγαλύτερο από πριν, άρα
κορυφές και μέγιστο βαθμό όχι μεγαλύτερο από πριν, άρα
![]() .
Συνεπώς, από την επαγωγική μας υπόθεση,
.
Συνεπώς, από την επαγωγική μας υπόθεση,
![]() , δηλ. μπορούμε
να χρωματίσουμε τις κορυφές του
, δηλ. μπορούμε
να χρωματίσουμε τις κορυφές του ![]() με τα χρώματα
με τα χρώματα
![]() .
.
Εστω τώρα οι γείτονες της ![]() στο
στο ![]() ,
,
![]() , με
, με ![]() .
Αρα υπάρχει κάποιο από τα χρώματα
.
Αρα υπάρχει κάποιο από τα χρώματα
![]() που δεν έχει
χρησιμοποιηθεί στο χρωματισμό των
που δεν έχει
χρησιμοποιηθεί στο χρωματισμό των
![]() , έστω το χρώμα
, έστω το χρώμα ![]() .
Χρωματίζουμε τότε την κορυφή
.
Χρωματίζουμε τότε την κορυφή ![]() με το χρώμα
με το χρώμα ![]() και κρατάμε τα χρώματα
των υπολοίπων κορυφών όπως στο χρωματισμό του
και κρατάμε τα χρώματα
των υπολοίπων κορυφών όπως στο χρωματισμό του ![]() .
Εχουμε έτσι κατασκευάσει ένα χρωματισμό του
.
Εχουμε έτσι κατασκευάσει ένα χρωματισμό του ![]() με
με ![]() χρώματα.
χρώματα.
![]()
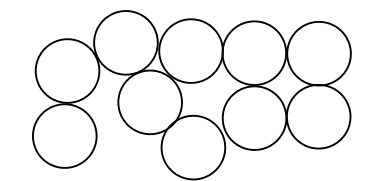
Στο επίπεδο εχουμε ![]() ίσους κύκλους οι οποίοι δεν τέμνονται ανά δύο αλλά μπορούν να εφάπτονται (εξωτερικά, αφού είναι ίσοι).
Δείξτε ότι μπορούμε να χρωματίσουμε τα εσωτερικά των κύκλων αυτών με το πολύ 4 διαφορετικά χρώματα με τρόπο τέτοιο ώστε
αν δύο κύκλοι εφάπτονται τότε αυτοί να έχουν διαφορετικό χρώμα στο εσωτερικό τους.
ίσους κύκλους οι οποίοι δεν τέμνονται ανά δύο αλλά μπορούν να εφάπτονται (εξωτερικά, αφού είναι ίσοι).
Δείξτε ότι μπορούμε να χρωματίσουμε τα εσωτερικά των κύκλων αυτών με το πολύ 4 διαφορετικά χρώματα με τρόπο τέτοιο ώστε
αν δύο κύκλοι εφάπτονται τότε αυτοί να έχουν διαφορετικό χρώμα στο εσωτερικό τους.
Υπόδειξη: Επαγωγή ως προς ![]() . Εστιάσετε την προσοχή σας σε ένα κύκλο με ελάχιστη τετμημένη του κέντρου του.
. Εστιάσετε την προσοχή σας σε ένα κύκλο με ελάχιστη τετμημένη του κέντρου του.
Mihalis Kolountzakis 2015-11-28