6.3 Μέγιστα ταιριάσματα

Υπάρχουν πολλές ενδιαφέρουσες περιπτώσεις διμερών γραφημάτων που δεν έχουν πλήρη ταιριάσματα του συνόλου κορυφών $A$. Σέ τέτοια περίπτωση ενδιαφερόμαστε να βρούμε μέγιστα ταιριάσματα, ταιριάσματα δηλ. που καλύπτουν το μέγιστο δυνατό αριθμό κορυφών (εναλλακτικά, που έχουν όσο γίνεται περισσότερες ακμές).

Ορισμός 6.4   (Εναλλακτικά μονοπάτια, επαυξάνοντα μονοπάτια) Μια κορυφή ενός διμερούς γραφήματος που δεν καλύπτεται από κάποια ακμή ενός ταιριάσματος λέγεται αταίριαστη (ως προς το ταίριασμα αυτό).

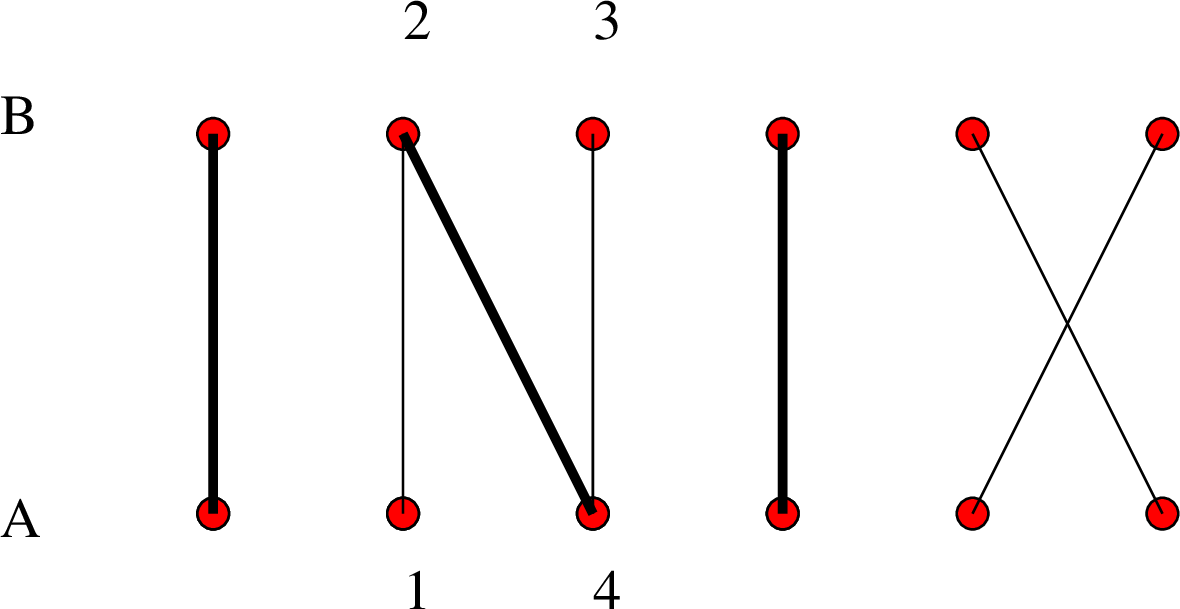
Σε ένα διμερές γράφημα με σύνολα κορυφών $A$ και $B$ και ένα ταίριασμα $M$ ένα μονοπάτι, χωρίς επαναλαμβανόμενες ακμές, που αρχίζει από μια αταίριαστη κορυφή του $A$ και περιέχει εναλλακτικά ακμές από το $E \setminus M$ και το $M$, λέγεται εναλλακτικό μονοπάτι.

Αν ένα εναλλακτικό μονοπάτι τελειώνει σε μια αταίριαστη κορυφή του $B$ τότε λέγεται επαυξάνον μονοπάτι.

Σχήμα 6.5: Το μονοπάτι 1243 είναι επαυξάνον για το σημειωμένο ταίριασμα

Παράδειγμα 6.4   Στο Σχ. 6.5 το μονοπάτι 1243 είναι επαυξάνον για το ταίριασμα που έχει σημειωθεί με έντονες γραμμές.

Παρατήρηση 6.4  

Σχήμα 6.6: Ένα επαυξάνον μονοπάτι (πάνω). Οι έντονες ακμές είναι στο ταίριασμα $M$. Αν αφαιρέσουμε τις ακμές αυτές από το $M$ και προσθέσουμε στο $M$ τις υπόλοιπες ακμές του μονοπατιού τότε το ταίριασμά μας κερδίζει μια ακμή

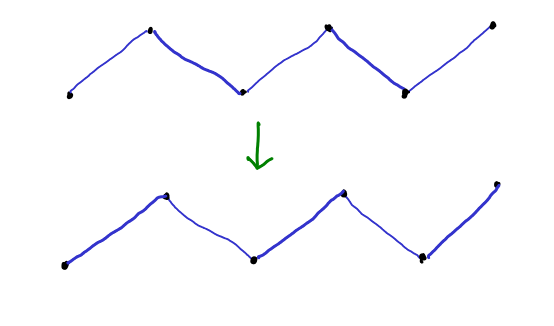
Τα επαυξάνοντα μονοπάτια είναι σημαντικά γιατί η ύπαρξη ενός τέτοιου μονοπατιού συνεπάγεται την ύπαρξη ενός μεγαλύτερου ταιριάσματος από το υπάρχον. Πράγματι, σε ένα επαυξάνον μονοπάτι οι ακμές είναι εναλλακτικά εκτός του $M$, από το $M$, εκτός του $M$, κ.ο.κ., και τελειώνουν με μια ακμή εκτός του $M$, μια και η τελευταία κορυφή του μονοπατιού είναι στο $B$ και αταίριαστη στο ταίριασμα $M$. Αν λοιπόν αφαιρέσουμε από το $M$ τις ακμές του που συμμετέχουν σε ένα επαυξάνον μονοπάτι $\pi$ και προσθέσουμε στο $M$ τις ακμές του $\pi$ που δεν ανήκαν στο $M$, παίρνουμε ένα άλλο σύνολο ακμών $M'$ που είναι μεγαλύτερο του $M$ κατά μία ακμή. Το σημαντικό εδώ είναι ότι και το $M'$ είναι ταίριασμα (Άσκηση 6.15 παρακάτω), άρα, χρησιμοποιώντας το $\pi$ καταφέραμε να αυξήσουμε το μέγεθος του δοθέντος ταιριάσματος.

Δείτε το Σχήμα 6.6 και το Παράδειγμα 6.5.

Παράδειγμα 6.5   Στο ταίριασμα του Σχ. 6.5 αν αφαιρέσουμε την ακμή 24 και προσθέσουμε τις 12 και 34 παίρνουμε πάλι ένα ταίριασμα κατά μία ακμή μεγαλύτερο από πριν.

Άσκηση 6.15   Αποδείξτε τον ισχυρισμό της Παρατήρησης 6.4, ότι το σύνολο ακμών $M'$ είναι ταίριασμα. Συνεπώς αν το $M$ είναι μέγιστο ταίριασμα τότε δεν υπάρχουν επαυξάνοντα μονοπάτια.

Είναι σημαντικό ότι ισχύει και το αντίστροφο της Άσκησης 6.15, και αυτό δεν είναι καθόλου προφανές.

Θεώρημα 6.4   Αν ένα ταίριασμα δεν έχει επαυξάνοντα μονοπάτια τότε είναι μέγιστο ταίριασμα.

Απόδειξη. Έστω $M_1$ ένα ταίριασμα (ενός διμερούς γραφήματος $G$, με σύνολα κορυφών $A$ και $B$) που δεν έχει επαυξάνοντα μονοπάτια, και $M_2$ ένα μέγιστο ταίρασμα. Θεωρούμε το γράφημα $G'$ με σύνολο ακμών το $M_1 \bigtriangleup M_2$ (το σύνολο αυτό είναι η συμμετρική διαφορά των $M_1$ και $M_2$, οι ακμές εκείνες του $G$ δηλ. που ανήκουν σε ακριβώς ένα από τα σύνολα $M_1$ και $M_2$).

Επειδή τα $M_1$ και $M_2$ είναι ταιριάσματα έπεται ότι οι κορυφές του $G'$ έχουν όλες βαθμό 0, 1 ή 2 (στο $G'$, όχι στο $G$). Αυτό ισχύει γιατί αν μια κορυφή του $G'$ έχει βαθμό 3 ή περισσότερο τότε υπάρχουν είτε δύο ακμές του $M_1$ είτε δύο ακμές του $M_2$ που καταλήγουν στην κορυφή αυτή, πράγμα που αντιφάσκει με τον ορισμό του ταιριάσματος που απαιτεί όλες οι ακμές του ταιριάσματος να μη μοιράζονται καμία κορυφή.

Από αυτό προκύπτει ότι κάθε συνεκτική συνιστώσα του $G'$ είναι είτε ένας κύκλος είτε ένα μονοπάτι (ενδεχομένως μήκους 0, μια μόνη κορυφή δηλαδή). Και στις δύο αυτές περιπτώσεις οι ακμές σε κάθε συνεκτική συνιστώσα προέρχονται εναλλάξ από το $M_1$ και το $M_2$. Όταν η συνιστώσα είναι κύκλος χρησιμοποιούνται σε αυτή ίσο πλήθος ακμών από το $M_1$ και το $M_2$. Όταν η συνιστώσα δεν είναι κύκλος αλλά μονοπάτι, ο μόνος τρόπος να εμφανίζονται σε αυτή λιγότερες $M_1$-ακμές απ' ότι $M_2$-ακμές είναι το μονοπάτι αυτό να αρχίζει και να τελειώνει με $M_2$-ακμή πράγμα που θα σήμαινε ότι το μονοπάτι αυτό θα ήταν επαυξάνον για το ταίριασμα $M_1$, με ενδεχόμενη εναλλαγή των ρόλων των πλευρών $A$ και $B$.

Επειδή έχουμε υποθέσει ότι επαυξάνοντα μονοπάτια δεν υπάρχουν έπεται ότι και σε αυτή την περίπτωση (η συνιστώσα είναι μονοπάτι καί όχι κύκλος) χρησιμοποιούνται τουλάχιστον τόσες $M_1$-ακμές όσες και $M_2$. Και αφού το $M_2$ είναι μέγιστο ταίριασμα έπεται ότι το πλήθος ακμών του $M_1$ είναι ίσο με αυτό του $M_2$ και άρα είναι κι αυτό μέγιστο, όπως έπρεπε να δείξουμε. $\qedsymbol$

Παρατήρηση 6.5   Λόγω του Θεωρήματος 6.4 μπορούμε να ακολουθήσουμε την εξής διαδικασία για την εύρεση ενός μέγιστου ταιριάσματος ενός διμερούς γραφήματος: ξεκινάμε από ένα οποιοδήποτε ταίριασμα (π.χ. το κενό) και ψάχνουμε να βρούμε επαυξάνοντα μονοπάτια. Κάθε φορά που βρίσκουμε ένα τέτοιο ακολουθούμε τη διαδικασία της Παρατήρησης 6.4 ώστε να αυξήσουμε κατά μία το σύνολο των ακμών που συμμετέχουν στο ταίριασμά μας. Όταν δε μπορούμε πλέον να βρούμε επαυξάνον μονοπάτι είμαστε σίγουροι, από το Θεώρημα 6.4 ότι έχουμε βρεί ένα μέγιστο ταίριασμα.

Ορισμός 6.5   (Κάλυμμα κορυφών) Ένα σύνολο κορυφών $U$ σε ένα γράφημα $G$ λέγεται κάλυμμα κορυφών του $G$ αν κάθε ακμή του $G$ έχει μια τουλάχιστον κορυφή στο $U$.

Παράδειγμα 6.6   Στο Σχ. 6.3(a) το σύνολο ${\left\{{1,6,8}\right\}}$ είναι κάλυμμα κορυφών.

Άσκηση 6.16   Έστω γράφημα $G$ με ταίριασμα $M$ και κάλυμμα κορυφών $U$. Δείξτε ότι

$${\left\vert{U}\right\vert} \ge {\left\vert{M}\right\vert}.$$

Υπόδειξη: Κάθε ακμή του $M$ πρέπει να περιέχει τουλάχιστον μια κορυφή του $U$. Μπορεί μια τέτοια κορυφή να περιέχεται και σε άλλη ακμή του $M$;

Θεώρημα 6.5   (König, 1931, και Egerváry, 1931) Σε ένα διμερές γράφημα το μέγεθος ενός μεγίστου ταιριάσματος ισούται με το μέγεθος ενός ελαχίστου καλύμματος κορυφών.

Απόδειξη. Έστω $G$ διμερές γράφημα με σύνολα κορυφών τα $A$ και $B$ και $M$ ένα ταίριασμα του $G$ με μέγιστο πλήθος ακμών. Θα κατασκευάσουμε ένα σύνολο κορυφών $U$, μεγέθους ${\left\vert{U}\right\vert} = {\left\vert{M}\right\vert}$, που θα είναι κάλυμμα κορυφών του $G$. Αυτό θα σημαίνει ότι το ελάχιστο μέγεθος καλύμματος κορυφών του $G$ είναι το πολύ ${\left\vert{M}\right\vert}$. Από την άλλη μεριά όμως, εύκολα βλέπει κανείς (Άσκηση 6.16) ότι κάθε κάλυμμα κορυφών πρέπει να έχει τουλάχιστον ${\left\vert{M}\right\vert}$ κορυφές, οπότε η απόδειξη του Θεωρήματος 6.5 θα είναι πλήρης.

Επιλέγουμε λοιπόν να βάλουμε στο σύνολο $U$ μια ακριβώς κορυφή από κάθε ακμή του $M$, και θα πρέπει να επιλέξουμε με κάποιο τρόπο ποια από τις δύο κορυφές να βάλουμε. Το κριτήριό μας θα είναι το παρακάτω:

Έστω $uv \in M$, με $u \in A, v \in B$. Αν υπάρχει εναλλακτικό μονοπάτι που καταλήγει στο $v$ τότε βάζουμε την κορυφή $v$ στο σύνολο $U$, αλλιώς βάζουμε την κορυφή $u$.

Είναι φανερό ότι με αυτή την κατασκευή ισχύει

$${\left\vert{U}\right\vert} = {\left\vert{M}\right\vert}.$$

Απομένει να δείξουμε ότι το σύνολο $U$ που κατασκευάσαμε είναι όντως κάλυμμα κορυφών του γραφήματος. Έστω λοιπόν $ab$ μια ακμή του γραφήματος με $a \in A, b \in B$. Πρέπει να δείξουμε ότι τουλάχιστον ένα από τα $a, b$ ανήκει στο $U$. Αν $ab \in M$ αυτό είναι προφανές οπότε υποθέτουμε ότι $ab \notin M$. Επειδή το $M$ είναι μέγιστο ταίριασμα έπεται ότι υπάρχει $a'b' \in M$, με $a = a'$ ή $b = b'$, αλλιώς η ακμή $a'b'$ θα μπορούσε να προστεθεί στο $M$ και το $M$ να παραμείνει ταίριασμα, άρα αυτό δε μπορεί να ήταν μέγιστο ταίριασμα. Αν η $a$ είναι αταίριαστη τότε $b = b'$ και η ακμή $ab$ αποτελεί από μόνη της εναλλακτικό μονοπάτι, οπότε η κορυφή της $a'b'$ που επιλέχτηκε για το $U$ ήταν η $b' = b$, και άρα πάλι δείξαμε αυτό που θέλουμε.

Μπορούμε συνεπώς να υποθέσουμε ότι $a = a'$. Αν το $a = a'$ δεν είναι στο $U$ τότε $b' \in U$, άρα υπάρχει κάποιο εναλλακτικό μονοπάτι $\pi$ που καταλήγει στο $b'$. (Δείτε την περίπτωση αυτή στο Σχήμα 6.7.)

Σχήμα 6.7: Μια περίπτωση στην απόδειξη του Θεωρήματος 6.5 (König-Egervary).

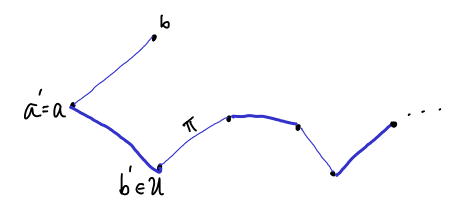
Οι βαριές ακμές είναι στο ταίριασμα $M$ και οι άλλες όχι. Τότε όμως υπάρχει και κάποιο εναλλακτικό μονοπάτι $\pi'$ που καταλήγει στο $b$: είτε το μέρος του $\pi$ έως το $b$ αν $b \in \pi$ είτε το $\pi' = \pi a b$ (το $\pi$ ακολουθούμενο από το μονοπάτι $b'ab$). Επειδή το $M$ είναι μέγιστο το $\pi'$ πέρα από εναλλακτικό δε μπορεί να είναι και επαυξάνον μονοπάτι, άρα το $b$ είναι ταιριασμένο στο $M$ και είχε επιλεγεί για το $U$ λόγω της ύπαρξης του εναλλακτικού μονοπατιού $\pi'$ που καταλήγει στο $b$. $\qedsymbol$

Παρατήρηση 6.6   Το Θεώρημα 6.5 μας δίνει τη δυνατότητα να πιστοποιήσουμε ένα μέγιστο ταίριασμα. Φανταστείτε, για παράδειγμα, ότι έχετε μια εταιρεία που πουλάει μέγιστα ταιριάσματα σε διμερή γραφήματα. Έρχεται δηλ. ο πελάτης σας και σας δίνει ένα (τεράστιο) διμερές γράφημα, και ζητά από σας να βρείτε ένα μέγιστο ταίριασμα γι' αυτό. Για να σας πληρώσει όμως ζητάει και εγγυήσεις ότι το ταίριασμα που του βρήκατε είναι όντως μέγιστο. Τότε εσείς δεν έχετε παρά να του δώσετε, μαζί με το ταίριασμα $M$ που υπολογίσατε, και ένα σύνολο κορυφών $U$, με τόσες κορυφές όσες το ταίριασμα έχει ακμές, και τέτοιo ώστε το $U$ να είναι κάλυμμα όλων των ακμών του γραφήματος (κάθε ακμή του γραφήματος δηλ. να περιέχει κάποια κορυφή του $U$). Τέτοιο σύνολο κορυφών $U$ υπάρχει λόγω του Θεωρήματος 6.4. Τότε, πάλι λόγω του Θεωρήματος 6.4, ο πελάτης σας (ο οποίος εύκολα μπορεί να επιβεβαιώσει τον ισχυρισμό σας ότι ${\left\vert{U}\right\vert} = {\left\vert{M}\right\vert}$ και ότι το $U$ είναι κάλυμμα κορυφών) είναι βέβαιος ότι το $M$ είναι μέγιστο ταίριασμα.

Άσκηση 6.17   Δίδεται ένας $m\times n$ πίνακας $A$ με στοιχεία $A_{ij} \in {\left\{{0,1}\right\}}$. Με ευθεία του πίνακα εννούμε μια οποιαδήποτε γραμμή ή στήλη του. Δείξτε ότι το ελάχιστο πλήθος ευθειών που περιέχει όλα τα 1 του $A$ είναι ίσο με το μέγιστο πλήθος από 1 που ανά δύο δε βρίσκονται πάνω στην ίδια ευθεία.

Υπόδειξη: Φτιάξτε ένα γράφημα $G$ που έχει ως κορυφές όλες τις ευθείες του πίνακα $A$ (το πλήθος τους είναι $m+n$) και ενώστε δύο ευθείες με μια ακμή αν και μόνο αν οι δύο αυτές ευθείες τέμνονται στον $A$ και στην τομή τους υπάρχει άσος. Το γράφημα που δημιουργείται είναι φυσικά διμερές με τις δύο πλευρές να είναι οι γραμμές και οι στήλες του πίνακα. Ερμηνεύστε σε αυτό το γράφημα τις έννοιες «ταίριασμα» και «κάλυμμα» και εφαρμόστε το Θεώρημα 6.5.

Παρατήρηση 6.7   Ας δείξουμε τώρα ότι το Θεώρημα 6.3 μπορεί να αποδειχθεί εύκολα χρησιμοποιώντας το Θεώρημα 6.5. Ουσιαστικά δίνουμε μια διαφορετική απόδειξη του Θεωρήματος του Γάμου η οποία χρησιμοποιεί το Θεώρημα König-Egerváry.

Πράγματι ας υποθέσουμε ότι σε ένα διμερές γράφημα ισχύει η συνθήκη (6.1) αλλά δεν υπάρχει πλήρες ταίριασμα του $A$. Από το Θεώρημα 6.5 υπάρχει σύνολο κορυφών $U$, με ${\left\vert{U}\right\vert}<{\left\vert{A}\right\vert}$, που είναι κάλυμμα κορυφών, έστω $U = A' \cup B'$ με $A' \subseteq A$ και $B' \subseteq B$. Έπεται ότι ${\left\vert{B'}\right\vert} < {\left\vert{A\setminus A'}\right\vert}$. Επειδή το $U$ είναι κάλυμμα κορυφών έχουμε ότι δεν υπάρχουν στο $G$ ακμές ανάμεσα στα σύνολα $A\setminus A'$ και $B \setminus B'$, άρα

$${\left\vert{N(A \setminus A')}\right\vert} \le {\left\vert{B'}\right\vert} < {\left\vert{A \setminus A'}\right\vert},$$

και αυτό αντιφάσκει με την συνθήκη (6.1) για το σύνολο $J = A \setminus A'$.