Μια πολύ χρήσιμη έννοια είναι η έννοια του ταιριάσματος σε ένα γράφημα.
Ορισμός 6.2
(Ανεξάρτητες ακμές, Ταιριάσματα)
Δύο ακμές λέγονται ανεξάρτητες αν δεν έχουν κοινή κορυφή.
Ένα σύνολο ανεξαρτήτων ακμών 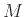 σε ένα γράφημα λέγεται ταίριασμα (matching).
Αν το γράφημα είναι διμερές με σύνολα κορυφών
σε ένα γράφημα λέγεται ταίριασμα (matching).
Αν το γράφημα είναι διμερές με σύνολα κορυφών  και
και  τότε ένα ταίριασμα
τότε ένα ταίριασμα 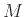 λέγεται πλήρες ταίριασμα του
λέγεται πλήρες ταίριασμα του  (ομοίως για το
(ομοίως για το  ) αν κάθε κορυφή του
) αν κάθε κορυφή του  περιέχεται
σε κάποια ακμή του
περιέχεται
σε κάποια ακμή του 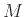 .
.
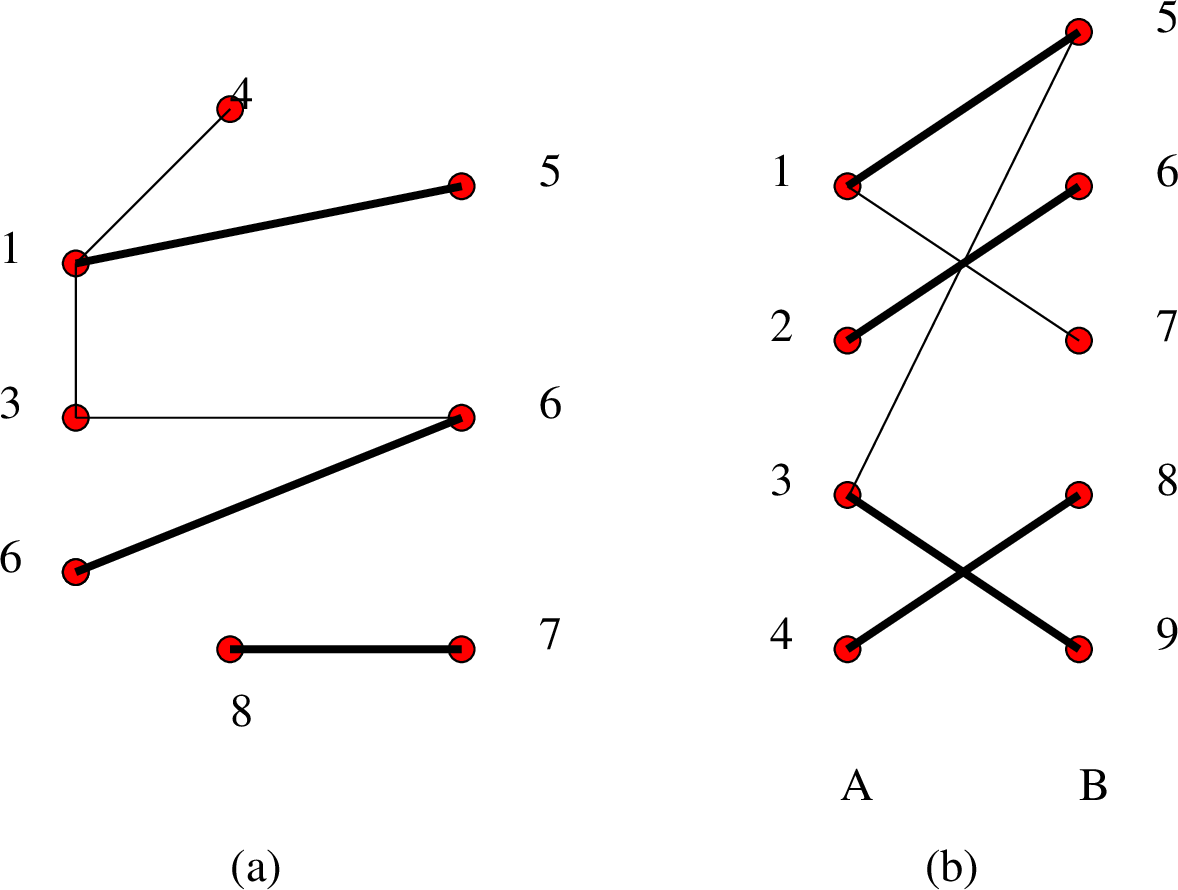
Σχήμα
6.3: Οι ακμές με έντονη γραμμή αποτελούν ταίριασμα
Παράδειγμα 6.2
Στο Σχ. 6.3(a) το σύνολο των ακμών που έχουν σχεδιαστεί έντονα
αποτελεί ένα ταίριασμα.
Στο Σχ. 6.3(b) έχουμε ένα διμερές γράφημα με ένα ταίριασμα του
πλήρες συνόλου κορυφών  (αριστερές κορυφές).
Το ταίριασμα αυτό δεν αποτελεί
πλήρες ταίριασμα του
(αριστερές κορυφές).
Το ταίριασμα αυτό δεν αποτελεί
πλήρες ταίριασμα του  αφού η κορυφή 9 του
αφού η κορυφή 9 του  δεν «καλύπτεται» από ακμή του ταιριάσματος.
δεν «καλύπτεται» από ακμή του ταιριάσματος.
Παράδειγμα 6.3
Ας υποθέσουμε ότι έχουμε προκηρύξει κάποιες θέσεις εργασίας
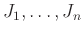 και ότι έχουν κάνει αίτηση γι' αυτές κάποιοι
υποψήφιοι
και ότι έχουν κάνει αίτηση γι' αυτές κάποιοι
υποψήφιοι
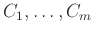 , με
, με 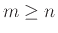 .
Δεν έχει κατ' ανάγκην κάνει αίτηση ο κάθε υποψήφιος για όλες τις θέσεις, αλλά
κάθε υποψήφιος έχει κάνει αίτηση για κάποιες από τις προσφερόμενες θέσεις.
Σκοπός μας είναι να γεμίσουμε όλες τις θέσεις εργασίας.
Δε μπορούμε φυσικά να προσλάβουμε για μια θέση εργασίας
κάποιον που δεν έχει κάνει αίτηση γι' αυτή.
Φτιάχνουμε ένα διμερές γράφημα με σύνολα κορυφών
.
Δεν έχει κατ' ανάγκην κάνει αίτηση ο κάθε υποψήφιος για όλες τις θέσεις, αλλά
κάθε υποψήφιος έχει κάνει αίτηση για κάποιες από τις προσφερόμενες θέσεις.
Σκοπός μας είναι να γεμίσουμε όλες τις θέσεις εργασίας.
Δε μπορούμε φυσικά να προσλάβουμε για μια θέση εργασίας
κάποιον που δεν έχει κάνει αίτηση γι' αυτή.
Φτιάχνουμε ένα διμερές γράφημα με σύνολα κορυφών
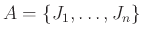 και
και
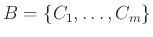 και βάζουμε μια ακμή ανάμεσα στις κορυφές
και βάζουμε μια ακμή ανάμεσα στις κορυφές
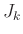 και
και 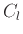 αν και μόνο αν ο υποψήφιος
αν και μόνο αν ο υποψήφιος 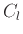 έχει κάνει αίτηση για τη θέση
έχει κάνει αίτηση για τη θέση
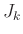 .
Είναι φανερό τώρα ότι μπορούμε να γεμίσουμε όλες τις θέσεις εργασίας αν
και μόνο αν υπάρχει πλήρες ταίριασμα του
.
Είναι φανερό τώρα ότι μπορούμε να γεμίσουμε όλες τις θέσεις εργασίας αν
και μόνο αν υπάρχει πλήρες ταίριασμα του  στο γράφημα αυτό.
στο γράφημα αυτό.
Άσκηση 6.11
Αν ένα διμερές γράφημα με σύνολα κορυφών  και
και  έχει πλήρες ταίριασμα
του
έχει πλήρες ταίριασμα
του  τότε
τότε
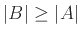 .
.
Ορισμός 6.3
Σε ένα διμερές γράφημα, για κάθε σύνολο 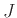 αριστερών
κορυφών, συμβολίζουμε με
αριστερών
κορυφών, συμβολίζουμε με 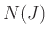 το σύνολο όλων των δεξιών κορυφών
που ενώνονται με κάποια κορυφή από το
το σύνολο όλων των δεξιών κορυφών
που ενώνονται με κάποια κορυφή από το 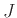 .
.
Το αποτέλεσμα που ακολουθεί περιγράφει ακριβώς πότε ένα διμερές γράφημα
έχει πλήρες ταίριασμα της μιας πλευράς του.
Απόδειξη.
Το Θεώρημα
6.3 αποτελεί ουσιαστικά μια αναδιατύπωση
του Θεωρήματος του Γάμου (Θεώρημα
1.5).
Φτιάχνουμε από το διμερές μας γράφημα
ένα σύστημα υποσυνόλων του

, όπως στην Παρατήρηση
6.3.
Η συνθήκη του Θεωρήματος
6.3 αποτελεί
απλά αναδιατύπωση της συνθήκης (
1.21) του Hall.
Το γράφημά μας έχει πλήρες ταίριασμα του

αν και μόνο αν
το σύστημα υποσυνόλων του

που φτιάξαμε έχει σύστημα ξένων αντιπροσώπων,
πράγμα που, σύμφωνα με το Θεώρημα του Γάμου, ισχύει ακριβώς όταν ισχύει
η συνθήκη του Hall, δηλ. η συνθήκη που διατυπώνεται στο Θεώρημα
6.3.

Μια εύκολη συνέπεια του θεωρήματος του Γάμου είναι η εξής:
Πόρισμα 6.1
Κάθε κανονικό διμερές γράφημα έχει πλήρες ταίριασμα (και των δύο μεριών του, αναγκαστικά).
Απόδειξη.
Εστω ότι το
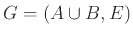
είναι
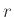
-κανονικό,
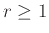
.
Θα αποδείξουμε ότι ισχύει η υπόθεση του Θεωρήματος
6.3.
Εστω
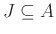
και
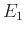
το σύνολο των ακμών που ξεκινούν από κάποια
κορυφή του
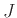
. Επειδή το
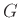
είναι
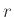
-κανονικό έχουμε ότι
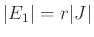
.
Εστω επίσης 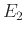 το σύνολο των ακμών που καταλήγουν σε κάποια από τις
κορυφές του
το σύνολο των ακμών που καταλήγουν σε κάποια από τις
κορυφές του 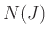 , δηλ. σε κάποιο από τους γείτονες του
, δηλ. σε κάποιο από τους γείτονες του 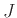 .
Ξανά έχουμε
.
Ξανά έχουμε
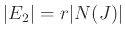 .
.
Αλλά προφανώς ισχύει
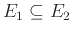 . Αρα
. Αρα
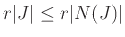 ,
το οποίο συνεπάγεται
,
το οποίο συνεπάγεται

Άσκηση 6.13
Αν ένα διμερές γράφημα είναι 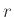 -κανονικό δείξτε ότι έχει
-κανονικό δείξτε ότι έχει 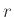 ξένα μεταξύ τους πλήρη ταιριάσματα.
ξένα μεταξύ τους πλήρη ταιριάσματα.
Υπόδειξη: Χρησιμοποιήστε το Πόρισμα 6.1. Αφού βρείτε ένα πλήρες ταίρασμα διαγράψτε όλες
τις ακμές του από το γράφημά σας. Τι ιδιότητες έχει το γράφημα που απομένει;
Άσκηση 6.14
Παίρνουμε μια συνηθισμένη τράπουλα (52 φύλλα σε 13 είδη (
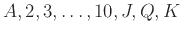 ),
από 4 κάθε είδος (
),
από 4 κάθε είδος (
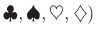 ),
την ανακατεύουμε και την μοιράζουμε σε 13 σωρούς των 4 φύλλων.
(Τα περιεχόμενα των σωρών τα βλέπουμε, τα φύλλα δηλ. κοιτάνε προς τα πάνω.)
),
την ανακατεύουμε και την μοιράζουμε σε 13 σωρούς των 4 φύλλων.
(Τα περιεχόμενα των σωρών τα βλέπουμε, τα φύλλα δηλ. κοιτάνε προς τα πάνω.)
Δείξτε ότι είναι πάντα δυνατό να επιλέξουμε ένα φύλλο από κάθε σωρό
ώστε στο τέλος να έχουμε ένα φύλλο από κάθε είδος.
Υπόδειξη: Φτιάξτε ένα διμερές γράφημα με τους 13 σωρούς αριστερά και τα 13 είδη δεξιά. Βάλτε μια ακμή από ένα σωρό σε ένα είδος αν και μόνο αν
το είδος αυτό εμφανίζεται στο σωρό. Δείξτε ότι το διμερές γράφημα έχει πλήρες ταίριασμα και των δύο πλευρών του. Ένα τέτοιο ταίριασμα σας λέει
τι είδος να διαλέξετε από κάθε σωρό.
Mihalis Kolountzakis
2015-11-28

![]() και σύστημα
και σύστημα
![]() υποσυνόλων του.
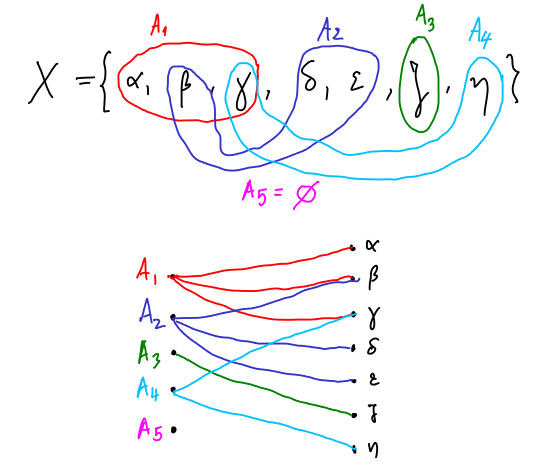
Υπάρχει ένας πολύ φυσιολογικός τρόπος να αντιστοιχίσουμε
σε αυτό το σύστημα υποσυνόλων ένα διμερές γράφημα:
υποσυνόλων του.
Υπάρχει ένας πολύ φυσιολογικός τρόπος να αντιστοιχίσουμε
σε αυτό το σύστημα υποσυνόλων ένα διμερές γράφημα:
και σύνολο δεξιών κορυφών είναι το
. Ενώνουμε την αριστερή κορυφή
με τη δεξιά κορυφή
αν και μόνο αν
.
![]() και συνδέσετέ τις με όλες τις κορυφές του
και συνδέσετέ τις με όλες τις κορυφές του ![]() .
Το νέο αυτό διμερές γράφημα τώρα ικανοποιεί τη συνθήκη του Hall (6.1).
Αφού χρησιμοποιήσετε το Θεώρημα 6.3 θα πρέπει από το συμπέρασμά σας να
«ξεφορτωθείτε» τις παραπανίσιες κορυφές που εισαγάγατε προηγουμένως.
.
Το νέο αυτό διμερές γράφημα τώρα ικανοποιεί τη συνθήκη του Hall (6.1).
Αφού χρησιμοποιήσετε το Θεώρημα 6.3 θα πρέπει από το συμπέρασμά σας να
«ξεφορτωθείτε» τις παραπανίσιες κορυφές που εισαγάγατε προηγουμένως.![]() το σύνολο των ακμών που καταλήγουν σε κάποια από τις
κορυφές του
το σύνολο των ακμών που καταλήγουν σε κάποια από τις
κορυφές του ![]() , δηλ. σε κάποιο από τους γείτονες του
, δηλ. σε κάποιο από τους γείτονες του ![]() .
Ξανά έχουμε
.
Ξανά έχουμε
![]() .
.
![]() . Αρα
. Αρα
![]() ,
το οποίο συνεπάγεται
,
το οποίο συνεπάγεται