Next: 5.7 Ο αλγόριθμος του Up: 5. Εισαγωγή στη θεωρία Previous: 5.5 Δέντρα και δάση Contents Index
Ανάλογα με την περίπτωση μπορεί κανείς να επιτρέπει ή όχι και ζευγάρια
της μορφής ![]() (τέτοιες ακμές ονομάζονται βρόχοι).
Το σημαντικό πάντως είναι ότι δε μπορεί πλέον κανείς
να λέει ότι «
(τέτοιες ακμές ονομάζονται βρόχοι).
Το σημαντικό πάντως είναι ότι δε μπορεί πλέον κανείς
να λέει ότι «![]() συνδέεται με το
συνδέεται με το ![]() » αλλά πρέπει να προσδιορίζει
και την κατεύθυνση της σύνδεσης.
» αλλά πρέπει να προσδιορίζει
και την κατεύθυνση της σύνδεσης.
Αυτά τα βάρη είναι συνήθως μη αρνητικοί αριθμοί, αλλά αυτό δεν είναι απαραίτητο και εξαρτάται από την εφαρμογή. Για παράδειγμα, αν οι κορυφές παριστάνουν πόλεις σε μία χώρα και οι ακμές κάποιους δρόμους που τις συνδέουν, τα βάρη μπορούν να παριστάνουν τα μήκη των δρόμων.
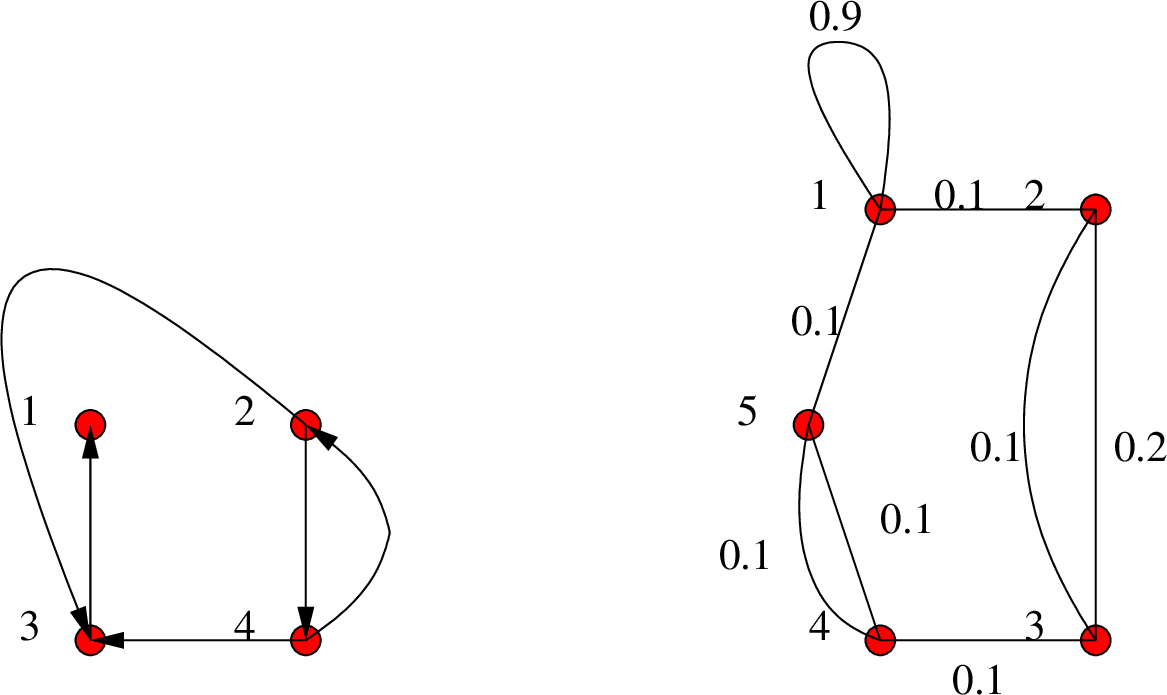
Στο Σχήμα 5.25 δείχνουμε δύο γραφήματα. Το αριστερό είναι ένα κατευθυνόμενο γράφημα με σύνολα κορυφών και ακμών τα
Η έννοια του μονοπατιού σε μη απλά γραφήματα είναι σχεδόν ταυτόσημη με αυτή που ισχύει στα απλά γραφήματα, αν όμως το γράφημα είναι κατευθυνόμενο τότε φυσιολογικά απαιτούμε οι ακμές να έχουν όλες φορά από μια κορυφή του μονοπατιού προς την επόμενη.
Ειδικά για τα γραφήματα με μη αρνητικά βάρη υπάρχει μια επιπλέον έννοια της απόστασης ανάμεσα σε δύο κορυφές που λαμβάνει υπόψην της τα «μήκη» (ή βάρη) των ακμών.
Υπόδειξη: Η απόδειξη είναι σχεδόν ταυτόσημη με αυτή για τη συνηθισμένη έννοι απόστασης σε απλά γραφήματα.
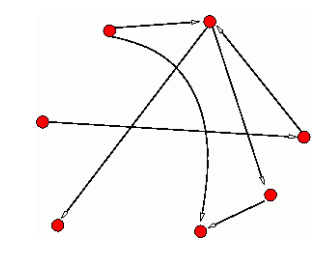
Ας ονομάσουμε ![]() τον αριθμό των πόλεων στις οποίες δεν καταλήγει κανείς δρόμος και
τον αριθμό των πόλεων στις οποίες δεν καταλήγει κανείς δρόμος και ![]() τον αριθμό των πόλεων
στις οποίες καταλήγει άρτιος αριθμός δρόμων (του 0 συμπεριλαμβανομένου). Στο Σχήμα 5.26 έχουμε
τον αριθμό των πόλεων
στις οποίες καταλήγει άρτιος αριθμός δρόμων (του 0 συμπεριλαμβανομένου). Στο Σχήμα 5.26 έχουμε ![]() και
και ![]() .
.
Δείξτε ότι ![]() .
.
Mihalis Kolountzakis 2015-11-28