5.7 Ο αλγόριθμος του Kruskal για ελάχιστα δέντρα που παράγουν σε γραφήματα με βάρη

Εστω $G=(V,E)$ ένα συνεκτικό γράφημα με μη αρνητικά βάρη στις ακμές του

$$w:E\to {\mathbb{R}}^+.$$

Μας ενδιαφέρει να επιλέξουμε εκείνο το δέντρο $T$ από όλα τα δυνατά δέντρα που παράγουν το $G$ που το βάρος του, δηλ. το άθροισμα των ακμών που συμμετέχουν στο δέντρο, να είναι όσο γίνεται πιο μικρό. Θέλουμε δηλ. να ελαχιστοποιήσουμε την ποσότητα

$$w(T) = \sum_{e \in T} w(e),$$

όπου το άθροισμα παίρνεται πάνω απ'όλες τις ακμές $e$ που εμφανίζονται στο δέντρο ($e \in T$), και το $T$ είναι ένα δέντρο που παράγει το $G$, έχει δηλ. το ίδιο σύνολο κορυφών με το γράφημα $G$.

Ορισμός 5.20   (Ελάχιστο δέντρο που παράγει) Αν και η ποσότητα $w(T)$ έχει μοναδικό ελάχιστο, αυτό μπορεί να «πιάνεται» για παραπάνω από ένα δέντρα που παράγουν. Ολα αυτά τα δέντρα με ελάχιστο βάρος τα ονομάζουμε ελάχιστα δέντρα του $G$.

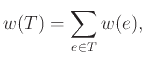
Μπορεί κανείς σχετικά εύκολα να δείξει ότι ο παρακάτω αλγόριθμος όντως βρίσκει ένα ελάχιστο δέντρο που παράγει στο $G$.

Ο αλγόριθμος του Kruskal

1. Δημιουργούμε ένα δάσος $F$ από δέντρα όπου κάθε κορυφή του $G$ αποτελεί και ένα δέντρο.
2. Δημιουργούμε ένα σύνολο $S$ που περιέχει όλες τις ακμές του $G$, διατεταγμένες σε αύξουσα σειρά βάρους.
3. Όσο ισχύει $S \neq \emptyset$ επαναλαμβάνουμε τα παρακάτω:
   1. Αφαιρούμε την πρώτη ακμή του $S$ (που είναι μια από αυτές που έχουν το ελάχιστο βάρος ανάμεσα στις ακμές που περιέχονται στο $S$).
   2. Αν αυτή η ακμή ενώνει μεταξύ τους δύο διαφορετικά δέντρα του δάσους $F$, τότε προσθέτουμε αυτή την ακμή στο $F$, ενώνοντας έτσι σε ένα δύο δέντρα του $F$. Αλλιώς την πετάμε αυτή την ακμή.

Αποδεικνύεται ότι στο τέλος του αλγορίθμου το δάσος $F$ περιέχει μόνο ένα δέντρο που είναι ένα ελάχιστο δέντρο του $G$. (Με τις κατάλληλες δομές δεδομένων ο αλγόριθμος του Kruskal χρειάζεται χρόνο $O(m \log m)$ για να τελειώσει, όπου $m$ είναι το πόσες ακμές έχει το γράφημα $G$.)

Θεώρημα 5.3   Ο αλγόριθμος του Kruskal που περιγράψαμε προηγουμένως όντως βρίσκει ένα ελάχιστο δέντρο για το γράφημα $G$.

Απόδειξη. Το ότι το γράφημα που παράγεται από τον αλγόριθμο του Kruskal είναι ανά πάσα χρονική στιγμή ένα δάσος είναι φανερό, αφού κάθε τέτοιο γράφημα προκύπτει από το προηγούμενο με την προσθήκη μιας ακμής η οποία ενώνει δύο διαφορετικά δέντρα του προηγουμένου, και επειδή είναι φανερό ότι αν ενώσουμε με μια ακμή δύο δέντρα με διαφορετικό σύνολο κορυφών παίρνουμε πάλι ένα δέντρο.

Επίσης το δάσος $F$ είναι, στο τέλος του αλγορίθμου, ένα και μόνο δέντρο. Αλλιώς το $F$ θα περιείχε τις συνεκτικές συνιστώσες $C_1,\ldots,C_k$.$k>1$, και, από τον τρόπο που δουλεύει ο αλγόριθμος, αυτό συνεπάγεται ότι καμιά από τις ακμές του $G$ δεν ενώνει μεταξύ τους δύο διαφορετικά $C_j$. Αυτό σημαίνει όμως ότι το $G$ δεν είναι συνεκτικό, άτοπο.

Είναι λοιπόν το $F$ ένα και μόνο δέντρο και μάλιστα παράγει το $G$ και μένει να δειχτεί ότι το $F$ είναι επιπλέον και ελάχιστο δέντρο που παράγει το $G$. Ας είναι λοιπόν $T$ ένα ελάχιστο δέντρο από αυτά που παράγουν το $G$ που το επιλέγουμε ούτως ώστε να συμφωνεί με το $F$ για το μέγιστο δυνατό διάστημα Το διάστημα συμφωνίας είναι ο χρόνος μέχρι να βρεθεί η πρώτη ακμή (με τη διάταξη του $S$) η οποία ανήκει στο ένα αλλά όχι στο άλλο. Αν όλες οι ακμές τους ταυτίζονται τότε έχουμε $F=T$ και άρα το $F$ είναι και αυτό ελάχιστο. Άρα μπορούμε να υποθέσουμε ότι υπάρχει μια ακμή $e$ που είτε περιέχεται στο $F$ αλλά όχι στο $T$ είτε περιέχεται στο $T$ αλλά όχι στο $F$. Ας πάρουμε να είναι η $e$ η πρώτη από τις ακμές που κοιτάει ο αλγόριθμος για την οποία συμβαίνει αυτό.

Η πρώτη παρατήρηση είναι ότι

$$e \in F \setminus T.$$ (5.5)

Ο λόγος είναι ότι όταν μια ακμή εξετάζεται από τον αλγόριθμο του Kruskal και απορρίπτεται αυτό συνεπάγεται ότι εκείνη τη στιγμή τα δύο άκρα της είναι ήδη συνδεδεμένα στο $F$. Αλλά, μέχρι εκείνη τη στιγμή το $T$ συμφωνεί με το $F$, άρα τα δύο άκρα της $e$ είναι ήδη συνδεδεμένα και στο $T$, πράγμα που απαγορεύει στην $e$ να ανήκει στο $T$ αφού αυτό είναι δέντρο. Άρα η ακμή αυτή δεν απορρίπτεται από τον αλγόριθμο και ισχύει η (5.5).

Σχήμα 5.27: Βοηθητικό σχήμα για την απόδειξη του Θεωρήματος 5.3

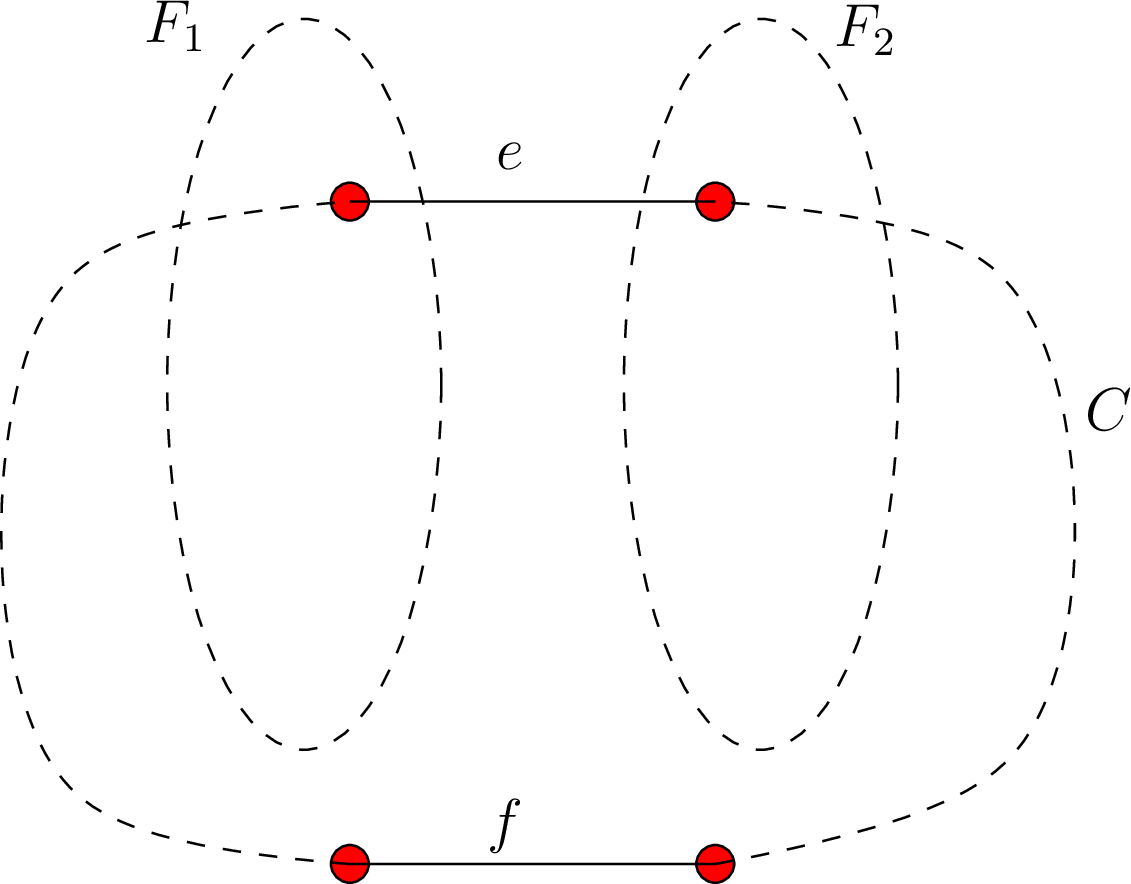
Ας εστιάσουμε την προσοχή μας στη χρονική στιγμή που εξετάζεται από τον αλγόριθμο η ακμή $e$ και ας είναι $F_1$ και $F_2$ τα δύο δέντρα του (τρέχοντος) $F$ τα οποία η ακμή αυτή ενώνει. Αφού $e \notin T$ αν την προσθέσουμε στο $T$ δημιουργείται ένας κύκλος $C$ και έπεται ότι υπάρχει κάποια από τις ακμές του $C \setminus{\left\{{e}\right\}}$, έστω η $f$, που έχει βάρος

$$w(f) \ge w(e).$$

Αυτό συμβαίνει γιατί στην αντίθετη περίπτωση όλες οι ακμές του $C \setminus{\left\{{e}\right\}}$ θα είχαν εξεταστεί από τον αλγόριθμο πριν από την $e$, και, λόγω της συμφωνίας μεταξύ $F$ και $T$ ως εκείνη τη στιγμή, και επειδή οι ακμές του $C \setminus{\left\{{e}\right\}}$ ανήκουν όλες στο $T$, έπεται ότι θα ανήκουν και στο $F$, πράγμα ασυμβίβαστο με το ότι η $e$ συνδέει δύο διαφορετικές συνεκτικές συνιστώσες $F_1$ και $F_2$. (Δείτε το Σχήμα 5.27.)

Θεωρούμε τώρα το δέντρο

$$T' = T \cup {\left\{{e}\right\}} \setminus{f}.$$

Αυτό το δέντρο είναι επίσης ελάχιστο και επίσης συμφωνεί με το $F$ για παραπάνω χρόνο απ' ότι το $T$, άτοπο διότι το $T$ είχε υποτεθεί ότι μεγιστοποιεί αυτό το χρόνο συμφωνίας. Άρα $F=T$ και το $F$ είναι ελάχιστο. $\qedsymbol$

Σχήμα 5.28: Ένα γράφημα με βάρη

Άσκηση 5.41   Εφαρμόστε με το χέρι τον αλγόριθμο του Kruskal στο γράφημα του Σχήματος 5.28 και βρείτε ένα ελάχιστο δέντρο που το παράγει.

Άσκηση 5.42   Υλοποιήστε τον αλγόριθμο του Kruskal στην αγαπημένη σας γλώσσα προγραμματισμού με τρόπο ώστε ο χρόνος εκτέλεσης να είναι της τάξης του $m \log m$, όπου $m$ είναι το πλήθος των ακμών (που αναγκαστικά είναι τουλάχιστον $n-1$, όπου $n$ είναι το πλήθος των κορυφών, μια και το γράφημα υποτίθεται συνεκτικό. Εξηγήστε το χρόνο εκτέλεσης του αλγορίθμου.

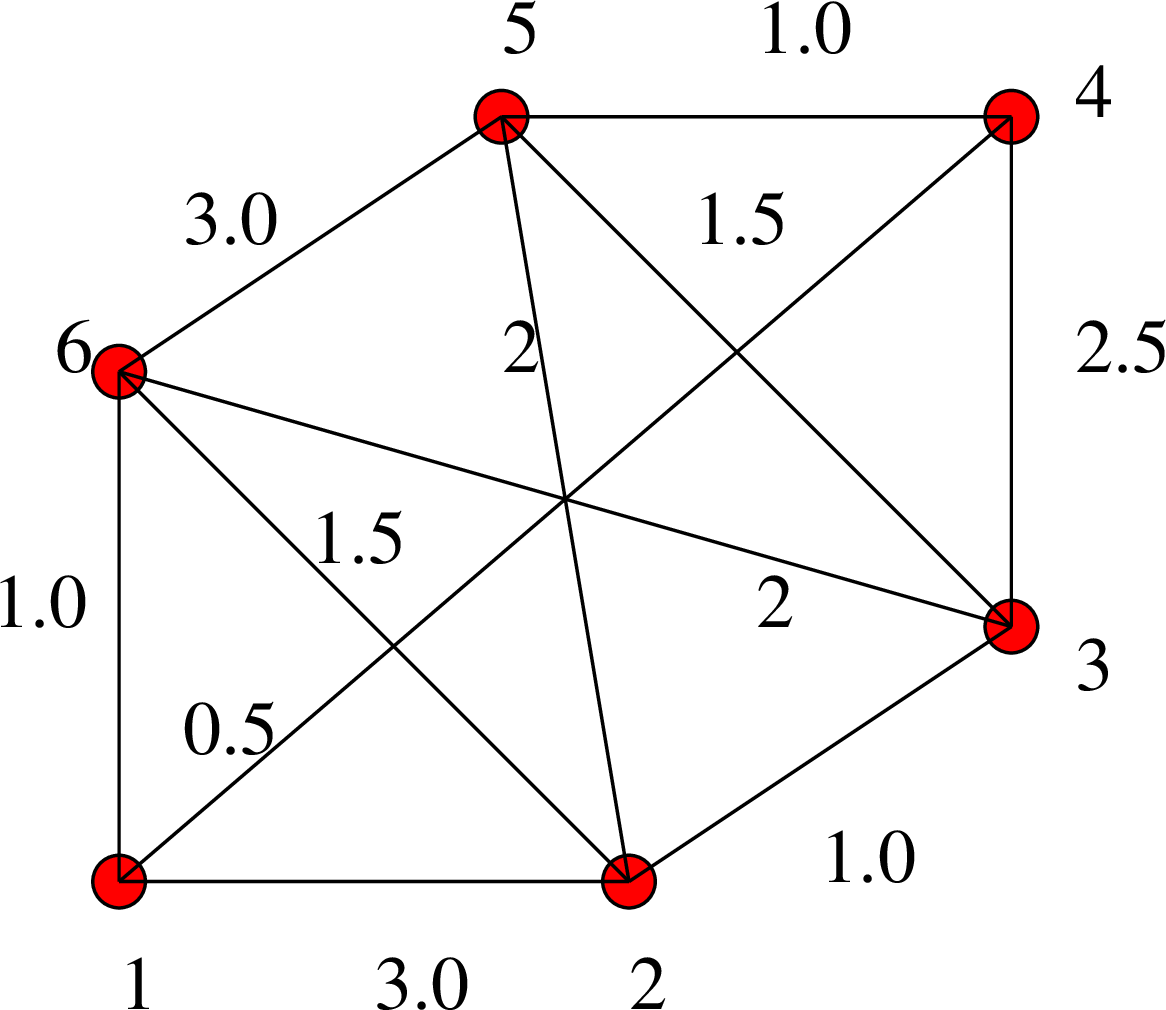
Ο αλγόριθμος του Kruskal ανήκει σ'εκείνη την κατηγορία αλγορίθμων που ονομάζονται «μυωπικοί» (greedy) μια και προσπαθούν να πετύχουν μια συνολική βελτιστοποίηση (στην περίπτωσή μας την εύρεση ενός ελάχιστου δέντρου) βελτιστοποιώντας, κατά τη διάρκεια της εκτέλεσης τους, κάθε επιλογή που έχουν να κάνουν με κάποια κριτήρια «της στιγμής». Τέτοιοι αλγόριθμοι σπανίως βελτιστοποιούν το συνολικό πρόβλημα, και αυτός ο αλγόριθμος για ελάχιστα δέντρα είναι μια από τις εξαιρέσεις όπου αποδεδειγμένα επιτυγχάνεται συνολική βελτιστοποίηση.