Next: 4.4 Συνδυαστικές αποδείξεις ταυτοτήτων Up: 4. Προχωρημένη απαρίθμηση Previous: 4.2 Πολυωνυμικοί συντελεστές Contents Index
Το Διωνυμικό Θεώρημα (Θεώρημα 4.4 είναι ένα ισχυρότατο εργαλείο για υπολογισμούς που αναφέρονται σε ποσότητες με διωνυμικούς συντελεστές. Είναι επίσης η πρώτη σύνδεση των συνδυαστικών ποσοτήτων που συναντάμε με αλγεβρικές μεθόδους. Αργότερα θα δούμε και τις γεννήτριες συναρτήσεις ακολουθιών σα μια φυσική επέκταση της μεθόδου.
Είναι φανερό ότι, εφόσον οι προσθετέοι από κάθε παράδειγμα είναι
![]() ή
ή ![]() και το πλήθος των παραγόντων είναι
και το πλήθος των παραγόντων είναι ![]() , όλα τα μονώνυμα
που θα εμφανιστούν είναι της μορφής
, όλα τα μονώνυμα
που θα εμφανιστούν είναι της μορφής
Το Διωνυμικό Θεώρημα (Θεώρημα 4.4) έχει πολλές εφαρμογές σε υπολογισμούς αθροισμάτων.
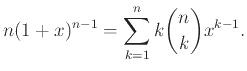
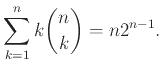
Αν γράψουμε
![]() δείξτε ότι και η συνάρτηση
δείξτε ότι και η συνάρτηση ![]() είναι πολυώνυμο Laurent
και ότι οι συντελεστές της δίνονται από τον τύπο
είναι πολυώνυμο Laurent
και ότι οι συντελεστές της δίνονται από τον τύπο
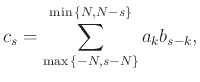
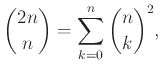
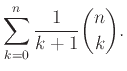
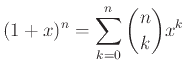
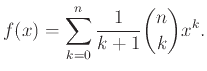
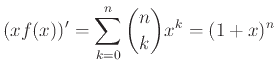
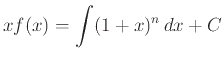
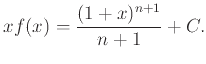
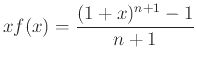
Mihalis Kolountzakis 2015-11-28