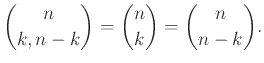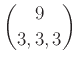4.2 Πολυωνυμικοί συντελεστές
Έχουμε δεί ότι αν θέλουμε να επιλέξουμε  αντικείμενα από
αντικείμενα από 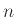 ,
χωρίς επανάθεση, το πλήθος των τρόπων να γίνει αυτό είναι
,
χωρίς επανάθεση, το πλήθος των τρόπων να γίνει αυτό είναι
Τι γίνεται αν θέλουμε να επιλέξουμε, πάλι χωρίς επανάθεση,
μια ομάδα στοιχείων του
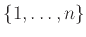 μεγέθους
μεγέθους 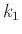 , μια ομάδα μεγέθους
, μια ομάδα μεγέθους 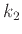 , κλπ,
και τέλος μια ομάδα μεγέθους
, κλπ,
και τέλος μια ομάδα μεγέθους 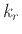 , όπου για
, όπου για
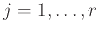 έχουμε
έχουμε
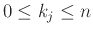 και επιπλέον ισχύει
και επιπλέον ισχύει
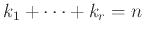 ;
Με πόσους τρόπους δηλ. μπορούμε να διαμερίσουμε το
;
Με πόσους τρόπους δηλ. μπορούμε να διαμερίσουμε το
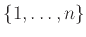 σε ένα σύνολο μεγέθους
σε ένα σύνολο μεγέθους 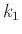 , σε ένα σύνολο μεγέθους
, σε ένα σύνολο μεγέθους 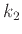 και τέλος
σε ένα σύνολο μεγέθους
και τέλος
σε ένα σύνολο μεγέθους 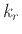 ;
;
Απόδειξη.
Το πρώτο σύνολο μπορεί να επιλεγεί με
τρόπους.
Μετά από την επιλογή του πρώτου συνόλου απομένουν
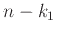
στοιχεία
αχρησιμοποίητα, άρα το δεύτερο σύνολο μπορεί να επιλεγεί
με
τρόπους.
Συνεχίζονας κατ' αυτόν τον τρόπο παίρνουμε ότι η επιλογή
του προτελευταίου συνόλου (με
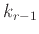
στοιχεία) μπορεί
να γίνει με
τρόπους.
Επίσης, αφού έχουν επιλεγεί τα
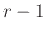
πρώτα σύνολα δεν υπάρχει πλέον
καμιά επιλογή να γίνει αφου τα υπόλοιπα
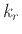
στοιχεία που απομένουν
ακόμη αχρησιμοποίητα αναγκαστικά πάνε στο τελευταίο σύνολο που
πρέπει να επιλέξουμε.
Έτσι πολλαπλασιάζοντας τις δυνατότητες επιλογών μας για τα πρώτα
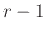 σύνολα, και κάνοντας τις απλοποιήσεις παίρνουμε τον
τύπο (4.4).
σύνολα, και κάνοντας τις απλοποιήσεις παίρνουμε τον
τύπο (4.4).

Το σύμβολο
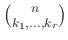 ονομάζεται πολυωνυμικός
συντελεστής (κατ' αναλογία με τα
ονομάζεται πολυωνυμικός
συντελεστής (κατ' αναλογία με τα
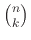 που ονομάζονται
διωνυμικοί συντελεστές).
Παρατηρήστε επίσης ότι
που ονομάζονται
διωνυμικοί συντελεστές).
Παρατηρήστε επίσης ότι
Παρατήρηση 4.1
Ο πολυωνυμικός συντελεστής
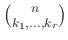 δεν αλλάζει αν τα
δεν αλλάζει αν τα
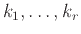 αντικατασταθούν από μια μετάθεσή τους
(αν αλλάξει δηλ. απλώς η σειρά τους).
αντικατασταθούν από μια μετάθεσή τους
(αν αλλάξει δηλ. απλώς η σειρά τους).
Παρατήρηση 4.2
Πρέπει να τονίσουμε εδώ ότι, αν και δε μας ενδιαφέρει η εσωτερική σειρά των συνόλων
των στοιχείων που επιλέγουμε, η σειρά των ίδιων των συνόλων είναι προκαθορισμένη.
Αυτό είναι ίσως φανερό όταν όλα τα
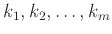 είναι μεταξύ τους διαφορετικά
αλλά δημιουργεί κάποια σύγχυση όταν μερικά από αυτά είναι μεταξύ τους ίσα. Μια ακραία
περίπτωση αυτού είναι όταν όλα είναι ίδια. Για παράδειγμα, ο πολυωνυμικός συντελεστής
είναι μεταξύ τους διαφορετικά
αλλά δημιουργεί κάποια σύγχυση όταν μερικά από αυτά είναι μεταξύ τους ίσα. Μια ακραία
περίπτωση αυτού είναι όταν όλα είναι ίδια. Για παράδειγμα, ο πολυωνυμικός συντελεστής
μετράει με πόσους τρόπους μπορούμε να χωρίσουμε τους αριθμούς
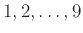 σε τρείς ομάδες.
Αν δύο τρόποι διαφέρουν μόνο ως προς τον εσωτερικό
τρόπο γραφής της κάθε ομάδας τότε δε θεωρούνται διαφορετικοί.
Έτσι οι τρόποι
σε τρείς ομάδες.
Αν δύο τρόποι διαφέρουν μόνο ως προς τον εσωτερικό
τρόπο γραφής της κάθε ομάδας τότε δε θεωρούνται διαφορετικοί.
Έτσι οι τρόποι
θεωρούνται ίδιοι και μετράνε ως ένα.
Αν όμως δύο τρόποι διαφέρουν ως προς τον τρόπο γραφής των ομάδων τότε μετράνε ως διαφορετικοί.
Οι τρόποι, π.χ.,
μετράνε ως διαφορετικοί τρόποι.
Άσκηση 4.11
Έχουμε 10 αριθμημένες μπάλες και τρία κουτιά με χωρητικότητες
5, 3 και 2 μπάλες. Με πόσους τρόπους μπορούμε να βάλουμε τις μπάλες
στα κουτιά; (Δεν υπάρχει εσωτερική σειρά στα κουτιά αλλά τα κουτιά είναι
μεταξύ τους διακεκριμένα.)
Άσκηση 4.12
Με πόσους τρόπους μπορούμε να τοποθετήσουμε 12 αριθμημένες μπάλες σε 4 όμοια (μη αριθμημένα)
κουτιά χωρητικότητας 3 το καθένα;
Άσκηση 4.13
Με πόσους τρόπους μπορούμε να διατάξουμε 5 γράμματα Α, 3 γράμματα Β και 4 γράμματα Γ;
Εκφράστε την απάντησή σας σαν ένα πολυωνυμικό συντελεστή.
Mihalis Kolountzakis
2015-11-28
![]() αντικείμενα από
αντικείμενα από ![]() ,
χωρίς επανάθεση, το πλήθος των τρόπων να γίνει αυτό είναι
,
χωρίς επανάθεση, το πλήθος των τρόπων να γίνει αυτό είναι
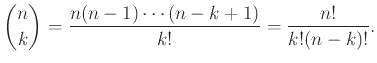
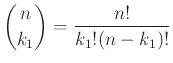
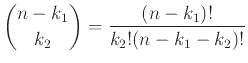
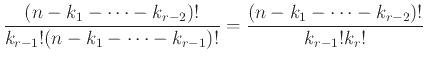
![]() σύνολα, και κάνοντας τις απλοποιήσεις παίρνουμε τον
τύπο (4.4).
σύνολα, και κάνοντας τις απλοποιήσεις παίρνουμε τον
τύπο (4.4).
![]()
![]() ονομάζεται πολυωνυμικός
συντελεστής (κατ' αναλογία με τα
ονομάζεται πολυωνυμικός
συντελεστής (κατ' αναλογία με τα
![]() που ονομάζονται
διωνυμικοί συντελεστές).
Παρατηρήστε επίσης ότι
που ονομάζονται
διωνυμικοί συντελεστές).
Παρατηρήστε επίσης ότι