3.2 Αρχή πολλαπλασιασμού ημι-ανεξάρτητων επιλογών

Είδαμε στην §3.1 ότι όταν έχουμε να παραγματοποιήσουμε μια σύνθετη επιλογή που αποτελείται από πολλές επί μέρους επιλογές, οι οποίες είναι ανεξάρτητες η μια από την άλλη, μπορούμε δηλ. να πραγματοποιήσουμε τις επί μέρους επιλογές όλες ταυτόχρονα, τότε το πλήθος δυνατοτήτων για τη σύνθετη επιλογή ισούται με το γινόμενο των δυανατοτήτων για τις επί μέρους επιλογές.

Η αρχή πολλαπλασιασμού γίνεται πολύ χρησιμότερη μετά από την εξής παρατήρηση. Δε χρειάζεται οι επί μέρους επιλογές μας να είναι ανεξάρτητες. Μπορούμε να επιτρέψουμε η πρώτη μας επί μέρους επιλογή να επηρεάζει τις δυνατότητές μας για τη δεύτερη (ή κάποια άλλη) επιλογή, αρκεί να μην επηρεάζει το πλήθος των δυνατοτήτων για την επιλογή αυτή. Δεν απαιτούμε δηλ. να μένει το σύνολο δυνατοτήτων της κάθε επί μέρους επιλογής αναλλοίωτο από κάθε προηγούμενή μας απόφαση, αρκεί να μένει το μέγεθος του συνόλου αναλλοίωτο. Λέμε τότε ότι οι επί μέρους επιλογές μας είναι ημι-ανεξάρτητες (ο όρος δεν είναι καθιερωμένος).

Παράδειγμα 3.2   Ας υποθέσουμε ότι, παράλληλα με τις υποθέσεις της Άσκησης 3.1, σε ένα περιέργο τόπο ο κόσμος δεν πίνει ποτέ σκέτο καφέ χωρίς γάλα και ότι δεν πίνει επίσης ποτέ γλυκό (2 φακελάκια ζάχαρη) με γάλα. Το πλήθος των δυνατών τύπων καφέ είναι πάλι $2\cdot 2$ αν και τώρα οι επιλογές (γάλα, ζάχαρη) δεν είναι πλέον ανεξάρτητες, αφού αν κάποιος επιλέξει πρώτα καφέ χωρίς γάλα οι επιλογές του ως προς τη ζάχαρη είναι 1 ή 2 φακελάκια ενώ αν επιλέξει καφέ με γάλα οι επιλογές του ως προς τη ζάχαρη είναι 0 ή 1 φακελάκι. Οι επιλογή δηλ. που κάνουμε για το γάλα επηρεάζει τις επιλογές μας για τη ζάχαρη, αλλά όχι το πλήθος των επιλογών αυτών, είναι δηλ. η επιλογή της ζάχαρης ημιανεξάρτητη από την επιλογή του γάλακτος.

Παρατήρηση 3.1   Είναι πάρα πολύ σημαντικό να παρατηρήσουμε εδώ ότι η έννοια της ημι-ανεξαρτησίας όπως την ορίσαμε περιγραφικά εδώ εξαρτάται από τη σειρά με την οποία πραγματοποιούνται οι επί μέρους επιλογές. Αν στο Παράδειγμα 3.2 επιλέξει κανείς πρώτα το επίπεδο ζάχαρης και μετά το αν θα έχει ο καφές του γάλα ή όχι, παύει η ημι-ανεξαρτησία. Αν επιλέξει κάποιος ο καφές του να είναι σκέτος (καθόλου ζάχαρη) τότε έχει μία επιλογή για το γάλα: πρέπει οπωσδήποτε να βάλει. Αν επιλέξει 1 φακελάκι ζάχαρη μπορεί βάλει γάλα ή όχι, ενώ αν επιλέξει 2 φακελάκια ζάχαρη πάλι έχει 1 επιλογή: να μη βάλει γάλα. Αν αθροίσουμε το πλήθος των επιλογών τότε παίρνουμε πάλι $1+2+1=4$ φυσικά. Αλλά παρατηρήστε ότι αυτός ο τρόπος μετρήματος είναι πιο περίπλοκος μια και δεν μπορούμε πλέον να πολλαπλασιάσουμε τις επιλογές, αλλά πρέπει να αθροίσουμε. Γι' αυτό και ένα μεγάλο κομμάτι από την τέχνη του μετρήματος έγκειται στο να διαλέξουμε μια καλή σειρά μετρήματος, που θα οδηγήσει σε απλό μέτρημα.

Παράδειγμα 3.3   Μια 10-μελής ομάδα επιλέγει αρχηγό και (διαφορετικό) υπαρχηγό. Με πόσους τρόπους μπορεί να γίνει αυτό;

Η απάντηση είναι με $10\cdot9 = 90$ διαφορετικούς τρόπους. Πρώτα επιλέγεται ο αρχηγός και μετά ο υπαρχηγός. Για τον αρχηγό έχουμε 10 επιλογές. Αφού επιλεγεί αυτός, έστω ο $x$, στη θέση του υπαρχηγού μπορούμε να επιλέξουμε οποιονδήποτε εκτός του $x$, έχουμε δηλ. 9 επιλογές. Παρατηρήστε ότι οι δύο επιλογές δεν είναι ανεξάρτητες αφού η επιλογή του αρχηγού επηρεάζει το σύνολο των δυνατών επιλογών για υπαρχηγό, δεν επηρεάζει όμως το πλήθος των δυνατών υπαρχηγών. Είναι δηλ. οι δύο αυτές επιλογές ημι-ανεξάρτητες.

Άσκηση 3.19   Έστω μια ομάδα 5 ανδρών και μια ομάδα 7 γυναικών. Με πόσους τρόπους μπορούμε να παντρέψουμε και τους 5 άνδρες με γυναίκες από αυτή την ομάδα των 7; Ισχύουν οι συνήθεις κανόνες (όχι διγαμία).

Άσκηση 3.20   Για $m\le n$ πόσες 1-1 συναρτήσεις υπάρχουν από το $[m]$ στο $[n]$;

Υπόδειξη: Επιλέγετε την εικόνα των $1, 2, \ldots, m$ με τη σειρά. Έχοντας επιλέξει τις εικόνες των $1, 2, \ldots, k-1$ πόσες επιλογές έχετε για την εικόνα του $k$;

Άσκηση 3.21   Στην Άσκηση 3.19 αλλάξτε τους κοινωνικούς κανόνες ώστε να επιτρέπουν σε μια γυναίκα να παντρευτεί ταυτόχρονα όσους άντρες θέλει. Και πάλι πρέπει να παντρευτούν όλοι οι άντρες και ο ίδιος άντρας δε μπορεί να είναι παντρεμένος με δύο γυναίκες.

3.2.1 Πλήθος διατεταγμένων επιλογών. Μεταθέσεις συνόλου

Με πόσους τρόπους μπορούμε να διαλέξουμε, κατά τρόπο διατεταγμένο, $r$ άτομα από $n$;

Θεώρημα 3.4   Το πλήθος των διατεταγμένων $r$-άδων ($r\le n$)

$$(x_1,\ldots,x_r),$$ (3.6)

με $x_j \in [n]$ όλα διαφορετικά, είναι

$$n(n-1)(n-2)\cdots(n-r+1).$$

Απόδειξη. Επιλέγουμε πρώτα το $x_1$. Γι' αυτό έχουμε $n$ δυνατότητες. Έχοντας επιλέξει το $x_1$ δεν μπορούμε πλέον να διαλέξουμε το ίδιο στοιχείο και για $x_2$. Οι δυνατότητες που έχουμε άρα για το $x_2$ είναι μία λιγότερες, δηλ. $n-1$. Έχοντας επιλέξει τα $x_1, x_2$ οι δυνατότητες για το $x_3$ είναι πλέον $n-2$, κλπ. Παρατηρούμε ότι οι επιλογές είναι ημι-ανεξάρτητες. Δεν επηρεάζουν δηλ. οι μέχρι κάποια στιγμή επιλογές μας το πλήθος των μετέπειτα επιλογών μας. Εφαρμόζοντας την αρχή του πολλαπλασιασμού παίρνουμε το αποτέλεσμα, αφού για το $x_r$ θα έχουμε $n-r+1=n-(r-1)$ δυνατότητες αφού θα έχουν ήδη χρησιμοποιηθεί ακριβώς $r-1$ στοιχεία από τα $n$. $\qedsymbol$

Πόρισμα 3.1   Το πλήθος των τρόπων να διατάξουμε στη σειρά τα στοιχεία ενός συνόλου με $n$ στοιχεία είναι

$$n! = 1\cdot2\cdot3\cdots n.$$

Οι διαφορετικοί αυτοί τρόποι διάταξης όλων των στοιχείων ενός συνόλου λέγονται μεταθέσεις του συνόλου.

Απόδειξη. Το να διατάξουμε τα στοιχεία του συνόλου στη σειρά είναι το ίδιο πράγμα με το να διαλέξουμε μια διατεταγμένη $n$-άδα από αυτά. Εφαρμόζουμε λοιπόν το Θεώρημα 3.4 με $r=n$. $\qedsymbol$

Άσκηση 3.22   Το παρακάτω πρόγραμμα σε python βρίσκει όλες τις μεταθέσεις ενός συνόλου (το οποίο, ως συνήθως, αναπαριστούμε ως μια λίστα με διαφορετικά στοιχεία).

def permutations(s):
    """
    Returns a list of all perumatations of the set (list) s.
    Each element of this list is a permutation of s (again, a list).
    The list s is assumed to be nonempty.
    """
    n = len(s)
    if n==1:
        return [s] # One permutation only
    else:
        result = [] # we will return this variable
        for x in s: # list all permutations of s with first element x
            ss = s[:] # make a copy of s
            ss.remove(x) # now ss is the original list with x removed
            for l in permutations(ss):
                result.append([x] + l) # we add each of them to result
        return result

Μπορείτε π.χ. να καλέσετε τη συνάρτηση δίνοντας

print permutations(['a', 'b', 'c', 'd'])

οπότε θα πάρετε το output

[['a', 'b', 'c', 'd'], ['a', 'b', 'd', 'c'],
['a', 'c', 'b', 'd'], ['a', 'c', 'd', 'b'],
['a', 'd', 'b', 'c'], ['a', 'd', 'c', 'b'],
['b', 'a', 'c', 'd'], ['b', 'a', 'd', 'c'],
['b', 'c', 'a', 'd'], ['b', 'c', 'd', 'a'],
['b', 'd', 'a', 'c'], ['b', 'd', 'c', 'a'],
['c', 'a', 'b', 'd'], ['c', 'a', 'd', 'b'],
['c', 'b', 'a', 'd'], ['c', 'b', 'd', 'a'],
['c', 'd', 'a', 'b'], ['c', 'd', 'b', 'a'],
['d', 'a', 'b', 'c'], ['d', 'a', 'c', 'b'],
['d', 'b', 'a', 'c'], ['d', 'b', 'c', 'a'],
['d', 'c', 'a', 'b'], ['d', 'c', 'b', 'a']]

Το πρόγραμμα είναι αναδρομικό (recursive). Βεβαιωθείτε ότι καταλαβαίνετε πώς δουλεύει.

Άσκηση 3.23   Γράψτε ένα πρόγραμμα στη γλώσσα python που να υπολογίζει το παραγοντικό του $n$, το οποίο το δίνει ο χρήστης. Προσέξτε ότι το $n$ θα πρέπει να είναι ακέραιος και ότι για $n<0$ το παραγοντικό δεν ορίζεται (το πρόγραμμα θα πρέπει να τυπώνει κάποιο μήνυμα σε αυτή την περίπτωση). Επίσης προσέξτε ότι $0! = 1$.

Γράψτε το πρόγραμμά σας συμπληρώνοντας τα κενά στον παρακάτω κώδικα:

def factorial(n):
    # n should be >= 0
    if n<0:
        .............
    else:
        t=1
        .............
        return t

Έχοντας γράψει τη συνάρτησή σας μπορείτε να την ελέγξετε με την εντολή π.χ.

print factorial(5)

Άσκηση 3.24   Γράψτε όλες τις μεταθέσεις του συνόλου ${\left\{{A,B,C}\right\}}$.

Υπόδειξη: Μπορείτε αν θέλετε να χρησιμοποιήσετε το πρόγραμμα της Άσκησης 3.22.

Άσκηση 3.25   Με πόσους τρόπους μπορούν να διαταχθούν τα ψηφία 1,2,3,4,5; Με πόσους τα ψηφία 1,1,3,4,5;

Υπόδειξη: Για το δεύτερο ερώτημα βρείτε πρώτα με πόσους τρόπους μπορούν να μπουν στη σειρά τα σύμβολα 1, 1', 3, 4, 5. Με ποια διαδικασία μπορείτε να πάρετε από αυτούς τους τρόπους όλους τους τρόπους διάταξης των 1, 1, 3, 4, 5;

Με πόσους τρόπους μπορείτε να διατάξετε τα ψηφία 1, 1, 1, 2, 2, 3, 4, 5;

Άσκηση 3.26   Σε μια πόλη με εξαψήφια τηλέφωνα πόσα νούμερα το πολύ μπορεί να υπάρχουν χωρίς επαναλαμβανόμενα ψηφία;

Άσκηση 3.27   Ένα μήνυμα στον κώδικα Morse είναι μια πεπερασμένη ακολουθία (μια λέξη όπως λέμε) από κουκίδες, παύλες και κενά. Πόσα διαφορετικά μηνύματα φτιάχνονται με 7 κουκίδες, 3 παύλες και 2 κενά.

Πόσα αν απαγορεύεται ένα μήνυμα να ξεκινάει ή να τελειώνει με κενό;

Άσκηση 3.28   Η νεοσύστατη εταιρεία πληροφορικής «Faster Than Light» ετοιμάζεται να φτιάξει ένα σύστημα για online email το οποίο φιλοδοξεί να καλύψει στο μέλλον πάνω από 100 εκατομμύρια χρήστες. Η εταιρεία έχει αποφασίσει ότι όλες οι διευθύνσεις email των χρηστών της θα είναι της μορφής

username@does-not-get-there.ever

όπου το username του χρήστη θα απαρτίζεται από το πολύ $N$ γράμματα από το σύνολο

A, B, C, D, ..., Z, 0, 1, ..., 9

(36 σύμβολα συνολικά) με τον περιορισμό ότι το πρώτο γράμμα του username πρέπει να είναι γράμμα και όχι αριθμός. (Τα κεφαλαία γράμματα ταυτίζονται με τα μικρά.) Ποια είναι η ελάχιστη τιμή του $N$ που πρέπει να προβλέψει η εταιρεία ώστε να μπορεί να ικανοποιήσει το στόχο της και να έχει τουλάχιστον 100 εκατομμύρια διαθέσιμες διευθύνσεις στην αρχή της λειτουργίας της;

Άσκηση 3.29   Αποδείξτε ότι $\frac{n!}{2^n} \to \infty$, για $n\to\infty$.

3.2.2 Μη διατεταγμένες επιλογές. Συνδυασμοί

Πόσα υποσύνολα του συνόλου $[n]$ (ή, εν γένει, ενός συνόλου με $n$ στοιχεία) υπάρχουν με μέγεθος $k$;

Θεώρημα 3.5   Αν $0\le k \le n$ τότε το σύνολο $[n]$ (ή οποιοδήποτε σύνολο με $n$ στοιχεία) έχει

$${n \choose k} := \frac{n(n-1)\cdots(n-k+1)}{k!}$$

υποσύνολα μεγέθους $k$ (ακολουθούμε τη σύμβαση ότι ένα γινόμενο με 0 παράγοντες ισούται με 1, έτσι $0! = 1$).

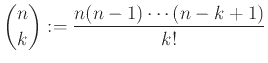
Το σύμβολο ${n \choose k}$ προφέρεται: $n$ ανά $k$.

Πόρισμα 3.2   Αν $n, k$ φυσικοί αριθμοί, $0\le k \le n$, τότε α αριθμός

$${n(n-1)\cdots(n-k+1) \over k!}$$

είναι ακέραιος.

Απόδειξη. Αυτό που ζητάμε να μετρήσουμε είναι το πλήθος των μη διατεταγμένων $k$-άδων με διαφορετικά στοιχεία από το $[n]$. Λέγοντας ότι θέλουμε να μετρήσουμε «μη διατεταγμένες» $k$-άδες εννούμε ότι αν δύο $k$-άδες διαφέρουν μόνο ως προς τη σειρά που εμφανίζονται τα στοιχεία τους, τότε αυτές τις θεωρούμε ίδιες και τις μετράμε μία φορά. Αν αυτό δεν ίσχυε, αν δηλ. διαφορετικά διατεταγμένες $k$-άδες θεωρούνταν διαφορετικές, τότε την απάντηση τη δίνει το Θεώρημα 3.4, δηλ. $n(n-1)\cdots(n-k+1)$.

Παρατηρήστε τώρα ότι σε κάθε μη διατεταγμένη $k$-άδα, σε κάθε δηλ. $k$-μελές υποσύνολο του $[n]$, αντιστοιχούν ακριβώς $k!$ διατεταγμένες $k$-άδες, μια και με τόσους τρόπους μπορούν να διαταχθούν τα στοιχεία ενός $k$-μελούς συνόλου (Πόρισμα 3.1). Άρα, στον αριθμό $n(n-1)\cdots(n-k+1)$ κάθε $k$-μελές υποσύνολο του $[n]$ έχει μετρηθεί ακριβώς $k!$ φορές. Για να βρούμε συνεπώς το πλήθος των $k$-μελών υποσυνόλων του $[n]$ αρκεί να διαιρέσουμε αυτό τον αριθμό με $k!$. $\qedsymbol$

Παρατήρηση 3.2   Είναι σημαντικό να τονίσουμε εδώ ότι η προηγούμενη απόδειξη δουλεύει ακριβώς επειδή κάθε $k$-μελές σύνολο είχε μετρηθεί τον ίδιο αριθμό φορών στην ποσότητα $n(n-1)\cdots(n-k+1)$, και άρα δικαιούμασταν να διαιρέσουμε δια αυτό τον αριθμό φορών.

Άσκηση 3.30   Το παρακάτω πρόγραμμα σε python υπολογίζει το διωνυμικό συντελεστή ${n \choose k}$ και τυπώνει για δοκιμή την τιμή ${5 \choose 2}$:

def binomial(n,k):
    if k<0:
        print "Error"
        return -1
    else:
        t=1.0
        for i in range(k):
            t = t*(n-i)/(k-i)
        return t

print binomial(5,2)

Βεβαιωθείτε ότι καταλαβαίνετε τον τρόπο λειτουργίας του και τρέξτε μερικά παραδείγματα. Παρατηρήστε ότι αν στη θέση του $n$ βάλουμε έναν οποιοδήποτε πραγματικό αριθμό το πρόγραμμα τρέχει κανονικά αλλά προκύπτει σφάλμα αν στη θέση του $k$ βάλουμε κάποιον αριθμό που δεν είναι φυσικός αριθμός.

Στην πραγματικότητα το πρόγραμμα αυτό υπολογίζει το πολυώνυμο

$${x \choose k} = \frac{x(x-1)(x-2)\cdots(x-k+1)}{k!}, x\in{\mathbb{R}}.$$ (3.7)

Όταν $x=n$ είναι ένας φυσικός αριθμός η τιμή του πολυωνύμου αυτού είναι ${n \choose k}$ και έχει τη συνδυαστική ερμηνεία που είδαμε παραπάνω. Όμως είναι χρήσιμο να ξέρουμε ότι η συνάρτηση αυτή του $x$ ορίζεται μια χαρά και όταν το $x$ είναι οποιοσδήποτε πραγματικός (ή μιγαδικός) αριθμός και μάλιστα η συνάρτηση αυτή είναι πολυώνυμο του $x$.

Άσκηση 3.31   Δείξτε ότι το πολυώνυμο $f(x) = {x \choose k}$ που ορίζεται στην (3.7) είναι ακεραιότιμο, ισχύει δηλ. για κάθε ακέραιο $k \ge 0$

$$x \in {\mathbb{Z}}\Longrightarrow f(x) \in {\mathbb{Z}}.$$

Βρείτε τις ρίζες αυτού του πολυωνύμου. Επίσης εκφράστε το διωνυμικό συντελεστή ${-n \choose k}$, όπου $n$ θετικός ακέραιος, μέσω κάποιου άλλου διωνυμικού συντελεστή ${N \choose k}$, όπου $N$ επίσης είναι θετικός ακέραιος.

Άσκηση 3.32   Ποια είναι τα διμελή υποσύνολα του $[4]={\left\{{1,2,3,4}\right\}}$.

Γράψτε μια συνάρτηση σε python που δοθέντος ενός συνόλου (ως μια λίστα python) να επιστρέφει μια λίστα με όλα τα διμελή υποσύνολα του συνόλου αυτού. Δουλέψτε συμπληρώνοντας την παρακάτω ημιτελή συνάρτηση.

def subsets2(s):
    n = len(s)
    ss = []
    if n <= 1:
        return ss
    else:
        for i in range(n):
	.......
        return ss

Η κλήση

s = ['a', 'b', 'c', 'd']
print subsets2(s)

θα πρέπει να σας επιστρέφει

[['a', 'b'], ['a', 'c'], ['a', 'd'], ['b', 'c'], ['b', 'd'], ['c', 'd']]

Παράδειγμα 3.4   Με πόσους τρόπους μπορούμε να διαλέξουμε τέσσερεις διαφορετικούς διψήφιους ακεραίους (δε μας ενδιαφέρει η σειρά τους) ούτως ώστε να χωρίζονται αυτοί σε δύο ζεύγη και οι αριθμοί κάθε ζεύγους να έχουν το ίδιο δεύτερο (χαμηλότερο) ψηφίο αλλά αριθμοί σε διαφορετικά ζεύγη να έχουν διαφορετικό δεύτερο ψηφίο;

Για να μετρήσουμε τους τρόπους σκεφτόμαστε με ποια διαδικασία θα παράγουμε μονοσήμαντα ένα τέτοιο αποτέλεσμα. Παρατηρούμε ότι στη δεύτερη θέση χρησιμοποιούνται ακριβώς δύο ψηφία, ένα στο ένα ζεύγος και ένα για το άλλο. Αποφασίζουμε λοιπόν κάθε τετράδα τέτοιων αριθμών να τη γράφουμε ως εξής:

$$xa, ya, zb, wb$$ (3.8)

όπου ισχύει

$$a,b \in {\left\{{0,\ldots,9}\right\}}, x,y,z,w \in {\left\{{1,\ldots,9}\right\}}, a>b, x>y, z>w.$$ (3.9)

Την τελευταία αυτή απαίτηση τη βάζουμε ώστε κάθε τετράδα από αυτές που θέλουμε να μετρήσουμε να γράφεται με μοναδικό τρόπο στη μορφή (3.8). Πάντα δηλ. όταν είναι να γράψουμε μια τετράδα κάτω γράφουμε πρώτα το ζευγάρι όπου το ψηφίο των μονάδων είναι το μεγαλύτερο, και μέσα σε κάθε ζευγάρι γράφουμε πρώτα αυτόν τον αριθμό του οποίο το ψηφίο των δεκάδων είναι το μεγαλύτερο.

Τα αντικείμενα δηλ. που θέλουμε να μετρήσουμε είναι σε ένα προς ένα αντιστοιχία με τις εξάδες

$$(a,b,x,y,z,w)$$

που ικανοποιούν την (3.9). Για να μετρήσουμε τις εξάδες αυτές μετράμε πρώτα πόσες είναι οι επιλογές μας για το ζεύγος $a, b$, πόσες για το ζεύγος $x, y$ και πόσες για το ζεύγος $z,w$. Επειδή, λόγω της φύσης της συνθήκης (3.9), αυτές οι επιλογές είναι ανεξάρτητες μεταξύ τους μπορούμε να τις πολλαπλασιάσουμε. Αλλά για να επιλέξουμε το ζεύγος $a,b \in {\left\{{0,\ldots,9}\right\}}$ με $a>b$ μπορούμε απλά να επιλέξουμε ένα διμελές υποσύνολο του ${\left\{{0,\ldots,9}\right\}}$ και να ονομάσουμε $a$ το μεγαλύτερο στοιχείο του και $b$ το μικρότερο. Το πλήθος επιλογών μας δηλ. είναι ${10 \choose 2}$ και, ομοίως σκεπτόμενοι, βλέπουμε ότι για το ζεύγος $x, y$ έχουμε ${9 \choose 2}$ επιλογές και ομοίως για το ζεύγος $z,w$.

Το τελικό αποτέλεσμα είναι λοιπόν

$${10 \choose 2} {9 \choose 2}^2.$$

Παράδειγμα 3.5   Από μια συνηθισμένη τράπουλα με πόσους τρόπους μπορούμε να επιλέξουμε μια εξάδα από φύλλα υπό τον περιορισμό ότι ακριβώς τρία από αυτά είναι σπαθιά ($\clubsuit$); Οι εξάδες που επιλέγουμε είναι μη διατεταγμένες.

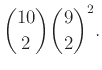
Για να απαντήσουμε βρίσκουμε μια διαδικασία παραγωγής του τυπικού αποτελέσματος. Αφού λοιπόν πρέπει τρία από αυτά τα χαρτιά να είναι σπαθιά ξεκινάμε διαλέγοντας πρώτα απ' όλα αυτά. Τα τρία αυτά φύλλα επιλέγονται χωρίς κανένα περιορισμό από τα 13 συνολικά σπαθιά της τράπουλας. Άρα οι δυνατότητες γι' αυτή την επιλογή είναι ${13 \choose 3}$.

Στη συνέχεια επιλέγουμε τα υπόλοιπα τρία φύλλα που πρέπει απλά να μην είναι σπαθιά, επιλέγονται δηλ. από τα $3\times 13 = 39$ φύλλα που δεν είναι σπαθιά, δίνοντάς μας ${39 \choose 3}$ δυνατότητες.

Επειδή η πρώτη επιλογή (των σπαθιών) είναι ανεξάρτητη από τη δεύτερη το τελικό αποτέλεσμα είναι

$${13 \choose 3} \cdot {39 \choose 3}.$$

Παράδειγμα 3.6   Είναι πολύ σημαντικό να τονίσουμε ότι η απαρίθμηση που κάναμε στο Παράδειγμα 3.5 είναι σωστή επειδή η μέθοδος κατασκευής έχει τις ακόλουθες ιδιότητες

• Είναι τέτοια ώστε διαφορετικές επί μέρους επιλογές (στη μέθοδο κατασκευής που περιγράψαμε οι επί μέρους επιλογές ήταν δύο: πρώτα η επιλογή των σπαθιών και μετά η επιλογή των μη σπαθιών) οδηγούν αναγκαστικά σε διαφορετικό αποτέλεσμα, και
• Κάθε δυνατό αποτέλεσμα είναι δυνατό να κατασκευαστεί με τη μέθοδό μας.

Οι δύο αυτές ιδιότητες μαζί εξασφαλίζουν ότι υπάρχει αμφιμονοσήμαντη αντιστοιχία ανάμεσα σε αυτά που κατασκευάζουμε και σε αυτά που θέλουμε να μετρήσουμε, άρα μπορούμε απλά να μετρήσουμε το πλήθος των αντικειμένων που κατασκευάζουμε.

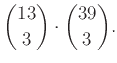
Για να τονίσουμε το πόσο σημαντικές είναι αυτές οι δύο ιδιότητες και πόσο προσεκτικοί πρέπει να είμαστε σε αντίστοιχα μετρήματα, ας παραλλάξουμε λίγο το ερώτημα του Παραδείγματος 3.5. Ας ρωτήσουμε το ίδιο με μόνη διαφορά ότι τώρα δεν απαιτούμε ακριβώς τρία φύλλα να είναι σπαθιά αλλά τουλάχιστον τρία.

Ας βρούμε μια διαδικασία κατασκευής (σύνθετη επιλογή). Αφού όπωσδήποτε θέλουμε τρία σπαθιά ας ξεκινήσουμε επιλέγοντάς τα. Έχουμε πάλι ${13 \choose 3}$ δυνατότητες γι' αυτή την επιλογή. Στο δεύτερο στάδιο μένει απλά να επιλέξουμε άλλα τρία φύλλα από τα εναπομέναντα $49$, αφού τώρα δε μας πειράζει να έχουμε επιπλέον σπαθιά. Στο δεύτερο στάδιο λοιπόν έχουμε ${49 \choose 3}$ δυνατότητες. Εφ' όσον τα δύο στάδια επιλογής είναι ημι-ανεξάρτητα (προηγουμένως ήταν ανεξάρτητα) μπορούμε και πάλι να πολλαπλασιάσουμε και παίρνουμε τελικό αποτέλεσμα

$${13 \choose 3} \cdot {49 \choose 3}.$$

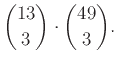
ΛΑΘΟΣ!

Και ο λόγος είναι ότι μπορούμε να έχουμε το ίδιο αποτέλεσμα ακόμη κι αν η σύνθετη επιλογή μας αλλάξει. Για παράδειγμα, η κατασκευή μας μπορεί στο πρώτο στάδιο να μας δώσει 1 $\clubsuit$, 2 $\clubsuit$, 3 $\clubsuit$ και στο δεύτερο 4 $\clubsuit$, 1 $\heartsuit$ και 2 $\heartsuit$. Μπορεί επίσης να μας δώσει στο πρώτο στάδιο 1 $\clubsuit$, 2 $\clubsuit$, 4 $\clubsuit$ και στο δεύτερο να μας δώσει 3 $\clubsuit$, 1 $\heartsuit$ και 2 $\heartsuit$. Η τελική εξάδα είναι στις δύο αυτές περιπτώσεις η ίδια. Άρα ο αριθμός ${13 \choose 3} \cdot {49 \choose 3}$ που υπολογίσαμε προηγουμένως είναι αυστηρά (και μάλλον κατά πολύ) μεγαλύτερος της πραγματικότητας.

Πώς μπορούμε να διορθώσουμε τη μέθοδό μας; Μια απλή απάντηση είναι ότι μπορούμε να διαχωρίσουμε τις δυνατές εξάδες σε τέσσερεις κατηγορίες: αυτές που έχουν ακριβώς 3, ακριβώς 4, ακριβώς 5 ή ακριβώς 6 σπαθιά. Μπορούμε εύκολα να μετρήσουμε τις εξάδες κάθε κατηγορίας, ουσιαστικά με τη μέθοδο του Παραδείγματος 3.5, και στο τέλος να προσθέσουμε αυτά τα τέσσερα νούμερα. Έτσι το αποτέλεσμα είναι

$${13 \choose 3}{39 \choose 3} + {13 \choose 4}{39 \choose 2} + {13 \choose 5}39 + {13 \choose 6}$$

όπου ο κάθε προσθετέος αντιπροσωπεύει και μια κατηγορία. (Βεβαιωθείτε ότι καταλαβαίνετε αυτή την αντιστοιχία.)

Παράδειγμα 3.7   Αν αναπτύξουμε (γράψουμε δηλ. στη μορφή $a_0 + a_1 x + a_2 x^2 + \cdots + a_n x^n$) το πολυώνυμο $(1+x)^{10}$ ποιος είναι ο συντελεστής του $x^4$;

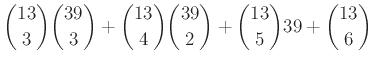
Ας σκεφτούμε λίγο πώς υπολογίζει κανείς το ανάπτυγμα ενός γινομένου, για απλότητα του $(a+b)^2 = (a+b)(a+b)$ που έχει δύο μόνο παράγοντες και όχι 10 όπως αυτό που ζητάμε. Το βρίσκουμε παίρνοντας κάθε προσθετέο του πρώτου αθροίσματος πολλαπλασιασμένο με κάθε προσθετέο του δεύτερου, και αθροίζουμε τα αποτελέσματα. Αν λοιπόν ρωτήσουμε ποιός είναι ο συντελεστής του $ab$ στο ανάπτυγμα, είναι σα να ρωτάμε με πόσους τρόπους μπορεί να εμφανιστεί το γινόμενο $ab$ κάνοντας το ανάπτυγμα όπως παραπάνω.

Λόγω αντιμεταθετικότητας του πολλαπλασιασμού αυτό μπορεί να εμφανιστεί είτε ως $ab$ είτε ως $ba$. Το $ab$ εμφανίζεται ακριβώς μία φορά, όταν συνδυάζουμε στο ανάπτυγμα το $a$ από την πρώτη παρένθεση με το $b$ από τη δεύτερη. Δεν υπάρχει άλλος τρόπος. Ομοίως μία φορά εμφανίζεται και το $ba$ όταν συνδυάζεται το $b$ από την πρώτη παρένθεση με το $a$ από τη δεύτερη. Άρα ο συντελεστής του $ab$ στο ανάπτυγμα είναι $1+1=2$. Ομοίως τα $a^2$ και $b^2$ μπορούν το καθένα να προκύψουν με ένα μόνο τρόπο. Για το $a^2$, π.χ., πρέπει να επιλεγεί το $a$ και από την πρώτη και από τη δεύτερη παρένθεση, ομοίως και για το $b^2$. Επιβεβαιώνεται έτσι ο γνωστός μας τύπος $(a+b)^2 = a^2 + 2ab + b^2$.

Αν ρωτήσουμε για το συντελεστή του $a^2b$ στο ανάπτυγμα του $(a+b)^3$ είναι σα να ρωτάμε με πόσους τρόπους μπορούμε να συνδυάσουμε ένα $b$ με δύο $a$ από τις τρείς παρενθέσεις $(a+b)$ που υπάρχουν στο γινόμενο. Αυτό μπορεί να γίνει με ακριβώς τρείς τρόπους μια και αρκεί να πούμε από ποια παρένθεση επιλέγουμε να πάρουμε το $b$. Αυτό προσδιορίζει ότι από τις άλλες δύο παίρνουμε από ένα $a$.

Επανερχόμαστε τώρα στο αρχικό μας ερώτημα και ρωτάμε για το συντελεστή του $x^4$ στο ανάπτυγμα του $(1+x)^{10}$. Στο ανάπτυγμα αυτό οι προσθετέοι προκύπτουν με επιλογή, ο καθένας, ενός $1$ ή ενός $x$ από κάθε μία από τις 10 παρενθέσεις. Το $x^4$ λοιπόν μπορεί να προκύψει με τόσους τρόπους όσοι είναι οι τρόποι να επιλέξουμε τις 4 παρενθέσεις, από τις οποίες θα πάρουμε τα $x$. Άρα το αποτέλεσμα είναι

$${10 \choose 4}.$$

Άσκηση 3.33   Από μια ομάδα 10 ατόμων, με πόσους τρόπους μπορεί να επιλεγεί ένα τριμελές προεδρείο χωρίς διακριτούς ρόλους; Ένα 5μελές προεδρείο με πρόεδρο, αντιπρόεδρο και 3 μέλη;

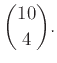
Υπόδειξη: Για το δεύτερο ερώτημα, επιλέξτε το προεδρείο επιλέγοντας πρώτα τον πρόεδρο, μετά τον αντιπρόεδρο και, τέλος, τα τρία μέλη μαζί.

Άσκηση 3.34   Μέ πόσους τρόπους μπορούμε να επιλέξουμε, από μια συνηθισμένη τράπουλα με 52 φύλλα (που χωρίζονται σε 4 χρώματα και 13 είδη), πέντε φύλλα από τα οποία 2 κόκκινα ( $\diamondsuit$ ή $\heartsuit$) και 3 σπαθιά; Δε μας ενδιαφέρει η σειρά επιλογής των φύλλων.

Άσκηση 3.35   Αν $n$ άρτιο για ποιο $k\in{\left\{{0,1,\ldots,n}\right\}}$ μεγιστοποιείται η ποσότητα ${n \choose k}$; Τι γίνεται αν $n$ περιττός;

Άσκηση 3.36   Δείξτε την ταυτότητα

$$\sum_{k=0}^n {n \choose k} = {n \choose 0} + {n \choose 1} + \cdots + {n \choose n-1} + {n \choose n} = 2^n,$$

για κάθε $n \ge 0$.

Άσκηση 3.37   Δείξτε την ταυτότητα

$${n \choose k} = {n \choose n-k}$$

για κάθε $n \ge 0$ και $0\le k \le n$.

Άσκηση 3.38   Αν $r, s, k$ είναι φυσικοί αριθμοί με $r \ge s$ δείξτε ότι ο αριθμός $s!$ είναι διαιρέτης του

$$(k+1)(k+2)\cdots(k+r).$$