Next: 4.5 Επαναληπτικές ασκήσεις Κεφαλαίου Up: 4. Προχωρημένη απαρίθμηση Previous: 4.3 Το Διωνυμικό Θεώρημα Contents Index
Σε αυτή την παράγραφο θα δούμε πώς μπορούμε πολλές φορές να αποδεικνύουμε ταυτότητες χωρίς ιδιαίτερες πράξεις, απλά ερμηνεύοντας το αριστερό και το δεξί μέλος με συνδυαστικό τρόπο και παρατηρώντας ότι απαριθμούν τα ίδια αντικείμενα (άρα είναι και ίσα). Αυτή η τεχνική ονομάζεται και διπλό μέτρημα μια και μετράμε τα ίδια αντικείμενα δύο φορές, άρα τα δύο αποτελέσματα είναι ίσα.
Έστω
![]() οι καλεσμένοι. Θεωρούμε το σύνολο των ζευγών
οι καλεσμένοι. Θεωρούμε το σύνολο των ζευγών
![]() τέτοια ώστε ο
τέτοια ώστε ο ![]() χαιρετάει τον
χαιρετάει τον ![]() , και ας είναι
, και ας είναι
![]() ο αριθμός των χειραψιών που ανταλλάσσει ο
ο αριθμός των χειραψιών που ανταλλάσσει ο ![]() και
και ![]() ο συνολικός
αριθμός χειραψιών που ανταλλάσονται.
Το πλήθος των ζευγών
ο συνολικός
αριθμός χειραψιών που ανταλλάσονται.
Το πλήθος των ζευγών
![]() ισούται, από τη μια μεριά, με
ισούται, από τη μια μεριά, με
![]() , και, από την άλλη, με
, και, από την άλλη, με ![]() , αφού σε κάθε χειραψία
αντιστοιχούν ακριβώς δύο ζευγάρια
, αφού σε κάθε χειραψία
αντιστοιχούν ακριβώς δύο ζευγάρια
![]() και
και
![]() .
Έτσι έχουμε
.
Έτσι έχουμε
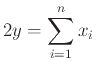
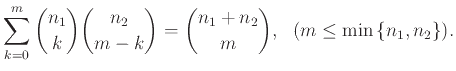
Δεξιά μετράμε τα υποσύνολα μεγέθους ![]() του
του ![]() .
Βάφουμε τα
.
Βάφουμε τα ![]() αντικείμενα άσπρα και τα άλλα μαύρα. Τα υποσύνολα μεγέθους
αντικείμενα άσπρα και τα άλλα μαύρα. Τα υποσύνολα μεγέθους
![]() που μας ενδιαφέρουν χωρίζονται στις
που μας ενδιαφέρουν χωρίζονται στις ![]() σε πλήθος κατηγορίες
σε πλήθος κατηγορίες ![]() ,
,
![]() . Η κατηγορία
. Η κατηγορία ![]() περιλαμβάνει όλα τα
περιλαμβάνει όλα τα ![]() -μελή υποσύνολα
του
-μελή υποσύνολα
του ![]() που περιέχουν ακριβώς
που περιέχουν ακριβώς ![]() άσπρα.
Προφανώς έχουμε
άσπρα.
Προφανώς έχουμε
![]() αφού
για να φτιάξουμε ένα υποσύνολα κατηγορίας
αφού
για να φτιάξουμε ένα υποσύνολα κατηγορίας ![]() πρέπει να επιλέξουμε
πρέπει να επιλέξουμε
![]() άσπρα και τα υπόλοιπα
άσπρα και τα υπόλοιπα ![]() μαύρα.
Άρα το αριστερό μέλος της ισότητας είναι ίσο με
μαύρα.
Άρα το αριστερό μέλος της ισότητας είναι ίσο με
![]() .
.
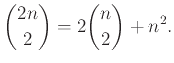
Αριστερά μετράμε διμελή υποσύνολα του ![]() . Έστω ότι χρωματίζουμε
. Έστω ότι χρωματίζουμε ![]() από τα
από τα ![]() αντικείμενα σε άσπρα και τα άλλα μαύρα. Τα διμελή υποσύνολα του
αντικείμενα σε άσπρα και τα άλλα μαύρα. Τα διμελή υποσύνολα του ![]() είναι τριών τύπων:
(Α) δύο στοιχεία άσπρα, (Β) δύο στοιχεία μαύρα, (Γ) ένα άσπρο κι ένα μαύρο.
Τα υποσύνολα τύπου (Α) είναι
είναι τριών τύπων:
(Α) δύο στοιχεία άσπρα, (Β) δύο στοιχεία μαύρα, (Γ) ένα άσπρο κι ένα μαύρο.
Τα υποσύνολα τύπου (Α) είναι
![]() σε πλήθος αφού διαλέγουμε δύο από
τα
σε πλήθος αφού διαλέγουμε δύο από
τα ![]() άσπρα. Τόσα είναι και τα υποσύνολα τύπου (Β). Τα σύνολα τύπου (Γ) είναι
σε πλήθος
άσπρα. Τόσα είναι και τα υποσύνολα τύπου (Β). Τα σύνολα τύπου (Γ) είναι
σε πλήθος ![]() , μια και πρέπει να διαλέξουμε ένα από
, μια και πρέπει να διαλέξουμε ένα από ![]() άσπρα
και ένα από
άσπρα
και ένα από ![]() μαύρα. Το σύνολο για τις τρεις κατηγορίες συνόλων εμφανίζεται στο
δεξί μέλος.
μαύρα. Το σύνολο για τις τρεις κατηγορίες συνόλων εμφανίζεται στο
δεξί μέλος.
Υπάρχουν
![]() σύνολα
σύνολα
![]() με μέγεθος
με μέγεθος ![]() , και
για κάθε ένα από αυτά μπορούμε να επιλέξουμε ως
, και
για κάθε ένα από αυτά μπορούμε να επιλέξουμε ως ![]() οποιοδήποτε από τα
οποιοδήποτε από τα ![]() στοιχεία του, άρα το πλήθος των ζευγών
στοιχεία του, άρα το πλήθος των ζευγών ![]() τέτοια ώστε
τέτοια ώστε
![]() ισούται με το δεξί μέλος της (4.8).
ισούται με το δεξί μέλος της (4.8).
Όμως τα ζεύγη αυτά μπορούν να αριθμηθούν επιλέγοντας πρώτα το ![]() και μετά επιλέγοντας τα υπόλοιπα στοιχεία του
και μετά επιλέγοντας τα υπόλοιπα στοιχεία του ![]() ,
το σύνολο δηλ.
,
το σύνολο δηλ.
![]() .
Όμως όλα τα σημεία του
.
Όμως όλα τα σημεία του ![]() εκτός το
εκτός το ![]() συμμετέχουν στον καθορισμό του
συμμετέχουν στον καθορισμό του
![]() , και άρα οι δυνατότητες γι' αυτό είναι
, και άρα οι δυνατότητες γι' αυτό είναι ![]() , άρα
οι δυνατότητες για τα ζεύγη είναι
, άρα
οι δυνατότητες για τα ζεύγη είναι ![]() , που είναι το αριστερό μέλος.
, που είναι το αριστερό μέλος.
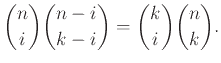
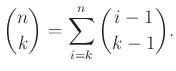
Υπόδειξη: Πόσα υποσύνολα του ![]() μεγέθους
μεγέθους ![]() υπάρχουν τ.ώ. το μεγαλύτερο
στοιχείο τους να είναι το
υπάρχουν τ.ώ. το μεγαλύτερο
στοιχείο τους να είναι το ![]() ;
;
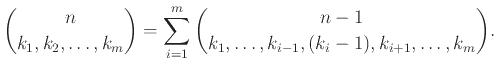
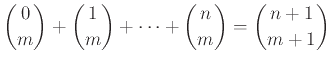
Mihalis Kolountzakis 2015-11-28