3.1 Αρχή πολλαπλασιασμού ανεξάρτητων επιλογών

Περπατώντας έξω από ένα κατάστημα που σερβίρει καφέδες διαφόρων ειδών συναντά κανείς τον ισχυρισμό που φαίνεται στο Σχήμα 3.1, που αρχικά φαίνεται μάλλον εξωφρενικός. Είναι όμως;

Σχήμα 3.1: Πόσους διαφορετικούς καφέδες μπορεί να φτιάξει ένα καφενείο;

Ας υποθέσουμε ότι κάποιος πίνει τον καφέ του με ή χωρίς ζάχαρη, με ή χωρίς γάλα. (Οι ποσότητες γάλατος και ζάχαρης που μπορεί κανείς να έχει είναι σταθερές. Δεν υπάρχει με ολίγη.) Πόσα διαφορετικά είδη από καφέ πρέπει να μπορεί να φτιαξει ένα καφενείο ώστε να μπορεί να εξυπηρετήσει όλους τους πελάτες;

Η απάντηση είναι 4:

1. Χωρίς γάλα, χωρίς ζάχαρη
2. Χωρίς γάλα, με ζάχαρη
3. Με γάλα, χωρίς ζάχαρη
4. Με γάλα, με ζάχαρη

Αν σκεφτούμε λίγο προσεκτικότερα θα συνειδητοποιήσουμε ότι $4=2\cdot 2$ και ότι ο λόγος που η απάντηση είναι αυτή είναι ότι κάθε μια από τις δύο δυνατές επιλογές όσον αφορά το περιεχόμενο σε γάλα μπορεί να συνδυαστεί με κάθε μία από τις δύο δυνατές επιλογές που αφορούν στο περιεχόμενο σε ζάχαρη.

Άσκηση 3.1   Ποια η απάντηση στο άνω «πρόβλημα του καφέ» αν οι επιλογές μας ως προς τη ζάχαρη δεν είναι πλέον οι ΝΑΙ, ΟΧΙ, αλλά μπορούμε είτε να μην έχουμε καθόλου ζάχαρη, είτε να έχουμε ένα φακελάκι, είτε δύο;

Άσκηση 3.2   Αν το αρχικό «πρόβλημα του καφέ» προστεθεί η επιλογή ΚΡΥΟΣ ή ΖΕΣΤΟΣ, την οποία μπορούμε να έχουμε ανεξάρτητα από το γάλα ή τη ζάχαρη που διαλέγουμε, ποια είναι η απάντηση;

Η αρχή του πολλαπλασιασμού ανεξάρτητων επιλογών κωδικοποιεί την απλή αυτή παρατήρηση που κάναμε:

Ας υποθέσουμε ότι έχουμε να παραγματοποιήσουμε μια σύνθετη επιλογή, η οποία συνίσταται από την πραγματοποίηση $k$ επί μέρους επιλογών, που πραγματοποιούνται ανεξάρτητα η μία από την άλλη, είναι δηλ. τέτοιες οι επί μέρους επιλογές ώστε η επιλογή τιμών για κάποιες από αυτές να μην επηρεάζει τις δυνατότητες που υπάρχουν για τις υπόλοιπες. Τότε το συνολικό πλήθος δυνατοτήτων που έχουμε για τη σύνθετή μας επιλογή είναι το γινόμενο των $k$ δυνατοτήτων για τις επί μέρους επιλογές μας.

Σε πιο αυστηρή γλώσσα η αρχή του πολλαπλασιασμού ανεξαρτήτων επιλογών εκφράζεται ως εξής (γενικά με ${\left\vert{X}\right\vert}$ συμβολίζουμε τον πληθάριθμο-πόσα στοιχεία έχει-του συνόλου $X$):

Θεώρημα 3.1   Έστω $k$ φυσικός αριθμός και $E$ το σύνολο όλων των διαφορετικών $k$-άδων

$$(x_1, \ldots, x_k)$$

όπου $x_1 \in E_1, x_2 \in E_2, \ldots, x_k \in E_k$, και τα $E_j$ είναι όλα πεπερασμένα σύνολα. Τότε

$${\left\vert{E}\right\vert} = {\left\vert{E_1}\right\vert} \cdot {\left\vert{E_2}\right\vert} \cdots {\left\vert{E_k}\right\vert}.$$

Απόδειξη. Απόδειξη με επαγωγή ως προς $k$. Αν $k=1$ πρόκειται περί ταυτολογίας, αφού $E=E_1$. Υποθέτουμε τώρα ότι η πρόταση ισχύει για $k=n$ και τη δείχνουμε για $k=n+1$. Θέλουμε να μετρήσουμε τα διατεταγμένα αντικείμενα της μορφής

$$(x_1, \ldots, x_n, x_{n+1})$$ (3.1)

όπου $x_j \in E_j$, για $j=1,\ldots,n+1$. Αν $E_{n+1} = {\left\{{e_1,\ldots,e_r}\right\}}$ αυτά τα αντικείμενα (3.1) χωρίζονται στις εξής ξένες μεταξύ τους $r$ ομάδες: $G_1$ είναι εκείνα τα αντικείμενα που στην τελευταία θέση τους έχουν $e_1$, δηλ. όλα τα αντικείμενα της μορφής

$$(x_1,\ldots,x_n,e_1), \mu\epsilon x_j\in E_j,$$ (3.2)

$G_2$ είναι εκείνα τα αντικείμενα με $e_2$ στην τελευταία θέση, κ.ο.κ. Οι ομάδες αυτές είναι μεταξύ τους ισοπληθείς, αφού, π.χ. μπορεί η $G_1$ να τεθεί σε 1-1 και επί αντιστοιχία με τη $G_2$ μέση της απεικόνισης $G_1 \to G_2$

$$(x_1, \ldots, x_n, e_1) \to (x_1, \ldots,x_n, e_2).$$

Το συνολικό πλήθος λοιπόν των αντικειμένων τύπου (3.1) είναι

$${\left\vert{G_1}\right\vert}\cdot r = {\left\vert{G_1}\right\vert}\cdot{\left\vert{E_{n+1}}\right\vert}.$$ (3.3)

Αλλά, είναι φανερό, το πλήθος στοιχείων της $G_1$ είναι όσα και τα διατεταγμένα αντικείμενα

$$(x_1,\ldots,x_n), \mu\epsilon x_j\in E_j,$$

που, λόγω της επαγωγικής υπόθεσης, είναι ίσο με ${\left\vert{E_1}\right\vert}\cdots{\left\vert{E_n}\right\vert}$. Αντικαθιστώντας στην (3.3) παίρνουμε το αποτέλεσμα. $\qedsymbol$

Άσκηση 3.3   Το παρακάτω πρόγραμμα σε python υπολογίζει όλα τα ζεύγη $(x,y)$ όπου $x \in A, y \in B$, όλα τα στοιχεία δηλ. του καρτεσιανού γινομένου $A\times B$.

A = ['Sweet', 'Medium', 'No Sugar']
B = ['With milk', 'No milk']
for x in A:
    for y in B:
        print "Sugar: ", x, " Milk: ", y

Τρέξτε το πρόγραμμα. Πόσες γραμμές τυπώνει; Τροποποιήστε το πρόγραμμα ώστε να συμπεριλαμβάνει και ένα επιπλέον χαρακτηριστικό του καφέ, το μέγεθος, το οποίο έχει τρεις δυνατές τιμές:

C = ['Large', 'Medium', 'Small']

Άσκηση 3.4   Σε μια χώρα οι τηλεφωνικοί αριθμοί είναι όλοι δεκαψήφιοι. Το πρώτο ψηφίο κάθε τηλεφωνικού αριθμού μπορεί να είναι 2 ή 3 μόνο. Δεν υπάρχει περιορισμός για τα άλλα 9 ψηφία. Ποιος είναι ο μέγιστος αριθμός τηλεφώνων που μπορεί να υπάρξει ταυτόχρονα σε αυτή τη χώρα;

Άσκηση 3.5   Πόσους δεκαδικούς ακεραίους με το πολύ τρία ψηφία μπορεί κανείς να γράψει χρησιμοποιώντας μόνο τα γράμματα 2,3,5;

Υπόδειξη: Πόσους μονοψήφιους, πόσους διψήφιους και πόσους τριψήφιους μπορείτε να φτιάξετε;

Άσκηση 3.6   Πόσες διαφορετικές στήλες ΠΡΟ-ΠΟ υπάρχουν (μήκους 14, με 1,2 ή Χ σε κάθε θέση);

Άσκηση 3.7   Πόσες διαφορετικές τριάδες γραμμάτων μπορούν να εμφανιστούν σε ελληνικές πινακίδες αυτοκινήτων; (Σε αυτές χρησιμοποιούνται μόνο γράμματα που ανήκουν και στο ελληνικό και στο λατινικό αλφάβητο. Αυτά τα γράμματα είναι 14 τον αριθμό.) Αν κάθε τέτοια τριάδα ακολουθείται από ένα τετραψήφιο φυσικό αριθμό (με πρώτο ψηφίο διαφορετικό από το 0) πόσα το πολύ αυτοκίνητα μπορούν να ταξινομηθούν στην Ελλάδα;

Λύστε το ίδιο πρόβλημα για πινακίδες μοτοσυκλετών: 3 γράμματα ακολουθούμενα από ένα αριθμό που μπορεί να είναι μονοψήφιος, διψήφιος ή τριψήφιος αλλά όχι 0.

Άσκηση 3.8   Αν ρίχνετε συνεχώς ένα ζευγάρι τίμια ζάρια, πόσο συχνά περιμένετε να φέρετε δύο άσους; Άσο και δύο;

Υπόδειξη: Εμμέσως υποθέτουμε εδώ ότι όλα τα δυνατά αποτελέσματα αυτού του πειράματος είναι εξίσου πιθανά. Αν είναι λοιπόν $N$ ο αριθμός όλων των δυνατών αποτελεσμάτων τότε το κάθε ένα από αυτά εμφανίζεται περίπου το $1/N$ του χρόνου (με συχνότητα δηλ. $1/N$). Πρώτα λοιπόν θα πρέπει να βρείτε το $N$: πόσα είναι τα δυνατά αποτελέσματα αυτού του πειράματος; Πόσα είναι δηλ. τα δυνατά ζεύγη $(x,y)$, με

$$x, y \in {\left\{{1, 2, 3, 4, 5, 6}\right\}};$$

Εδώ $x$ συμβολίζει την ένδειξη του πρώτου ζαριού και $y$ συμβολίζει την ένδειξη του δεύτερου ζαριού. Προσέξτε μόνο ότι το δεύτερο ερώτημα αντιστοιχεί σε δύο τέτοια ζεύγη και όχι μόνο σε ένα όπως το πρώτο ερώτημα.

3.1.1 Πλήθος υποσυνόλων ενός πεπερασμένου συνόλου

Η πρώτη σημαντική εφαρμογή της αρχής πολλαπλασιασμού των ανεξάρτητων επιλογών είναι το ακόλουθο.

Θεώρημα 3.2   Έστω σύνολο $A$ με $n$ στοιχεία, και ${\mathcal{P}}(A)$ το δυναμοσύνολο του $A$, δηλ. το σύνολο όλων των υποσυνόλων του $A$. Τότε

$${\left\vert{{\mathcal{P}}(A)}\right\vert} = 2^n.$$

Απόδειξη. Μπορεί κανείς εύκολα να αποδείξει το Θεώρημα με επαγωγή ως προς το $n$, αλλά ας δούμε πώς αποδεικνύεται εφαρμόζοντας την αρχή πολλαπλασιασμού. Η βασική παρατήρηση είναι ότι το πλήθος όλων των υποσυνόλων του $A = {\left\{{a_1, \ldots, a_n}\right\}}$ μπορεί να τεθεί σε 1-1 και επί αντιστοιχία με το σύνολο όλων των διατεταγμένων $n$-άδων

$$(x_1, \ldots, x_n) \mu\epsilon x_1, \ldots, x_n \in {\left\{{0,1}\right\}}.$$ (3.4)

Όντως, η 1-1 και επί αυτή αντιστοιχία είναι αυτή που στέλνει το τυχόν υποσύνολο $B \subseteq A$ στη $n$-άδα $(x_1,\ldots,x_n)$ όπου $x_j = 1$ αν και μόνο αν $j \in B$ (βεβαιωθείτε ότι αυτή η απεικόνιση όντως είναι 1-1 και επί).

Αντί να μετρήσουμε λοιπόν τα στοιχεία του

$${\mathcal{P}}(A) = {\left\{{B: B \subseteq A}\right\}}$$

μπορούμε να μετρήσουμε το πλήθος των $n$-άδων (3.4). Το αποτέλεσμα είναι το ίδιο.

Για να μετρήσουμε τώρα τις $n$-άδες (3.4) σκεφτόμαστε ως εξής: για να επιλέξουμε μια τυχούσα $n$-άδα πρέπει να κάνουμε $n$ ανεξάρτητες επιλογές, μια για κάθε $x_j$, και σε κάθε μια από αυτές τις επιλογές έχουμε δύο δυνατότητες. Άρα, το πλήθος δυνατοτήτων για τη συνολική επιλογή είναι $\underbrace{2 \cdot 2 \cdots 2}_n = 2^n$. $\qedsymbol$

Άσκηση 3.9   Δώστε επαγωγική απόδειξη (ως προς το $n$) του Θεωρήματος 3.2.

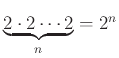Άσκηση 3.10   Το παρακάτω πρόγραμμα σε python υπολογίζει το δυναμοσύνολο ενός συνόλου. Το σύνολο το αναπαριστάμε με μια λίστα (που φροντίζουμε να μην έχει στοιχεία που επαναλαμβάνονται).

def subsets(s):
    n = len(s)
    # empty set contains only the empty set
    if n==0:
        return [[]]
    # s1 is set s without its first element
    s1 = s[1:]
    f = s[0] # f is the first element of set s
    # all subsets of s not containing its first element, f
    p1 = subsets(s1)
    # p2 will contain all subsets of s containing f
    p2 = []
    for x in p1:
        p2.append([f]+x)
    return p2+p1

Κατανοήστε το πώς δουλεύει αυτή η συνάρτηση subsets. (Η συνάρτηση αυτή είναι αναδρομική (recursive), καλεί δηλ. τον εαυτό της.) Μπορείτε να τη δοκιμάσετε ως εξής:

s = ['a', 'b', 'c', 'd']
print subsets(s)

για να πάρετε το output

[['a', 'b', 'c', 'd'], ['a', 'b', 'c'], ['a', 'b', 'd'],
 ['a', 'b'], ['a', 'c', 'd'], ['a', 'c'], ['a', 'd'], ['a'],
 ['b', 'c', 'd'], ['b', 'c'], ['b', 'd'],
 ['b'], ['c', 'd'], ['c'], ['d'], []]

Παράδειγμα 3.1   Μέ πόσους τρόπους μπορεί κανείς να επιλέξει δύο ξένα μεταξύ τους υποσύνολα $A$ και $B$ του συνόλου $[n] = {\left\{{1,2,\ldots,n}\right\}}$;

Τα σύνολα αυτά μπορούν να είναι και κενά.

Για να απαντήσουμε σκεφτόμαστε ως εξής, και ο τρόπος αυτός σκέψης αποτελεί υπόδειγμα για το πώς σκεφτόμαστε στην πλειονότητα των περιπτώσεων. Για να μετρήσουμε λοιπόν τα συγκεκριμένα αντικείμενα βρίσκουμε, κατ' αρχήν, μια διαδικασία για να τα κατασκευάσουμε. Αυτή η διαδικασία πρέπει να είναι τέτοια ώστε

• Να κωδικοποιείται με μια ακολουθία από επιλογές μετά από τις οποίες καταλήγουμε σε ένα από τα αντικείμενα της κλάσης που προσπαθούμε να μετρήσουμε,
• Για κάθε μια από τις δυνατές ακολουθίες επιλογών που κάνουμε να προκύπτει και ένα διαφορετικό αντικείμενο από την κλάση, και
• Για κάθε στοιχείο της κλάσης των προς μέτρηση αντικειμένων υπάρχει μια ακολουθία επιλογών (που είναι και μοναδική, από την προηγούμενη απαίτηση) που μας δίνει το στοιχείο αυτό.

Η κατασκευή που δίνουμε για το συγκεκριμένο πρόβλημα είναι η εξής. Προχωράμε για $i=1$ έως $i=n$ και για κάθε $i$ επιλέγουμε αν θα είναι στο σύνολο $A$, στο σύνολο $B$ ή αν δε θα είναι σε κανένα από αυτά. Δε μπορεί να είναι και στα δύο αφού τα $A$ και $B$ τα θέλουμε ξένα μεταξύ τους. (Δείτε Σχήμα 3.2.)

Σχήμα 3.2: Τοποθετούμε κάθε ένα από τα $1,2,\ldots,n$ σε ακριβώς ένα από τα τρία σακιά

Είναι φανερό πως αν έχουμε δύο διαφορετικές ακολουθίες από τις $n$ αυτές επιλογές, τότε αυτές οδηγούν σε δύο διαφορετικά αντικείμενα, σε δύο διαφορετικά δηλ. ζεύγη ξένων υποσυνόλων $A, B \subseteq [n]$. Έτσι, το πλήθος των αντικειμένων που μας ενδιαφέρει είναι ίσο με το πλήθος των δυνατών ακολουθιών επιλογών μας. Είναι επίσης φανερό ότι οι $n$ απλές επιλογές που απαρτίζουν αυτή την ακολουθία επιλογών είναι ανεξάρτητες μεταξύ τους, αφού κάθε φορά, και ότι και να έχουμε επιλέξει μέχρι στιγμής, τρείς είναι οι δυνατές επιλογές μας για τον τρέχοντα αριθμό $i$, δηλ. να επιλέξουμε $i\in A$.$i\in B$ ή $i \notin A \cup B$. Έτσι, το τελικό αποτέλεσμα είναι

$$\underbrace{3\cdots3}_n = 3^n.$$

Άσκηση 3.11   Με πόσους τρόπους μπορούμε να επιλέξουμε δύο υποσύνολα $A$ και $B$ του $[n]$ ώστε $A \subseteq B$;

Υπόδειξη:

Σχήμα 3.3: Τα σακιά που πρέπει να χρησιμοποιήσετε για την Άσκηση 3.11

Άσκηση 3.12   Ποια η απάντηση στο ερώτημα του Παραδείγματος 3.1 αν απαιτήσουμε τα σύνολα $A$ και $B$ να είναι μη κενά;

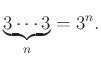
Υπόδειξη: Αφαιρέστε από την απάντηση που δόθηκε στο Παράδειγμα 3.1 μια κατάλληλη ποσότητα που αντιπροσωπεύει επιλογές που δεν πληρούν το κριτήριο της μη κενότητας που έχουμε θέσει.

3.1.2 Πλήθος συναρτήσεων από σύνολο $A$ σε σύνολο $B$

Μια συνάρτηση από το σύνολο $A$ στο σύνολο $B$ είναι απλά μια αντιστοίχιση κάθε στοιχείου του $A$ σε κάποιο στοιχείο του $B$. Αν ${\left\vert{A}\right\vert}=m$ και ${\left\vert{B}\right\vert}=n$ πόσες τέτοιες συναρτήσεις υπάρχουν; Η απάντηση είναι $n^m$:

Θεώρημα 3.3   Αν $A$ και $B$ είναι δύο πεπερασμένα σύνολα, και με $B^A$ συμβολίσουμε το σύνολο όλων των συναρτήσεων από το $A$ στο $B$, τότε

$${\left\vert{B^A}\right\vert} = {\left\vert{B}\right\vert}^{\left\vert{A}\right\vert}.$$

Απόδειξη. Το να επιλέξουμε μια συνάρτηση από το $A$ στο $B$ (ένα μέλος δηλ. του συνόλου $B^A$) σημαίνει απλούστατα να επιλέξουμε την εικόνα κάθε στοιχείου του $A$ ανάμεσα σε όλα τα στοιχεία του $B$. Οι επιλογές αυτές είναι προφανώς ανεξάρτητες μεταξύ τους αφού δεν έχουμε θέσει κανένα περιορισμό στο τι είδους συναρτήσεις θέλουμε (π.χ., θα μπορούσαμε να θέλουμε 1-1 συναρτήσεις μόνο-σε αυτή την περίπτωση οι επιλογές δε θα ήταν φυσικά ανεξάρτητες). Έτσι το πλήθος των δυνατών επιλογών είναι

$$\underbrace{{\left\vert{B}\right\vert}\cdots{\left\vert{B}\right\... ...\vert{A}\right\vert}} = {\left\vert{B}\right\vert}^{\left\vert{A}\right\vert}.$$

$\qedsymbol$

Άσκηση 3.13   Ποιο το πλήθος των συναρτήσεων $[n]\to{\left\{{0,1}\right\}}$; (Περιγράψτε μια φυσιολογική σχέση με τα υποσύνολα του $[n]$.)

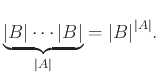
Υπόδειξη:

Σχήμα 3.4: Μια κωδικοποίηση υποσυνόλων του $X$ με μια απεικόνιση $X \to {\left\{{0, 1}\right\}}$, για την Άσκηση 3.13

Άσκηση 3.14   Πόσοι $m\times n$ πίνακες υπάρχουν με στοιχεία 0, 1 ή 3;

Άσκηση 3.15   Ποιο το πλήθος των συναρτήσεων $f:[n] \to {\mathbb{N}}={\left\{{0,1,2,\ldots}\right\}}$ που πληρούν την ανισότητα $f(k) < k$ για κάθε $k\in[n]$;

Υπόδειξη: Πόσες επιλογές έχετε για την εικόνα του $k$;

Άσκηση 3.16   Αν $A={\left\{{-n,-n+1,\ldots,n-1,n}\right\}}$ ποιο το πλήθος των συναρτήσεων $A \to A$ που είναι άρτιες, πληρούν δηλ. $f(-x)=f(x)$ για όλα τα $x \in A$;

Άσκηση 3.17   Πόσοι μη αρνητικοί ακέραιοι αριθμοί, μικρότεροι από $10^6$, έχουν κάποιο 2 στο δεκαδικό τους ανάπτυγμα;

Υπόδειξη: Πόσοι δεν έχουν;

Άσκηση 3.18   Πόσους διαιρέτες έχει ο φυσικός αριθμός

$$n=p_1^{\nu_1}\cdots p_k^{\nu_k} ;$$ (3.5)

Ο $n$ έχει γραφεί σαν γινόμενο δυνάμεων ξένων μεταξύ τους πρώτων αριθμών $p_j$. (Πρώτος λέγεται ένας ακέραιος μεγαλύτερος του $1$ αν δεν έχει άλλους διαιρέτες παρά μόνο τον εαυτό του και το 1. Π.χ. πρώτοι αριθμοί είναι οι 2, 3, 5, 7, 11, 13, ενώ ο 6 δεν είναι πρώτος, αλλά σύνθετος αριθμός. Υπάρχουν άπειροι πρώτοι αριθμοί.) Μπορείτε να χρησιμοποιήσετε το θεμελιώδες θεώρημα (Θεώρημα 2.6) που λέει ότι κάθε φυσικός αριθμός $n$ γράφεται κατά μοναδικό τρόπο στη μορφή (3.5), εκτός ίσως από τη σειρά των παραγόντων.

Εφαρμόστε το αποτέλεσμά σας στον αριθμό $100$ και απαριθμήστε και τους διαιρέτες του έναν-έναν μαζί με το ανάπτυγμα του καθενός σε γινόμενο πρώτων.