Άσκηση 3.39
Πόσα διμελή υποσύνολα του
![$ [50]={\left\{{1,2,\ldots,50}\right\}}$](img1033.png) υπάρχουν όπου ο ένας αριθμός του ζεύγους
είναι διπλάσιος από τον άλλο;
υπάρχουν όπου ο ένας αριθμός του ζεύγους
είναι διπλάσιος από τον άλλο;
Άσκηση 3.40
Σε μια 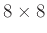 σκακιέρα πόσα διαφορετικά ορθογώνια ορίζονται; Ένα ορθογώνιο είναι ένα υποσύνολο
των κελιών (τετραγώνων) της σκακιέρας που έχει σχήμα ορθογωνίου. Δύο ορθογώνια θεωρούνται διαφορετικά
αν είναι διαφορετικά ως σύνολα κελιών.
σκακιέρα πόσα διαφορετικά ορθογώνια ορίζονται; Ένα ορθογώνιο είναι ένα υποσύνολο
των κελιών (τετραγώνων) της σκακιέρας που έχει σχήμα ορθογωνίου. Δύο ορθογώνια θεωρούνται διαφορετικά
αν είναι διαφορετικά ως σύνολα κελιών.

Σχήμα 3.5: Μια 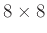 σκακιέρα κι ένα από τα ορθογώνια τα οποία θέλουμε να μετρήσουμε
σκακιέρα κι ένα από τα ορθογώνια τα οποία θέλουμε να μετρήσουμε
Δείτε στο Σχήμα 3.5.
Άσκηση 3.41
Με πόσους τρόπους μπορούμε να διατάξουμε τα ψηφία
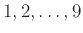 ώστε ανάμεσα στο 1 και το 2 να υπάρχουν
ακριβώς τρία ψηφία;
ώστε ανάμεσα στο 1 και το 2 να υπάρχουν
ακριβώς τρία ψηφία;
Άσκηση 3.42
Με πόσους τρόπους μπορούμε να διατάξουμε τα ψηφία
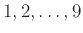 ώστε
το 1 να προηγείται του 2 και το 2 να προηγείται του 3;
ώστε
το 1 να προηγείται του 2 και το 2 να προηγείται του 3;
Άσκηση 3.43
Πόσες μεταθέσεις των αριθμών
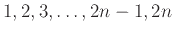 υπάρχουν που στις άρτιες
θέσεις έχουν μόνο άρτιους αριθμούς;
υπάρχουν που στις άρτιες
θέσεις έχουν μόνο άρτιους αριθμούς;
Πόσες υπάρχουν που σε τουλάχιστον μια άρτια θέση υπάρχει άρτιος αριθμός;
Άσκηση 3.44
Πόσα υποσύνολα του
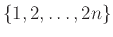 περιέχουν ακριβώς
περιέχουν ακριβώς  περιττούς αριθμούς;
περιττούς αριθμούς;
Άσκηση 3.45
Σε μια σχολή χορού μια τάξη αποτελείται από 12 άνδρες και 10 γυναίκες. Με πόσους
τρόπους μπορούν να επιλεγούν 5 άνδρες και 5 γυναίκες και να σχηματίσουν ζεύγη χορού;
Δε μας ενδιαφέρει η σειρά των ζευγών, μόνο το ποια ζεύγη σχηματίζονται.
Άσκηση 3.46
Με πόσους τρόπους μπορούμε να επιλέξουμε ένα άνδρα και μια γυναίκα, που να μην είναι
μεταξύ τους παντρεμένοι, από 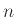 παντρεμένα ζευγάρια;
παντρεμένα ζευγάρια;
Άσκηση 3.47
Με πόσους τρόπους μπορούμε να χωρίσουμε τους αριθμούς
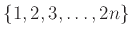 σε
σε 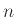 ζεύγη όταν (α) μας ενδιαφέρει η σειρά των ζευγών και (β) όταν δε μας ενδιαφέρει;
ζεύγη όταν (α) μας ενδιαφέρει η σειρά των ζευγών και (β) όταν δε μας ενδιαφέρει;
Άσκηση 3.48
Στην Άσκηση 3.19 υποθέστε ότι κάθε άνδρας παντρεύεται όσες γυναίκες θέλει
αλλά μια γυναίκα δε μπορεί να παντρευτεί ταυτόχρονα παραπάνω από έναν άνδρα.
Με πόσους τρόπους μπορείτε να παντρέψετε και τους 5 άνδρες ώστε και οι 7 γυναίκες να
παντρευτούν.
Άσκηση 3.49
Με πόσους τρόπους μπορούν να υπάρξουν 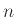 ζευγαρώματα ανάμεσα σε
ζευγαρώματα ανάμεσα σε 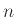 άνδρες και
άνδρες και 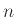 γυναίκες;
γυναίκες;
Άσκηση 3.50
Πόσους διαιρέτες έχει ο αριθμός 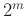 ; Ο αριθμός
; Ο αριθμός 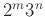 ;
;
Άσκηση 3.52
Αν 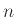 είναι περιττός αριθμός δείξτε ότι
είναι περιττός αριθμός δείξτε ότι
Υπόδειξη: Ερμηνεύστε και τις δυο μεριές της ισότητας ως το πλήθος κάποιων υποσυνόλων του ![$ [n]$](img665.png) .
Δείξτε έπειτα ότι οι δυο αυτές οικογένειες υποσυνόλων του
.
Δείξτε έπειτα ότι οι δυο αυτές οικογένειες υποσυνόλων του ![$ [n]$](img665.png) (των οποίων τα μεγέθη είναι
το αριστερό και το δεξί μέλος της ισότητας) είναι ισοπληθικές δείχνοντας μια μεταξύ τους
1-1 και επί αντιστοίχιση.
(των οποίων τα μεγέθη είναι
το αριστερό και το δεξί μέλος της ισότητας) είναι ισοπληθικές δείχνοντας μια μεταξύ τους
1-1 και επί αντιστοίχιση.
Άσκηση 3.53
Από μια συνηθισμένη τράπουλα με πόσους τρόπους μπορούμε να επιλέξουμε
6 χαρτιά (δε μας ενδιαφέρει η σειρά τους) από τα οποία τα τρία να είναι κόκκινα
(
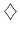 ή
ή
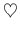 ) και τα τρία μαύρα (
) και τα τρία μαύρα (
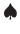 ή
ή 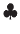 ),
και τα δύο από τα τρία κόκκινα να είναι ίδιου είδους (αριθμού).
),
και τα δύο από τα τρία κόκκινα να είναι ίδιου είδους (αριθμού).
Μια τέτοια δυνατή εξάδα είναι η:
Άσκηση 3.54
Πόσες διαφορετικές λέξεις με 10 γράμματα
υπάρχουν που να έχουν μέσα τρία γράμματα Α, τέσσερα Β
και στις υπόλοιπες θέσεις οποιαδήποτε άλλα γράμματα (από τα 24 κεφαλαία
της ελληνικής γλώσσας);
Δε μας ενδιαφέρει να είναι λέξεις με κάποιο νόημα. Λέξη μήκους 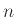 είναι μια σειρά από
είναι μια σειρά από 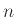 γράμματα από αυτά που επιτρέπουμε και τίποτα παραπάνω.
γράμματα από αυτά που επιτρέπουμε και τίποτα παραπάνω.
Άσκηση 3.55
Σ' ένα μικροβιολογικό εργαστήριο έχουν 100 φιάλες αίματος από διαφορετικά άτομα και γνωρίζουν ότι ακριβώς μια από αυτές
περιέχει αίμα μολυσμένο με μια ουσία Α.
Ο έλεγχος για το αν ένα δείγμα αίματος περιέχει την ουσία Α είναι πολύ ακριβός και το εργαστήριο θέλει
να ελαχιστοποιήσει τον αριθμό δειγμάτων που θα ελέγξει για να βρει τη μολυσμένη φιάλη.
Γι' αυτό το λόγο το εργαστήριο δημιουργεί 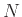 μίγματα από τα 100 μπουκάλια που θέλει να ελέγξει και στέλνει αυτά τα
μίγματα από τα 100 μπουκάλια που θέλει να ελέγξει και στέλνει αυτά τα 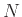 δείγματα σε ένα εργαστήριο στην Αμερική το οποίο στέλνει πίσω τις απαντήσεις.
(Τα ταχυδρομικά είναι επίσης πανάκριβα, οπότε το εργαστήριο στέλνει και τα
δείγματα σε ένα εργαστήριο στην Αμερική το οποίο στέλνει πίσω τις απαντήσεις.
(Τα ταχυδρομικά είναι επίσης πανάκριβα, οπότε το εργαστήριο στέλνει και τα 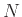 μίγματα με μια αποστολή.)
μίγματα με μια αποστολή.)
Αν κάποιο από αυτά τα μίγματα προκύψει θετικό αυτό σημαίνει ότι κάποιο από τα μπουκάλια που χρησιμοποιήθηκαν στο μίγμα αυτό είναι μολυσμένο.
Ποιος είναι ο ελάχιστος αριθμός μιγμάτων 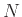 που πρέπει να στείλει το εργαστήριο για να βρει τη μολυσμένη φιάλη, και με ποια μίγματα;
που πρέπει να στείλει το εργαστήριο για να βρει τη μολυσμένη φιάλη, και με ποια μίγματα;
Άσκηση 3.57
Μια ομάδα 7 ληστών μόλις διέπραξε μια πολύ επιτυχημένη ληστεία τράπεζας.
Τα χρήματα που σήκωσαν τα έχουν βάλει σε ένα χρηματοκιβώτιο στο καταφύγιό τους.
Πρέπει όμως να διαφυλάξουν αυτά τα χρήματα πρώτ' απ' όλα από τους ίδιους τους τους εαυτούς.
Τι θα γίνει π.χ. αν σηκωθεί ένας από αυτούς τα πάρει και φύγει;
Αυτό φυσικά δεν είναι αποδεκτό στην ομάδα.
Ή αν δύο από αυτούς συμφωνήσουν μεταξύ τους και τα πάρουν και φύγουν;
Ούτε κι αυτό είναι αποδεκτό.
Όμως πρόκειται για μια ομάδα κλεφτών μεγαλωμένη από τους γονείς τους με πίστη στα δημοκρατικά ιδεώδη.
Αν λοιπόν κάποιοι 4 από αυτούς αποφασίσουν να τα πάρουν αυτό γίνεται αποδεκτό γιατί οι 4 είναι πλειοψηφία στους 7. Όχι όμως 3 ή λιγότεροι.
Πώς θα το υλοποιήσουν αυτό;
Το χρηματοκιβώτιο έχει απ' έξω ένα μεγάλο σίδερο πάνω στο οποίο μπορούν να μπουν πολλά λουκέτα και όλα αυτά πρέπει να ξεκλειδωθούν για να ανοίξει.
Για κάθε λουκέτο μπορούμε να έχουμε όσα αντικλείδια χρειαζόμαστε.
Πρέπει λοιπόν να δώσουμε σε κάθε κλέφτη ένα σετ από κλειδιά με τέτοιο τρόπο ώστε:
- Οποιοιδήποτε 4 κλέφτες να έχουν μεταξύ τους όλα τα κλειδιά που απαιτούνται για να ανοίξει το χρηματοκιβώτιο.
- Για οποιουσδήποτε 3 κλέφτες αυτό δε συμβαίνει.
Πώς μπορεί να γίνει αυτό; Πόσα λουκέτα συνολικά χρειάζονται και ποια κλειδιά θα πάρει κάθε κλέφτης;
Mihalis Kolountzakis
2015-11-28

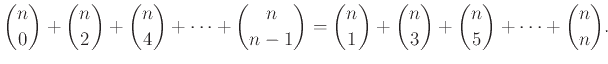
![]() .
Δείξτε έπειτα ότι οι δυο αυτές οικογένειες υποσυνόλων του
.
Δείξτε έπειτα ότι οι δυο αυτές οικογένειες υποσυνόλων του ![]() (των οποίων τα μεγέθη είναι
το αριστερό και το δεξί μέλος της ισότητας) είναι ισοπληθικές δείχνοντας μια μεταξύ τους
1-1 και επί αντιστοίχιση.
(των οποίων τα μεγέθη είναι
το αριστερό και το δεξί μέλος της ισότητας) είναι ισοπληθικές δείχνοντας μια μεταξύ τους
1-1 και επί αντιστοίχιση.![]() είναι μια σειρά από
είναι μια σειρά από ![]() γράμματα από αυτά που επιτρέπουμε και τίποτα παραπάνω.
γράμματα από αυτά που επιτρέπουμε και τίποτα παραπάνω.![]() μίγματα από τα 100 μπουκάλια που θέλει να ελέγξει και στέλνει αυτά τα
μίγματα από τα 100 μπουκάλια που θέλει να ελέγξει και στέλνει αυτά τα ![]() δείγματα σε ένα εργαστήριο στην Αμερική το οποίο στέλνει πίσω τις απαντήσεις.
(Τα ταχυδρομικά είναι επίσης πανάκριβα, οπότε το εργαστήριο στέλνει και τα
δείγματα σε ένα εργαστήριο στην Αμερική το οποίο στέλνει πίσω τις απαντήσεις.
(Τα ταχυδρομικά είναι επίσης πανάκριβα, οπότε το εργαστήριο στέλνει και τα ![]() μίγματα με μια αποστολή.)
μίγματα με μια αποστολή.)
![]() που πρέπει να στείλει το εργαστήριο για να βρει τη μολυσμένη φιάλη, και με ποια μίγματα;
που πρέπει να στείλει το εργαστήριο για να βρει τη μολυσμένη φιάλη, και με ποια μίγματα;![]() το πλήθος των τρόπων με τους οποίους μπορούν αυτές οι μπάλες να τοποθετηθούν αποκλειστικά στα άβαφα κουτιά και
το πλήθος των τρόπων με τους οποίους μπορούν αυτές οι μπάλες να τοποθετηθούν αποκλειστικά στα άβαφα κουτιά και
![]() το πλήθος των τρόπων με τους οποίους μπορούν αυτές οι μπάλες να τοποθτηθούν σε κουτιά που είναι όλα του ίδιου χρώματος (κόκκινου ή μπλε).
το πλήθος των τρόπων με τους οποίους μπορούν αυτές οι μπάλες να τοποθτηθούν σε κουτιά που είναι όλα του ίδιου χρώματος (κόκκινου ή μπλε).
![]() .
.