Ορισμός 2.6
(Πρώτος αριθμός)
Ένας ακέραιος 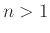 λέγεται πρώτος αριθμός αν δεν έχει μη τετριμμένους διαιρέτες, αν δηλ.
λέγεται πρώτος αριθμός αν δεν έχει μη τετριμμένους διαιρέτες, αν δηλ.
Ένας ακέραιος 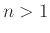 που δεν είναι πρώτος λέγεται σύνθετος αριθμός.
που δεν είναι πρώτος λέγεται σύνθετος αριθμός.
Η ακολουθία των πρώτων αριθμών έχει το αρχικό κομμάτι
Η ακολουθία των σύνθετων αριθμών έχει το αρχικό κομμάτι
Άσκηση 2.15
Ελέγξτε αν οι αριθμοί 101, 103, 107, 111, 113, 121 είναι πρώτοι.
Άσκηση 2.16
Αν ο 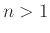 δεν είναι πρώτος τότε έχει κάποιο γνήσιο διαιρέτη (όχι το 1 ή το
δεν είναι πρώτος τότε έχει κάποιο γνήσιο διαιρέτη (όχι το 1 ή το 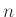 δηλ.)
δηλ.)
Υπόδειξη: Αφού δεν είναι πρώτος θα έχει κάποιο γνήσιο διαιρέτη  . Υποθέστε ότι
. Υποθέστε ότι
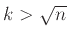 και εξετάστε
το μέγεθος του
και εξετάστε
το μέγεθος του 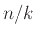 .
.
Άσκηση 2.17
 Με βάση το αποτέλεσμα της Άσκησης 2.16 για να ελέγξουμε αν ένα θετικός ακέραιος
Με βάση το αποτέλεσμα της Άσκησης 2.16 για να ελέγξουμε αν ένα θετικός ακέραιος 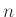 είναι πρώτος αρκεί να ελέγξουμε αν τον διαιρεί κάποιος από τους ακεραίους από το 2 έως τον ακέραιο
είναι πρώτος αρκεί να ελέγξουμε αν τον διαιρεί κάποιος από τους ακεραίους από το 2 έως τον ακέραιο
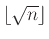 . Αυτή τη μέθοδο υλοποιεί η παρακάτω συνάρτηση python.
. Αυτή τη μέθοδο υλοποιεί η παρακάτω συνάρτηση python.
def isprime(n):
if n<=1:
return False
d = 2
while d*d <= n: # Check only up to the square root of n
if n%d == 0:
return False
d = d+1
return True
Δοκιμάστε την παραπάνω συνάρτηση σε κάποιους αριθμούς και καταλάβετε πώς δουλεύει. Μπορείτε επίσης να υπολογίσετε όλους τους πρώτους έως το 49 με την εντολή
print [x for x in range(2,50) if isprime(x)]
οπότε παίρνετε
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47]
Την ίδια δουλειά κάνει και η παρακάτω συνάρτηση αλλά είναι κάπως πιο γρήγορη γιατί αποφεύγει να κάνει τον πολλπλασιασμό d*d αντικαθιστώντας τον με μερικές προσθέσεις (που είναι συνήθως πιο γρήγορες στην υλοποίηση, ειδικά για πολύ μεγάλους αριθμούς).
def isprime(n):
if n<=1:
return False
d = 2
d2 = 4
while d2 <= n: # Check only up to the square root of n
if n%d == 0:
return False
d2 = d2 + d + d +1
d = d+1
return True
Γιατί δουλεύει;
Άσκηση 2.18
Έστω 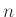 σύνθετος και υποθέστε ότι ο μικρότερος πρώτος παράγοντας
σύνθετος και υποθέστε ότι ο μικρότερος πρώτος παράγοντας 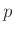 του
του 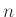 είναι
είναι 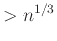 .
Δείξτε τότε ότι ο
.
Δείξτε τότε ότι ο 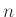 είναι γινόμενο δύο πρώτων (όχι αναγκαστικά διαφορετικών μεταξύ τους).
είναι γινόμενο δύο πρώτων (όχι αναγκαστικά διαφορετικών μεταξύ τους).
Απόδειξη.
Ας υποθέσουμε ότι υπάρχουν πεπερασμένοι μόνο πρώτοι αριθμοί, οι
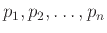
, και έστω
Με βάση την υπόθεσή μας ο

δεν είναι πρώτος, άρα έχει κάποιο μη τετριμμένο διαιρέτη
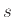
, και ας υποθέσουμε ότι ο
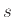
είναι ο μικρότερος μη τετριμμένος διαιρέτης του

. Τότε ο
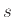
πρέπει να είναι πρώτος, αλλιώς θα είχε κι αυτός ένα μη τετριμμένο διαιρέτη, που θα ήταν και διαιρέτης του

και μικρότερος από τον
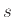
, πράγμα που αντιφάσκει με το ότι ο
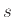
είναι ο μικρότερος μη τετριμμένος διαιρέτης του

.
Αφού ο 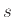 είναι πρώτος τότε είναι κάποιος από τους
είναι πρώτος τότε είναι κάποιος από τους
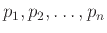 , έστω
, έστω 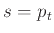 .
Όμως
.
Όμως
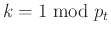 , άτοπο.
, άτοπο.

Άσκηση 2.19
Δείξτε ότι υπάρχουν οσοδήποτε μεγάλα διαστήματα
![$ [a, b] \subseteq {\mathbb{N}}$](img817.png) που δεν περιέχουν πρώτους αριθμούς.
που δεν περιέχουν πρώτους αριθμούς.
Υπόδειξη: Υπάρχει πρώτος αριθμός ανάμεσα στους αριθμούς
Άσκηση 2.20
Βρείτε τους μικρότερους 5 διαδοχικούς σύνθετους ακεραίους.
Βρείτε 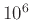 διαδοχικούς ακεραίους που να είναι σύνθετοι.
διαδοχικούς ακεραίους που να είναι σύνθετοι.
Υπόδειξη: Ο αριθμός
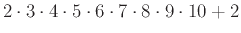 και οι επόμενοι 8 αριθμοί είναι όλοι σύνθετοι.
και οι επόμενοι 8 αριθμοί είναι όλοι σύνθετοι.
Άσκηση 2.21
Ας είναι
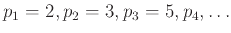 οι πρώτοι αριθμοί σε αύξουσα σειρά.
Χρησιμοποιώντας τη μέθοδο του Ευκλείδη (για το το ότι υπάρχουν άπειροι πρώτοι, Θεώρημα 2.4) δείξτε ότι
οι πρώτοι αριθμοί σε αύξουσα σειρά.
Χρησιμοποιώντας τη μέθοδο του Ευκλείδη (για το το ότι υπάρχουν άπειροι πρώτοι, Θεώρημα 2.4) δείξτε ότι
χρησιμοποιώντας επαγωγή.
Απόδειξη.
Έστω
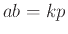
,
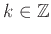
, και
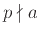
.
Αφού
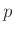
πρώτος αυτό σημαίνει ότι
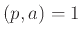
, και άρα, από το Θεώρημα
2.2,
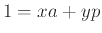
για κάποιους
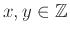
. Πολλαπλασιάζοντας επί
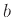
παίρνουμε
άρα
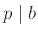
όπως έπρεπε να δείξουμε.

Παρατήρηση 2.1
Ομοίως αν
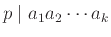 τότε το
τότε το 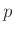 διαιρεί κάποιο από τα
διαιρεί κάποιο από τα 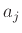 (επαγωγή ως προς
(επαγωγή ως προς  ).
).
Θεώρημα 2.6
(Θεμελιώδες Θεώρημα της Αριθμητικής)
Κάθε ακέραιος 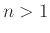 μπορεί να γραφεί με μοναδικό τρόπο ως γινόμενο πρώτων αριθμών στη μορφή
μπορεί να γραφεί με μοναδικό τρόπο ως γινόμενο πρώτων αριθμών στη μορφή
όπου
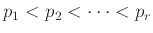 είναι διαφορετικοί πρώτοι αριθμοί και
είναι διαφορετικοί πρώτοι αριθμοί και
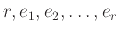 είναι
θετικοί ακέραιοι.
είναι
θετικοί ακέραιοι.
Παρατήρηση 2.2
Ένας άλλος τρόπος να εκφράσει κανείς αυτό το αποτέλεσμα είναι να πει ότι για κάθε ακέραιο είναι μοναδικά καθορισμένο το ποιοι πρώτοι αριθμοί (και πόσες φορές ο καθένας) εμφανίζονται αν τον διασπάσουμε πολλαπλασιαστικά όσο περισσότερο μπορούμε. Όποτε δηλ. υπάρχει κάποιος μη τετριμμένος διαιρέτης 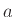 του αριθμού
του αριθμού 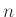 τότε γράφουμε
τότε γράφουμε
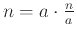 και συνεχίζουμε διασπώντας τους δύο ακεραίους
και συνεχίζουμε διασπώντας τους δύο ακεραίους 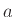 και
και
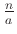 όσο αυτό είναι δυνατό (μέχρι αυτοί να γίνουν πρώτοι δηλαδή).
όσο αυτό είναι δυνατό (μέχρι αυτοί να γίνουν πρώτοι δηλαδή).
Απόδειξη.
[Απόδειξη του Θεωρήματος
2.6]
Είναι φανερό (ακολουθώντας την προηγούμενη παρατήρηση) ότι κάθε ακέραιος
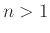
μπορεί να γραφεί ως γινόμενο πρώτων. Απλά διασπάμε συνεχώς σε γινόμενο μικρότερων αριθμών, όσο μπορούμε να το κάνουμε αυτό. Όταν δε μπορούμε πλέον έχουμε φτάσει σε γινόμενο πρώτων. Αν θέλουμε μπορούμε να δώσουμε και μια πιο τυπική (αλλά όχι περισσότερο διαφωτιστική) απόδειξη με επαγωγή ως προς
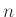
.
Συνεχίζουμε με επαγωγή για τη μοναδικότητα του αναπτύγματος σε γινόμενο πρώτων.
Για 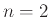 προφανώς ισχύει (η μικρότερη περίπτωση του
προφανώς ισχύει (η μικρότερη περίπτωση του 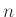 ). Ας υποθέσουμε τώρα ότι ισχύει το θεώρημα για όλους τους ακεραίους μικροτερους από
). Ας υποθέσουμε τώρα ότι ισχύει το θεώρημα για όλους τους ακεραίους μικροτερους από 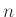 και πάμε να το αποδείξουμε για το
και πάμε να το αποδείξουμε για το 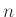 .
.
Ας υποθέσουμε ότι
όπου
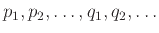
πρώτοι αριθμοί, όχι κατ' ανάγκη πρώτοι μεταξύ τους.
Τότε, με βάση το Θεώρημα
2.5 και την παρατήρηση που το ακολουθεί, έπεται ότι το
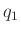
είναι ένα από τα
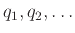
. Διαγράφοντας το
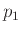
και από τις δύο μεριές προκύπτει ένας μικρότερος ακέραιος
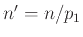
που γράφεται με δύο τρόπους ως γινόμενο πρώτων. Από επαγωγή αυτοί οι τρόποι πρέπει να είναι οι ίδιοι.

Λήμμα 2.2
Αν
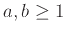 τότε
τότε 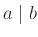 αν και μόνο αν όλοι οι πρώτοι αριθμοί που εμφανίζονται στην ανάλυση του
αν και μόνο αν όλοι οι πρώτοι αριθμοί που εμφανίζονται στην ανάλυση του 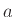 εμφανίζονται και στην ανάλυση του
εμφανίζονται και στην ανάλυση του 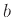 και μάλιστα σε εκθέτη μεγαλύτερο ή ίσο από τον εκθέτη τους στον
και μάλιστα σε εκθέτη μεγαλύτερο ή ίσο από τον εκθέτη τους στον 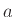 .
.
Απόδειξη.
Ας υποθέσουμε ότι ο πρώτος
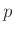
εμφανίζεται στην ανάλυση του
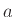
με εκθέτη
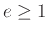
:
(ακολουθούν διαφορετικοί πρώτοι).
Αν
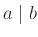
τότε
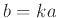
, για κάποιο
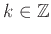
, οπότε
και άρα ο
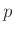
εμφανίζεται στον
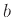
με εκθέτη τουλάχιστον
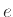
.
Η αντίστροφη κατεύθυνση είναι εξίσου φανερή αφού αν
και
με
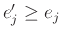
,
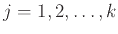
, τότε είναι προφανές ότι ο
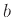
είναι πολλαπλάσιο
του
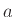
.

Άσκηση 2.24
Αν 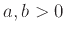 είναι μεταξύ τους πρώτοι βρείτε τον
είναι μεταξύ τους πρώτοι βρείτε τον
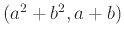 .
.
Άσκηση 2.25
Αν 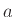 άρτιος και
άρτιος και 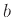 περιττός δείξτε
περιττός δείξτε
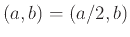 . Αν και οι δύο είναι άρτιοι δείξτε
. Αν και οι δύο είναι άρτιοι δείξτε
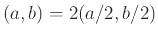 .
.
Άσκηση 2.26
Αν 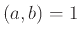 και
και 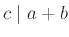 δείξτε
δείξτε
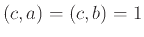 .
.
Άσκηση 2.28
Βρείτε την ανάλυση του 4849845 σε γινόμενο πρώτων.
Άσκηση 2.29
Βρείτε όλους τους πρώτους που διαιρούν το 10!. Ομοίως για τον αριθμό
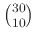 .
.
Άσκηση 2.30
Περιγράψτε όλους τους θετικούς ακεραίους που έχουν ακριβώς 3 διαιρέτες (συμπεριλαμβανομένου του 1 και τους εαυτού τους). Ομοίως για ακριβώς 4 διαιρέτες. Ομοίως για ακριβώς 5 διαιρέτες.
Άσκηση 2.31
Δείξτε ότι κάθε θετικός ακέραιος γράφεται σα γινόμενο ενός τέλειου τετραγώνου και ενός αριθμού ελεύθερου τετραγώνων (αυτοί είναι οι ακέραιοι πο
υ δε διαιρούνται από το 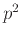 για κανένα πρώτο
για κανένα πρώτο 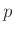 ).
).
Άσκηση 2.32
Δείξτε ότι η δύναμη με την οποία ο πρώτος 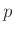 εμφανίζεται στο
εμφανίζεται στο 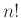 είναι το άθροισμα
είναι το άθροισμα
Παρατηρήστε ότι το άθροισμα αυτό έχει πεπερασμένους σε πλήθος μη μηδενικούς όρους αφού για αρκετά μεγάλο 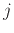 θα έχουμε
θα έχουμε 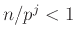 .
.
Βρείτε την ανάλυση του 20! σε γινόμενο πρώτων.
Πόσα μηδενικά υπάρχουν στο τέλος του αριθμού 1000!; Πόσα αν τον ίδιο αριθμό τον γράψουμε στο 8-αδικό σύστημα;
Άσκηση 2.33
Ποια ζεύγη ακεραίων 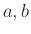 έχουν μέγιστο κοινό διαιρέτη
έχουν μέγιστο κοινό διαιρέτη 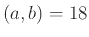 και ελάχιστο κοινό πολλαπλάσιο
και ελάχιστο κοινό πολλαπλάσιο ![$ [a,b]=240$](img875.png) ;
;
Άσκηση 2.34
Δείξτε
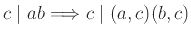 .
.
Άσκηση 2.35
Δείξτε
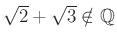 .
.
Άσκηση 2.36
Δείξτε
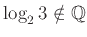 .
.
Άσκηση 2.37
Δείξτε ότι ο αριθμός
δεν είναι ποτέ ακέραιος αν 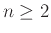 .
.
Άσκηση 2.38
Δείξτε
![$ (a,b) = (a+b, [a,b])$](img880.png) .
.
Άσκηση 2.39
Πόσα ζεύγη θετικών ακεραίων 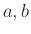 υπάρχουν με
υπάρχουν με ![$ [a,b]=n$](img881.png) .
Η απάντηση εξαρτάται από την ανάλυση του
.
Η απάντηση εξαρτάται από την ανάλυση του 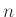 σε πρώτους παράγοντες.
σε πρώτους παράγοντες.
Άσκηση 2.41
Αν πάρουμε ένα σύνολο από 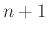 διαφορετικούς ακεραίους από 1 έως
διαφορετικούς ακεραίους από 1 έως 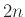 δείξτε ότι υπάρχει κάποιος στο σύνολο που διαιρεί κάποιον άλλο αριθμό του συνόλου.
δείξτε ότι υπάρχει κάποιος στο σύνολο που διαιρεί κάποιον άλλο αριθμό του συνόλου.
Mihalis Kolountzakis
2015-11-28
![]() . Υποθέστε ότι
. Υποθέστε ότι
![]() και εξετάστε
το μέγεθος του
και εξετάστε
το μέγεθος του ![]() .
. Με βάση το αποτέλεσμα της Άσκησης 2.16 για να ελέγξουμε αν ένα θετικός ακέραιος
Με βάση το αποτέλεσμα της Άσκησης 2.16 για να ελέγξουμε αν ένα θετικός ακέραιος ![]() είναι πρώτος αρκεί να ελέγξουμε αν τον διαιρεί κάποιος από τους ακεραίους από το 2 έως τον ακέραιο
είναι πρώτος αρκεί να ελέγξουμε αν τον διαιρεί κάποιος από τους ακεραίους από το 2 έως τον ακέραιο
![]() . Αυτή τη μέθοδο υλοποιεί η παρακάτω συνάρτηση python.
. Αυτή τη μέθοδο υλοποιεί η παρακάτω συνάρτηση python.
![]() είναι πρώτος τότε είναι κάποιος από τους
είναι πρώτος τότε είναι κάποιος από τους
![]() , έστω
, έστω ![]() .
Όμως
.
Όμως
![]() , άτοπο.
, άτοπο.
![]()
![]() και οι επόμενοι 8 αριθμοί είναι όλοι σύνθετοι.
και οι επόμενοι 8 αριθμοί είναι όλοι σύνθετοι.![]() προφανώς ισχύει (η μικρότερη περίπτωση του
προφανώς ισχύει (η μικρότερη περίπτωση του ![]() ). Ας υποθέσουμε τώρα ότι ισχύει το θεώρημα για όλους τους ακεραίους μικροτερους από
). Ας υποθέσουμε τώρα ότι ισχύει το θεώρημα για όλους τους ακεραίους μικροτερους από ![]() και πάμε να το αποδείξουμε για το
και πάμε να το αποδείξουμε για το ![]() .
.
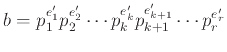
![]() εμφανίζονται ακριβώς εκείνοι οι πρώτοι αριθμοί που εμφανίζονται και στον
εμφανίζονται ακριβώς εκείνοι οι πρώτοι αριθμοί που εμφανίζονται και στον ![]() και στον
και στον ![]() και μάλιστα με εκθέτη ίσο με τον ελάχιστο εκθέτη που έχουν στους
και μάλιστα με εκθέτη ίσο με τον ελάχιστο εκθέτη που έχουν στους ![]() .
.
![]() εμφανίζονται ακριβώς εκείνοι οι πρώτοι αριθμοί που εμφανίζονται στον
εμφανίζονται ακριβώς εκείνοι οι πρώτοι αριθμοί που εμφανίζονται στον ![]() ή στον
ή στον ![]() και μάλιστα με εκθέτη ίσο με το μέγιστο εκθέτη που έχουν στους
και μάλιστα με εκθέτη ίσο με το μέγιστο εκθέτη που έχουν στους ![]() .
.
![]() είναι άρρητοι.
είναι άρρητοι.
![]() με
με ![]() και
και ![]() . Ας είναι
. Ας είναι ![]() κάποιος πρώτος
διαιρέτης του
κάποιος πρώτος
διαιρέτης του ![]() .
.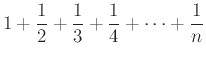
![]() ή
ή ![]() .
Υποθέστε ότι υπάρχουν πεπερασμένοι σε πλήθος πρώτοι της μορφής
.
Υποθέστε ότι υπάρχουν πεπερασμένοι σε πλήθος πρώτοι της μορφής ![]() , οι
, οι
![]() , και εξετάστε τον αριθμό
, και εξετάστε τον αριθμό
![]() .
.