Παράρτημα AΣτοιχεία από τη Θεωρία Συνόλων
Ας ξενικήσουμε με μερικούς συμβολισμούς. Για δύο σύνολα Α,Β ορίζουμε τα εξής σύνολα: ένωση (), τομή (), διαφορά () και καρτεσιανό γινόμενο ():
όπου το
σημαίνει «ανήκει», το
σημαίνει ((δεν ανήκει)), με
συμβολίζουμε το «ορίζω» και με
συμβολίζουμε το κενό σύνολο, δηλ. και το σύμβολο
σημαίνει «για κάθε».
Αν είναι ένα μη κενό σύνολο σχέση (relation) στο λέγεται ένα υποσύνολο του καρτεσιανού γινομένου .
Έστω μία σχέση στο . Η λέγεται:
-
i.
ανακλαστική (reflective), αν , ,
-
ii.
συμμετρική (symmetric), αν για κάθε , τότε ,
-
iii.
μεταβατική (transitive), αν και συνεπάγεται ότι .
Μία σχέση στο Χ λέγεται σχέση ισοδυναμίας (equivalence relation) αν είναι ανακλαστική, συμμετρική και μεταβατική. Για μία σχέση ισοδυναμίας στο σύνολο Χ, κλάση του σημείου λέγεται το σύνολο και συμβολίζεται .
Πρόταση A.1
Αν είναι μία σχέση ισοδυναμίας στο μη κενό σύνολο , τότε για δύο στοιχεία του ισχύει ή , ή . Ακόμη
| (A.1) |
Απόδειξη Έστω ότι και . Τότε . Για το αντίστροφο από τη σχέση . Άρα και αποδείχθηκε το πρώτο μέρος της πρότασης. Το δεύτερο μέρος προκύπτει αμέσως από το πρώτο και το γεγονός ότι η είναι ανακλαστική.
Από την Πρόταση (A.1) συνάγεται ότι μία σχέση ισοδυναμίας στο μη κενό σύνολο χωρίζεται με υποσύνολα, τις κλάσεις, που είναι ξένα μεταξύ τους ανά δυο και η ένωσή τους είναι όλο το σύνολο . Ένας τέτοιος χωρισμός του λέγεται διαμέριση (partition). Αλλά και αντίστροφα κάθε διαμέριση του οδηγεί σε μία σχέση ισοδυναμίας στο . Πράγματι, έστω
| (A.2) |
μία διαμέριση του . Τότε η σχέση στο που ορίζεται ως εξής
| (A.3) |
είναι εύκολο να αποδειχθεί ότι είναι σχέση ισοδυναμίας.
Κάθε στοιχείο μίας κλάσης ισοδυναμίας λέγεται αντιπρόσωπος της κλάσης αυτής. Πλήρες σύστημα αντιπροσώπων (complete representative system) της σχέσης ισοδυναμίας στο σύνολο λέγεται ένα σύνολο με στοιχεία έναν ακριβώς αντιπρόσωπο από κάθε κλάση ισοδυναμίας.
Το σύνολο των κλάσεων ισοδυναμίας της σχέσης ισοδυναμίας λέγεται σύνολο πηλίκο (quotient set) και συμβολίζεται , δηλ.
| (A.4) |
όπου είναι ένα σύστημα αντιπροσώπων της σχέσης .
Μία σχέση στο μη κενό σύνολο λέγεται διάταξη (order) στο αν είναι:
-
i.
ανακλαστική, δηλ. , ,
-
ii.
αντισυμμετρική (antisymmetric), δηλ. αν και τότε , και
-
iii.
μεταβατική, δηλ. αν και , τότε .
Ένα σύνολο στο οποίο έχει οριστεί μία σχέση διάταξης λέγεται μερικά διατεταγμένο (partially ordered) ή διατεταγμένο (ordered) και συμβολίζεται .
Σε ένα μερικά διατεταγμένο σύνολο είναι δυνατό να υπάρχουν στοιχεία που να μη συνδέονται με τη σχέση ή με τη σχέση . Αν, όμως, για κάθε ζεύγος στοιχείων του συμβαίνει ή , τότε η σχέση στο λέγεται σχέση ολικής διάταξης (total order) και το ολικά διατεταγμένο (totally ordered) ή γραμμικά διατεταγμένο (linearly ordered) σύνολο.
Αν είναι ένα μερικά διατεταγμένο σύνολο και τότε το λέγεται προηγούμενο (precedent) του ή το επόμενο (next) του αν . Το λέγεται αμέσως επόμενο του αν : . Σε αυτή την περίπτωση το λέγεται αμέσως προηγούμενο του . Συνήθως παριστάνουμε τα στοιχεία του με σημεία και αν το είναι αμέσως επόμενο του , τότε θέτουμε το υψηλότερα του και ενώνουμε το με το με μία ευθεία γραμμή. Έτσι αν δύο στοιχεία του συνδέονται με τη σχέση , τότε θα ενώνονται με μία πολυγωνική γραμμή. Το διάγραμμα που δημιουργείται με αυτόν τον τρόπο λέγεται διάγραμμα του Hasse (Hasse diagram). Π.χ. το σύνολο με τη συνήθη διάταξη του συνόλου των φυσικών αριθμών παριστάνεται με ένα διάγραμμα όπως το σχήμα 1. Το σύνολο των υποσυνόλων του συνόλου είναι μερικά διατεταγμένο με τη σχέση και παριστάνεται με το διάγραμμα του σχήματος 2.
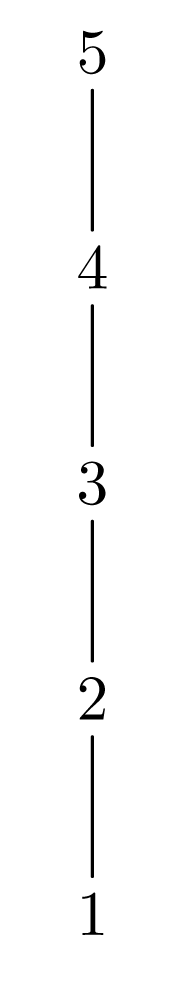 Σχήμα Π.1 Σχήμα Π.1 |
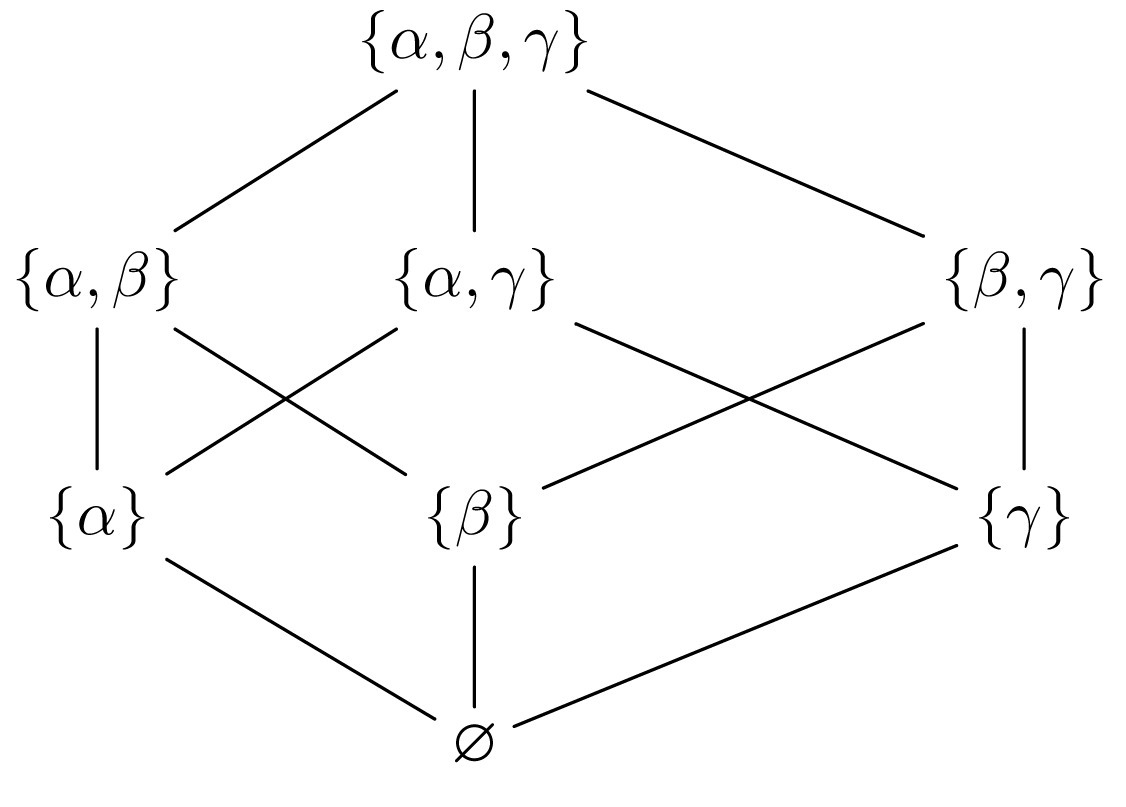 Σχήμα Π.2 Σχήμα Π.2 |
(A.5) |
Ένα στοιχείο του διατεταγμένου συνόλου λέγεται μέγιστο (maximal) αν δεν είναι προηγούμενο κανενός στοιχείου του και ελάχιστο (minimal) αν δεν είναι επόμενο κανενός στοιχείου του . Πρώτο (first ή least ή minimum) λέγεται ένα στοιχείο του που είναι προηγούμενο όλων των άλλων στοιχείων του και τελευταίο (maximum greater) αν είναι επόμενο όλων των άλλων στοιχείων του . Από τους ορισμούς αυτούς φαίνεται ότι το πρώτο στοιχείο του είναι και ελάχιστο στοιχείο και το τελευταίο είναι και μέγιστο στοιχείο. Δεν ισχύει, όμως, το αντίστροφο κάθε μίας εκ των δύο αυτών προτάσεων. Ακόμα από τους παραπάνω ορισμούς είναι φανερό ότι το πρώτο και το τελευταίο στοιχείο, αν υπάρχουν, είναι μοναδικά ενώ είναι δυνατόν να υπάρχουν περισσότερα από ένα μέγιστα ή ελάχιστα στοιχεία. Π.χ. στο διάγραμμα
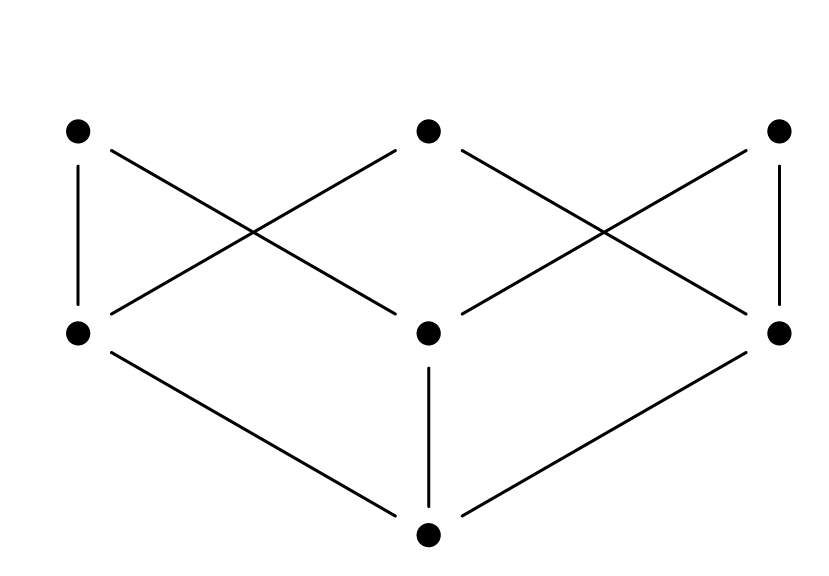 Σχήμα Π.3 Σχήμα Π.3 |
(A.6) |
υπάρχουν τρία μέγιστα στοιχεία, ένα ελάχιστο στοιχείο που είναι και πρώτο, αλλά δεν υπάρχει τελευταίο στοιχείο.
Έστω , δύο μη κενά σύνολα. Συνάρτηση (function ή map) από το στο είναι μία αντιστοιχία που σε κάθε στοιχείο του αντιστοιχεί ένα μόνο στοιχείο του . Το σύνολο λέγεται σύνολο ορισμού (domain) και το σύνολο τιμών (codomain). Ο τρόπος που απεικονίζεται το τυχόν στοιχείο του μέσω της συνάρτησης λέγεται κανόνας αντιστοιχίας. Μία συνάρτηση από το στο συμβολίζεται ως εξής: , , όπου είναι η εικόνα (image) του μέσω της . Δύο συναρτήσεις λέγονται ίσες αν έχουν ίσα σύνολα ορισμού, ίσα σύνολα τιμών και τον ίδιο κανόνα αντιστοιχίας.
Έστω , μία συνάρτηση. Το σύνολο λέγεται σύνολο εικόνων του ή εικόνα του μέσω της . Είναι φανερό ότι . Αν , τότε η λέγεται επί συνάρτηση (surjection). Αν από τη σχέση συνεπάγεται , όπου , τότε η λέγεται αμφιμονότιμη συνάρτηση (injection). Μία αμφιμονότιμη και επί συνάρτηση λέγεται επίσης ένα προς ένα και συμβολίζεται . Ιδιαίτερα η συνάρτηση , λέγεται ταυτοτική συνάρτηση (identity map) στο και συμβολίζεται .
Αν , το σύνολο λέγεται αντίστροφη εικόνα (inverse image) του και συμβολίζεται .
Αν , , είναι μη κενά σύνολα και , , , είναι δύο συναρτήσεις, τότε ορίζεται μία νέα συνάρτηση , η οποία λέγεται σύνθεση των συναρτήσεων και συμβολίζεται . Η περιγράφεται με το διάγραμμα
| (A.7) |
Έστω μία συνάρτηση. Μπορούμε τότε να ορίσουμε τη συνάρτηση , που λέγεται αντίστροφη συνάρτηση (inverse map) της και συμβολίζεται . Είναι εύκολο να διαπιστωθεί ότι η ικανοποιεί τις σχέσεις
| (A.8) |
Θεώρημα A.2
Δίνεται μία συνάρτηση . i.. Η είναι αμφιμονότιμη αν και μόνον αν υπάρχει συνάρτηση τέτοια ώστε . ii.. Η είναι επί αν και μόνον αν υπάρχει συνάρτηση τέτοια ώστε .
Απόδειξη i.. Έστω μία αμφιμονότιμη συνάρτηση. Ορίζουμε μία αντιστοιχία ως εξής: Κάθε στοιχείο της μορφής , για κάποιο στοιχείο αντιστοιχείται στο στοιχείο , που είναι μοναδικό για το , αφού η είναι αμφιμονότιμη. Κάθε στοιχείο του που δεν ανήκει στο σύνολο αντιστοιχείται στο στοιχείο για κάποιο τυχαίο αλλά από τη στιγμή της επιλογής του σταθερό στοιχείο του . Είναι εύκολο να διαπιστώσει κανείς ότι η είναι συνάρτηση και ικανοποιεί τη σχέση . Αντίστροφα, τώρα, έστω μία συνάρτηση που ικανοποιεί τη σχέση . Τότε από τη σχέση για δύο στοιχεία του , έπεται ότι , δηλ. , επομένως , που σημαίνει ότι η είναι αμφιμονότιμη.
ii.. Έστω μία επί συνάρτηση. Για κάθε εκλέγουμε ένα στοιχείο του συνόλου που από τη στιγμή της επιλογής του είναι σταθερό. Θεωρούμε, τώρα, την αντιστοιχία , . Είναι εύκολο να αποδειχθεί ότι η είναι συνάρτηση και ότι ικανοποιεί τη σχέση .
Αντίστροφα, τώρα, έστω μία συνάρτηση τέτοια ώστε . Τότε για κάθε , δηλ. για κάθε υπάρχει το στοιχείο έτσι ώστε , που σημαίνει ότι η είναι επί συνάρτηση.
Παρατηρήσεις
. Η απόδειξη του ii) στηρίχθηκε στο Αξίωμα της Επιλογής (Axiom of Choise): αν τότε μπορούμε να επιλέξουμε ένα στοιχείο από κάθε σύνολο .
Πράξη σε ένα μη κενό σύνολο λέγεται μία συνάρτηση
| (A.9) |
Συνήθως μία πράξη στο σύνολο συμβολίζεται με τα σύμβολα , , , .
Ένα σύνολο εφοδιασμένο με μία πράξη, έστω , λέγεται αλγεβρική δομή (algebraic structure) και συμβολίζεται με . Ιδιαίτερα μία αλγεβρική δομή που το σύνολο είναι ένα υποσύνολο του συνόλου των μιγαδικών αριθμών και η πράξη είναι η πρόσθεση ή ο πολλαπλασιασμός των αριθμών, τότε η λέγεται αριθμητική δομή (arithmetic structure) ή αριθμητικό σύστημα (arithmetic system). Έτσι έχουμε τις αριθμητικές δομές , , , , , , , , όπου είναι το σύνολο των ακεραίων αριθμών, είναι το σύνολο των ρητών αριθμών, είναι το σύνολο των πραγματικών αριθμών και είναι το σύνολο των μιγαδικών αριθμών.
Σε ένα σύνολο μπορούν να οριστούν περισσότερες από μία πράξεις, έστω οι και και τότε η αλγεβρική αυτή δομή συμβολίζεται ως . Τέτοια παραδείγματα μας προσφέρουν οι αριθμητικές δομές. Μας είναι γνωστές από τη μέση εκπαίδευση οι αριθμητικές δομές: , , , . Θα αναφέρουμε τις βασικές ιδιότητες των πράξεων σε ένα σύνολο που κυρίως θα χρησιμοποιούμε σε αυτό το κείμενο.
Μία πράξη στο σύνολο λέγεται προσεταιριστική (associative) αν
| (A.10) |
για όλα τα .
Μία πράξη στο σύνολο λέγεται αντιμεταθετική (commutative) αν
| (A.11) |
για όλα τα .
Η αλγεβρική δομή , όπου η είναι μία προσεταιριστική πράξη λέγεται ημιομάδα (semigroup), ενώ αν η είναι μία αντιμεταθετική πράξη η λέγεται αντιμεταθετική.
Έτσι παρατηρούμε ότι οι αριθμητικές δομές , είναι αντιμεταθετικές ημιομάδες. Επίσης η είναι αντιμεταθετική ημιομάδα ως προς τις δύο πράξεις.
Συμβολίζουμε με
| (A.12) |
το σύνολο των φυσικών αριθμών και με
| (A.13) |
το σύνολο των ακεραίων αριθμών.
Αρχή της Μαθηματικής Επαγωγής (Principle of Mathematical Induction): Έστω ένα υποσύνολο του συνόλου των φυσικών αριθμών που περιέχει το και για κάθε , το . Τότε το περιέχει όλους τους φυσικούς αριθμούς, δηλαδή .
Η αρχή της μαθηματικής επαγωγής είναιι ένα αξίωμα που ενυπάρχει στον ορισμό του συνόλου των φυσικών αριθμών σύμφωνα με τα αξιώματα του Peano. Στα μαθηματικά δεχόμαστε την αρχή της μαθηματικής επαγωγής η οποία μας παρέχει ένα εξαιρετικό αποδεικτικό εργαλείο, τη μέθοδο της μαθηματικής επαγωγής, για την απόδειξη προτάσεων που εξαρτώνται από έναν φυσικό αριθμό.
Μέθοδος της μαθηματικής επαγωγής (Mathematical Induction): Έστω μία πρόταση που εξαρτάται από τον φυσικό αριθμό .
-
(i)
Η πρόταση είναι αληθής (απόδειξη).
-
(i)
Με την υπόθεση ότι η είναι αληθής, για κάποιον φυσικό αριθμό , αποδεικνύεται ότι η είναι αληθής.
Αν τα και , ισχύουν τότε η πρόταση είναι αληθής για κάθε φυσικό αριθμό .
Η υπόθεση ότι η είναι αληθής αναφέρεται και ως υπόθεση της μαθηματικής επαγωγής.
Η μέθοδος της μαθηματικής επαγωγής προκύπτει αμέσως από την Αρχή της Μαθηματικής Επαγωγής.
Αναφέρουμε τώρα την αρχή της καλής διάταξης την οποία δεχόμαστε ως αξίωμα επίσης.
Αρχή της Καλής Διάταξης (Principle of Well ordering): Κάθε μη κενό υποσύνολο του συνόλου των φυσικών αριθμών έχει ελάχιστο στοιχείο.
Την αρχή της καλής διάταξης διαισθητικά την δεχόμαστε αμέσως, είναι όμως ιδιαίτερης αξίας η χρήση αυτής της αρχής όταν το σύνολο που μας απασχολεί ορίζεται από μία σχέση και δεν είναι εύκολος ο ορισμός του με την αναγραφή των στοιχείων του.
Είναι σημαντικό να παρατηρήσουμε εδώ ότι η Αρχή της Μαθηματικής Επαγωγής και η Αρχή της Καλής Διάταξης είναι ισοδύναμες προτάσεις, δηλαδή από την ισχύ της πρώτης αποδεικνύεται η δεύτερη και αντίστροφα.
Στην πράξη, ως αποδεικτικό εργαλείο επίσης, είναι χρήσιμη η λεγόμενη Β μορφή της Μαθηματικής Επαγωγής, που διατυπώνεται με το επόμενο θεώρημα και αποδεικνύεται με τη χρήση της αρχής της καλής διάταξης.
Θεώρημα A.3 (Δεύτερη μορφή της μαθηματικής επαγωγής)
Έστω μία πρόταση που εξαρτάται από τον φυσικό αριθμό . Υποθέτουμε ότι από την ισχύ της , για όλα τα , αποδεικνύεται η αλήθεια της πρότασης . Τότε η ισχύει για κάθε φυσικό αριθμό .
Τέλος αναφέρουμε μία ακόμη πρόταση χρήσιμη ως επαγωγική αποδεικτική μέθοδος.
Θεώρημα A.4
Έστω , , μία πρόταση που εξαρτάται από τον φυσικό αριθμό , για , όπου είναι επίσης ένας φυσικός αριθμός. Αν η πρόταση είναι αληθής και με την υπόθεση ότι η είναι αληθής, για , αποδεικνύεται ότι η είναι αληθής, τότε η είναι αληθής, για κάθε φυσικό αριθμό .