9.1 Ελλειπτική εξίσωση
Θεωρούμε το ακόλουθο πρόβλημα: Ζητείται μια συνάρτηση , τέτοια ώστε
| (9.1) |
όπου και , για κάθε . Στη συνέχεια, θα συμβολίζουμε με .
Θεωρούμε και πάλι έναν φυσικό αριθμό και διαμερίζουμε το διάστημα σε ισαπέχοντα σημεία , όπου , . Επίσης θέτουμε , και τότε τα σημεία , δημιουργούν έναν διαμερισμό του . Τότε, σε κάθε σημείο του διαμερισμού , , θα ισχύει:
| (9.2) |
για Θα κατασκευάσουμε όπως και στα προηγούμενα κεφάλαια προσεγγίσεις των τιμών , . Λόγω των ομογενών συνοριακών συνθηκών Dirichlet, θέτουμε , . Για την κατασκευή των υπολοίπων θα προσεγγίσουμε τις και στην (9.2) με την , θεωρώντας την πεπερασμένη διαφορά τη μία φορά ως προς τη μεταβλητή και την αλλή ως προς τη μεταβλητή , βλ. (2.8). Στο Σχήμα 9.1, βλέπουμε ένα παράδειγμα πλέγματος σημείων, όπου σημειώνουμε τα σημεία των άγνωστων ή γνωστών τιμών της λύσης του (9.1). Έτσι, αν υποθέσουμε ότι , λόγω της (2.11), η (9.2) γίνεται,
| (9.3) |
όπου
| (9.4) |

Θεωρούμε λοιπόν τις προσεγγίσεις της , , οι οποίες θα ικανοποιούν τις ακόλουθες εξισώσεις
| (9.5) |
Στο Σχήμα 9.2 φαίνεται ένα παράδειγμα πλέγματος όπου σημειώνουμε τις άγνωστες τιμές της προσέγγισης σύμφωνα με τη μέθοδο (9.5).
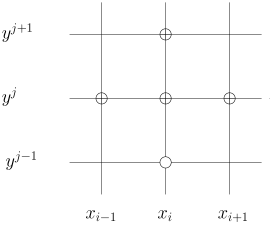
Επομένως, αν συμβολίσουμε με το διάνυσμα με συνιστώσες , , , , , μπορούμε να γράψουμε τις εξισώσεις (9.5) ως γραμμικό σύστημα
όπου , , , , .
Για να κατανοήσουμε τη δομή του πίνακα , θεωρούμε την περίπτωση και παρατηρούμε ότι για και οι εξισώσεις (9.5) γίνονται
| (9.6) |
Επομένως, οι πρώτες γραμμές του πίνακα Α είναι
\begin{equation*}%\label{A-matrix-partI} \begin{aligned} &\left( \begin{array}{cccccc} 4 & -1 & 0 & &0 &|\\ -1& 4 & -1 & 0 &0 &|\\ 0 &\ddots&\ddots&\ddots&0 &|\\ & &-1 & 4 &-1&|\\ & & & -1 & 4&|\\ \end{array}\right.\!\!\!\!\! &&\begin{array}{cccccc} 1 &0&0 & &0 &|\\ 0 &1&0 & &0 &|\\ 0 & &\ddots& &0 &|\\ 0 & & 0 &1&0 &|\\ 0 & & &0&1 &|\\ \end{array}\!\!\!\!\! &&\left.\begin{array}{ccc} 0& &0\\ 0&\dots &0\\ 0&\dots &0\\ 0& &0\\ 0& &0\\ \end{array} \right)\\ &\hspace{1cm}\underbrace{\hspace{3cm}} &&\hspace{0.1cm}\underbrace{\hspace{3cm}} &&\hspace{0.1cm}\underbrace{\hspace{1.5cm}}\\ &\hspace{2cm}\text{$N$ στήλες} &&\hspace{1cm}\text{$N$ στήλες} &&\text{$N^2-2N$ στήλες} \end{aligned}\end{equation*}Συμβολίζουμε με τον πίνακα
\[B= \left( \begin{array}{rrrrr} 4 & -1 & 0 & &0 \\ -1& 4 & -1 & 0 &0 \\ 0 &\ddots&\ddots&\ddots&0 \\ & &-1 & 4 &-1\\ & & & -1 & 4\\ \end{array}\right) \]και με \(\mathcal{I}\) τον μοναδιαίο πίνακα, και λόγω των εξισώσεων (9.5) για και , οι έως γραμμές του πίνακα Α είναι
\begin{equation*} \begin{aligned} \left( \begin{array}{cccccccccc} & & &|& & & |& & &|\\ & \mathcal{I}& & |& B& &|& \mathcal{I} & &|\\ & & & |& & &|& & &|\\ % \multicolumn{9}{c}{}& &\multicolumn{3}{c}{\myunderbrace{}{\text{$N^2-3N$ στήλες}}} \end{array} \right. &\left. \begin{array}{ccc} 0&0&0\\ 0&0&0\\ 0&0&0\\ % \multicolumn{9}{c}{}& &\multicolumn{3}{c}{\myunderbrace{}{\text{$N^2-3N$ στήλες}}} \end{array} \right)\\ &\hspace{.1cm}\underbrace{\hspace{1.5cm}}\\ &\hspace{.1cm}{\text{$N^2-3N$ στήλες}} \end{aligned}\end{equation*}Οπότε, ο πίνακας έχει τη μορφή
\begin{equation}\label{9.9} A= \left( \begin{array}{rrrrr} B & \mathcal{I} & 0 & &0 \\ \mathcal{I}& B & -1 & 0 &0 \\ 0 &\ddots&\ddots&\ddots&0 \\ & &\mathcal{I} & B &\mathcal{I}\\ & & & \mathcal{I} & B\\ \end{array}\right)\tag{9.9} \end{equation}ο οποίος δεν έχει αυστηρά κυριαρχική διαγώνιο, είναι όμως αντιστρέψιμος. Αν υποθέσουμε τώρα ότι και ότι , τότε το γραμμικό σύστημα που προκύπτει από τις (9.5) είναι
| (9.10) |
και όπως παραπάνω και ένας διαγώνιος πίνακας με στοιχεία στη διαγώνιο , , , , , , , , , . Είναι απλό να δούμε ότι ο πίνακας έχει όμοια μορφή με αυτή της (\ref{9.9}), διότι αλλάζουν μόνο τα διαγώνια στοιχεία και έχει αυστηρά κυριαρχική διαγώνιο, αν .
Επομένως, μπορούμε να επιλέξουμε μια άμεση μέθοδο, όπως είναι αυτή της απαλοιφής Gauss, για να λύσουμε το γραμμικό σύστημα (9.10), βλ. π.χ. (Ακρίβης και Δουγαλής, (2015)). Ο πίνακας του γραμμικού συστήματος (9.10) είναι μεγάλος σε διάσταση και είναι και αραιός, έχει δηλαδή πολλά μηδενικά στοιχεία. Λόγω της (9.6), μπορούμε να δούμε ότι κάθε γραμμή του πίνακα έχει το πολύ 5 μη-μηδενικά στοιχεία. Στην πράξη, δεν επιλέγουμε τη μέθοδο απαλοιφής Gauss για την αριθμητική επίλυση μεγάλων αραιών γραμμικών συστημάτων, αλλά άλλες μεθόδους όπως είναι οι επαναληπτικές μέθοδοι, Jacobi, Gauss-Seidel, SOR και άλλες, βλ. π.χ. (Ακρίβης και Δουγαλής, (2015), Strikwerda, (2004)).