Θεώρημα 8.1: ΄Εστω G μια ομάδα Lie με άλγεβρα Lie 𝔤 και έστω X,Y ∈ 𝔤. Τότε υπάρχει καμπύλη
Z : I ⊆ ℝ → 𝔤, t Z(t) τέτοια ώστε
Z(t) τέτοια ώστε
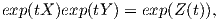 | (8.1) |
όπου το Z(t) αναπτύσεται σε σειρά Taylor Z(t) = ∑ n=0∞tnZn(X,Y ), με
![Z1(X, Y ) = X + Y
Z (X, Y ) = 1[X, Y]
2 2
1-- -1-
Z3(X, Y ) = 12[[X, Y ],Y ]- 12 [[X, Y],X ].](02_chapter_082x.png)
Σύνοψη
Στο κεφάλαιο αυτό παρουσιάζουμε κάποια χρήσιμα εργαλεία τόσο για τη μελέτη της δομής μιας ομάδας Lie όσο
και για τη μελέτη της γεωμετρίας τους. Αυτά είναι κάποια στοιχεία θεωρίας αναπαραστάσεων, με έμφαση στη
συζυγή αναπαράσταση μιας ομάδας Lie, στη μορφή Killing και στους μεγιστικούς δακτυλίους. Θα
παρουσιάσουμε (χωρίς απόδειξη) το θεώρημα ταξινόμησης των συμπαγών και συνεκτικών ομάδων Lie και
έτσι να αναδειχτεί το γεγονός ότι η μελέτη των ομάδων πινάκων μας δίνει μία πολύ καλή εικόνα της
γενικής θεωρίας. Οι αναφορές σε αύξοντα βαθμό δυσκολίας είναι τα βιβλία [3], [4], [8], [1], [12] και
[11].
Προαπαιτούμενη γνώση
Διαφορικός Λογισμός μιας και πολλών μεταβλητών, Εισαγωγή στις Πολλαπλότητες, Γραμμική Άλγεβρα, Θεωρία
Ομάδων.
Είναι μια συνήθης πρακτική στα μαθηματικά να γίνεται προσπάθεια ταξινόμησης των μαθηματικών αντικειμένων τα οποία έχουν κάποιες κοινές ιδιότητες (π.χ. ομάδες, τοπολογικοί χώροι, πολλαπλότητες, κ.λπ.). Κάποια προβλήματα ταξινόμησης είναι αρκετά απλά (π.χ. διανυσματικοί χώροι) και άλλα εξαιρετικά δύσκολα (π.χ. πεπερασμένες απλές ομάδες). Η πλήρης ταξινόμηση των ομάδων Lie δεν είναι και αυτή εύκολη υπόθεση. Ακόμα και με κάποιες γενικές υποθέσεις (π.χ. συμπάγεια) το πρόβλημα εινα δύσκολο. Παρ΄ όλα αυτά, κάποια εργαλεία που χρησιμοποιούνται έχουν μια γενικότερη αξία και χρησιμότητα (π.χ. μεγιστικοί δακτύλιοι), γι΄ αυτό στο κεφάλαιο αυτό θα ασχοληθούμε κάπως με τη δομή μιας ομάδας Lie. Στο τέλος θα παρουσιάσουμε την ταξινόμηση των απλών, συμπαγών, συνεκτικών και απλά συνεκτικών ομάδων Lie.
Η παρακολούθηση του κεφαλαίου αυτού απαιτεί μια ελαφρώς αυξημένη μαθηματική ωριμότητα, αν και η μόνη προαπαιτούμενη γνώση είναι γραμμική άλγεβρα δύο εξαμήνων (π.χ. [9]) και βασική άλγεβρα (π.χ. [7]). Ταυτόχρονα όμως αποτελεί ένα ενδιαφέρον πεδίο ανάδειξης των τεχνικών και των εφαρμογών της. ΄Οπως και να έχει, αρκετές αποδείξεις μπορούν να παραληφθούν από τον αναγνώστη και να επικεντρωθεί στα αποτελέσματα και τις εφαρμογές αυτών.
Η ακριβής σχέση μεταξύ των expX expY και exp(X + Y ) δίνεται από τον τύπο των Campbell-Baker-Hausdorff1, ο οποίος ουσιαστικά δίνει τη λύση της εξίσωσης Z = log(expX expY ). Ο τύπος είναι αρκετά δύσκολος στην απόδειξη, αλλά έχει σημαντικές εφαρμογές σχετικά με την σχέση ανάμεσα στη δομή της ομάδας Lie και της άλγεβρας Lie. Για παραδειγμα, το Θεώρημα 7.1 (της κλειστής υποομάδας) αποδεικνύεται χρησιμοποιώντας τον τύπο των Campbell-Baker-Hausdorff.
Θεώρημα 8.1: ΄Εστω G μια ομάδα Lie με άλγεβρα Lie 𝔤 και έστω X,Y ∈ 𝔤. Τότε υπάρχει καμπύλη
Z : I ⊆ ℝ → 𝔤, t Z(t) τέτοια ώστε
Z(t) τέτοια ώστε
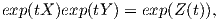 | (8.1) |
όπου το Z(t) αναπτύσεται σε σειρά Taylor Z(t) = ∑ n=0∞tnZn(X,Y ), με
![Z1(X, Y ) = X + Y
Z (X, Y ) = 1[X, Y]
2 2
1-- -1-
Z3(X, Y ) = 12[[X, Y ],Y ]- 12 [[X, Y],X ].](02_chapter_082x.png)
Στις περισσότερες εφαρμογές χρησιμοποιούμε μόνο τους όρους Z1(X,Y ) και Z2(X,Y ), οπότε η (8.1) γράφεται αντίστοιχα ως
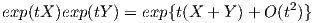
![t2- 3
exp(tX )exp(tY ) = exp{t(X + Y )+ 2 [X, Y] + O(t )},](02_chapter_084x.png)
όπου O(t2) και O(t3) είναι λείες συναρτήσεις του t με τιμές στην 𝔤, τέτοιες ώστε η 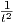 O(t2) να είναι φραγμένη στο
t = 0 και για τη δεύτερη, υπάρχει κάποιο ϵ > 0 τέτοιο ώστε η
O(t2) να είναι φραγμένη στο
t = 0 και για τη δεύτερη, υπάρχει κάποιο ϵ > 0 τέτοιο ώστε η 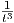 O(t3) να είναι φραγμένη για κάθε
O(t3) να είναι φραγμένη για κάθε
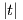 < ϵ.
< ϵ.
Θα αποδείξουμε δύο εφαρμογές του τύπου αυτού σχετικά με αβελιανές ομάδες Lie. Η πρώτη αναφέρει ότι η εκθετική απεικόνιση μιας συνεκτικής και αβελιανής ομάδας Lie είναι επί και η δεύτερη ότι κάθε συνεκτική και αβελιανή ομάδα Lie είναι της μορφής Tk × ℝn-k, όπου T είναι ένας δακτύλιος.
Το παρακάτω αποτέλεσμα αφορά οποιαδήποτε τοπολογική ομάδα.
Λήμμα 8.1: ΄Εστω G μια συνεκτική ομάδα Lie και U ⊂ G μια περιοχή του ουδέτερου στοιχείου e ∈ G. Τότε η G παράγεται από την περιοχή U.
Απόδειξη. ΄Εστω W ένα υποσύνολο της G και συμβολίζουμε με W-1 = {g-1 ∈ G | g ∈ W} και
Wk = {g1g2 gk : gi ∈ W}, όπου k ένας θετικός ακέραιος. ΄Εστω U η ανοικτή περιοχή του ουδέτερου
στοιχείου e και θέτουμε V = U ∩ U-1 ⊆ U. Τότε το σύνολο V είναι ανοικτό ως τομή των δύο ανοικτών
συνόλων U και U-1 και ισχύει V = V -1. ΄Εστω H η τοπολογική ομάδα η οποία παράγεται από το σύνολο
V , δηλαδή
gk : gi ∈ W}, όπου k ένας θετικός ακέραιος. ΄Εστω U η ανοικτή περιοχή του ουδέτερου
στοιχείου e και θέτουμε V = U ∩ U-1 ⊆ U. Τότε το σύνολο V είναι ανοικτό ως τομή των δύο ανοικτών
συνόλων U και U-1 και ισχύει V = V -1. ΄Εστω H η τοπολογική ομάδα η οποία παράγεται από το σύνολο
V , δηλαδή
Τότε η H είναι υποομάδα της G και επιπλέον η H παράγεται από την ανοικτή περιοχή U. Πράγματι, είναι
Η τοπολογική ομάδα H είναι από τον ορισμό της ανοικτή. Για κάθε g ∈ G το σύνολο gH = {gh : h ∈ H} περιέχει το στοιχείο g, άρα είναι ανοικτό, επειδή η αριστερή μεταφορά Lg-1 : G → G είναι ομοιομορφισμός (λόγω του ότι είναι αμφιδιαφόριση). Συνεπώς, το σύνολο G γράφεται ως ένωση ξένων μεταξύ τους αριστερών συμπλόκων gH ως
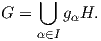
Επειδή όμως η τοπολογική ομάδα G είναι συνεκτική και τα gαH είναι ανοικτά, αυτό μπορεί να γίνει μόνο στην περίπτωση που έχουμε μόνο ένα σύμπλοκο, δηλαδή eH = G. ▄
Πρόταση 8.1: ΄Εστω G μια ομάδα Lie με άλγεβρα Lie 𝔤. Τότε η G είναι αβελιανή εάν και μόνο εάν η 𝔤 είναι αβελιανή.
Απόδειξη. ϒποθέτουμε ότι η άλγεβρα Lie 𝔤 είναι αβελιανή. Τότε για X,Y ∈ 𝔤 και για κάποιο αρκετά μικρό t, ο τύπος των Campbell-Baker-Hausdorff δίνει
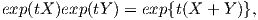
συνεπώς θα έχουμε
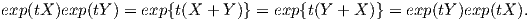 | (8.2) |
Επειδή η εκθετική απεικόνιση είναι μια αμφιδιαφόριση μεταξύ των περιοχών Ũ ∋ 0 ∈ 𝔤 και U ∋ e ∈ G, έπεται ότι η ομάδα G είναι αβελιανή στην περιοχή U του ουδέτερου στοιχείου e. Λόγω της συνεκτικότητας της G από το Λήμμα 8.1 προκύπτει ότι αυτή θα παράγεται από την περιοχή U, συνεπώς θα είναι αβελιανή.
Αντίστροφα, έστω ότι η ομάδα G είναι αβελιανή. Τότε θα είναι:
![t2
exptXexptY = exp{t(X + Y )+ --[X,Y ]+ O (t3)}
2](02_chapter_0814x.png)
και
![t2 3
exptY exptX = exp{t(Y + X )+ 2 [Y,X ]+ O (t )}.](02_chapter_0815x.png)
Λόγω της (8.2) τα πρώτα μέλη στις παραπάνω εξισώσεις θα είναι, ίσα οπότε εξισώνοντας τα δεύτερα μέλη θα πάρουμε [X,Y ] = [Y,X] και επειδή το γινόμενο Lie είναι αντισυμμετρικό θα έχουμε ότι [X,Y ] = 0, επομένως η 𝔤 θα είναι αβελιανή. ▄
Θεώρημα 8.2: Αν μια ομάδα Lie G είναι αβελιανή τότε η εκθετική απεικόνιση exp : 𝔤 → G είναι ομομορφισμός ομάδων Lie.
Απόδειξη. Επειδή η εκθετική απεικόνιση είναι λεία, αρκεί να δείξουμε ότι exp(X)exp(Y ) = exp(X + Y ). Στον τύπο των Campbell-Baker-Hausdorff θέτουμε t = 1∕n, όπου n αρκετά μεγάλος αριθμός, οπότε
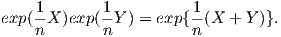
Συνεπώς
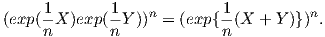
Επειδή η ομάδα G είναι αβελιανή, θα ισχύει η σχέση (8.2) από την οποία θα πάρουμε:
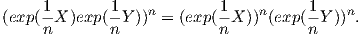
Επομένως,
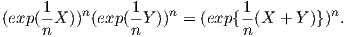
Η παραπάνω ισότητα μπορεί να γραφτεί ως
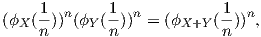
όπου ϕX,ϕY και ϕX+Y είναι οι αντίστοιχες μονοπαραμετρικές υποομάδες των X,Y και X + Y . Χρησιμοποιώντας το γεγονός ότι οι μονοπαραμετρικές υποομάδες είναι ομομορφισμοί, θα ισχύει η εξής ιδιότητα:
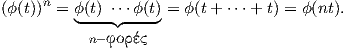
Η προηγούμενη σχέση θα μας δώσει ότι ϕX(1)ϕY (1) = ϕX+Y (1), δηλαδή
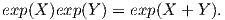
▄
Στη συνέχεια θα δούμε πότε η εκθετική απεικόνιση είναι επί.
Πρόταση 8.2: Αν μια ομάδα Lie G είναι αβελιανή και συνεκτική, τότε η εκθετική απεικόνιση exp : 𝔤 → G είναι επί.
Απόδειξη. Για να είναι η ακεικόνιση exp επί θα πρέπει για κάθε g ∈ G να υπάρχει κάποιο X ∈ 𝔤
τέτοιο ώστε exp(X) = g. ΄Εστω g ∈ G και V μια ανοιχτή περιοχή του 0 ∈ 𝔤 τέτοια ώστε η exp
να είναι αμφιδιαφόριση. Τότε η U = exp(V ) είναι μια ανοιχτή περιοχή του e ∈ G η οποία λόγω της
συνεκτικότητας θα παράγει την G (Λήμμα 8.1). ΄Αρα μπορούμε να γράψουμε g = exp(X1) exp(Xn)
(όπου n = dimG). Επειδή όμως η ομάδα G είναι αβελιανή, λόγω του Θεωρήματος 8.2 η εκθετική απεικόνιση
θα είναι ομομορφισμός, δηλαδή για κάθε X,Y ∈ 𝔤 θα ισχύει exp(X)exp(Y ) = exp(X + Y ). Συνεπώς,
προκύπτει ότι g = exp(X1)
exp(Xn)
(όπου n = dimG). Επειδή όμως η ομάδα G είναι αβελιανή, λόγω του Θεωρήματος 8.2 η εκθετική απεικόνιση
θα είναι ομομορφισμός, δηλαδή για κάθε X,Y ∈ 𝔤 θα ισχύει exp(X)exp(Y ) = exp(X + Y ). Συνεπώς,
προκύπτει ότι g = exp(X1) exp(Xn) = exp(
exp(Xn) = exp(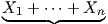 X∈𝔤). ▄
X∈𝔤). ▄
Παρατήρηση. Η προηγούμενη πρόταση δεν ισχύει, αν κάποια από τις προ᾽υποθέσεις δεν ικανοποιείται. Πράγματι, για
την μη συνεκτική ομάδα Lie G = GLnℝ, η εκθετική απεικόνιση exp : Mnℝ → GLnℝ δεν είναι επί, διότι π.χ. για
τον πίνακα g = 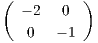 ∈ GLnℝ, δεν υπάρχει A ∈ Mnℝ τέτοιος ώστε ≡ eA = g (βλ. και ΄Ασκηση 18 του
Κεφαλαίου 7).
∈ GLnℝ, δεν υπάρχει A ∈ Mnℝ τέτοιος ώστε ≡ eA = g (βλ. και ΄Ασκηση 18 του
Κεφαλαίου 7).
Ερχόμαστε τώρα στη δεύτερη εφαρμογή του τύπου Campbell-Baker-Hausdorff.
Ορισμός 8.2: ΄Εστω G μια τοπολογική ομάδα και N μια υποομάδα αυτής. Η N ονομάζεται διακριτή (discete) υποομάδα της G, εάν υπάρχει μια περιοχή U του e τέτοια ώστε N ∩ U = {e}.
Παράδειγμα. Το σύνολο ℤ των ακεραίων είναι μια διακριτή υποομάδα της προσθετικής ομάδας των πραγματικών αριθμών ℝ, αλλά το σύνολο ℚ των ρητών αριθμών δεν είναι διακριτή υποομάδα του ℝ.
Πρόταση 8.3: ΄Εστω G μια ομάδα Lie και 𝔤 η άλγεβρα Lie αυτής. Αν η G είναι αβελιανή και συνεκτική τότε το σύνολο Ker(exp) = {X ∈ 𝔤 : exp(X) = e} είναι μια διακριτή υποομάδα της 𝔤.
Απόδειξη. Επειδή η ομάδα G είναι αβελιανή, η εκθετική απεικόνιση θα είναι ομομορφισμός, δηλαδή exp(0) = e. Επιπλέον, γνωρίζουμε ότι η εκθετική είναι μια τοπική αμφιδιαφόριση από μια περιοχή V ∋ 0 ∈ 𝔤 σε μια περιοχή U ∋ e ∈ G. Δηλαδή θα έχουμε Ker(exp) ∩ V = {0}. ▄
Πριν παρουσιάσουμε το θεώρημα που ταξινομεί όλες τις αβελιανές και συνεκτικές ομάδες Lie χρειαζόμαστε το ακόλουθο αποτέλεσμα σχετικά με τις διακριτές υποομάδες ενός διανυσματικού χώρου (συνδυάστε τα παρακάτω και με την ΄Ασκηση 7).
Λήμμα 8.2: `Εστω V ένας πραγματικός διανυσματικός χώρος πεπερασμένης διάστασης και έστω K μια
διακριτή υποομάδα του V . Τότε υπάρχει ένα γραμμικώς ανεξάρτητο υποσύνολο {υ1,…,υk} του V , ώστε
K = span{υ1,…,υk}. Επιπλέον, εάν dimV = n τότε V∕K (ℝk∕ℤk) × ℝn-k.
(ℝk∕ℤk) × ℝn-k.
Θεώρημα 8.3: Κάθε συνεκτική και αβελιανή ομάδα Lie G είναι της μορφής Tk × ℝn-k, όπου Tk είναι ο k-διάστατος δακτύλιος2 και n η διάσταση της ομάδας G. Αν επιπλέον η G είναι συμπαγής τότε αυτή είναι κάποιος δακτύλιος.
Απόδειξη. Επειδή η ομάδα G είναι συνεκτική και αβελιανή, η εκθετική απεικόνιση exp : 𝔤 → G θα είναι επί,
άρα από το πρώτο θεώρημα ισομορφισμού3
θα έχουμε ότι G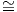 𝔤∕Ker(exp). Από την Πρόταση 8.3 ο πυρήνας Ker(exp) της εκθετικής απεικόνισης
είναι διακριτή υποομάδα της 𝔤, οπότε από το προηγούμενο λήμμα είναι ότι Ker(exp) = spanℤ{X1,…,Xk}
για κάποια Xi ∈ 𝔤. Τότε, λαμβάνοντας υπόψη τον ισομορφισμό 𝔤
𝔤∕Ker(exp). Από την Πρόταση 8.3 ο πυρήνας Ker(exp) της εκθετικής απεικόνισης
είναι διακριτή υποομάδα της 𝔤, οπότε από το προηγούμενο λήμμα είναι ότι Ker(exp) = spanℤ{X1,…,Xk}
για κάποια Xi ∈ 𝔤. Τότε, λαμβάνοντας υπόψη τον ισομορφισμό 𝔤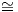 ℝn, προκύπτει ότι
ℝn, προκύπτει ότι
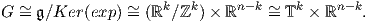
▄
Γενικά μια αναπαράσταση μιας ομάδας G είναι ένας λείος ομομορφισμός από την G στους αυτομορφισμούς ενός διανυσματικού χώρου V ή σε ένα σύνολο πινάκων. Οι αναπαραστάσεις αποτελούν ένα χρήσιμο εργαλείο στη θεωρία ομάδων, επειδή ανάγουν το δύσκολο πρόβλημα της μελέτης τους, στη μελέτη γραμμικών απεικονίσεων σε κατάλληλους διανυσματικούς χώρους. Η θεωρία αναπαραστάσεων αναπτύχθηκε κυρίως από τους Ferdinand Georg Frobenius, Felix Bernstein και Issai Schur. Αποτελεί ένα ιδιαίτερα σημαντικό εργαλείο στα μαθηματικά και στη φυσική, αλλά και ξεχωριστό ερευνητικό κλάδο.
Στην παρούσα παράγραφο θα παρουσιάσουμε βασικές έννοιες από τη θεωρία αναπαραστάσεων ομάδων Lie, οι οποίες είναι χρήσιμες στη μελέτη τόσο της δομής των ομάδων Lie, όσο και της γεωμετρίας των ομογενών χώρων που θα δούμε στα δύο επόμενα κεφάλαια.
Θυμίζουμε ότι για έναν διανυσματικό χώρο V , συμβολίζουμε με Aut(V ) το σύνολο των αντιστρέψιμων γραμμικών μετασχηματισμών του V .
Ορισμός 8.3: ΄Εστω G μια ομάδα Lie. Μια αναπαράσταση της G είναι ένας ομομορφισμός ομάδων Lie ϕ : G → Aut(V ). Αν ο διανυσματικός χώρος V είναι πεπερασμένης διάστασης, τότε η αναπαράσταση ονομάζεται πεπερασμένης διάστασης και η διάστασή της ορίζεται ως η διάσταση του διανυσματικού χώρου V .
Πολλές φορές μια αναπαράσταση της G στον V συμβολίζεται με (G,V ) ή απλά με V . ΄Οταν η απεικόνιση ϕ είναι 1 - 1, τότε η αναπαράσταση καλείται pist� (faithful). Αν η ϕ απεικονίζει κάθε στοιχείο g ∈ G στην ταυτοτική απεικόνιση του χώρου Aut(V ), δηλαδή ϕ(g) = IdV , τότε λέγεται tetrimm�nh (trivial) και συμβολίζεται με 1. Σύμφωνα με τον ορισμό κάθε αναπαράσταση ορίζει μια δράση της ομάδας G στον διανυσματικό χώρο V ως εξής:
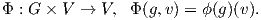
Για τον λόγο αυτό μια αναπαράσταση λέγεται και G-χώρος (G-space). Αν ο V είναι πραγματικός (αντ. μιγαδικός, ή υπερμιγαδικός) διανυσματικός χώρος και η απεικόνιση Φg = ϕ(g) : V → V είναι γραμμική για κάθε g ∈ G, τότε η αναπαράσταση καλείται πραγματική (αντ. μιγαδική ή υπερμιγαδική). Σε επόμενο κεφάλαιο θα δούμε αναλυτικότερα την έννοια της δράσης.
Με ανάλογο τρόπο, αν 𝔤 είναι μια άλγεβρα Lie τότε μια αναπαράσταση της 𝔤 είναι ένας ομομορφισμός αλγεβρών Lie ϕ : 𝔤 → End(V ).
Ορισμός 8.4: ΄Εστω (G,V ) μια αναπαράσταση. ΄Ενας υπόχωρος U του V καλείται αναλλοίωτος ή G-αναλλοίωτος (G-invariant), αν για κάθε g ∈ G ισχύει
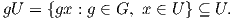
΄Ενα εσωτερικό γινόμενο 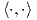 στον χώρο V θα λέγεται G-αναλλοίωτο, εάν
στον χώρο V θα λέγεται G-αναλλοίωτο, εάν
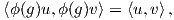
για κάθε g ∈ G και u,υ ∈ V .
Κάθε αναπαράσταση (G,V ) έχει τουλάχιστον δύο αναλλοίωτους υπόχωρους τον τετριμμένο {0} και τον ευατό της V . Στην περίπτωση που ο χώρος V είναι εφοδιασμένος με ένα G-αναλλοίωτο εσωτερικό γινόμενο τότε η αναπαράσταση καλείται orjog�nia (orthogonal), αν V = ℝ και monadia�a (unitary), αν V = ℂ.
Ορισμός 8.5: Μια αναπαράσταση ϕ : G → Aut(V ) καλείται μη αναγώγιμη (irreducible), αν οι μόνοι αναλλοίωτοι υπόχωροι είναι οι {0} και V .
Δύο αναπαραστάσεις ϕ : G → Aut(V ) και ψ : G → Aut(W) ονομάζονται ισοδύναμες (equivalent) (συμβολικά
γράφουμε ϕ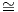 ψ), εάν υπάρχει ισομορφισμός διανυσματικών χώρων A : V → W τέτοιος ώστε για κάθε g ∈ G και
υ ∈ V να ισχύει
ψ), εάν υπάρχει ισομορφισμός διανυσματικών χώρων A : V → W τέτοιος ώστε για κάθε g ∈ G και
υ ∈ V να ισχύει
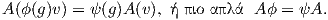

Κάθε απεικόνιση A που ικανοποιεί την παραπάνω ιδιότητα ονομάζεται G-ισοαναλλοίωτη (G-equivariant).
΄Εστω οι αναπαραστάσεις ϕi : G → Aut(V i),i = 1,2 της ομάδας G. Τότε ορίζονται δύο νέες αναπαραστάσεις της G ως εξής:
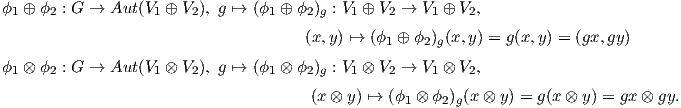
Ορισμός 8.6: Μια αναπαράσταση ϕ : G → Aut(V ) ονομάζεται aναγώγιμη (reducible), αν εκφράζεται ως ευθύ άθροισμα μη αναγώγιμων αναπαραστάσεων ϕ1,…,ϕk, δηλαδή ισχύει
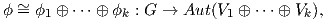
όπου V i είναι G-αναλλοίωτοι υπόχωροι του διανυσματικού χώρου V και ϕi : G → Aut(V i).
Αποδεικνύεται ότι κάθε αναπαράσταση (G,V ) μιας πεπερασμένης ομάδας G έχει ένα G-αναλλοίωτο εσωτερικό γινόμενο4. Το ίδιο αποτέλεσμα γενικεύεται και στις συμπαγείς τοπολογικές ομάδες. Πριν περάσουμε στην απόδειξη θα χρειαστούμε το ακόλουθο αποτέλεσμα (από τις τοπολογικές ομάδες), δηλαδή ότι σε κάθε τοπικά συμπαγή τοπολογική ομάδα G ορίζεται μοναδική απεικόνιση από το σύνολο των πραγματικών συνεχών συναρτήσεων στους πραγματικούς αριθμούς
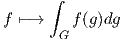
η οποία ικανοποιεί τις παρακάτω ιδιότητες:
Ο αριθμός ∫ Gf(g)dg καλείται ολοκλήρωμα του Haar5.
Θεώρημα 8.4: ΄Εστω ϕ : G → Aut(V ) μια αναπαράσταση μιας συμπαγούς ομάδας Lie. Τότε υπάρχει ένα
G-αναλλοίωτο εσωτερικό γινόμενο 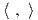 στον V , δηλαδή
στον V , δηλαδή
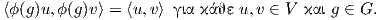
Απόδειξη. Θεωρούμε ένα τυχαίο εσωτερικό γινόμενο 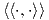 στον διανυσματικό χώρο V και ορίζουμε
στον διανυσματικό χώρο V και ορίζουμε
 είναι εσωτερικό γινόμενο, αποδεικνύεται εύκολα
ότι η σχέση (8.3) ορίζει ένα εσωτερικό γινόμενο στον χώρο V . Θα αποδείξουμε ότι αυτό είναι G-αναλλοίωτο.
Πράγματι, έστω h ∈ G. Τότε
είναι εσωτερικό γινόμενο, αποδεικνύεται εύκολα
ότι η σχέση (8.3) ορίζει ένα εσωτερικό γινόμενο στον χώρο V . Θα αποδείξουμε ότι αυτό είναι G-αναλλοίωτο.
Πράγματι, έστω h ∈ G. Τότε 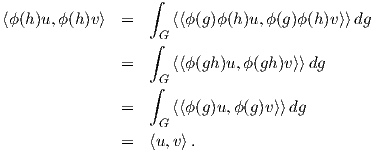
Για μια συμπαγή ομάδα Lie οι μη αναγώγιμες αναπαραστάσεις αποτελούν τους θεμέλιους λίθους για κάθε αναπαράσταση πεπερασμένης διάστασης. Χρειαζόμαστε πρώτα το εξής:
Λήμμα 8.3: ΄Εστω G μια συμπαγής ομάδα Lie, V πραγματικός ή μιγαδικός χώρος, ϕ : G → Aut(V ) μια
αναπαράσταση και έστω U ένας G-αναλλοίωτος υπόχωρος του V . Εφοδιάζουμε τον V με ένα G-αναλλοίωτο
εσωτερικό γινόμενο 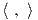 . Τότε ο υπόχωρος
. Τότε ο υπόχωρος
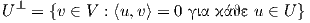
είναι G-αναλλοίωτος.
Απόδειξη. Θα πρέπει να δείξουμε ότι ϕ(g)U⊥ ⊆ U⊥ για κάθε g ∈ G. Επειδή το εσωτερικό γινόμενο είναι G-αναλλοίωτο, για κάθε u ∈ U, υ ∈ U⊥ και g ∈ G, έχουμε ότι
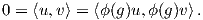
Επομένως θα πρέπει το ϕ(g)υ να ανήκει στον U⊥, άρα το ορθογώνιο συμπλήρωμα του U είναι πράγματι G-αναλλοίωτος υπόχωρος. ▄
Θεώρημα 8.5: ΄Εστω G μια συμπαγής ομάδα Lie και V ένας πραγματικός ή μιγαδικός διανυσματικός χώρος. Τότε κάθε αναπαράσταση ϕ : G → Aut(V ) πεπερασμένης διάστασης εκφράζεται ως ευθύ άθροισμα μη αναγώγιμων αναπαραστάσεων, δηλαδή η ϕ είναι αναγώγιμη.
Απόδειξη. Εφοδιάζουμε τον διανυσματικό χώρο V με ένα G-αναλλοίωτο εσωτερικό γινόμενο 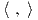 το
οποίο υπάρχει από το Θεώρημα 8.4. ΄Εστω U ένας μη αναγώγιμος G-αναλλοίωτος υπόχωρος του V
τέτοιος ώστε dim(U) > 0 και έστω U⊥ = {υ ∈ V :
το
οποίο υπάρχει από το Θεώρημα 8.4. ΄Εστω U ένας μη αναγώγιμος G-αναλλοίωτος υπόχωρος του V
τέτοιος ώστε dim(U) > 0 και έστω U⊥ = {υ ∈ V : 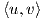 = 0 για κάθε u ∈ U} το ορθογώνιο
συμπλήρωμα. Τότε ο V γράφεται ως ευθύ άθροισμα δύο G-αναλλοίωτων υποχώρων, δηλαδή V = U ⊕ U⊥
και dim(V ) = dim(U) + dim(U⊥). Στην περίπτωση που οι χώροι U και U⊥ είναι μη αναγώγιμοι τότε η
αναπαράσταση ϕ θα γράφεται ως ευθύ άθροισμα δύο μη αναγώγιμων αναπαραστάσεων
= 0 για κάθε u ∈ U} το ορθογώνιο
συμπλήρωμα. Τότε ο V γράφεται ως ευθύ άθροισμα δύο G-αναλλοίωτων υποχώρων, δηλαδή V = U ⊕ U⊥
και dim(V ) = dim(U) + dim(U⊥). Στην περίπτωση που οι χώροι U και U⊥ είναι μη αναγώγιμοι τότε η
αναπαράσταση ϕ θα γράφεται ως ευθύ άθροισμα δύο μη αναγώγιμων αναπαραστάσεων
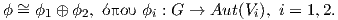
Αν όμως οι χώροι U, U⊥ είναι αναγώγιμοι, τότε ο καθένας θα γράφεται ως ευθύ άθροισμα ορθογώνιων G-αναλλοίωτων υπόχωρων, όπως και προηγουμένως. Αν αυτοί οι υπόχωροι είναι μη αναγώγιμοι, θα έχουμε το ζητούμενο, αν όχι θα επαναλάβουμε την ίδια διαδικασία. Επειδή ο διανυσματικός χώρος V είναι πεπερασμένης διάστασης, έστω n, από την παραπάνω διαδικασία θα έχουμε ότι
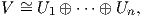
όπου Ui,i = 1,…n είναι μη αναγώγιμοι G-αναλλοίωτοι υπόχωροι, δηλαδή
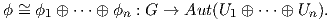
▄
΄Εστω (G,V ) μια αναπαράσταση πεπερασμένης διάστασης. Σύμφωνα με το Θεώρημα 8.4, όταν η ομάδα G είναι
συμπαγής, τότε υπάρχει πάντα ένα G-αναλλοίωτο εσωτερικό γινόμενο στον χώρο V . Θα αποδείξουμε ότι, αν η
(G,V ) είναι μη αναγώγιμη (δηλαδή οι μόνοι G-αναλλοίωτοι υπόχωροι του V είναι ο {0} και ο εαυτός του) και ο
V είναι μιγαδικός διανυσματικός χώρος, τότε το G-αναλλοίωτο εσωτερικό γινόμενο 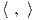 στον V
είναι μοναδικό. Ειδικότερα θα δούμε ότι, αν
στον V
είναι μοναδικό. Ειδικότερα θα δούμε ότι, αν 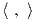 ′ είναι κάποιο τυχαίο εσωτερικό γινόμενο του V ,
τότε
′ είναι κάποιο τυχαίο εσωτερικό γινόμενο του V ,
τότε
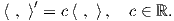
Το ίδιο αποτέλεσμα ισχύει και στην περίπτωση που η αναπαράσταση (G,V ) είναι πραγματική.
Θα χρειαστούμε ένα εξαιρετικά χρήσιμο αποτέλεσμα, γνωστό ως Λήμμα του Schur, το οποίο εμφανίζεται με διάφορες εκδοχές.
Θεώρημα 8.6: (Λήμμα του Schur, Πρώτη εκδοχή).
΄Εστω ϕi : G → Aut(V i), i = 1,2 δύο μη αναγώγιμες αναπαραστάσεις της G και έστω f : V 1 → V 2
μια G-ισοαναλλοίωτη απεικόνιση. Τότε είτε η f είναι ισομορφισμός διανυσματικών χώρων (οπότε η ϕ1 είναι
ισοδύναμη με την ϕ2), είτε f = 0.
Απόδειξη. Αρκεί να αποδείξουμε ότι οι χώροι Kerf = {x ∈ V 1 : f(x) = 0} ⊂ V 1 και Imf = {f(x) : x ∈ V 1}⊂ V 2 είναι αντίστοιχα ϕi(g)-αναλλοίωτοι για κάθε g ∈ G. Επειδή η απεικόνιση f είναι G-ισοαναλλοίωτη, θα ισχύει f ∘ ϕ1(g) = ϕ2(g) ∘ f για κάθε g ∈ G.
΄Εστω x ∈ Kerf. Τότε f(x) = 0, επομένως για κάθε g ∈ G είναι:
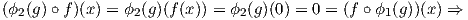
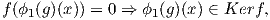
άρα ο χώρος Kerf είναι ϕ1(g)-αναλλοίωτος. Επειδή η αναπαράσταση ϕ1 : G → Aut(V 1) είναι μη αναγώγιμη, θα πρέπει Kerf = 0 ή Kerf = V 1. Στη συνέχεια, θα δείξουμε ότι το σύνολο Imf είναι ϕ2(g)-αναλλοίωτο. ΄Εστω y ∈ Imf. Τότε υπάρχει x ∈ V 1 τέτοιο ώστε y = f(x). Επομένως, για κάθε g ∈ G έχουμε ότι
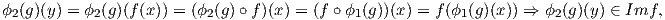
δηλαδή ο Imf είναι πράγματι ϕ2(g)-αναλλοίωτος. Αφού η αναπαράσταση ϕ2 : G → Aut(V 2) είναι μη αναγώγιμη, θα πρέπει Imf = 0 ή Imf = V 2.
Συνδυάζοντας τα παραπάνω παίρνουμε τις εξής περιπτώσεις:
▄
Θεώρημα 8.7: (Λήμμα του Schur, Δεύτερη εκδοχή).
΄Εστω ϕ : G → Aut(V ) μια μη αναγώγιμη αναπαράσταση της G στον μιγαδικό χώρο V και f ∈ End(V )
μια G-ισοαναλλοίωτη απεικόνιση. Τότε f = cIdV , για κάποιο c ∈ ℂ.
Απόδειξη. ΄Εστω A = (αij) ο πίνακας του ενδομορφισμού f ως προς κάποια βάση του V . Τότε από το θεμελιώδες θεώρημα της άλγεβρας το χαρακτηριστικό πολυώνυμο p(x) της f έχει μια ρίζα c ∈ ℂ. Επομένως
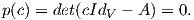
Αυτό σημαίνει ότι ο πυρήνας του ενδομορφισμού f1 := cIdV - f δεν είναι ο μηδενικός υπόχωρος, δηλαδή Ker(cIdV - f)≠{0}. Επίσης, για κάθε g ∈ G έχουμε ότι
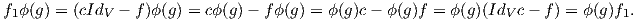
Αυτό σημαίνει ότι η f1 είναι μια ισοαναλλοίωτη απεικόνιση και ο V είναι μη αναγώγιμος υπόχωρος, άρα από την πρώτη εκδοχή του Λήμματος του Schur προκύπτει ότι f1 = 0 και άρα f = cIdV . ▄
Θα δούμε τώρα το βασικό θεώρημα της παραγράφου. Το θεώρημα αυτό έχει πολλές εφαρμογές στη γεωμετρία των ομάδων Lie και των ομογενών χώρων. Για παράδειγμα, όπως θα δούμε αργότερα, μας βοηθάει να περιγράψουμε τις αναλλοίωτες μετρικές σε έναν ομογενή χώρο.
Θεώρημα 8.8: ΄Εστω V ένας μιγαδικός διανυσματικός χώρος διάστασης n και ϕ : G → Aut(V ) μια μη αναγώγιμη αναπαράσταση της G. Τότε υπάρχει ένα και μοναδικό G-αναλλοίωτο εσωτερικό γινόμενο στον V , αγνοώντας πολλαπλασιασμό με θετικές σταθερές.6
Απόδειξη. Η ύπαρξη εξασφαλίζεται από το Θεώρημα 8.4. ΄Εστω 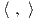 1 και
1 και 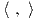 2 δύο G-αναλλοίωτα
εσωτερικά γινόμενα στον V . Τότε (βλ. Ασκηση 1) υπάρχει μοναδικός γραμμικός τελεστής T : V → V
τέτοιος ώστε
2 δύο G-αναλλοίωτα
εσωτερικά γινόμενα στον V . Τότε (βλ. Ασκηση 1) υπάρχει μοναδικός γραμμικός τελεστής T : V → V
τέτοιος ώστε
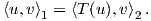
Ο T είναι αυτοσυζυγής ως προς το εσωτερικό γινόμενο 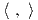 2. Επίσης, για κάθε g ∈ G ισχύει ότι
T(ϕ(g)υ) = ϕ(g)T(υ). Πράγματι,
2. Επίσης, για κάθε g ∈ G ισχύει ότι
T(ϕ(g)υ) = ϕ(g)T(υ). Πράγματι,
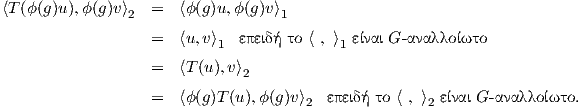
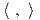 2-ορθοκανονική βάση απο ιδιοδιανύσματα και επιπλέον ο τελεστής T θα έχει τουλάχιστον μία πραγματική ιδιοτιμή
λ ∈ ℝ. 7
Θεωρούμε τον υπόχωρο Ker(T - λIdV ) του V . Επειδή το λ είναι ιδιοτιμή, τότε ο πυρήνας της γραμμικής
απεικόνισης T - λIdV : V → V θα είναι μη μηδενικός, διότι θα υπάρχει κάποιο υ ∈ V τέτοιο ώστε
(T - λIdV )(υ) = 0, δηλαδή υ ∈ Ker(T - λIdV ), οπότε
2-ορθοκανονική βάση απο ιδιοδιανύσματα και επιπλέον ο τελεστής T θα έχει τουλάχιστον μία πραγματική ιδιοτιμή
λ ∈ ℝ. 7
Θεωρούμε τον υπόχωρο Ker(T - λIdV ) του V . Επειδή το λ είναι ιδιοτιμή, τότε ο πυρήνας της γραμμικής
απεικόνισης T - λIdV : V → V θα είναι μη μηδενικός, διότι θα υπάρχει κάποιο υ ∈ V τέτοιο ώστε
(T - λIdV )(υ) = 0, δηλαδή υ ∈ Ker(T - λIdV ), οπότε
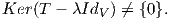
Αρκεί να δείξουμε ότι ο χώρος Ker(T - λIdV ) είναι G-αναλλοίωτος, δηλαδή ότι για κάθε g ∈ G
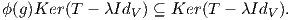
Πιο αναλυτικά θα πρέπει να ισχύει ϕ(g)υ ∈ Ker(T -λIdV ) εάν και μόνο εάν (T -λIdV )(ϕ(g)υ) = 0, για κάθε υ ∈ Ker(T - λIdV ).
Η απεικόνιση T - λIdV είναι G-ισοαναλλοίωτη, επειδή ισχύει
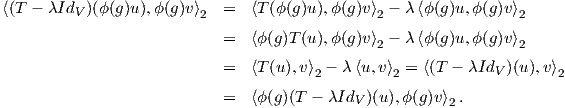
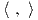 i, i = 1,2 είναι G-αναλλοίωτα. Οπότε (T -λIdV )(ϕ(g)u) = ϕ(g)(T -λIdV )(u),
επομένως για κάθε υ ∈ Ker(T - λIdV ) θα είναι
i, i = 1,2 είναι G-αναλλοίωτα. Οπότε (T -λIdV )(ϕ(g)u) = ϕ(g)(T -λIdV )(u),
επομένως για κάθε υ ∈ Ker(T - λIdV ) θα είναι 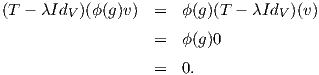
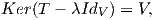
δηλαδή κάθε στοιχείο του χώρου V είναι ιδιοδιάνυσμα του τελεστή T. ΄Εστω τώρα u,υ ∈ V . Τότε
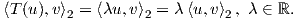
Αλλά 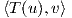 2 =
2 = 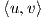 1, άρα θα έχουμε το ζητούμενο:
1, άρα θα έχουμε το ζητούμενο:
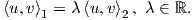
▄
Στην περίπτωση που η αναπαράσταση ϕ : G → Aut(V ) είναι αναγώγιμη, δηλάδη ϕ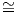 ϕ1 ⊕
ϕ1 ⊕ ⊕ϕn, όπου κάθε
υποαναπαράσταση ϕi : G → Aut(Ui), i = 1,…,n είναι μη αναγώγιμη, τότε ισχύει το εξής σημαντικό
αποτέλεσμα:
⊕ϕn, όπου κάθε
υποαναπαράσταση ϕi : G → Aut(Ui), i = 1,…,n είναι μη αναγώγιμη, τότε ισχύει το εξής σημαντικό
αποτέλεσμα:
Θεώρημα 8.9: ΄Εστω μια αναγώγιμη αναπαράσταση ϕ : G → Aut(V ) τέτοια ώστε ϕ ϕ1 ⊕ ϕ2, όπου
ϕi : G → Aut(Ui), i = 1,2 είναι δύο μη ισοδύναμες υποαναπαραστάσεις, δηλαδή ϕ1 ≇ ϕ2. Τότε ως προς
ένα G-αναλλοίωτο εσωτερικό γινόμενο του διανυσματικού χώρου V οι υπόχωροι U1 και U2 είναι κάθετοι
μεταξύ τους (U1⊥U2).
ϕ1 ⊕ ϕ2, όπου
ϕi : G → Aut(Ui), i = 1,2 είναι δύο μη ισοδύναμες υποαναπαραστάσεις, δηλαδή ϕ1 ≇ ϕ2. Τότε ως προς
ένα G-αναλλοίωτο εσωτερικό γινόμενο του διανυσματικού χώρου V οι υπόχωροι U1 και U2 είναι κάθετοι
μεταξύ τους (U1⊥U2).
Απόδειξη. Εφοδιάζουμε τον διανυσματικό χώρο V  U1 ⊕ U2 με ένα G-αναλλοίωτο εσωτερικό γινόμενο.
Θεωρούμε την ορθογώνια προβολή σ : U2 → U1, u
U1 ⊕ U2 με ένα G-αναλλοίωτο εσωτερικό γινόμενο.
Θεωρούμε την ορθογώνια προβολή σ : U2 → U1, u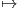 x του U2 επί του U1, όπου το u ∈ U2 γράφεται
κατά μοναδικό τρόπο ως u = x + y, με x ∈ U1 και y ∈ U1⊥. Προφανώς η απεικόνιση IdU2 - σ είναι η
ορθογώνια προβολή του U2 επί του U1⊥, δηλαδή για κάθε u ∈ U2 θα είναι
x του U2 επί του U1, όπου το u ∈ U2 γράφεται
κατά μοναδικό τρόπο ως u = x + y, με x ∈ U1 και y ∈ U1⊥. Προφανώς η απεικόνιση IdU2 - σ είναι η
ορθογώνια προβολή του U2 επί του U1⊥, δηλαδή για κάθε u ∈ U2 θα είναι
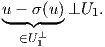 | (8.4) |
Επομένως, αρκεί να αποδείξουμε ότι η απεικόνιση σ είναι η μηδενική. Η σ : U2 → U1 είναι G-ισοαναλλοίωτη. Πράγματι, για κάθε g ∈ G έχουμε
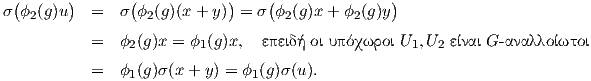
Σημειώνουμε ότι τα παραπάνω ισχύουν για οποιαδήποτε αναπαράσταση μιας ομάδας.
Μια ιδιαίτερα σημαντική αναπαράσταση για τη μελέτη της δομής μιας ομάδας Lie είναι η συζυγής αναπαράσταση αυτής. ΄Εστω G μια ομάδα Lie. ΄Ενας ισομορφισμός ομάδων Lie ϕ : G → G καλείται αυτομορφισμός (automorphism) της G. Για κάθε g ∈ G η απεικόνιση
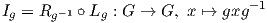
Ορισμός 8.7: Η συζυγής αναπαράσταση (adjoint representation) της ομάδας Lie G είναι ο ομομορφισμός Ad : G → Aut(𝔤), με τιμή Ad(g) = (dIg)e.
Επειδή Ixy = Ix ∘Iy, παίρνοντας τα διαφορικά και στα δύο μέλη, θα έχουμε Ad(xy) = Ad(x) ∘Ad(y), δηλαδή είναι ομομορφισμός ομάδων Lie. Αποδεικνύεται ότι η Ad είναι λεία, άρα είναι πράγματι ένας ομομορφισμός ομάδων Lie.
Το διαφορικό της Ad ορίζει τη συζυγή αναπαράσταση της άλγεβρας Lie 𝔤:
Ορισμός 8.8: Η συζυγής αναπαράσταση της άλγεβρας Lie 𝔤 είναι ο ομομορφισμός ad : 𝔤 → End(𝔤), με τιμή ad(X) = (dAd)e(X).
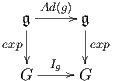
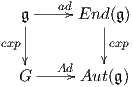
΄Εστω G μια ομάδα Lie. Τότε για κάθε t ∈ ℝ, g ∈ G και X ∈ 𝔤 ισχύουν οι παρακάτω σχέσεις:
Πράγματι, για την πρώτη σχέση λαμβάνοντας υπόψη τη φυσιολογική συμπεριφορά της εκθετικής απεικόνισης (Θεώρημα 7.6), το παρακάτω διάγραμμα θα είναι μεταθετικό:
Με τον ίδιο τρόπο η δεύτερη σχέση προκύπτει εύκολα από το διάγραμμα
Γνωρίζουμε ότι το κέντρο μιας ομάδας είναι μια υπομάδα ιδιαίτερης σημασίας. Το κέντρο της ομάδας Lie G να είναι το σύνολο
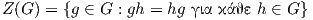
και είναι μια υποομάδα Lie της G. Εύκολα προκύπτει ότι το Z(G) είναι μια κανονική αβελιανή υποομάδα της G και στην περίπτωση που η G είναι αβελιανή τότε Z(G) = G. Με ανάλογο σκεπτικό ορίζουμε το κέντρο της άλγεβρας Lie 𝔤 ως το σύνολο
![Z (𝔤) = {X ∈ 𝔤 : [X, Y] = 0 γ ια κάθε Y ∈ 𝔤}.](02_chapter_08102x.png)
Αν η ομάδα Lie G είναι συνεκτική τότε KerAd = Z(G) και Ker ad = Z(𝔤). Επιπλέον, η άλγεβρα Lie του Z(G) είναι το σύνολο Z(𝔤). Η πρόταση που ακολουθεί δίνει ένα κριτήριο του κάτα πόσον η ομαδά G είναι αβελιανή.
Η απόδειξη είναι κάπως τεχνική και την παραλείπουμε.
Πολλές φορές, η συζυγής αναπαράσταση μιας άλγεβρας Lie ορίζεται από την σχέση ad(X)Y = [X,Y ] (ιδιαιτέρως όταν κάποιος μελετά αποκλειστικά θεωρία αλγεβρών Lie).
Παρατήρηση. Εάν η ομάδα Lie G είναι αβελιανή τότε Ig = Id, άρα Adg = Id για κάθε g ∈ G. Τότε από την προηγούμενη πρόταση προκύπτει ότι [X,Y ] = 0 για κάθε X,Y ∈ 𝔤. Μια άλγεβρα Lie 𝔤 που ικανοποιεί την συνθήκη αυτή ονομάζεται αβελιανή. Αποδεικνύεται ότι το αντίστροφο ισχύει, εάν η G είναι συνεκτική ομάδα Lie.
Στην περίπτωση που η ομάδα Lie G είναι μια ομάδα πινάκων, δηλαδή κάποια κλειστή υποομάδα της γενικής γραμμικής ομάδας GLnK, K ∈{ℝ, ℂ, ℍ}, τότε η συζυγής αναπαράσταση έχει μια ιδιαίτερα απλή μορφή:
Πρόταση 8.5: Αν η G είναι μια ομάδα πινάκων, τότε Ad(g)X = gXg-1 για κάθε g ∈ G, X ∈ 𝔤 (πολλαπλασιασμός πινάκων).
Απόδειξη. ΄Εστω t exp(tX) η μονοπαραμετρική υποομάδα του X. Τότε
exp(tX) η μονοπαραμετρική υποομάδα του X. Τότε
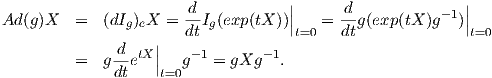
Παράδειγμα. ΄Εστω η ομάδα Lie G = SU(2) = {A ∈ U(2) : det(A) = 1} με άλγεβρα Lie 𝔰𝔲(2) = {A ∈ GL2ℂ : A + t = 0, trA = 0}. Από την σχέση (7.6) έχουμε ότι
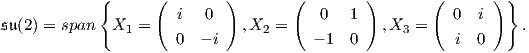
Θα υπολογίσουμε πρώτα τη συζυγή αναπαράσταση Ad : SU(2) → Aut(𝔰𝔲(2)). Γνωρίζουμε ότι τα στοιχεία της
SU(2) έχουν τη μορφή A = 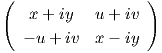 , οπότε αρκεί να βρούμε τον πίνακα της γραμμικής απεικόνισης
Ad(A) : 𝔰𝔲(2) → 𝔰𝔲(2), με τύπο Ad(A)B = ABA-1, ως προς τη βάση {X1,X2,X3} της 𝔰𝔲(2). Είναι
, οπότε αρκεί να βρούμε τον πίνακα της γραμμικής απεικόνισης
Ad(A) : 𝔰𝔲(2) → 𝔰𝔲(2), με τύπο Ad(A)B = ABA-1, ως προς τη βάση {X1,X2,X3} της 𝔰𝔲(2). Είναι
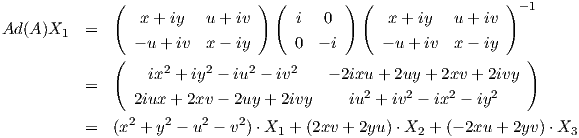
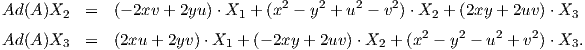
![( 2 2 2 2 )
| x + y - u - v - 2xv + 2yu 2xu + 2yv |
[Ad (A)] = ( 2xv + 2yu x2 - y2 + u2 - v2 - 2xy + 2uv ) .
- 2xu + 2yv 2xy + 2uv x2 - y2 - u2 + v2](02_chapter_08109x.png)
Για την ειδική περίπτωση όπου A = g = 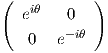 , παίρνουμε ότι
, παίρνουμε ότι
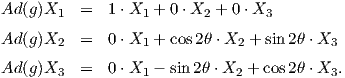
![( )
1 0 0
[Ad (g )] = | | .
( 0 cos2θ - sin2θ )
0 sin2θ cos2 θ](02_chapter_08112x.png)
Στη συνέχεια, θα υπολογίσουμε τη συζυγή αναπαράσταση ad : 𝔰𝔲(2) → End(𝔰𝔲(2)) της άλγεβρας Lie 𝔰𝔲(2). Για
X ∈ 𝔰𝔲(2) θα βρούμε τον πίνακα της γραμμικής απεικόνισης ad(X) : 𝔰𝔲(2) → 𝔰𝔲(2) με τύπο ad(X)Y = [X,Y ] ως
προς τη βάση {X1,X2,X3}. ΄Οπως θα εξηγηθεί στη συνέχεια, αρκεί να επιλέξουμε 𝔰𝔲(2) ∋ X = 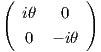 .
Τότε
.
Τότε
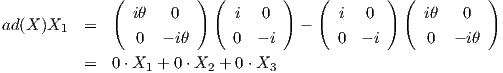
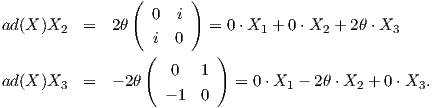
![( )
0 0 0
[ad(X )] = |( 0 0 - 2θ |) .
0 2θ 0](02_chapter_08116x.png) |
΄Εχουμε δει ότι μια αναπαράσταση ϕ : G → Aut(V ) ορίζει μια δράση της ομάδας G στον διανυσματικό χώρο V
μέσω της απεικόνισης G×V → V, (g,υ)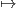 ϕ(g)υ. Γενικά ισχύει και το αντίστροφο, δηλαδή κάθε δράση ορίζει μια
αναπαράσταση. Ιδιαιτέρως, όταν η ομάδα G είναι μια από τις ομάδες πινάκων GLnℝ, SO(n) ή O(n), τότε η
δράση
ϕ(g)υ. Γενικά ισχύει και το αντίστροφο, δηλαδή κάθε δράση ορίζει μια
αναπαράσταση. Ιδιαιτέρως, όταν η ομάδα G είναι μια από τις ομάδες πινάκων GLnℝ, SO(n) ή O(n), τότε η
δράση
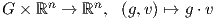
όπου g ⋅υ είναι ο συνήθης πολλαπλασιασμός πινάκων, ορίζει μια αναπαράσταση ϕ : G → Aut(ℝn), η οποία καλείται
sun�jhc anapar�stash thc G (standard representation). Ανάλογα ορίζεται και η συνήθης αναπαράσταση των
ομάδων πινάκων GLnℂ, SU(n) και U(n) στον διανυσματικό χώρο ℂn. Συμβολίζουμε με 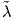 n τη συνήθη
αναπαράσταση της GLnℝ και με λn τη συνήθη αναπαράσταση της SO(n), όπου ισχύει λn =
n τη συνήθη
αναπαράσταση της GLnℝ και με λn τη συνήθη αναπαράσταση της SO(n), όπου ισχύει λn = 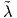 n
n SO(n).
Συχνά με λn θα συμβολίζουμε και τη συνήθη αναπαράσταση της O(n). Επίσης με
SO(n).
Συχνά με λn θα συμβολίζουμε και τη συνήθη αναπαράσταση της O(n). Επίσης με 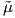 n συμβολίζουμε τη
συνήθη αναπαράσταση της GLnℂ και με μn τη συνήθη αναπαράσταση της SU(n) (ή αντ. της U(n)).
Τέλος, θα συμβολίζουμε με νn τη συνήθη αναπαράσταση της Sp(n). Αποδεικνύεται ότι η συζυγής
αναπαράσταση των προηγούμενων ομάδων Lie με βάση αυτόν τον συμβολισμό εκφράζεται ως εξής:
n συμβολίζουμε τη
συνήθη αναπαράσταση της GLnℂ και με μn τη συνήθη αναπαράσταση της SU(n) (ή αντ. της U(n)).
Τέλος, θα συμβολίζουμε με νn τη συνήθη αναπαράσταση της Sp(n). Αποδεικνύεται ότι η συζυγής
αναπαράσταση των προηγούμενων ομάδων Lie με βάση αυτόν τον συμβολισμό εκφράζεται ως εξής:
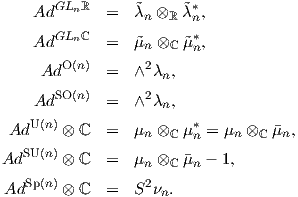
Παράδειγμα. Θα αποδείξουμε αναλυτικά ότι AdSO(3) = ∧2λ3, όπου λ3 : SO(3) → Aut(ℝ3),
A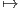 λ3(A)(υ) = A ⋅ υ, υ ∈ ℝ3 η συνήθης αναπαράσταση της SO(3). Η άλγεβρα Lie της SO(3) είναι
𝔰𝔬(3) = {A ∈ GL3ℝ : At = -A} = span{X1,X2,X3}, όπου
λ3(A)(υ) = A ⋅ υ, υ ∈ ℝ3 η συνήθης αναπαράσταση της SO(3). Η άλγεβρα Lie της SO(3) είναι
𝔰𝔬(3) = {A ∈ GL3ℝ : At = -A} = span{X1,X2,X3}, όπου
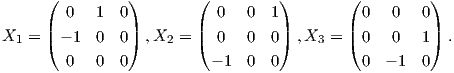
![( ( ) )
|{ cos θ sinθ 0 |}
T = |( - sinθ cos θ 0 |) : θ ∈ (0,2π ]
|( |)
0 0 1](02_chapter_08126x.png)
(βλ. Θεώρημα 8.12). ΄Εστω A ∈ T. Τότε ο πίνακας της απεικόνισης Ad(A) : 𝔰𝔬(3) → 𝔰𝔬(3), Ad(A)(B) = ABA-1, B ∈ 𝔰𝔬(3) ως προς τη βάση {X1,X2,X3} είναι
![(1 0 0 )
| |
[Ad (A)] = (0 cosθ sinθ) .
0 - sinθ cosθ](02_chapter_08127x.png)
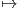 ∧2λ3(A) : ∧2ℝ3 →∧2ℝ3, ei ∧ej
∧2λ3(A) : ∧2ℝ3 →∧2ℝ3, ei ∧ej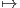 ∧2λ3(A)(ei ∧ej) = Aei ∧Aej.
Τότε για κάθε A ∈ T έχουμε ότι
∧2λ3(A)(ei ∧ej) = Aei ∧Aej.
Τότε για κάθε A ∈ T έχουμε ότι
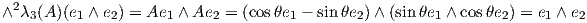
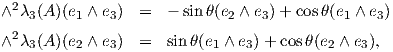
![( )
1 0 0
[∧2λ3(A )] = |(0 cosθ sinθ|) = [Ad(A )].
0 - sinθ cosθ](02_chapter_08132x.png)
΄Εστω V ένας διανυσματικός χώρος επί του ℝ. Τότε μπορούμε να ορίσουμε τον διανυσματικό χώρο V ℂ = V ⊗ℝℂ (ή πιο απλά V ⊗ ℂ) επί του ℂ, όπου
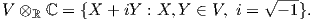
Ο διανυσματικός χώρος V ℂ λέγεται μιγαδοποίηση (complexification) του V . Η διάσταση του V ℂ επί του ℂ είναι ίση με τη διάσταση του V επί του ℝ, δηλαδή
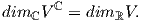
Αν 𝔤 είναι μια άλγεβρα Lie επί του ℝ, τότε η μιγαδοποίηση της 𝔤 είναι η άλγεβρα Lie 𝔤ℂ = 𝔤 ⊗ ℂ (ή μερικές φορές γράφουμε 𝔤 + i𝔤), όπου το γινόμενο Lie δίνεται ως εξής:
![[U + iV,X + iY] = [U, X]- [V,Y ]+ i([V, X]+ [U,Y ]).](02_chapter_08135x.png)
Αν ϕ : G → Aut(V ) είναι μια αναπαράσταση της ομάδας Lie G στον διανυσματικό χώρο V επί του ℝ, τότε συνδυάζοντας τα προηγούμενα μπορούμε να ορίσουμε τη μιγαδοποιημένη αναπαράσταση (complexified representation) της G ως εξής:
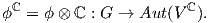
Αντίστοιχα ορίζεται και η μιγαδοποιημένη αναπαράσταση μιας άλγεβρας Lie 𝔤. Ακριβώς λόγω της παραπάνω ισότητας των διαστάσεων, η μιγαδοποίηση είναι μια πολύ χρήσιμη διαδικασία στη θεωρία αναπαραστάσεων και γενικά στη θεωρία των ομάδων και αλγεβρών Lie, αλλά χρειάζεται προσοχή στον χειρισμό της.8
Σύμφωνα με το Θεώρημα 8.4, κάθε αναπαράσταση (G,V ) μιας συμπαγούς ομάδας Lie G έχει ένα G-αναλλοίωτο εσωτερικό γινόμενο (στον χώρο V ). Το ίδιο ισχύει ιδιαίτερα και για τη συζυγή αναπαράσταση (G,𝔤) της ομάδας G. Σε αυτή την ενότητα θα ορίσουμε ένα πολύ χρήσιμο εσωτερικό γινόμενο στην άλγεβρα Lie 𝔤, χρησιμοποιώντας τη συζυγή αναπαράσταση.
Η μορφή Killing μιας ομάδας Lie είναι η μορφή Killing της αντίστοιχης άλγεβρας.
Πρόταση 8.6: Η μορφή Killing B : 𝔤 × 𝔤 → ℝ έχει τις εξής ιδιότητες:
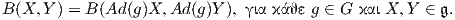
Αυτό σημαίνει ότι η απεικόνιση Ad(g) είναι ορθογώνια ως προς τη μορφή Killing, ή απλά B-ορθογώνια.
![B (ad(Z)X, Y) = - B(X, ad(Z)Y ) ή B ([X, Z],Y ) = B (X,[Z,Y ]).](02_chapter_08139x.png)
Απόδειξη. Η πρώτη ιδιότητα είναι απλή και την αφήνουμε για άσκηση. Για τη δεύτερη ιδιότητα, θεωρούμε έναν αυτομορφισμό σ ∈ Aut(𝔤). Αυτό σημαίνε ότι η απεικόνιση σ : 𝔤 → 𝔤 είναι ισομορφισμός διανυσματικών χώρων και επιπλέον ισχύει η σχέση σ[X,Y ] = [σX,σY ]. Από την ισότητα αυτή προκύπτει ότι ad(σX) ∘ σ = σ ∘ ad(X) ή ad(σX) = σ ∘ ad(X) ∘ σ-1. Πράγματι, για κάθε Y ∈ 𝔤 είναι
![-1 -1 -1
ad(σX )Y = [σX, Y ] = [σX, σσ Y ] = σ [X, σ Y ] = σ ∘ ad(X )∘σ Y.](02_chapter_08140x.png)
Χρησιμοποιώντας την παραπάνω σχέση θα έχουμε:
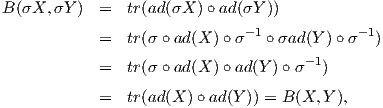
Θα δείξουμε τώρα την τρίτη ιδιότητα, δηλαδή ότι η απεικόνιση ad(Z) είναι αντισυμμετρική ως προς την B. Εφαρμόζουμε δύο φορές την ταυτότητα του Jacobi και παίρνουμε
![[Z,[X, [Y, W ]]] = [[Z,X ],[Y, W ]]+ [X, [Z,[Y,W ]]]
= [[Z,X ],[Y, W ]]+ [X, [[Z, Y],W ]]+ [X, [Y,[Z, W ]]].](02_chapter_08142x.png)
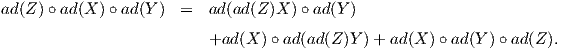
![[ad(Z ), ad(X )∘ ad(Y )] = ad (Z )∘ ad(X )∘ad (Y )- ad (X ) ∘ad(Y )∘ ad(Z)
= ad (ad (Z )X )∘ad (Y )+ ad (X ) ∘ad(ad(Z )Y )
+ad (X )∘ ad(Y) ∘ad(Z )- (ad(X )∘ ad(Y))∘ ad(Z)
= ad (ad (Z )X )∘ad (Y )+ ad (X ) ∘ad(ad(Z )Y ).](02_chapter_08144x.png)
![0 = tr([ad(Z), ad(X )∘ ad(Y)]) = tr(ad(ad(Z)X )∘ ad(Y)) + tr(ad(X )∘ ad(ad(Z)Y ))
= B(ad(Z )X,Y )+ B (X, ad(Z)Y ).](02_chapter_08145x.png)
Παρατηρούμε ότι λόγω της ταυτότητας Jacobi ισχύει
![ad (X )[Y,Z ] = [ad (X )Y,Z ]+ [Y,ad(X )Z],](02_chapter_08146x.png)
το οποίο σημαίνει ότι η απεικόνιση ad(X) : 𝔤 → 𝔤 είναι μια παραγώγιση της άλγεβρας Lie 𝔤 (δηλαδή ad(X) ∈ Der(𝔤). Γενικά ισχύει ότι
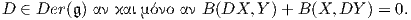
Ορισμός 8.10: Μια ομάδα Lie G (αντ. άλγεβρα Lie) ονομάζεται ημιαπλή (semisimple), εάν η μορφή Killing είναι μη εκφυλισμένη (non degenerate).
Το να είναι η μορφή Killing μη εκφυλισμένη σημαίνει ότι εάν B(X,Y ) = 0 για κάθε X ∈ 𝔤, τότε Y = 0. Ισοδύναμα, εάν ο πίνακας της απεικόνισης B ως προς μια βάση του χώρου έχει αντίστροφο.
Στην περίπτωση που η ομάδα Lie G είναι ημιαπλή, τότε το κέντρο της άλγεβρας Lie 𝔤 είναι τετριμμένο. Πράγματι, έστω X ∈ Z(𝔤). Τότε για κάθε Y ∈ 𝔤 θα είναι [X,Y ] = 0, δηλαδή η απεικόνιση ad(X) είναι ο μηδενικός τελεστής του χώρου End(𝔤). Επομένως,
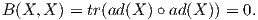
Επειδή η G είναι ημιαπλή, θα πρέπει X = 0, άρα Z(𝔤) = {0}.
Το επόμενο θεώρημα είναι χρήσιμο, διότι καθιστά τη μορφή Killing ένα εσωτερικό γινόμενο σε συμπαγείς και ημιαπλές ομάδες Lie.
Θεώρημα 8.10: Αν η ομάδα Lie G είναι συμπαγής και ημιαπλή, τότε η μορφή Killing είναι αρνητικά ορισμένη.
Απόδειξη. ΄Εστω Ad : G → Aut(𝔤) η συζυγής αναπαράσταση της G. Επειδή η ομάδα G είναι συμπαγής,
από το Θεώρημα 8.4 υπάρχει ένα G-αναλλοίωτο εσωτερικό γινόμενο 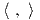 στον χώρο 𝔤, δηλαδή
στον χώρο 𝔤, δηλαδή
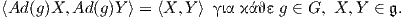
Αυτό σημαίνει ότι η απεικόνιση Ad(g) είναι 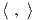 -ορθογώνια. Επομένως, από την τρίτη ιδιότητα της
Πρότασης 8.6, για κάθε X ∈ 𝔤, η απεικόνιση ad(X) : 𝔤 → 𝔤 θα είναι αντισυμμετρική ως προς το εσωτερικό
γινόμενο
-ορθογώνια. Επομένως, από την τρίτη ιδιότητα της
Πρότασης 8.6, για κάθε X ∈ 𝔤, η απεικόνιση ad(X) : 𝔤 → 𝔤 θα είναι αντισυμμετρική ως προς το εσωτερικό
γινόμενο 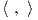 . ΄Εστω (αij) ο πίνακας της απεικόνισης ad(X) ως προς μια ορθοκανονική βάση του χώρου
𝔤. Τότε
. ΄Εστω (αij) ο πίνακας της απεικόνισης ad(X) ως προς μια ορθοκανονική βάση του χώρου
𝔤. Τότε
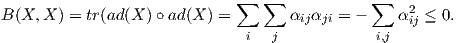
Επειδή η G είναι ημιαπλή η B είναι μη εκφυλισμένη, οπότε το παραπάνω άθροισμα θα είναι αυστηρά αρνητικό. ▄
Το συμπέρασμα που παίρνουμε από το παραπάνω θεώρημα είναι ότι, όταν έχουμε μια συμπαγή και ημιαπλή ομάδα Lie G, τότε μπορούμε να ορίσουμε το εσωτερικό γινόμενο
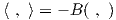
στην άλγεβρα Lie 𝔤. Το αντίστροφο του παραπάνω θεωρήματος ισχύει, όταν η ομάδα Lie G είναι συνεκτική και είναι αρκετά πιο δύσκολο στην απόδειξη. Συγκεριμένα:
Θεώρημα 8.11: Αν η G είναι μια συνεκτική ομάδα Lie και η μορφή Killing B είναι αρνητικά ορισμένη στην 𝔤, τότε η G είναι συμπαγής και ημιαπλή.
Παραδείγματα.
1. Θα υπολογίσουμε τη μορφή Killing της SU(2) περιορισμένης στα διαγώνια στοχεία. Θα δούμε στη συνέχεια ότι αυτό δεν είναι ιδιαίτερα περιοριστικό.
Στο προηγούμενο παράδειγμα είχαμε βρει ότι
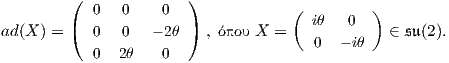 |
Για X = 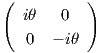 ,Y =
,Y = 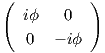 ∈ 𝔰𝔲(2), με απλές πράξεις προκύπτει ότι
∈ 𝔰𝔲(2), με απλές πράξεις προκύπτει ότι
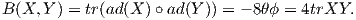
Για τον πίνακα της απεικόνισης B ως προς τη συνήθη βάση {X1,X2,X3} της 𝔰𝔲(2) με στοιχεία Bij = B(Xi,Xj), θα έχουμε
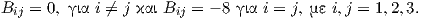
΄Αρα τελικά προκύπτει ότι
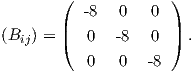
Παρατηρούμε ότι det(Bij)≠0 δηλαδή η μορφή Killing είναι μη εκφυλισμένη, επομένως η ομάδα SU(2) είναι ημιαπλή.
2. Θα υπολογίσουμε τη μορφή Killing της U(2). Θεωρούμε τη βάση της 𝔲(2) = {A ∈ GL2ℂ : A + t = I}
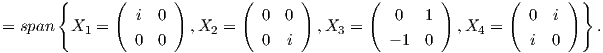
Αρχικά υπολογίζουμε τον πίνακα της γραμμικής απεικόνισης ad(X) : 𝔲(2) → 𝔲(2) ως προς την προηγούμενη βάση.
Επιλέγουμε για ευκολία στους υπολογισμούς έναν πίνακα με διαγώνια στοιχεία 𝔲(2) ∋ X = 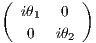 . Τότε
. Τότε
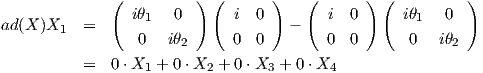
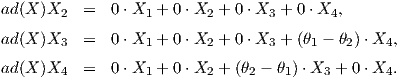
![( )
0 0 0 0
| |
[ad(X )] = || 0 0 0 0 || .
|( 0 0 0 θ2 - θ1 |)
0 0 θ - θ 0
1 2](02_chapter_08165x.png) |
Επομένως, αν X = 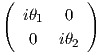 ,Y =
,Y = 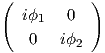 ∈ 𝔲(2), τότε η μορφή Killing της 𝔲(2) θα είναι
∈ 𝔲(2), τότε η μορφή Killing της 𝔲(2) θα είναι
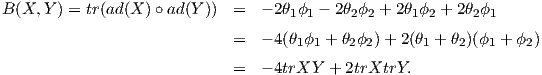
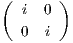 και B(X,X) = 0, δηλαδή η ομάδα U(2)
δεν είναι ημιαπλή.
και B(X,X) = 0, δηλαδή η ομάδα U(2)
δεν είναι ημιαπλή.
Με εκτενείς υπολογισμούς προκύπτει ότι η μορφή Killing μερικών ομάδων πινάκων είναι οι εξής:

Οι μεγιστικοί δακτύλιοι αποτελούν τους δομικούς λίθους των συμπαγών ομάδων Lie. Σε αυτή την ενότητα θα αναφέρουμε κάποια χρήσιμα αποτελέσματα που αφορούν τους μεγιστικούς δακτυλίους των ομαδών Lie και αποτελούν το κλειδί για την ταξινόμηση των συμπαγών και συνεκτικών ομάδων Lie. Για εύληπτες παρουσιάσεις παραπέμπουμε στα βιβλία [5], [14] και στην εργασία [13].
Ο κύκλος S1 είναι η μοναδική συμπαγής και συνεκτική ομάδα Lie διάστασης 1 και το καρτεσιανό γινόμενο πολλών τέτοιων κύκλων είναι, λόγω του Θεωρήματος 8.3, η μόνη συμπαγής, συνεκτική και αβελιανή ομάδα Lie. ΄Ενα τέτοιο γινόμενο κύκλων ονομάζεται δακτύλιος.
΄Ενας μεγιστικός δακτύλιος μιας ομάδας Lie G θα συμβολίζεται με T και είναι ουσιαστικά μια μέγιστη συνεκτική, αβελιανή υποομάδα της. Στα παραδείγματα υπολογισμού της συζυγούς αναπαράστασης και της μορφής Killing χρησιμοποιήσαμε στοιχεία του δακτυλίου T.
Ορισμός 8.11: ΄Ενας n-διάστατος δακτύλιος (torus) Tn σε μια ομάδα Lie G είναι μια υποομάδα αυτής η
οποία είναι ισόμορφη με το καρτεσιανό γινόμενο n κύκλων S1, δηλαδή Tn S1 ×
S1 × ×S1. ΄Ενας δακτύλιος
T ονομάζεται μεγιστικός δακτύλιος (maximal torus) της G, αν για οποιονδήποτε άλλο δακτύλιο S της G
με T ⊂ S ⊂ G ισχύει T = S.
×S1. ΄Ενας δακτύλιος
T ονομάζεται μεγιστικός δακτύλιος (maximal torus) της G, αν για οποιονδήποτε άλλο δακτύλιο S της G
με T ⊂ S ⊂ G ισχύει T = S.
Παρατηρήσεις.
1. Αν G,H είναι δύο ομάδες, τότε το καρτεσιανό γινόμενο G×H γίνεται ομάδα με πράξη (g,h)(g1,h1) = (gg1,hh1), (g,g1 ∈ G και h,h1 ∈ H). Στην περίπτωση που οι ομάδες G και H είναι υποσύνολα του Mn(K) και Mm(K) αντίστοιχα, τότε ένα τυχαίο στοιχείο (g,h) του γινομένου G × H γράφεται ως (g,h) = diag(g,h), δηλαδή είναι ένας (n + m) × (n + m) πίνακας. Τότε για (A1,B1),(A2,B2) ∈ G × H είναι
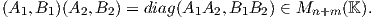
Επομένως, με βάση τα παραπάνω είναι εύκολο να δούμε ότι ο 2-διάστατος δακτύλιος T2 S1 × S1 εκφράζεται
ως
S1 × S1 εκφράζεται
ως
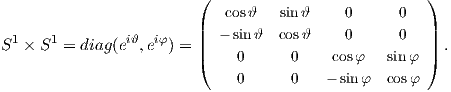
Γενικά ένας n-διάστατος δακτύλιος Tn είναι ένας 2n × 2n διαγώνιος πίνακας της μορφής
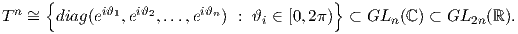
Τέλος, θυμίζουμε ότι Tn ℝn∕ℤn, δηλαδή ένας δακτύλιος είναι μια συμπαγής, συνεκτική και αβελιανή
ομάδα.
ℝn∕ℤn, δηλαδή ένας δακτύλιος είναι μια συμπαγής, συνεκτική και αβελιανή
ομάδα.
2. Μια ομάδα Lie G περιέχει πάντα κάποιον δακτύλιο, αφού αποδεικνύεται ότι για οποιοδήποτε X ∈ 𝔤 η κλειστότητα του συνόλου {exp(tX) : t ∈ ℝ} (γνωστή και ως κλειστή θήκη), είναι μια συμπαγής, συνεκτική και αβελιανή ομάδα, άρα από το Θεώρημα 8.3 είναι ένας δακτύλιος.
Απόδειξη. Πράγματι, αν T ⊂ T1 ⊂ T2 ⊂ είναι μια αύξουσα ακολουθία από δακτυλίους της G, αρκεί
να δείξουμε ότι αυτή είναι πεπερασμένη. Παίρνοντας τις άλγεβρες Lie των παραπάνω δακτυλίων, έχουμε
την ακολουθία 𝔱 ⊂ 𝔱1 ⊂ 𝔱2 ⊂
είναι μια αύξουσα ακολουθία από δακτυλίους της G, αρκεί
να δείξουμε ότι αυτή είναι πεπερασμένη. Παίρνοντας τις άλγεβρες Lie των παραπάνω δακτυλίων, έχουμε
την ακολουθία 𝔱 ⊂ 𝔱1 ⊂ 𝔱2 ⊂ δηλαδή είναι μια αύξουσα ακολουθία διανυσματικών χώρων πεπερασμένης
διάστασης, οπότε πρέπει και αυτή να είναι πεπερασμένη. ▄
δηλαδή είναι μια αύξουσα ακολουθία διανυσματικών χώρων πεπερασμένης
διάστασης, οπότε πρέπει και αυτή να είναι πεπερασμένη. ▄
Πρόταση 8.8: ΄Εστω G μια συμπαγής ομάδα Lie. Τότε κάθε μεγιστικός δακτύλιος T είναι μια μεγιστική συνεκτική αβελιανή υποομάδα της G.
Απόδειξη. Πράγματι, αν T ⊂ A, όπου A είναι μια συνεκτική και αβελιανή ομάδα, τότε T ⊂ ( η κλειστή θήκη της A). Επειδή η G είναι συμπαγής και η είναι κλειστή, θα είναι και συμπαγής, άρα η είναι μια συνεκτική, συμπαγής και αβελιανή ομάδα, δηλαδή είναι ένας δακτύλιος. Τέλος, αφού T ⊂ και T μεγιστικός δακτύλιος, θα πρέπει T = . ▄
Παρατήρηση. Αν T είναι ένας μεγιστικός δακτύλιος της ομάδας Lie G, τότε μέσω του εσωτερικού αυτομορφισμού Ig : G → G, το σύνολο gTg-1 = {gαg-1 : α ∈ T} είναι ένας μεγιστικός δακτύλιος της G. Πράγματι, επειδή η απεικόνιση Ig είναι ισομορφισμός (g ∈ G), το σύνολο gTg-1 θα είναι ισόμορφο με τον T, άρα θα είναι ένας δακτύλιος. Αυτός είναι μεγιστικός δακτύλιος. Πράγματι, έστω T′⊂ G ένας μεγιστικός δακτύλιος της G. Τότε είναι gTg-1 ⊂ T′, άρα T ⊂ Ig-1(T′), πράγμα άτοπο, διότι ο T είναι μεγιστικός. Επομένως, ο gTg-1 είναι μεγιστικός.
Το κεντρικό θεώρημα στη θεωρία δακτυλίων είναι το εξής:
Θεώρημα 8.12: ΄Εστω G μια συμπαγής και συνεκτική ομάδα Lie. Τότε
(α) Κάθε στοιχείο g ∈ G περιέχεται σε κάποιον μεγιστικό δακτύλιο.
(β) Οποιοιδήποτε δύο μεγιστικοί δακτύλιοι είναι συζυγείς. Δηλαδή αν T1,T2 είναι μεγιστικοί δακτύλιοι της
G, τότε υπάρχει ένα στοιχείο g ∈ G τέτοιο ώστε gT1g-1 = T2.
Από το δεύτερο σκέλος του προηγούμενου θεωρήματος, προκύπτει ότι δύο τυχαίοι μεγιστικοί δακτύλιοι έχουν την ίδια διάσταση, δηλαδή η διάσταση των δακτυλίων ορίζει μια αναλλοίωτη ποσότητα στις συμπαγείς και συνεκτικές ομάδες Lie ως ακολούθως:
Ορισμός 8.12: Η τάξη (rank) μιας συμπαγούς και συνεκτικής ομάδας Lie είναι η διάσταση ενός μεγιστικού δακτυλίου.
Κάποιες συνέπειες του παραπάνω κεντρικού θεωρήματος είναι οι εξής:
Πρόταση 8.9: ΄Εστω G μια συμπαγής και συνεκτική ομάδα Lie με άλγεβρα Lie 𝔤. Τότε:
(1) ϒπάρχει μια 1-1 αντιστοιχία μεταξύ μεγιστικών δακτυλίων T της G και μεγιστικών αβελιανών υποχώρων
𝔥 της 𝔤, η οποία δίνεται μέσω της απεικόνισης T ↔ 𝔥 = exp(𝔱), όπου 𝔱 είναι η άλγεβρα Lie του T.
(2) Αν T είναι ένας μεγιστικός δακτύλιος της G με άλγεβρα Lie 𝔱, τότε G = ⋃
g∈GgTg-1 και 𝔤 =
⋃
g∈GAd(g)𝔱.
(3) Το κέντρο της G είναι ίσο με την τομή όλων των μεγιστικών δακτυλίων της G.
(4) Αν S είναι ένα υποσύνολο της G, ορίζουμε την κεντροποιούσα (centralizer) υποομάδα του S ως το
σύνολο C(S) = {g ∈ G : gx = xg για κάθε x ∈ S}. Τότε, αν T είναι μεγιστικός δακτύλιος της G, ισχύει
C(T) = T.
(5) Οι μεγιστικοί δακτύλιοι είναι επίσης μεγιστικές αβελιανές υποομάδες της G.
Στη συνέχεια θα δούμε κάποια παραδείγματα μεγιστικών δακτυλίων των γνωστών μας ομάδων Lie.
Παραδείγματα.
1. ΄Ενας μεγιστικός δακτύλιος της U(n) είναι το σύνολο
![( eiθ1 0 ⋅⋅⋅ 0 )
{ | 0 eiθ2 ⋅⋅⋅ 0 | }
T = diag (eiθ1,...,eiθn) = || . . . || : θi ∈ (0,2π] .
( .. .. ... .. )
0 0 ⋅⋅⋅ eiθn](02_chapter_08180x.png)
Το σύνολο T είναι ένας δακτύλιος, διότι είναι ισόμορφος με το καρτεσιανό γινόμενο n κύκλων. Θα αποδείξουμε ότι είναι μεγιστικός, δηλαδή δεν υπάρχει άλλος δακτύλιος που να τον περιέχει. Αυτό είναι ισοδύναμο με το να δείξουμε ότι κάθε στοιχείο A ∈ U(n), που μετατίθεται με όλα τα στοιχεία του T, ανήκει στον T (αν υπήρχε για παράδειγμα κάποιος άλλος δακτύλιος T′ ο οποίος να περιέχει τον T, τότε όλα τα στοιχεία του T′ θα μετατίθενται με όλα τα στοιχεία του T, οπότε ο T δεν θα είναι μεγιστικός). ΄Εστω ένας πίνακας A ∈ U(n) που αντιμετατίθεται με κάθε στοιχείο του T. ΄Εστω Tj η υποομάδα του T η οποία αποτελείται από τους πίνακες με 1 στο j-στοιχείο της διαγωνίου. Τότε, αν πάρουμε
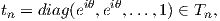
παρατηρούμε ότι tnAen = Atnen = Aen, (όπου en είναι το διάνυσμα στήλη με 1 στην n-γραμμή και μηδέν αλλού). Αυτό σημαίνει ότι το διάνυσμα Aen διατηρείται σταθερό από την δράση των στοιχείων του Tn, οπότε θα έχουμε Aen = λnen για κάποιο λn ∈ ℂ, δηλαδή η n-στήλη του A θα είναι της μορφής (0,0,…,λn). Επειδή A ∈ U(n), οι στήλες του θα αποτελούν βάση του χώρου ℝn2 , οπότε το μέτρο κάθε στήλης θα είναι ίσο με 1, επομένως μπορούμε να θέσουμε λn = eiϕn, για κάποιο ϕn ∈ (0,2π). Επαναλαμβάνοντας την παραπάνω διαδικασία για n = 1,2,…,n- 1, προκύπτει ότι
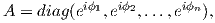
άρα A ∈ T, δηλαδή ο T είναι μεγιστικός δακτύλιος της U(n). Η τάξη της U(n) θα είναι n.
2. ΄Ενας μεγιστικός δακτύλιος της SU(n) είναι το σύνολο των διαγώνιων πινάκων της μορφής
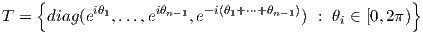
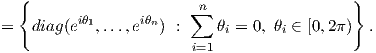
Το παραπάνω σύνολο είναι ισόμορφο με το καρτεσιανό γινόμενο n- 1 κύκλων, οπότε είναι δακτύλιος και η τάξη της SU(n) είναι n - 1.
Για το ότι είναι μεγιστικός, θα αποδείξουμε πρώτα την απλή περίπτωση για n = 2, δηλαδή θα δείξουμε ότι το σύνολο
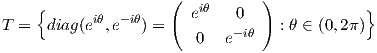
είναι ένας μεγιστικός δακτύλιος της SU(2). Είναι γνωστό ότι ένα τυχαίο στοιχείο της SU(2) γράφεται ως
A = 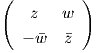 . Ο πίνακας A μετατίθεται με τα στοιχεία του συνόλου T, επομένως θα έχουμε
. Ο πίνακας A μετατίθεται με τα στοιχεία του συνόλου T, επομένως θα έχουμε
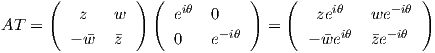
και
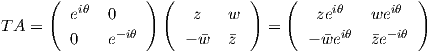
Από ισότητα πινάκων παίρνουμε ότι
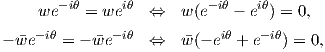
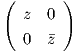 . ΄Ομως A ∈ SU(2), οπότε det(A) = 1
δηλαδή z = 1 ή
. ΄Ομως A ∈ SU(2), οπότε det(A) = 1
δηλαδή z = 1 ή 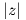 2 = 1, άρα μπορούμε να θέσουμε z = eiφ για κάποιο φ ∈ (0,2π). Οπότε τελικά ο A θα έχει τη
μορφή
2 = 1, άρα μπορούμε να θέσουμε z = eiφ για κάποιο φ ∈ (0,2π). Οπότε τελικά ο A θα έχει τη
μορφή
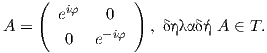
Στη συνέχεια, θα αποδείξουμε την περίπτωση για n = 3 και με όμοιο τρόπο αποδεικνύεται για n > 3. Αποδεικνύουμε ότι το σύνολο
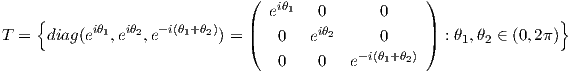
είναι ένας μεγιστικός δακτύλιος της SU(3) (διάστασης 2). ΄Εστω A =  ∈ SU(3), ο οποίος
μετατίθεται με κάθε στοιχείο της T. Θα δείξουμε ότι A ∈ T. Ο A θα μετατίθεται με το στοιχείο
B =
∈ SU(3), ο οποίος
μετατίθεται με κάθε στοιχείο της T. Θα δείξουμε ότι A ∈ T. Ο A θα μετατίθεται με το στοιχείο
B =  του T, οπότε θα ισχύει ότι AB = BA όπου
του T, οπότε θα ισχύει ότι AB = BA όπου
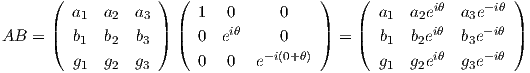
και
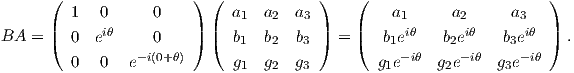
΄Αρα για κάθε θ ∈ (0,2π) από ισότητα πινάκων θα πάρουμε
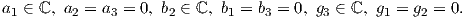
΄Αρα ο πίνακας A θα έχει τη μορφή A = 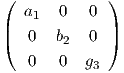 και παρατηρούμε ότι κάθε γραμμή είναι
πολλαπλάσιο των e1 =
και παρατηρούμε ότι κάθε γραμμή είναι
πολλαπλάσιο των e1 = 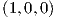 ,e2 =
,e2 = 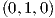 και e3 =
και e3 = 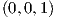 . Επειδή A ∈ SU(3) = U(3) ∩ SL3(ℂ), οι
γραμμές του θα έχουν μοναδιαίο μήκος, δηλαδή
. Επειδή A ∈ SU(3) = U(3) ∩ SL3(ℂ), οι
γραμμές του θα έχουν μοναδιαίο μήκος, δηλαδή 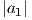 =
= 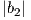 =
= 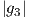 = 1, οπότε μπορούμε να θέσουμε
a1 = eiφ1,b2 = eiφ2 και g3 = eiφ3 για κάποια φ1,φ2,φ3 ∈ (0,2π). Επίσης θα ισχύει και det(A) = 1 δηλαδή
a1b2g3 = 1 ή eiφ3 =
= 1, οπότε μπορούμε να θέσουμε
a1 = eiφ1,b2 = eiφ2 και g3 = eiφ3 για κάποια φ1,φ2,φ3 ∈ (0,2π). Επίσης θα ισχύει και det(A) = 1 δηλαδή
a1b2g3 = 1 ή eiφ3 = 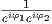 = e-i(φ1+φ2). Επομένως, ο A θα είναι
= e-i(φ1+φ2). Επομένως, ο A θα είναι
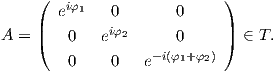
΄Ενας εναλλακτικός τρόπος να αποδείξουμε ότι το σύνολο T του προηγούμενου παραδείγματος είναι μεγιστικός δακτύλιος της ομάδας SU(n), είναι να θεωρήσουμε τον ισομορφισμό
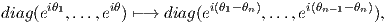
ο οποίος απεικονίζει τον T σε έναν δακτύλιο της U(n - 1). Το ότι είναι μεγιστικός αποδεικνύεται, όπως στο Παράδειγμα 1.
3. Οι τάξη των ομάδων Sp(n),SO(2n) και SO(2n + 1) είναι n (βλ. ΄Ασκηση 5).
Από το πρώτο μέρος του Θεωρήματος 8.12 και με βάση τα προηγούμενα παραδείγματα, γίνεται κατανοητός ο λόγος που πήραμε πίνακες με διαγώνια στοιχεία για να υπολογίσουμε τη μορφή Killing των ομάδων SU(2) και U(2).
Η ταξινόμηση των συμπαγών και συνεκτικών ομάδων Lie δεν είναι μια εύκολη υπόθεση. Σε μια απο τις παρατηρήσεις που ακολουθούν το παρακάτω θεώρημα ταξινόμησης, αναφέρουμε το γενικό σκεπτικό της απόδειξης.
Ορισμός 8.13: Μια ομάδα Lie ονομάζεται απλή (simple) εάν δεν είναι αβελιανή και δεν περιέχει κάποια γνήσια κανονική υποομάδα Lie. Μια άλγεβρα Lie ονομάζεται απλή, εάν δεν είναι μεταθετική και δεν περιέχει κάποιο γνήσιο ιδεώδες.
Θεώρημα 8.13: (Θεώρημα ταξινόμησης συμπαγών και συνεκτικών ομάδων Lie).
(1) ΄Εστω G μια συμπαγής και συνεκτική ομάδα Lie. Τότε υπάρχει ένας χώρος κάλυψης της G 9
ο οποίος είναι ισόμορφος με το ευθύ γινόμενο ενός δακτυλίου και μιας συμπαγούς, συνεκτικής και απλά
συνεκτικής ομάδας Lie.
(2) Κάθε συμπαγής, συνεκτική και απλά συνεκτική ομάδα Lie είναι ισόμορφη με το ευθύ γινόμενο απλών,
συμπαγών, συνεκτικών και απλά συνεκτικών ομάδων Lie.
(3) Οι απλές, συμπαγείς, συνεκτικές και απλά συνεκτικές ομάδες Lie είναι οι εξής:
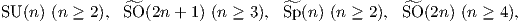
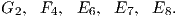
Παρατηρήσεις.
1. Η ομάδα  (n) είναι ο καθολικός χώρος κάλυψης της SO(2n + 1), συμβολίζεται με Spin(n) και
ονομάζεται ομάδα στροφορμής (spin group). Οι ομάδες στροφορμής έχουν ιδιαίτερη σημασία
στη φυσική και μπορούν να οριστούν μέσω κάποιων σημαντικών αλγεβρών, τις άλγεβρες
Clifford10
(n) είναι ο καθολικός χώρος κάλυψης της SO(2n + 1), συμβολίζεται με Spin(n) και
ονομάζεται ομάδα στροφορμής (spin group). Οι ομάδες στροφορμής έχουν ιδιαίτερη σημασία
στη φυσική και μπορούν να οριστούν μέσω κάποιων σημαντικών αλγεβρών, τις άλγεβρες
Clifford10
2. Οι άλγεβρες Lie των τεσσάρων πρώτων ομάδων Lie συμβολίζονται με An-1,Bn,Cn και Dn αντίστοιχα,
συμβολισμός που αποδίδεται στον Cartan. Ισχύουν οι εξής ισομορφισμοί: A1 B1
B1 C1, B2
C1, B2 C2, A3
C2, A3 D3 και
D2 = A1 ⊕ A1.
D3 και
D2 = A1 ⊕ A1.
3. Οι επόμενες πέντε ομάδες ονομάζονται ασυνήθιστες ομάδες Lie (exceptional Lie groups) και οι αριθμοί που τις συνοδεύουν είναι η τάξη τους. ΄Εχουν διαστάσεις 14,52,78,133 και 248 αντίστοιχα. Η ύπαρξη και ορισμός της καθεμίας από αυτές σχετίζεται με ενδιαφέρουσες και όχι εύκολες στην περιγραφή αλγεβρικές και γεωμετρικές δομές. Για μια παρουσίαση παραπέμπουμε στο βιβλίο [2].
4. ΄Οσον αφορά την ιδέα της απόδειξης του θεωρήτος της ταξινόμησης των συμπαγών και συνεκτικτικών ομάδων Lie, αυτή είναι η εξής: ϒπάρχει μια 1 - 1 αντιστοιχία μεταξύ συμπαγών ομάδων Lie και συμπαγών ημιαπλών αλγεβρών Lie. Η αντιστοιχία αυτή διατηρείται και μετά τη μιγαδοποίηση των αλγεβρών αυτών. Οι μιγαδικές ημιαπλές άλγεβρες Lie έχουν τη δική τους θεωρία ανάπτυξης, η οποία, επειδή είναι καθαρά αλγεβρική, είναι πιο προσπελάσιμη (αν και όχι τετριμμένη). Σύμφωνα με τη θεωρία αυτή, η μελέτη των μιγαδικών ημιαπλών αλγεβρών Lie ανάγεται στη μελέτη των διαγραμμάτων Dynkin11 (Dynkin diagrams), η ταξινόμηση των οποίων ανάγεται σε ένα στοιχειώδες, αλλά όχι εύκολο, συνδυαστικό πρόβλημα. Συνεπώς, τελικά λαμβάνουμε μια 1 - 1 αντιστοιχία μεταξύ συμπαγών, συνεκτικών και απλά συνεκτικών ομάδων Lie και διαγραμμάτων Dynkin.
1. ΄Εστω V ένας διανυσματικός χώρος με εσωτερικό γινόμενο 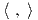 και T : V → V ένας θετικά ορισμένος
γραμμικός τελεστής. Τότε είναι εύκολο να δούμε ότι η σχέση
και T : V → V ένας θετικά ορισμένος
γραμμικός τελεστής. Τότε είναι εύκολο να δούμε ότι η σχέση 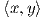 ′ =
′ = 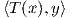 ορίζει ένα νέο εσωτερικό
γινόμενο στον V . Αποδείξτε το αντίστροφο: ΄Εστω
ορίζει ένα νέο εσωτερικό
γινόμενο στον V . Αποδείξτε το αντίστροφο: ΄Εστω 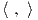 και
και 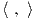 ′ δύο εσωτερικά γινόμενα σε έναν διανυσματικό
χώρο V πεπερασμένης διάστασης. Τότε υπάρχει μοναδικός τελεστής T : V → V τέτοιος ώστε
′ δύο εσωτερικά γινόμενα σε έναν διανυσματικό
χώρο V πεπερασμένης διάστασης. Τότε υπάρχει μοναδικός τελεστής T : V → V τέτοιος ώστε 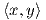 ′ =
′ = 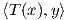 ,
για κάθε x,y ∈ V .
,
για κάθε x,y ∈ V .
(ϒπόδειξη. Συμβουλευτείτε κάποιο βιβλίο γραμμικής άλγεβρας στα κεφάλαιο σχετικά με χώρους με εσωτερικό γινόμενο και αυτοσυζυγείς τελεστές.)
2. ΄Εστω ϕ : G → Aut(V ) μια αναπαράσταση της G τέτοια ώστε ϕ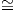 ϕ1 ⊕ ϕ2, όπου ϕi : G → Aut(Ui) είναι μη
ισοδύναμες υποαναπαραστάσεις της ϕ. ΄Εστω Q,B δύο τυχαία G-αναλλοίωτα εσωτερικά γινόμενα στους
υπόχωρους U1,U2 του V αντίστοιχα. Αποδείξτε ότι κάθε G-αναλλοίωτο εσωτερικό γινόμενο στον V έχει τη
μορφή
ϕ1 ⊕ ϕ2, όπου ϕi : G → Aut(Ui) είναι μη
ισοδύναμες υποαναπαραστάσεις της ϕ. ΄Εστω Q,B δύο τυχαία G-αναλλοίωτα εσωτερικά γινόμενα στους
υπόχωρους U1,U2 του V αντίστοιχα. Αποδείξτε ότι κάθε G-αναλλοίωτο εσωτερικό γινόμενο στον V έχει τη
μορφή
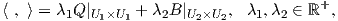
για το οποίο ισχύει 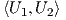 = 0.
= 0.
3. ΄Εστω G μια αβελιανή ομάδα Lie. Αποδείξτε ότι κάθε μιγαδική μη αναγώγιμη αναπαράσταση της G έχει διάσταση 1.
(ϒπόδειξη. Χρησιμοποιείστε το Λήμμα του Schur (δεύτερη εκδοχή).)
4. ΄Εστω G μια ομάδα πινάκων με άλγεβρα Lie 𝔤. Δείξτε ότι για κάθε g ∈ G και για κάθε X,Y ∈ 𝔤 ισχύει
![[Ad (g)(X ),Ad (g )(Y )] = Ad (g )([X,Y ]).](02_chapter_08230x.png)
5. Αποδείξτε ότι η μορφή Killing μιας άλγεβρας Lie είναι μια συμμετρική διγραμμική μορφή (Θεώρημα 8.6).
6. ΄Εστω (ℝn,+) η προσθετική ομάδα Lie. Συμβολίζουμε με
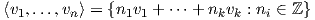
(α) ΄Εστω {e1,…,en} η κανονική βάση του ℝn. Αποδείξτε ότι η απεικόνιση
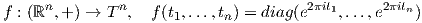
(β) Αποδείξτε το (α) παίρνοντας μια τυχαία βάση {υ1,…,υn} του ℝn.
(γ) Αν {υ1,…,υk} είναι ένα τυχαίο γραμμικώς ανεξάρτητο υποσύνολο του ℝn, αποδείξτε ότι η ομάδα (ℝn,+)∕⟨υ1,…,υk⟩ είναι ισόμορφη με την Tk × (ℝn-k,+).
7. (α) Αποδείξτε ότι ένας μεγιστικός δακτύλιος της ομάδας Sp(n) έχει τη μορφή
![{ }
T = diag(eiθ1,...,eiθn) : θi ∈ (0,2π] .](02_chapter_08233x.png)
(β) ΄Εστω rotθ ο 2 × 2 πίνακας περιστροφής, δηλαδή rotθ = 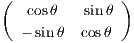 . Δείξτε ότι το σύνολο των
διαγώνιων πινάκων
. Δείξτε ότι το σύνολο των
διαγώνιων πινάκων
![T = {diag(rotθ1,...,rotθn) : θi ∈ (0,2π]} ,](02_chapter_08235x.png)
αποτελεί έναν μέγιστο δακτύλιο της ομάδας SO(2n).
(γ) Δείξτε ότι το σύνολο
![T = {diag(rotθ1,...,rotθn,1) : θi ∈ (0,2 π]} ,](02_chapter_08236x.png)
είναι ένας μεγιστικός δακτύλιος της SO(2n + 1).
(δ) Βρείτε τις άλγεβρες Lie των παραπάνω δακτυλίων.
8. Αποδείξτε ότι για κάθε x ∈ SO(3), υπάρχει g ∈ SO(3) έτσι ώστε
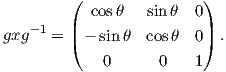
[1] J. F Adams, Lectures on Lie Groups, The University of Chicago Press, 1969.
[2] J. F. Adams, Z. Mahmud and M. Mimura, Lectures on Exceptional Lie Groups, The University of Chicago Press, 1996.
[3] A. Arvanitoyeorgos, An Introduction to Lie Groups and the Geometry of Homogeneous Spaces, American Mathematical Society, 2003.
[4] Α. Αρβανιτογεώργος, Ομάδες Lie, Ομογενείς Χώροι και Διαφορική Γεωμετρία, Εκδόσεις Τροχαλία, Αθήνα 1999.
[5] A. Baker, Matrix groups: An Introduction to Lie Group Theory, Springer 2003.
[6] T. Bröcker and T. tom Dieck, Representations of Compact Lie Groups, Springer, 1985.
[7] D.S. Dummit and R.M. Foote, Abstract Algebra, Third Edition, John Wiley, NJ 2014.
[8] H.D. Fegan, Introduction to Compact Lie Groups, Word Scientific, Singapore, 1991.
[9] S.H. Friedberg and A.J. Insel, Linear Algebra, Fourth Edition, 2002.
[10] W. Fulton and J. Harris, Representation Theory: A First Course, Springer 1999.
[11] B.C. Hall, Lie Groups, Lie Algebras and Representations: An Elementary Introduction, Springer 2004.
[12] A. A. Sagle and R.E. Walde, Introduction to Lie Groups and Lie Algebras, Academic Press, New York 1973.
[13] Μ. Σταθά, Μέγιστοι Δακτύλιοι των Ομάδων Πινάκων, Μαθηματική Επιθεώρηση, 74 (2010) 43–60.
[14] K. Tapp, Matrix groups for Undergraduates, American Mathematical Society, 2005.