Κεφάλαιο 7
Ομάδες Lie
Σύνοψη
Μια ομάδα Lie είναι μια λεία πολλαπλότητα και ταυτόχρονα ομάδα, τέτοια ώστε οι πράξεις της ομάδας να είναι λείες
απεικονίσεις. Η δομή της ομάδας προσδίδει ιδιαίτερα πλούσια χαρακτηριστικά στις πολλαπλότητες αυτές. Για
παράδειγμα, η μελέτη του εφαπτόμενου χώρου αρκεί να γίνει μόνο στο ουδέτερο στοιχείο της ομάδας. Τα πιο
σημαντικά παραδείγματα ομάδων Lie είναι οι ομάδες πινάκων, δηλαδή κλειστές υποομάδες της γενικής γραμμικής
ομάδας. Μια ιδιαίτερα σημαντική κλάση διανυσματικών πεδίων σε μια ομάδα Lie είναι τα αριστερά αναλλοίωτα
διανυσματικά πεδία. Μέσω αυτών ορίζεται ένα αλγεβρικό αντικείμενο, η άλγεβρα Lie μιας ομάδας
Lie. ΄Ετσι ορίζεται ένα γινόμενο Lie στο εφαπτόμενο χώρο της στο ουδέτερο στοιχείο. Ιδιαίτερα
χρήσιμες καμπύλες σε μια ομάδα Lie είναι οι μονοπαραμετρικές υποομάδες και μέσω αυτών ορίζεται η
εκθετική απεικόνιση. Για την περίπτωση των ομάδων πινάκων, αυτή είναι η συνηθισμένη εκθετική
απεικόνιση πινάκων. Οι αναφορές μας είναι τα βιβλία [1], [2], [6], [8] και [11]. Το βιβλίο [12] είναι πιο
προχωρημένο.
Προαπαιτούμενη γνώση
Διαφορικός Λογισμός μιας και πολλών μεταβλητών, Εισαγωγή στις Πολλαπλότητες, Γραμμική Άλγεβρα.
Μια ομάδα Lie είναι μια λεία πολλαπλότητα G, η οποία είναι ταυτόχρονα και ομάδα (υπό την γνωστή αλγεβρική
έννοια), έτσι ώστε οι πράξη της ομάδας, καθώς και η απεικόνιση αντιστροφής να είναι λείες απεικονίσεις.
Αποτελούν μια εξαιρετικά σημαντική κλάση πολλαπλοτήτων με μεγάλο εύρος εφαρμογών στη γεωμετρία, στη
φυσική, στην αρμονική ανάλυση, στις διαφορικές εξισώσεις, αλλά και σε άλλους κλάδους των μαθηματικών όπως
στατιστική, θεωρία ελέγχου κ.ά. Οι ομάδες Lie χρησιμοποιήθηκαν από τον Felix Klein για τη θεμελίωση της
γεωμετρίας στο πρόγραμμα του Erlangen, θέμα το οποίο θα συζητήσουμε στο Κεφάλαιο 10. Για τους
λόγους αυτούς, ένα μεγάλο τμήμα του βιβλίου αυτού ασχολείται με τις ομάδες Lie και τη γεωμετρία
τους.
Ο σπόρος της θεωρίας των ομάδων Lie βρίσκεται στις προσπάθειες του Sophus Lie περί το 1870 να
αναπτύξει μια θεωρία συμμετριών για την επίλυση συστημάτων διαφορικών εξισώσεων. Η αρχική ονομασία
που έδωσε ο Lie στις συμμετρίες αυτές ήταν συνεχείς ομάδες. Ο όρος ομάδα Lie δόθηκε το 1893
από τον μαθητή του Lie, Arthur Tresse ([10]), αλλά η πιο ευρεία χρήση του οφείλεται στον Henri
Cartan περί το 1930. Για διάφορα ιστορικά θέματα σχετικά με ομάδες Lie παραπέμπουμε στο βιβλίο
[5].
Ο στόχος του Lie ήταν η ανάπτυξη μια θεωρίας ανάλογης αυτής της θεωρίας του 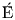 variste Galois, σύμφωνα
με την οποία τη θέση της λύσης μιας πολυωνυμικής εξίσωσης με ριζικά, θα έπαιρνε μια πεπερασμένη ομάδα
συμμετριών μιας διαφορικής εξίσωσης. Οι διαφορικές εξισώσεις που μελετούσε τότε ο Lie είναι γνωστές ως
εξισώσεις τύπου Lie, τυπικό παράδειγμα των οποίων είναι η εξίσωση Riccati. Τα απλούστερα παραδείγματα ομάδων
Lie είναι οι ομάδες ισομετρικών των ℝn, ℂn και ℍn (ℍ είναι το σύνολο των υπερμιγαδικών αριθμών),
απ΄ όπου προκύπτουν η ορθογώνια ομάδα O(n), η μοναδιαία ομάδα U(n) και η συμπλεκτική ομάδα
Sp(n).
variste Galois, σύμφωνα
με την οποία τη θέση της λύσης μιας πολυωνυμικής εξίσωσης με ριζικά, θα έπαιρνε μια πεπερασμένη ομάδα
συμμετριών μιας διαφορικής εξίσωσης. Οι διαφορικές εξισώσεις που μελετούσε τότε ο Lie είναι γνωστές ως
εξισώσεις τύπου Lie, τυπικό παράδειγμα των οποίων είναι η εξίσωση Riccati. Τα απλούστερα παραδείγματα ομάδων
Lie είναι οι ομάδες ισομετρικών των ℝn, ℂn και ℍn (ℍ είναι το σύνολο των υπερμιγαδικών αριθμών),
απ΄ όπου προκύπτουν η ορθογώνια ομάδα O(n), η μοναδιαία ομάδα U(n) και η συμπλεκτική ομάδα
Sp(n).
7.1 Ορισμός και παραδείγματα
Ορισμός 7.1: ΄Εστω G μια λεία πολλαπλότητα. Τότε η G ονομάζεται ομάδα Lie, εάν
(i) Η G είναι ομάδα.
(ii) Οι απεικονίσεις μ : G × G → G, (x,y) xy και i : G → G, x
xy και i : G → G, x x-1 να είναι λείες.
x-1 να είναι λείες.
Επειδή σε κάθε ομάδα Lie οι πράξεις της ομάδας είναι λείες απεικονίσεις, τότε θα είναι και συνεχείς, οπότε οι ομάδες Lie είναι
τοπολογικές ομάδες.
Η διάσταση μιας ομάδας Lie G είναι η διάσταση της G ως λεία πολλαπλότητα.
Παραδείγματα.
1. Τα σύνολα ℝn, ℂn και ℍn είναι ομάδες Lie με πράξη την πρόσθεση και αν εξαιρέσουμε το μηδενικό
στοιχείο γίνονται ομάδες Lie με πράξη τον πολλαπλασιασμό. Εδώ με ℍ συμβολίζουμε το σύνολο
των upermigadik�n arijm�n (quaternions), δηλαδή αριθμών της μορφής q = t + xi + yj + zk,
t,x,y,z ∈ ℝ, όπου {1,i,j,k} είναι μια βάση του ℝ4. Ο πολλαπλασιασμός ορίζεται από τις σχέσεις
i2 = j2 = k2 = -1,ij = k,ji = -k,ik = -j,ki = j,kj = -i,jk = i και στη συνέχεια με γραμμική επέκταση στο
ℍ. Ισχύει ότι ℍ ℝ4
ℝ4 ℂ2. Θα αναφερθούμε εκτενέστερα στους υπερμιγαδικούς αριθμούς και στους
ισομορφισμούς αυτούς, πιο κάτω.
ℂ2. Θα αναφερθούμε εκτενέστερα στους υπερμιγαδικούς αριθμούς και στους
ισομορφισμούς αυτούς, πιο κάτω.
2. Ο μοναδιαίος κύκλος S1 είναι μια ομάδα Lie. Μπορούμε να ταυτίσουμε τον κύκλο S1 με το σύνολο
{z ∈ ℂ : 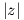 = 1}, όλων των μιγαδικών αριθμών με μέτρο μονάδα, το οποίο είναι ομάδα με πράξη τον
πολλαπλασιασμό στο ℂ. Η ταύτιση αυτή γίνεται ως εξής: (cosθ,sinθ) ↔ eiθ, i =
= 1}, όλων των μιγαδικών αριθμών με μέτρο μονάδα, το οποίο είναι ομάδα με πράξη τον
πολλαπλασιασμό στο ℂ. Η ταύτιση αυτή γίνεται ως εξής: (cosθ,sinθ) ↔ eiθ, i = 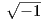 . Βλέπε περισσότερα στην
υποπαράγραφο 7.1.1.
. Βλέπε περισσότερα στην
υποπαράγραφο 7.1.1.
3. Αν G1,G2 είναι δύο ομάδες Lie, τότε το γινόμενο αυτών G1 ×G2 είναι λεία πολλαπλότητα και γίνεται ομάδα Lie
με πράξη τον πολλαπλασιασμό στην ομάδα G1 × G2, ο οποίος ορίζεται ως εξής: αν (g1,h1),(g2,h2) ∈ G1 × G2,
τότε (g1,h1) ⋅ (g2,h2) = (g1g2,h1h2).
Ο n-διάστατος δακτύλιος Tn = S1 × × S1 είναι ένα τέτοιο παράδειγμα.
× S1 είναι ένα τέτοιο παράδειγμα.
4. Η γενική γραμμική ομάδα (general linear group) GLnℝ είναι το πιο σημαντικό παράδειγμα ομάδας Lie. Το
σύνολο GLnℝ αποτελείται από όλους τους n × n αντιστρέψιμους πίνακες, δηλαδή
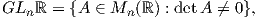 και
αποτελεί ομάδα με πράξη τον πολλαπλασιασμό πινάκων. Γνωρίζουμε από το Κεφάλαιο 2 ότι το σύνολο GLnℝ είναι
μια πολλαπλότητα διάστασης n2. Θα δείξουμε ότι οι πράξεις του γινομένου πινάκων και του αντιστρόφου ενός
πίνακα, είναι λείες απεικονίσεις. Πράγματι, το γινόμενο δύο πινάκων A = (αij) και B = (βij) της γενικής
γραμμικής ομάδας δίνεται ως AB = ∑
k=1nαikβkj, δηλαδή τα στοιχεία του γινομένου είναι πολυώνυμα. Συνεπώς, ο
πολλαπλασιασμός πινάκων,
και
αποτελεί ομάδα με πράξη τον πολλαπλασιασμό πινάκων. Γνωρίζουμε από το Κεφάλαιο 2 ότι το σύνολο GLnℝ είναι
μια πολλαπλότητα διάστασης n2. Θα δείξουμε ότι οι πράξεις του γινομένου πινάκων και του αντιστρόφου ενός
πίνακα, είναι λείες απεικονίσεις. Πράγματι, το γινόμενο δύο πινάκων A = (αij) και B = (βij) της γενικής
γραμμικής ομάδας δίνεται ως AB = ∑
k=1nαikβkj, δηλαδή τα στοιχεία του γινομένου είναι πολυώνυμα. Συνεπώς, ο
πολλαπλασιασμός πινάκων,
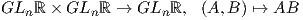
είναι λεία συνάρτηση. Επίσης, γνωρίζουμε ότι ο αντίστροφος πίνακας του A δίνεται από τη σχέση
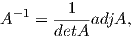
όπου adjA είναι ο προσαρτημένος πίνακας του A, άρα τα στοιχεία του A-1 θα είναι πολυώνυμα, οπότε η
απεικόνιση
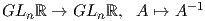
θα είναι λεία. Συνεπώς, η GLnℝ είναι μια ομάδα Lie. Με το ίδιο σκεπτικό οι ομάδες GLnℂ και GLnℍ είναι
ομάδες Lie. Από την γραμμική άλγεβρα γνωρίζουμε ότι η GLnℝ είναι ισόμορφη με την ομάδα όλων
των αντιστρέψιμων γραμμικών απεικονίσεων f : ℝn → ℝn (με πράξη τη σύνθεση απεικονίσεων),
δηλαδή το σύνολο των αυτομορφισμών του ℝn. Η ομάδα αυτή συμβολίζεται με Aut(ℝn). Ανάλογα,
αποδεικνύεται ότι η ειδική γραμμική ομάδα GLnℂ όλων των αντιστρέψιμων μιγαδικών πινάκων είναι ομάδα
Lie.
5. Η ειδική γραμμική ομάδα (special linear group) SLnℝ είναι η υποομάδα της GLnℝ που αποτελείται από όλους
τους πίνακες με ορίζουσα ίση με 1. ΄Εχουμε αποδείξει στο Κεφάλαιο 3 ότι η SLnℝ είναι μια κανονική
υποπολλαπλότητα της GLnℝ διάστασης n2 - 1. Το ότι οι πράξεις του γινομένου και της αντιστροφής είναι λείες
απεικονίσεις είναι κάπως πιο δύσκολο να αποδειχθεί και το παραλείπουμε. Ανάλογα προκύπτει ότι η ομάδα
SLnℂ = {A ∈ GLnℂ : detA = 1} είναι ομάδα Lie.
6. Η ορθογώνια ομάδα (orthogonal group) ορίζεται ως O(n) = {A ∈ GLnℝ : AAt = I}, (όπου At είναι ο
ανάστροφος του πίνακα A). Θα αποδείξουμε ότι η ορθογώνια ομάδα είναι μια κανονική υποπολλαπλότητα της
GLnℝ. Το ότι οι πράξεις της ομάδας είναι λείες απεικονίσεις, δεν είναι προφανές και το παραλείπουμε. ΄Εστω
Symnℝ το σύνολο όλων των n × n συμμετρικών πινάκων. Το σύνολο Symnℝ είναι ένας διανυσματικός χώρος
διάστασης n(n + 1)∕2 (άσκηση). Θεωρούμε την απεικόνιση
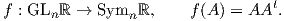 Θα
χρησιμοποιήσουμε το θεώρημα του κανονικού συνόλου στάθμης (Θεώρημα 3.2), συνεπώς πρέπει να αποδείξουμε
ότι το διαφορικό
Θα
χρησιμοποιήσουμε το θεώρημα του κανονικού συνόλου στάθμης (Θεώρημα 3.2), συνεπώς πρέπει να αποδείξουμε
ότι το διαφορικό
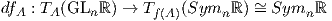 είναι
επί, για κάθε A ∈ GLnℝ, n ≥ 2. Επειδή το σύνολο GLnℝ είναι ανοικτό υποσύνολο του Mn(ℝ) θα έχουμε ότι
TA(GLnℝ) = TA(Mn(ℝ)) = Mn(ℝ), για κάθε A ∈ GLnℝ. Λόγω της Πρότασης 3.9, για κάθε πίνακα X ∈ Mn(ℝ)
υπάρχει καμπύλη γ(s) στην GLnℝ, τέτοια ώστε γ(0) = A και γ′(0) = X. Χρησιμοποιούμε την Πρόταση 3.11 και
υπολογίζουμε: Για να αποδείξουμε ότι η f είναι επί, αρκεί να δείξουμε ότι για κάθε A ∈ O(n) και για κάθε B ∈ Symnℝ υπάρχει
ένας n × n πίνακας X τέτοιος ώστε
είναι
επί, για κάθε A ∈ GLnℝ, n ≥ 2. Επειδή το σύνολο GLnℝ είναι ανοικτό υποσύνολο του Mn(ℝ) θα έχουμε ότι
TA(GLnℝ) = TA(Mn(ℝ)) = Mn(ℝ), για κάθε A ∈ GLnℝ. Λόγω της Πρότασης 3.9, για κάθε πίνακα X ∈ Mn(ℝ)
υπάρχει καμπύλη γ(s) στην GLnℝ, τέτοια ώστε γ(0) = A και γ′(0) = X. Χρησιμοποιούμε την Πρόταση 3.11 και
υπολογίζουμε: Για να αποδείξουμε ότι η f είναι επί, αρκεί να δείξουμε ότι για κάθε A ∈ O(n) και για κάθε B ∈ Symnℝ υπάρχει
ένας n × n πίνακας X τέτοιος ώστε
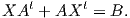 Πράγματι, η παραπάνω εξίσωση έχει τη λύση X =
Πράγματι, η παραπάνω εξίσωση έχει τη λύση X = 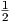 B(At)-1 (άσκηση). Συνεπώς, από το θεώρημα του
κανονικού συνόλου στάθμης το σύνολο O(n) = f-1(I) είναι μια κανονική υποπολλαπλότητα της GLnℝ
διάστασης
B(At)-1 (άσκηση). Συνεπώς, από το θεώρημα του
κανονικού συνόλου στάθμης το σύνολο O(n) = f-1(I) είναι μια κανονική υποπολλαπλότητα της GLnℝ
διάστασης
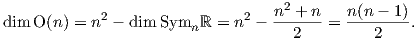
7. Η μοναδιαία ομάδα (unitary group) ορίζεται ως U(n) = {A ∈ GLnℂ : AAt = I}. Με παρόμοιο τρόπο
και ελαφρά προσαρμογή του Παραδείγματος 6 προκύτει ότι η U(n) είναι ομάδα Lie. Η διάστασή της
είναι
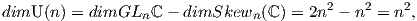
όπου Skewn(ℂ) είναι το σύνολο των αντιερμιτιανών πινάκων.
8. Η συμπλεκτική ομάδα (symplectic group) Sp(n) = {A ∈ GLnℍ : AAt = I}. Ο συζυγής ενός υπερμιγαδικού
q = t + ix + jy + kz ορίζεται ως q = t - ix - iy - kz. Βλέπε περισσότερα στην υποπαράγραφο 7.1.1.
Αποδεικνύεται ότι η συμπλεκτική ομάδα είναι ομάδα Lie διάστασης 2n2 + n. Πολλές φορές αυτή εκφράζεται και
ως
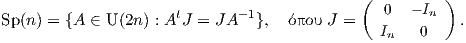
9. Η ειδική ορθογώνια ομάδα (special linear group) και η ειδική μοναδιαία ομάδα (special unitary group) ορίζονται
αντίστοιχα ως SO(n) = {A ∈ O(n) : detA = 1} και SU(n) = {A ∈ U(n) : detA = 1}. Ισχύει ότι
SO(n) = O(n) ∩ SLnℝ και SU(n) = U(n) ∩ SLnℂ. Η διάσταση αυτών είναι αντίστοιχα 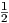 n(n - 1) και
n2 - 1.
n(n - 1) και
n2 - 1.
10. Η Ευκλείδεια ομάδα ορίζεται ως
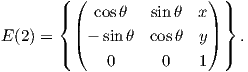 Βρείτε τη διάστασή της. Για ποιό λόγο πιστεύετε ότι ονομάζεται έτσι;
Βρείτε τη διάστασή της. Για ποιό λόγο πιστεύετε ότι ονομάζεται έτσι;
Οι παραπάνω διαστάσεις μπορούν να υπολογιστούν και μέσω της εύρεσης του εφαπτόμενου χώρου μιας ομάδας Lie,
όπως θα δούμε στην παράγραφο 7.2.
Οι ομάδες Lie O(n),U(n) και Sp(n) μπορούν να οριστούν και ως οι ομάδες ισομετριών του ℝn, ℂn και ℍn
αντίστοιχα, ως εξής. ΄Εστω K ∈{ℝ, ℂ, ℍ} και ορίζουμε στο K το εσωτερικό γινόμενο ⟨ , ⟩ με τιμή
⟨(x1,…,xn),(y1,…,yn)⟩ = x1y1 + … + xnyn. Θεωρούμε το σύνολο
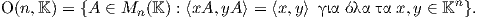
Τότε είναι εύκολο να δούμε ότι το σύνολο O(n, K) ισούται με τις ομάδες O(n),U(n) και Sp(n), όταν K = ℝ, ℂ
και ℍ αντίστοιχα.
Οι ομάδες Lie GLnℝ, SLnℝ, SO(n), O(n), GLnℂ, U(n), κ.λπ. είναι γνωστές και ως οι κλασικές ομάδες Lie
(classical Lie groups). Ταυτόχρονα, είναι και παραδείγματα ομάδων πινάκων (matrix groups). Μια ομάδα πινάκων
είναι μια κλειστή υποομάδα μιας γενικής γραμμικής ομάδας (GLnℝ, κ.λπ.). Για εύληπτες εισαγωγές στις ομάδες
πινάκων παραπέμπουμε στα βιβλία [3] και [9].
Θα αναφέρουμε παρακάτω ένα σημαντικό αποτέλεσμα για τις κλειστές υποομάδες μιας ομάδας Lie.
Χρειαζόμαστε αρχικά τους εξής ορισμούς.
Ορισμός 7.2: (α) Μια υποομάδα Lie H μιας ομάδας Lie G είναι μια υποομάδα της G υπό την αλγεβρική
έννοια, η οποία είναι ταυτόχρονα μια εμβαπτισμένη υποπολλαπλότητα της G, ώστε οι πράξεις της ομάδας H
να είναι λείες .
(β) Μια κλειστή υποομάδα H μιας ομάδας Lie G είναι μια υποομάδα της G, η οποία είναι κλειστό υποσύνολο
της G.
Μια υποομάδα Lie H ⊂ G δεν έχει απαραίτητα την επαγόμενη τοπολογία της G. Το παρακάτω θεώρημα είναι
αρκετά δύσκολο στην απόδειξή του.
Θεώρημα 7.1: (Θεώρημα της κλειστής υποομάδας). Μια κλειστή υποομάδα H μιας ομάδας Lie G είναι μια
κανονική υποπολλαπλότητα της G, άρα και μια υποομάδα Lie της G. Ειδικότερα, η H έχει την επαγόμενη
τοπολογία.
Παράδειγμα. Οι ομάδες SLnℝ, O(n), SO(n) είναι κλειστές υποομάδες της GLnℝ, άρα σύμφωνα με το παραπάνω
θεώρημα είναι υποομάδες Lie της GLnℝ.
Παρατήρηση. Αν και η μελέτη των ομάδων πινάκων μας δίνει μια πολύ καλή πληροφόρηση για την όλη θεωρία των
ομάδων Lie, δεν ισχύει ότι μια ομάδα Lie είναι ομάδα πινάκων. ΄Ενα τέτοιο παράδειγμα είναι η oμάδα του
Heisenberg
H, η ακριβής περιγραφή της οποίας απαιτεί κάποια στοιχεία άλγεβρας. Παρόλα αυτά, αναφέρουμε ότι αυτή είναι της
μορφής H = Nil3∕Z, όπου Nil3 είναι το σύνολο των πινάκων της μορφής
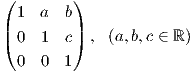 και Z
μια διακριτή κανονική υποομάδα της H. Αποδεικνύεται ότι η H είναι μια ομάδα Lie, αλλά δεν είναι δυνατόν να
εκφραστεί ως κλειστή υποομάδα της GLnℂ.
και Z
μια διακριτή κανονική υποομάδα της H. Αποδεικνύεται ότι η H είναι μια ομάδα Lie, αλλά δεν είναι δυνατόν να
εκφραστεί ως κλειστή υποομάδα της GLnℂ.
7.1.1 Ομάδες Lie μικρής διάστασης
Θα περιγράψουμε αναλυτικά κάποιες υποομάδες της O(n, K) για μικρές τιμές του n. Συγκεκριμένα, θα
περιγράψουμε τους ισομορφισμούς
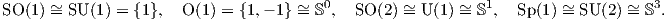 Οι
δύο πρώτοι είναι προφανείς, οπότε θα συζητήσουμε τις δύο τελευταίες ομάδες ισομορφισμών.
Οι
δύο πρώτοι είναι προφανείς, οπότε θα συζητήσουμε τις δύο τελευταίες ομάδες ισομορφισμών.
Από την ΄Ασκηση 2 έχουμε ότι
![{( ) }
cosθ sin θ
SO(2) = : θ ∈ [0,2π]
- sin θ cosθ](02_chapter_0725x.png) και
επιπλέον είναι
και
επιπλέον είναι
![S1 = {(x,y ) ∈ ℝ2 : x2 + y2 = 1} = {eiθ : θ ∈ [0,2π]}.](02_chapter_0726x.png) Επίσης, έχουμε ότι
Επίσης, έχουμε ότι
![U (1) = {z = x+ yi ∈ ℂ : z?z = 1} = {eiθ : θ ∈ [0,2π ]}.](02_chapter_0727x.png) Οι
πράξεις των ομάδων είναι, στην SO(2) ο πολλαπλασιασμός πινάκων και στον κύκλο S1 ο πολλαπλασιασμός
μιγαδικών αριθμών eiθ1eiθ2 = ei(θ1+θ2), άρα U(1)
Οι
πράξεις των ομάδων είναι, στην SO(2) ο πολλαπλασιασμός πινάκων και στον κύκλο S1 ο πολλαπλασιασμός
μιγαδικών αριθμών eiθ1eiθ2 = ei(θ1+θ2), άρα U(1) S1
S1 SO(2) (ισομορφισμός ομάδων). Είναι μια ενδιαφέρουσα
άσκηση ότι οι ισομορφισμοί αυτοί είναι και αμφιδιαφορίσεις λείων πολλαπλοτήτων.
SO(2) (ισομορφισμός ομάδων). Είναι μια ενδιαφέρουσα
άσκηση ότι οι ισομορφισμοί αυτοί είναι και αμφιδιαφορίσεις λείων πολλαπλοτήτων.
Ερχόμαστε τώρα στους επόμενους ισομορφισμούς. Από τον ορισμό της Sp(1) έχουμε ότι
Sp(1) = 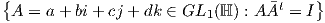 . Κάνοντας πράξεις προκύπτει ότι
. Κάνοντας πράξεις προκύπτει ότι
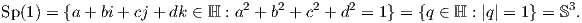 Προκειμένου να δείξουμε ότι Sp(1)
Προκειμένου να δείξουμε ότι Sp(1) S3 ως ομάδες, χρειάζεται να ορίσουμε πράξη πολλαπλασιασμού στην σφαίρα
S3. Αυτό θα γίνει ορίζοντας έναν πολλαπλασιασμό στο σύνολο των υπερμιγαδικών αριθμών ℍ, οπότε θα κάνουμε
μια μικρή παρένθεση για το θέμα αυτό.
S3 ως ομάδες, χρειάζεται να ορίσουμε πράξη πολλαπλασιασμού στην σφαίρα
S3. Αυτό θα γίνει ορίζοντας έναν πολλαπλασιασμό στο σύνολο των υπερμιγαδικών αριθμών ℍ, οπότε θα κάνουμε
μια μικρή παρένθεση για το θέμα αυτό.
Θεωρούμε μια βάση του ℝ4, έστω 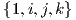 και ορίζουμε έναν πολλαπλασιαστικό κανόνα για τα στοιχεία της
με τον εξής τρόπο:
και ορίζουμε έναν πολλαπλασιαστικό κανόνα για τα στοιχεία της
με τον εξής τρόπο:
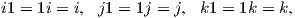
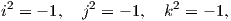
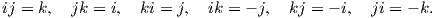
Επεκτείνουμε τώρα το γινόμενο αυτό σε ένα γινόμενο δύο οποιωνδήποτε στοιχείων του ℝ4 ως εξής: ΄Εστω
q1 = a + bi + cj + dk,q2 = x + yi + zj + wk. Τότε
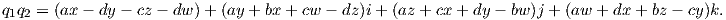 Η
πρόσθεση και ο βαθμωτός πολλαπλασιασμός ορίζονται κατά συντεταγμένη ως
Η
πρόσθεση και ο βαθμωτός πολλαπλασιασμός ορίζονται κατά συντεταγμένη ως
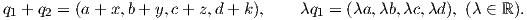 Ο διανυσματικός χώρος ℝ4 εφοδιασμένος με αυτές τι πράξεις γίνεται (μη μεταθετικό) σώμα,
συμβολίζεται με ℍ και καλείται σώμα των υπερμιγαδικών αριθμών (quaternions). Αναφέρονται και ως
τετράνια ή κβατέρνια. Το σύνολο αυτό έχει ιδιαίτερη σημασία στα μαθηματικά και τη φυσική
.
Ο διανυσματικός χώρος ℝ4 εφοδιασμένος με αυτές τι πράξεις γίνεται (μη μεταθετικό) σώμα,
συμβολίζεται με ℍ και καλείται σώμα των υπερμιγαδικών αριθμών (quaternions). Αναφέρονται και ως
τετράνια ή κβατέρνια. Το σύνολο αυτό έχει ιδιαίτερη σημασία στα μαθηματικά και τη φυσική
.
Το συζυγές ενός κβατερνίου q = a + bi + cj + dk ορίζεται ως q = a - bi - cj - dk, το μέτρο του ως
|q| = 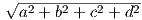 = qq = qq και το αντίστροφο ως q-1 =
= qq = qq και το αντίστροφο ως q-1 = 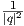 q.
q.
Με πράξη λοιπόν τον πολλαπλασιασμό κβατερνίων η σφαίρα S3 = {q ∈ ℍ : |q| = 1} εφοδιάζεται με δομή ομάδας
και έτσι προκύπτει ο ισομορφισμός Sp(1) S3.
S3.
Θα αποδείξουμε τώρα ότι Sp(1)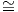 SU(2).
SU(2).
Ταυτίζουμε τον υπερμιγαδικό αριθμό q με την τετράδα (a,b,c,d) ∈ ℝ4 και στη συνέχεια με το ζεύγος
(u1,u2) ∈ ℂ2, όπου u1 = a + ib και u2 = c + id. Ορίζουμε την απεικόνιση
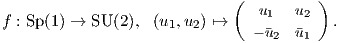
Η απεικόνιση αυτή παίρνει πράγματι τιμές στην SU(2). Για να το δείξουμε αυτό, υπολογίζουμε την
ορίζουσα
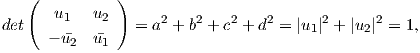 συνεπώς λόγω της ΄Ασκησης 2 προκύπτει ότι η f παίρνει τιμές στην SU(2). Για να δείξουμε το επί,
έστω
συνεπώς λόγω της ΄Ασκησης 2 προκύπτει ότι η f παίρνει τιμές στην SU(2). Για να δείξουμε το επί,
έστω
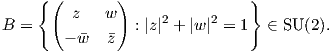 Τότε
θέτοντας q = (z,w) = z + wj ∈ Sp(1) παίρνουμε ότι f(q) = B. Αξίζει να σημειώσουμε ότι οι S0, S1, S3 είναι οι
μόνες σφαίρες που επιδέχονται δομή ομάδας, άρα οι μόνες που είναι ομάδες Lie.
Τότε
θέτοντας q = (z,w) = z + wj ∈ Sp(1) παίρνουμε ότι f(q) = B. Αξίζει να σημειώσουμε ότι οι S0, S1, S3 είναι οι
μόνες σφαίρες που επιδέχονται δομή ομάδας, άρα οι μόνες που είναι ομάδες Lie.
7.2 Ο Εφαπτόμενος χώρος μιας ομάδας Lie
Οι ομάδες Lie ως μη γραμμικά αντικείμενα, είναι αρκετά δύσκολα στη μελέτη. ΄Οπως και για μια οποιαδήποτε
πολλαπλότητα ο εφαπτόμενος χώρος σε κάθε σημείο τους αποτελεί τη βέλτιστη γραμμική προσέγγιση στο σημείο
αυτό. Ωστόσο, το σημαντικό με τη θεωρία των ομάδων Lie είναι ότι χρησιμοποιώντας απεικονίσεις μεταφοράς, (εδώ
η δομή ομάδας παίζει σημαντικό ρόλο) αρκεί να μελετήσουμε τον εφαπτόμενο χώρο μόνο στο ουδέτερο σημείο.
Επιπλέον, ο εφαπτόμενος χώρος στο ουδέτερο σημείο αποκτά δομή μιας άλγεβρας Lie (ένα καθαρά αλγεβρικό
αντικείμενο) και το πιο συναρπαστικό σημείο της θεωρίας είναι ότι κάθε ομάδα Lie καθορίζεται τοπικά από την
αντίστοιχη άλγεβρα Lie.
΄Εστω G μια ομάδα Lie και a ∈ G. Οι απεικονίσεις
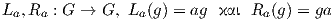 ονομάζονται αριστερή μεταφορά (left translation) και δεξιά μεταφορά (right translation) αντίστοιχα. Είναι και οι
δύο αμφιδιαφορίσεις με αντιστρόφους (La)-1 = La-1 και (Ra)-1 = Ra-1 (άσκηση). Η αμφιδιαφόριση La επάγει
τον ισομορφισμό διανυσματικών χώρων
ονομάζονται αριστερή μεταφορά (left translation) και δεξιά μεταφορά (right translation) αντίστοιχα. Είναι και οι
δύο αμφιδιαφορίσεις με αντιστρόφους (La)-1 = La-1 και (Ra)-1 = Ra-1 (άσκηση). Η αμφιδιαφόριση La επάγει
τον ισομορφισμό διανυσματικών χώρων
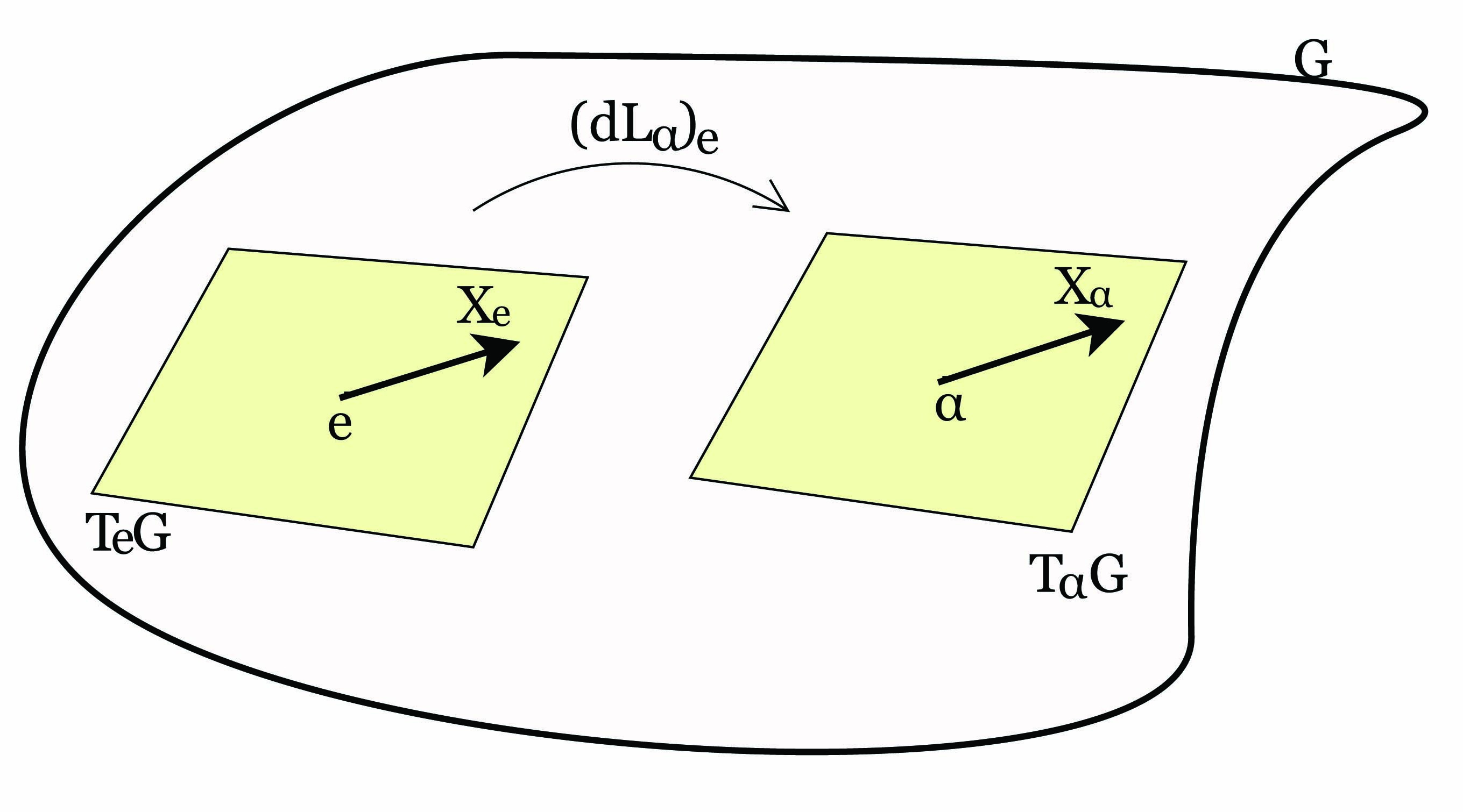
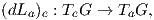 συνεπώς, αν περιγράψουμε τον εφαπτόμενο χώρο TeG στο ουδέτερο σημείο e ∈ G, τότε η εικόνα (dLa)e(TeG)
περιγράφει τον εφαπτόμενο χώρο TaG σε οποιοδήποτε σημείο a της ομάδας Lie G. Πιο γενικά, ορίζονται οι
ισομορφισμοί (dLα)g : TgG → TαgG και (dRα)g : TgG → TgαG, (a,g ∈ G).
συνεπώς, αν περιγράψουμε τον εφαπτόμενο χώρο TeG στο ουδέτερο σημείο e ∈ G, τότε η εικόνα (dLa)e(TeG)
περιγράφει τον εφαπτόμενο χώρο TaG σε οποιοδήποτε σημείο a της ομάδας Lie G. Πιο γενικά, ορίζονται οι
ισομορφισμοί (dLα)g : TgG → TαgG και (dRα)g : TgG → TgαG, (a,g ∈ G).
Πριν προχωρήσουμε σε μερικά παραδείγματα υπολογισμών εφαπτόμενων χώρων κάποιων ομάδων Lie στο
ουδέτερο σημείο τους, θα χρειαστούμε κάποιες ιδιότητες της εκθετικής απεικόνισης πινάκων. Για περισσότερες
λεπτομέρειες παραπέμπουμε σε βιβλία γραμμικής άλγεβρας.
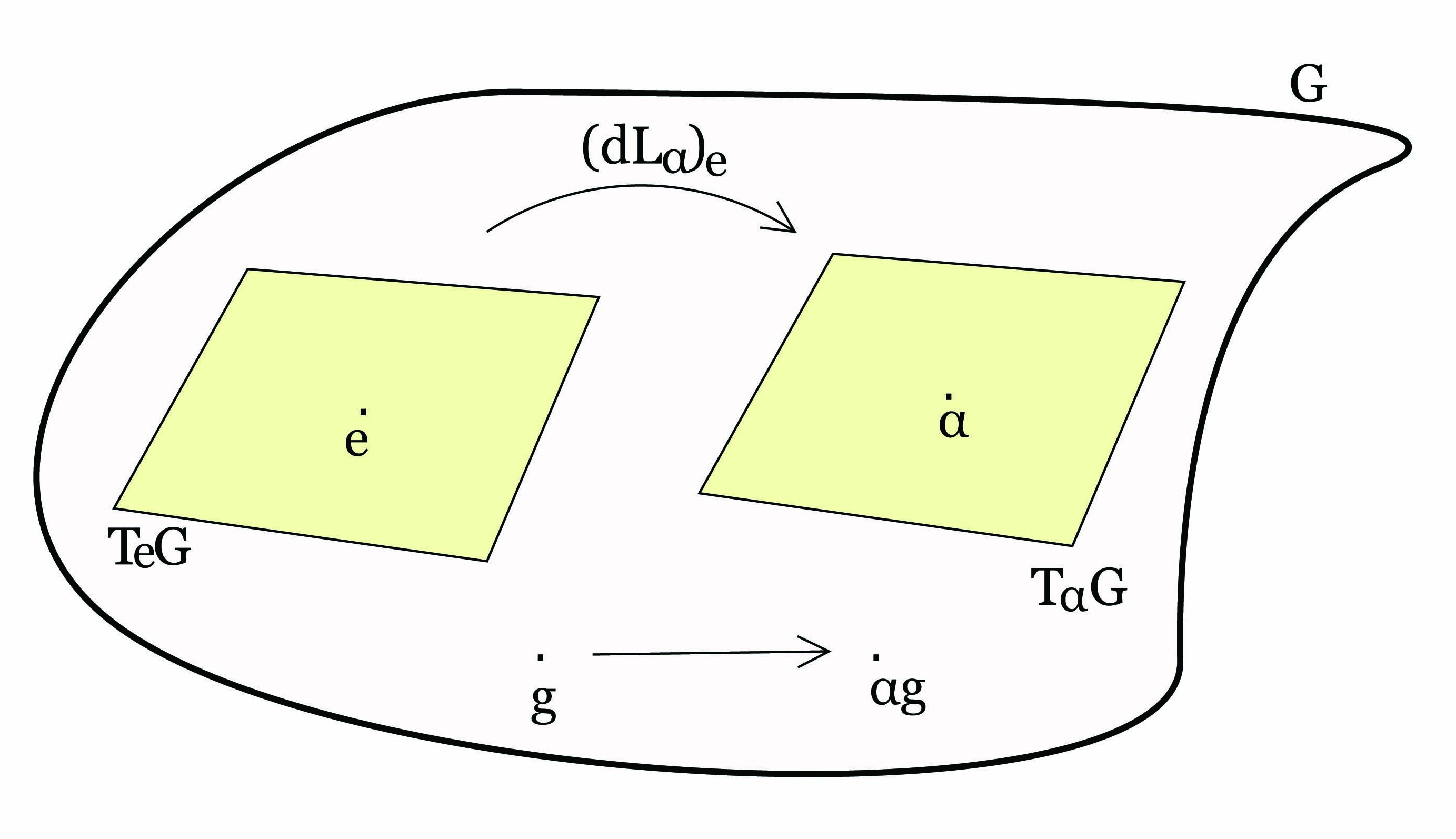
Πρόταση 7.1: ΄Εστω exp : Mn(ℂ) → Mn(ℂ) η εκθετική απεικόνιση πινάκων, η οποία ορίζεται μέσω της
συγκλίνουσας δυναμοσειράς
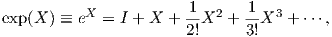
όπου
I είναι ο
n×n ταυτοτικός πίνακας.
Τότε ισχύουν οι εξής ιδιότητες:
(α) det(eX) = etrX,
(β) eXt
= (eX)t,
(γ) Εάν XY = Y X τότε eX+Y = eXeY .
Η εκθετική απεικόνιση είναι μια πολύ σημαντική απεικόνιση, διότι μέσω αυτής μπορούμε να πάρουμε καμπύλες
στην GLnℂ, οι οποίες να διέρχονται από δοθέν σημείο και να έχουν συγκεκριμένη αρχική ταχύτητα. Για
παράδειγμα, η καμπύλη γ : ℝ → GLnℂ, γ(t) = etX ικανοποιεί
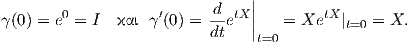
Λήμμα 7.1: ΄Εστω det : Mn(ℂ) → ℂ η απεικόνιση ορίζουσας. Τότε για κάθε X ∈ Mn(ℂ) ισχύει
d(det)I(X) = trX.
Απόδειξη. Θεωρούμε την καμπύλη γ(t) = etX, η οποία ικανοποιεί γ(0) = I και γ′(0) = X. Τότε έχουμε
ότι
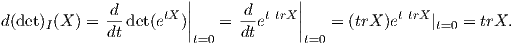
▄
Παραδείγματα.
1. Ο εφαπτόμενος χώρος της GLnℝ. Γνωρίζουμε από το Κεφάλαιο 3 ότι ο εφαπτόμενος χώρος της γενικής
γραμμικής ομάδας GLnℝ σε ένα οποιοδήποτε σημείο της g ταυτίζεται με το σύνολο Mnℝ όλων των n × n
πραγματικών πινάκων. Επιπλέον, ως εφαρμογή της Πρότασης 3.11 είχαμε υπολογίσει ότι ο ισομορφισμός
(dLg)I : TI(GLnℝ) → Tg(GLnℝ) Mnℝ είναι η αριστερή μεταφορά (dLg)I(X) = gX (εδώ I είναι ο n × n
ταυτοτικός πίνακας).
Mnℝ είναι η αριστερή μεταφορά (dLg)I(X) = gX (εδώ I είναι ο n × n
ταυτοτικός πίνακας).
2. Ο εφαπτόμενος χώρος της SLnℝ. Θυμίζουμε ότι ο εφαπτόμενος χώρος μιας λείας πολλαπλότητας M
στο σημείο p ∈ M εκφράζεται ως TpM = {γ′(0) : γ : (-ε,ε) → M, λεία καμπύλη με γ(0) = p}
(Πρόταση 3.9). ΄Εστω X ∈ TI(SLnℝ). Τότε υπάρχει λεία καμπύλη γ : (-ε,ε) → SLnℝ τέτοια ώστε
γ(0) = I και γ′(0) = X. Επειδή η καμπύλη αυτή ανήκει στην SLnℝ, ισχύει ότι detγ(t) = 1 για
κάθε t ∈ (-ε,ε), συνεπώς παραγωγίζοντας τα δύο μέλη και υπολογίζοντας για t = 0, προκύτει ότι
Αν V είναι ο διανυσματικός χώρος όλων των πραγματικών n × n πινάκων με ίχνος 0, αποδείξαμε ότι
TI(SLnℝ) ⊂ V . Επειδή dimV = n2 - 1 = dimTI(SLnℝ) = dimSLnℝ, προκύπτει τελικά ότι
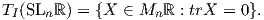
3. Ο εφαπτόμενος χώρος της O(n). ΄Εστω X ∈ TI(O(n)). Επιλέγουμε μια λεία καμπύλη γ : (-ε,ε) → O(n) τέτοια
ώστε γ(0) = I και γ′(0) = X. Επειδή η καμπύλη αυτή ανήκει στην O(n), ισχύει ότι γ(s)γ(s)t = I για κάθε
t ∈ (-ε,ε). Παραγωγίζουμε και τα δύο μέλη χρησιμοποιώντας την ΄Ασκηση 1 και παίρνουμε
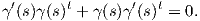 Θέτοντας t = 0 παίρνουμε την ισότητα X + Xt = 0, δηλαδή ο X είναι ένας αντισυμμετρικός πίνακας. Αν
Skewn(ℝ) είναι ο διανυσματικός χώρος όλων των n × n αντισυμμετρικών πινάκων, τότε έχουμε αποδείξει
ότι TI(O(n)) ⊂ Skewn(ℝ). Είναι μια απλή άσκηση γραμμικής άλγεβρας το να δείξει κάποιος ότι
dimSkewn(ℝ) =
Θέτοντας t = 0 παίρνουμε την ισότητα X + Xt = 0, δηλαδή ο X είναι ένας αντισυμμετρικός πίνακας. Αν
Skewn(ℝ) είναι ο διανυσματικός χώρος όλων των n × n αντισυμμετρικών πινάκων, τότε έχουμε αποδείξει
ότι TI(O(n)) ⊂ Skewn(ℝ). Είναι μια απλή άσκηση γραμμικής άλγεβρας το να δείξει κάποιος ότι
dimSkewn(ℝ) = 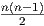 . Επιπλέον, επειδή είναι dimTI(O(n)) = dimO(n) =
. Επιπλέον, επειδή είναι dimTI(O(n)) = dimO(n) = 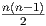 , καταλήξαμε στο
ότι
, καταλήξαμε στο
ότι
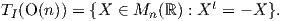 Εναλλακτικά, μπορούμε να δείξουμε τον εγκλεισμό Skewn(ℝ) ⊂ TI(O(n)) ως εξής: ΄Εστω X ∈ Skewn(ℝ).
Ορίζουμε την καμπύλη γ : ℝ → Mn(ℝ) γ(s) = esX. Τότε έχουμε ότι
Εναλλακτικά, μπορούμε να δείξουμε τον εγκλεισμό Skewn(ℝ) ⊂ TI(O(n)) ως εξής: ΄Εστω X ∈ Skewn(ℝ).
Ορίζουμε την καμπύλη γ : ℝ → Mn(ℝ) γ(s) = esX. Τότε έχουμε ότι
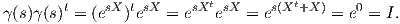 Αυτό
σημαίνει ότι η καμπύλη γ ανήκει στην O(n) και ικανοποιεί τις σχέσεις γ(0) = I και γ′(0) = X, άρα
X ∈ TI(O(n)).
Αυτό
σημαίνει ότι η καμπύλη γ ανήκει στην O(n) και ικανοποιεί τις σχέσεις γ(0) = I και γ′(0) = X, άρα
X ∈ TI(O(n)).
3. Ο εφαπτόμενος χώρος της SO(n). Γνωρίζουμε ότι SO(n) = O(n) ∩ SLnℝ. Επειδή κάθε αντισυμμετρικός πίνακας
έχει ίχνος μηδέν, από τα Παραδείγματα 2 και 3 προκύπτει ότι TI(SO(n)) = TI(O(n)).
7.3 Η άλγεβρα Lie μιας ομάδας Lie
Θα ορίσουμε αρχικά μια σημαντική κατηγορία διανυσματικών πεδίων σε μια ομάδα Lie και στη συνέχεια, σε κάθε
ομάδα Lie G θα αντιστοιχίσουμε ένα αλγεβρικό αντικείμενο, την άλγεβρα Lie 𝔤 της G.
Ορισμός 7.3: ΄Ενα διανυσματικό πεδίο X σε μια ομάδα Lie ονομάζεται αριστερά αναλλοίωτο (left invariant)
εάν X ∘ Lα = dLα(X) για κάθε α ∈ G, ή πιο αναλυτικά εάν Xαg = (dLα)g(Xg) για κάθε α,g ∈ G.
Ισοδύναμα, ένα διανυσματικό πεδίο X στην ομάδα Lie G θα λέγεται αριστερά αναλλοίωτο, εάν το παρακάτω
διάγραμμα είναι μεταθετικό.
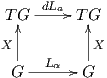
Μια σημαντική ιδιότητα ενός αριστερά αναλλοίωτου διανυσματικού πεδίου είναι ότι αυτό καθορίζεται από την τιμή
του στο ουδέτερο στοιχείο e ∈ G, αφού Xα = (dLα)e(Xe) για κάθε α ∈ G. Επιπλέον, αποδεικνύεται ότι κάθε
αριστερά αναλλοίωτο διανυσματικό πεδίο είναι λείο.
Συμβολίζουμε με 𝔤 το σύνολο όλων των αριστερά αναλλοίωτων διανυσματικών πεδίων στην ομάδα Lie G. Τότε
ο διανυσματικός χώρος 𝔤 είναι υπόχωρος του διανυσματικού χώρου X(G), όλων των λείων διανυσματικών πεδίων
της G.
Εάν X,Y ∈𝔤, τότε ισχύει ότι [X,Y ] ∈𝔤. Πράγματι, έστω α,p ∈ G και f ∈ F(G). Τότε
όπου στην τρίτη ισότητα χρησιμοποιήσαμε τον ορισμό του διαφορικού. Εναλλακτικά αυτό μπορεί να αποδειχθεί
ως εξής: ΄Ενα αριστερά αναλλοίωτο διανυσματικό πεδίο είναι από τον ορισμό La-συσχετισμένο με
τον εαυτό του, για κάθε a ∈ G (Ορισμός 4.10). Τότε το αποτέλεσμα προκύπτει από την Πρόταση
4.4.
Θυμίζουμε ότι μια άλγεβρα Lie είναι ένας διανυσματικός χώρος 𝔤 εφοδιασμένος με μια πράξη
[ , ] : 𝔤 ×𝔤 →𝔤 (γινόμενο Lie) με τις εξής ιδιότητες: (1) [x,y] = -[y,x], (2) [αx + βy,z] = α[x,z] + β[y,z],
[z,αx + βy] = α[z,x] + β[z,y], (3) [[x,y],z] + [[y,z],x] + [[z,x],y] = 0.
Μια υποάλγεβρα Lie (Lie subalgebra) μιας άλγεβρας Lie 𝔤 είναι ένας διανυσματικός υπόχωρος 𝔥 ⊂𝔤, ο οποίος
είναι κλειστός ως προς το γινόμενο Lie
Συνεπώς, καταλήγουμε στο συμπέρασμα ότι το σύνολο όλων των αριστερά αναλλοίωτων διανυσματικών πεδίων
μιας ομάδας Lie είναι μια άλγεβρα Lie, η οποία είναι υποάλγεβρα Lie της άλγεβρας Lie X(G), όλων των λείων
διανυσματικών πεδίων της G.
Ορισμός 7.4: Η άλγεβρα Lie μιας ομάδας Lie G είναι το σύνολο 𝔤 όλων των αριστερά αναλλοίωτων
διανυσματικών πεδίων της G.
Οι άλγεβρες Lie των ομάδων πινάκων GLnℝ, SLnℝ, SO(n), GLnℂ,U(n), κ.λπ. συμβολίζονται αντίστοιχα
με
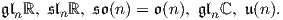 Στη
συνέχεια, θα δούμε έναν πολύ σημαντικό ισομορφισμό.
Στη
συνέχεια, θα δούμε έναν πολύ σημαντικό ισομορφισμό.
Πρόταση 7.2: Η απεικόνιση ϕ : 𝔤 → TeG, X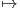 Xe είναι ισομορφισμός διανυσματικών χώρων.
Xe είναι ισομορφισμός διανυσματικών χώρων.
Απόδειξη. Η ϕ είναι προφανώς γραμμική. Επίσης είναι 1-1. Πράγματι, αν X ∈𝔤 με ϕ(X) = Xe = 0, τότε
για κάθε g ∈ G είναι
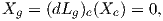
συνεπώς X = 0. Για να δείξουμε ότι η ϕ είναι επί, αρκεί να δειχθεί ότι για κάθε εφαπτόμενο διάνυσμα
υ ∈ TeG υπάρχει ένα αριστερά αναλλοίωτο διανυσματικό πεδίο Xυ τέτοιο ώστε ϕ(Xυ) = υ. Πράγματι, αν
υ ∈ TeG, ορίζουμε το διανυσματικό πεδίο Xυ ∈𝔤 ως Xgυ = (dLg)e(υ), (g ∈ G), για το οποίο έχουμε
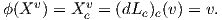
Το
πεδίο αυτό είναι αριστερά αναλλοίωτο. Πράγματι, αν
α,g ∈ G τότε
Τέλος, το
Xυ είναι ένα λείο διανυσματικό πεδίο. Αρκεί να δείξουμε ότι για κάθε
f ∈ F(G) η απεικόνιση
Xυf : G → ℝ είναι λεία. Πράγματι, για κάθε
g ∈ G είναι
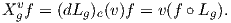
Η απεικόνιση f ∘Lg είναι λεία ως σύνθεση λείων απεικονίσεων, οπότε η υ(f ∘Lg) είναι λεία και κατ΄ επέκταση η
ζητούμενη απεικόνιση Xυf είναι λεία, άρα το πεδίο Xυ είναι λείο. ▄
Μέσω του παραπάνω ισομορφισμού μπορούμε να ορίσουμε ένα γινόμενο Lie στον εφαπτόμενο χώρο TeG ως
εξής: για κάθε u,υ ∈ TeG θέτουμε
Παρατηρείστε ότι [Xu,Xυ]e = ϕ-1([Xu,Xυ]).
Παραδείγματα.
1. Θα αποδείξουμε ότι τα αριστερά αναλλοίωτα διανυσματικά πεδία της ομάδας Lie G = (ℝ,+) (με ουδέτερο
στοιχείο το 0), είναι πολλαπλάσια του διανυσματικού πεδίου 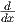 ∈ X(ℝ). Οι αριστερές μεταφορές είναι της μορφής
Lg(x) = g + x και υπολογίζουμε αρχικά την τιμή (dLg)0(
∈ X(ℝ). Οι αριστερές μεταφορές είναι της μορφής
Lg(x) = g + x και υπολογίζουμε αρχικά την τιμή (dLg)0(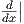 0). Αυτή είναι ένα εφαπτόμενο διάνυσμα στο σημείο
g ∈ ℝ, άρα ένα πολλαπλάσιο του
0). Αυτή είναι ένα εφαπτόμενο διάνυσμα στο σημείο
g ∈ ℝ, άρα ένα πολλαπλάσιο του 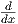 |g, δηλαδή της μορφής λ
|g, δηλαδή της μορφής λ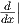 g. Προκειμένου να βρούμε τον αριθμό λ, παίρνουμε
την συνάρτηση f(x) = x και υπολογίζουμε:
g. Προκειμένου να βρούμε τον αριθμό λ, παίρνουμε
την συνάρτηση f(x) = x και υπολογίζουμε:
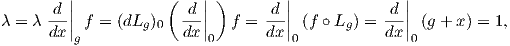 συνεπώς
συνεπώς
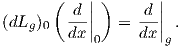 ΄Αρα
το
΄Αρα
το 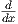 είναι ένα αριστερά αναλλοίωτο διανυσματικό πεδίο της πολλαπλότητας ℝ και κάθε άλλο αριστερά αναλλοίωτο
διανυσματικό πεδίο της ℝ είναι πολλαπλάσιο αυτού.
είναι ένα αριστερά αναλλοίωτο διανυσματικό πεδίο της πολλαπλότητας ℝ και κάθε άλλο αριστερά αναλλοίωτο
διανυσματικό πεδίο της ℝ είναι πολλαπλάσιο αυτού.
2. Θα προσδιορίσουμε τα αριστερά αναλλοίωτα διανυσματικά πεδία της γενικής γραμμικής ομάδας GLnℝ.
Θυμίζουμε ότι για κάθε g ∈ GLnℝ ο εφαπτόμενος χώρος Tg(GLnℝ) είναι ισόμορφος με τον διανυσματικό χώρο
Mn(ℝ), μέσω του οποίου έχουμε την παρακάτω αντιστοιχία μεταξύ εφαπτόμενων διανυσμάτων και n × n
πινάκων:
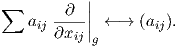 | (7.2) |
΄Εστω B = ∑
bij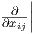 I ∈ TI(GLnℝ) και έστω XB το αντίστοιχο αριστερά αναλλοίωτο διανυσματικό πεδίο.
Συμβολίζουμε επίσης με B = (bij) τον αντίστοιχο n × n πίνακα. ΄Εχουμε υπολογίσει στο Κεφάλαιο 3
(εφαρμογή της Πρότασης 3.11) ότι XgB = (dLg)I(B) = gB (λαμβάνοντας υπόψη και την ταύτιση
(7.2). Ως προς τη συνηθισμένη βάση {
I ∈ TI(GLnℝ) και έστω XB το αντίστοιχο αριστερά αναλλοίωτο διανυσματικό πεδίο.
Συμβολίζουμε επίσης με B = (bij) τον αντίστοιχο n × n πίνακα. ΄Εχουμε υπολογίσει στο Κεφάλαιο 3
(εφαρμογή της Πρότασης 3.11) ότι XgB = (dLg)I(B) = gB (λαμβάνοντας υπόψη και την ταύτιση
(7.2). Ως προς τη συνηθισμένη βάση {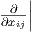 g} του Tg(GLnℝ) η τιμή του πεδίου XB στο σημείο g
είναι
g} του Tg(GLnℝ) η τιμή του πεδίου XB στο σημείο g
είναι
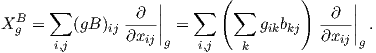
3. ΄Εστω V ένας πραγματικός διανυσματικός χώρος διάστασης n. Θεωρούμε το σύνολο των ενδομορφισμών
(endomorphisms) του V , δηλαδή End(V ) = {f : V → V, f γραμμική} και το σύνολο Aut(V )
όλων των αντιστρέψιμων ενδομορφισμών του V , δηλαδή τους αυτομορφισμούς (automorphisms) του
V . Το σύνολο End(V ) είναι ισόμορφο με το σύνολο όλων των n × n πραγματικών πινάκων Mnℝ
(ως προς κάποια επιλογή βάσης του V ) και είναι επιπλέον άλγεβρα Lie διάστασης n2 με γινόμενο
Lie
![[f,g] = f ∘g - g ∘ f.](02_chapter_0780x.png)
Επίσης, επειδή V  ℝn θα είναι Aut(V )
ℝn θα είναι Aut(V ) GLnℝ. ΄Ετσι το σύνολο Aut(V ) ως ανοικτό υποσύνολο του End(V )
είναι μια λεία πολλαπλότητα και εφοδιασμένο με την πράξη της σύνθεσης απεικονίσεων γίνεται ομάδα Lie. Επειδή
είναι
GLnℝ. ΄Ετσι το σύνολο Aut(V ) ως ανοικτό υποσύνολο του End(V )
είναι μια λεία πολλαπλότητα και εφοδιασμένο με την πράξη της σύνθεσης απεικονίσεων γίνεται ομάδα Lie. Επειδή
είναι
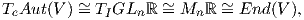 όπου
e είναι ο ταυτοτικός ενδομορφισμός του V , η άλγεβρα Lie του Aut(V ) είναι το σύνολο των ενδομορφισμών
End(V ).
όπου
e είναι ο ταυτοτικός ενδομορφισμός του V , η άλγεβρα Lie του Aut(V ) είναι το σύνολο των ενδομορφισμών
End(V ).
4. Θα αποδείξουμε ότι το γινόμενο Lie στην GLnℝ δίνεται ως
![[A, B] = AB - BA,](02_chapter_0784x.png) όπου
A,B ∈ TI(GLnℝ) = Mn(ℝ). ΄Εστω XA,XB ∈𝔤𝔩nℝ τα αντίστοιχα αριστερά αναλλοίωτα διανυσματικά πεδία.
Θεωρούμε μια λεία συνάρτηση f : U ⊂ GLnℝ → ℝ ορισμένη σε μια περιοχή του ταυτοτικού πίνακα I και έστω
g ∈ U (πίνακας). Τότε έχουμε ότι
όπου
A,B ∈ TI(GLnℝ) = Mn(ℝ). ΄Εστω XA,XB ∈𝔤𝔩nℝ τα αντίστοιχα αριστερά αναλλοίωτα διανυσματικά πεδία.
Θεωρούμε μια λεία συνάρτηση f : U ⊂ GLnℝ → ℝ ορισμένη σε μια περιοχή του ταυτοτικού πίνακα I και έστω
g ∈ U (πίνακας). Τότε έχουμε ότι
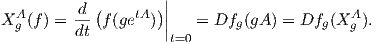 Επειδή το σύνολο GLnℝ είναι ανοικτό υποσύνολο του Mnℝ
Επειδή το σύνολο GLnℝ είναι ανοικτό υποσύνολο του Mnℝ ℝn2
, μπορούμε να χρησιμοποιήσουμε κανόνες του
απειροστικού λογισμού και υπολογίζουμε:
ℝn2
, μπορούμε να χρησιμοποιήσουμε κανόνες του
απειροστικού λογισμού και υπολογίζουμε:
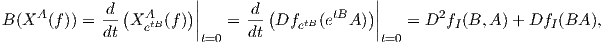 όπου
D2fI είναι η δεύτερη παράγωγος f στον πίνακα I, την οποία θεωρούμε ως μια συμμετρική διγραμμική μορφή.
Παρόμοια, προκύπτει ότι A(XB(f)) = D2fI(A,B) + DfI(AB), συνεπώς, έχουμε ότι
όπου
D2fI είναι η δεύτερη παράγωγος f στον πίνακα I, την οποία θεωρούμε ως μια συμμετρική διγραμμική μορφή.
Παρόμοια, προκύπτει ότι A(XB(f)) = D2fI(A,B) + DfI(AB), συνεπώς, έχουμε ότι
![[XA, XB ]I(f) = A (XB (f))- B (XA (f)) = DfI (AB - BA ),](02_chapter_0789x.png) απ΄
όπου προκύπτει το ζητούμενο (επεξεργαστείτε τις λεπτομέρειες της απόδειξης).
απ΄
όπου προκύπτει το ζητούμενο (επεξεργαστείτε τις λεπτομέρειες της απόδειξης).
7.4 Η σχέση μεταξύ ομάδων Lie και αλγεβρών Lie
Μέχρι στιγμής σε κάθε ομάδα Lie G έχουμε αντιστοιχίσει μια άλγβερα Lie 𝔤, ως το σύνολο όλων των αριστερά
αναλλοίωτων διανυσματικών πεδίων της G. Η 𝔤 είναι ισόμορφη με τον εφαπτόμενο χώρο TeG και μέσω αυτού του
ισομορφισμού το γινόμενο Lie διανυσματικών πεδίων στην 𝔤 μεταφέρεται στον εφαπτόμενο χώρο TeG. Το φυσικό
ερώτημα είναι, αν δοθεί μια τυχαία (πραγματική) άλγεβρα Lie 𝔤, κατά πόσον υπάρχει ομάδα Lie της οποίας η
άλγεβρα Lie να ισούται με την 𝔤. Η τεκμηρίωση της απάντησης δεν είναι εύκολο να παρουσιαστεί στα πλαίσια του
παρόντος βιβλίου, οπότε θα δώσουμε μια γενική περιγραφή της σχετικής θεωρίας, η κατάληξη της οποίας είναι τα
θεωρήματα του Lie.
΄Εστω G,H δύο ομάδες Lie. Μια απεικόνιση ϕ : G → H καλείται ομομορφισμός ομάδων Lie, αν είναι λεία και
ομομορφισμός ομάδων. Επιπλέον, αν η ϕ είναι ισομορφισμός και αμφιδιαφόριση, τότε λέγεται ισομορφισμός ομάδων
Lie και οι ομάδες Lie G,H ισόμορφες. Αν 𝔤 και 𝔥 είναι δύο άλγεβρες Lie, τότε η απεικόνιση τ : 𝔤 →𝔥 θα λέγεται
ομομορφισμός αλγεβρών Lie αν είναι γραμμική και ισχύει
![τ([X,Y ]𝔤) = [τ(X ),τ(Y )]𝔥, για κάθε X, Y ∈ 𝔤.](02_chapter_0790x.png)
Στην περίπτωση που η απεικόνιση τ είναι ισομορφισμός, τότε οι δύο άλγεβρες είναι ισόμορφες. Θα ορίσουμε στη
συνέχεια την έννοια της υποάλγεβρας Lie.
Ορισμός 7.5: ΄Εστω 𝔤 μια άλγεβρα Lie και 𝔥 ένας διανυσματικός υπόχωρος της 𝔤.
(α) Ο 𝔥 θα λέγεται υποάλγεβρα Lie (Lie subalgebra) της 𝔤, αν [X,Y ] ∈𝔥 για κάθε X,Y ∈𝔥.
(β) Ο 𝔥 θα λέγεται ιδεώδες (ideal) της 𝔤, αν [A,X] ∈𝔥 για κάθε A ∈𝔤 και X ∈𝔥.
Η επόμενη πρόταση μας δίνει μια πρώτη σχέση ανάμεσα στις ομάδες Lie και τις άλγεβρες Lie.
Πρόταση 7.3: ΄Εστω ϕ : G → H ένας ομομορφισμός ομάδων Lie. Τότε η απεικόνιση dϕe : TeG → Tϕ(e)H
είναι ένας ομομορφισμός αλγεβρών Lie.
Απόδειξη. Θα αποδείξουμε ότι η απεικόνιση dϕe : TeG → Tϕ(e)H είναι ομομορφισμός αλγεβρών Lie, δηλαδή
θα πρέπει για κάθε u,υ ∈ TeG να ισχύει dϕe([u,υ]) = [dϕeu,dϕeυ]. Τα εφαπτόμενα διανύσματα u,υ μέσω
της απεικόνισης dϕe απεικονίζονται στα διανύσματα x = dϕe(u) και y = dϕe(υ) του εφαπτόμενου χώρου
Tϕ(e)H. Θεωρούμε τα αντίστοιχα αριστερά αναλλοίωτα διανυσματικά πεδία των προηγούμενων διανυσμάτων,
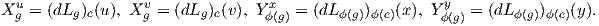
Τότε θα έχουμε ότι
![x y
[dϕeu,dϕev ] = [x,y] = [Y ,Y ]ϕ(e).](02_chapter_0792x.png) | (7.3) |
Επειδή η ϕ είναι ομομορφισμός, το ϕ(e) είναι το ουδέτερο στοιχείο της ομάδας H. Επιπλέον, τα διανυσματικά πεδία
Xu,Xυ ∈𝔤 είναι ϕ-συσχετισμένα με τα πεδία Y x,Y y ∈𝔥. Πράγματι, είναι
Στην τρίτη ισότητα χρησιμοποιήσαμε την υπόθεση ότι η απεικόνιση
ϕ είναι ομομορφισμός ομάδων
Lie, το οποίο
είναι ισοδύναμο με την σχέση
ϕ∘Lg = Lϕ(g) ∘ϕ. Με τον ίδιο τρόπο προκύπτει ότι το διανυσματικό πεδίο
Xυ είναι
ϕ-συσχετισμένο με το πεδίο
Y y, άρα λόγω της Πρότασης 4.4 το πεδίο
[Xu,Xυ] θα είναι
ϕ-συσχετισμένο με το
πεδίο
[Y x,Y y]. Αυτό σημαίνει ότι
![dϕ ([u,v ]) = dϕ ([Xu, Xv ]) = [Yx,Y y] .
e e e ϕ(e)](02_chapter_0794x.png) | (7.4) |
Επομένως από τις σχέσεις (7.3) και (7.4) προκύπτει ότι dϕe([u,υ]) = [dϕeu,dϕeυ], δηλαδή η ϕ είναι ομομορφισμός
αλγεβρών Lie. ▄
Λόγω του ισομορφισμού 𝔤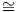 TeG γράφουμε τον παραπάνω ομομορφισμό αλγεβρών Lie και ως
dϕe : 𝔤 →𝔥.
TeG γράφουμε τον παραπάνω ομομορφισμό αλγεβρών Lie και ως
dϕe : 𝔤 →𝔥.
Πόρισμα 7.1: ΄Εστω G μια ομάδα Lie με άλγεβρα Lie 𝔤 και H μια υποομάδα Lie της G. Τότε η ένθεση
j : H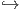 G επάγει μια αντιστοιχία dje : 𝔥
G επάγει μια αντιστοιχία dje : 𝔥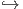 𝔤, μεταξύ της άλγεβρας Lie 𝔥 της H και μιας υποάλγεβρας Lie
dje(𝔥) της 𝔤.
𝔤, μεταξύ της άλγεβρας Lie 𝔥 της H και μιας υποάλγεβρας Lie
dje(𝔥) της 𝔤.
Η απόδειξη του πορίσματος είναι άμεση, αφού, όπως γνωρίζουμε, το διαφορικό της ένθεσης είναι απεικόνιση
1 - 1.
Στη συνέχεια, θα εξετάσουμε υπό ποιές συνθήκες ισχύει το αντίστροφο. Δηλαδή, αν έχουμε μια υποάλγεβρα
Lie 𝔥 της 𝔤 κατά πόσον υπάρχει υποομάδα Lie H της ομάδας Lie G με άλγεβρα Lie την 𝔥. Η απάντηση δίνεται στο
ακόλουθο θεώρημα:
Θεώρημα 7.2: ΄Εστω G μια ομάδα Lie με άλγεβρα Lie 𝔤 και έστω 𝔥 μια υποάλγεβρα Lie της 𝔤. Τότε υπάρχει
μοναδική συνεκτική υποομάδα Lie H της G της οποίας η άλγεβρα Lie είναι η 𝔥.
Η απόδειξη δεν είναι εύκολη και στηρίζεται στο θεώρημα κατανομών του Frobenius. Επίσης, αν δεν
απαιτήσουμε η υποομάδα H να είναι συνεκτική, τότε αυτή δεν είναι μοναδική. Για παράδειγμα, οι ομάδες Lie O(n)
(μη συνεκτική) και SO(n) (συνεκτική) έχουν την ίδια άλγεβρα Lie 𝔬(n).
Ισχύει επίσης και το εξής:
Θεώρημα 7.3: ΄Εστω G και H δύο ομάδες Lie με την G απλά συνεκτική και έστω 𝔤 και 𝔥 οι άλγεβρες Lie
αυτών. Τότε για κάθε ομομορφισμό ψ : 𝔤 →𝔥 υπάρχει μοναδικός ομομορφισμός ομάδων Lie ϕ : G → H
τέτοιος ώστε dϕe = ψ.
Το παρακάτω θεώρημα συνοψίζει τα αποτελέσματα του Lie και δίνει την ακριβή σχέση μεταξύ ομάδων Lie και
αλγεβρών Lie.
Θεώρημα 7.4:
- Για κάθε άλγεβρα Lie 𝔤 υπάρχει μια ομάδα Lie G, όχι απαραίτητα μοναδική, της οποίας η άλγεβρα Lie
είναι η 𝔤.
- ΄Εστω G1,G2 δύο ομάδες Lie με αντίστοιχες άλγεβρες Lie 𝔤1,𝔤2. Αν οι άλγεβρες Lie 𝔤1 και 𝔤2 είναι
ισόμορφες, τότε οι ομάδες Lie G1,G2 είναι τοπικά ισομορφικές. Στην περίπτωση που οι G1,G2 είναι
απλά συνεκτικές,
τότε οι ομάδες Lie G1,G2 είναι ισόμορφες.
- Για κάθε άλγεβρα Lie V υπάρχει μια ομάδα Lie G της οποίας η άλγεβρα Lie 𝔤 να είναι ισόμορφη με
την V .
Παρατηρήσεις.
1. Η απόδειξη του (1) του παραπάνω θεωρήματος στηρίζεται στο θεώρημα του
Ado,
στο οποίο αναφέρεται ότι κάθε πραγματική άλγεβρα Lie πεπερασμένης διάστασης είναι ισόμορφη με μια υποάλγεβρα
Lie της άλγεβρας Lie Mn(ℝ) όλων των n × n πραγματικών πινάκων.
2. Η συνθήκη της απλής συνεκτικότητα στο (3) του θεωρήματος είναι απαραίτητη. Για παράδειγμα,
αν G1 = S1 και G2 = ℝ, τότε οι ομάδες αυτές έχουν την ίδια άλγεβρα Lie 𝔤 = ℝ, αλλά δεν είναι
ισόμορφες. Η θεμελιώδης ομάδα της πρώτης είναι το σύνολο των ακεραίων, ενώ της δεύτερης είναι
τετριμμένη.
7.5 Μονοπαραμετρικές υποομάδες και η εκθετικη απεικόνιση
Θα δώσουμε έναν δεύτερο χαρακτηρισμό του εφαπτόμενου χώρου μιας ομάδας Lie G, ως το σύνολο των
μονοπαραμετρικών υποομάδων της. Στη συνέχεια, θα ορίσουμε την εκθετική απεικόνιση, η οποία είναι ιδιαίτερα
σημαντική στη θεωρία των ομάδων Lie. Για την περίπτωση των ομάδων πινάκων αυτή είναι η συνηθισμένη
εκθετική απεικόνιση πινάκων.
Ορισμός 7.6: ΄Ενα λείος ομομορφισμός ϕ : (ℝ,+) → G από την προσθετική ομάδα (ℝ,+) σε μια ομάδα Lie
G, καλείται μονοπαραμετρική υποομάδα (one-parametric subgroup) της G.
Βλέπουμε ότι η μονοπαραμετρική υποομάδα ϕ είναι μια λεία καμπύλη της ομάδας Lie G, η οποία ως
ομομορφισμός θα ικανοποιεί τις σχέσεις ϕ(s + t) = ϕ(s)ϕ(t), ϕ(0) = e και ϕ(-t) = ϕ(t)-1.
Παρατήρηση. Ο ορισμός είναι κάπως παραπλανητικός, αλλά έχει παραδοσιακά επικρατήσει. Γενικά δεν ισχύει ότι η
εικόνα ϕ(ℝ) ⊂ G είναι μια υποομάδα της G, εκτός εάν η ϕ είναι 1 - 1. Στην περιπτωση αυτή, η εικόνα ϕ(ℝ) είναι
ισόμορφη με το ℝ (ως προσθετική ομάδα).
Παραδείγματα
1. Η απεικόνιση ℝ → S1, με ϕ(t) = eit είναι μια μονοπαραμετρική υποομάδα του μοναδιαίου κύκλου
S1 U(1).
U(1).
2. Η απεικόνιση ϕ : ℝ → GL3(ℝ), με ϕ(t) = 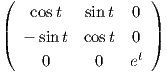 είναι μια μονοπαραμετρική υποομάδα της
GL3(ℝ).
είναι μια μονοπαραμετρική υποομάδα της
GL3(ℝ).
3. Η απεικόνιση ϕ : ℝ → SO(2), με ϕ(t) = 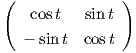 είναι μια μονοπαραμετρική υποομάδα της SO(2).
Πράγματι, η ϕ είναι λεία απεικόνιση. Θα δείξουμε ότι είναι ομομορφισμός. ΄Εχουμε,
είναι μια μονοπαραμετρική υποομάδα της SO(2).
Πράγματι, η ϕ είναι λεία απεικόνιση. Θα δείξουμε ότι είναι ομομορφισμός. ΄Εχουμε,
Με παρόμοιο τρόπο αποδεικνύονται και τα άλλα παραδείγματα.
Ερχόμαστε τώρα στο κεντρικό θεώρημα της ενότητας αυτής, το οποίο είναι η ταύτιση του εφαπτόμενου χώρου
μιας ομάδας Lie G με το σύνολο των μονοπαραμετρικών υποομάδων της. Ας συμβολίσουμε το σύνολο αυτό με
S.
Θεώρημα 7.5: Η απεικόνιση μ : S → TeG, ϕ dϕ0(1) ορίζει μια 1 - 1 αντιστοιχία μεταξύ
μονοπαραμετρικών υποομάδων της G και του εφαπτόμενου χώρου TeG.
dϕ0(1) ορίζει μια 1 - 1 αντιστοιχία μεταξύ
μονοπαραμετρικών υποομάδων της G και του εφαπτόμενου χώρου TeG.
Απόδειξη. ΄Εστω υ ∈ TeG και έστω Xgυ = (dLg)e(υ) το αντίστοιχο αριστερά αναλλοίωτο διανυσματικό
πεδίο (g ∈ G). Πρέπει να βρούμε μια μονοπαραμετρική υποομάδα ϕυ : ℝ → G της G. Από τα Θεωρήματα
4.3 και 4.4 υπάρχει μοναδική ολοκληρωτική καμπύλη
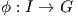
του πεδίου Xυ, τέτοια ώστε ϕ(0) = e και 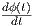 = Xϕ(t)υ. Η καμπύλη ϕ είναι ένας ομομορφισμός. Πράγματι,
για σταθερό s ∈ I τέτοιο ώστε s + t ∈ I για κάθε t ∈ I, οι καμπύλες ϕ1,ϕ2 : I → G με ϕ1(t) = ϕ(s + t),
ϕ2(t) = ϕ(s)ϕ(t) ικανοποιούν ϕ1(0) = ϕ2(0) = ϕ(s) και
= Xϕ(t)υ. Η καμπύλη ϕ είναι ένας ομομορφισμός. Πράγματι,
για σταθερό s ∈ I τέτοιο ώστε s + t ∈ I για κάθε t ∈ I, οι καμπύλες ϕ1,ϕ2 : I → G με ϕ1(t) = ϕ(s + t),
ϕ2(t) = ϕ(s)ϕ(t) ικανοποιούν ϕ1(0) = ϕ2(0) = ϕ(s) και
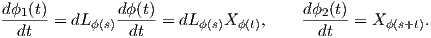
Επειδή το X είναι ένα αριστερά αναλλοίωτο θα ισχύει dLϕ(s)Xϕ(t) = Xϕ(s)ϕ(t). Αυτό σημαίνει ότι οι
καμπύλες ϕ1 και ϕ2 είναι και οι δύο ολοκληρωτικές καμπύλες του διανυσματικού πεδίου X, άρα λόγω της
μοναδικότητας της λύσης θα πρέπει ϕ1(t) = ϕ2(t), δηλαδή ϕ(s + t) = ϕ(s)ϕ(t), (s,t ∈ I). Τέλος, για να
είναι η ϕ μια μονοπαραμετρική υποομάδα της G πρέπει να την επεκτείνουμε σε όλο το ℝ. Αυτό γίνεται ως
εξής: Για κάθε t ∈ ℝ υπάρχει n ∈ ℕ τέτοιο ώστε 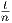 ∈ I, οπότε ορίζουμε
∈ I, οπότε ορίζουμε
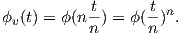
Συνεπώς η ϕυ είναι ένας ομομορφισμός που για t = 0 διέρχεται από το e ∈ G, άρα αποτελεί μια
μονοπαραμετρική υποομάδα της G. ▄
Χρησιμοποιώντας την ταύτηση του εφαπτόμενου χώρου TeG με το σύνολο όλων των αριστερά αναλλοίωτων
διανυσματικών πεδίων 𝔤 της ομάδας Lie G παίρνουμε το παρακάτω συμπέρασμα.
Πόρισμα 7.2: Για κάθε αριστερά αναλλοίωτο διανυσματικό πεδίο X ∈𝔤 υπάρχει μοναδική μονοπαραμετρική
υποομάδα ϕX : ℝ → G τέτοια ώστε ϕX′(0) = X.
Απόδειξη. ΄Εστω X ∈𝔤. Θεωρούμε την απεικόνιση αλγεβρών Lie τ : ℝ →𝔤 με τιμή τ(t) = X. Επειδή
το σύνολο των πραγματικών αριθμών ℝ είναι απλά συνεκτικό, από το Θεώρημα 7.3 υπάρχει μοναδικός
ομομορφισμός ομάδων Lie ϕX : ℝ → G τέτοιος ώστε (dϕX)0 = τ, δηλαδή 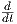
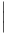 t=0ϕX(t) = X. ▄
t=0ϕX(t) = X. ▄
Μπορούμε τώρα να περιγράψουμε όλες τις μονοπαραμετρικές υποομάδες μιας ομάδας Lie G μέσω μιας
απεικόνισης 𝔤 → G ως εξής:
Ορισμός 7.7: ΄Εστω G μια ομάδα Lie με αντίστοιχη άλγεβρα Lie 𝔤. Η εκθετική απεικόνιση (exponential
map) exp : 𝔤 → G ορίζεται ως εξής:
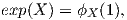
όπου ϕX είναι η μοναδική μονοπαραμετρική υποομάδα του πεδίου X.
Παρατηρήσεις.
1. Στο Κεφάλαιο 5 είχαμε ορίσει την εκθετική απεικόνιση σε μια πολλαπλότητα Riemann. Οι έννοιες γενικά δεν
σχετίζονται. Στην περίπτωση όμως που μια ομάδα Lie είναι εφοδιασμένη με μια αμφιαναλλοίωτη μετρική Riemann
(βλ. Κεφάλαιο 9), οι δύο αυτές εκθετικές απεικονίσεις ταυτίζονται.
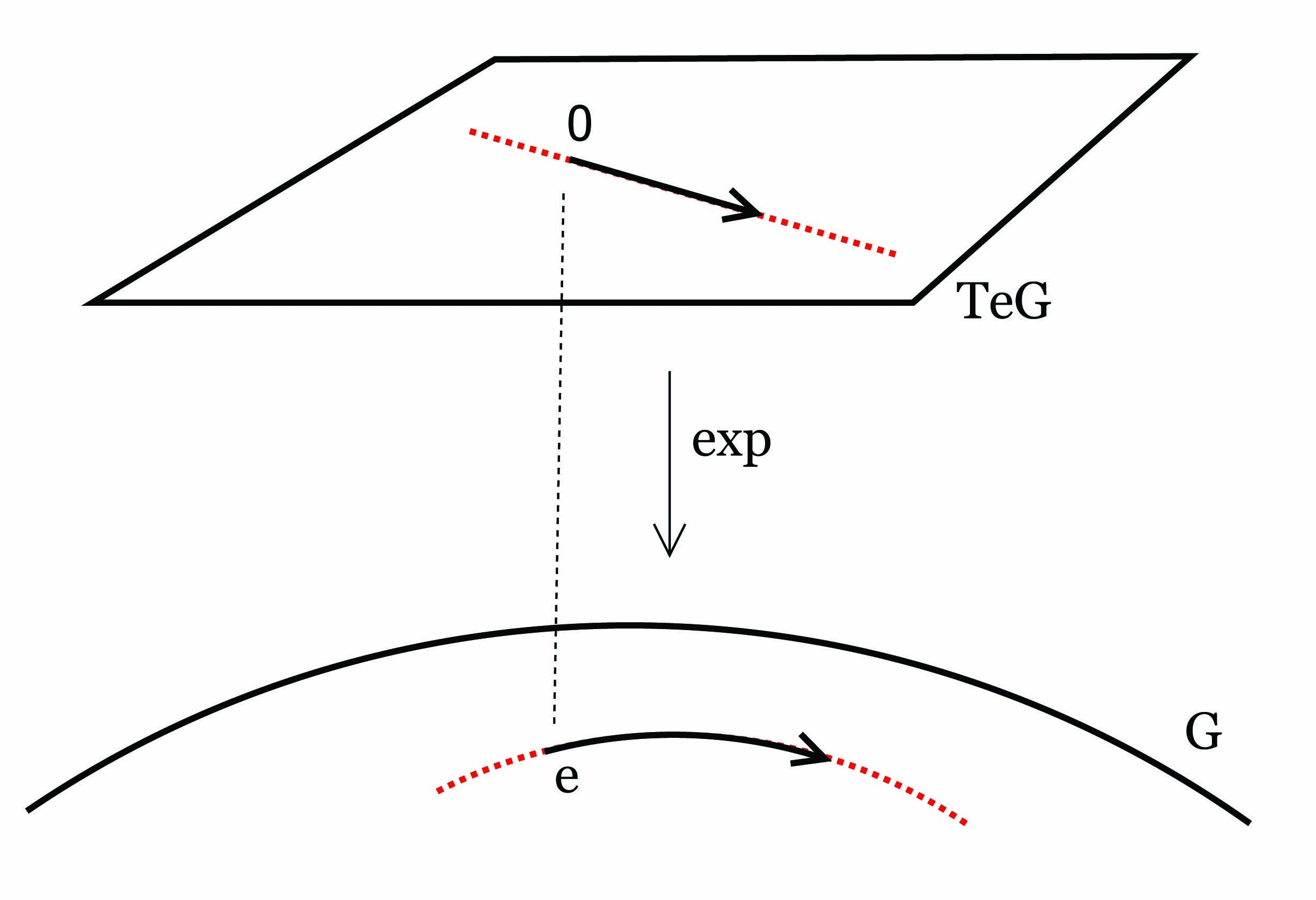
2. Το παρακάτω σχόλιο αφορά την ιστορική χρήση του όρου απειροστική ομάδα (infinitesimal group) την οποία
είχε πρωτοχρησιμοποιήσει ο Lie για μια ομάδα Lie. Χρησιμοποιείται τακτικά και στη Φυσική. Αν ϕ(t)
είναι μια μονοπαραμετρική ομάδα μιας ομάδας Lie G, τότε η παράγωγός της μπορεί να εκφραστεί
ως
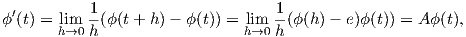 όπου
A = limh→0
όπου
A = limh→0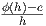 . Το όριο αυτό υπάρχει επειδή η ομάδα Lie είναι πολλαπλότητα της οποίας οι συναρτήσεις
συντεταγμένων είναι λείες. Στην περίπτωση που το A είναι ένας πίνακας (π.χ. όταν η G είναι μια ομάδα πινάκων),
τότε η καμπύλη ϕ(t) = etA είναι η (μοναδική) λύση της παραπάνω διαφορικής εξίσωσης με την αρχική συνθήκη
ϕ(0) = A. Ο πίνακας A ονομάζεται απειροστικός γεννήτορας (infinitesimal generator) της μονοπαραμετρικής
υποομάδας ϕ(t). Για παράδειγμα, για τη μονοπαραμετρική υποομάδα ϕ(t) =
. Το όριο αυτό υπάρχει επειδή η ομάδα Lie είναι πολλαπλότητα της οποίας οι συναρτήσεις
συντεταγμένων είναι λείες. Στην περίπτωση που το A είναι ένας πίνακας (π.χ. όταν η G είναι μια ομάδα πινάκων),
τότε η καμπύλη ϕ(t) = etA είναι η (μοναδική) λύση της παραπάνω διαφορικής εξίσωσης με την αρχική συνθήκη
ϕ(0) = A. Ο πίνακας A ονομάζεται απειροστικός γεννήτορας (infinitesimal generator) της μονοπαραμετρικής
υποομάδας ϕ(t). Για παράδειγμα, για τη μονοπαραμετρική υποομάδα ϕ(t) = 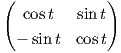 της SU(2)
είναι
της SU(2)
είναι
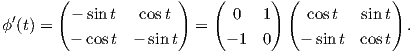 Τότε
ο απειροστικός γεννήτορας της ϕ(t) είναι ο πίνακας
Τότε
ο απειροστικός γεννήτορας της ϕ(t) είναι ο πίνακας
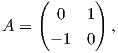 επειδή
πράγματι ισχύει ϕ(t) = etA (εκθετική απεικόνιση πινάκων).
επειδή
πράγματι ισχύει ϕ(t) = etA (εκθετική απεικόνιση πινάκων).
Παράδειγμα. ΄Εστω G = GLnℝ. Γνωρίζουμε ότι η άλγεβρα Lie 𝔤𝔩nℝ είναι το σύνολο Mnℝ. Θα δείξουμε ότι η
εκθετική απεικόνιση exp : 𝔤𝔩nℝ → GLnℝ είναι απλά η συνήθης εκθετική απεικόνιση πινάκων, δηλαδή ότι
exp(A) = eA. ΄Εστω A ∈𝔤𝔩nℝ. Τότε η απεικόνιση
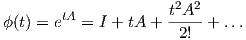
είναι μια μονοπαραμετρική υποομάδα της GLnℝ με ϕ′(0) = A (εύκολα έχουμε ότι ϕ(t + s) = ϕ(t)ϕ(s)). Τότε από
το Πόρισμα 7.2 η εκθετική απεικόνιση θα δίνεται ως
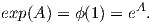
Τα παραπάνω ισχύουν και στην περίπτωση, όπου G = GLnℂ ή G = GLnℍ.
Θα αποδείξουμε στη συνέχεια την απλή σχέση
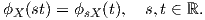 Πράγματι, έστω η μονοπαραμετρική υποομάδα h(t) = ϕX(st) με h′(t) = sϕX′(st), οπότε h′(0) = sϕX′(0) = sX.
Από το προηγούμενο πόρισμα είναι ϕsX′(0) = sX, άρα λόγω της μοναδικότητας θα πρέπει ϕX(st) = ϕsX(t).
Πράγματι, έστω η μονοπαραμετρική υποομάδα h(t) = ϕX(st) με h′(t) = sϕX′(st), οπότε h′(0) = sϕX′(0) = sX.
Από το προηγούμενο πόρισμα είναι ϕsX′(0) = sX, άρα λόγω της μοναδικότητας θα πρέπει ϕX(st) = ϕsX(t).
Εναλλάσσοντας τους ρόλους των s,t και θέτοντας s = 1, προκύπτει ότι
Η παραπάνω σχέση σημαίνει ότι η εκθετική απεικόνιση απεικονίζει τις ευθείες {tX : t ∈ ℝ} του εφαπτόμενου
χώρου TeG σε μονοπαραμετρικές υποομάδες {ϕX(t) : t ∈ ℝ} της ομάδας Lie G.
Παρακάτω δίνουμε κάποιες βασικές ιδιότητες της εκθετικής απεικόνισης.
Πρόταση 7.4: ΄Εστω μια ομάδα Lie G με άλγεβρα Lie 𝔤. Τότε η εκθετική απεικόνιση exp : 𝔤 → G ικανοποιεί
τα εξής:
(1) Η καμπύλη ϕX(t) = exp(tX) για κάθε X ∈𝔤 είναι ο μοναδικός ομομορφισμός της G με ϕX′(0) = X
και επειδή η ϕX είναι ομομορφισμός θα έχουμε:
(2) exp(s + t)X = exp(sX) ⋅ exp(tX).
(3) exp(-tX) = (exp(tX))-1.
Η απόδειξη της πρότασης είναι άμεση συνέπεια των όσων έχουμε αναφέρει μέχρι στιγμής. Ενδεικτικά
αποδεικνύουμε την ιδιότητα (2). Είναι
Θα υπολογίσουμε τώρα το διαφορικό της εκθετικής απεικόνισης στο ουδέτερο στοιχείο 0 ∈𝔤.
Πρόταση 7.5: ΄Εστω G μια ομάδα Lie και 𝔤 η άλγεβρα Lie αυτής. Τότε το διαφορικό (dexp)0 : 𝔤 →𝔤 είναι
η ταυτοτική απεικόνιση του χώρου 𝔤.
Απόδειξη. Θεωρούμε την καμπύλη α : I →𝔤 με α(t) = tX για την οποία είναι α(0) = 0 και α′(0) = X ∈𝔤.
Τότε
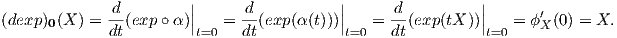
▄
Επειδή το διαφορικό (dexp)0 είναι η ταυτοτική απεικόνιση, αποτελεί έναν ισομορφισμό της 𝔤 στο 0 ∈𝔤. ΄Αρα
από το θεώρημα αντίστροφης απεικόνισης η exp είναι τοπική αμφιδιαφόριση. Συγκεκριμένα, ισχύει το
εξής:
Πρόταση 7.6: ϒπάρχει μια περιοχή Ũ του 0 ∈𝔤 η οποία να απεικονίζεται αμφιδιαφορικά μέσω της exp σε
μια περιοχή U του e ∈ G.
Η ανοικτή περιοχή U = exp(Ũ) ονομάζεται κανονική περιοχή του e (normal neighborhood) και χρησιμοπείται
ως ένας βολικός τοπικός χάρτης στο ουδέτερο της G.
Μέσω της εκθετικής απεικόνισης παίρνουμε μια σημαντική σχέση ανάμεσα στους ομομορφισμούς ομάδων Lie
και τους ομομορφισμούς αλγεβρών Lie. Συγκεκριμένα, ισχύει το εξής θεώρημα, το οποίο είναι γνωστό ως η
φυσιολογική συμπεριφορά (naturality) της εκθετικής απεικόνισης.
Θεώρημα 7.6: ΄Εστω G, H δύο ομάδες Lie με αντίστοιχες άλγεβρες Lie 𝔤, 𝔥. ΄Εστω ϕ : H → G ένας
ομομορφισμός ομάδων Lie. Τότε το παρακάτω διάγραμμα είναι μεταθετικό:
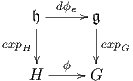
Δηλαδή ισχύει ότι ϕ(expHX) = expG(dϕeX) για κάθε X ∈𝔥.
Απόδειξη. ΄Εστω X ∈𝔥. Θεωρούμε τις καμπύλες σ,τ : ℝ → G με
Αρκεί να αποδείξουμε ότι οι
σ,τ είναι ίσες, οπότε για
t = 1 θα έχουμε το ζητούμενο. Παρατηρούμε ότι η καμπύλη
τ
είναι η μονοπαραμετρική υποομάδα της
G που αντιστοιχεί στο
dϕeX ∈𝔤, άρα θα είναι ένας ομομορφισμός της
G.
Το ίδιο ισχύει και για την καμπύλη
σ, αφού
Επίσης, είναι
σ(0) = τ(0) = e, οπότε θα έχουμε
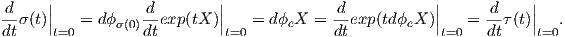
΄Αρα για κάθε t ∈ ℝ θα είναι σ(t) = τ(t), επομένως για t = 1 έχουμε ότι σ(1) = τ(1), δηλαδή
ϕ(exp(X)) = exp(dϕeX) ▄
Παρακάτω, στην έκφραση expG ο δείκτης G θα συμβολίζει την εκθετική απεικόνιση της ομάδας Lie G, δηλαδή
expG : 𝔤 → G.
Πόρισμα 7.3: ΄Εστω H μια υποομάδα Lie της ομάδας Lie G. Τότε για κάθε X ∈ 𝔥, ισχύει expG(X) =
expH(X). Ειδικότερα, ισχύει ότι X ∈𝔥 εάν και μόνο εάν exp(tX) ∈ H για κάθε t.
Παρατήρηση. Χρησιμοποιώντας το παραπάνω πόρισμα, η υποομάδα H του Θεωρήματος 7.2, είναι αυτή που
παράγεται από το σύνολο {exp(tX) : X ∈𝔥}.
Το Πόρισμα 7.3 είναι ιδιαίτερα χρήσιμο στο υπολογισμό των αλγεβρών Lie των κλειστών υποομάδων της
γενικής γραμμικής ομάδας. Πράγματι, αν G είναι μια κλειστή υποομάδα Lie της GLnK με K ∈{ℝ, ℂ} και 𝔤 η
άλγεβρα Lie αυτής, τότε
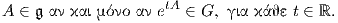
Παράδειγμα. Θα αποδείξουμε ότι η άλγεβρα Lie της SU(n) = U(n) ∩ SLnℂ είναι το σύνολο
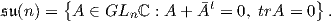
Αρκεί να δείξουμε ότι TISU(n) = 𝔰𝔲(n). ΄Εστω A ∈ TISU(n). Τότε η καμπύλη γ : I → SU(n) με
γ(s) = esA ικανοποιεί γ(0) = I και γ′(0) = A. Επειδή γ(s) ⊂ SU(n) = U(n) ∩ SLnℂ θα έχουμε
ότι
 | (7.5) |
Απο την πρώτη σχέση παίρνουμε ότι γ(s)γ(s)t = I και παραγωγίζοντας στο s = 0 παίρνουμε ότι
![---- -- --
γ′(0)γ(0)t + γ(0)[γ ′(0)]t = 0 ⇒ γ ′(0)+ [γ′(0)]t = 0 ⇒ A + A?t = 0.](02_chapter_07129x.png)
Επίσης, από τη δεύτερη σχέση (7.5) έχουμε ότι det(γ(s)) = 1 και παραγωγίζοντάς στο s = 0 παίρνουμε
ότι
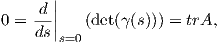
άρα, A ∈𝔰𝔲(n). Αντίστροφα, έστω A ∈𝔰𝔲(n), δηλαδή A + At = 0 και trA = 0. Θα δείξουμε ότι
esA ∈ SU(n) = U(n) ∩ SLnℂ. Πράγματι, είναι
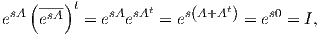
δηλαδή esA ∈ U(n) και
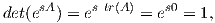
άρα esA ∈ SLnℂ. Επίσης ισχύει e0A = I και 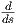
 s=0esA = A, οπότε A ∈ TISU(n).
s=0esA = A, οπότε A ∈ TISU(n).
Μπορούμε εύκολα να δούμε ότι ένας πίνακας A που ανήκει στην 𝔰𝔲(2) έχει τη μορφή
απ΄ όπου πράγματι βλέπουμε ότι dim𝔰𝔲(2) = dimSU(2) = 3.
Οι πίνακες στην παραπάνω βάση της 𝔰𝔲(2) ονομάζονται πίνακες του
Pauli
και έχουν εκτενή χρήση στην κβαντομηχανική.
7.6 Ασκήσεις
1. Θεωρούμε τις απεικονίσεις A : (-ε,ε) → Mm×n(ℝ) και B : (-ε,ε) → Mn×p με την ιδιότητα τα στοιχεία των
πινάκων A(t) και B(t) να είναι διαφορίσιμες συναρτήσεις του t ∈ (-ε,ε). Αποδείξτε ότι για κάθε t ∈ (-ε,ε)
ισχύει
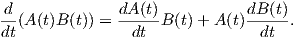
2. Αποδείξτε ότι η SO(2) εκφράζεται ως το σύνολο
![{( cosθ sin θ) }
SO(2) = : θ ∈ [0,2π]
- sin θ cosθ](02_chapter_07137x.png) και
ότι η SU(2) ως το σύνολο
και
ότι η SU(2) ως το σύνολο
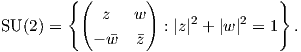
3. Αποδείξτε αναλυτικά ότι οι ομάδες U(n) και SU(n) είναι ομάδες Lie διάστασης n2 και n2 - 1
αντίστοιχα.
4. Αποδείξτε ότι η ορθογώνια ομάδα O(n) είναι ένα κλειστό και φραγμένο υποσύνολο του Mn(ℝ), άρα είναι μια
συμπαγής ομάδα.
5. ΄Εστω n περιττός. Αποδείξτε ότι η απεικόνιση f : O(n) → SO(n) ×{-1,+1} με τύπο f(A) = ((detA)A,detA)
είναι ισομορφισμός ομάδων. Αποδείξτε ότι η SO(2) δεν είναι ισόμορφη με την O(2) ×{-1,+1}.
6. Αποδείξτε ότι η απεικόνιση f : SU(n) × S1 → U(n) με τύπο f(A,u) = Aσ(u), όπου σ(u) = 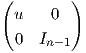 , είναι
αμφιδιαφόριση.
, είναι
αμφιδιαφόριση.
(ϒπόδειξη. Για το επί υπολογίστε την ορίζουσα της εικόνας.)
7. Αναζητήστε στην εργασία [7] ή σε άλλες πηγές τον ορισμό και μερικές ιδιότητες της νηματοποίησης του Hopf
(Hopf fibration). Η απεικόνιση αυτή ορίζεται ως h : S3 → S2, h(z,w) = (2zw,|z|2 -|w|2), (όπου
S3 ⊂ ℝ4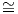 ℂ2). Ισχύει ότι h-1(q) = S1 για κάθε q ∈ S2. Η πιο σημαντική της ιδιότητα είναι ότι μέσω
της απεικόνισης αυτής η σφαίρα S3 είναι δυνατόν να εκφραστεί ως ένωση κύκλων S1, ξένων μεταξύ
τους.
ℂ2). Ισχύει ότι h-1(q) = S1 για κάθε q ∈ S2. Η πιο σημαντική της ιδιότητα είναι ότι μέσω
της απεικόνισης αυτής η σφαίρα S3 είναι δυνατόν να εκφραστεί ως ένωση κύκλων S1, ξένων μεταξύ
τους.
8. Αποδείξτε ότι για κάθε a ∈ G η απεικόνιση La : G → G, La(g) = ag είναι αμφιδιαφόριση.
9. ΄Εστω G μια ομάδα Lie και H μια υποομάδα της G η οποία είναι κανονική υποπολλαπλότητα της G. Αποδείξτε
ότι η H είναι μια υποομάδα Lie της G.
10. ΄Εστω G μια ομάδα πινάκων με άλγεβρα Lie 𝔤. Αποδείξτε ότι για κάθε g ∈ G
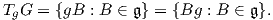
11. ΄Εστω λ ένας άρρητος αριθμός και έστω
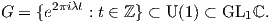 Αποδείξτε ότι η G είναι μια υποομάδα της GL1ℂ, αλλά δεν είναι ομάδα πινάκων.
Αποδείξτε ότι η G είναι μια υποομάδα της GL1ℂ, αλλά δεν είναι ομάδα πινάκων.
(ϒπόδειξη. Αποδείξτε ότι το G είναι πυκνό στην U(1).)
12. ΄Εστω λ ένας άρρητος αριθμός και έστω η απεικόνιση
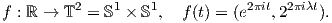 Αποδείξτε ότι η f είναι ένας μονομορφισμός ομάδων Lie και ότι η εικόνα f(ℝ) είναι ένα πυκνό υποσύνολο του
δακτυλίου T2. Είναι μια ευθεία με άρρητη κλίση στον T2. (Το πρώτο ερώτημα είνα απλό, ενώ το δεύτερο δύσκολο.
Αναζητήσε το στη βιβλιογραφία).
Αποδείξτε ότι η f είναι ένας μονομορφισμός ομάδων Lie και ότι η εικόνα f(ℝ) είναι ένα πυκνό υποσύνολο του
δακτυλίου T2. Είναι μια ευθεία με άρρητη κλίση στον T2. (Το πρώτο ερώτημα είνα απλό, ενώ το δεύτερο δύσκολο.
Αναζητήσε το στη βιβλιογραφία).
Συνεπώς, η εικόνα f(G) ενός ομομορφισμού f : G → H ομάδων Lie, δεν είναι γενικά μια κανονική
υποπολλαπλότητα της H ([4]).
13. Αποδείξτε ότι TI(U(n)) = {X ∈ Mn(ℂ) : Xt = -X}, το σύνολο όλων των n × n αντιερμητιανών
πινάκων.
14. ΄Εστω Sp(n) = {A ∈ U(2n) : AtJ = JA-1}, όπου J = 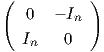 . Αποδείξτε ότι
TI(Sp(n) = {X ∈ M2n(ℂ) : Xt = -X, XtJ + JX = 0}.
. Αποδείξτε ότι
TI(Sp(n) = {X ∈ M2n(ℂ) : Xt = -X, XtJ + JX = 0}.
15. ΄Εστω u,υ ∈ TeG με Xu,Xυ τα αντίστοιχα αριστερά αναλλοίωτα διανυσματικά πεδία. Αποδείξτε
ότι
![[Xu, Xv] = X [u,v].](02_chapter_07145x.png)
16. Βρείτε όλα τα αριστερά αναλλοίωτα διανυσματικά πεδία στον ℝn και στον μοναδιαίο κύκλο S1.
17. Θεωρούμε το σύνολο πινάκων της μορφής
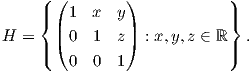 Αποδείξτε τα εξής:
Αποδείξτε τα εξής:
(α) Το σύνολο H είναι μια λεία πολλαπλότητα αμφιδιαφορική με τον ℝ3.
(β) Το H με πράξη πολλαπλασιασμό πινάκων είναι μια ομάδα Lie.
(γ) Το σύνολο {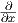 ,
,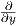 ,x
,x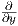 +
+ 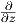 } αποτελεί μια βάση της άλγεβρας Lie 𝔥 της H.
} αποτελεί μια βάση της άλγεβρας Lie 𝔥 της H.
(δ) Βρείτε την άλγεβρα Lie της H.
(ε) Βρείτε την εκθετική απεικόνιση της H.
(ϒποδείξεις: Για το (γ): Επειδή dimH = 3, αρκεί να δειχθεί ότι τα διανυσματικά αυτά πεδία είναι γραμμικώς
ανεξάρτητα (που είναι άμεσο) και ότι είναι αριστερά αναλλοίωτα διανυσματικά πεδία της H. Για το (δ):
Βρείτε τον εφαπτόμενο χώρο στο ουδέτερο. Αυτός αποτελείται από τους αυστηρά άνω τριγωνικούς
πίνακες.)
18. Αποδείξτε ότι ο πίνακας 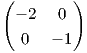 δεν μπορεί να εκφραστεί ως eA για κάποιον πίνακα A ∈ GLnℝ. Συνεπώς,
η εκθετική απεικόνιση γενικά δεν είναι επί.
δεν μπορεί να εκφραστεί ως eA για κάποιον πίνακα A ∈ GLnℝ. Συνεπώς,
η εκθετική απεικόνιση γενικά δεν είναι επί.
Βιβλιογραφία
[1] A. Arvanitoyeorgos, An Introduction to Lie Groups and the Geometry of Homogeneous Spaces,
American Mathematical Society, 2003.
[2] Α. Αρβανιτογεώργος, Ομάδες Lie, Ομογενείς Χώροι και Διαφορική Γεωμετρία, Εκδόσεις
Τροχαλία, Αθήνα 1999.
[3] A. Baker, Matrix groups: An Introduction to Lie Group Theory, Springer 2003.
[4] N. Bourbaki, Topologie général, Ch. 5, 6, Herman, Paris 1947.
[5] A. Borel, Essays in the History of Lie Groups and Algebraic Groups, American Mathematical
Society, 2001.
[6] H.D. Fegan, Introduction to Compact Lie Groups, Word Scientific, Singapore, 1991.
[7] D.W. Lyons, An elementary introduction to the Hopf fibration, Mathematics Magazine, 76(2)
(2003) 87–98.
[8] A. A. Sagle and R.E. Walde, Introduction to Lie Groups and Lie Algebras, Academic Press,
New York 1973.
[9] K. Tapp, Matrix groups for Undergraduates, American Mathematical Society, 2005.
[10] A. Tresse, Sur les invariants différentiels des groups continus de transformations, Acta
Mathematica, 18 (1893) 1–88.
[11] L. Tu, An Introduction to Manifolds, Second Edition, Springer-Verlag New York, 2011.
[12] F. W. Warner, Foundations of Differentiable Manifolds and Lie Groups, Springer-Verlag New
York, 1983.
 variste Galois, σύμφωνα
με την οποία τη θέση της λύσης μιας πολυωνυμικής εξίσωσης με ριζικά, θα έπαιρνε μια πεπερασμένη ομάδα
συμμετριών μιας διαφορικής εξίσωσης. Οι διαφορικές εξισώσεις που μελετούσε τότε ο Lie είναι γνωστές ως
εξισώσεις τύπου Lie, τυπικό παράδειγμα των οποίων είναι η εξίσωση Riccati. Τα απλούστερα παραδείγματα ομάδων
Lie είναι οι ομάδες ισομετρικών των ℝn, ℂn και ℍn (ℍ είναι το σύνολο των υπερμιγαδικών αριθμών),
απ΄ όπου προκύπτουν η ορθογώνια ομάδα O(n), η μοναδιαία ομάδα U(n) και η συμπλεκτική ομάδα
Sp(n).
variste Galois, σύμφωνα
με την οποία τη θέση της λύσης μιας πολυωνυμικής εξίσωσης με ριζικά, θα έπαιρνε μια πεπερασμένη ομάδα
συμμετριών μιας διαφορικής εξίσωσης. Οι διαφορικές εξισώσεις που μελετούσε τότε ο Lie είναι γνωστές ως
εξισώσεις τύπου Lie, τυπικό παράδειγμα των οποίων είναι η εξίσωση Riccati. Τα απλούστερα παραδείγματα ομάδων
Lie είναι οι ομάδες ισομετρικών των ℝn, ℂn και ℍn (ℍ είναι το σύνολο των υπερμιγαδικών αριθμών),
απ΄ όπου προκύπτουν η ορθογώνια ομάδα O(n), η μοναδιαία ομάδα U(n) και η συμπλεκτική ομάδα
Sp(n).




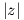
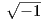 . Βλέπε περισσότερα στην
υποπαράγραφο
. Βλέπε περισσότερα στην
υποπαράγραφο 
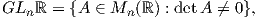
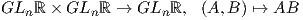
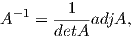
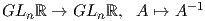
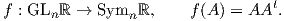
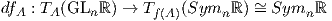
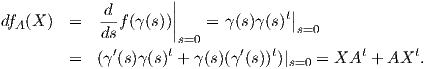
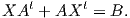
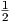
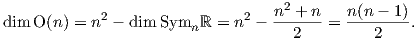
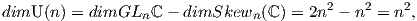
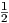
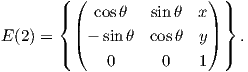
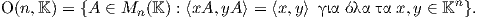
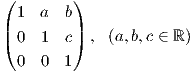
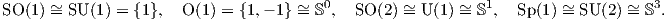
![{( ) }
cosθ sin θ
SO(2) = : θ ∈ [0,2π]
- sin θ cosθ](02_chapter_0725x.png)
![S1 = {(x,y ) ∈ ℝ2 : x2 + y2 = 1} = {eiθ : θ ∈ [0,2π]}.](02_chapter_0726x.png)
![U (1) = {z = x+ yi ∈ ℂ : z?z = 1} = {eiθ : θ ∈ [0,2π ]}.](02_chapter_0727x.png)


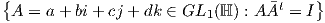 . Κάνοντας πράξεις προκύπτει ότι
. Κάνοντας πράξεις προκύπτει ότι
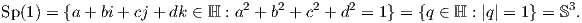

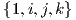 και ορίζουμε έναν πολλαπλασιαστικό κανόνα για τα στοιχεία της
με τον εξής τρόπο:
και ορίζουμε έναν πολλαπλασιαστικό κανόνα για τα στοιχεία της
με τον εξής τρόπο:
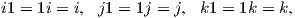
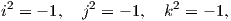
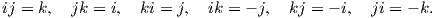
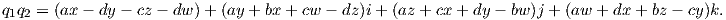
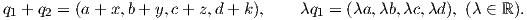
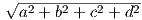
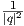

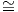
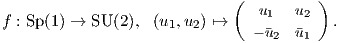
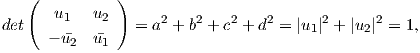
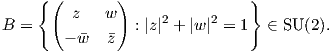
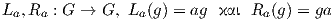
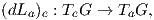
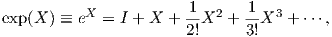
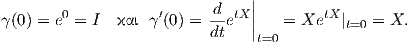
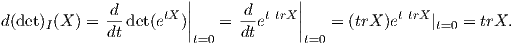

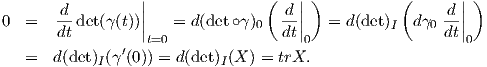
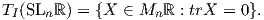
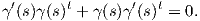
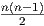 . Επιπλέον, επειδή είναι
. Επιπλέον, επειδή είναι 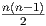 , καταλήξαμε στο
ότι
, καταλήξαμε στο
ότι
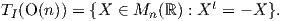
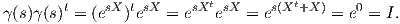
![dL α[X, Y ]pf = [X,Y ]p(f ∘L α) = Xp(Y (f ∘ Lα))- Yp (X (f ∘L α))
= Xp (dL αY )f - Yp(dL αX )f = XpY f - YpXf
= (XpY - YpX )f = [X, Y]pf,](02_chapter_0761x.png)
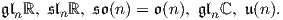
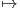
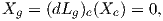
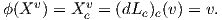
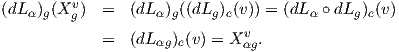
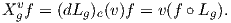
![[u,v] = [Xu, Xv ]e ∈ TeG. (7.1)](02_chapter_0768x.png)
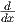
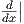
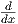
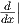
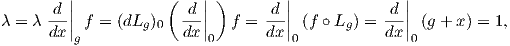
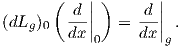
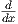 είναι ένα αριστερά αναλλοίωτο διανυσματικό πεδίο της πολλαπλότητας
είναι ένα αριστερά αναλλοίωτο διανυσματικό πεδίο της πολλαπλότητας 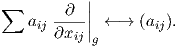
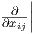
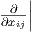
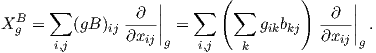
![[f,g] = f ∘g - g ∘ f.](02_chapter_0780x.png)


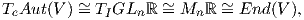
![[A, B] = AB - BA,](02_chapter_0784x.png)
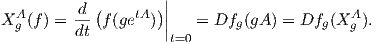

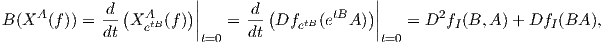
![[XA, XB ]I(f) = A (XB (f))- B (XA (f)) = DfI (AB - BA ),](02_chapter_0789x.png)
![τ([X,Y ]𝔤) = [τ(X ),τ(Y )]𝔥, για κάθε X, Y ∈ 𝔤.](02_chapter_0790x.png)
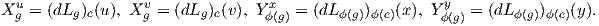
![x y
[dϕeu,dϕev ] = [x,y] = [Y ,Y ]ϕ(e).](02_chapter_0792x.png)
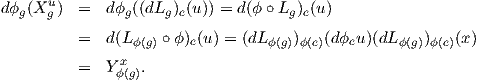
![dϕ ([u,v ]) = dϕ ([Xu, Xv ]) = [Yx,Y y] .
e e e ϕ(e)](02_chapter_0794x.png)
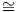
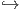
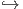

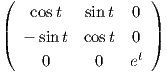 είναι μια μονοπαραμετρική υποομάδα της
είναι μια μονοπαραμετρική υποομάδα της
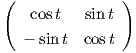 είναι μια μονοπαραμετρική υποομάδα της
είναι μια μονοπαραμετρική υποομάδα της 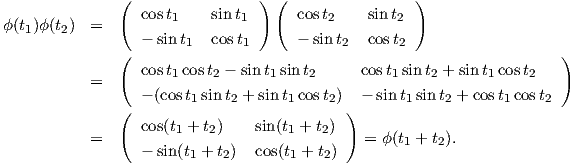

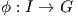
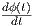
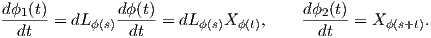
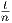
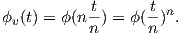
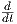
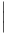
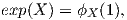
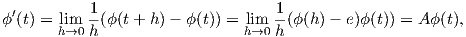
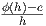 . Το όριο αυτό υπάρχει επειδή η ομάδα
. Το όριο αυτό υπάρχει επειδή η ομάδα 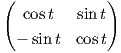 της
της 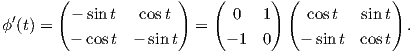
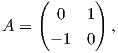
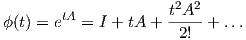
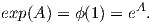
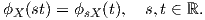
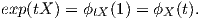
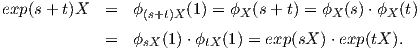
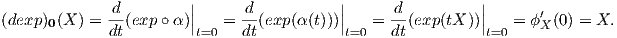

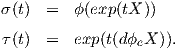
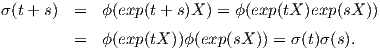
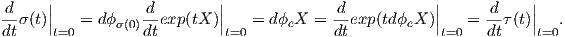
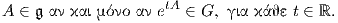
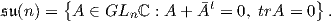

![---- -- --
γ′(0)γ(0)t + γ(0)[γ ′(0)]t = 0 ⇒ γ ′(0)+ [γ′(0)]t = 0 ⇒ A + A?t = 0.](02_chapter_07129x.png)
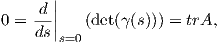
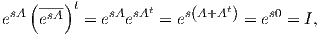
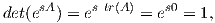
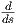

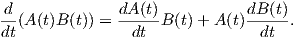
![{( cosθ sin θ) }
SO(2) = : θ ∈ [0,2π]
- sin θ cosθ](02_chapter_07137x.png)
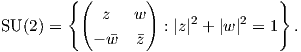
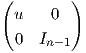 , είναι
αμφιδιαφόριση.
, είναι
αμφιδιαφόριση.
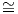
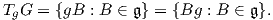
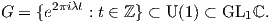
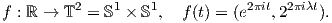
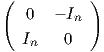 . Αποδείξτε ότι
. Αποδείξτε ότι
![[Xu, Xv] = X [u,v].](02_chapter_07145x.png)
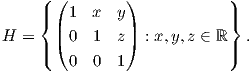
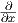
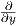
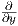
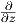
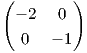 δεν μπορεί να εκφραστεί ως
δεν μπορεί να εκφραστεί ως