⁶Θα θέλαμε να δώσουμε κάποια εξήγηση για τον ορισμό της δεύτερης παραγώγου D²f _I, η οποία δεν παρουσιάζεται τακτικά σε μαθήματα. ΄Εστω f : U ⊂ ℝⁿ → ℝ^m μια διαφορίσιμη συνάρτηση. Τότε το διαφορικό της f στο p ∈ U είναι η γραμμική απεικόνιση Df_p : ℝⁿ → ℝ^m, δηλαδή Df _p ∈ L(ℝⁿ, ℝ^m), άρα ορίζεται η απεικόνιση Df : U → L(ℝⁿ, ℝ^m), p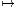Df _p. Η δεύτερη παράγωγος της f στο p ορίζεται από τον τύπο D²f _p = D(Df)_p ∈ L(ℝⁿ,L(ℝⁿ, ℝ^m)) (υπό την προϋπόθεση ότι τα απαραίτητα όρια υπάρχουν). Από τη γραμμική άλγεβρα γνωρίζουμε ότι, αν L²(ℝⁿ, ℝ^m) είναι ο διανυσματικός χώρος των διγραμμικών απεικονίσεων από τον ℝⁿ × ℝⁿ στον ℝ^m, τότε οι διανυσματικοί χώροι L(ℝⁿ,L(ℝⁿ, ℝ^m)) και L²(ℝⁿ, ℝ^m) είναι ισόμορφοι. Ο ισομορφισμός αυτός δίνεται ως εξής: έστω X,Y ∈ ℝⁿ. Τότε για κάθε B ∈ L(ℝⁿ,L(ℝⁿ, ℝ^m)) ορίζουμε B′∈ L²(ℝⁿ, ℝ^m) με B′(X,Y ) = (B(X))(Y ). Ιδιαιτέρως, για τη διαφορίσιμη συνάρτηση f : U → ℝ για την οποία υποθέτουμε ότι υπάρχει η δεύτερη παράγωγος B = D²f _p (p ∈ U), ορίζουμε F(p) = Df_p ∈ L(ℝⁿ, ℝ^m). Τότε, για κάθε X,Y ∈ ℝⁿ είναι D²f _p(X,Y ) = (DF_p(X))Y . Αποδεικνύεται ότι ο πίνακας της διγραμμικής μορφής D²f _p : ℝⁿ × ℝⁿ → ℝ (ως προς τις κανονικές βάσεις) είναι ο Εσσιανός πίνακας της f.