Ορισμός 6.1: ΄Εστω (M,g) μια πολλαπλότητα Riemann με συνοχή Levi-Civita ∇. Η απεικόνιση
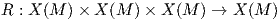
![R (X,Y )Z = ∇X ∇Y Z - ∇Y ∇X Z - ∇ [X,Y]Z](02_chapter_061x.png)
Σύνοψη
Το κεντρικό αντικείμενο μελέτης της γεωμετρίας Riemann είναι η καμπυλότητα. Παρουσιάζουμε σε σύγχρονη
γλώσσα τον ιστορικό ορισμό της καμπυλότητας τομής που έδωσε ο Riemann. Στη συνέχεια, αναπτύσσουμε
αναλυτικά τις (ισοδύναμες) έννοιες του τανυστή καμπυλότητας και την καμπυλότητα τομής. Η καμπυλότητα Ricci
και η βαθμωτή αποτελούν δύο άλλα είδη καμπυλοτήτων που ορίζονται σε μια πολλαπλότητα Riemann. Στην
περίπτωση μιας κανονικής επιφάνειας στον ℝ3, όλα τα είδη αυτά των καμπυλοτήτων ταυτίζονται. Οι βασικές
αναφορές στο κεφάλαιο αυτό είναι τα βιβλία [3], [4], [6], [8], [10] και [11]. Σε πιο προχωρημένο επίπεδο είναι τα
βιβλία [2] και [7].
Προαπαιτούμενη γνώση
Διαφορικός Λογισμός μιας και πολλών μεταβλητών, Γραμμική Άλγεβρα, Θεωρία Επιφανειών.
Γνωρίζουμε από τη θεωρία επιφανειών όπως αυτή αναπτύχθηκε μετά το 1700, ότι η καμπυλότητα Gauss αποτελεί ένα μέτρο της κύρτωσης μιας επιφάνειας στον ℝ3. Θυμίζουμε ότι ένας τρόπος να οριστεί η καμπυλότητα Gauss είναι μέσω των κύριων καμπυλοτήτων, δηλαδή λαμβάνοντας υπόψη ότι η επιφάνεια βρίσκεται εμβαπτισμένη στον ℝ3. Με το περίφημο Theorema Egregium ο Gauss απέδειξε το απροσδόκητο αποτέλεσμα ότι η καμπυλότητα Gauss αποτελεί μια ισομετρική αναλλοίωτη της επιφάνειας, δηλαδή ότι δεν εξαρτάται από το γεγονός ότι η επιφάνεια βρίσκεται στον ℝ3. Το σημαντικό αυτό θεώρημα οδήγησε τον Riemann1 στην ανακάλυψη της ομώνυμης γεωμετρίας, κεντρικό αντικείμενο της οποίας είναι η γενίκευση της καμπυλότητας Gauss σε οποιαδήποτε πολλαπλότητα Riemann ([13]).
Από ιστορικής απόψεως ο Riemann όρισε μια έννοια καμπυλότητας για μια πολλαπλότητα Riemann, γενικεύοντας την καμπυλότητα Gauss. Η καμπυλότητα αυτή σήμερα ονομάζεται καμπυλότητα τομής. Παρακάτω θα περιγράψουμε σύντομα τον αρχικό ορισμό του Riemann. Για περισσότερα ιστορικά και μαθηματικά θέματα σχετικά με την συνεισφορά του Riemann, παραπέμπουμε στα βιβλία [1], [4] και στην εργασία [9].
΄Εστω M μια πολλαπλότητα Riemann, p ∈ M και έστω Π ένας υπόχωρος του TpM διάστασης 2. Θεωρούμε το σύνολο όλων των γεωδαισιακών με αρχή το p και με διανύσματα ταχύτητάς τους να ανήκουν στον υπόχωρο Π. Τα τμήματα των γεωδαισιακών αυτών τα οποία βρίσκονται σε μια κανονική περιοχή U του p, ορίζουν μια υποπολλαπλότητα N της M, διάστασης 2. Σε σύγχρονη γλώσσα N = expp(Π ∩ expp-1(U)). Η υποπολλαπλότητα N της M έχει μια επαγόμενη μετρική. Σύμφωνα με το Theorema Egregium η καμπυλότητα Gauss της N μπορεί να υπολογιστεί από τη μετρική αυτή. Αυτή ακριβώς είναι η καμπυλότητα τομής την οποία εισήγαγε ο Riemann στο p για το επίπεδο Π και συμβολίζεται με K(p,Π). Προφανώς, αν M = ℝn, τότε K(p,Π) = 0 για κάθε p και για κάθε Π.
Αν και γεωμετρικά εύληπτη, η καμπυλότητα τομής είναι δύσκολο να υπολογιστεί με τον τρόπο που την όρισε ο Riemann και πέρασε αρκετός χρόνος μέχρι να αναπτυχθεί ένα πιο χρηστικό εργαλείο. Ο τανυστής καμπυλότητας, τον οποίο θα ορίσουμε στη συνέχεια, αν και ως έννοια είναι πιο αφηρημένη και μακριά από την αρχική ιδέα του Riemann, εντούτοις αποτελεί ένα λειτουργικό εργαλείο, προκειμένου να δοθούν ορισμοί και να γίνονται υπολογισμοί.
Για τον ορισμό του τανυστή καμπυλότητας, αρκεί να έχουμε μια λεία πολλαπλότητα εφοδιασμένη με μια ομοπαραλληλική συνοχή. Είναι δυνατόν να αναπτυχθούν διάφορα ήδη γεωμετρίας με την προσέγγιση αυτή. Επειδή όμως εμείς στο παρόν βιβλίο (αλλά και γενικά στην μαθηματική πρακτική) ασχολούμαστε με τη γεωμετρία των πολλαπλοτήτων Riemann, η συνοχή που θα χρησιμοποιούμε είναι η συνοχή Levi-Civita.
Ορισμός 6.1: ΄Εστω (M,g) μια πολλαπλότητα Riemann με συνοχή Levi-Civita ∇. Η απεικόνιση
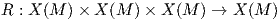
![R (X,Y )Z = ∇X ∇Y Z - ∇Y ∇X Z - ∇ [X,Y]Z](02_chapter_061x.png)
Παρατήρηση. Εφιστούμε την προσοχή στον αναγνώστη στο ότι πολλές φορές η καμπυλότητα ορίζεται στην βιβλιογραφία με αντίθετο πρόσημο, δηλαδή R(X,Y )Z = ∇[X,Y ]Z -∇X∇Y Z + ∇Y ∇XZ. Σε αυτή την περίπτωση διάφοροι τύποι έχουν αντίθετο πρόσημο.
Η παραπάνω απεικόνιση είναι πράγματι ένας τανυστής τύπου (1,3), όπως θα αποδείξουμε αμέσως. Αποτελεί εσωτερική ποσότητα της πολλαπλότητας, επειδή εξαρτάται μόνο από τη συνοχή Levi-Civita.
Για κάθε X,Y ∈ X(M) ορίζεται ο τελεστής
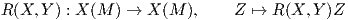
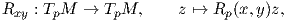
Πρόταση 6.1: Για κάθε X,Y,Z ∈ X(M) η συνάρτηση R(X,Y )Z είναι F(M)-γραμμική ως προς τις μεταβλητές X,Y και Z. Συνεπώς, η συνάρτηση R είναι ένας τανυστής τύπου (1,3).
Απόδειξη. Θα αποδείξουμε πρώτα την F(M)-γραμμικότητα της R(X,Y )Z ως προς X. Θα χρησιμοποιήσουμε την εξής σχέση (βλ. Κεφάλαιο 4, ΄Ασκηση 12):
![[f X,gY ] = f g[X, Y ]+ f(Xg )Y - g(Yf )X,](02_chapter_064x.png) | (6.1) |
για κάθε f,g ∈ F(M),X,Y ∈ X(M). Από το ορισμό της καμπυλότητας έχουμε ότι
![R(f X,Y )Z = ∇fX ∇Y Z - ∇Y ∇fX Z - ∇ [fX,Y]Z.](02_chapter_065x.png) | (6.2) |
Λόγω της F(M)-γραμμικότητας της συνοχής ∇ ως προς X, ο πρώτος όρος της (6.2) ισούται με f∇X∇Y Z και λόγω του κανόνα Leibnitz ο δεύτερος όρος της (6.2) ισούται με
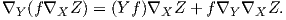
![∇[fX,Y]Z = ∇f[X,Y]- (Y f)X Z = f∇ [X,Y ]Z - (Y f)∇X Z.](02_chapter_067x.png)
![R (fX, Y)Z = f (∇X ∇Y Z - ∇Y ∇X Z - ∇[X,Y]Z ) = fR(X, Y )Z.](02_chapter_068x.png)
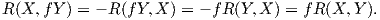
Παράδειγμα. Αν M = ℝn τότε R(X,Y )Z = 0 για κάθε X,Y,Z ∈ X(ℝn). Πράγματι, αν Z = ∑
Zi = (Z1,…,Zn),
όπου ui οι φυσικές συντεταγμένες του ℝn, τότε
= (Z1,…,Zn),
όπου ui οι φυσικές συντεταγμένες του ℝn, τότε
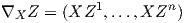
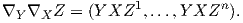
![R (X, Y )Z = ∇X ∇Y Z - ∇Y ∇X Z - ∇ [X,Y]Z = 0.](02_chapter_0613x.png)
Ας δούμε τώρα τοπική έκφραση του τανυστή καμπυλότητας (ιδιαίτερα τακτική σε βιβλιογραφία Φυσικής). ΄Εστω
(U;x1,…,xn) ένας τοπικός χάρτης της M και θέτουμε Xi = 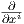 . Τότε, επειδή ισχύει [Xi,Xj] = 0, θα έχουμε
ότι
. Τότε, επειδή ισχύει [Xi,Xj] = 0, θα έχουμε
ότι
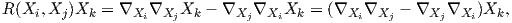
Πρόταση 6.2: ΄Εστω (M,g) μια πολλαπλότητα Riemann διάστασης n και οι συναρτήσεις Rijkl = g(R(Xi,Xj)Xk,Xl), (i,j,k,l = 1,…,n). Τότε
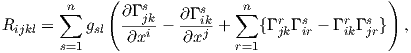
Πολλές φορές ορίζουμε και τις συναρτήσεις Rijkl από την σχέση
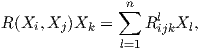
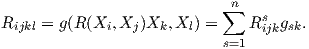
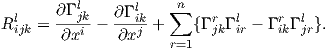
Επίσης, αν X = ∑ iuiXi,Y = ∑ jυjXj και Z = ∑ kwkXk, τότε η σχέση
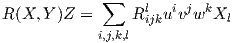
Παράδειγμα. ΄Εστω M = ℝn εφοδιασμένος με τη μετρική gij = δij. Τότε ως γνωστόν είναι Γijk = 0 για κάθε i,l,k, συνεπώς παίρνουμε πάλι ότι R ≡ 0.
Απόδειξη. Με κυκλική εναλλαγή στην σχέση ∇XY -∇Y X = [X,Y ] και χρησιμοποιώντας την ταυτότητα Jacobi προκύπτει ότι
![R (X,Y )Z + R (Y, Z)X + R(Z,X )Y = ∇X ∇Y Z - ∇Y ∇X Z - ∇[X,Y]Z
+ ∇ ∇ X - ∇ ∇ X - ∇ X + ∇ ∇ Y - ∇ ∇ Y - ∇ Y
Y Z Z Y [Y,Z] Z X X Z [Z,X]
= ∇Z [X, Y] + ∇Y [Z, X ]+ ∇X [Y,Z]- ∇[X,Y]Z - ∇[Y,Z]X - ∇ [Z,X ]Y
= [Z,[X, Y]]+ [X,[Y,Z ]]+ [Y,[Z,X ]] = 0.](02_chapter_0623x.png)
ϒπάρχει και η ονομαζόμενη δεύτερη ταυτότητα του Bianchi, σύμφωνα με την οποία
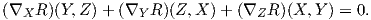
Ο τανυστής καμπυλότητας ικανοποιεί τις εξής ταυτότητες συμμετρίας. Θέτουμε
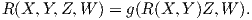
Πρόταση 6.4: Για κάθε X,Y,Z,W ∈ X(M) ισχύουν οι σχέσεις:
Απόδειξη. Η ταυτότητα (i) προκύπτει άμεσα από τον ορισμό του τανυστή καμπυλότητας. Θα αποδείξουμε την (ii) και αφήνουμε την (iii) ως άσκηση.
Αρκεί να δείξουμε την ταυτότητα R(X,Y,Z,Z) = 0. Τότε η ζητούμενη σχέση προκύπτει άμεσα από το ότι R(X,Y,Z + W,Z + W) = 0. Πράγματι, έχουμε ότι
![R(X, Y,Z, Z) = g(∇X ∇Y Z - ∇Y ∇X Z - ∇[X,Y]Z,Z ).](02_chapter_0626x.png) | (6.3) |
Στη συνέχεια, θα χρησιμοποιήσουμε τη συμβατότητα της μετρικής με τη συνοχή Levi-Civita
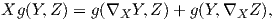
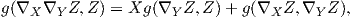
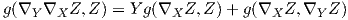
![1
g(∇ [X,Y ]Z, Z) = -[X, Y]g(Z,Z ).
2](02_chapter_0630x.png)
![R(X, Y,Z, Z) = g (∇X ∇Y Z,Z )- g(∇Y ∇X Z, Z) - g(∇[X,Y]Z, Z)
1
= Xg (∇Y Z, Z) - Yg(∇X Z, Z) - -[X, Y]g(Z,Z )
2
= 1X (Yg(Z, Z))- 1Y(Xg (Z,Z ))- 1-[X, Y ]g(Z, Z)
2 2 2
= 1[X,Y ]g (Z, Z) - 1[X,Y ]g(Z,Z ) = 0.
2 2](02_chapter_0631x.png)
Χρησιμοποιώντας την τοπική έκφραση του τανυστή καμπυλότητας, η πρώτη ταυτότητα του Bianchi, καθώς και οι ταυτότητες συμμετρίας της Πρότασης 6.4 εκφράζονται αντίστοιχα ως εξής:
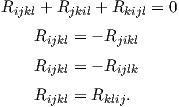
΄Αμεσα συνδεδεμένη με τον τανυστή καμπυλότητας και ταυτόχρονα πιο κοντά στον αρχικό ορισμό του Riemann, είναι η καμπυλότητα τομής.
΄Εστω (M,g) μια πολλαπλότητα Riemann και p ∈ M. ΄Εστω Π ένας δισδιάστατος υπόχωρος του TpM (ένας τέτοιος ονομάζεται εφαπτόμενο επίπεδο της M στο p) και έστω x,y ∈ Π. Ορίζουμε
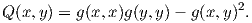
Λήμμα 6.1: Εάν Π είναι ένα μη ιδιάζον εφαπτόμενο επίπεδο της M στο σημείο p, τότε ο αριθμός
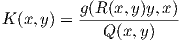
Απόδειξη. Δύο βάσεις {x,y}, {υ,w} του Π σχετίζονται μέσω των εξισώσεων
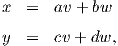
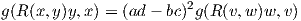
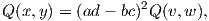
Ορισμός 6.2: ΄Εστω Π ένας δισδιάστατος υπόχωρος του TpM και {x,y} μια τυχαία βάση του Π. Τότε ο αριθμός
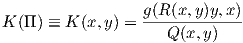
Εάν θεωρήσουμε την πολλαπλότητα Grassmann Gr2(TpM) όλων των δισδιάστατων υποχώρων του TpM, δηλαδή
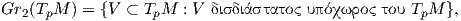
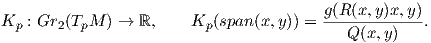
Παρατήρηση. Εάν dimM = 2, τότε η καμπυλότητα τομής στο σημείο p είναι η γνωστή μας καμπυλότητα Gauss της M στο σημείο p. Εδώ είναι Π = TpM και η K είναι μια συνάρτηση του σημείου p και μόνο, η οποία δίνεται ως
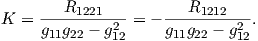
Παράδειγμα. Θεωρούμε την σφαίρα S2 εφοδιασμένη με τη μετρική
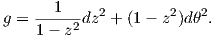
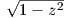
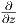 και Y =
και Y = 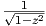
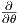 . Τότε είναι
. Τότε είναι
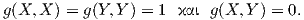
![--z---∂f- --z---
[X,Y ]f = 1- z2 ∂θ άρα [X, Y] = 1- z2Y.](02_chapter_0648x.png)
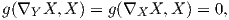
![g(∇ Y,X ) = g(∇ X, X) + g([X, Y ],X ) = 0, οπότε ∇ Y = 0.
X Y X](02_chapter_0650x.png)
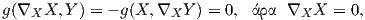
![z z
g(∇Y X, Y ) = g(∇X Y, Y) - g([X, Y ],Y ) = - √----2, άρα ∇Y X = - √-----2-Y,
1- z 1- z](02_chapter_0652x.png)
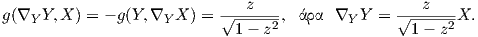
![K = g (R (X,Y )Y,X ) = g(∇X ∇Y Y - ∇Y ∇X Y - ∇ [X,Y]Y,X )
= g (∇ (√--z---X )- √--z---∇ Y, X)
X 1 - z2 1 - z2 Y
∘ ------∂ z z z
= 1- z2---√-----2-- √------2√------2 = 1.
∂z 1- z 1 - z 1- z](02_chapter_0654x.png)
Η καμπυλότητα τομής σε ένα σημείο είναι λοιπόν γνωστή, όταν γνωρίζουμε τον τανυστή καμπυλότητας R στο σημείο αυτό, όπως προκύπτει από τον ορισμό. Το ενδιαφέρον είναι ότι ισχύει και το αντίστροφο: η γνώση της καμπυλότητας τομής K(Π) για κάθε Π ⊂ TpM δισδιάστατο υπόχωρο, προσδιορίζει πλήρως τον R στο σημείο p. Αυτό είναι ένα καθαρά αλγεβρικό αποτέλεσμα, το οποίο αν και δεν θα αποδείξουμε εδώ, σημαίνει το εξής:
΄Εστω F : TpM × TpM × TpM → TpM μια τριγραμμική απεικόνιση, η οποία ικανοποιεί την ταυτότητα Bianchi (Πρόταση 6.3), καθώς και τις συμμετρίας του τανυστή καμπυλότητας (Πρόταση 6.4). Ορίζουμε
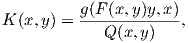
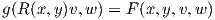
Μια πολλαπλότητα Riemann ονομάζεται πολλαπλότητα σταθερής καμπυλότητας (constant curvature), εάν η καμπυλότητα τομής είναι σταθερή σε κάθε σημείο p και για κάθε επίπεδο Π. Τότε γράφουμε K = K(p,Π) ≡ σταθερά. Η μελέτη τέτοιων πολλαπλοτήτων αποτελεί σημαντικό πεδίο της διαφορικής γεωμετρίας. Παραδείγματα τέτοιων πολλαπλοτήτων είναι ο Ευκλείδειος χώρος ℝn, όπου K ≡ 0, η σφαίρα Sn όπου K ≡ 1 και ο υπερβολικός χώρος ℍn όπου K ≡-1.
Θα αποδείξουμε στη συνέχεια μια απλή έκφραση του τανυστή καμπυλότητας μιας πολλαπλότητας Riemann, η οποία έχει σταθερή καμπυλότητα τομής. Δεν υπάρχει κάποια ιδιαίτερα εύκολη απόδειξη του αποτελέσματος αυτού, και αυτή που παραθέτουμε έχει προσαρμοστεί από το βιβλίο [5]. Για εναλλακτικές αποδείξεις παραπέμπουμε στα βιβλία των [7] και [10].
Αρχίζουμε με έναν ισοδύναμο ορισμό του να είναι μια πολλαπλότητα Riemann σταθερής καμπυλότητας. Ορίζουμε τις συναρτήσεις δ,Δ : M → ℝ με τύπους

(α) (γνήσια) θετικής καμπυλότητας εάν δ ≥ 0 (> 0) για κάθε p.
(β) (γνήσια) αρνητικής καμπυλότητας εάν Δ ≤ 0 (< 0) για κάθε p.
(γ) σταθερής καμπυλότητας εάν δ = Δ = σταθερά.
(δ) επίπεδη (flat) εάν δ ≡ Δ ≡ 0.
Λήμμα 6.2: ΄Εστω (M,g) μια πολλαπλότητα Riemann, p ∈ M και Y ∈ TpM. Τότε ο τελεστής

΄Εστω Y ∈ TpM με |Y | = 1. Ορίζουμε
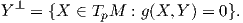

Ορίζουμε το τανυστικό πεδίο τύπου (1,3)
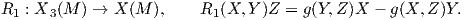
Πρόταση 6.5: ΄Εστω (M,g) μια πολλαπλότητα Riemann και έστω X,Y,Z λεία διανυσματικά πεδία στην M. Τότε ισχύουν οι εξής ανισότητες:
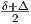 R1(X,Y )Y |≤
R1(X,Y )Y |≤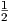 (Δ - δ)|X||Y |2.
(Δ - δ)|X||Y |2.
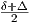 R1(X,Y )Z|≤
R1(X,Y )Z|≤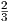 (Δ - δ)|X||Y ||Z|.
(Δ - δ)|X||Y ||Z|.Απόδειξη. Χωρίς βλάβη της γενικότητας μπορούμε να υποθέσουμε ότι |X| = |Y | = |Z| = 1. ΄Εστω ότι X = X⊥ + X⊤ με X⊥⊥ Y και X⊤ παράλληλο του Y . Τότε R(X,Y )Z = R(X⊥,Y )Z, άρα μπορούμε να υποθέσουμε επιπλέον ότι X ⊥ Y . Τότε θα έχουμε ότι R1(X,Y )Y = g(Y,Y )X - g(X,Y )Y = X.
Η πρώτη ανισότητα προπύπτει από το γεγονός ότι οι ιδιοτιμές του αυτοσυζυγούς τελεστή
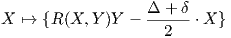
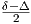 ,
,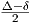 ].
].
΄Οσον αφορά τη δεύτερη ανισότητα, παρατηρούμε ότι ο τελεστής R1 ικανοποιεί την πρώτη ταυτότητα
του Bianchi, καθώς και τις ταυτότητες συμμετρίας του τανυστή καμπυλότητας, συνεπώς το ίδιο θα συμβαίνει
και για τον τελεστή D = R -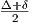 ⋅ R1. Τότε προκύπτει η ταυτότητα
⋅ R1. Τότε προκύπτει η ταυτότητα
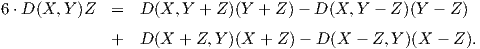
Τελικά παίρνουμε ότι
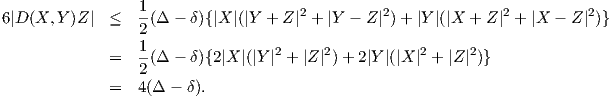
Ως συνέπεια παίρνουμε τελικά το παρακάτω χρήσιμο αποτέλεσμα:
Πόρισμα 6.1: ΄Εστω (M,g) μια πολλαπλότητα Riemann σταθερής καμπυλότητας κ. Τότε ο τανυστής καμπυλότητας έχει τη μορφή
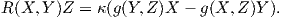
Απόδειξη. Είναι άμεσο αποτέλεσμα της Πρότασης 6.5 θέτοντας Δ = δ = c. ▄
΄Ενα ακόμα σχετικό αποτέλεσμα είναι το παρακάτω θεώρημα, την απόδειξη του οποίου παραλείπουμε (βλ. [4]).
Θεώρημα 6.1: (Θεώρημα του Schur.) ΄Εστω (M,g) μια συνεκτική πολλαπλότητα Riemann διάστασης n ≥ 3. Εάν για κάθε p ∈ M η καμπυλότητα τομής Kp(Π) δεν εξαρτάται από το επίπεδο Π (άρα είναι συνάρτηση μόνο του σημείου p), τότε η M είναι πολλαπλότητα σταθερής καμπυλότητας τομής, δηλαδή K(p) = K, σταθερή.
Παράδειγμα. Θεωρούμε τον μοναδιαίο ανοικτό δίσκο U του επιπέδου ℝ2 εφοδιασμένον με τη μετρική Riemann
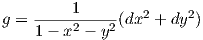
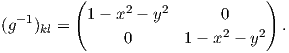
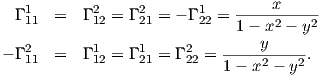
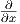 ,
,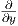 )
)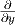 ,
,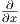 ) καθορίζει πλήρως την καμπυλότητα τομής και λόγω της Πρότασης 6.2,
ισούται με
) καθορίζει πλήρως την καμπυλότητα τομής και λόγω της Πρότασης 6.2,
ισούται με
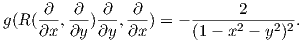
Ο τανυστής καμπυλότητας αποτελεί ένα αρκετά δύσκολο αντικείμενο στον χειρισμό του. Για τον λόγο αυτό εισάγονται δύο άλλα είδη καμπυλοτήτων, η καμπυλότητα Ricci 3 και η βαθμωτή καμπυλότητα, οι οποίες είναι μεν πιο απλές και εύκολες στον χειρισμό τους, χάνεται όμως η πλήρης γεωμετρική πληροφόρηση για την πολλαπλότητα (M,g). Οι νέοι αυτοί τανυστές ουσιαστικά προκύπτουν με συστολή (contraction) του τανυστή καμπυλότητας, αλλά δεν θα χρησιμοποιήσουμε εδώ την έννοια αυτή. Το όφελος είναι (και ουσιαστικά αυτή ήταν ιστορικά η αρχική επιδίωξη του Ricci) η εισαγωγή ενός είδους καμπυλότητας (εν προκειμένω η καμπυλότητα Ricci), η οποία να έχει ως τανυστής τον ίδιο τύπο με τη μετρική g, δηλαδή να είναι τύπου (0,2). Η βαθμωτή καμπυλότητα είναι στη συνέχεια μια πραγματική συνάρτηση στην πολλαπλότητα M.
Θυμίζουμε από την γραμμική άλγεβρα ότι αν (V,⟨ , ⟩) είναι ένας διανυσματικός χώρος με εσωτερικό γινόμενο, T : V → V ένας γραμμικός τελεστής και {e1,…,en} μια ορθοκανονική βάση του V , τότε το ίχνος του τελεστή T εκφράζεται ως
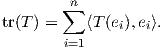
Ορισμός 6.3: ΄Εστω (M,g) μια πολλαπλότητα Riemann. Ο τανυστής Ricci (Ricci tensor) ή καμπυλότητα Ricci (Ricci curvature) είναι ο τανυστής τύπου (0,2)
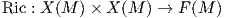
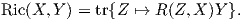
Εάν {e1,…,en} είναι μια ορθοκανονική βάση του TpM τότε για κάθε x,y ∈ TpM έχουμε ότι
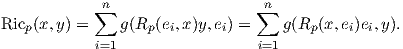
Εύκολα προκύπτει ότι ο τανυστής Ricci είναι συμμετρικός, δηλαδή ισχύει Ric(X,Y ) = Ric(Y,X). Τακτικά χρησιμοποιούμε αντί για τον τανυστή Ricci τον τελεστή Ricci (Ricci operator)
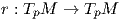
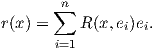
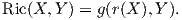
Επειδή η καμπυλότητα τομής K καθορίζει τον τανυστή καμπυλότητα R, θα καθορίζει και τον τανυστή Ricci. Πράγματι, αν u ∈ TpM είναι ένα μοναδιαίο διάνυσμα και {e1,…,en} μια ορθοκανονική βάση του TpM τέτοια ώστε u = e1, τότε η καμπυλότητα Ricci της (M,g) ως προς τη διεύθυνση u είναι
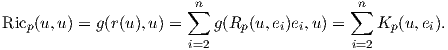
Ορισμός 6.4: Η βαθμωτή καμπυλότητα (scalar curvature) μιας πολλαπλότητας Riemann είναι η συνάρτηση S : M → ℝ με τιμή
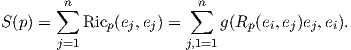
Εάν {e1,…,en} είναι μια ορθοκανονική βάση του TpM, τότε η βαθμωτή καμπυλότητα εκφράζεται ως
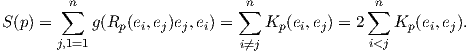
Ως προς ένα τοπικό σύστημα συντεταγμένων ο τανυστής Ricci και η βαθμωτή καμπυλότητα δίνονται αντίστοιχα
ως εξής. Αν Rij = Ric(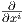 ,
,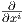 ), τότε
), τότε
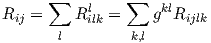
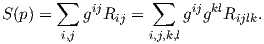
Παράδειγμα. ΄Εστω M μια κανονική επιφάνεια στον ℝ3. Τότε η βαθμωτή καμπυλότητα καθορίζει πλήρως τον τανυστή καμπυλότητας (άρα και την καμπυλότητα τομής K), αφού ισχύει ότι
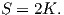
Πρόταση 6.6: ΄Εστω (M,g) μια πολλαπλότητα Riemann διάστασης n και σταθερής καμπυλότητα κ. Τότε ισχύουν τα εξής:
Απόδειξη. ΄Εστω {E1,…,En} ένα ορθοκανονικό πλαίσιο της M και έστω X,Y ∈ X(M). Τότε από το Πόρισμα 6.1 προκύπτει ότι
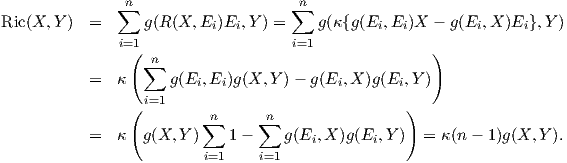
Επίσης, είναι
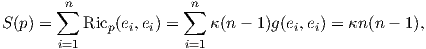
Ορισμός 6.5: Μια πολλαπλότητα Riemann ονομάζεται πολλαπλότητα Einstein, εάν ο τανυστής Ricci ικανοποιεί την εξίσωση Ric(X,Y ) = cg(X,Y ), για κάποια σταθερά c.
Θέτοντας X = Y = ei, ({ei} μια ορθοκανονική βάση του TpM) στην παραπάνω εξίσωση και αθροίζοντας για 1 ≤ i ≤ n, προκύπτει ότι
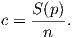
 ∫
MSgdvolg, επί του συνόλου των μετρικών με όγκο μονάδα. Αυτό σημαίνει ότι υπάρχει
συσχέτιση με θεωρία λογισμού των μεταβολών, κάτι ιδιαίτερα σημαντικό στην γεωμετρία και την
φυσική. Τέλος, η εξίσωση Ric(X,Y ) = cg(X,Y ) αποτελεί ειδική περίπτωση της εξίσωσης πεδίου του
Einstein.5
∫
MSgdvolg, επί του συνόλου των μετρικών με όγκο μονάδα. Αυτό σημαίνει ότι υπάρχει
συσχέτιση με θεωρία λογισμού των μεταβολών, κάτι ιδιαίτερα σημαντικό στην γεωμετρία και την
φυσική. Τέλος, η εξίσωση Ric(X,Y ) = cg(X,Y ) αποτελεί ειδική περίπτωση της εξίσωσης πεδίου του
Einstein.5
Εάν μια πολλαπλότητα Riemann έχει σταθερή καμπυλότητα τομής, τότε σύμφωνα με την παραπάνω πρόταση είναι πολλαπλότητα Einstein. Στην περίπτωση που η διάσταση της πολλαπλότητας είναι 3 τότε ισχύει και το αντίστροφο.
Πρόταση 6.7: ΄Εστω (M,g) μια πολλαπλότητα Einstein διάστασης 3. Τότε η M έχει σταθερή καμπυλότητα τομής.
Απόδειξη. ΄Εστω p ένα τυχαίο σημείο της M και {e1,…,en} μια ορθοκανονική βάση του TpM. Θα πρέπει αν αποδείξουμε ότι για όλους τους υποχώρους Πij = span{ei,ej} (i≠j) η καμπυλότητα τομής είναι σταθερή. Είναι
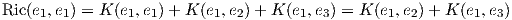
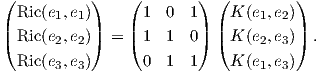
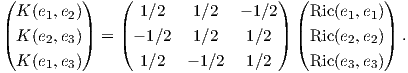
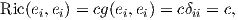
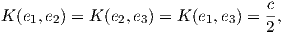
Ορισμός 6.6: Μια λεία απεικόνιση f : (M,g) → (N,h) μεταξύ δύο πολλαπλοτήτων Riemann ονομάζεται τοπική ισομετρία εάν το διαφορικό dfp : TpM → Tf(p)N είναι μια γραμμική ισομετρία, δηλαδή ισχύει
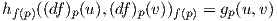
Μια ισομετρία είναι μια τοπική ισομετρία εάν επιπλέον η f είναι αμφιδιαφόριση.
Ορισμός 6.7: Μια αμφιδιαφόριση f : (M,g) → (N,h) ονομάζεται ομοιοθεσία κατά παράγοντα c≠0 εάν ισχύει
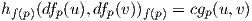
Προφανώς μια ισομετρία είναι μια ομοιθεσία κατά παράγοντα c = 1.
Είναι φυσικό να αναμένουμε ότι οι ισομετρίες διατηρούν όλες τις γεωμετρικές έννοιες που σχετίζονται με μια πολλαπλότητα Riemann (συνοχή Levi-Civita, καμπυλότητα κ.λπ.). Θα δούμε στη συνέχεια συνοπτικά το θέμα αυτό.
Ορισμός 6.8: ΄Εστω f : M → N μια αμφιδιαφόριση. Τότε για κάθε διανυσματικό πεδίο X ∈ X(M) ορίζουμε το διανυσματικό πεδίο f*X ∈ X(M) ως
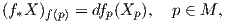
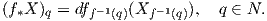
Χρησιμοποιώντας τον τύπο του Koszul αποδεικνύεται το εξής:
Πρόταση 6.8: ΄Εστω f : M → N μια ισομετρία μεταξύ πολλαπλοτήτων Riemann. Τότε
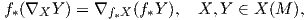
Ως συνέπεια, ο τανυστής καμπυλότητας διατηρείται μέσω μιας τοπικής ισομετρίας f : M → N, δηλαδή ισχύει
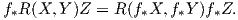
Πρόταση 6.9: ΄Εστω f : M → N μια τοπική ισομετρία. Τότε οι παρακάτω γεωμετρικές έννοιες διατηρούνται μέσω της f:
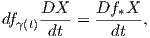
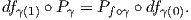
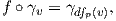
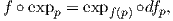
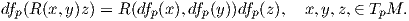
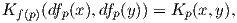
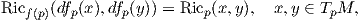
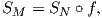
΄Οσον αφορά τις ομοιοθεσίες, οι συνοχές Levi-Civita διατηρούνται μέσω αυτών. Επιπλέον, οι ομοιοθεσίες διατηρούν τη συναλλοίωτη παράγωγο, την παράλληλη μεταφορά, τις γεωδαισιακές, τον τανυστή καμπυότητας R και τον τανυστή Ricci. ΄Ομως η καμπυλότητα τομής και η βαθμωτή καμπυλότητα δεν διιατηρούνται μέσω ομοιοθεσιών. Συγκεκριμένα, αν f : M → N είναι μια ομοιοθεσία κατά παράγοντα c, τότε ισχύουν οι σχέσεις
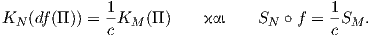
1. Αποδείξτε ότι η συνάρτηση R(X,Y )Z = ∇X∇Y Z -∇Y ∇XZ -∇[X,Y ]Z είναι F(M)-γραμμική ως προς Z.
2. Αποδείξτε την ταυτότητα (iii) της Πρότασης 6.4.
3. Αναζητήστε στην βιβλιογραφία μια απόδειξη του Θεωρήματος του Schur (Θεώρημα 6.1).
4. Αποδείξτε ότι ο τανυστής Ricci είναι συμμετρικός, δηλαδή για κάθε x,y ∈ TpM ισχύει Ricp(x,y) = Ricp(y,x).
5. Αποδείξτε ότι αν μια πολλαπλότητα Riemann έχει διάσταση 3 η καμπυλότητα Ricci καθορίζει την καμπυλότητα τομής. Το ίδιο συμβαίνει αν η διάσταση της πολλαπλότητας είναι 2. (ϒπόδειξη: Πάρτε μια ορκοκανονική βάση {e1,e2,e3} του TpM και υπολογίστε διαδοχικά τις τιμές Ric(ei,ei),i = 1,2,3. Στη συνέχεια, εκφράστε τις τιμές αυτές ως γραμμικές εκφράσεις των K(ei,ej).)
6. Θεωρούμε τον Ευκλείδειο χώρο ℝ3 εφοδιασμένον με τη μετρική Riemann
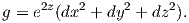
 ,
, )
)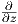 ,
, ) = 0.
) = 0.
7. Θεωρούμε τον Ευκλείδειο χώρο ℝ3 εφοδιασμένον με τη μετρική Riemann
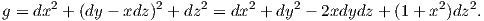
(β) Βρείτε τις συναρτήσεις Rijkl και στη συνέχεια τις μη μηδενικές συναρτήσεις Rijkl = ∑ sRijksgsk (συνιστώσες του τανυστή καμπυλότητας).
(γ) Αποδείξτε ότι οι μη μηδενικές συνιστώσες του τανυστή Ricci δίνονται από τις συναρτήσεις
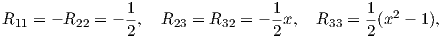
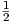 .
.
8. ΄Ενα διανυσματικό πεδίο X σε μια πολλαπλότητα Riemann (M,g) ονομάζεται πεδίο Killing εάν ισχύει
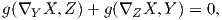
![Xg (Y, Z) = g([X, Y ],Z )+ g(Y,[X, Z]).](02_chapter_06133x.png)
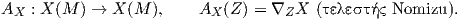
(α) gp(AX(Z),X) = 0.
(β) gp(AX(Z),AX(Z)) = 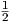 Zp(Zg(X,X)) + g(R(X,Z)Z,X).
Zp(Zg(X,X)) + g(R(X,Z)Z,X).
(ϒπόδειξη: ΄Εστω T = 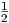 Z(Zg(X,X)) + g(R(X,Z)Z,X). Χρησιμοποιείστε την εξίσωση Killing και θα προκύψει
ότι T = -g(∇XX,∇ZZ) - g(∇X∇ZX,Z) - g(∇ZX,∇XZ) + g(∇ZX,∇ZX). Με χρήση πάλι της εξίσωσης
Killing παίρνουμε ότι T = -g(∇XX,∇ZZ) + g(∇ZX,∇ZX). Αλλά ∇XpX = 0, απ΄ όπου προκύπτει το
ζητούμενο.)
Z(Zg(X,X)) + g(R(X,Z)Z,X). Χρησιμοποιείστε την εξίσωση Killing και θα προκύψει
ότι T = -g(∇XX,∇ZZ) - g(∇X∇ZX,Z) - g(∇ZX,∇XZ) + g(∇ZX,∇ZX). Με χρήση πάλι της εξίσωσης
Killing παίρνουμε ότι T = -g(∇XX,∇ZZ) + g(∇ZX,∇ZX). Αλλά ∇XpX = 0, απ΄ όπου προκύπτει το
ζητούμενο.)
(γ) Αναζητήστε στην βιβλιογραφία μια απόδειξη για το εξής: ΄Εστω M μια συμπαγής πολλαπλότητα Riemann άρτιας διάστασης με θετική καμπυλότητα τομής. Τότε κάθε πεδίο Killing X έχει ένα ιδιάζον σημείο (singular point), δηλαδή υπάρχει p ∈ M ώστε Xp = 0.
[1] M. Berger, A Panoramic View of Riemannian Geometry, Springer, 2002.
[2] A. Besse, Einstein Manifolds, Springer, 2008.
[3] W. Boothby, An Introduction to Differentiable Manifolds and Riemannian Geometry, 2nd ed., Academic Press, Boston, 1986.
[4] M. do Carmo, Riemannian Geometry, Birkhäuser, Boston 1992.
[5] S. Gallot, D. Hulin and J. Lafontaine, Riemannian Geometry, 3rd ed. Springer, 2004.
[6] L. Godinho and J. Natário, An Introduction to Riemannian Geometry: With Applications to Mechanics and Relativity , Springer, 2014.
[7] S. Kobayashi and K. Nomizu, Foundations of Differential Geometry, Vol. I, Wiley Classics, 1996.
[8] J.M. Lee, Riemannian Manifolds: An Introduction to Curvatute, Springer, New York, 1997.
[9] A.M. Naveira, The Riemann Curvature Through History, Rev. R. Acad. Cien. Serie A. Mat. 99 (2) 195–210.
[10] B. O’ Neill, Semi-Riemannian Geometry with Applications to Relativity, Academic Press 1983.
[11] P. Petersen, Riemannian Geometry, Springer, New York, 1998.
[12] A.N. Pressley, Elementary Differential Geometry Geometry, 2nd ed. Springer, New York, 2010. Μετάφραση: Στοιχειώδης Διαφορική Γεωμετρία, Πανεπιστημιακές Εκδόσεις Κρήτης, Κρήτη 2012.
[13] B. Riemann, On the hypotheses which lie at the foundations of geometry, Μετάφραση από τα Γερμανικά από τον Henry S. White στο βιβλίο: D.E. Smith: A Source Book in Mathematics, Dover ed. Vol. 2, Dover, New York, 1959, 411–425. Μετάφραση στα Ελληνικά: Επί των Σχετικών με την Γεωμετρία ϒποθέσεων, Εκδόσεις Τροχαλία, Αθήνα 1999.