Ορισμός 1.16
(Πράξεις σε σύνολα)
Αν δοθούν δύο σύνολα 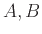 μπορούμε να ορίσουμε τρία άλλα σύνολα ως εξής:
μπορούμε να ορίσουμε τρία άλλα σύνολα ως εξής:
-
Την ένωση των
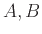 που τη συμβολίζουμε με
που τη συμβολίζουμε με 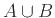 και είναι το σύνολο που αποτελείται από τα στοιχεία του
και είναι το σύνολο που αποτελείται από τα στοιχεία του  ή του
ή του  ή και των δύο, δηλαδή:
ή και των δύο, δηλαδή:
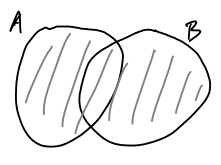
Σχήμα
1.3: Η ένωση των

.

(σκιασμένο) σε διάγραμμα Venn
-
Την τομή των
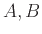 που τη συμβολίζουμε με
που τη συμβολίζουμε με 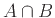 και είναι το σύνολο που αποτελείται από τα κοινά στοιχεία των
και είναι το σύνολο που αποτελείται από τα κοινά στοιχεία των  και
και  :
:
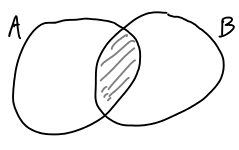
Σχήμα
1.4: Η τομή των

.

(σκιασμένο) σε διάγραμμα Venn
-
Την διαφορά των
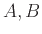 , που τη συμβολίζουμε με
, που τη συμβολίζουμε με
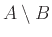 και είναι το σύνολο που προκύπτει αν από τα στοιχεία του
και είναι το σύνολο που προκύπτει αν από τα στοιχεία του  αφαιρέσουμε εκείνα που ανήκουν στο
αφαιρέσουμε εκείνα που ανήκουν στο  :
:
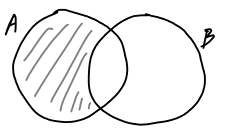
Σχήμα
1.5: Η διαφορά των
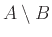
(σκιασμένο) σε διάγραμμα Venn
Συχνά τα σύνολα που θεωρούμε, όπως θα δούμε παρακάτω, είναι υποσύνολα ενός ευρύτερου συνόλου, έστω 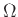 .
Στην περίπτωση αυτή ορίζουμε το συμπλήρωμα ενός
.
Στην περίπτωση αυτή ορίζουμε το συμπλήρωμα ενός
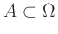 , που το συμβολίζουμε με
, που το συμβολίζουμε με 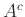 ,
να είναι το σύνολο:
,
να είναι το σύνολο:
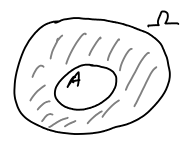
Σχήμα
1.6: Το συμπλήρωμα του

μέσα στο
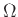
(σκιασμένο) σε διάγραμμα Venn
Παράδειγμα 1.11
Ρίχνουμε δύο ζάρια. Το σύνολο των δυνατών αποτελεσμάτων είναι
Το 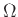 αποτελείται από 36 διατεταγμένα ζεύγη.
Θεωρούμε τα εξής υποσύνολα του
αποτελείται από 36 διατεταγμένα ζεύγη.
Θεωρούμε τα εξής υποσύνολα του 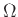 :
:
Έχουμε
Γιά τις πράξεις μεταξύ συνόλων 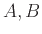 τα οποία θεωρούμε ότι είναι υποσύνολα ενός ευρύτερου συνόλου
τα οποία θεωρούμε ότι είναι υποσύνολα ενός ευρύτερου συνόλου 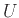 (το οποίο λέγεται σύνολο αναφοράς ή καθολικό σύνολο)ισχύουν οι ιδιότητες που καταγράφουμε στον παρακάτω πίνακα.
(το οποίο λέγεται σύνολο αναφοράς ή καθολικό σύνολο)ισχύουν οι ιδιότητες που καταγράφουμε στον παρακάτω πίνακα.
Ιδιότητες των συνολοθεωρητικών πράξεων
- Νόμος Ατομικότητας:
α)
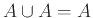 , β)
, β)
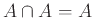 .
.
- Προσεταιριστικός Νόμος:
α)
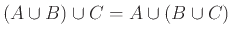 , β)
, β)
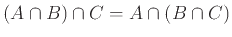 .
.
- Μεταθετικός Νόμος:
α)
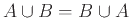 , β)
, β)
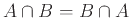 .
.
- Επιμεριστικός Νόμος:
α)
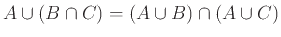 ,
β)
,
β)
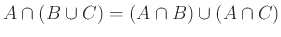 .
.
- Νόμοι Ταυτότητας:
α)
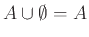 , β)
, β)
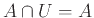
α')
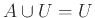 , β')
, β')
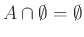 .
.
- Νόμοι Συμπληρώματος:
α)
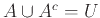 , β)
, β)
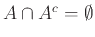 ,
,
α')
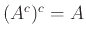 , β')
, β')
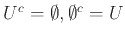 .
.
- Νόμοι De Morgan:
α)
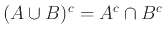 , β)
, β)
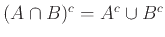 .
.
- Νόμος Διάταξης:
α)
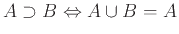 , β)
, β)
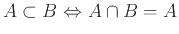 .
.
Παράδειγμα 1.12
Ισχύει
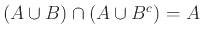 .
.
Έχουμε
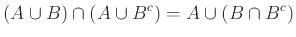 |
(1.5) |
και
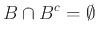 |
(1.6) |
(ιδιότητα 7β).
Με αντικατάσταση παίρνουμε
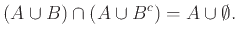 |
(1.7) |
Ομως ισχύει
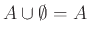 |
(1.8) |
(ιδιότητα 5α).
Οπότε, αντικαθιστώντας την (1.8) στην (1.7) προκύπτει το ζητούμενο.
Αν σε μία σχέση με σύνολα ανταλλάξουμε τα 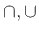 , τα
, τα
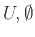 και τα
και τα
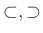 προκύπτει μία νέα σχέση που λέγεται δυϊκή της αρχικής.
προκύπτει μία νέα σχέση που λέγεται δυϊκή της αρχικής.
Παρατηρούμε ότι η δυϊκή κάθε ιδιότητας του παραπάνω πίνακα είναι επίσης ιδιότητα του πίνακα.
Αυτό το γεγονός έχει σαν αποτέλεσμα το επόμενο πολύ σπουδαίο θεώρημα που είναι γνωστό σαν αρχή δυϊσμού.
Η απόδειξη του θεωρήματος αυτού είναι ουσιαστικά μια επανειλημμένη χρήση των παραπάνω κανόνων και παραλείπεται.
Σε κάθε συγκεκριμένη χρήση του είναι συνήθως προφανές το πώς να πάει κανείς από μια πρόταση στη δυϊκή της και το γιατί ισχύει αυτή η ισοδυναμία.
Θεώρημα 1.1
(Αρχή δυϊσμού)
Η δυϊκή σχέση κάθε σχέσης που προκύπτει απο τις ιδιότητες των πράξεων, είναι επίσης αληθής.
Παράδειγμα 1.13
Η δυϊκή σχέση του Παραδείγματος 1.12 είναι η
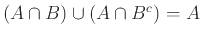 ,
η οποία είναι επίσης αληθής από την αρχή δυϊσμού. Αν θέλουμε να την αποδείξουμε απλώς θα χρησιμοποιήσουμε τις δυϊκές ιδιότητες στην απόδειξη του Παραδείγματος 1.12.
,
η οποία είναι επίσης αληθής από την αρχή δυϊσμού. Αν θέλουμε να την αποδείξουμε απλώς θα χρησιμοποιήσουμε τις δυϊκές ιδιότητες στην απόδειξη του Παραδείγματος 1.12.
Mihalis Kolountzakis
2015-11-28



![]() .
Στην περίπτωση αυτή ορίζουμε το συμπλήρωμα ενός
.
Στην περίπτωση αυτή ορίζουμε το συμπλήρωμα ενός
![]() , που το συμβολίζουμε με
, που το συμβολίζουμε με ![]() ,
να είναι το σύνολο:
,
να είναι το σύνολο:

![]() αποτελείται από 36 διατεταγμένα ζεύγη.
Θεωρούμε τα εξής υποσύνολα του
αποτελείται από 36 διατεταγμένα ζεύγη.
Θεωρούμε τα εξής υποσύνολα του ![]() :
:
![]() τα οποία θεωρούμε ότι είναι υποσύνολα ενός ευρύτερου συνόλου
τα οποία θεωρούμε ότι είναι υποσύνολα ενός ευρύτερου συνόλου ![]() (το οποίο λέγεται σύνολο αναφοράς ή καθολικό σύνολο)ισχύουν οι ιδιότητες που καταγράφουμε στον παρακάτω πίνακα.
(το οποίο λέγεται σύνολο αναφοράς ή καθολικό σύνολο)ισχύουν οι ιδιότητες που καταγράφουμε στον παρακάτω πίνακα.
![]() , τα
, τα
![]() και τα
και τα
![]() προκύπτει μία νέα σχέση που λέγεται δυϊκή της αρχικής.
προκύπτει μία νέα σχέση που λέγεται δυϊκή της αρχικής.