Συνάρτηση 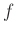 απο το σύνολο
απο το σύνολο  στο σύνολο
στο σύνολο  ονομάζεται κάθε «κανόνας» ο οποίος σε κάποια στοιχεία του
ονομάζεται κάθε «κανόνας» ο οποίος σε κάποια στοιχεία του  (τα οποία, ως γνωστό, λέμε ότι αποτελούν το πεδίο ορισμού της
(τα οποία, ως γνωστό, λέμε ότι αποτελούν το πεδίο ορισμού της 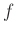 ) αντιστοιχεί ένα ακριβώς στοιχείο του
) αντιστοιχεί ένα ακριβώς στοιχείο του  . Έτσι μία συνάρτηση ορίζει ένα σύνολο από ζευγάρια αντιστοίχων τιμών (ο λεγόμενος πίνακας τιμών ή γράφημα της
. Έτσι μία συνάρτηση ορίζει ένα σύνολο από ζευγάρια αντιστοίχων τιμών (ο λεγόμενος πίνακας τιμών ή γράφημα της 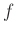 ). Χρησιμοποιώντας την έννοια της σχέσης,μπορούμε να ορίσουμε αυστηρότερα την έννοια της συνάρτησης.
). Χρησιμοποιώντας την έννοια της σχέσης,μπορούμε να ορίσουμε αυστηρότερα την έννοια της συνάρτησης.
Ορισμός 1.11
(Συνάρτηση)
Συνάρτηση 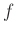 από το
από το  στο
στο  ονομάζουμε μία σχέση
ονομάζουμε μία σχέση
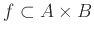 με την εξής ιδιότητα:
με την εξής ιδιότητα:
Για κάθε
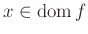 το σύνολο
το σύνολο
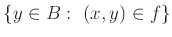 είναι μονοσύνολο.
είναι μονοσύνολο.
Ως συνήθως αντί
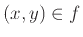 γράφουμε
γράφουμε 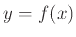 .
.
Το σύμβολο
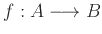 δηλώνει μία συνάρτηση με πεδίο ορισμού
το
δηλώνει μία συνάρτηση με πεδίο ορισμού
το  .
Στην περίπτωση αυτή για να ορίσουμε τη συνάρτηση γράφουμε με τι ισούται το
.
Στην περίπτωση αυτή για να ορίσουμε τη συνάρτηση γράφουμε με τι ισούται το 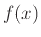 για οποιδήποτε
για οποιδήποτε 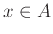 .
.
Παράδειγμα 1.8
Έστω 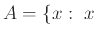 κράτος
κράτος 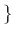 .
.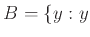 πόλη
πόλη 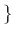 .
Ορίζουμε
.
Ορίζουμε
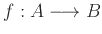 με
με
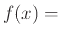 η πρωτεύουσα του
η πρωτεύουσα του 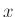 .
.
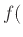 Γαλλία)=Παρίσι.
Γαλλία)=Παρίσι.
Άσκηση 1.5
Δίνονται οι παρακάτω σχέσεις από το
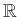 στο
στο
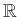 :
:
Βρείτε ποιές από τις παραπάνω σχέσεις είναι συναρτήσεις.
Στη συνέχεια βρείτε το πεδίο ορισμού των παραπάνω σχέσεων.
Με άλλα λόγια,
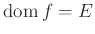 και
και
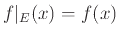 , αν
, αν 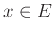 .
.
Παράδειγμα 1.9
Έστω
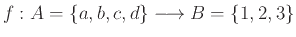 με
με
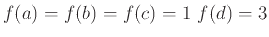 .
Ισχύουν:
.
Ισχύουν:
και
Ορισμός 1.14
Εστω 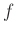 συνάρτηση από το
συνάρτηση από το  στο
στο  .
Η
.
Η 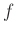 λέγεται 1-1 (ένα προς ένα), αν για
λέγεται 1-1 (ένα προς ένα), αν για
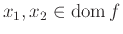 με
με
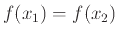 , έχουμε ότι
, έχουμε ότι
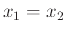 .
Δηλαδή διαφορετικά στοιχεία του πεδίου ορισμού έχουν διαφορετικές εικόνες.
Η
.
Δηλαδή διαφορετικά στοιχεία του πεδίου ορισμού έχουν διαφορετικές εικόνες.
Η 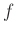 λέγεται επί αν
λέγεται επί αν
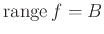 .
.
Παράδειγμα 1.10
Η συνάρτηση 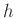 του Παρεδείγματος 1.7 και η συνάρτηση
του Παρεδείγματος 1.7 και η συνάρτηση 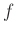 του Παραδείγματος 1.8
είναι 1-1, ενώ η
του Παραδείγματος 1.8
είναι 1-1, ενώ η 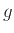 του Παραδείγματος 1.7 δεν είναι 1-1.
Επίσης από τις παραπάνω συναρτήσεις επί είναι μόνο η
του Παραδείγματος 1.7 δεν είναι 1-1.
Επίσης από τις παραπάνω συναρτήσεις επί είναι μόνο η 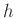 .
.
Άσκηση 1.6
Έστω 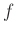 συνάρτηση από το
συνάρτηση από το  στο
στο  .
Δείξτε ότι η αντίστροφη σχέση
.
Δείξτε ότι η αντίστροφη σχέση 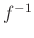 είναι συνάρτηση αν και μόνο αν η
είναι συνάρτηση αν και μόνο αν η 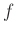 είναι 1-1.
είναι 1-1.
Άσκηση 1.7
Έστω
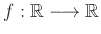 με τύπο
με τύπο
- α)
- Δείξτε ότι η
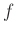 είναι 1-1 και όχι επί.
είναι 1-1 και όχι επί.
- β)
- Βρείτε το σύνολο τιμών και την
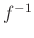 .
.
Λύση:
α) Έχουμε
Αρα
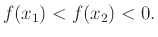 |
(1.1) |
Ομοίως
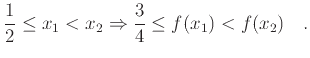 |
(1.2) |
Από τις (1.1), (1.2)
έπεται ότι για
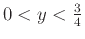 δεν υπάρχει
δεν υπάρχει
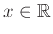 με
με 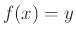 .
Άρα η
.
Άρα η 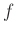 δεν είναι επί. Επίσης εύκολα βλέπουμε ότι οι (1.1), (1.2) εξασφαλίζουν ότι ικανοποιείται ο ορισμός της 1-1 συνάρτησης.
δεν είναι επί. Επίσης εύκολα βλέπουμε ότι οι (1.1), (1.2) εξασφαλίζουν ότι ικανοποιείται ο ορισμός της 1-1 συνάρτησης.
β) Αν
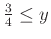 τότε
τότε
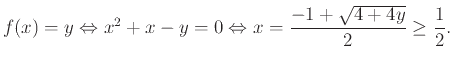 |
(1.3) |
Ομοίως αν 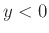 τότε
τότε
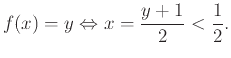 |
(1.4) |
Από τις (1.1), (1.2), (1.3), (1.4) προκύπτουν οι
και
Θυμίζουμε ότι από τον ορισμό τής 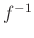 ισχύει:
ισχύει:
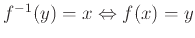 .
Επίσης
.
Επίσης
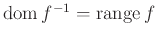 .
.
Άσκηση 1.8
Δίνονται οι συναρτήσεις
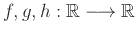 με τύπους
με τύπους
Εξετάστε αυτές τις συναρτήσεις ως προς το αν είναι 1-1 και επί.
Υπόδειξη: Για την 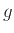 βρείτε τα
βρείτε τα 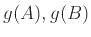 όπου
όπου
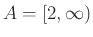 ,
,
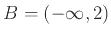 και συμπεράνετε ότι δεν είναι επί.
και συμπεράνετε ότι δεν είναι επί.
Ορισμός 1.15
(Σύνθεση συναρτήσεων)
Η σύνθεση συναρτήσεων ορίζεται όπως η σύνθεση των σχέσεων. Έστω
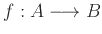 ,
,
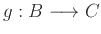 .
Ορίζουμε
.
Ορίζουμε
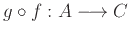 την συνάρτηση
την συνάρτηση
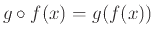 .
.
Άσκηση 1.9
Έστω ότι οι συναρτήσεις
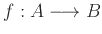 ,
,
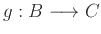 είναι 1-1.
Δείξτε ότι η
είναι 1-1.
Δείξτε ότι η 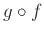 είναι επίσης 1-1.
είναι επίσης 1-1.
Mihalis Kolountzakis
2015-11-28
![]() απο το σύνολο
απο το σύνολο ![]() στο σύνολο
στο σύνολο ![]() ονομάζεται κάθε «κανόνας» ο οποίος σε κάποια στοιχεία του
ονομάζεται κάθε «κανόνας» ο οποίος σε κάποια στοιχεία του ![]() (τα οποία, ως γνωστό, λέμε ότι αποτελούν το πεδίο ορισμού της
(τα οποία, ως γνωστό, λέμε ότι αποτελούν το πεδίο ορισμού της ![]() ) αντιστοιχεί ένα ακριβώς στοιχείο του
) αντιστοιχεί ένα ακριβώς στοιχείο του ![]() . Έτσι μία συνάρτηση ορίζει ένα σύνολο από ζευγάρια αντιστοίχων τιμών (ο λεγόμενος πίνακας τιμών ή γράφημα της
. Έτσι μία συνάρτηση ορίζει ένα σύνολο από ζευγάρια αντιστοίχων τιμών (ο λεγόμενος πίνακας τιμών ή γράφημα της ![]() ). Χρησιμοποιώντας την έννοια της σχέσης,μπορούμε να ορίσουμε αυστηρότερα την έννοια της συνάρτησης.
). Χρησιμοποιώντας την έννοια της σχέσης,μπορούμε να ορίσουμε αυστηρότερα την έννοια της συνάρτησης.
το σύνολο
είναι μονοσύνολο.
![]() γράφουμε
γράφουμε ![]() .
.
![]() δηλώνει μία συνάρτηση με πεδίο ορισμού
το
δηλώνει μία συνάρτηση με πεδίο ορισμού
το ![]() .
Στην περίπτωση αυτή για να ορίσουμε τη συνάρτηση γράφουμε με τι ισούται το
.
Στην περίπτωση αυτή για να ορίσουμε τη συνάρτηση γράφουμε με τι ισούται το ![]() για οποιδήποτε
για οποιδήποτε ![]() .
.
![]() και
και
![]() , αν
, αν ![]() .
.
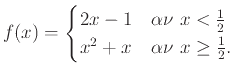
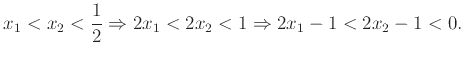
![]() τότε
τότε
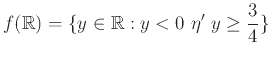
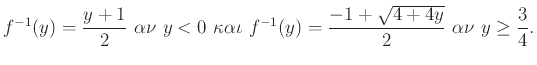
![]() ισχύει:
ισχύει:
![]() .
Επίσης
.
Επίσης
![]() .
.
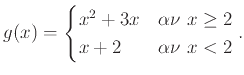
![]() βρείτε τα
βρείτε τα ![]() όπου
όπου
![]() ,
,
![]() και συμπεράνετε ότι δεν είναι επί.
και συμπεράνετε ότι δεν είναι επί.