1.6 Γενικευμένες πράξεις συνόλων

Έστω $F$ μία οικογένεια συνόλων, δηλαδή ένα σύνολο που τα στοιχεία του είναι επίσης σύνολα. (Λέμε «οικογένεια συνόλων» αντί για «σύνολο συνόλων» απλά επειδή είναι πιο εύηχο.) Υποθέτουμε επίσης ότι έχουμε μία συνάρτηση $A:I\longrightarrow{F}$, η οποία είναι 1-1 και επί. Στην περίπτωση αυτή αντι $A(i)$ γράφουμε $A_{i}$ οπότε η οικογένεια $F$ γράφεται $\{A_{i}: i\in{I}\}$ ή απλούστερα $\{A_{i}\}_{i\in{I}}$.

Ορίζουμε:

$$\bigcup{F} = \bigcup_{A \in F} A = \bigcup_{i\in{I}}A_{i}=\{x: \exists i\in{I} \mu\epsilon x\in{A_{i}}\}$$

και

$$\bigcap{F} = \bigcap_{A \in F} A = \bigcap_{i\in{I}}A_{i}=\{x: x\in{A_{i}} \forall i\in{I}\}.$$

Δηλαδή η ένωση $\bigcup{F}$ περιέχει τα στοιχεία που ανήκουν σε τουλάχιστο ένα μέλος της οικογένειας και η τομή $\bigcap{F}$ περιέχει τα στοιχεία που ανήκουν ταυτόχρονα σε όλα τα μέλη της οικογένειας.

Παράδειγμα 1.14   Έστω $I={{\mathbb{N}}}=\{n:n=1,2,3,\ldots\}$ και $A_{n}=\left[0,n\right] = \{x\in{{\mathbb{R}}}: 0\leq{x}\leq{n}\}$.

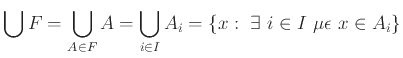
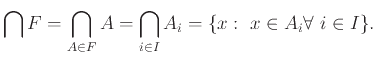
Έχουμε τότε

$$\bigcup_{n\in{{\mathbb{N}}}} A_{n}=\{x\in{{\mathbb{R}}}: x\geq0\},$$

και

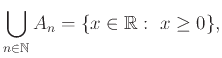
$$\bigcap_{n\in{{\mathbb{N}}}}A_{n} = \left[0,1\right].$$

Μία σημαντική ειδική περίπτωση έχουμε όταν η οικογένεια είναι πεπερασμένη, έστω $F=\{A_{1},A_{2},...,A_{n}\}$. Τότε οι ενώσεις και τομές γράφονται επίσης ως εξής:

$$\bigcup{F}=\bigcup_{i=1}^{n}A_{i} = A_{1}\cup{A_{2}}\cup...\cup{A_{n}},$$

$$\bigcap{F} = \bigcap_{i=1}^{n}A_{i} = A_{1}\cap...\cap{A_{n}}.$$

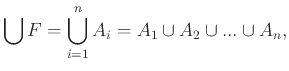
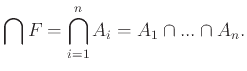
Εύκολα μπορεί να αποδειχθούν οι επόμενες ιδιότητες των γενικευμένων πράξεων, την απόδειξη των οποίων αφήνουμε σαν άσκηση. Έστω $\{A_{i}\}_{i\in{I}}$ οικογένεια συνόλων και $B$ ένα σύνολο. Έστω $U$ ένα σύνολο αναφοράς που περιέχει τα προηγούμενα σύνολα. Τότε ισχύουν:

1. Γενικευμένος επιμεριστικός νόμος:
   
   $$B\cap \bigcup_{i\in{I}}A_{i} =\bigcup_{i\in{I}}(B\cap{A_{i}}).$$
   $$B\cup \bigcap_{i\in{I}}A_{i} = \bigcap_{i\in{I}}(B\cup{A_{i}}).$$

2. Γενικευμένοι τύποι De Morgan:
   
   $$\left(\bigcup_{i\in{I}}A_{i}\right)^{c} = \bigcap_{i\in{I}}A_{i}^... ... \ \left(\bigcap_{i\in{I}}A_{i} \right)^{c} = \bigcup_{i\in{I}}A_{i}^{c}.$$
   $$B\setminus \bigcup_{i\in{I}}A_{i} = \bigcap_{i\in{I}}(B\setminus ... ... \ B\setminus\bigcap_{i\in{I}}A_{i} = \bigcup_{i\in{I}}(B\setminus A_{i}).$$

Άσκηση 1.10   Έστω συνάρτηση $f:X\longrightarrow{Y}$ με $X_{1},X_{2}\subset{X}$ και $Y_{1},Y_{2}\subset{Y}$. Δείξτε ότι

$$f(X_{1}\setminus X_{2})\supset{f(X_{1})}\setminus f(X_{2}), {f^{-1}}(Y_{1}\setminus Y_{2})=f^{-1}(Y_{1})\setminus f^{-1}(Y_{2}).$$

Με παράδειγμα δείξτε ότι ο εγκλεισμός στην πρώτη σχέση μπορεί να είναι γνήσιος.

Υπόδειξη: Γιά την απόδειξη της πρώτης σχέσης, έστω $y\in{f(X_{1})}\setminus f(X_{2})$. Αυτό σημαίνει από τον ορισμό της πράξης της διαφοράς ότι υπάρχει $x_{1}\in{X_{1}}$ με $f(x_{1})=y$ και για κάθε $x\in{X_{2}},f(x)\neq{y}$.

Άσκηση 1.11   Έστω $f:A\longrightarrow{B}$ συνάρτηση και $\{A_{i}\}_{i\in{I}}$ οικογένεια υποσυνόλων του $A$, και $\{B_{j}\}_{j\in{J}}$ οικογένεια υποσυνόλων του $B$. Δείξτε ότι:

α)

$$f\left(\bigcup_{i\in{I}}A_{i}\right) = \bigcup_{i\in{I}}f(A_{i}),... ...f}^{-1}\left(\bigcup_{j\in {J}}B_{j}\right) = \bigcup_{j\in{J}}f^{-1}(B_{j}).$$

β)

$$f\left(\bigcap_{i\in{I}}A_{i}\right) \subset {\bigcap}_{i\in{I}}f... ... f^{-1}\left(\bigcap_{j\in{J}}B_{j}\right) = \bigcap_{j\in{J}}f^{-1}(B_{j}).$$

γ)

Με παράδειγμα δείξτε ότι ο εγκλεισμός του ερωτήματος β) μπορεί να είναι και γνήσιος.

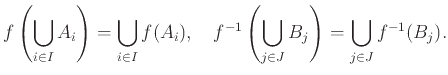
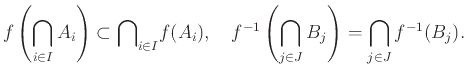
Υπόδειξη: Γιά το ερώτημα γ) μπορείτε να θεωρήσετε ότι η οικογένεια είναι πεπερασμένη, π.χ. ότι αποτελείται από δύο σύνολα.

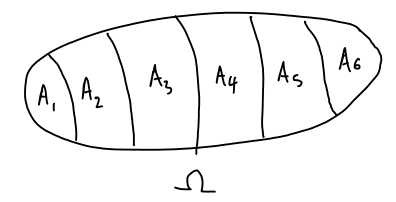
Κλείνουμε την παρούσα παράγραφο με την πολύ βασική ένοια της διαμέρισης, η οποία είναι, όπως θα δούμε στην επόμενη παράγραφο, αλληλένδετη με την ένοια της σχέσης ισοδυναμίας. Υπενθυμίζουμε πρώτα ότι δύο σύνολα λέγονται ξένα μεταξύ τους, αν η τομή τους ισούται με το κενό σύνολο, αν δεν έχουν δηλ. κανένα κοινό στοιχείο.

Ορισμός 1.17   (Διαμέριση) Έστω $A$ σύνολο και $\{A_{i}\}_{i\in{I}}$ μία οικογένεια υποσυνόλων του. Λέμε ότι η $\{A_{i}\}_{i\in{I}}$ είναι διαμέριση του $A$ αν ισχύουν τα εξής:

1. $A_{i}\cap{A_{j}} = \emptyset$ για $i\neq{j}, i, j\in{I}$, δηλαδή τα σύνολα της οικογένειας είναι ξένα ανά δύο.
2. $\bigcup_{i\in{I}}A_{i} = A$.

Σχήμα 1.7: Η διαμέριση $\Omega = \bigcup_{i=1}^6 A_i$ σε διάγραμμα Venn