Ένα σύνολο είναι μία συλλογή από αντικείμενα που ονομάζονται μέλη ή στοιχεία ή σημεία του συνόλου.
Τα σύνολα τα συμβολίζουμε συνήθως με κεφαλαία γράμματα.
Για να δηλώσουμε ότι ένα αντικείμενο 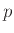 είναι μέλος ενός συνόλου
είναι μέλος ενός συνόλου  , γράφουμε:
, γράφουμε:
(διαβάζεται: το 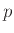 ανήκει στο
ανήκει στο  ).
Για να δηλώσουμε ότι δεν ανήκει στο
).
Για να δηλώσουμε ότι δεν ανήκει στο  γράφουμε:
γράφουμε:
(διαβάζεται: το 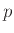 δεν ανήκει στο
δεν ανήκει στο  ).
).
Ορισμός 1.1
(Κενό Σύνολο)
Το σύνολο που δεν έχει μέλη, κάτι σα μία άδεια τσάντα,
ονομάζεται κενό σύνολο και συμβολίζεται με το σύμβολο 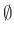 .
.
Παράσταση Συνόλου:
Για να περιγράψουμε ένα σύνολο υπάρχουν διάφοροι τρόποι:
- Να καταγράψουμε μία λίστα με τα στοιχεία του μέσα σε άγγιστρα,
π.χ. το σύνολο με μέλη τα αντικείμενα
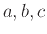 γράφεται
γράφεται
Το σύνολο με μόνο στοιχείο ένα αντικείμενο 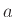 γράφεται
γράφεται
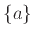 και λέγεται μονοσύνολο.
και λέγεται μονοσύνολο.
- Να τα παραστήσουμε σχηματικά με ένα διάγραμμα Venn. Π.χ., μπορούμε να παραστήσουμε σχηματικά τα δύο σύνολα
και
με το παρακάτω Σχήμα 1.1.
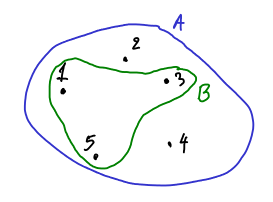
Σχήμα
1.1: Τα δύο σύνολα

και

σε διάγραμμα Venn
- Συχνότερα όμως για να ορίσουμε ένα σύνολο δηλώνουμε μια ιδιότητα (πρόταση)
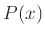 που αφορά αντικείμενα, πραγματικά ή ιδεατά, (όπως π.χ. είναι οι αριθμοί), η επαλήθευση της οποίας από ένα αντικείμενο
που αφορά αντικείμενα, πραγματικά ή ιδεατά, (όπως π.χ. είναι οι αριθμοί), η επαλήθευση της οποίας από ένα αντικείμενο 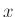 είναι αναγκαία και ικανή συνθήκη για να ανήκει το αντικείμενο αύτο στο σύνολο.
Γράφουμε
είναι αναγκαία και ικανή συνθήκη για να ανήκει το αντικείμενο αύτο στο σύνολο.
Γράφουμε
για να δηλώσουμε το σύνολο που έχει σαν μέλη τα αντικείμενα 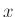 ικανοποιούν την ιδιότητα
ικανοποιούν την ιδιότητα 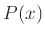 .
.
Επίσης συνήθως αντί να γράφουμε:
γράφουμε:
Παράδειγμα 1.1
Το σύνολο
περιέχει εκείνους τους ακεραίους που έχουν τετράγωνο μικρότερο από 100.
Το ίδιο σύνολο πιο σύντομα γράφεται
Πρόκειται βεβαίως για ένα διαφορετικό τρόπο γραφής του συνόλου (βλέπουμε εδώ μια νέα συντομογραφία)
που περιέχει όλους τους ακεραίους από το -9 έως το 9.
Από αυτό προκύπτει ότι:
για κάθε σύνολο  .
Στην περίπτωση που
.
Στην περίπτωση που
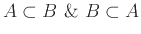 τα σύνολα λέγονται ίσα και γράφουμε
τα σύνολα λέγονται ίσα και γράφουμε 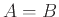 .
Με άλλα λόγια ίσα σύνολα σημαίνει ότι τα σύνολα έχουν ακριβώς τα ίδια στοιχεία.
.
Με άλλα λόγια ίσα σύνολα σημαίνει ότι τα σύνολα έχουν ακριβώς τα ίδια στοιχεία.
Παράδειγμα 1.2
-
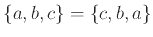 .
.
- Εστω ότι
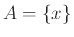 . Τότε ισχύουν τα εξής:
. Τότε ισχύουν τα εξής:
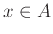 ,
,
-
 .
.
Αν
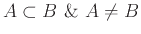 τότε το
τότε το  λέγεται γνήσιο υποσύνολο του
λέγεται γνήσιο υποσύνολο του  και γράφουμε
και γράφουμε
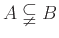 .
Αν το
.
Αν το  δεν είναι υποσύνολο του
δεν είναι υποσύνολο του  τότε γράφουμε:
τότε γράφουμε:
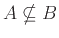 .
.
Άσκηση 1.1
Εστω
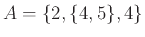 . Ποια από τις παρακάτω προτάσεις είναι λάθος και γιατί;
. Ποια από τις παρακάτω προτάσεις είναι λάθος και γιατί;
-
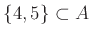
-
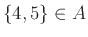
-
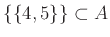 .
.
Άσκηση 1.2
Δίνονται τα σύνολα:
Συμπληρώστε τα κενά με 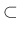 ,
,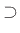 ή μσ (μη συγκρίσιμα),
ώστε να προκύψουν αληθείς προτάσεις.
ή μσ (μη συγκρίσιμα),
ώστε να προκύψουν αληθείς προτάσεις.
-
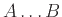
-
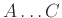
-
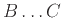
-
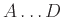
-
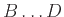
-
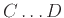
Άσκηση 1.3
Βρείτε ποιά από τα παρακάτω είναι σωστά και ποιά λάθος:
-
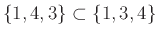 ,
,
-
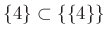 ,
,
-
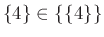 ,
,
-
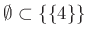 .
.
Παράδειγμα 1.3
Εστω
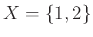 . Τότε,
. Τότε,
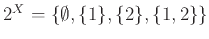 .
.
Ορισμός 1.5
(Καρτεσιανό γινόμενο συνόλων)
Εστω 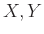 σύνολα.
Το καρτεσιανό γινόμενο των
σύνολα.
Το καρτεσιανό γινόμενο των 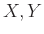 ορίζεται να είναι το σύνολο:
ορίζεται να είναι το σύνολο:
Αν 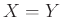 τότε το καρτεσιανό γινόμενο γράφεται και
τότε το καρτεσιανό γινόμενο γράφεται και 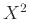 .
Δηλαδή:
.
Δηλαδή:
Η έννοια του διατεταγμένου ζεύγους και του καρτεσιανού γινομένου
μπορεί να γενικευτεί για περισότερα από δύο αντικείμενα και σύνολα.
Διατεταγμένη 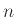 -άδα ονομάζεται η τοποθέτηση
-άδα ονομάζεται η τοποθέτηση 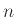 αντικειμένων στη σειρά.
Μία διατεταγμένη
αντικειμένων στη σειρά.
Μία διατεταγμένη 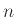 -άδα συμβολίζεται ως εξής:
-άδα συμβολίζεται ως εξής:
Αν
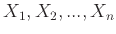 είναι σύνολα, σαν καρτεσιανό γινόμενό τους ορίζουμε το σύνολο:
είναι σύνολα, σαν καρτεσιανό γινόμενό τους ορίζουμε το σύνολο:
Στη περίπτωση που
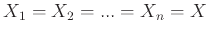 τότε το καρτεσιανό γινόμενο συμβολίζεται απλώς με
τότε το καρτεσιανό γινόμενο συμβολίζεται απλώς με 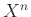 .
.
Mihalis Kolountzakis
2015-11-28
![]() είναι μέλος ενός συνόλου
είναι μέλος ενός συνόλου ![]() , γράφουμε:
, γράφουμε:

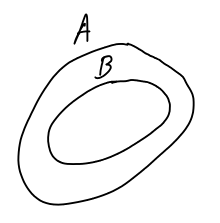
![]() παριστάνονται όπως στο Σχήμα 1.2.
παριστάνονται όπως στο Σχήμα 1.2.
![]() τότε το
τότε το ![]() λέγεται γνήσιο υποσύνολο του
λέγεται γνήσιο υποσύνολο του ![]() και γράφουμε
και γράφουμε
![]() .
Αν το
.
Αν το ![]() δεν είναι υποσύνολο του
δεν είναι υποσύνολο του ![]() τότε γράφουμε:
τότε γράφουμε:
![]() .
.
![]() -άδα ονομάζεται η τοποθέτηση
-άδα ονομάζεται η τοποθέτηση ![]() αντικειμένων στη σειρά.
Μία διατεταγμένη
αντικειμένων στη σειρά.
Μία διατεταγμένη ![]() -άδα συμβολίζεται ως εξής:
-άδα συμβολίζεται ως εξής:
![]() είναι σύνολα, σαν καρτεσιανό γινόμενό τους ορίζουμε το σύνολο:
είναι σύνολα, σαν καρτεσιανό γινόμενό τους ορίζουμε το σύνολο: