7.6 Ισοδυναμία ε-NFA και NFA

Εδώ θα αποδείξουμε ότι τα $\epsilon$-NFA είναι ισοδύναμα με τα NFA, και άρα και με τα DFA. Για κάθε $\epsilon$-NFA δηλ. υπάρχει ένα NFA χωρίς $\epsilon$-κινήσεις που αναγνωρίζει την ίδια γλώσσα.

Ορισμός 7.17   ($\epsilon$-μονοπάτι) Ένα $\epsilon$-μονοπάτι στο γράφημα ενός $\epsilon$-NFA είναι μια πεπερασμένη ακολουθία διαδοχικών $\epsilon$-ακμών (ακμών δηλ. που φέρουν την ετικέτα $\epsilon$).

Ορισμός 7.18   ($\alpha$-μονοπάτι) Ένα $\alpha$-μονοπάτι, όπου $\alpha\in\Sigma$, είναι ένα μονοπάτι στο γράφημα ενός $\epsilon$-NFA που απαρτίζεται από ένα αρχικό $\epsilon$-μονοπάτι, ακολουθούμενο από μια ακμή με ετικέτα $\alpha$, ακολουθούμενο από ένα $\epsilon$-μονοπάτι. Τα δύο $\epsilon$-μονοπάτια μπορούν να είναι και κενά.

Θεώρημα 7.2   (Ισοδυναμία $\epsilon$-NFA και NFA) Για κάθε $\epsilon$-NFA $M$ υπάρχει ισοδύναμο NFA $M'$.

Απόδειξη. Για να μεταβούμε από ένα $\epsilon$-NFA $M$ σε ένα ισοδύναμο NFA $M'$ κάνουμε τα εξής:

• Το σύνολο καταστάσεων του $M'$ είναι ίδιο με του $M$.
• Η αρχική κατάσταση του $M'$ είναι ίδια με αυτή του $M$.
• Οι τελικές καταστάσεις του $M'$, το σύνολο των οποίων συμβολίζουμε με $F'$, είναι όλες εκείνες τις καταστάσεις από τις οποίες μπορούμε να φτάσουμε σε κάποια κορυφή του $F$ (το σύνολο τελικών καταστάσεων του $M$) με ένα $\epsilon$-μονοπάτι. Επειδή ένα κενό μονοπάτι είναι $\epsilon$-μονοπάτι, ο ορισμός αυτός συνεπάγεται ότι $F \subseteq F'$.
• Για κάθε κατάσταση $q$ και γράμμα $\alpha\in\Sigma$ θέτουμε στο $M'$ ως $\delta_{M'}(q,\alpha)$ το σύνολο όλων των καταστάσεων στις οποίες μπορεί κανείς να μεταβεί από την $q$ στο $M$ διανύοντας κάποιο $\alpha$-μονοπάτι.
• Καταργούμε όλες τις $\epsilon$-κινήσεις.

Έστω τώρα $w=w_1 w_2 \cdots w_n \in \Sigma^*$.$n \ge 0$. Πρέπει να δείξουμε ότι η λέξη $w$ γίνεται δεκτή από το $M$ αν και μόνο αν γίνεται δεκτή από το $M$.

Αν $w\in L(M)$ αυτό σημαίνει ότι υπάρχει τρόπος κίνησης πάνω στο $M$, διαβάζοντας τα γράμματα της λέξης $w$ είτε ακολουθώντας $\epsilon$-κινήσεις, ώστε να μεταβούμε από την $q_0$ σε κάποια κατάσταση $f \in F$. Σε αυτή την περίπτωση δείχνουμε ότι υπάρχει τρόπος κίνησης πάνω στο $M$ τέτοιος που να οδηγεί από την $q_0$ σε κάποια κατάσταση του $F'$.

Έστω λοιπόν ότι $w\in L(M)$. Αυτό σημαίνει ότι υπάρχει μια ακολουθία καταστάσεων του $M$ έστω $q_0,q_1,\ldots,q_{k-1},q_k$.$k \ge 0$, τέτοια ώστε $q_k \in F$ και η μετάβαση από την $q_j$ στην $q_{j+1}$, $0\le j < k$, γίνεται είτε με κάποιο γράμμα $w_j$ είτε με μια $\epsilon$-ακμή, και τα γράμματα $w_j$ χρησιμοποιούνται όλα, από μια φορά το καθένα, και με τη σειρά.

Χωρίζουμε την πεπερασμένη αυτή ακολουθία των μεταβάσεων $q_0 \to q_1, q_1 \to q_2, \ldots, q_{k-1}\to q_k$ σε κομμάτια $q_{a_0} \to q_{a_1}, q_{a_1} \to q_{a_2}, \ldots, q_{a_{n-1}}\to q_{a_n}$ (με $a_0 = 0$.$a_n = k$) τα οποία αντιστοιχούν σε ένα $w_1$-μονοπάτι, ακολουθούμενο από ένα $w_2$-μονοπάτι, κλπ., τελειώνοντας με ένα $w_n$-μονοπάτι. Από τον ορισμό του NFA $M'$ προκύπτει ότι στο $M'$ είναι δυνατή η μετάβαση από την κορυφή $q_{a_0}$ στην $q_{a_1}$ με μια $w_1$-ακμή, από την $q_{a_1}$ στην $q_{a_2}$ με μια $w_2$-ακμή, κλπ. Επειδή η κατάσταση $q_k$ παραμένει τελική κατάσταση και του $M'$ προκύπτει ότι $w \in L(M')$.

Ο εγκλεισμός $L(M') \subseteq L(M)$ αφήνεται ως άσκηση (Άσκηση 7.25). $\qedsymbol$

Άσκηση 7.25   Με το συμβολισμό της άνω απόδειξης δείξτε ότι αν μια λέξη αναγνωρίζεται από το NFA $M'$ τότε αναγνωρίζεται και από το $\epsilon$-NFA $M$.

Παράδειγμα 7.23   Με τη μέθοδο της απόδειξης του Θεωρήματος 7.2 το $\epsilon$-NFA του Σχήματος 7.10

Σχήμα 7.11: Το $\epsilon$-NFA του Σχήματος 7.10 όπως έχει μετατραπεί σε NFA

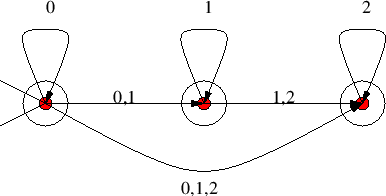
μετατρέπεται στο NFA του Σχήματος 7.11.