Next: 7.6 Ισοδυναμία ε-NFA και Up: 7. Τυπικές γλώσσες και Previous: 7.4 Ισοδυναμία NFA και Contents Index
Μια ακόμη παραλλαγή του μοντέλου του πεπερασμένου αυτομάτου είναι το
μη ντετερμινιστικό αυτόματο με ![]() -κινήσεις.
Αυτό είναι ένα NFA που έχει, ενδεχομένως, και κάποιες ακμές που αντί να
έχουν ως ετικέτα ένα γράμμα του αλφαβήτου έχουν την κενή λέξη
-κινήσεις.
Αυτό είναι ένα NFA που έχει, ενδεχομένως, και κάποιες ακμές που αντί να
έχουν ως ετικέτα ένα γράμμα του αλφαβήτου έχουν την κενή λέξη ![]() .
Κινούμενοι πάνω στο αυτόματο αυτό για να αναγνωρίσουμε μια λέξη έχουμε το
δικαίωμα να διανύσουμε μια
.
Κινούμενοι πάνω στο αυτόματο αυτό για να αναγνωρίσουμε μια λέξη έχουμε το
δικαίωμα να διανύσουμε μια ![]() -ακμή οποτεδήποτε υπάρχει μια τέτοια
από την τρέχουσα κατάσταση χωρίς να μας ενδιαφέρει ποιο είναι το επόμενο
γράμμα της λέξης. Η διάνυση μιας
-ακμή οποτεδήποτε υπάρχει μια τέτοια
από την τρέχουσα κατάσταση χωρίς να μας ενδιαφέρει ποιο είναι το επόμενο
γράμμα της λέξης. Η διάνυση μιας ![]() -ακμής δε συνοδεύεται από
μεταπήδηση στο επόμενο γράμμα της λέξης.
Ας τα λέμε αυτά
-ακμής δε συνοδεύεται από
μεταπήδηση στο επόμενο γράμμα της λέξης.
Ας τα λέμε αυτά ![]() -NFA.
-NFA.
Κάθε φορά που διαβάζουμε ένα γράμμα ![]() , και ευρισκόμενοι στην
κατάσταση
, και ευρισκόμενοι στην
κατάσταση ![]() , επιλέγουμε ως επόμενη κατάσταση
μια από τις καταστάσεις του συνόλου
, επιλέγουμε ως επόμενη κατάσταση
μια από τις καταστάσεις του συνόλου
![]() .
(Αν το σύνολο αυτό είναι κενό η λέξη απορρίπτεται.)
Αν επιλέξουμε να μη διαβάσουμε το επόμενο γράμμα της λέξης
μπορούμε να μεταβούμε σε νέα κατάσταση ακολουθώντας μια
.
(Αν το σύνολο αυτό είναι κενό η λέξη απορρίπτεται.)
Αν επιλέξουμε να μη διαβάσουμε το επόμενο γράμμα της λέξης
μπορούμε να μεταβούμε σε νέα κατάσταση ακολουθώντας μια ![]() -ακμή,
μπορούμε δηλ. να μεταβούμε σε μια αποιαδήποτε από τις καταστάσεις
του συνόλου
-ακμή,
μπορούμε δηλ. να μεταβούμε σε μια αποιαδήποτε από τις καταστάσεις
του συνόλου
![]() , όπου
, όπου ![]() είναι η τρέχουσα κατάσταση.
(Αν το σύνολο αυτό είναι κενό η λέξη απορρίπτεται.)
Είναι φανερό ότι για κάθε λέξη υπάρχουν ενδεχομένως περισσότεροι από ένας
τρόποι να κινηθούμε πάνω στο αυτόματο διαβάζοντας τα γράμματα αυτής
της λέξης, αφού σε κάθε βήμα ενδέχεται να έχουμε τη δυνατότητα να επιλέξουμε
την επόμενή μας κατάσταση.
Απορρίπτεται η λέξη
είναι η τρέχουσα κατάσταση.
(Αν το σύνολο αυτό είναι κενό η λέξη απορρίπτεται.)
Είναι φανερό ότι για κάθε λέξη υπάρχουν ενδεχομένως περισσότεροι από ένας
τρόποι να κινηθούμε πάνω στο αυτόματο διαβάζοντας τα γράμματα αυτής
της λέξης, αφού σε κάθε βήμα ενδέχεται να έχουμε τη δυνατότητα να επιλέξουμε
την επόμενή μας κατάσταση.
Απορρίπτεται η λέξη ![]() αν και μόνο αν κανείς από τους δυνατούς τρόπους
κίνησης δεν καταλήγει σε τελική κορυφή.
αν και μόνο αν κανείς από τους δυνατούς τρόπους
κίνησης δεν καταλήγει σε τελική κορυφή.
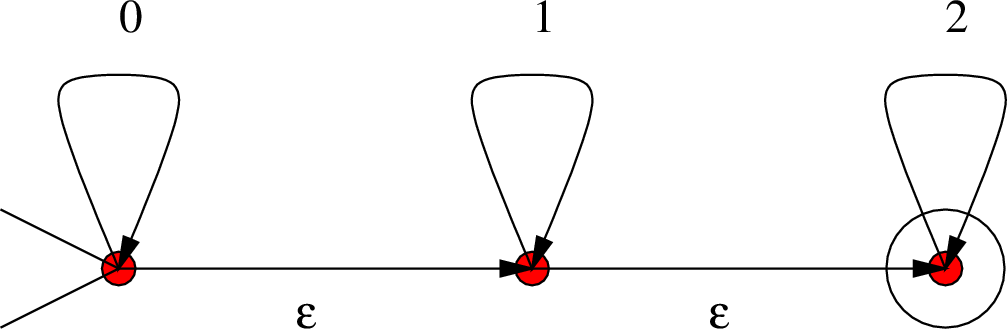
Υπόδειξη: Χρησιμοποιήστε τα ![]() και
και ![]() βάζοντας πριν από αυτά μια κοινή κατάσταση
εισόδου με
βάζοντας πριν από αυτά μια κοινή κατάσταση
εισόδου με ![]() -κινήσεις μόνο προς τα δύο DFA.
-κινήσεις μόνο προς τα δύο DFA.
Υπόδειξη: Χρησιμοποιήστε το ![]() ακολουθούμενο από το
ακολουθούμενο από το ![]() . Από τις τελικές καταστάσεις του
. Από τις τελικές καταστάσεις του
![]() θα φεύγουν κάποιες
θα φεύγουν κάποιες ![]() -ακμές.
-ακμές.
Mihalis Kolountzakis 2015-11-28