7.7 Κανονικές εκφράσεις και οι γλώσσες τους
Οι κανονικές εκφράσεις που θα δούμε σε αυτή την παράγραφο είναι ένας διαφορετικός τρόπος περιγραφής
μιας γλώσσας που αναγνωρίζεται από ένα DFA. Είναι μάλιστα ένας αρκετά πιο συνοπτικός και διαισθητικός τρόπος να περιγράψει
κανείς μια τέτοια γλώσσα και γι' αυτό το λόγο είναι ένας τρόπος που χρησιμοποιείται πολύ στην πράξη.
Θα δώσουμε κατ' αρχήν ένα αναδρομικό ορισμό για το
τι είναι μια κανονική έκφραση (regular expression) και το ποια γλώσσα παριστάνει.
Ορισμός 7.19
(Κανονικές εκφράσεις και οι γλώσσες τους)
Οι παρακάτω λέξεις ορίζονται να είναι κανονικές εκφράσεις
με τις αντίστοιχες γλώσσες.
(Με 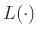 συμβολίζουμε τη γλώσσα μιας έκφρασης.)
συμβολίζουμε τη γλώσσα μιας έκφρασης.)
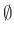 , και
, και
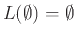 (η κενή γλώσσα, που δεν περιέχει καμία λέξη)
(η κενή γλώσσα, που δεν περιέχει καμία λέξη)
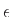 , και
, και
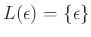 (η γλώσσα που περιέχει μόνο μια λέξη, την κενή λέξη
(η γλώσσα που περιέχει μόνο μια λέξη, την κενή λέξη 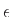 )
)
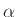 , για κάθε
, για κάθε
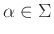 , και
, και
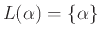 .
.
Επίσης, αν 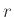 και
και 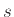 είναι κανονικές εκφράσεις τότε και οι ακόλουθες λέξεις είναι
επίσης κανονικές εκφράσεις.
είναι κανονικές εκφράσεις τότε και οι ακόλουθες λέξεις είναι
επίσης κανονικές εκφράσεις.
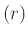 , και
, και
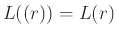 .
.
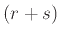 , και
, και
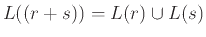 ,
,
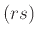 , και
, και
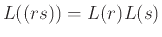 ,
,
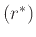 , και
, και
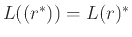 .
.
Μια γλώσσα 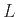 λέγεται κανονική αν υπάρχει κανονική έκφραση
λέγεται κανονική αν υπάρχει κανονική έκφραση 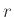 με
με 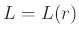 .
.
Παρατήρηση 7.10
Αν μπορούμε να παρελείψουμε τις παρανθέσεις χωρίς να αλλάξουμε το νόημα
τότε το κάνουμε αυτό. Λαμβάνουμε υπόψιν ότι τη μεγαλύτερη προτεραιότητα
έχει ο εκθέτης 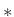 , μετά έρχεται η συγκόλληση και τέλος η πρόσθεση.
Για παράδειγμα η κανονική έκφραση
, μετά έρχεται η συγκόλληση και τέλος η πρόσθεση.
Για παράδειγμα η κανονική έκφραση 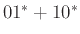 ερμηνεύεται ως
ερμηνεύεται ως
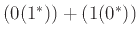 .
Αν
.
Αν 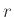 είναι μια κανονική έκφραση τότε χρησιμοποιούμε επίσης τη
συντομογραφία
είναι μια κανονική έκφραση τότε χρησιμοποιούμε επίσης τη
συντομογραφία 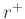 αντί για
αντί για 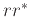 .
.
Άσκηση 7.26
Γράψτε κανονικές εκφράσεις για τις ακόλουθες γλώσσες:
- Λέξεις που δεν περιέχουν τη μορφή 101.
- Λέξεις όπου όλες οι εμφανίσεις διαδοχικών 0 συμβαίνουν πριν από οποιαδήποτε εμφάνιση
διαδοχικών 1.
Άσκηση 7.27
Περιγράψτε τις γλώσσες που ορίζονται από τις κανονικές εκφράσεις:
-
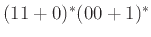
-
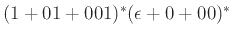
-
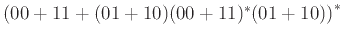
Άσκηση 7.28
Δείξτε τις παρακάτω ταυτότητες όπου 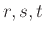 είναι οποιεσδήποτε κανονικές εκφράσεις.
Η ισότητα παρακάτω δε σημαίνει ότι οι δύο εκφράσεις είναι ίσες (και δεν είναι,
μια και οι εκφράσεις είναι λέξεις, και ως τέτοιες διαφέρουν) αλλά ότι οι αντίστοιχες
γλώσσες είναι ίσες.
είναι οποιεσδήποτε κανονικές εκφράσεις.
Η ισότητα παρακάτω δε σημαίνει ότι οι δύο εκφράσεις είναι ίσες (και δεν είναι,
μια και οι εκφράσεις είναι λέξεις, και ως τέτοιες διαφέρουν) αλλά ότι οι αντίστοιχες
γλώσσες είναι ίσες.
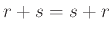
-
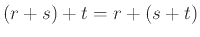
-
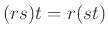
-
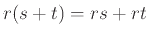
-
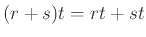
-
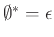
-
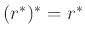
-
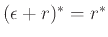
-
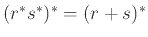
Mihalis Kolountzakis
2015-11-28