Next: 7.5 NFA με ε-κινήσεις Up: 7. Τυπικές γλώσσες και Previous: 7.3 Μη ντετερμινιστικά αυτόματα Contents Index
Επαναλαμβάνουμε ότι για ένα NFA η συνάρτηση μετάβασης ![]() είναι ο τρόπος
κωδικοποίησης των μεταβάσεων του.
Αν δηλ.
είναι ο τρόπος
κωδικοποίησης των μεταβάσεων του.
Αν δηλ. ![]() είναι μια κατάσταση και
είναι μια κατάσταση και
![]() είναι ένα
γράμμα του αλφαβήτου, το σύνολο
είναι ένα
γράμμα του αλφαβήτου, το σύνολο
![]() είναι το σύνολο όλων των καταστάσεων του NFA στις οποίες μπορεί αυτό
να μεταβεί όντας στην κατάσταση
είναι το σύνολο όλων των καταστάσεων του NFA στις οποίες μπορεί αυτό
να μεταβεί όντας στην κατάσταση ![]() και διαβάζοντας το γράμμα
και διαβάζοντας το γράμμα ![]() .
.
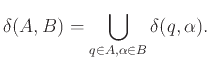
Επεκτείνουμε τώρα το πεδίο ορισμού της συνάρτησης ![]() όσον αφορά το δεύτερο όρισμά της.
όσον αφορά το δεύτερο όρισμά της.
Με άλλα λόγια
![]() , είναι το σύνολο όλων εκείνων των καταστάσεων
του αυτομάτου στις οποίες μπορεί κανείς να βρεθεί ξεκινώντας από την κατάσταση
, είναι το σύνολο όλων εκείνων των καταστάσεων
του αυτομάτου στις οποίες μπορεί κανείς να βρεθεί ξεκινώντας από την κατάσταση ![]() και
ακολουθώντας τη λέξη
και
ακολουθώντας τη λέξη ![]() .
Και, αν
.
Και, αν
![]() είναι ένα σύνολο καταστάσεων, με
είναι ένα σύνολο καταστάσεων, με
![]() συμβολίζεται
το σύνολο όλων των καταστάσεων στις οποίες μπορεί κανείς να πάει ξεκινώντας
από κάποια κατάσταση στο
συμβολίζεται
το σύνολο όλων των καταστάσεων στις οποίες μπορεί κανείς να πάει ξεκινώντας
από κάποια κατάσταση στο ![]() και ακολουθώντας τη λέξη
και ακολουθώντας τη λέξη ![]() .
.
Έστω λοιπόν ότι το NFA ![]() είναι η πεντάδα
είναι η πεντάδα
![]() .
Το DFA
.
Το DFA
![]() θα έχει σύνολο καταστάσεων
θα έχει σύνολο καταστάσεων
![]() το δυναμοσύνολο (σύνολο όλων
των υποσυνόλων) του
το δυναμοσύνολο (σύνολο όλων
των υποσυνόλων) του ![]() ,
αρχική κατάσταση
,
αρχική κατάσταση
![]() , ίδιο αλφάβητο
, ίδιο αλφάβητο ![]() και τελικές
καταστάσεις όλα εκείνα τα σύνολα καταστάσεων του
και τελικές
καταστάσεις όλα εκείνα τα σύνολα καταστάσεων του ![]() που περιέχουν κάποια
τελική κατάσταση
που περιέχουν κάποια
τελική κατάσταση
Με άλλα λόγια: στο DFA ![]() που κατασκευάζουμε από την κατάσταση
που κατασκευάζουμε από την κατάσταση ![]() (υποσύνολο
του
(υποσύνολο
του ![]() ) με το σύμβολο
) με το σύμβολο
![]() μεταβαίνουμε στην κατάσταση
μεταβαίνουμε στην κατάσταση ![]() , που είναι
το σύνολο όλων εκείνων των καταστάσεων του
, που είναι
το σύνολο όλων εκείνων των καταστάσεων του ![]() στις οποίες μπορούμε να μεταβούμε
από κάποια κατάσταση του συνόλου
στις οποίες μπορούμε να μεταβούμε
από κάποια κατάσταση του συνόλου ![]() με το γράμμα
με το γράμμα ![]() κινούμενοι πάνω στο
κινούμενοι πάνω στο ![]() .
Δείτε το Παράδειγμα 7.21 παρακάτω.
.
Δείτε το Παράδειγμα 7.21 παρακάτω.
Για να δείξουμε το Θεώρημα αρκεί να δείξουμε την ισοδυναμία
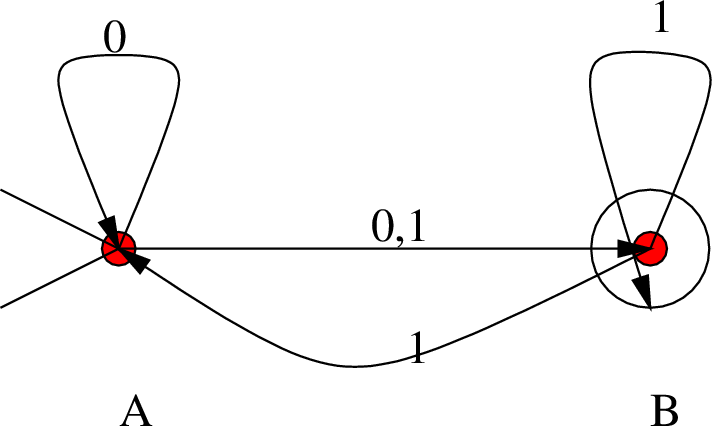
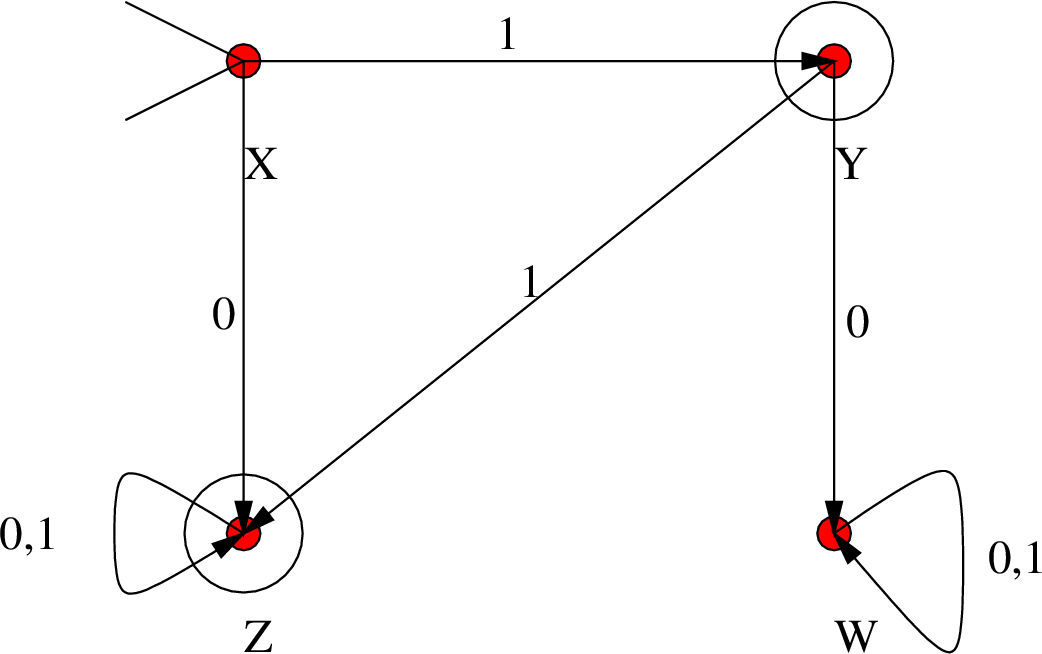
Το σύνολο καταστάσεων του ![]() θα είναι το δυναμοσύνολο
του συνόλου καταστάσεων του
θα είναι το δυναμοσύνολο
του συνόλου καταστάσεων του ![]() δηλ. του
δηλ. του
![]() .
Είναι δηλ. το σύνολο
.
Είναι δηλ. το σύνολο
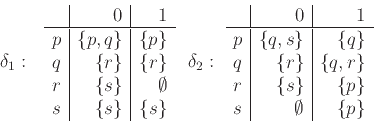
Mihalis Kolountzakis 2015-11-28