7.3 Μη ντετερμινιστικά αυτόματα

Εισάγουμε τώρα μια παραλλαγή των ντετερμινιστικών αυτομάτων, τα μη ντετερμινιστικά αυτόματα (Non-deterministic Finite Automata ή NFA). Αυτά αποτελούν, φαινομενικά, μια ενίσχυση του μοντέλου των ντετερμινιστικών αυτομάτων, αφού, από τον ορισμό που θα δώσουμε, κάθε DFA θα είναι και NFA, και άρα οι γλώσσες που αναγνωρίζονται από τα NFA είναι ένα υπερσύνολο των γλωσσών που αναγνωρίζονται από DFA.

Θα δούμε όμως σύντομα ότι αυτό είναι μόνο φαινομενικό, και ότι τα δύο μοντέλα είναι απολύτως ισοδύναμα, όσον αφορά τουλάχιστον το ποιες γλώσσες αναγνωρίζουν. Με άλλα λόγια, θα δούμε μια μέθοδο που για κάθε NFA θα κατασκευάζει ένα ισοδύναμο DFA, ένα DFA δηλ. που θα αναγνωρίζει ακριβώς την ίδια γλώσσα με το δοθέν NFA. Παρ' όλα αυτα το να μελετούμε NFA προσφέρει μερικά πλεονεκτήματα σε σχέση με τα DFA σε ορισμένες περιπτώσεις, όπως θα δούμε στα παραδείγματα.

Ορισμός 7.8   (Μη ντετερμινιστικό Αυτόματο (NFA) ) Ένα μη ντετερμινιστικό αυτόματο είναι μια πεντάδα

$$(Q, \Sigma, \delta, q_0, F)$$

όπου

• $Q$ είναι ένα πεπερασμένο σύνολο καταστάσεων,
• $\Sigma$ είναι ένα πεπερασμένο αλφάβητο,
• $\delta$ είναι η συνάρτηση μετάβασης (transition function) με πεδίο ορισμού το $Q \times \Sigma$ και πεδίο τιμών το δυναμοσύνολο $2^Q$, το σύνολο δηλ. όλων των υποσυνόλων του $Q$.
• $q_0\in Q$ είναι μια από τις καταστάσεις που ονομάζεται αρχική, και
• $F \subseteq Q$ είναι το σύνολο των τελικών καταστάσεων.

Ένα μη ντετερμινιστικό αυτόματο είναι σαν ένα DFA αλλά για κάθε κορυφή και για κάθε γράμμα του αλφαβήτου μπορεί κανεις να έχει οποιοδήποτε πεπερασμένο πλήθος από ακμές που ξεκινούν από την κορυφή και έχουν το γράμμα ως ετικέτα Μπορεί ακόμη και να μην υπάρχει καμία ακμή από κάποια κορυφή για κάποιο γράμμα. (Αν $\delta(q,\alpha)=\emptyset$ είναι το κενό σύνολο τότε δεν υπάρχει στο γράφημα καμία ακμή από την κορυφή $q$ με ετικέτα $\alpha$.)

Η σημαντική διαφορά με πριν είναι ότι, όταν διαβάζουμε μια λέξη, δεν είναι πλέον μονοσήμαντα καθορισμένη η κίνησή μας πάνω στο γράφημα αφού ενδέχεται να έχουμε περισσότερες από μία επιλογές μετάβασης όντας σε μία κορυφή και διαβάζοντας ένα γράμμα. Το σε ποιες καταστάσεις μπορούμε να πάμε από μια κατάσταση $q\in Q$ αφού διαβάσουμε το γράμμα $\alpha$ μας το λέει η συνάρτηση μετάβασης. Το σύνολο αυτών των δυνατών καταστάσεων είναι το $\delta(q,\alpha)\subseteq Q$.

Παρατήρηση 7.4   Αν για μια κατάσταση $q$ ενός NFA και για ένα γράμμα $\alpha\in\Sigma$ έχουμε $\delta(q,\alpha)=\emptyset$ αυτό ερμηνεύεται ως να μην είναι δυνατή η μετάβαση από την κατάσταση $q$ προς οποιαδήποτε άλλη κατάσταση με το γράμμα $\alpha$.

Ορισμός 7.9   (Αναγνώριση λέξης από NFA) Θεωρούμε ότι μια λέξη $w=w_1 w_2 \ldots w_n$, $w_j \in \Sigma$, αναγνωρίζεται από ένα NFA αν υπάρχει τρόπος να κινηθούμε, διαβάζοντας το $w$, πάνω στο γράφημα ώστε να καταλήξουμε σε τελική κορυφή. Ξεκινούμε ευρισκόμενοι στην αρχική κατάσταση $q_0$ και διαβάζουμε τα γράμματα $w_1$ έως $w_n$ με αυτή τη σειρά. Κάθε φορά που διαβάζουμε ένα γράμμα $w_j$, και ευρισκόμενοι στην κατάσταση $q$, επιλέγουμε ως επόμενη κατάσταση μια από τις καταστάσεις του συνόλου $\delta(q,w_j)$. (Αν το σύνολο αυτό είναι κενό η λέξη απορρίπτεται.) Είναι φανερό ότι για κάθε λέξη υπάρχουν ενδεχομένως περισσότεροι από ένας τρόποι να κινηθούμε πάνω στο αυτόματο διαβάζοντας τα γράμματα αυτής της λέξης, αφού σε κάθε βήμα ενδέχεται να έχουμε τη δυνατότητα να επιλέξουμε την επόμενή μας κατάσταση. Απορρίπτεται η λέξη $w$ αν και μόνο αν κανείς από τους δυνατούς τρόπους κίνησης δεν καταλήγει σε τελική κορυφή.

Ορισμός 7.10   (Γλώσσα ενός NFA) Το σύνολο των λέξεων που αποδέχεται το μη ντετερμινιστκό αυτόματο $M$ ονομάζεται η γλώσσα που αναγνωρίζει το αυτόματο και συμβολίζεται με $L(M)$.

Παράδειγμα 7.19   Το ακόλουθο παράδειγμα μη ντετερμινιστικού αυτομάτου αναγνωρίζει τη γλώσσα $00{\left\{{0,1}\right\}}^*11$.

Σχήμα 7.6: NFA για τη γλώσσα $00{\left\{{0,1}\right\}}^*11$

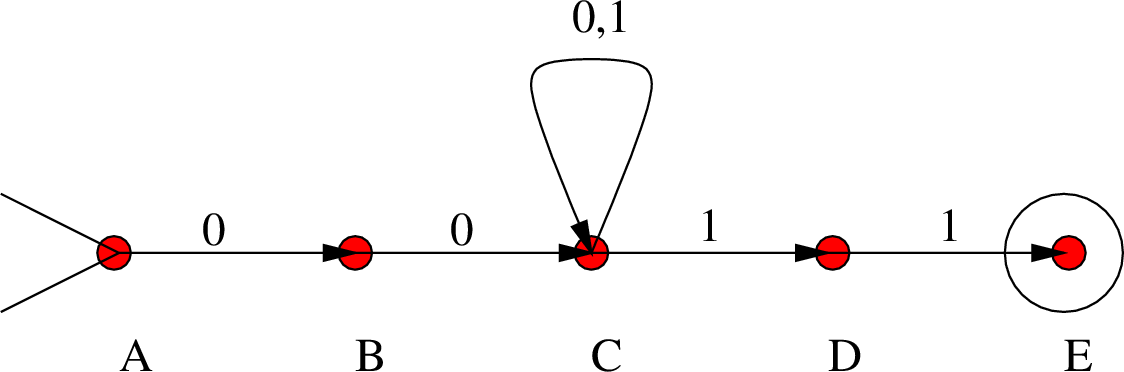
Πρόκειται για NFA και όχι για DFA μια και στη μεσαία κορυφή υπάρχουν δύο ακμές με ετικέτα 1. Παρατηρήστε τη συντομογραφία που επιλέξαμε εδώ: ο βρόχος (loop) από τη μεσαία κορυφή στον εαυτό της έχει δύο ετικέτες 0 και 1. Αυτό σημαίνει ότι επιτρέπεται να διανύσουμε την κορυφή αυτή όταν διαβάσουμε είτε 0 είτε 1. Θα μπορούσαμε να είχαμε το ίδιο αποτέλεσμα αν φτιάχναμε δύο βρόχους από την κορυφή αυτή στον εαυτό της, ένα με ετικέτα 0 κι ένα με ετικέτα 1. Επιλέγουμε τη συντομογραφία για καθαρότητα στο σχήμα και τίποτε άλλο.

Γιατί το NFA του σχήματος 7.6 αναγνωρίζει τη γλώσσα $L = 00{\left\{{0,1}\right\}}^*11$; Παρατηρήστε ότι η $L$ αποτελείται από εκείνες ακριβώς τις λέξεις που αρχίζουν με $00$ και τελειώνουν με $11$. Κάθε τέτοια λέξη περνάει από το NFA ως εξής: με τα δύο πρώτα 0 μεταβαίνει στη μεσαία κορυφή, στην οποία και παραμένει χρησιμοποιώντας το βρόχο μέχρι να διαβάσει και το προπροτελευταίο γράμμα. Με τα δύο τελευταία 1 επιλέγει να κινηθεί προς τα δεξιά για να καταλήξει στη μοναδική τελική κορυφή. Θα μπορούσε να επιλέξει με τα δύο τελευταία 1 να κινηθεί πάνω στο βρόχο της μεσαίας κορυφής, αλλά με αυτό τον τρόπο δεν καταλήγει σε τελική κορυφή. Αρκεί όμως για την αποδοχή μιας λέξης να υπάρχει έστω και ένας τρόπος να γίνει αποδεκτή.

Αντίστροφα τώρα, αν η λέξη $w$ περνά από το NFA τότε υποχρεωτικά αρχίζει από δύο 0 (αλλιώς δε μπορεί να πάει δεξιότερα από τη δεύτερη κορυφή) και τελειώνει σε δύο 1 (αλλιώς δε μπορεί να καταλήξει στην τελική κορυφή).

Ας δώσουμε τώρα και ένα DFA για την ίδια γλώσσα:

Σχήμα 7.7: DFA για τη γλώσσα $00{\left\{{0,1}\right\}}^*11$

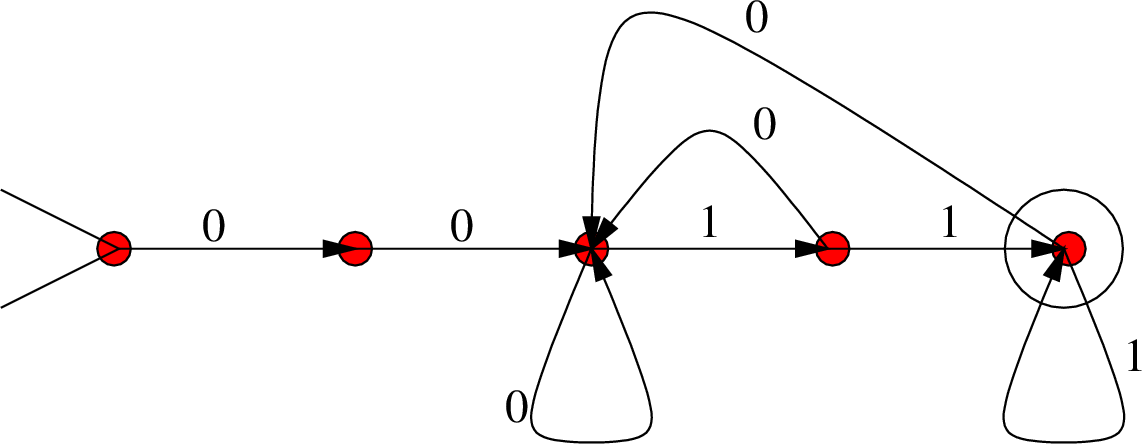
Είναι μια καλή άσκηση να να αποδείξετε ότι το άνω αυτόματο αναγνωρίζει τη γλώσσα $00{\left\{{0,1}\right\}}^*11$. Για να το κάνετε δώστε κάποιο «νόημα» στις καταστάσεις, όπως κάναμε παραπάνω για να δείξουμε ότι το DFA του σχήματος 7.5 δουλεύει.

Παρατήρηση 7.5   Συγκρίνοντας το NFA και το DFA για τη γλώσσα $00{\left\{{0,1}\right\}}^*11$ φαίνεται καθαρά το πλεονέκτημα του να σχεδιάζουμε NFA αντί για DFA. Επιτρέποντας στον εαυτό μας ένα πιο διευρυμένο μοντέλο μπορούμε να σχεδιάζουμε ευκολότερα αυτόματα για συγκεκριμένες γλώσσες, και η απλούστερη κατασκευή συνήθως επιτρέπει και μια ευκολότερη ανάλυση τού γιατί το συγκεκριμένο αυτόματο δουλεύει. Και, θα δούμε αργότερα, δε χάνεται τίποτα σχεδιάζοντας NFA αντί για DFA, γιατί αυτά τα δύο υπολογιστικά μοντέλα είναι ισοδύναμα. Όχι μόνο αυτό, αλλά ο τρόπος μετατροπής ενός NFA σε DFA μπορεί να είναι τελείως μηχανικός (αλγοριθμικός).

Παράδειγμα 7.20   Στο αυτόματο που φαίνεται στο σχήμα 7.6 παραπάνω έχουμε $Q = {\left\{{A, B, C, D, E}\right\}}$, $\Sigma = {\left\{{0,1}\right\}}$.$q_0 = A$, $F = {\left\{{E}\right\}}$, και

$$\delta(A,0) = {\left\{{B}\right\}}$$

$$\delta(A,1) = \emptyset$$

$$\delta(B,0) = {\left\{{C}\right\}}$$

$$\delta(B,1) = \emptyset$$

$$\delta(C,0) = {\left\{{C}\right\}}$$

$$\delta(C,1) = {\left\{{C, D}\right\}}$$

$$\delta(D,0) = \emptyset$$

$$\delta(D,1) = {\left\{{E}\right\}}$$

$$\delta(E,0) = \emptyset$$

$$\delta(E,1) = \emptyset$$

Άσκηση 7.16   Κατασκευάστε ένα NFA που να αναγνωρίζει τη γλώσσα της άσκησης 7.11.

Άσκηση 7.17   Κατασκευάστε ένα NFA που να αναγνωρίζει εκείνες τις λέξεις πάνω από το $\Sigma = {\left\{{0,1}\right\}}$ που περιέχουν δύο μηδενικά που απέχουν μεταξύ τους στη λέξη κατά πολλαπλάσιο του 4. Δύο διαδοχικά μηδενικά θεωρούνται ότι απέχουν απόσταση μηδέν, άρα πολλαπλάσιο του 4.