7.2 Ντετερμινιστικά Αυτόματα

Ένα Ντετερμινιστικό Αυτόματο (Deterministic Finite Automaton ή DFA) είναι ουσιαστικά ένα κατευθυνόμενο γράφημα, του οποίου οι κορυφές $Q$ ονομάζονται καταστάσεις (states) και από κάθε κορυφή φεύγει ακριβώς μια ακμή για κάθε γράμμα του αλφαβήτου $\Sigma$. Υπάρχει μια διακεκριμένη κατάσταση $q_0$, η αρχική κατάσταση και ένα μη-κενό σύνολο $F$ από τελικές καταστάσεις.

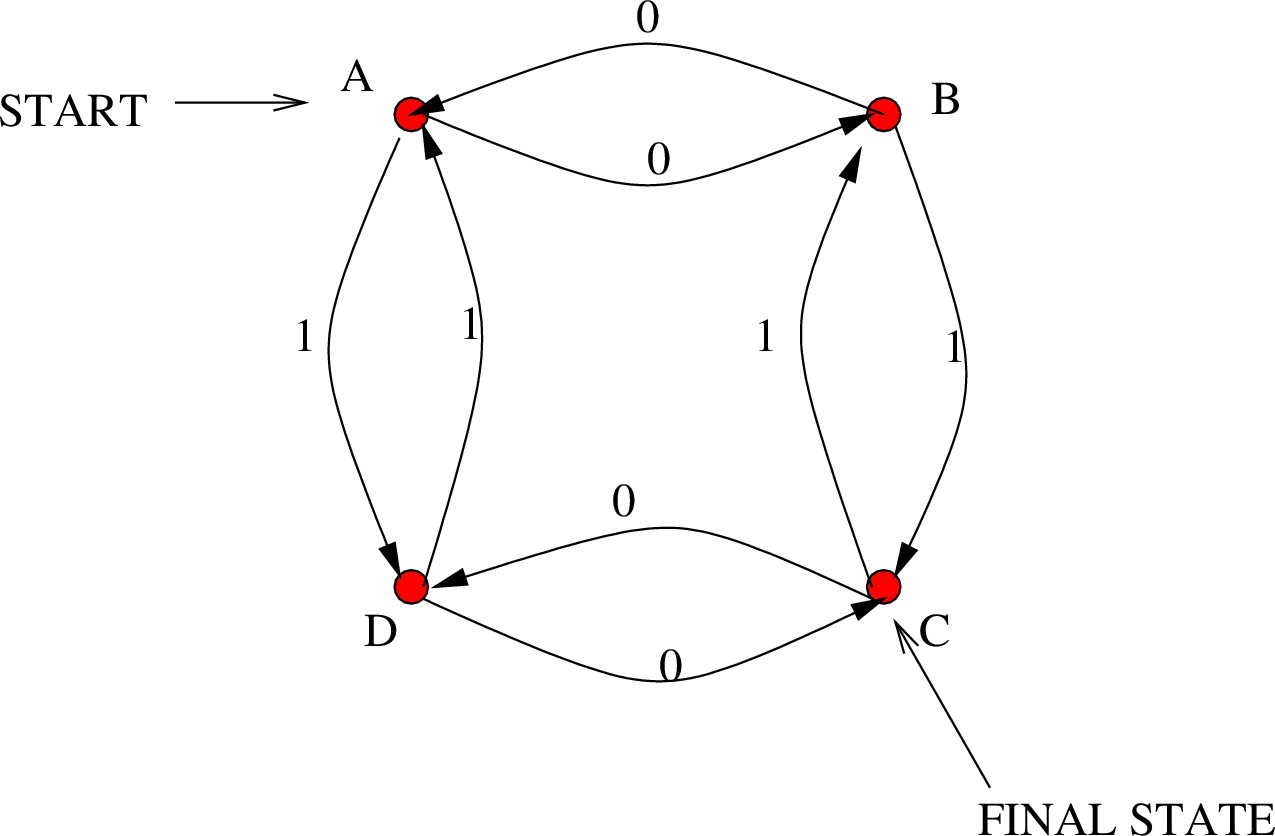
Δείτε π.χ. ένα τέτοιο αυτόματο στο Σχήμα 7.1.

Σχήμα 7.1: Ένα απλό ντετερμινιστικό αυτόματο

Ορισμός 7.6   (Ντετερμινιστικό Αυτόματο)
Ένα ντετερμινιστικό αυτόματο είναι μια πεντάδα

$$(Q, \Sigma, \delta, q_0, F)$$

όπου

• $Q$ είναι ένα πεπερασμένο σύνολο καταστάσεων,
• $\Sigma$ είναι ένα πεπερασμένο αλφάβητο,
• $\delta$ είναι η συνάρτηση μετάβασης (transition function) με πεδίο ορισμού το $Q \times \Sigma$ και πεδίο τιμών το $Q$,
• $q_0\in Q$ είναι μια από τις καταστάσεις που ονομάζεται αρχική, και
• $F \subseteq Q$ είναι το σύνολο των τελικών καταστάσεων.

Παρατήρηση 7.3   Ένα DFA το σχεδιάζουμε συνήθως ως ένα κατευθυνόμενο γράφημα με σύνολο κορυφών ίδιο με το σύνολο καταστάσεων $Q$. Από κάθε κατάσταση/κορυφή $q$ φεύγει ακριβώς μια ακμή για κάθε γράμμα $a \in \Sigma$ η οποία καταλήγει στην κατάσταση $\delta(q, a)$.

Παράδειγμα 7.14   Στο αυτόματο που φαίνεται στο Σχήμα 7.1 έχουμε $Q = {\left\{{A, B, C, D}\right\}}$, $\Sigma = {\left\{{0,1}\right\}}$.$q_0 = A$, $F = {\left\{{C}\right\}}$.

Για να μιλήσουμε για τη συνάρτηση μετάβασης $\delta$ θα πρέπει πρώτα να αναφερθούμε στον τρόπο «λειτουργίας » του αυτομάτου. Ένα αυτόματο χρησιμεύει για να αναγνωρίζει, όπως λέμε, μια γλώσσα $L \subseteq \Sigma^*$. Η διαδικασία αναγνώρισης είναι η εξής.

Έστω λέξη $w \in \Sigma^*$, $w = w_1\ldots w_n$, μήκους $n$ ( $w_i \in \Sigma$).

• Το αυτόματο αρχίζει τη λειτουργία του στην αρχική κατάσταση $q_0$.
• Διαβάζει έπειτα τα γράμματα της λέξης ένα προς ένα, από τα αριστερά προς τα δεξιά πάντα. Πρώτο διαβάζεται το γράμμα $w_1$ και τελευταίο το $w_n$.
• Μόλις διαβάσει το γράμμα $\alpha\in\Sigma$ και ευρισκόμενο στην κατάσταση $q$ το αυτόματο μεταβαίνει στην κατάσταση $r$ αν και μόνο αν η ακμή $q \to r$ έχει ετικέτα (label) ίση με $\alpha$. Για κάθε κατάσταση του αυτομάτου και κάθε γράμμα του αλφαβήτου υπάρχει εξ ορισμού ακριβώς μια ακμή που ξεκινά από την κατάσταση αυτή και έχει ετικέτα αυτό το γράμμα. Ισχύει τότε για τη συνάρτηση μετάβασης $\delta(q, \alpha) = r$, χρησιμεύει δηλ. η συνάρτηση μετάβασης για να μας προσδιορίσει σε ποια κατάσταση πάει το αυτόματο αν βρίσκεται σε μια δεδομένη κατάσταση $q$ και διαβάσει ένα συγκεκριμένο γράμμα $\alpha$. Όλη η συνδεσμολογία του αυτομάτου δηλ. είναι κωδικοποιημένη στη συνάρτηση $\delta$.
• Αφού διαβάσει το αυτόματο το τελευταίο γράμμα της λέξης και κάνει την τελευταία του μετάβαση δηλώνει ότι αποδέχεται τη λέξη αν και μόνο αν βρίσκεται σε τελική κατάσταση, σε μια κατάσταση δηλ. του συνόλου $F$. Αλλιώς η λέξη απορρίπτεται.

Ορισμός 7.7   (Γλώσσα ενός DFA)
Το σύνολο των λέξεων που αποδέχεται το αυτόματο $M$ ονομάζεται η γλώσσα που αναγνωρίζει το αυτόματο και συμβολίζεται με $L(M)$.

Παράδειγμα 7.15   Ποια είναι η γλώσσα $L$ που αναγνωρίζεται από το αυτόματο της εικόνας 7.1;

Δε θέλει και πολλή σκέψη για να πειστούμε ότι στην $L$ ανήκουν ακριβώς εκείνες οι λέξεις του ${\left\{{0,1}\right\}}^*$ που έχουν περιττό αριθμό από 0 και περιττό αριθμό από 1. Για να το δούμε αυτό παρατηρούμε ότι οποτεδήποτε το αυτόματο βρίσκεται σε μια από τις δύο αριστερές καταστάσεις το πλήθος των μηδενικών που έχει διαβάσει είναι άρτιο. Αυτό γίνεται γιατί αυτή η πρόταση ισχύει προφανέστατα τη χρονική στιγμή 0, αφού τότε δεν έχει διαβάσει κανένα μηδενικό και βρίσκεται στην αρχική κατάσταση $A$ που είναι στην αριστερή μεριά. Οποτεδήποτε διαβάσει επίσης κάποιο μηδενικό το αυτόματο αλλάζει μεριά και διατηρείται έτσι η ιδιότητα αυτή. Ομοίως επιχειρηματολογώντας βλέπουμε ότι το αυτόματο βρίσκεται σε μια από τις δύο πάνω καταστάσεις ($A$ και $B$) αν και μόνο αν έχει διαβάσει άρτιο αριθμό από 1. Έτσι, το να είναι το αυτόματο στην κατάσταση $C$ (τελική) σημαίνει ότι έχει δει περιττό αριθμό από ένα και περιττό από μηδέν, αφού η $C$ είναι κάτω (περιττοί άσοι) και δεξιά (περιττά μηδενικά).

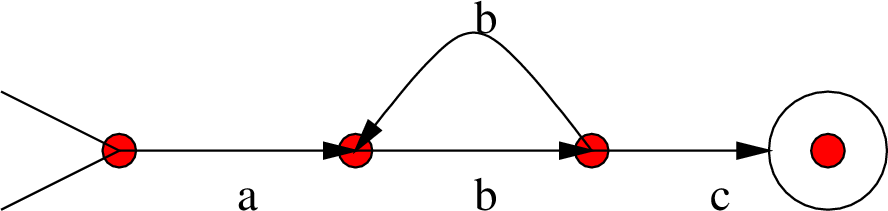
Αν π.χ. θελήσουμε να έχουμε ένα αυτόματο που θα αναγνωρίζει ακριβώς εκείνες τις λέξεις του ${\left\{{0,1}\right\}}^*$ που έχουν περιττά μηδενικά ή άρτιους άσους η μόνη αλλαγή που χρειάζεται να κάνουμε στην περιγραφή του αυτομάτου είναι να αλλάξουμε το σύνολο $F$ των τελικών καταστάσεων και να το θέσουμε ίσο με το ${\left\{{A,B,C}\right\}}$.

Άσκηση 7.8   Σχεδιάστε ένα DFA που να αναγνωρίζει εκείνες τις λέξεις πάνω από το $\Sigma = {\left\{{0,1}\right\}}$ που έχουν άρτιο πλήθος άσων και πλήθος μηδενικών που είναι πολλαπλάσιο του 3.

Υπόδειξη: Δείτε το Σχήμα 7.2.

Σχήμα 7.2: Για την Άσκηση 7.8 δουλέψτε με 6 καταστάσεις όπως αυτές.

Άσκηση 7.9   Σχεδιάστε ένα DFA που αναγνωρίζει εκείνες τις λέξεις πάνω από το $\Sigma = {\left\{{0,1}\right\}}$ που αρχίζουν από 11011.

Παράδειγμα 7.16   Στο σχήμα 7.3 βλέπουμε ένα αυτόματο που αναγνωρζει τη γλώσσα $a{\left\{{bb}\right\}}^*bc$, δηλ. όλες εκείνες τις λέξεις στο αλφάβητο $\Sigma = {\left\{{a, b}\right\}}$ που αρχίζουν με $a$, ακολουθεί ένας οποιοσδήποτε αριθμός (ακόμη και μηδέν) από αντίγραφα της λέξης $bb$, και τελειώνουν με τη λέξη $bc$.

Σχήμα 7.3: DFA για τη γλώσσα $a{\left\{{bb}\right\}}^*bc$

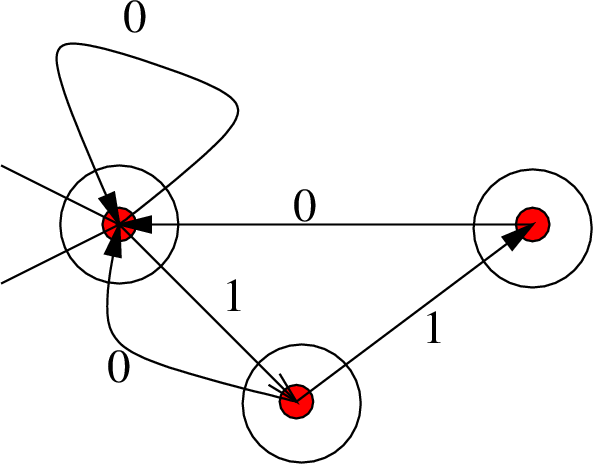
Συμβολισμός: Στο Σχήμα 7.3, όπως και παρακάτω, συμβολίζουμε την αρχική κατάσταση με μια ανοιχτή γωνία (σα «χωνί», απ' όπου μπαίνουμε στο αυτόματο) και κάθε τελική κατάσταση μπαίνει μέσα σ'ένα κύκλο.

Συμβολισμός: Προσέξτε ότι στο αυτόματο του Σχήματος 7.3 δεν ισχύει η αρχική μας απαίτηση ότι από κάθε κορυφή πρέπει να φεύγει ακριβώς μια ακμή για κάθε γράμμα του αλφαβήτου (ώστε ό,τι και να διαβάσουμε όταν είμαστε σε κάποια κατάσταση να έχουμε που να πάμε). Για παράδειγμα, για τη δεύτερη κορυφή από αριστερά δεν υπάρχει ακμή με ετικέτα $a$ που να ξεκινάει από αυτή. Η σύμβαση που ακολουθούμε είναι ότι αν διαβάσουμε ένα σύμβολο και βρισκόμαστε σε μια κατάσταση από την οποία δεν ξεκινάει ακμή με ετικέτα αυτό το σύμβολο, τότε η λέξη δεν αναγνωρίζεται από το αυτόματο.

Η σύμβαση αυτή ακολουθείται καθαρά για λόγους αισθητικής και κατανόησης του σχεδίου και δεν αλλάζει απολύτως τίποτα στην ουσία. Κάθε αυτόματο που ακολουθεί τη σύμβαση αυτή μπορεί εύκολα να μετατραπεί σε ένα αυτόματο που δε χρησιμοποιεί αυτή τη σύμβαση και έχει πράγματι μια ακμή για κάθε γράμμα από κάθε κορυφή. Απλά δηλώνουμε μια νέα μη τελική κατάσταση $K$, την κατάσταση καταστροφής, όπως επιλέγουμε να την ονομάσουμε, και από κάθε άλλη κατάσταση του αυτομάτου που δεν έχει ακμή από αυτή με ετικέτα έστω $x$ ορίζουμε μια τέτοια ακμή προς την $K$. Όλες οι ακμές από το $K$ επιστρέφουν πάλι στο $K$. Είναι εύκολο να δούμε ότι οι ίδιες ακριβώς λέξεις αναγνωρίζονται από το αρχικό και το νέο αυτόματο.

Παράδειγμα 7.17   Ακολουθεί στο Σχήμα 7.4 ένα αυτόματο που αναγνωρίζει τη γλώσσα $L$ εκείνων των λέξεων του ${\left\{{0,1}\right\}}^*$ που έχουν μέσα το πολύ δύο διαδοχικά 1. Ισοδύναμα, είναι εκείνες οι λέξεις στις οποίες δεν εμφανίζεται η μορφή 111.

Σχήμα 7.4: DFA για τις λέξεις χωρίς τρία διαδοχικά 1

Στο αυτόματο αυτό όλες οι καταστάσεις είναι τελικές, αλλά αυτό δεν αποτελεί αντίφαση, αφού ακολουθούμε τη σύμβαση της άνω παρατήρησης. Έτσι υπάρχουν πράγματι λέξεις που δεν αναγνωρίζονται από το αυτόματο, μια και κάποιες κορυφές δεν έχουν ακμές που ξεκινάνε από αυτές και για το 0 και το 1. Η μόνη τέτοια κορυφή είναι η δεξιά, και, όντως, η μόνη περίπτωση να απορριφθεί μια λέξη από το αυτόματο είναι να είμαστε στη δεξιά κατάσταση και να διαβάσουμε 1, πράγμα το οποίο συμβαίνει αν και μόνο αν υπάρχουν τρία διαδοχικά 1 στη λέξη.

Παράδειγμα 7.18   Το παράδειγμα αυτό είναι κάπως πιο ενδιαφέρον: $L$ είναι η γλώσσα εκείνων των λέξεων του ${\left\{{0,1}\right\}}^*$ που είναι τέτοιες ώστε, μετά το πρώτο 0 υπάρχει τουλάχιστον ένα 0 σε κάθε πεντάδα διαδοχικών γραμμάτων της λέξης. Για παράδειγμα, οι λέξεις 11111111111, 11111110111101111 είναι στην $L$ ενώ η λέξη 111111011111 δεν είναι (η τελευταία πεντάδα δεν έχει 0). Το αυτόματο δίνεται στο Σχήμα 7.5.

Σχήμα 7.5: DFA για τις λέξεις με τουλάχιστον ένα 0 σε κάθε πεντάδα, μετά το πρώτο 0

Πώς πρέπει να σκεφθεί κανείς για να καταλάβει πώς δουλεύει το συγκεκριμένο αυτόματο;

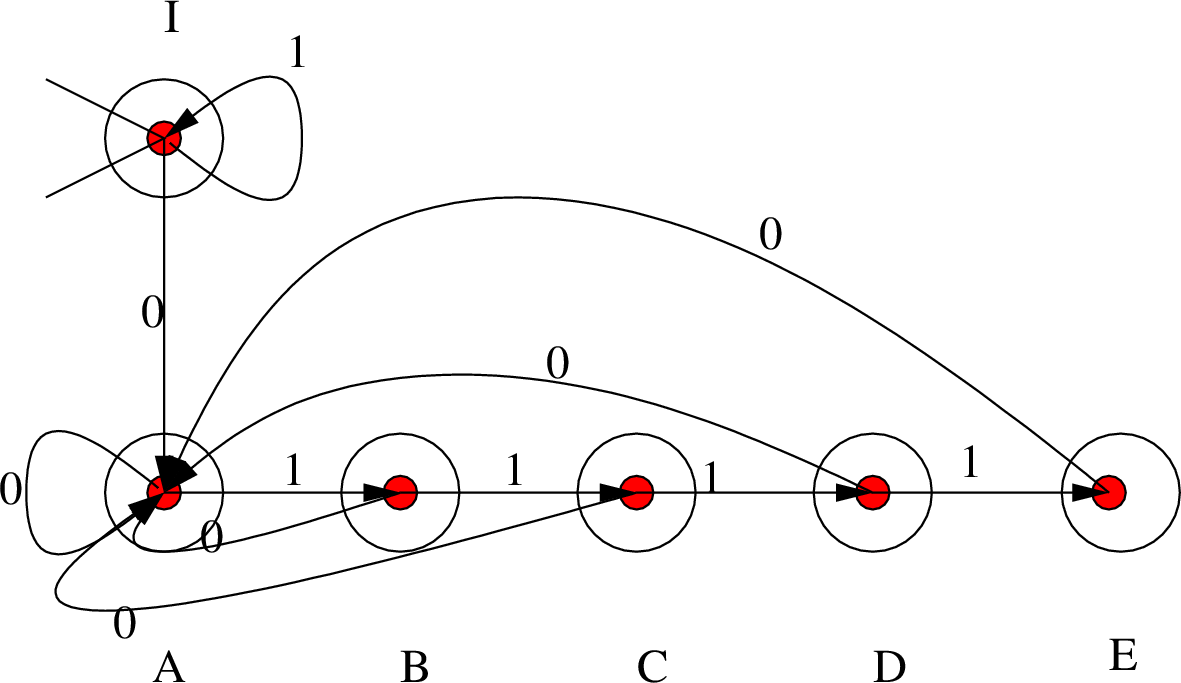
Το κλειδί σε αυτή την περίπτωση, όπως και στις περισσότερες, είναι να αποδώσουμε κάποιο νόημα στην πρόταση «βρισκόμαστε στην τάδε κατάσταση». Για παράδειγμα, στην κατάσταση $I$ βρισκόμαστε ακριβώς όταν δεν έχουμε διαβάσει ακόμη το πρώτο 0 της λέξης. Η πρόταση αυτή ισχύει κατ' αρχήν (πριν έχουμε διαβάσει τίποτε) και διατηρείται από οποιαδήποτε μετάβαση, αφού φεύγουμε από την κατάσταση $I$ ακριβώς μόλις διαβάσουμε το πρώτο μηδενικό και δεν ξαναγυρνάμε σε αυτή. Είναι τώρα φανερό, έχοντας ξεκαθαρίσει τι σημαίνει να βρισκόμαστε στην κατάσταση $I$, ότι αυτή πρέπει να είναι τελική κατάσταση, μια και αν ποτέ δε διαβάσουμε κάποιο 0, ισχύει ο κανόνας που βάλαμε στην αρχή για το ποιες λέξεις ανήκουν στην $L$ και άρα πρέπει να δεχτούμε τη λέξη.

Κάνουμε τώρα την εξής παρατήρηση. Ας πούμε πως ένας άνθρωπος, με λίγη μνήμη, έχει επιφορτισθεί με το καθήκον να αναγνωρίζει ακριβώς αυτές τις λέξεις. Αυτός μαθαίνει τα σύμβολα της λέξης ένα-ένα, πρώτα από τα αριστερά, όπως ακριβώς και το αυτόματο, και πρέπει κάποια στιγμή να πεί αν αυτή η λέξη ανήκει ή όχι στην $L$. Επειδή ακριβώς ο άνθρωπος αυτός έχει λίγη μνήμη, κι επειδή οι λέξεις τις οποίες κρίνει μπορούν να έχουν οσοδήποτε μεγάλο μήκος, αποφασίζει αντί ανά πάσα στιγμή να θυμάται ολόκληρη τη λέξη που έχει δει μέχρι τότε, να θυμάται απλώς πόσο χρόνο πριν είδε το τελευταίο μηδενικό. Είναι φανερό ότι αυτή η πληροφορία του αρκεί για να αποφασίσει. Θα απορρίψει δε τη λέξη αν και μόνο αν αυτός ο χρόνος ξεπεράσει το 5 σε κάποια χρονική στιγμή, γιατί ακριβώς τότε έχει δει μια πεντάδα γεμάτη με 1.

Μετά από αυτή την παρατήρηση το νόημα της κατάστασης $A$ είναι ότι βρίσκεται εκεί αν έχει δεί 0 ακριβώς πριν από χρόνο 1. Το νόημα της κατάστασης $B$ ομοίως είναι ότι έχει δεί το τελευταίο 0 ακριβώς πριν από χρόνο 2, κ.ο.κ., ενώ στην κατάσταση $E$ βρισκόμαστε αν έχουμε δεί το τελευταίο 0 ακριβώς 5 χρονικές στιγμές πριν. Είναι φανερό τώρα γιατί η κατάσταση $E$ δεν έχει μετάβαση που ξεκινά από αυτή με 1: αν είδαμε το τελευταίο 0 χρόνο 5 πίσω και μας έρθει 1 πάει να πει πως έχουμε μόλις συμπληρώσει μια πεντάδα γεμάτη με 1. Άρα δεν υπάρχει λόγος να συνεχίσουμε γιατί, ό,τι και να δούμε από δω και πέρα, η λέξη πρέπει να απορριφθεί.

Έυκολα μπορούμε τώρα να ελέγξουμε ότι οι διάφορες μεταβάσεις στο σχήμα 7.5 είναι φτιαγμένες ακριβώς ώστε ακολουθώντας αυτές να διατηρείται το νόημα της κάθε κατάστασης, και άρα το αυτόματο δουλεύει. Αν, για παράδειγμα, βρισκόμαστε σε μια οποιαδήποτε από τις καταστάσεις $A,\ldots,E$ και διαβάσουμε 0 πρέπει να μεταβούμε στην κατάσταση $A$ αφού μετά τη μετάβασή μας θα έχουμε διαβάσει 0 ακριβώς χρόνο 1 πριν, και αυτό είναι το νόημα της κατάστασης $A$.

Άσκηση 7.10   Κατασκευάστε ένα DFA που αναγνωρίζει εκείνες τις λέξεις πάνω από το $\Sigma = {\left\{{0,1}\right\}}$ που έχουν μήκος τουλάχιστον 5 και το 5ο γράμμα τους από τα αριστερά είναι 1.

Άσκηση 7.11   Κατασκευάστε ένα DFA που αναγνωρίζει εκείνες τις λέξεις πάνω από το $\Sigma = {\left\{{0,1}\right\}}$ που έχουν μήκος τουλάχιστον 5 και το 5ο γράμμα τους από τα δεξιά είναι 1.

Άσκηση 7.12   $L$ είναι η γλώσσα εκείνων των λέξεων του ${\left\{{0,1}\right\}}^*$ που είναι τέτοιες ώστε, μετά το πρώτο 0 υπάρχουν τουλάχιστον δύο 0 σε κάθε πεντάδα διαδοχικών γραμμάτων της λέξης. Κατασκευάστε ένα DFA που αναγνωρίζει την $L$.

Άσκηση 7.13   Κατασκευάστε DFA για τις γλώσσες του ${\left\{{0,1}\right\}}^*$:

1. Λέξεις που τελειώνουν σε 00
2. Λέξεις που περιέχουν τρία διαδοχικά 0

Άσκηση 7.14   Κατασκευάστε DFA για τις γλώσσες

(α)

$00^*1^*1$, και

(β)

${\left\{{w\in{\left\{{a,b}\right\}}^*:    6 \mid A(w)+2B(w)}\right\}}$,

όπου $A(w)$, και $B(w)$ είναι το πλήθος των $a$ και των $b$ στη λέξη $w$ και $x\vert y$ σημαίνει ότι το $x$ διαιρεί το $y$.

Άσκηση 7.15   Αν $M$ είναι DFA δείξτε πώς να κατασκευάσετε ένα DFA για τη γλώσσα $\Sigma^* \setminus L(M)$ (το συμπλήρωμα της γλώσσας $L(M)$).