Next: 7.2 Ντετερμινιστικά Αυτόματα Up: 7. Τυπικές γλώσσες και Previous: 7. Τυπικές γλώσσες και Contents Index
Ο αριθμός ![]() λέγεται μήκος της λέξης
λέγεται μήκος της λέξης ![]() και συμβολίζεται
με
και συμβολίζεται
με
![]() .
.
Η κενή λέξη συμβολίζεται πάντα με το ![]() .
.
Με ![]() συμβολίζουμε το σύνολο όλων των λέξεων πάνω από το αλφάβητο
συμβολίζουμε το σύνολο όλων των λέξεων πάνω από το αλφάβητο
![]() .
.
 Το παρακάτω πρόγραμμα σε python τυπώνει όλες τις λέξεις με δεδομένο μήκος
πάνω από ένα δοσμένο αλφάβητο.
Το παρακάτω πρόγραμμα σε python τυπώνει όλες τις λέξεις με δεδομένο μήκος
πάνω από ένα δοσμένο αλφάβητο.
def words_of_length(S, k):
""" Return a list with all words over alphabet S of length k"""
if k==0:
return ['']
result = []
tails = words_of_length(S, k-1)
for first in S:
for t in tails:
result.append(first+t)
return result
S = ['a', 'b']
print words_of_length(S, 3)
SS = ['a', 'b', 'c']
print words_of_length(SS, 3)
print words_of_length(SS, 0)
Το αποτέλεσμα αυτού του προγράμματος είναι:
['aaa', 'aab', 'aba', 'abb', 'baa', 'bab', 'bba', 'bbb'] ['aaa', 'aab', 'aac', 'aba', 'abb', 'abc', 'aca', 'acb', 'acc', 'baa', 'bab', 'bac', 'bba', 'bbb', 'bbc', 'bca', 'bcb', 'bcc', 'caa', 'cab', 'cac', 'cba', 'cbb', 'cbc', 'cca', 'ccb', 'ccc'] ['']Βεβαιωθείτε ότι καταλαβαίνετε πώς δουλεύει και πειραματιστείτε με αυτό ορίζοντας μερικά δικά σας αλφάβητα. Τροποποιήστε το ώστε να τυπώνει όλες τις λέξεις μήκους μέχρι
Η γλώσσα ![]() είναι εκείνο το σύνολο από λέξεις του
είναι εκείνο το σύνολο από λέξεις του
![]() που αποτελούν
συντακτικά σωστά προγράμματα στη γλώσσα προγραμματισμού python.
Αν δεν είστε γνώστες της γλώσσας αυτής αλλά κάποιας άλλης, μπορείτε να ορίσετε
την αντίστοιχη γλώσσα.
Ένα πρόγραμμα λοιπόν δεν είναι τίποτε άλλο από μια λέξη σε ένα κατάλληλο
αλφάβητο.
Αν αυτό ξενίζει να θυμίσουμε ότι και οι χαρακτήρες αλλαγής γραμμής βρίσκονται
μέσα στο αλφάβητο, και άρα μια λέξη του
που αποτελούν
συντακτικά σωστά προγράμματα στη γλώσσα προγραμματισμού python.
Αν δεν είστε γνώστες της γλώσσας αυτής αλλά κάποιας άλλης, μπορείτε να ορίσετε
την αντίστοιχη γλώσσα.
Ένα πρόγραμμα λοιπόν δεν είναι τίποτε άλλο από μια λέξη σε ένα κατάλληλο
αλφάβητο.
Αν αυτό ξενίζει να θυμίσουμε ότι και οι χαρακτήρες αλλαγής γραμμής βρίσκονται
μέσα στο αλφάβητο, και άρα μια λέξη του ![]() μπορεί να περιέχει τα γράμματα
ενός ολόκληρου αρχείου κειμένου.
μπορεί να περιέχει τα γράμματα
ενός ολόκληρου αρχείου κειμένου.
Το ![]() είναι μια άπειρη γλώσσα αφού δεν υπάρχει άνω όριο στο μέγεθος
ενός συντακτικά σωστού προγράμματος, και άρα υπάρχουν άπειρα τέτοια.
είναι μια άπειρη γλώσσα αφού δεν υπάρχει άνω όριο στο μέγεθος
ενός συντακτικά σωστού προγράμματος, και άρα υπάρχουν άπειρα τέτοια.
Μια λέξη ![]() λέγεται πρόθεμα (prefix)
μιας λέξης
λέγεται πρόθεμα (prefix)
μιας λέξης ![]() αν υπάρχει λέξη
αν υπάρχει λέξη
![]() τ.ώ.
τ.ώ.
![]() .
Ομοίως η
.
Ομοίως η ![]() λέγεται επίθεμα (suffix)
της
λέγεται επίθεμα (suffix)
της ![]() αν υπάρχει
αν υπάρχει ![]() τ.ώ.
τ.ώ.
![]() .
.
Τέλος, μια λέξη ![]() λέγεται υπολέξη της
λέγεται υπολέξη της ![]() αν υπάρχουν λέξεις
αν υπάρχουν λέξεις ![]() , και
, και ![]() ,
ενδεχομένως κενές, τέτοιες ώστε
,
ενδεχομένως κενές, τέτοιες ώστε
![]() .
.
Είναι φανερό ότι μια λέξη με μήκος ![]() έχει ακριβώς
έχει ακριβώς ![]() προθέματα και άλλα
τόσα επιθέματα.
προθέματα και άλλα
τόσα επιθέματα.
Επίσης η συγκόλληση λέξεων είναι μια πράξη μη αντιμεταθετική, αφού, για παράδειγμα, αν
![]() και
και ![]() τότε
τότε
![]() .
.
Ορίζουμε επίσης
![]() και, για
και, για ![]() ,
,
![]() (συγκόλληση της
(συγκόλληση της ![]() με τον εαυτό της
με τον εαυτό της
![]() φορές).
φορές).
Τέλος ορίζουμε
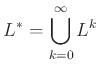
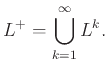
Mihalis Kolountzakis 2015-11-28