5.8 Ο αλγόριθμος Floyd-Warshall για εύρεση αποστάσεων πάνω σε γραφήματα

Εδώ θα περιγράψουμε ένα αλγόριθμο που βρίσκει όλες τις αποστάσεις ανάμεσα σε όλα τα ζευγάρια κορυφών, σε ένα γράφημα $G$ με (μη αρνητικά) βάρη στις ακμές του. Πρέπει να τονίσουμε ότι το πρόβλημα που λύνουμε εδώ αλγοριθμικά είναι το πρόβλημα των αποστάσεων από «οποιαδήποτε σε οποιαδήποτε» κορυφή. Στο τέλος του αλγορίθμου δηλ. θα μπορούμε να απαντήσουμε άμεσα (σε σταθερό χρόνο, όπως λέμε) σε κάθε ερώτημα «ποια είναι η απόσταση ανάμεσα στις κορυφές $i$ και $j$ του γραφήματος;».

Αν δε μας ενδιέφερε αυτή η γενικότητα αλλά θέλαμε, π.χ., να γνωρίζουμε, μετά το πέρας του αλγορίθμου, όλες τις αποστάσεις από την κορυφή $1$ προς όλες τις άλλες, τότε θα χρησιμοποιούσαμε διαφορετικό αλγόριθμο. Ο αλγόριθμος που δίνουμε σε αυτή την παράγραφο θα αποτελούσε «overkill» για ένα τέτοιο ερώτημα: υπολογίζει πολλά αδιάφορα πράγματα.

Θεωρούμε, ως συνήθως, το σύνολο κορυφών του γραφήματος να είναι το $[n] = {\left\{{1,2,\ldots,n}\right\}}$ και γράφουμε $w(i,j)$ για το βάρος της ακμής $(i,j)$ (το οποίο συμφωνούμε να θεωρούμε $+\infty$ αν η ακμή αυτή δεν υπάρχει).

Ο παρακάτω αλγόριθμος τροποποιεί σε κάθε επανάληψή του τον $n\times n$ πίνακα $A$ ο οποίος παίρνει αρχικές τιμές στο βήμα 1 και ενημερώνεται $n$ φορές στο βήμα 3.

Αλγόριθμος Floyd-Warshall

1. Θέτουμε $A^{(0)}_{ij} = w(i,j)$, για $i,j=1,\ldots,n$.
2. Επαναλαμβάνουμε για $k=1,2,\ldots,n$ το παρακάτω βήμα.
3. $A^{(k)}_{ij} = \min {\left\{{A^{(k-1)}_{ij}, A^{(k-1)}_{ik}+A^{(k-1)}_{kj}}\right\}}$, για $i,j=1,\ldots,n$.

Θεώρημα 5.4   Στο τέλος του προηγούμενου αλγορίθμου η απόσταση ανάμεσα στις κορυφές $i$ και $j$ είναι ίση με $A^{(n)}_{ij}$.

Απόδειξη. Θα δείξουμε με επαγωγή ως προς το $k$ ότι $A^{(k)}_{ij}$ ισούται με $L^{(k)}_{ij} =$ το μήκος του ελάχιστου μονοπατιού από το $i$ στο $j$ το οποίο όμως χρησιμοποιεί ενδιάμεσες κορυφές μόνο από το σύνολο ${\left\{{1,\ldots,k}\right\}}$.

Για $k=0$ το παραπάνω σύνολο είναι κενό και ο ισχυρισμός σημαίνει ότι $A^{(0)}_{ij}$ ισούται με το βάρος της πλευράς $(i,j)$ μια και το σύνολο των μονοπατιών από το $i$ στο $j$ που δε χρησιμοποιούν καμία ενδιάμεση κορυφή αποτελείται από την ακμή $(i,j)$ και μόνο. Άρα ο ισχυρισμός είναι αληθής για $k=0$.

Υποθέτουμε τώρα ότι ο ισχυρισμός ισχύει μέχρι και για $k-1$, θεωρούμε ένα ελάχιστο μονοπάτι από το $i$ στο $j$ που χρησιμοποιεί ενδιάμεσες κορυφές μόνο από το σύνολο ${\left\{{1,\ldots,k}\right\}}$, και ξεχωρίζουμε δύο περιπτώσεις.

(α)

Το ελάχιστο αυτό μονοπάτι δε χρησιμοποιεί την κορυφή $k$.

(β)

Χρησιμοποιεί την κορυφή $k$.

Στην πρώτη περίπτωση έχουμε φυσικά $L^{(k)}_{ij} = L^{(k-1)}_{ij}$.

Εστω ότι ισχύει το (β). Μπορούμε εύκολα να δείξουμε ότι όποιο και να είναι το ελάχιστο μονοπάτι από το $i$ στο $j$ περιέχει το $k$ ακριβώς μια φορά (αν το περιέχει δυο ή παραπάνω μπορούμε να το μικρύνουμε το μονοπάτι παραλείποντας ένα κομμάτι ανάμεσα σε δύο εμφανίσεις του $k$). Επίσης, το κομμάτι του μονοπατιού από το $i$ στο $k$ είναι ένα ελάχιστο μονοπάτι από το $i$ στο $k$ που χρησιμοποιεί ενδιάμεσες κορυφές από το σύνολο ${\left\{{1,\ldots,k-1}\right\}}$. Αρα το μήκος του είναι $L^{(k-1)}_{ik}$ και, ομοίως, το μήκος του μονοπατιού από το $k$ στο $j$ είναι $L^{(k-1)}_{kj}$. Το συνολικό μήκος του μονοπατιού είναι λοιπόν σ'αυτή την περίπτωση

$$L^{(k)}_{ij} = L^{(k-1)}_{ik} + L^{(k-1)}_{kj}.$$

Επίσης, σε κάθε περίπτωση, έχουμε τις ανισότητες

$$L^{(k)}_{ij} \le L^{(k-1)}_{ij} \kappa\alpha\iota \ L^{(k)}_{ij} \le L^{(k-1)}_{ik} + L^{(k-1)}_{kj},$$

η πρώτη από τον ορισμό του του συμβόλου $L$ και μόνο και η δεύτερη παρατηρώντας ότι μπορούμε να πάμε από το $i$ στο $j$ (με ενδιάμεσους από το $[k]$) ακολουθώντας πρώτα ένα ελάχιστο μονοπάτι από το $i$ στο $k$ και μετά ένα ελάχιστο μονοπάτι από το $k$ στο $j$ (με ενδιάμεσους από το $[k-1]$).

Από τα παραπάνω προκύπτει ότι

$$L^{(k)}_{ij} = \min{\left\{{L^{(k-1)}_{ij}, L^{(k-1)}_{ik} + L^{(k-1)}_{kj}}\right\}}$$

και άρα, από τον τρόπο υπολογισμού των πινάκων $A^{(k)}$, έχουμε $A^{(k)}_{ij} = L^{(k)}_{ij}$, για κάθε $i,j=1,\ldots,n$, $k=0,\ldots,n$. $\qedsymbol$

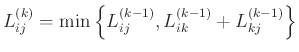
Μπορεί κανείς εύκολα να δεί ότι ο αλγόριθμος Floyd-Warshall που περιγράψαμε παίρνει περίπου $n^3$ υπολογιστικά βήματα για να τελειώσει.

Άσκηση 5.43   Πόσες πράξεις (προσθέσεις και πολλαπλασιασμούς) χρειάζεται ο αλγόριθμος Floyd-Warshall για να υπολογίσει το ζητούμενο; Πόσο χώρο (θέσεις για αριθμούς) χρειάζεται ο αλγόριθμος αυτός;

Άσκηση 5.44   Γράψτε ένα πρόγραμμα που θα υλοποιεί τον αλγόριθμο Floyd-Warshall και εφαρμόστε τον στο γράφημα του Σχήματος 5.28.