4.5 Επαναληπτικές ασκήσεις Κεφαλαίου

Άσκηση 4.24   Με πόσους τρόπους μπορούμε να μοιράσουμε 21 δαφορετικά βιβλία στα άτομα Α, Β και Γ, ούτως ώστε οι Α και Β μαζί να πάρουν διπλάσια βιβλία από τον Γ;

Άσκηση 4.25   Μια ομάδα 20 ατόμων θέλει να φτιάξει τρεις, ξένες μεταξύ τους, επιτροπές με 6, 5 και 4 άτομα η κάθε μία. (Μέσα σε κάθε επιτροπή δεν υπάρχουν χωριστά αξιώματα-τα μέλη τους είναι ισοδύναμα.) Με πόσους τρόπους μπορεί να γίνει αυτό;

Άσκηση 4.26   Υπολογίστε το άθροισμα

$$\sum_{k=1}^n k^2 {n \choose k}.$$

Άσκηση 4.27   Δείξτε ότι, για 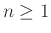$n\ge 1$ ισχύει

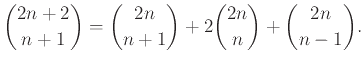$${2n+2 \choose n+1} = {2n \choose n+1} + 2{2n \choose n} + {2n \choose n-1}.$$ (4.9)