Next: 4.2 Πολυωνυμικοί συντελεστές Up: 4. Προχωρημένη απαρίθμηση Previous: 4. Προχωρημένη απαρίθμηση Contents Index
Ας συμβολίσουμε με ![]() το πλήθος των τρόπων με τους οποίους
μπορούμε να γράψουμε τον φυσικό αριθμό
το πλήθος των τρόπων με τους οποίους
μπορούμε να γράψουμε τον φυσικό αριθμό ![]() ως άθροισμα
ως άθροισμα ![]() μη αρνητικών ακεραίων
μη αρνητικών ακεραίων
![]() :
:
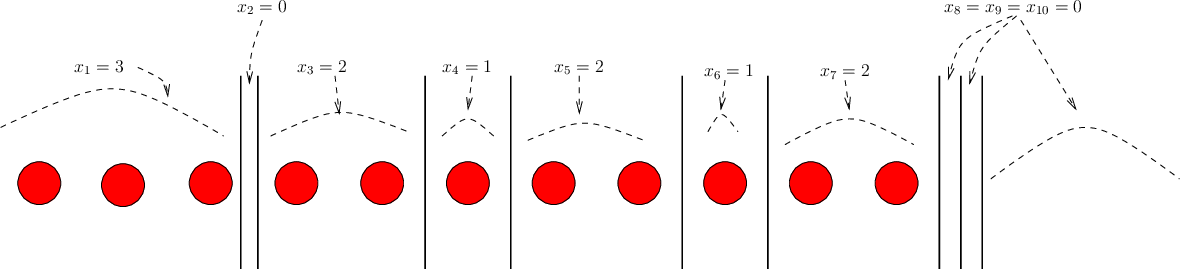
Η τιμή του ![]() βρίσκεται αν μετρήσουμε πόσες μπάλες υπάρχουν από το
βρίσκεται αν μετρήσουμε πόσες μπάλες υπάρχουν από το ![]() έως το πρώτο τοίχωμα, το
έως το πρώτο τοίχωμα, το ![]() αν μετρήσουμε τις μπάλες από το πρώτο έως το δεύτερο
τοίχωμα, κλπ. Τέλος το
αν μετρήσουμε τις μπάλες από το πρώτο έως το δεύτερο
τοίχωμα, κλπ. Τέλος το ![]() βρίσκεται αν μετρήσουμε τις μπάλες από το τελευταίο
(υπ' αριθμόν
βρίσκεται αν μετρήσουμε τις μπάλες από το τελευταίο
(υπ' αριθμόν ![]() ) τοίχωμα έως το
) τοίχωμα έως το ![]() .
.
Άρα, για να μετρήσουμε το πλήθος των διαμερίσεων ![]() αρκεί να μετρήσουμε
πόσα διαφορετικά σχήματα σαν και αυτό του Σχήματος 4.1
υπάρχουν, αφού είναι φανερό ότι σε κάθε τέτοιο σχήμα αντιστοιχεί και μια διαφορετική
διαμέριση, και αντίστροφα.
αρκεί να μετρήσουμε
πόσα διαφορετικά σχήματα σαν και αυτό του Σχήματος 4.1
υπάρχουν, αφού είναι φανερό ότι σε κάθε τέτοιο σχήμα αντιστοιχεί και μια διαφορετική
διαμέριση, και αντίστροφα.
Με ποια διαδικασία μπορούμε λοιπόν να κατασκευάσουμε μονοσήμαντα ένα τέτοιο σχήμα;
Το κάνουμε ως εξής: βάζουμε πρώτα στη σειρά ![]() αντικείμενα και κατόπιν
ονομάζουμε τα
αντικείμενα και κατόπιν
ονομάζουμε τα ![]() από αυτά μπάλες και τα υπόλοιπα
από αυτά μπάλες και τα υπόλοιπα ![]() τοιχώματα.
Αυτό μπορεί να γίνει ακριβώς με
τοιχώματα.
Αυτό μπορεί να γίνει ακριβώς με
![]() τρόπους.
Η δεύτερη ισότητα μέσα στο συμπέρασμα του Θεωρήματος 4.1
είναι απλή συνέπεια της ταυτότητας
τρόπους.
Η δεύτερη ισότητα μέσα στο συμπέρασμα του Θεωρήματος 4.1
είναι απλή συνέπεια της ταυτότητας
![]() (δείτε την Άσκηση 3.37).
(δείτε την Άσκηση 3.37).
![]()
Για παράδειγμα σύμφωνα με το Θεώρημα 4.1
ισχύει
![]() το οποίο συμφωνεί με την (4.1).
το οποίο συμφωνεί με την (4.1).
Πέρα από τη σημασία που έχει το ίδιο το πρόβλημα του
να μετρήσουμε το πλήθος των διαμερίσεων του ![]() σε
σε ![]() κομμάτια,
το ερώτημα αποκτά μεγαλύτερη σημασία γιατί είναι ένας ισοδύναμος
τρόπος του να ρωτήσουμε το εξής:
κομμάτια,
το ερώτημα αποκτά μεγαλύτερη σημασία γιατί είναι ένας ισοδύναμος
τρόπος του να ρωτήσουμε το εξής:
Με πόσους τρόπους μπορούμε να επιλέξουμεΈνας ισοδύναμος τρόπος να θέσουμε το ίδιο ερώτημα είναι ο ακόλουθος. Έχουμε ένα σάκο που έχει μέσααπό
στοιχεία όταν κάθε στοιχείο από τα
μπορεί να επιλεγεί ένα απεριόριστο αριθμό από φορές, και όταν δε μας ενδιαφέρει η σειρά των επιλεγέντων στοιχείων;
Παίρνουμε μια μπάλα από το σάκο και γράφουμε σ' ένα χαρτί τον αριθμό της. Έπειτα επανατοποθετούμε τη μπάλα στο σάκο.Στο τέλος παρατηρούμε τους
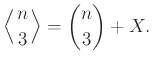
Ομοίως σκεπτόμενοι βρείτε τη διαφορά
![]() .
.
Στο τέλος αυτής της διαδικασίας επιλογής ![]() στοιχείων με επανάθεση
έχουμε στα χέρια μας
στοιχείων με επανάθεση
έχουμε στα χέρια μας ![]() αριθμούς, όχι κατ' ανάγκη διαφορετικούς μεταξύ τους,
κάθε ένας από τους οποίους ανήκει στο σύνολο
αριθμούς, όχι κατ' ανάγκη διαφορετικούς μεταξύ τους,
κάθε ένας από τους οποίους ανήκει στο σύνολο
![]() .
Έστω
.
Έστω ![]() ,
,
![]() , το πλήθος αυτών των αριθμών που είναι ίσοι με
, το πλήθος αυτών των αριθμών που είναι ίσοι με ![]() .
Επειδή δε μας ενδιαφέρει η σειρά που εμφανίζεται κάθε ένα από τα νούμερα
που επιλέγουμε, αλλά μόνο το πόσες φορές εμφανίζεται,
γίνεται φανερό ότι
.
Επειδή δε μας ενδιαφέρει η σειρά που εμφανίζεται κάθε ένα από τα νούμερα
που επιλέγουμε, αλλά μόνο το πόσες φορές εμφανίζεται,
γίνεται φανερό ότι
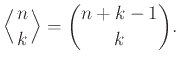
Ίδιο ερώτημα αν τα κουτιά δεν είναι αριθμημένα.
Με πόσους διαφορετικούς τρόπους μπορεί να έχουν συμβεί οι αποβιβάσεις των 8 ατόμων αν
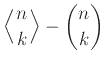
Το 1954 ο G. Gamow πρότεινε ότι δύο αλυσίδες DNA κωδικοποιούν το ίδιο αμινοξύ αν και μόνο αν περιέχουν τις ίδιες βάσεις ανεξαρτήτως σειράς. Οι αλυσίδες δηλ. ACC και CAC, αν και διαφορετικές, κωδικοποιούν το ίδιο αμινοξύ. Αν η υπόθεση του Gamow είναι σωστή πόσα διαφορετικά αμινοξέα κωδικοποιούνται με αλυσίδες DNA μήκους 3; Με λίγη σκέψη βλέπουμε ότι το πλήθος των διαφορετικών αμινοξέων είναι το ίδιο με το πλήθος των διαφορετικών συνδυασμών των τεσσάρων γραμμάτων A, C, G και T ανά τρία, με επανάθεση. Ο αριθμός αυτός είναι δηλ.
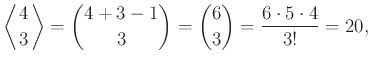
Ίδιο ερώτημα όταν και οι μπάλες είναι αριθμημένες.
Στο μοντέλο Bose-Einstein πόσες διαφορετικές καταστάσεις
του συστήματος υπάρχουν;
Αν θέσουμε ![]() ,
,
![]() , να είναι το πλήθος των σωματίων στο
ενεργειακό επίπεδο
, να είναι το πλήθος των σωματίων στο
ενεργειακό επίπεδο ![]() , τότε πρέπει απλά να διαλέξουμε τους
μη αρνητικούς ακεραίους
, τότε πρέπει απλά να διαλέξουμε τους
μη αρνητικούς ακεραίους ![]() ώστε να έχουν άθροισμα
ώστε να έχουν άθροισμα ![]() .
Δηλαδή το πλήθος καταστάσεων του συστήματος είναι ίσο με το πλήθος
των διαμερίσεων του
.
Δηλαδή το πλήθος καταστάσεων του συστήματος είναι ίσο με το πλήθος
των διαμερίσεων του ![]() σε
σε ![]() κομμάτια, δηλ.
κομμάτια, δηλ.
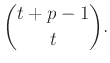
Mihalis Kolountzakis 2015-11-28