1.7 Σχέσεις ισοδυναμίας

Ορισμός 1.18   (Σχέση ισοδυναμίας) Ας είναι $X$ ένα σύνολο και $R$ μια σχέση από το $X$ στο $X$, δηλαδή $R\subset{X}\times{X}$. Η $R$ λέγεται σχέση ισοδυναμίας στο $X$ αν ισχύουν τα εξής:

1. $(x,x)\in{R}$, για κάθε $x\in{X}$ (Ανακλαστική ιδιότητα).
2. $(x,y)\in{R}\Rightarrow{(y,x)}\in{R}$ (Συμμετρική ιδιότητα).
3. $(x,y)\in{R} \& (y,z)\in{R}\Rightarrow{(x,z)} \in {R}$ (Μεταβατική ιδιότητα).

Από το 1 προκύπτει ότι, αν $R$ είναι σχέση ισοδυναμίας στο $X$ τότε,

$${\rm dom }{R} = {\rm range }{R} = X.$$

Oι περισσότερες σχέσεις ισοδυναμίας στα Μαθηματικά είναι οι λεγόμενες ισότητες. Χαρακτηριστική περίπτωση είναι η σχέση ισοδυναμίας που ορίζει την ισότητα στους ρητούς αριθμούς.

Παράδειγμα 1.15   Έστω ${{\mathbb{Q}}}=\{(a,b): a\in{{\mathbb{Z}}} \& b\in{{\mathbb{N}}}\}$. Ως συνήθως, κάθε ρητό αντί $(a,b)$ τον γράφουμε $\frac{a}{b}$. Ορίζουμε

$$\frac{a}{b}R\frac{c}{d}\Leftrightarrow{ad=cb}.$$

Εύκολα βλέπουμε ότι η ανωτέρω σχέση ικανοποιεί τον Ορισμό 1.18. Τα ισοδύναμα κλάσματα με αυτή την σχέση είναι εκείνα πού ονομάζουμε ίσα κλάσματα.

Παράδειγμα 1.16   Ας είναι $R\subset{{\mathbb{Z}}}\times{{\mathbb{Z}}}$, $R=\{(x,y)\in{{\mathbb{Z}}}: x-y$ διαιρείται με το 3 $\}$. Δηλαδή:

$$xRy\Leftrightarrow{x-y=3l}$$

για κάποιο $l\in{{\mathbb{Z}}}$.

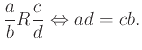
Εύκολα βλέπουμε ότι η σχέση αυτή είναι σχέση ισοδυναμίας (άσκηση). Λέγεται σχέση ισοδυναμίας modulo 3 στο ${{\mathbb{Z}}}$.

Ορισμός 1.19   (Κλάση ισοδυναμίας) Έστω $R$ σχέση ισοδυναμίας σε σύνολο $X$ και $x\in{X}$. Ορίζουμε κλάση ισοδυναμίας του $x$, και την συμβολίζουμε με $R(x)$, το σύνολο

$$R(x)=\{y\in{X}: x R y\}.$$

Παράδειγμα 1.17   Γιά την σχέση ισοδυναμίας του Παραδείγματος 1.15 έχουμε

$$R\left(\frac{2}{3}\right)={\left\{{\frac{2}{3},\frac{4}{6},\frac{6}{9},\ldots}\right\}}.$$

Παράδειγμα 1.18   Γιά τις κλάσεις ισοδυναμίας του Παραδείγματος 1.16 έχουμε τα παρακάτω (τις αποδείξεις τις αφήνουμε σαν άσκηση):

1. $R(1)={\left\{{k\in{{\mathbb{Z}}}: k=3l+1 \gamma\iota\alpha \kappa\alpha\pi o\iota o l\in{{\mathbb{Z}}}}\right\}}$.
2. $k\in{R(1)}\Rightarrow{R(k)}=R(1)$.
3. Οι διαφορετικές κλάσεις ισοδυναμίας είναι οι $R(0), R(1), R(2)$ και αποτελούν διαμέριση του ${{\mathbb{Z}}}$.

Οπως θα δούμε στο επόμενο θεώρημα οι σχέσεις ισοδυναμίας και οι διαμερίσεις είναι ταυτόσημες έννοιες: μπορεί κανείς να μιλήσει για μια διαμέριση ενός συνόλου μιλώντας για μια αντίστοιχη σχέση ισοδυναμίας που έχει τη διαμέριση αυτή ως σύνολο κλάσεων ισοδυναμίας. Ομοίως μπορεί κάποιος να μιλήσει για μια σχέση ισοδυναμίας περιγράφοντας απλά το ποια είναι η διαμέριση του συνόλου από τις κλάσεις ισοδυναμίας. Αυτό είναι το περιεχόμενο του επόμενου Θεωρήματος 1.2.

Θεώρημα 1.2   (Θεμελιώδες Θεώρημα των Σχέσεων Ισοδυναμίας) Αν $R$ είναι σχέση ισοδυναμίας σε ένα σύνολο $X$, τότε η οικογένεια των κλάσεων ισοδυναμίας $\{R(x)\}_{x\in{X}}$ είναι διαμέριση του $X$.

Αντίστροφα, αν η οικογένεια $\{X_{i}\}_{i\in{I}}$ είναι διαμέριση του $X$, τότε υπάρχει σχέση ισοδυναμίας $R$ τέτοια ώστε οι κλάσεις ισοδυναμίας της $R$ να είναι τα σύνολα της διαμέρισης.

Αφήνουμε την απόδειξη σαν άσκηση. Γιά το αντίστροφο να πούμε ότι η σχέση ισοδυναμίας ορίζεται ως εξής:

$${xRy}\Leftrightarrow{x,y\in{X_{i}}} \gamma\iota\alpha \kappa\alpha\pi o\iota o i\in{I}.$$

Άσκηση 1.12   Ας είναι $A=\{a,b,c,d\}$. Για κάθε μια από τις διαμερίσεις

$$P_{1}=\{\{a\},\{b,c,d\}\},$$

$$P_{2}=\{\{a,b\},\{c,d\}\},$$

$$P_{3}=\{\{a\},\{b\},\{c\},\{d\}\}$$

του $A$, γράψτε την αντίστοιχη σχέση ισοδυναμίας που ορίζει στο σύνολο $A$.