Κεφάλαιο 8Λανθάνουσα Σημασιολογική Ανάλυση

Έστω $M$ ένας πίνακας που αποτελείται από $n$ γραμμές και $m$ στήλες και κάθε στοιχείο $M[i,j]$ του πίνακα είναι μία πραγματική τιμή. Εάν $n$ = $m$ τότε ο πίνακας καλείται τετραγωνικός. Ο πίνακας $M^T$ καλείται ανάστροφος (transpose) του πίνακα $M$, έχει διαστάσεις $m$ $\times$ $n$ και προκύπτει από τον $M$ μετατρέποντας τις γραμμές του $M$ σε στήλες (άρα οι στήλες γίνονται γραμμές). Ο πίνακας $M^{-1}$ καλείται αντίστροφος (inverse) του πίνακα $M$ και έχει την ιδιότητα ότι αν πολλαπλασιαστεί με τον πίνακα $M$ το αποτέλεσμα είναι ο μοναδιαίος πίνακας $I_n$. Πιο συγκεκριμένα:

Σημαντικό ρόλο στη Γραμμική Άλγεβρα παίζουν οι συμμετρικοί πίνακες. Ένας τετραγωνικός πίνακας $M$ διαστάσεων $n\times n$ καλείται συμμετρικός όταν το στοιχείο που βρίσκεται στην $i$-οστή γραμμή και την $j$-οστή στήλη ισούται με το στοιχείο που βρίσκεται στην $j$-οστή γραμμή και την $i$-οστή στήλη.

Το άθροισμα δύο πινάκων προκύπτει με άθροιση των στοιχείων που βρίσκονται στις ίδιες θέσεις και στους δύο πίνακες. Απαραίτητη προϋπόθεση είναι οι πίνακες να έχουν τις ίδιες διαστάσεις. Έστω οι πίνακες $A$, $B$ και $C=A+B$ διαστάσεων $m\times n$. Αν συμβολίσουμε με $A[i,j]$ ($B[i,j]$) το στοιχείο του πίνακα $A$ ($B$) που βρίσκεται στην $i$-οστή γραμμή και την $j$-οστή στήλη τότε $C[i,j]$ = $A[i,j]$ + $B[i,j]$, $1\le i\le m$, $1\le j\le n$. Ο πολλαπλασιασμός δύο πινάκων $A$ και $B$ είναι εφικτός αν ο αριθμός των στηλών του $A$ είναι ίσος με τον αριθμό των γραμμών του $B$. Έτσι, αν ο $A$ έχει διαστάσεις $m$ $\times$ $n$ και ο $B$ έχει διαστάσεις $n$ $\times$ $k$ τότε ο πίνακας $C$ = $A$ $\cdot$ $B$ έχει διαστάσεις $m$ $\times$ $k$. Θυμίζουμε στον αναγνώστη ότι το στοιχείο στη γραμμή $i$ και στη στήλη $j$ του τελικού πίνακα ισούται με το άθροισμα των γινομένων των στοιχείων της $i$-οστής γραμμής και της $j$-οστής στήλης, όπως δίνεται παρακάτω:

Οι γραμμές και οι στήλες ενός πίνακα $M$ μπορούν να θεωρηθούν ως διανύσματα. Σε πολλές περιπτώσεις μας ενδιαφέρει να εξετάσουμε τη σχέση που έχουν δύο διανύσματα. Μία από αυτές τις σχέσεις είναι η γραμμική ανεξαρτησία.

Έστω $M$ ένας τετραγωνικός πίνακας διαστάσεων $n$ $\times$ $n$. Η τιμή $\lambda$ καλείται ιδιοτιμή (eigenvalue) του $M$ εάν υπάρχει ένα μή μηδενικό διάνυσμα $\overrightarrow{v}$ έτσι ώστε να ισχύει η ακόλουθη σχέση:

Στην περίπτωση αυτή, το διάνυσμα $v$⁶⁶Για λόγους απλούστευσης στη συνέχεια το διάνυσμα $\overrightarrow{v}$ θα αναγράφεται χωρίς το βέλος, δηλαδή $v$. καλείται ιδιοδιάνυσμα (eigenvector) του $M$. Παρατηρήστε ότι ενδεχομένως να υπάρχουν πολλά διανύσματα $v$ και πολλές τιμές $\lambda$ που να ικανοποιούν τη σχέση 8.5. Η γεωμετρική ερμηνεία της εξίσωσης 8.5 έχει ως εξής: εφαρμόζοντας το μετασχηματισμό που προσδιορίζεται από τον πίνακα $M$ στο ιδιοδιάνυσμα $v$ έχει ως αποτέλεσμα είτε την αλλαγή του μέτρου του $v$ είτε την αλλαγή της φοράς του $v$ είτε και τα δύο. Σε καμία όμως περίπτωση δε μεταβάλεται η διεύθυνση του $v$. Η μεταβολή του μέτρου ή της φοράς καθορίζεται από τις ιδιοτιμές του $M$. Επομένως, τα ιδιοδιανύσματα του $M$ έχουν μία ιδιαίτερη σημασία, και για το λόγο αυτό χαρακτηρίζουν τον πίνακα $M$. Η εξίσωση 8.5 μπορεί να γραφεί και ως εξής:

όπου $I_n$ είναι ο μοναδιαίος πίνακας διαστάσεων $n$ $\times$ $n$.

Για να εντοπιστούν οι ιδιοτιμές και τα ιδιοδιανύσματα του πίνακα $M$ θα πρέπει να επιλυθούν μερικά συστήματα εξισώσεων. Ας δούμε με ποιον τρόπο μπορεί να γίνει αυτό. Σύμφωνα με γνωστό θεώρημα της Γραμμικής Άλγεβρας, οι τιμές $\lambda$ που ικανοποιούν τη σχέση 8.6 είναι αυτές για τις οποίες ο πίνακας $M-\lambda \cdot I_n$ γίνεται μη-αντιστρέψιμος. Ένας πίνακας είναι μη-αντιστρέψιμος όταν η ορίζουσά του είναι μηδενική. Στην περίπτωση αυτή ο πίνακας καλείται επίσης και ιδιάζων (singular). Επομένως, για να εντοπιστούν οι ιδιοτιμές του πίνακα $M$ αρκεί να λυθεί το σύστημα εξισώσεων που περιγράφεται από την παρακάτω σχέση, που είναι γνωστή και ως χαρακτηριστική εξίσωση του πίνακα $M$:

Ο προσδιορισμός των ιδιοτιμών αποτελεί το πρώτο βήμα για την εύρεση των ιδιοδιανυσμάτων του πίνακα. Ωστόσο, για κάθε ιδιοτιμή υπάρχει ένα άπειρος αριθμός ιδιοδιανυσμάτων, όπως προκύπτει από την επίλυση του συστήματος εξισώσεων 8.6, όπου $\lambda$ είναι η εκάστοτε ιδιοτιμή που χρησιμοποιείται. Το σύνολο των ιδιοδιανυσμάτων που αντιστοιχούν σε μία ιδιοτιμή καλείται ιδιοχώρος (eigenspace). Ο αριθμός των διαστάσεων του ιδιοχώρου που αντιστοιχεί στην ιδιοτιμή $\lambda$ εξαρτάται από το πόσες εμφανίζεται το $\lambda$ ως ιδιοτιμή. Για παράδειγμα, εάν μία ιδιοτιμή εμφανίζεται δύο φορές τότε ο αντίστοιχος ιδιοχώρος είναι δισδιάστατος.

Τονίζεται ακόμη μία φορά, ότι υπάρχουν άπειρα ιδιοδιανύσματα που αντιστοιχούν στην ίδια ιδιοτιμή. Ωστόσο, μία από τις βασικές ιδιότητες αναφέρει ότι τα ιδιοδιανύσματα που αντιστοιχούν σε διαφορετικές ιδιοτιμές είναι γραμμικά ανεξάρτητα μεταξύ τους και επομένως, κανένα δεν μπορεί να εκφραστεί ως γραμμικός συνδυασμός των υπολοίπων, κάτι που δηλώνει τη σημαντική πληροφορία την οποία καταγράφουν. Είναι γνωστό από τη θεωρία της Γραμμικής Άλγεβρας (π.χ., [36]) ότι ένα σύνολο διανυσμάτων είναι γραμμικά ανεξάρτητα αν ο πίνακας που σχηματίζεται θέτοντας ως στήλες τα διανύσματα έχει μη μηδενική ορίζουσα. Σύμφωνα με το Παράδειγμα 8.3, τα δύο ιδιοδιανύσματα που προέκευψαν βασίζονται σε διαφορετικές ιδιοτιμές και επομένως θα πρέπει να είναι γραμμικά ανεξάρτητα. Πράγματι, η ορίζουσα του πίνακα που σχηματίζεται θεωρώντας το κάθε διάνυσμα ως στήλη του πίνακα είναι:

και επομένως μπορούμε να συμπεράνουμε ότι τα δύο ιδιοδιανύσματα είναι γραμμικά ανεξάρτητα.

Αν ο πίνακας $M$ διαστάσεων $n\times n$ είναι συμμετρικός, τότε έχει ακριβώς $n$ ιδιοτιμές όχι κατ’ ανάγκη διαφορετικές μεταξύ τους. Επίσης, δύο ιδιοδιανύσματα που αντιστοιχούν σε διαφορετικές ιδιοτιμές είναι μεταξύ τους ορθοκανονικά (κάθετα), επομένως το εσωτερικό γινόμενό τους ισούται με μηδέν.

Μερικές φορές μας ενδιαφέρει να κρατήσουμε μοναδιαία διανύσματα (unit vectors), τα οποία έχουν μέτρο τη μονάδα. Το μέτρο ενός διανύσματος $v$ στις $n$ διαστάσεις ορίζεται ως εξής:

όπου $x_i$, $1\le i\le n$ είναι οι συντεταγμένες του διανύσματος. Για να μετατρέψουμε ένα διάνυσμα $v$ σε μοναδιαίο αρκεί να διαιρέσουμε όλες τις συντεταγμένες του με το μέτρο του. Συμβολίζουμε με $\overline{v}$ το μοναδιαίο διάνυσμα που αντιστοιχεί στο διάνυσμα $v$. Ένα μοναδιαίο διάνυσμα μας δίνει πληροφορία για τη διεύθυνση στην οποία δείχνει.

Πολλές φορές, οι ιδιοτιμές και τα ιδιοδιανύσματα ενός πίνακα $M$ μπορούν να απεικονιστούν με τη βοήθεια της διαδικασίας της διαγωνιοποίησης (diagonalization), με την οποία ο πίνακας $M$ γράφεται ως γινόμενο τριών πινάκων ως εξής:

όπου $M$ είναι ένας πραγματικός πίνακας $n\times n$, $D$ είναι ένας διαγώνιος πίνακας $n\times n$ που περιέχει τις ιδιοτιμές του $M$ και $P$ είναι ένας τετραγωνικός πίνακας $n\times n$ του οποίου οι στήλες αποτελούν τα ιδιοδιανύσματα του $M$. Το επόμενο βασικό θεώρημα συνδέει την διαγωνιοποίηση με τον αριθμό των ιδιοδιανυσμάτων.

Μία από τις εφαρμογές που έχει η διαγωνιοποίηση ενός πίνακα $M$ είναι ο γρήγορος υπολογισμός των πινάκων $M^k$, $k\ge 1$. Μπορεί να αποδειχθεί ότι $M^k$ = $P\cdot D^k\cdot P^{-1}$, και εφόσον ο πίνακας $D^k$ υπολογίζεται πολύ εύκολα, το κόστος υπολογισμού του $M^k$ μειώνεται δραστικά.

Έως τώρα συναντήσαμε την έννοια του διαγωνιοποιήσιμου πίνακα. Ας δούμε τώρα πότε ένας πίνακας είναι ορθοκανονικά διαγωνιοποιήσιμος.

Επομένως, η ύπαρξη ενός ορθοκανονικού πίνακα $P$ στον παραπάνω ορισμό συνεπάγεται την ύπαρξη $n$ ορθοκανονικών ιδιοδιανσυμάτων. Έστω τώρα ότι ο πίνακας $M$ είναι συμμετρικός (άρα και τετραγωνικός). Υπάρχει κάποια ιδιαιτερότητα σε σχέση με τη διαγωνιοποίηση; Η απάντηση είναι ναι, και επαληθεύεται από την ακόλουθη συζήτηση. Προηγουμένως, μελετήσαμε την έννοια της διαγωνιοποίησης. Ας δούμε το συμβαίνει όταν ο πίνακας είναι συμμετρικός. Από το Θεώρημα 8.1 γνωρίζουμε ότι δύο ιδιοδιανύσματα που αντιστοιχούν σε διαφορετικές ιδιοτιμές είναι ορθοκανονικά μεταξύ τους αν ο πίνακας είναι συμμετρικός. Ειδικά για τους συμμετρικούς πίνακες ισχύει το ακόλουθο:

Το προηγούμενο θεώρημα είναι πολύ σημαντικό διότι μας εξασφαλίζει μία ισοδυναμία μεταξύ της διαγωνιοποιησιμότητας ενός πίνακα και της συμμετρίας συτού. Επομένως, η συμμετρία του πίνακα $M$ διαστάσεων $n\times n$ συνεπάγεται την ύπαρξη ενός ορθοκανονικού πίνακα $P$ έτσι ώστε $M$ = $P\cdot D\cdot P^T$, και το αντίστροφο. Σε περίπτωση που ο αριθμός των διακριτών ιδιοτιμών είναι ακριβώς $n$, τότε ο προσδιορισμός του πίνακα $P$ είναι πολύ απλή υπόθεση (τα $n$ ορθοκανονικά ιδιοσιανύσματα γίνονται οι στήλες του $P$). Διαφορετικά, θα πρέπει να εκτελεστούν κάποιες επιπλέον πράξεις ώστε να εντοπιστούν όλα τα ορθοκανονικά διανύσματα που θα αποτελέσουν τις στήλες του $P$. Για παράδειγμα, εάν μία ιδιοτιμή είναι διπλή (είναι δύο φορές ρίζα του χαρακτηριστικού πολυωνύμου) τότε πρέπει να εντοπιστούν δύο ορθοκανονικά διανύσματα για το συγκεκριμένο ιδιοχώρο. Εάν η ιδιοτιμή είναι τριπλή, θα πρέπει να εντοπιστούν τρία ορθοκανονικά διανύσματα του ιδιοχώρου. Ο πίνακας $P$ κατασκευάζεται από τα διανύσματα που έχουν εντοπιστεί σύμφωνα με την προηγούμενη μεθοδολογία. Άρα, σε κάθε περίπτωση, ανεξάρτητα από το αν οι ιδιοτιμές του πίνακα $M$ εμφανίζονται μία η περισσότερες φορές, η κατασκευή του ορθοκανονικού πίνακα $P$ είναι πάντα εφικτή.

Η διάσπαση ενός πίνακα $M$ σε γινόμενο τριών πινάκων χρησιμοποιώντας τη μέθοδο της διαγωνιοποίησης δεν είναι πάντοτε εφικτή, και εξαρτάται από τα χαρακτηριστικά του πίνακα $M$. Ωστόσο, υπάρχει μία μέθοδος διάσπασης σύμφωνα με την οποία ένας οποιοσδήποτε πίνακας $\mathrm{{\rm M}}$ με διαστάσεις $m\times n$ μπορεί να εκφραστεί ως γινόμενο τριών πινάκων:

όπου, $S$ είναι ένας διαγώνιος πίνακας $m\times n$ που περιέχει στην κύρια διαγώνιο τις ιδιάζουσες τιμές (singular values) του πίνακα $M$ σε φθίνουσα διάταξη, $U$ είναι ένας ορθοκανονικός πίνακας με διαστάσεις $m\times m$ και $V$ είναι ένας ορθοκανονικός πίνακας $n\times n$. Η διάσπαση αυτή καλείται επίσης και παραγοντοποίηση ιδιαζουσών τιμών (singular value decomposition). Οι ιδιάζουσες τιμές του πίνακα $M$ προκύπτουν από τις ιδιοτιμές του πίνακα $M^T\cdot M$. Πιο συγκεκριμένα, για κάθε ιδιοτιμή $\lambda$ του πίνακα $M^T\cdot M$ προκύπτει η ιδιάζουσα τιμή $\sqrt{\lambda }$.

Ο πίνακας $S$, όπως έχει αναφερθεί, περιέχει τις ιδιάζουσες τιμές του $M$ (που προκύπτουν από τις ιδιοτιμές του $M^T\cdot M$) στην κύρια διαγώνιο. Οι ιδιάζουσες τιμές ενός πίνακα έχουν παρόμοια φυσική σημασία με αυτή των ιδιοτιμών. Αν ο πίνακας $M$ είναι συμμετρικός, οι απόλυτες τιμές των ιδιοτιμών εκφράζουν το μέγεθος της συρρίκνωσης ή της επέκτασης των ιδιοδιανυσμάτων. Έστω $\lambda$ μία ιδιοτιμή του $M$ και $v$ το μοναδιαίο ιδιοδιάνυσμα⁷⁷Για τη συνέχεια δε θα χρησιμοποιείται ο συμβολισμός $\overline{v}$ για να δηλώσει μοναδιαίο διάνυσμα. Θα υπάρχει ειδική αναφορά στο κείμενο αν κάποιο διάνυσμα είναι μοναδιαίο ή όχι. που αντιστοιχεί στην ιδιοτιμή $\lambda$.

Ισχύει ότι: $M\cdot v$ = $\lambda \cdot v$ = $|\lambda |\cdot v$ = $|\lambda |$ (αφού το $v$ είναι μοναδιαίο και επομένως το μέτρο του ισούται με τη μονάδα). Έστω ${\lambda }_k$ η ιδιοτιμή του πίνακα $M$ με τη μεγαλύτερη απόλυτη τιμή και $v_k$ το μοναδιαίο ιδιοδιάνυσμα που αντιστοιχεί στην ${\lambda }_k$. Τότε, το $v_k$ προσδιορίζει τη διεύθυνση ως προς την οποία η επίδραση του $M$ μεγιστοποιείται. Αυτό συμβαίνει διότι η ποσότητα $M\cdot v$ μεγιστοποιείται όταν θέσουμε $\lambda$ = ${\lambda }_k$ και $v$ = $v_k$. Αντικαθιστώντας τις τιμές αυτές έχουμε:

Έστω $M$ πίνακας διαστάσεων $n\times m$. Ο πίνακας $M^T\cdot M$ είναι συμμετρικός και επομένως είναι ορθοκανονικά διαγωνιοποιήσιμος σύμφωνα με το Θεώρημα 8.3. Άρα, μπορούμε να βρούμε $n$ ορθοκανονικά μοναδιαία ιδιοδιανύσματα $v_1^{\prime },v_2^{\prime },\mathrm{\dots },v_n^{\prime }$ που αντιστοιχούν στις $n$ ιδιοτιμές ${\lambda }_1^{\prime },{\lambda }_2^{\prime },\mathrm{\dots },{\lambda }_n^{\prime }$. Για κάθε ιδιοτιμή ${\lambda }_i^{\prime }$ και ιδιοδιάνυσμα $v_i^{\prime }$ (που αντιστοιχεί στην ${\lambda }_i^{\prime }$) ισχύει ότι:

Από την παραπάνω σχέση προκύπτει ότι οι ιδιοτιμές του πίνακα $M^T\cdot M$ δεν μπορεί να είναι αρνητικοί αριθμοί, αφού ισχύει ότι ${M\cdot v_i^{\prime }}^2\ge 0$. Για κάθε ιδιοτιμή ${\lambda }_i^{\prime }$ του πίνακα $M^T\cdot M$ υπάρχει μία ιδιάζουσα τιμή ${\sigma }_i$ = $\sqrt{{\lambda }_i^{\prime }}$. Με βάση την προηγούμενη σχέση, η ιδιάζουσα τιμή ${\sigma }_i$ ισούται με το μέτρο του γινομένου $M\cdot v_i^{\prime }$. Έστω τώρα ${\sigma }_k$ η μεγαλύτερη ιδιάζουσα τιμή του $M$, που προφανώς αντιστοιχεί στη μεγαλύτερη ιδιοτιμή του πίνακα $M^T\cdot M$, και $v_k^{\prime }$ το σντίστοιχο μοναδιαίο ιδιοδιάνυσμα. Σύμφωνα με την προηγούμενη συζήτηση ισχύει η ακόλουθη σχέση:

Η ομοιότητα των σχέσεων 8.36 και 8.37 είναι εμφανής. Ωστόσο, η 8.36 δείχνει τη σχέση του πίνακα $M$ με τις ιδιοτιμές και τα ιδιοδιανύσματά του, ενώ η 8.37 συσχετίζει τον πίνακα $M$ με τις ιδιοτιμές και τα ιδιοδιανύσματα του πίνακα $M^T\cdot M$. Η μέθοδος SVD στηρίζεται ακριβώς σε αυτήν την παρατήρηση.

Ας εξετάσουμε τώρα πιο προσεκτικά τις ιδιότητες των πινάκων $U$, $S$ και $V$ της σχέσης 8.32. Θα ξεκινήσουμε από τον πίνακα $S$ για τον οποίο γνωρίζουμε ότι είναι διαγώνιος και περιέχει τις ιδιάζουσες τιμές του $M$ σε φθίνουσα διάταξη. Το ακόλουθο θεώρημα συνδέει το βαθμό του πίνακα με το πλήθος των μη μηδενικών ιδιαζουσών τιμών.

Επομένως, αναμένουμε ότι ο αριθμός των μη μηδενικών στοιχείων στην κύρια διαγώνιο του πίνακα $S$ είναι ίσος με το βαθμό του πίνακα $M$, δηλαδή με το μέγιστο αριθμό των γραμμικά ανεξάρτητων γραμμών. Ας δούμε τι συμβαίνει με τους πίνακες $U$ και $V$. Οι στήλες του πίνακα $U$ καλούνται αριστερά ιδιάζοντα διανύσματα (left singular vectors) και οι στήλες του $V$ ονομάζονται δεξιά ιδιάζοντα διανύσματα (right singular vectors). Πιο συγκεκριμένα, έστω $v_1$, …, $v_r$ είναι τα μοναδιαία ιδιοδιανύσματα του πίνακα $M^T\cdot M$ και ${\lambda }_1$, …, ${\lambda }_r$ οι αντίστοιχες ιδιοτιμές, όπου ${\lambda }_1$ $\ge$ ${\lambda }_2$ $\ge$ … $\ge$ ${\lambda }_r$. Από κάθε ιδιοτιμή του $M^T\cdot M$ προκύπτει μία ιδιάζουσα τιμή του $M$: ${\sigma }_i$ = $\sqrt{{\lambda }_i}$, $1\le i\le r$. Προφανώς ισχύει ότι: ${\sigma }_1$ $\ge$ ${\sigma }_2$ $\ge$ … $\ge$ ${\sigma }_r$.

Αφού ο βαθμός του $M$ είναι $r$ ισχύει ότι $r\le \min \{n,m\}$. Εφόσον τα διανύσματα $v_1$, …, $v_r$ είναι ορθοκανονικά, τα διανύσματα $M\cdot v_1$, …, $M\cdot v_r$ είναι επίσης ορθοκανονικά, και μάλιστα σύμφωνα με τη θεωρία, αποτελούν βάση του χώρου που παράγεται από τις στήλες του πίνακα $M$. Για κάθε διάνυσμα $v_i$ όπου $1\le i\le r$ ορίζουμε το διάνυσμα $u_i$ σύμφωνα με τον ακόλουθο τύπο:

Η παραπάνω σχέση δηλώνει ότι και τα διανύσματα $u_i$, $1\le i\le r$ είναι ορθοκανονικά και αποτελούν επίσης μία βάση του χώρου που παράγεται από τις στήλες του πίνακα $M$. Στη συνέχεια, επεκτείνουμε το σύνολο $\{u_1,\mathrm{\dots },u_r\}$ στο σύνολο $\{u_1,\mathrm{\dots },u_n\}$ και το σύνολο $\{v_1,\mathrm{\dots },v_r\}$ στο σύνολο $\{v_1,\mathrm{\dots },v_m\}$ έτσι ώστε τα $u_i$ να αποτελούν βάση του χώρου ${\mathrm{\Re }}^n$ και τα $v_i$ να αποτελούν βάση του χώρου ${\mathrm{\Re }}^m$. Στη συνέχεια κατασκευάζουμε τους ορθοκανονικούς πίνακες $U$ και $V$ που περιέχουν ως στήλες τα ορθοκανονικά διανύσματα $u_i$ και $v_i$ αντίστοιχα. Θα δείξουμε τώρα ότι $MV=US$.

Από τις σχέσεις 8.39 και 8.40 είναι προφανές ότι $MV$ = $US$. Ο πίνακας $V$ είναι ορθοκανονικός και επομένως $V^{-1}$ = $V^T$. Επομένως, πολλαπλασιάζοντας τα δύο μέλη με $V^T$ παίρνουμε ότι $M=US{V}^T$. Η παραπάνω μεθοδολογία μας επιτρέπει να προσδιορίσουμε τους πίνακες $U$, $S$ και $V$ έτσι ώστε η παραγοντοποίηση ιδιαζουσών τιμών να είναι πάντοτε εφικτή για οποιονδήποτε πίνακα $M$, ανεξαρτήτως διαστάσεων.

Ας εξετάσουμε στη συνέχεια μία πολύ σημαντική ιδιότητα της παραγοντοποίησης SVD. Όπως έχει αναφερθεί, αν ο πίνακας $M$ έχει διαστάσεις $m\times n$, τότε ο πίνακας $U$ είναι $m\times m$, ο $S$ είναι $m\times n$ και ο $V$ είναι $n\times n$. Επίσης, έχουμε δει ότι ο αριθμός των μη μηδενικών ιδιαζουσών τιμών του $M$ (που βρίσκονται στην κύρια διαγώνιο του $S$), ισούται με το βαθμό του πίνακα $M$. Έστω τώρα ότι εκτελούμε τις ακόλουθες ενέργειες επιλέγοντας έναν ακέραιο αριθμό $k\le r$:

• •

  διατηρούμε τις $k$ μεγαλύτερες ιδιάζουσες τιμές του $M$ και θέτουμε τις υπόλοιπες $r-k$ ίσες με μηδέν στον πίνακα $S$,

• •

  διατηρούμε τις πρώτες $k$ στήλες του πίνακα $U$ και θέτουμε τις υπόλοιπες $n-r$ στήλες σε μηδέν, και τέλος

• •

  διατηρούμε τις πρώτες $k$ γραμμές του πίνακα $V^T$ και θέτουμε τις υπόλοιπες $m-r$ στήλες σε μηδέν.

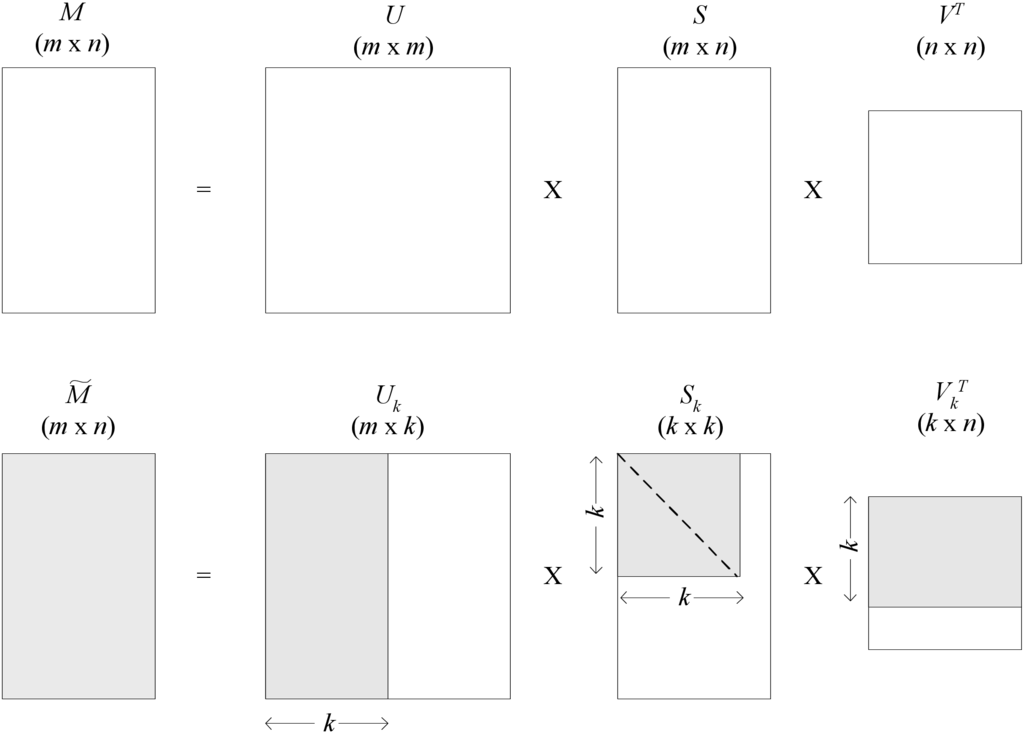
Η παραπάνω διαδικασία απεικονίζεται στο Σχήμα 8.1. Εφόσον ισχύει ότι $k\le r$ και $r\le \min \{n,m\}$ τότε προφανώς οι ποσότητες $r-k$, $n-k$ και $m-k$ θα είναι πάντοτε θετικές ή μηδέν. Το αποτέλεσμα των παραπάνω ενεργειών είναι να προκύψουν τρεις νέοι πίνακες, οι $U_k$, $S_k$ και $V_k$, διαστάσεων $m\times k$, $k\times k$ και $k\times n$ αντίστοιχα. Άρα, πολλαπλασιάζοντας τους τρεις πίνακες προκύπτει ο πίνακας $\tilde{M}$:

Ο πίνακας $\tilde{M}$ έχει διαστάσεις $m\times n$ (όπως και ο $M$). Ωστόσο, ο βαθμός του πίνακα $\tilde{M}$ είναι $k$, ενώ του $M$ είναι $r$, όπου $k\le r$. Τι σχέση έχουν όμως οι πίνακες $\tilde{M}$ και $M$; Εάν διατηρήσουμε όλες τις μη μηδενικές ιδιάζουσες τιμές του $M$, τότε προφανώς $\tilde{M}$ = $M$. Η διατήρηση όμως μερικών μόνο ($k$) ιδιαζουσών τιμών οδηγεί στην κατασκευή ενός πίνακα $\tilde{M}$ ο οποίος έχει τη μικρότερη δυνατή απόσταση από τον $M$ με βάση τη νόρμα Frobenius ⁸⁸Ferdinand Georg Frobenius (26 Οκτωβρίου 1849 - 3 Αυγούστου 1917). Γερμανός μαθηματικός που έγινε γνωστός κυρίως για τη συνεισφορά του στις διαφορικές εξισώσεις και τη θεωρία ομάδων. Επίσης, ήταν ο πρώτος που έχει δώσει πλήρη απόδειξη του θεωρήματος Cayley-Hamilton., που ορίζεται ως εξής:

Η σημαντικότητα της παραγοντοποίησης SVD γίνεται περισσότερο προφανής εάν αναλύσουμε τη σχέση $M=U\cdot S\cdot V^T$. Αν εκφράσουμε την παραπάνω σχέση με τη μορφή αθροίσματος (με εφαρμογή του ορισμού του πολλαπλασιασμού πινάκων) έχουμε:

Κάθε γινόμενο $u_i\cdot v_i^T$ είναι ένας πίνακας $M_i$ διαστάσεων $m\times n$, όπως ακριβώς και ο $M$. Ο κάθε πίνακας $M_i$ συμμετέχει στη σύνθεση του πίνακα $M$ με κάποιο βάρος που προσδιορίζεται από την ιδιάζουσα τιμή ${\sigma }_i$. Εφόσον τα διανύσματα $u_i$ και $v_i^T$ είναι μοναδιαία, είναι προφανές ότι η επίδραση του πίνακα $M_i$ καθορίζεται από τον παράγοντα ${\sigma }_i$. Επομένως, όσο μεγαλύτερη η τιμή του ${\sigma }_i$ τόσο μεγαλύτερη και η συμμετοχή του $M_i$ στη σύνθεση του αρχικού πίνακα $M$. Εάν κρατήσουμε τις $k$ μεγαλύτερες ιδιάζουσες τιμές (και θέσουμε τις υπόλοιπες στο μηδέν) θα έχουμε μία προσέγγιση του πίνακα $M$ η ποιότητα της οποίας εξαρτάται από το $k$ και από τις τιμές ${\sigma }_1$ έως ${\sigma }_k$.

Στη βιβλιογραφία, πολλές φορές συναντούμε έναν ισοδύναμο ορισμό για την παραγοντοποίηση SVD, όπου οι πίνακας $U$, $S$ και $V^T$ έχουν διαστάσεις $m\times r$, $r\times r$ και $r\times n$ αντίστοιχα, όπου $r$ είναι ο βαθμός του πίνακα $M$. Η αναπαράσταση αυτή θεωρείται οικονομικότερη από πλευράς χώρου αποθήκευσης, καθώς για το βαθμό του πίνακα $M$ ισχύει ότι $r\le min\{m,n\}$, οπότε ο πίνακας $S$ δε χρειάζεται να έχει περισσότερες από $r$ γραμμές και στήλες, διότι τα στοιχεία στις θέσεις αυτές θα είναι μηδενικά. Αντίστοιχα, ο πίνακας $U$ δε χρειάζεται να έχει πάνω από $r$ στήλες και ο $V^T$ πάνω από $r$ γραμμές.