Κεφάλαιο 6 Καταστατικοί νόμοι
Στο παρόν κεφάλαιο εξετάζεται η κλασική θεωρία της πλαστικότητας, παρουσιάζονται στοιχεία της μη γραμμικής ανάλυσης και εξετάζονται μη γραμμικοί καταστατικοί νόμοι που βρίσκουν ευρεία εφαρμογή σε προβλήματα γεωτεχνικής μηχανικής.
Αρχικά εξετάζεται η περίπτωση της μονοδιάστατης πλαστικότητας (Ενότητα 6.1). Παρουσιάζεται η περίπτωση της ιδεατής μονοδιάστατης πλαστικότητας (Ενότητα 6.1.1), όπου παρουσιάζονται οι καταστατικές εξισώσεις (Ενότητα 6.1.1), ορίζεται η παραμένουσα παραμόρφωση (Ενότητα 6.1.1) και δίνονται οι συνθήκες αποφόρτισης/επαναφόρτισης (Ενότητα 6.1.1).
Στη συνέχεια παρουσιάζεται η επέκταση στην κρατυνόμενη πλαστικότητα (Ενότητα 6.1.2), όπου συμπληρωματικά ορίζεται και το συνεχές εφαπτομενικό ελαστοπλαστικό μέτρο (Ενότητα 6.1.2).
Ακολουθεί η επέκταση στην τρισδιάστατη πλαστικότητα (Ενότητα 6.2), όπου παρουσιάζονται οι καταστατικές εξισώσεις (Ενότητα 6.2.1), ορίζεται η μη αναστρέψιμη πλαστική απόκριση (Ενότητα 6.2.2), δίνεται η ερμηνεία των συμπληρωματικών συνθηκών Karush-Kuhn-Tucker (Ενότητα 6.2.3) και τέλος παρουσιάζεται το συνεχές εφαπτομενικό ελαστοπλαστικό μέτρο (Ενότητα 6.2.4).
Η τρισδιάστατη πλαστικότητα που εξετάστηκε μέχρι στιγμής αφορά κριτήρια διαρροής που περιγράφονται από μία και μοναδική επιφάνεια διαρροής. Στην Ενότητα 6.3 εξετάζεται η περίπτωση της πλαστικότητας που περιγράφεται από κριτήρια διαρροής που χαρακτηρίζονται από πολλαπλές επιφάνειες διαρροής. Δίνονται αρχικά οι καταστατικές εξισώσεις για αυτή την οικογένεια των κριτηρίων (Ενότητα 6.3.1) και περιγράφονται οι συνθήκες φόρτισης/αποφόρτισης (Ενότητα 6.3.2). Στη συνέχεια ορίζεται η απαίτηση συνέπειας (Ενότητα 6.3.3) και τέλος δίνεται το συνεχές εφαπτομενικό ελαστοπλαστικό μέτρο (Ενότητα 6.3.4).
Ακολουθεί η επισκόπηση και η επαναδιατύπωση της μεθόδου των πεπερασμένων στοιχείων στο πλαίσιο πλέον της μη γραμμικής ανάλυσης (Ενότητα 6.4). Δίνεται η ασθενής διατύπωση του προβλήματος συνοριακών τιμών (Ενότητα 6.4.1), ορίζεται η χωρική διακριτοποίηση και επαναδιατυπώνεται η μέθοδος των πεπερασμένων στοιχείων (Ενότητα 6.4.2). Πιο συγκεκριμένα, διατυπώνονται οι εξισώσεις σε βηματική μορφή (Ενότητα 6.4.3) και δίνονται μέθοδοι επίλυσης του (μη γραμμικού) προβλήματος (Ενότητα 6.5). Αυτές αφορούν τη μέθοδο Newton-Raphson (Ενότητα 6.5.1) και τον γενικό κανόνα του μέσου σημείου (Ενότητα 6.5.2).
Στη συνέχεια εξετάζεται πλέον η αριθμητική επίλυση του προβλήματος, αρχικά για την περίπτωση της μονοδιάστατης πλαστικότητας (Ενότητα 6.6). Παρουσιάζεται ο αλγόριθμος επιστροφής των τάσεων return-mapping (Ενότητα 6.6.1) και, πιο συγκεκριμένα, ορίζεται η δοκιμαστική (trial) ελαστική εντατική κατάσταση (Ενότητα 6.6.1), ελέγχεται η συνθήκη διαρροής (Ενότητα 6.6.1), διατυπώνεται ο αλγόριθμος επιστροφής (Ενότητα 6.6.1) και παρουσιάζεται το αλγοριθμικό (συνεπές) εφαπτομενικό μέτρο (Ενότητα 6.6.2).
Ακολουθεί η αριθμητική επίλυση του προβλήματος της πλαστικότητας πολλών διαστάσεων που αφορά όμως μία επιφάνεια διαρροής (Ενότητα 6.7). Παρουσιάζεται ομοίως ο αλγόριθμος επιστροφής των τάσεων return-mapping (Ενότητα 6.7.1) και, πιο συγκεκριμένα, ορίζεται η δοκιμαστική (trial) ελαστική εντατική κατάσταση (Ενότητα 6.7.1), ελέγχεται η συνθήκη διαρροής (Ενότητα 6.7.1), διατυπώνεται ο αλγόριθμος επιστροφής (Ενότητα 6.7.1) και παρουσιάζεται το αλγοριθμικό (συνεπές) εφαπτομενικό μέτρο (Ενότητα 6.7.2).
Τέλος παρουσιάζεται η αριθμητική επίλυση του προβλήματος της πλαστικότητας πολλών διαστάσεων που αφορά κριτήρια πολλαπλών επιφανειών (Ενότητα 6.8). Παρουσιάζεται και για αυτή την περίπτωση ο αλγόριθμος επιστροφής των τάσεων return-mapping (Ενότητα 6.8.1) και, πιο συγκεκριμένα, ορίζεται πάλι η δοκιμαστική (trial) ελαστική εντατική κατάσταση (Ενότητα 6.8.1), ελέγχεται η συνθήκη διαρροής (Ενότητα 6.8.1), διατυπώνεται ο αλγόριθμος επιστροφής (Ενότητα 6.8.1), προσδιορίζονται οι ενεργές επιφάνειες (Ενότητα 6.8.2) και παρουσιάζεται το αλγοριθμικό (συνεπές) εφαπτομενικό μέτρο (Ενότητα 6.8.3).
Στη συνέχεια εξετάζεται η εφαρμογή των παραπάνω σε τυπικά κριτήρια διαρροής της γεωτεχνικής μηχανικής. Παρουσιάζεται αρχικά η γραφική απεικόνιση των κριτηρίων διαρροής γενικά (Ενότητα 6.9) και στη συνέχεια εξετάζεται το κριτήριο διαρροής Tresca (Ενότητα 6.10). Στην Ενότητα 6.10.1 δίνεται η πλήρης περιγραφή του κριτηρίου, ενώ η εφαρμογή των μεθόδων της αριθμητικής ανάλυσης που αναπτύχθηκαν προηγουμένως δίνεται στην Ενότητα 6.10.2.
Ακολουθεί η παρουσίαση του κριτηρίου διαρροής Mohr-Coulomb (Ενότητα 6.11). Η περιγραφή του κριτηρίου δίνεται στην Ενότητα 6.11.1, ενώ η αριθμητική επίλυσή του στην Ενότητα 6.11.2.
Στο τέλος του κεφαλαίου παρατίθεται η σχετική βιβλιογραφία (Ενότητα 6.12).
6.1 Θεωρία μονοδιάστατης πλαστικότητας
Παρουσιάζεται η κλασική θεωρία της πλαστικότητας, ξεκινώντας αρχικά από τη μονοδιάστατη πλαστικότητα.
6.1.1 Ιδεατή πλαστικότητα
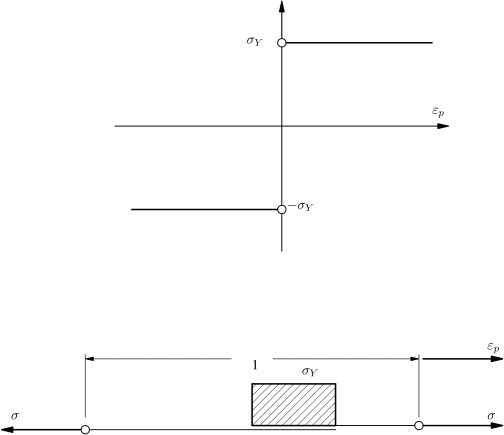
Εξετάζεται το μηχανικό ανάλογο μιας μονοδιάστατης συσκευής τριβής [8], το οποίο παρουσιάζεται στο Σχήμα 6.1.

Θεωρείται ότι η συσκευή καταλαμβάνει μοναδιαίο μήκος και εμβαδό και ότι αποτελείται από ένα ελατήριο με ελατηριακή σταθερά και ένα στοιχείο ολίσθησης με σταθερά . Έστω είναι η εφαρμοζόμενη τάση (δύναμη) και η συνολική παραμόρφωση (μεταβολή μήκους).
Καταστατικές εξισώσεις
Η συνολική παραμόρφωση της συσκευής αποτελείται από την παραμόρφωση του ελατηρίου , η οποία και θα αναφέρεται στη συνέχεια ως ελαστική παραμόρφωση, και από την παραμόρφωση του μηχανισμού τριβής , ή αλλιώς πλαστική παραμόρφωση, δηλαδή η συνολική παραμόρφωση ισούται με το άθροισμα [12]:
| (6.1) |
Επομένως, η σχέση τάσεων-παραμορφώσεων δίνεται από τη σχέση:
| (6.2) |
Παραμένουσα παραμόρφωση
Έστω τώρα ότι η πλαστική παραμόρφωση είναι χρονική συνάρτηση στο διάστημα και πιο συγκεκριμένα:
| (6.3) |
Τυχόν αλλαγή στη συσκευή τριβής είναι εφικτή μόνο όταν . Απομονώνοντας τη συσκευή τριβής, όπως φαίνεται στο Σχήμα 6.1, γίνονται δεκτές οι ακόλουθες παραδοχές [12]:
-
1.
Η τιμή της τάσης στη συσκευή δεν μπορεί να υπερβαίνει κατά απόλυτη τιμή τη σταθερή τιμή του συντελεστή ολίσθησης . Αυτό σημαίνει ότι επιτρεπτές τάσεις θεωρούνται εκείνες οι τάσεις που βρίσκονται στο κλειστό διάστημα , ορίζοντας έτσι το σύνολο των επιτρεπτών τάσεων ,
(6.4) όπου η συνάρτηση ,
(6.5) ονομάζεται συνάρτηση διαρροής.
-
2.
Αν η απόλυτη τιμή της εφαρμοζόμενης τάσης είναι μικρότερη από την τάση διαρροής , δεν παρατηρείται καμία αλλαγή στις πλαστικές παραμορφώσεις , δηλαδή θεωρούμε ότι ισχύει . Επομένως προκύπτει ότι:
(6.6) και σύμφωνα με την (6.2) ισχύει:
(6.7) δηλαδή η άμεση συμπεριφορά του μηχανικού αναλόγου είναι ελαστική με ελατηριακή σταθερά . Έτσι μπορεί να οριστεί η ελαστική περιοχή ως το ανοικτό (και φραγμένο στην προκειμένη περίπτωση) σύνολο
(6.8) καθώς και το σύνορο της ελαστικής περιοχής
(6.9) που ονομάζεται επιφάνεια διαρροής. Στο υπόψη μονοδιάστατο προσομοίωμα η επιφάνεια διαρροής εκφυλίζεται σε δύο σημεία, δηλαδή .
-
3.
Λόγω της παραδοχής 1, μια εντατική κατάσταση τέτοια ώστε τιμές δεν επιτρέπονται, και λόγω της παραδοχής 2, ο ρυθμός των πλαστικών παραμορφώσεων είναι μηδενικός όταν . Συνεπάγεται επομένως ότι η πλαστική παραμόρφωση μεταβάλλεται μόνο στην περίπτωση που . Σε αυτή την περίπτωση ο μηχανισμός τριβής εμφανίζει σταθερή πλαστική ροή κατά τη διεύθυνση της εφαρμοζόμενης τάσης . Αν είναι η απόλυτη τιμή της πλαστικής ροής, τότε
(6.10) (6.11) Η παραπάνω σχέση ονομάζεται κανόνας ροής και μπορεί να γραφτεί ως:
(6.12) όπου η συνάρτηση sign (προσήμου) ορίζεται ως:
(6.13) Ο κανόνας ροής όπως δίνεται στην (6.12) μπορεί να συσχετιστεί στο συγκεκριμένο παράδειγμα με τη συνάρτηση διαρροής (6.5) μέσω της εξίσωσης:
(6.14) εφόσον . Όπως θα δούμε και στη συνέχεια, όταν η (6.14) ισχύει, τότε ο κανόνας ροής αναφέρεται και ως συζευγμένος κανόνας ροής.
Συνθήκες αποφόρτισης/επαναφόρτισης
Για τον πλήρη ορισμό του προβλήματος και τον υπολογισμό της πλαστικής παραμόρφωσης θεωρείται ότι το και το υπόκεινται στους παρακάτω περιορισμούς [12]:
-
1.
Η τάση πρέπει να είναι επιτρεπτή, δηλαδή, σύμφωνα με την παραδοχή 1, και το πρέπει να είναι μη αρνητικό σύμφωνα με την παραδοχή 3. Επομένως θα πρέπει να ισχύει:
(6.15) -
2.
Σύμφωνα με την παραδοχή 2, αν . Σύμφωνα όμως με την παραδοχή 3, και επομένως ισχύει ότι αν και μόνο αν . Αυτές οι παρατηρήσεις συνοψίζονται ως:
(6.16) Από τις παραπάνω σχέσεις εύκολα συνεπάγεται ότι απαιτείται:
(6.17) Οι συνθήκες (6.15) και (6.17) εκφράζουν την απαίτηση ότι οι τάσεις πρέπει να είναι επιτρεπτές και ότι η πλαστική ροή, με την έννοια του μη μηδενικού ρυθμού πλαστικής παραμόρφωσης (), μπορούν να συμβούν μόνο στην επιφάνεια διαρροής . Αυτές οι συνθήκες είναι κλασικές σε προβλήματα βελτιστοποίησης και ονομάζονται συνθήκες Karush-Kuhn-Tucker.
-
3.
Τέλος θεωρείται ότι αν και μόνο αν και αν , δηλαδή
(6.18) ή
(6.19) Η σχέση (6.19) ονομάζεται απαίτηση συνέπειας και περιγράφει την απαίτηση ότι για να είναι ο ρυθμός της πλαστικής παραμόρφωσης μη μηδενικός (δηλαδή για να ισχύει ) πρέπει οι τάσεις να βρίσκονται στην επιφάνεια διαρροής έτσι ώστε .
Η θεωρία που αναπτύχθηκε στην παρούσα ενότητα λέγεται και θεωρία ιδεατής πλαστικότητας. Οι εξισώσεις της ιδεατής πλαστικότητας συνοψίζονται στο Πλαίσιο 6.1.1.
-
1.
Ελαστική σχέση τάσεων-παραμορφώσεων
-
2.
Συνάρτηση διαρροής
-
3.
Επιφάνεια διαρροής
-
4.
Ελαστική περιοχή
-
5.
Κανόνας ροής
-
6.
Karush-Kuhn-Tucker συμπληρωματικές συνθήκες
-
7.
Απαίτηση συνέπειας
6.1.2 Κρατυνόμενη πλαστικότητα
Η ιδεατή πλαστικότητα χαρακτηρίζεται από τη μη μεταβολή της ελαστικής περιοχής οδηγώντας στην καμπύλη τάσεων-παραμορφώσεων του Σχήματος 6.3 [12]. Η καμπύλη τάσεων-παραμορφώσεων του Σχήματος 6.4 περιγράφει μία συμπεριφορά που ονομάζεται κρατυνόμενη πλαστικότητα, σύμφωνα με την οποία το εύρος της ελαστικής περιοχής δεν είναι σταθερό, αλλά εξαρτάται από το μέγεθος της πλαστικής ολίσθησης [12]. Στη συνέχεια περιγράφεται αυτή η συμπεριφορά.
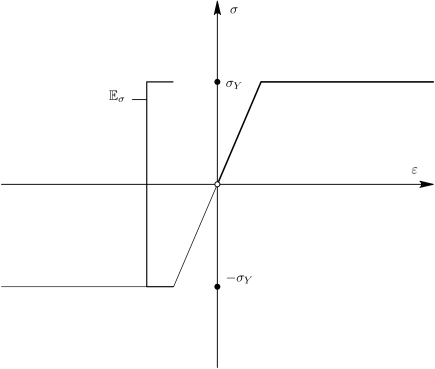
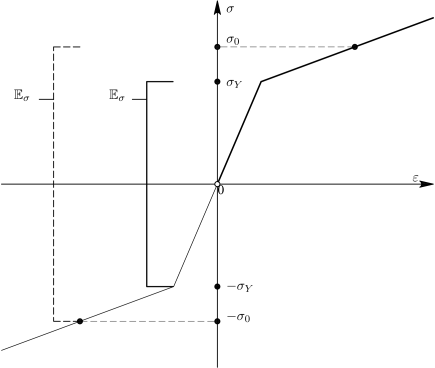
Οι βασικές παραδοχές που αφορούν την ελαστική συμπεριφορά παραμένουν αμετάβλητες, υιοθετώντας τον διαχωρισμό των παραμορφώσεων,
| (6.20) |
καθώς και τη σχέση τάσεων-παραμορφώσεων:
| (6.21) |
Επιπλέον, όμως, θεωρούμε ότι ισχύουν οι δύο παρακάτω παραδοχές [12]:
-
1.
Η κράτυνση είναι ισότροπη, δηλαδή θεωρείται ότι το κέντρο της ελαστικής περιοχής παραμένει σταθερό.
-
2.
Η κράτυνση είναι γραμμική όσον αφορά την πλαστική ροή, δηλαδή είναι γραμμική ως προς την πλαστική παραμόρφωση και ανεξάρτητη από το πρόσημό της.
Οι παραπάνω παραδοχές οδηγούν σε ένα κριτήριο διαρροής της μορφής:
| (6.22) |
όπου η τάση διαρροής και ο συντελεστής είναι γνωστοί, σταθεροί όροι. Ο συντελεστής αναφέρεται συχνά και ως μέτρο κράτυνσης. Η μεταβλητή είναι μια μη αρνητική μεταβλητή, εξαρτάται από το μέγεθος της πλαστικής ροής (ολίσθησης) και ονομάζεται εσωτερική μεταβλητή κράτυνσης. Σύμφωνα με τα παραπάνω, η απλούστερη εξίσωση που περιγράφει την εξέλιξη της εσωτερικής μεταβλητής είναι:
| (6.23) |
Το ελαστικό πεδίο ορίζεται πλέον ως:
| (6.24) |
και εξαρτάται από την εσωτερική μεταβλητή , όπως φαίνεται στο Σχήμα 6.5 [12].
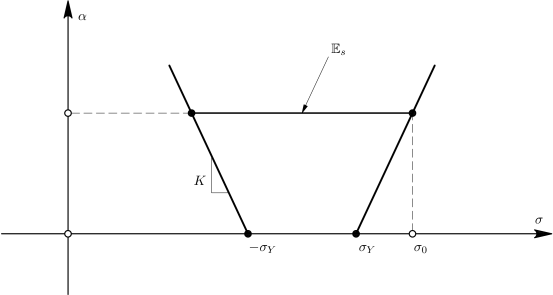
Ο μη αναστρέψιμος μηχανισμός που χαρακτηρίζει την εξέλιξη της ολίσθησης του προσομοιώματος (πλαστική ροή) και που χαρακτηρίζεται από τον κανόνα ροής παραμένει αμετάβλητος. Συνεπώς, θεωρείται όπως προηγουμένως ότι
| (6.25) |
όπου είναι ο ρυθμός με τον οποίο λαμβάνει χώρα η ολίσθηση. Επομένως από τις (6.23) και (6.25) προκύπτει ότι η εξέλιξη της εσωτερικής μεταβλητής κράτυνσης μπορεί να οριστεί από τη σχέση:
| (6.26) |
που είναι γνωστή και ως νόμος της κράτυνσης. Η μη αναστρεψιμότητα της πλαστικής ροής περιγράφεται και από τις συμπληρωματικές συνθήκες αποφόρτισης/επαναφόρτισης Karush-Kuhn-Tucker, οι οποίες όμως τώρα διατυπώνονται ως:
| (6.27) |
όπου και πάλι η παράμετρος καθορίζεται από την απαίτηση συνέπειας
| (6.28) |
Οι παραπάνω παρατηρήσεις συνοψίζονται στο Πλαίσιο 6.1.2.
-
1.
Ελαστική σχέση τάσεων-παραμορφώσεων
-
2.
Συνάρτηση διαρροής
-
3.
Επιφάνεια διαρροής
-
4.
Ελαστική περιοχή
-
5.
Κανόνας ροής και (ισότροπος) νόμος κράτυνσης
-
6.
Συμπληρωματικές συνθήκες Karush-Kuhn-Tucker
-
7.
Συνθήκη συνέπειας
Συνεχές εφαπτομενικό ελαστοπλαστικό μέτρο
Η απαίτηση συνέπειας της χρονικά ανεξάρτητης πλαστικότητας (6.28) επιτρέπει την απευθείας επίλυση για την παράμετρο και τη σύνδεση του ρυθμού μεταβολής των τάσεων με τον ρυθμό μεταβολής των παραμορφώσεων [12]. Από τις σχέσεις (6.22), (6.23) και (6.25) προκύπτει:
| (6.29) | ||||
| (6.30) | ||||
| (6.31) |
Εφόσον , από τις συνθήκες Karush-Kuhn-Tucker (6.27) και την απαίτηση συνέπειας (6.28) συνεπάγεται ότι το μπορεί να είναι μη μηδενικό αν και μόνο αν:
| (6.32) |
Επομένως, ο ρυθμός μεταβολής των τάσεων μπορεί να προσδιοριστεί από τη σχέση:
| (6.33) |
Το μέγεθος ονομάζεται συνεχές εφαπτομενικό ελαστοπλαστικό μέτρο.
6.2 Θεωρία τρισδιάστατης πλαστικότητας. Κριτήρια μίας επιφάνειας διαρροής
Στη συνέχεια επεκτείνεται η θεωρία της μονοδιάστατης πλαστικότητας σε περισσότερες της μίας διαστάσεις. Η διατύπωση των εξισώσεων γίνεται στον χώρο των τάσεων και, αν δεν υπάρχει σαφής αναφορά, θεωρείται ότι τα πεδία , και υπολογίζονται στο σημείο και στη χρονική στιγμή , όπου το κλειστό διάστημα λαμβάνεται συχνά ίσο με το συνολικό για ευκολία.
6.2.1 Καταστατικές εξισώσεις
Η θεωρία της μονοδιάστατης πλαστικότητας που εξετάστηκε στην Ενότητα 6.1.1 γενικεύεται στις τρεις διαστάσεις ως εξής [12]:
-
1.
Διαχωρισμός του τανυστή παραμορφώσεων. Αρχικά υποθέτουμε ότι ο τανυστής των παραμορφώσεων μπορεί να διαχωριστεί σε ένα ελαστικό και ένα πλαστικό μέρος τα οποία αναφέρονται ως και , αντίστοιχα, σύμφωνα με τη σχέση:
(6.34) ή σε τανυστική μορφή:
(6.35) Εφόσον η παραμόρφωση θεωρείται ανεξάρτητη μεταβλητή και ο ρυθμός μεταβολής των πλαστικών παραμορφώσεων ορίζεται μέσω του κανόνα ροής, η εξίσωση (6.34) μπορεί να θεωρηθεί και ως ο ορισμός των ελαστικών παραμορφώσεων. Θεωρείται δηλαδή ότι οι ελαστικές παραμορφώσεις ορίζονται από τη σχέση:
(6.36) -
2.
Ελαστική απόκριση. Ο τανυστής των τάσεων συνδέεται με τις ελαστικές παραμορφώσεις μέσω μιας συνάρτησης δυναμικού , όπου σύμφωνα με την (υπερελαστική) σχέση
(6.37) Για τη γραμμική ελαστικότητα η συνάρτηση δίνεται από τη δευτεροβάθμια εξίσωση , όπου είναι ο τανυστής ελαστικότητας, ο οποίος θεωρείται σταθερός. Επομένως από τις σχέσεις (6.34) και (6.37) προκύπτει:
(6.38) ή σε τανυστική μορφή:
(6.39)
6.2.2 Μη αναστρέψιμη πλαστική απόκριση
Το βασικό χαρακτηριστικό της πλαστικής ροής είναι η μη αναστρεψιμότητά της. Αυτή η ιδιότητα εξετάζεται στη συνέχεια ως μια απευθείας επέκταση των όσων αναφέρθηκαν στην Ενότητα 6.1.2.
-
1.
Ελαστική περιοχή και συνάρτηση διαρροής. Ορίζεται η συνάρτηση η οποία ονομάζεται συνάρτηση διαρροής και η οποία περιορίζει τις επιτρεπτές εντατικές καταστάσεις να ανήκουν στο σύνολο , το οποίο ορίζεται ως:
(6.40) Το εσωτερικό του συνόλου , που συμβολίζεται ως και δίνεται από τη σχέση:
(6.41) αναφέρεται ως ελαστική περιοχή. Το σύνορο του , που συμβολίζεται ως και δίνεται από τη σχέση:
(6.42) καλείται επιφάνεια διαρροής στον χώρο των τάσεων. Στις παραπάνω σχέσεις με συμβολίζονται οι εσωτερικές μεταβλητές στον χώρο των τάσεων σε αντιστοιχία με τη μεταβλητή της μονοδιάστατης πλαστικότητας. Όπως και στην περίπτωση της μονοδιάστατης πλαστικότητας, ισχύει ότι .
-
2.
Κανόνας ροής και νόμος κράτυνσης. Συνθήκες φόρτισης/αποφόρτισης. Η έννοια της μη αναστρεψιμότητας της πλαστικής ροής εισάγεται από τις εξισώσεις ρυθμού μεταβολής του τανυστή των τάσεων και των εσωτερικών μεταβλητών κράτυνσης , οι οποίες ονομάζονται κανόνας ροής και νόμος κράτυνσης αντίστοιχα:
(6.43) Οι συναρτήσεις και είναι συναρτήσεις που εξαρτώνται από το υλικό και καθορίζουν τη διεύθυνση της πλαστικής ροής και τον νόμο της κράτυνσης. Η παράμετρος είναι μια μη αρνητική παράμετρος, που ονομάζεται παράμετρος συνέπειας και θεωρείται ότι πληροί τις επόμενες Karush-Kuhn-Tucker συμπληρωματικές συνθήκες:
(6.44) Τέλος, συμπληρωματικά με τις συνθήκες (6.44), η παράμετρος οφείλει να ικανοποιεί την απαίτηση συνέπειας
(6.45)
Στην κλασική βιβλιογραφία, οι συνθήκες (6.44) και (6.45) αναφέρονται ως συνθήκες φόρτισης/αποφόρτισης και απαίτηση συνέπειας, αντίστοιχα. Όπως ήδη συζητήθηκε στην Ενότητα 6.1 και θα αναπτυχθεί περαιτέρω στη συνέχεια, οι σχέσεις αυτές περιγράφουν πλήρως τις έννοιες της πλαστικής φόρτισης και της ελαστικής αποφόρτισης.
6.2.3 Ερμηνεία των συμπληρωματικών συνθηκών Karush-Kuhn-Tucker
Θεωρείται ότι μία από τις παρακάτω περιπτώσεις μπορεί να συμβεί [12]:
-
1.
Οι τάσεις βρίσκονται εντός της ελαστικής περιοχής, δηλαδή , και επομένως, σύμφωνα με την (6.41), ισχύει . Από τις συνθήκες Karush-Kuhn-Tucker (6.44) συμπεραίνεται ότι:
(6.46) και από τη σχέση (6.43) συνεπάγεται ότι και . Επομένως, σύμφωνα με την εξίσωση (6.34) ισχύει και ο ρυθμός μεταβολής των παραμορφώσεων, όπως περιγράφεται από τη σχέση (6.38), οδηγεί στο συμπέρασμα ότι:
(6.47) Η συμπεριφορά που περιγράφεται από την εξίσωση (6.47) αναφέρεται και ως άμεσα ελαστική.
-
2.
Αν υποθέσουμε ότι , σύμφωνα με την (6.42), συνεπάγεται ότι και οι συνθήκες (6.44) ικανοποιούνται αυτόματα. Αν το είναι θετικό ή μηδενικό, εξαρτάται από την απαίτηση συνέπειας (6.45). Πιο συγκεκριμένα, διακρίνονται δύο περιπτώσεις:
- (α)
-
(β)
Αν θεωρηθεί ότι ισχύει και , τότε συνεπάγεται ότι και , μια κατάσταση που περιγράφεται ως πλαστική φόρτιση. Η κατάσταση κατά την οποία (και ) ονομάζεται ουδέτερη φόρτιση.
Συνοψίζοντας τα παραπάνω συμπεράσματα, για κάθε επιτρεπτή εντατική κατάσταση ισχύει:
| (6.49) |
Για την καλύτερη κατανόηση αλλά και για μελλοντικές αναφορές, οι βασικές καταστατικές εξισώσεις της τρισδιάστατης χρονικά μη εξαρτημένης πλαστικοποίησης συνοψίζονται στο Πλαίσιο 6.2.3.
-
1.
Ελαστική σχέση τάσεων-παραμορφώσεων
-
2.
Ελαστική περιοχή στον χώρο των τάσεων (για μία επιφάνεια διαρροής)
(6.50) -
3.
Κανόνας ροής και νόμος κράτυνσης
-
(α)
Μη συζευγμένος νόμος
(6.51) (6.52) -
(β)
Συζευγμένος νόμος
-
(α)
-
4.
Συμπληρωματικές συνθήκες φόρτισης/αποφόρτισης Karush-Kuhn-Tucker
-
5.
Απαίτηση συνέπειας
6.2.4 Συνεχές εφαπτομενικό ελαστοπλαστικό μέτρο
Το συνεχές εφαπτομενικό ελαστοπλαστικό μέτρο μπορεί να προσδιοριστεί από την απαίτηση συνέπειας (6.45). Εφαρμόζοντας τον κανόνα αλυσίδας, προκύπτει ότι [12]:
| (6.53) |
Θεωρείται στη συνέχεια ότι ο νόμος κράτυνσης και το κριτήριο διαρροής ικανοποιούν την ακόλουθη ανισότητα:
| (6.54) |
για όλες τις επιτρεπτές εντατικές καταστάσεις .
Σύμφωνα με τη παραπάνω παραδοχή και με την συνθήκη συνέπειας (6.45), συνεπάγεται ότι
| (6.55) |
όπου . Τέλος, σύμφωνα με τη σχέση τάσεων-παραμορφώσεων (6.38), τον κανόνα ροής και τον νόμο κράτυνσης (6.43), προκύπτει:
| (6.56) |
Αντικαθιστώντας την εξίσωση (6.55) στη σχέση (6.56), προκύπτει ο ρυθμός μεταβολής των τάσεων σε συνάρτηση του ρυθμού μεταβολής των συνολικών παραμορφώσεων ,
| (6.57) |
όπου η έκφραση αναφέρεται στον τανυστή του εφαπτομενικού ελαστοπλαστικού μέτρου, ο οποίος δίνεται από την εξίσωση:
| (6.58) |
Όπως διακρίνεται στη σχέση (6.58), ο τανυστής στη γενική του μορφή είναι μη συμμετρικός για τυχαίο , εκτός από την περίπτωση κατά την οποία
| (6.59) |
που έχει ιδιαίτερη σημασία και καλείται συζευγμένος κανόνας ροής. Ομοίως και ο νόμος της κράτυνσης μπορεί να είναι συζευγμένος ή ασύζευκτος. Καλείται συζευγμένος όταν στον χώρο των τάσεων έχει τη μορφή:
| (6.60) |
και επομένως στον χώρο των παραμορφώσεων δίνεται ως:
| (6.61) |
όπου το γενικευμένο μητρώο πλαστικότητας [12], που απεικονίζει τις εσωτερικές μεταβλητές κράτυνσης στον χώρο των παραμορφώσεων, σύμφωνα με τη σχέση:
| (6.62) |
6.3 Θεωρία τρισδιάστατης πλαστικότητας. Κριτήρια πολλαπλών επιφανειών διαρροής
Στη συνέχεια επεκτείνεται η θεωρία που αναπτύχθηκε στην Ενότητα 6.2 σε περιπτώσεις πλαστικότητας των οποίων το σύνολο των επιτρεπτών εντατικών καταστάσεων καθορίζεται από περισσότερες της μίας ομαλές επιφάνειες διαρροής, οι οποίες όμως ενδέχεται να αλληλοτέμνονται μεταξύ τους μη ομαλά. Αυτό έχει ως αποτέλεσμα να εμφανίζονται ανωμαλίες και ιδιάζουσες (singular) τιμές στο όριο της ελαστικής περιοχής και στα σημεία τομής των επιφανειών, που καθιστούν ιδιαίτερα την αριθμητική επίλυση εξαιρετικά επίπονη.
Η επέκταση της κλασικής θεωρίας πλαστικότητας ώστε να συμπεριλαμβάνει και κριτήρια αστοχίας πολλαπλών επιφανειών διαρροής πρωτοεμφανίζεται στις εργασίες των Koiter [6] και Mandel [9]. Νεότερες διατυπώσεις της θεωρίας πλαστικότητας εφαρμόζουν ιδέες της θεωρίας βελτιστοποίησης και ενσωματώνουν τις προηγούμενες προσεγγίσεις ως ειδικές περιπτώσεις.
6.3.1 Καταστατικές εξισώσεις
Το κύριο ζητούμενο της θεωρίας πλαστικότητας για κριτήρια με πολλαπλές επιφάνειες διαρροής είναι ο χαρακτηρισμός της ελαστικής περιοχής. Θεωρείται ότι η ελαστική περιοχή είναι το κυρτό υποσύνολο του , που ορίζεται ως [14]:
| (6.63) |
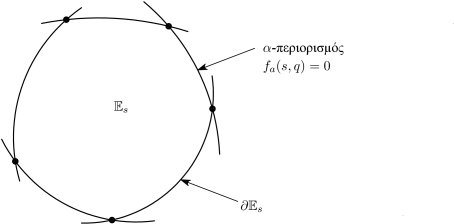
όπου οι συναρτήσεις είναι αλληλοτεμνόμενες (πιθανόν μη ομαλά) συναρτήσεις, όπως φαίνεται και στο Σχήμα 6.6 [14]. Αντίστοιχα, το σύνορο ορίζεται ως:
| (6.64) |
Στη συνέχεια, το ενδιαφέρον επικεντρώνεται στην περίπτωση κατά την οποία οι συναρτήσεις είναι ομαλές και ορίζουν ανεξάρτητους περιορισμούς για κάθε . Σε αυτή την περίπτωση η μεταβολή του ρυθμού της πλαστικής παραμόρφωσης καθορίζεται από τον κανόνα του Koiter:
| (6.65) |
Στην παραπάνω εξίσωση οι παράμετροι είναι οι παράμετροι συνέπειας, οι οποίες ικανοποιούν τις Karush-Kuhn-Tucker συμπληρωματικές συνθήκες, για ,
| (6.66) |
ταυτόχρονα με την απαίτηση συνέπειας,
| (6.67) |
Ομοίως, από τη γενίκευση των εξισώσεων που περιγράφουν τον ρυθμό μεταβολής των παραμέτρων κράτυνσης για την περίπτωση των πολλαπλών επιφανειών διαρροής προκύπτει ο νόμος κράτυνσης:
| (6.68) |
ο οποίος στον χώρο των παραμορφώσεων και για την περίπτωση συζευγμένου νόμου δίνεται ως:
| (6.69) |
6.3.2 Συνθήκες φόρτισης/αποφόρτισης
Στη συνέχεια διερευνώνται οι συνθήκες φόρτισης/αποφόρτισης για την περίπτωση των κριτηρίων που αποτελούνται από πολλαπλές επιφάνειες διαρροής. Έστω ο αριθμός των περιορισμών (επιφανειών) που είναι ενεργοί σε ένα σημείο στον χώρο των τάσεων και το σύνολο των δεικτών που αναφέρονται στους περιορισμούς, δηλαδή
| (6.70) |
Χρησιμοποιώντας τον κανόνα αλυσίδας, η παράγωγος των υπολογίζεται ως [14]:
| (6.71) |
όπου :
| (6.72) |
και για το οποίο υποθέτουμε ότι ισχύει:
| (6.73) |
για κάθε . Επομένως μπορεί εύκολα πλέον να αποδειχτεί ότι:
| (6.74) |
Έχοντας υπόψη τις παραπάνω σχέσεις, από τις συνθήκες Karush-Kuhn-Tucker (6.66) και την απαίτηση συνέπειας (6.67) συνεπάγονται τα ακόλουθα για τις συνθήκες φόρτισης/αποφόρτισης [14]:
| (6.75) |
Σημειώνεται ότι αν λαμβάνει χώρα πλαστική φόρτιση στο σημείο και κάποιες επιφάνειες είναι ενεργές, τότε η συνθήκη δεν εγγυάται ότι η επιφάνεια αυτή θα είναι οριστικά ενεργή.
6.3.3 Απαίτηση συνέπειας
Έστω τώρα ότι η ιστορία του ρυθμού των παραμορφώσεων είναι γνωστή τη χρονική στιγμή . Τότε από τις συμπληρωματικές συνθήκες Karush-Kuhn-Tucker (6.66) και την απαίτηση συνέπειας (6.67) μπορεί να καθοριστεί αν ένας περιορισμός (επιφάνεια) είναι ενεργός. Πιο συγκεκριμένα, από τις παραπάνω συνθήκες προκύπτει ότι [14]:
-
1.
Αν και , τότε .
-
2.
Αν και , τότε .
Οι περιπτώσεις 1 και 2 αποτελούν την επαναδιατύπωση των συνθηκών φόρτισης/αποφόρτισης για την περίπτωση της πλαστικοποίησης κριτηρίων πολλαπλών επιφανειών. Αν τώρα θεωρηθεί ότι είναι ο αριθμός των ενεργών περιορισμών σε ένα σημείο για το οποίο ισχύει η περίπτωση 2, τότε ορίζεται:
| (6.76) |
Εφόσον η παράμετρος συνέπειας είναι μη μηδενική μόνο για , και σύμφωνα με τη σχέση (6.71) συνεπάγεται ότι:
| (6.77) |
για κάθε . Συνεπώς έτσι ορίζεται ένα σύστημα εξισώσεων αγνώστων, στο οποίο οι συνθήκες (αν ) παρέχουν τις υπόλοιπες εξισώσεις ώστε το σύστημα (6.77) να είναι ορισμένο. Συνοπτικά, επομένως ισχύει:
| (6.78) |
όπου , και η συνάρτηση όπως έχει οριστεί στην (6.72).
Για την καλύτερη κατανόηση αλλά και για μελλοντικές αναφορές, οι εξισώσεις που εξετάστηκαν στην παρούσα ενότητα συνοψίζονται στο Πλαίσιο 6.3.3.
-
1.
Ελαστική σχέση τάσεων-παραμορφώσεων
-
2.
Κανόνας ροής
-
3.
Νόμος κράτυνσης
-
4.
Διαρροή και συνθήκες φόρτισης/αποφόρτισης
όπου , το σύνολο των επιφανειών διαρροής.
6.3.4 Συνεχές εφαπτομενικό ελαστοπλαστικό μέτρο
6.4 Επισκόπηση της μεθόδου των πεπερασμένων στοιχείων
Στη συνέχεια παρουσιάζεται συνοπτικά η μέθοδος των πεπερασμένων στοιχείων στο πλαίσιο της κλασικής θεωρίας πλαστικότητας και της μη γραμμικής ανάλυσης. Το πρόβλημα που εξετάζεται είναι το πρόβλημα αρχικών συνοριακών τιμών [7] που περιγράφεται από την εξίσωση ορμής
| (6.83) |
υποκείμενη στις συνοριακές συνθήκες
| (6.84) | ||||
| (6.85) |
με γνωστές αρχικές συνθήκες
| (6.86) | ||||
| (6.87) |
στον χώρο .
6.4.1 Ασθενής διατύπωση του προβλήματος συνοριακών τιμών
Για λόγους απλότητας θεωρείται στη συνέχεια ότι η επιρροή των αδρανειακών δυνάμεων είναι αμελητέα. Αρχικά ορίζεται ο συναρτησιακός χώρος ,
| (6.88) |
ο οποίος περιλαμβάνει όλες εκείνες τις συναρτήσεις που αποτελούν λύσεις του προβλήματος συνοριακών τιμών, και ο χώρος , που περιγράφει όλες τις κινηματικά αποδεκτές μεταβολές (ιδεατές μετακινήσεις), οι οποίες ικανοποιούν την ομογενή μορφή των συνθηκών Dirichlet, δηλαδή:
| (6.89) |
Στη γενική περίπτωση ισχύει ότι όπου με συμβολίζεται ο χώρος Sobolev. Έστω τώρα τυχαία συνάρτηση , για την οποία βάσει ορισμού ισχύει . Πολλαπλασιάζοντας την (6.83) με τη συνάρτηση και ολοκληρώνοντας κατά μέρη, προκύπτει η ασθενής διατύπωση του προβλήματος:
| (6.90) |
όπου ο τανυστής των τάσεων θεωρείται ότι πληροί τις καταστατικές εξισώσεις.
6.4.2 Χωρική διακριτοποίηση. Διατύπωση της μεθόδου των πεπερασμένων στοιχείων
Στη συνέχεια θεωρείται ότι η περιοχή διακριτοποιείται ακριβώς σε ένα σύνολο μη αλληλοεπικαλυπτόμενων υποπεριοχών , δηλαδή ισχύει:
| (6.91) |
και
| (6.92) |
Έστω τώρα ένας προσεγγιστικός χώρος του και μια δοκιμαστική συνάρτηση , , τέτοια ώστε
| (6.93) |
όπου η ορίζεται τοπικά με την παρεμβολή
| (6.94) |
είναι το μητρώο των συναρτήσεων παρεμβολής (μορφής) και είναι το τοπικό διάνυσμα των μετακινήσεων των κόμβων. Έχοντας υπόψη τη διακριτοποίηση, η (6.90) υπολογίζεται τοπικά σε επίπεδο στοιχείου, ενώ συνολικά προκύπτει ότι
| (6.95) |
Για ένα τυπικό στοιχείο υπολογίζεται αρχικά το μητρώο , όπως αυτό προκύπτει από την κινηματική εξίσωση
| (6.96) |
όπου το διάνυσμα επικόμβιων μετακινήσεων του στοιχείου .
Επομένως, μπορεί να οριστεί η ασθενής μορφή του προβλήματος τοπικά ως
| (6.97) |
όπου
| (6.98) |
είναι το διάνυσμα εσωτερικών δυνάμεων στο επίπεδο του στοιχείου το οποίο εξαρτάται από τον τανυστή των τάσεων , όπως αυτός ορίζεται από την ολοκλήρωση των καταστατικών εξισώσεων και
| (6.99) |
είναι το διάνυσμα εξωτερικών δυνάμεων σε επίπεδο στοιχείου.
Επομένως, σύμφωνα με την (6.97) και από τις (6.98) και (6.99) προκύπτει η (6.90) από τη συναρμολόγηση των συνεισφορών των στοιχείων, σύμφωνα με την παρακάτω σχέση:
| (6.100) |
όπου . Τα συνολικά διανύσματα και υπολογίζονται από τις συνεισφορές των στοιχείων,
| (6.101) | ||||
| (6.102) |
όπου ο τελεστής είναι ο τελεστής που απεικονίζει τις τοπικές συνεισφορές των στοιχείων στο συνολικό σύστημα. Εφόσον η συνάρτηση είναι τυχαία και η σχέση (6.100) πρέπει να ισχύει για όλα τα αποδεκτά σύνολα μετακινήσεων , η διακριτοποιημένη μορφή του προβλήματος αρχικών τιμών ορίζεται ως:
| (6.103) |
6.4.3 Διατύπωση των εξισώσεων σε βηματική μορφή
Έστω τώρα το χρονικό διάστημα μελέτης το οποίο διακριτοποιείται ως
| (6.104) |
Έστω επίσης τα σημεία ολοκλήρωσης ενός τυπικού πεπερασμένου στοιχείου και οι εσωτερικές μεταβλητές στο . Αρχικά, θεωρείται ότι το σώμα βρίσκεται σε ισορροπία κατά τη χρονική στιγμή , δηλαδή
| (6.105) |
Έστω τώρα ένα βήμα φόρτισης , τέτοιο ώστε
| (6.106) |
τη χρονική στιγμή .
Το πρόβλημα συνίσταται στον υπολογισμό του νέου πεδίου μετακινήσεων , των νέων εσωτερικών μεταβλητών και του νέου τασικού πεδίου στα διακριτά σημεία έτσι ώστε:
-
1.
(ισορροπία) και
-
2.
να πληρούνται οι καταστατικές εξισώσεις.
Η λύση στο παραπάνω πρόβλημα προσδιορίζεται μέσω της ακόλουθης επαναληπτικής διαδικασίας. Αν η τιμή μιας μεταβλητής κατά το χρονικό βήμα (ο εκθέτης παραλείπεται για λόγους απλότητας των συμβολισμών), τότε:
-
1.
Έστω η αύξηση των επικόμβιων μετακινήσεων κατά την επανάληψη στο χρονικό βήμα και
(6.107) το συνολικό διάνυσμα των επικόμβιων μετακινήσεων. Συνεπάγεται ότι για το πεδίο των μετακινήσεων ισχύει:
(6.108) -
2.
Με δεδομένες τις παραμορφώσεις στα σημεία υπολογίζεται το διάνυσμα μέσω του καταστατικού νόμου.
-
3.
Υπολογίζεται το διάνυσμα των εσωτερικών δυνάμεων σε επίπεδο στοιχείου και το συνολικό διάνυσμα των εσωτερικών δυνάμεων .
-
4.
Ελέγχεται η σύγκλιση της επαναληπτικής διαδικασίας. Αν ικανοποιείται, τότε η κατάσταση θεωρείται λύση του προβλήματος. Αλλιώς,
-
5.
υπολογίζεται το , τίθεται και επαναλαμβάνεται η παραπάνω επαναληπτική διαδικασία.
Ο υπολογισμός του γίνεται αρχικά θεωρώντας τον κανόνα της αλυσίδας:
| (6.109) |
Από την παραπάνω σχέση μπορεί να οριστεί το μητρώο δυσκαμψίας του στοιχείου
| (6.110) |
και η (6.109) διατυπώνεται ως:
| (6.111) |
όπου το συνολικό μητρώο δυσκαμψίας κατά τη χρονική στιγμή και την επανάληψη .
6.5 Αριθμητικές μέθοδοι επίλυσης
Στη συνέχεια εξετάζονται οι αριθμητικές μέθοδοι που εφαρμόζονται στην επίλυση του προβλήματος της πλαστικότητας στο πλαίσιο της μεθόδου των πεπερασμένων στοιχείων.
6.5.1 Η μέθοδος Newton-Raphson
Η μέθοδος Newton-Raphson αποτελεί την πλέον διαδεδομένη αριθμητική μέθοδο εύρεσης ριζών μη γραμμικών εξισώσεων και χρησιμοποιείται ευρέως σε μη γραμμικά προβλήματα και προβλήματα βελτιστοποίησης [10].
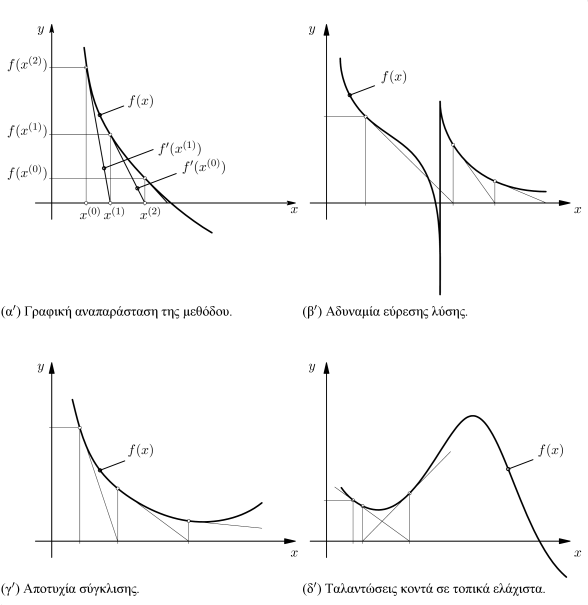
Στο Σχήμα 6.7 δίνεται γραφικά η εφαρμογή της μεθόδου στο μονοδιάστατο πρόβλημα . Ξεκινώντας από μια προσέγγιση της λύσης , η επόμενη προσέγγιση δίνεται από τον επαναληπτικό τύπο:
| (6.114) |
Η αρχική τιμή συνήθως επιλέγεται τυχαία και η επιθυμητή ακρίβεια της προσεγγιστικής λύσης ελέγχεται μέσω μίας ή περισσότερων σχετικών με το πρόβλημα νόρμες.
Στη γενική περίπτωση η μέθοδος Newton-Raphson μπορεί να προκύψει θεωρώντας μόνο τον πρώτο όρο του αναπτύγματος της σειράς Taylor της συνάρτησης :
| (6.115) |
Μέσω του παραπάνω ορισμού η μέθοδος γενικεύεται εύκολα σε περισσότερες της μίας διαστάσεις (-διαστάσεις). Σε αυτή τη περίπτωση το πρόβλημα ορίζεται ως εξής:
| (6.116) |
όπου , και οι άγνωστοι του προβλήματος και το αντίστοιχο ανάπτυγμα Taylor (6.115) για την -διάστατη περίπτωση ορίζεται ως:
| (6.117) |
Το μητρώο είναι ένα συναρτησιακό μητρώο, που ονομάζεται Ιακωβιανή, και ορίζεται ως:
| (6.118) |
Είναι προφανές ότι η σχέση (6.117) παριστάνει ένα γραμμικό σύστημα εξισώσεων από το οποίο προκύπτει το βήμα ,
| (6.119) |
όπου
| (6.120) |
Εύκολα αποδεικνύεται ότι για μια ομαλή συνάρτηση ο αλγόριθμος Newton-Raphson εγγυάται τετραγωνική σύγκλιση. Παρόλο το πλεονέκτημα της ταχύτατης σύγκλισης, το σχετικά υψηλό υπολογιστικό κόστος που απαιτείται στην -διάστατη περίπτωση για την αντιστροφή του -διάστατου εφαπτομενικού μητρώου καθιστά την παραπάνω μέθοδο πολλές φορές απαγορευτική. Έτσι χρησιμοποιείται συχνά η Τροποποιημένη Newton-Raphson μέθοδος, κατά την οποία το αντίστροφο του εφαπτομενικού μητρώου υπολογίζεται μόνο στην αρχή του κάθε βήματος και στη συνέχεια θεωρείται ότι παραμένει σταθερό στις επόμενες επαναλήψεις. Άλλες μέθοδοι που εφαρμόζονται όταν δεν θέλουμε ή και δεν μπορούμε να προσδιορίσουμε το αντίστροφο του εφαπτομενικού μητρώου είναι οι επονομαζόμενες μέθοδοι χορδής (ή τέμνουσας), στις οποίες η λύση προσεγγίζεται με την παραγωγή διαδοχικών χορδών μεταξύ δύο σημείων επί της άγνωστης καμπύλης.
Η μέθοδος Newton-Raphson συνήθως προτείνεται όταν το προς επίλυση πρόβλημα είναι έντονα μη γραμμικό. Παρ’ όλα αυτά, ανωμαλίες ή μη μονότονες συναρτήσεις μπορεί να οδηγήσουν σε αριθμητικά προβλήματα, όπως φαίνεται και στα Σχήματα 6.7(β), 6.7(γ) και 6.7(δ).
Σε αυτές τις περιπτώσεις συνήθως η μέθοδος Newton-Raphson συμπληρώνεται με κάποια τεχνική σταθεροποίησης, όπως η μέθοδος εύρεσης γραμμής, ή χρησιμοποιούνται άλλοι πιο εξειδικευμένοι αλγόριθμοι, όπως για παράδειγμα ο αλγόριθμος μήκους τόξου.
6.5.2 Ο γενικός κανόνας του μέσου σημείου
Έστω η συνάρτηση η οποία θεωρείται ομαλή. Εξετάζεται τώρα το πρόβλημα,
| (6.121) |
Για την αριθμητική επίλυση του παραπάνω προβλήματος χρησιμοποιείται συχνά ο γενικός κανόνας του μέσου σημείου, ο οποίος αναφέρεται σε μια οικογένεια σχημάτων χρονικής ολοκλήρωσης και ορίζεται ως:
| (6.122) |
Στην παραπάνω σχέση, το συμβολίζει την αριθμητική προσέγγιση στην ακριβή τιμή κατά τη χρονική στιγμή . Ο γενικός κανόνας του μέσου σημείου περιλαμβάνει μερικά από τα πιο γνωστά σχήματα χρονικής ολοκλήρωσης, και πιο συγκεκριμένα
| (6.123) |
Εκτενείς αναφορές για τη σύγκλιση, την ακρίβεια και την ευστάθεια των παραπάνω σχημάτων χρονικής ολοκλήρωσης μπορούν εύκολα να αναζητηθούν στη βιβλιογραφία [3]. Στη συνέχεια θα χρησιμοποιηθεί η έμμεση μέθοδος Euler, η οποία χαρακτηρίζεται από ακρίβεια πρώτης τάξης και απεριόριστη ευστάθεια. Κατά την εφαρμογή της μεθόδου απαιτείται η επίλυση ενός (πιθανώς) μη γραμμικού προβλήματος, για την οποία χρησιμοποιείται συνήθως η μέθοδος Newton-Raphson.
6.6 Αριθμητική επίλυση της μονοδιάστατης πλαστικότητας
Έστω ένα σημείο , όπου το είναι ένα κλειστό υποσύνολο του (τυπικό παράδειγμα και σημείο ολοκλήρωσης) του οποίου η καταστατική συμπεριφορά ορίζεται από τις σχέσεις του Πλαισίου 6.1.2. Η αρχική εντατική κατάσταση στο σημείο για το βήμα θεωρείται γνωστή και ότι περιγράφεται πλήρως από τις μεταβλητές . Το πρόβλημα μπορεί να οριστεί τώρα ως εξής:
Για δεδομένη αύξηση της παραμόρφωσης ζητείται να βρεθεί η τάση στο σημείο .
6.6.1 Ο αλγόριθμος return-mapping
Εφαρμόζοντας στον κανόνα ροής (6.25) και στον νόμο κράτυνσης (6.26) (βλ. και Πλαίσιο 6.1.2) τον γενικό κανόνα του μέσου σημείου (6.122) για , που αντιστοιχεί στην περίπτωση της έμμεσης μεθόδου Euler, προκύπτει:
| (6.124) | ||||
| (6.125) |
Η ολική παραμόρφωση ορίζεται σύμφωνα με τη σχέση
| (6.126) |
και θεωρείται σταθερή κατά τη διάρκεια του βήματος . Επομένως η ζητούμενη τάση δίνεται ως:
| (6.127) |
Οι μεταβλητές και η παράμετρος πρέπει επιπλέον να πληρούν τις ακόλουθες διακριτές συνθήκες Karush-Kuhn-Tucker, οι οποίες δίνονται ως:
| (6.128) |
Όπως διακρίνεται και από τις παραπάνω σχέσεις, με την εφαρμογή της έμμεσης μεθόδου Euler οδηγείται το αρχικό πρόβλημα βελτιστοποίησης με περιορισμούς στο διακριτό αντίστοιχο πρόβλημα για τις μεταβλητές .
Η δοκιμαστική (trial) ελαστική εντατική κατάσταση
Αρχικά ορίζεται μια μη πραγματική, δοκιμαστική (trial) ελαστική εντατική κατάσταση η οποία περιγράφεται από τις σχέσεις:
| (6.129) |
Η παραπάνω δοκιμαστική κατάσταση αντιστοιχεί σε μία πραγματική κατάσταση, αν και μόνο αν η αύξηση της παραμόρφωσης οδηγεί σε ελαστική φόρτιση/αποφόρτιση.
Η συνθήκη διαρροής
Με γνωστή τη δοκιμαστική κατάσταση, αρχικά εξετάζεται η περίπτωση κατά την οποία ισχύει:
| (6.130) |
Αν ισχύει η παραπάνω σχέση, τότε θεωρείται ότι η δοκιμαστική κατάσταση είναι αποδεκτή και επομένως τίθεται:
| (6.131) |
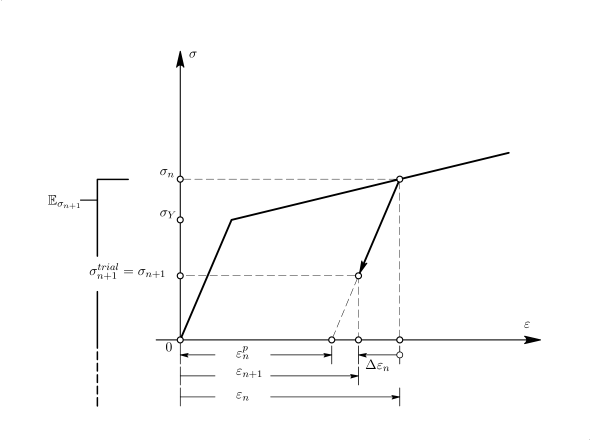
και θεωρείται ότι η δοκιμαστική κατάσταση αποτελεί τη λύση του προβλήματος (βλ. Σχήμα 6.8 για μια πιθανή περίπτωση ελαστικής αποφόρτισης).
Έστω τώρα η περίπτωση κατά την οποία ισχύει:
| (6.132) |
Η δοκιμαστική ελαστική κατάσταση προφανώς δεν μπορεί να αποτελεί λύση του προβλήματος, γιατί παραβιάζει τη συνθήκη . Επομένως ζητείται εκείνη η τιμή του για την οποία ισχύει έτσι ώστε . Από τις συμπληρωματικές συνθήκες Karush-Kuhn-Tucker είναι γνωστό ότι εφόσον , τότε ισχύει:
| (6.133) |
και το βήμα θεωρείται πλαστικό. Συνοψίζοντας, μπορεί να ισχύει:
| (6.134) |
Ο αλγόριθμος επιστροφής
Η ζητούμενη τάση επαναδιατυπώνεται συναρτήσει της πλαστικής παραμόρφωσης, σύμφωνα με την (6.124),
| (6.135) |
όπου η δοκιμαστική τάση θεωρείται σταθερή κατά τη διάρκεια του βήματος . Η εξίσωση (6.125) που αφορά τον νόμο κράτυνσης δίνεται ως:
| (6.136) |
Τέλος ορίζεται η συνάρτηση διαρροής στο βήμα , η οποία και θα πρέπει να είναι μηδενική:
| (6.137) |
Οι εξισώσεις (6.135), (6.136) και (6.137) αποτελούν για το απλό πρόβλημα που εξετάζεται ένα σύστημα γραμμικών εξισώσεων με αγνώστους τα , και . Η γραμμικότητα του παραπάνω συστήματος, όπως θα γίνει εμφανές και στις επόμενες ενότητες, δεν αποτελεί τον κανόνα, καθώς στην τυπική περίπτωση οι εξισώσεις (6.135), (6.136) και (6.137) είναι μη γραμμικές και απαιτείται η επίλυση ενός τοπικά μη γραμμικού συστήματος. Για τη συγκεκριμένη περίπτωση, εύκολα προκύπτει ότι:
| (6.138) |
και επομένως έχοντας γνωστό το
| (6.139) |
Οι ελαστοπλαστικές παραμορφώσεις υπολογίζονται από τη σχέση (6.124), δηλαδή
| (6.140) |
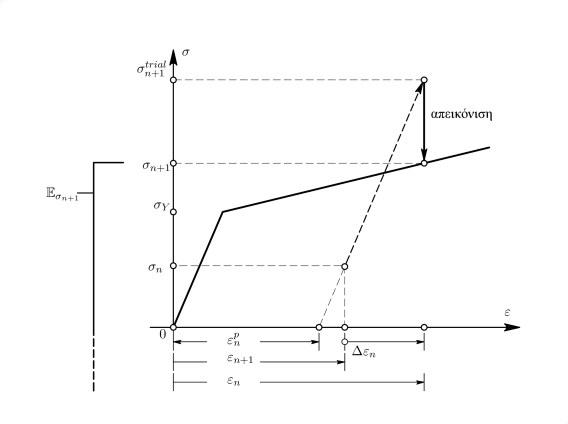
Η παραπάνω λύση παρουσιάζεται γραφικά στο Σχήμα 6.9 και δίνεται σε αλγοριθμική μορφή στο Πλαίσιο 6.6.1. Ιδιαίτερο ενδιαφέρον στον παραπάνω αλγόριθμο παρουσιάζει η σχέση (6.135), η οποία μπορεί να γραφτεί και ως:
| (6.141) |
Εφόσον , συμπεραίνεται ότι η τελική τάση είναι η προβολή της στην επιφάνεια διαρροής. Για αυτό τον λόγο, ο αλγόριθμος 6.6.1 ονομάζεται και αλγόριθμος return-mapping (επιστροφής-απεικόνισης).
-
Δεδομένα:
-
Είσοδος: Αύξηση παραμόρφωσης
-
1
-
2
-
3
-
4
Αν
-
ελαστική φόρτιση
-
-
-
-
-
-
αλλιώς
-
πλαστική φόρτιση
-
-
-
-
-
6.6.2 Το αλγοριθμικό (συνεπές) εφαπτομενικό μέτρο
Για λόγους πληρότητας της μεθόδου υπολογίζεται στη συνέχεια το αλγοριθμικό ελαστοπλαστικό μέτρο [13], το οποίο ενδέχεται να διαφέρει από το συνεχές μέτρο ελαστοπλαστικότητας (6.33), είναι συνεπές ως προς την εξωτερική επαναληπτική διαδικασία, εγγυάται τετραγωνική σύγκλιση και ορίζεται ως:
| (6.142) |
Για την περίπτωση όπου , εύκολα αποδεικνύεται ότι:
| (6.143) |
Στην περίπτωση που ισχύει , και σύμφωνα με τις αντίστοιχες σχέσεις του Πλαισίου 6.6.1, προκύπτει:
| (6.144) |
Από τις (6.143) και (6.144) και σε αντιστοιχία με τις (6.33) και (6.134), το αλγοριθμικό, ελαστοπλαστικό μέτρο δίνεται ως:
| (6.145) |
Σημειώνεται ότι το συνεχές (6.33) και το αλγοριθμικό μέτρο (6.145) ταυτίζονται για την περίπτωση της μονοδιάστατης πλαστικότητας. Αυτό όμως δεν ισχύει απαραίτητα σε μεγαλύτερες διαστάσεις.
6.7 Αριθμητική επίλυση του προβλήματος της πλαστικότητας πολλών διαστάσεων. Κριτήρια μίας επιφάνειας διαρροής
Το πρόβλημα της -διάστατης πλαστικότητας, σύμφωνα με όσα περιγράφονται στην Ενότητα 6.2 και συνοψίζονται στο Πλαίσιο 6.2.3, ορίζεται από τις παρακάτω εξισώσεις:
| (6.146) | ||||
| (6.147) | ||||
| (6.148) | ||||
| (6.149) | ||||
| (6.150) |
οι οποίες πρέπει να πληρούν τις Karush-Kuhn-Tucker συμπληρωματικές συνθήκες,
| (6.151) | ||||
| (6.152) | ||||
| (6.153) |
και την απαίτηση συνέπειας
| (6.154) |
υπό γνωστές αρχικές συνθήκες
| (6.155) |
6.7.1 Ο αλγόριθμος return-mapping
Στη συνέχεια εξετάζεται η εφαρμογή του αλγορίθμου return-mapping στην περίπτωση της πλαστικότητας πολλών διαστάσεων για κριτήρια διαρροής που αποτελούνται από μία επιφάνεια διαρροής.
Η δοκιμαστική (trial) ελαστική εντατική κατάσταση
Όπως και στην περίπτωση της μονοδιάστατης πλαστικότητας (Ενότητα 6.6), ορίζεται αρχικά μία μη πραγματική, δοκιμαστική (trial), ελαστική εντατική κατάσταση, η οποία περιγράφεται από τις σχέσεις:
| (6.156) |
Η συνθήκη διαρροής
Με γνωστή τη δοκιμαστική κατάσταση, αρχικά εξετάζεται η περίπτωση κατά την οποία ισχύει:
| (6.157) |
Αν ισχύει η παραπάνω σχέση, τότε θεωρείται ότι η δοκιμαστική κατάσταση είναι αποδεκτή, αποτελεί τη λύση του προβλήματος και επομένως τίθεται:
| (6.158) |
Ο αλγόριθμος επιστροφής
Αν τώρα ισχύει
| (6.159) |
δηλαδή η εντατική κατάσταση βρίσκεται εκτός του συνόλου των αποδεκτών εντατικών καταστάσεων , τότε η φόρτιση θεωρείται πλαστική. Η κατάσταση θεωρείται μη αποδεκτή, δηλαδή και επομένως θα πρέπει να προσδιοριστεί εκείνη η κατάσταση που αποτελεί τη λύση του προβλήματος.
Ξεκινώντας από την εξίσωση (6.148) και εφαρμόζοντας την έμμεση μέθοδο Euler, προκύπτει:
| (6.160) |
| (6.161) |
Γνωρίζοντας ότι , η παραπάνω σχέση μπορεί να γραφτεί ως:
| (6.162) |
και αντικαθιστώντας προκύπτει ότι:
| (6.163) |
η οποία βρίσκεται σε πλήρη αντιστοιχία με την αντίστοιχη εξίσωση που αφορά την περίπτωση της μονοδιάστατης πλαστικότητας. Η παραπάνω σχέση δίνεται σε μορφή υπολοίπου ως:
| (6.164) |
ή ισοδύναμα:
| (6.165) |
Στη συνέχεια, εφαρμόζοντας την έμμεση μέθοδο Euler στην εξίσωση (6.150), προκύπτει:
| (6.166) | ||||
| (6.167) |
ή με τη μορφή υπολοίπου:
| (6.168) |
και ισοδύναμα:
| (6.169) |
Τέλος, η συνθήκη διαρροής (6.151) γράφεται σε μορφή υπολοίπου ως:
| (6.170) |
Οι εξισώσεις (6.164), (6.168) και (6.170) αποτελούν ένα μη γραμμικό σύστημα εξισώσεων που επιλύεται με τη μέθοδο Newton-Raphson (βλ. Ενότητα 6.5.1) [1]. Συνεπώς ορίζονται τα διανύσματα των αγνώστων
| (6.171) |
και των υπολοίπων
| (6.172) |
από τα οποία προκύπτει η ακόλουθη Ιακωβιανή:
| (6.173) |
Η επαναληπτική επίλυση γίνεται κατά τα γνωστά:
| (6.174) |
όπου
| (6.175) |
και
| (6.176) |
Η παραπάνω διαδικασία περιγράφεται στο Πλαίσιο 6.7.1.
-
Δεδομένα:
-
Είσοδος: Αύξηση παραμόρφωσης
-
1
-
2
-
3
-
4
-
5
Αν
-
ελαστική φόρτιση
-
-
-
-
-
-
αλλιώς
-
πλαστική φόρτιση
-
-
Επανάλαβε
-
Υπολογισμός
-
Αν και
-
σύγκλιση
-
-
-
-
έξοδος
-
-
αλλιώς
-
υπολογισμός
-
επίλυση
-
καινούργια προσέγγιση
-
-
-
-
6.7.2 Το αλγοριθμικό (συνεπές) εφαπτομενικό μέτρο
Για λόγους πληρότητας δίνεται στη συνέχεια το αλγοριθμικό (συνεπές) εφαπτομενικό μέτρο ελαστοπλαστικότητας. Ξεκινώντας από το σύστημα των εξισώσεων, όπως αυτό δίνεται στην εξίσωση (6.172),
| (6.177) |
παραγωγίζοντας ως προς και επαναδιατυπώνοντας τις σχέσεις, προκύπτει:
| (6.178) |
Είναι προφανές ότι το ζητούμενο μητρώο προκύπτει ως το υπομητρώο του μητρώου .
6.8 Αριθμητική επίλυση του προβλήματος της πλαστικότητας πολλών διαστάσεων. Κριτήρια πολλαπλών επιφανειών
Τέλος εξετάζεται το πρόβλημα της -διάστατης πλαστικότητας για τα κριτήρια διαρροής που περιγράφονται από πολλαπλές επιφάνειες διαρροής. Το θεωρητικό υπόβαθρο έχει αναπτυχθεί πλήρως στην Ενότητα 6.3, συνοψίζεται στο Πλαίσιο 6.3.3 και περιγράφεται από τις παρακάτω εξισώσεις:
| (6.179) | ||||
| (6.180) | ||||
| (6.181) | ||||
| (6.182) | ||||
| (6.183) |
οι οποίες πρέπει να πληρούν τις Karush-Kuhn-Tucker συμπληρωματικές συνθήκες:
| (6.184) | ||||
| (6.185) | ||||
| (6.186) |
και την απαίτηση συνέπειας
| (6.187) |
υπό γνωστές αρχικές συνθήκες
| (6.188) |
όπου , το σύνολο των επιφανειών διαρροής.
6.8.1 Ο αλγόριθμος return-mapping
Στη συνέχεια εξετάζεται η εφαρμογή του αλγορίθμου return-mapping στην περίπτωση της πλαστικότητας πολλών διαστάσεων για κριτήρια διαρροής που αποτελούνται από πολλαπλές επιφάνειες διαρροής.
Σε αντίθεση με την περίπτωση κριτηρίων που χαρακτηρίζονται από μία επιφάνεια διαρροής, η διατύπωση του αλγορίθμου return-mapping θα γίνει στον χώρο των κυρίων τάσεων. Αυτή η προσέγγιση επιλέγεται γιατί τα πλέον συνήθη κριτήρια που αποτελούνται από πολλαπλές επιφάνειες χαρακτηρίζονται από μη ομαλές τομές μεταξύ αυτών των επιφανειών. Αυτές οι μη ομαλές τομές παρουσιάζουν προβλήματα κατά την αριθμητική επίλυση, τα οποία αίρονται για τα σημαντικότερα κριτήρια, όταν τα τελευταία επαναδιατυπωθούν στον χώρο των κυρίων τάσεων [5].
Η δοκιμαστική (trial) ελαστική εντατική κατάσταση
Όπως και στην περίπτωση της κλασικής επίλυσης της πλαστικότητας (Ενότητα 6.7), ορίζεται αρχικά μία μη πραγματική, δοκιμαστική (trial), ελαστική εντατική κατάσταση, η οποία περιγράφεται από τις σχέσεις:
| (6.189) |
Η συνθήκη διαρροής
Με γνωστή τη δοκιμαστική κατάσταση, εξετάζεται αρχικά η περίπτωση κατά την οποία ισχύει:
| (6.190) |
Αν ισχύει η παραπάνω σχέση, τότε θεωρείται ότι η δοκιμαστική κατάσταση είναι αποδεκτή, αποτελεί τη λύση του προβλήματος και επομένως τίθεται:
| (6.191) |
Ο αλγόριθμος επιστροφής
Έστω τώρα ότι ισχύει:
| (6.192) |
όπου . Η εντατική κατάσταση που περιγράφεται από βρίσκεται εκτός της ελαστικής περιοχής , επομένως η φόρτιση θεωρείται πλαστική και θα πρέπει να προσδιοριστεί εκείνη η κατάσταση που αποτελεί τη λύση του προβλήματος.
Αρχικά παραγοντοποιείται φασματικά ο τανυστής των τάσεων που περιγράφει τη δοκιμαστική εντατική κατάσταση, σύμφωνα με το Φασματικό Θεώρημα,
| (6.193) |
και επαναδιατυπώνεται ο κανόνας ροής (2) στον χώρο των φασματικών διευθύνσεων:
| (6.194) |
όπου πλέον το περιγράφει το σύνολο των ενεργών επιφανειών διαρροής , δηλαδή
| (6.195) |
Στον κανόνα ροής εφαρμόζεται η έμμεση μέθοδος Euler, οπότε και προκύπτει:
| (6.196) |
το οποίο σε μορφή υπολοίπου μπορεί να διατυπωθεί:
| (6.197) |
ή ισοδύναμα:
| (6.198) |
Ο νόμος της κράτυνσης (6.52) ολοκληρώνεται κατά τα γνωστά (βλ. και 6.168) με την έμμεση μέθοδο Euler,
| (6.199) | ||||
| (6.200) |
και γράφεται με τη μορφή υπολοίπου:
| (6.201) |
ή ισοδύναμα:
| (6.202) |
Τέλος, η συνθήκη διαρροής (3) γράφεται με τη μορφή υπολοίπου:
| (6.203) |
Οι εξισώσεις (6.197), (6.201) και (6.203) αποτελούν ένα μη γραμμικό σύστημα εξισώσεων που επιλύεται με τη μέθοδο Newton-Raphson (βλ. Ενότητα 6.5.1). Συνεπώς ορίζονται τα διανύσματα των αγνώστων
| (6.204) |
και των υπολοίπων
| (6.205) |
από τα οποία προκύπτει η ακόλουθη Ιακωβιανή:
| (6.206) |
Η επαναληπτική επίλυση γίνεται κατά τα γνωστά:
| (6.207) |
όπου
| (6.208) |
με αρχικές τιμές
| (6.209) |
και
| (6.210) |
6.8.2 Προσδιορισμός των ενεργών επιφανειών
Ο έλεγχος των ενεργών επιφανειών γίνεται με την ακόλουθη μεθοδολογία:
-
1.
Για θεωρείται ότι .
-
2.
Επιλύεται το πρόβλημα χρησιμοποιώντας το σύνολο .
-
3.
Ελέγχονται ως προς το πρόσημό τους οι περιορισμοί . Αν για κάποια ισχύει , τότε δημιουργείται ένα νέο σύνολο ενεργών περιορισμών εξαιρώντας τους παραπάνω περιορισμούς. Τίθεται και επαναλαμβάνεται το βήμα 2.
Η παραπάνω διαδικασία περιγράφεται στον αλγόριθμο που δίνεται στο Πλαίσιο 6.8.2.
-
Δεδομένα:
-
Είσοδος: Αύξηση παραμόρφωσης
-
1
-
2
-
3
-
4
-
5
Αν για όλα τα
-
ελαστική φόρτιση
-
-
-
-
-
-
αλλιώς
-
πλαστική φόρτιση
-
πήγαινε στο Πλαίσιο 6.8.2
-
-
1
φασματική παραγοντοποίηση των τάσεων
-
2
-
3
,
-
4
Υπολογισμός
-
5
Επανάλαβε
-
-
Υπολογισμός
-
Αν και για όλα
-
σύγκλιση
-
Αν
-
-
-
-
-
έξοδος
-
-
Αλλιώς
-
αφαίρεσε την -επιφάνεια από το
-
πήγαινε στο 3
-
-
-
αλλιώς
-
υπολογισμός
-
επίλυση
-
καινούργια προσέγγιση
-
-
-
6.8.3 Το αλγοριθμικό (συνεπές) εφαπτομενικό μέτρο
Τέλος, το συνεπές μέτρο ελαστοπλαστικότητας προκύπτει για τη χρονικά μη εξαρτώμενη πλαστικότητα ως το υπομητρώο του μητρώου , όπου
| (6.211) |
Ομοίως και εδώ οι ζητούμενες παράγωγοι εύκολα μπορούν να προκύψουν συναρτήσει των φασματικών συνιστωσών του τανυστή των τάσεων.
6.9 Γραφική απεικόνιση των κριτηρίων διαρροής
Οι κύριες τάσεις , και ορίζουν τον τρισδιάστατο χώρο που φαίνεται στο Σχήμα 6.10 και είναι γνωστός ως χώρος των τάσεων Haigh-Westergaard [11].
Στον χώρο Haigh-Westergaard μπορούν να απεικονιστούν γραφικά οι υδροστατικές και οι εκτροπικές συντεταγμένες μιας εντατικής κατάστασης. Θεωρώντας την εντατική κατάσταση που περιγράφεται από το σημείο , το διάνυσμα θέσης μπορεί να αναλυθεί σε δύο συνιστώσα διανύσματα και αντίστοιχα έτσι ώστε . Το πρώτο ορίζεται παράλληλο ως προς το μοναδιαίο διάνυσμα ενώ το δεύτερο κάθετο στο προηγούμενο, ισχύει δηλαδή .
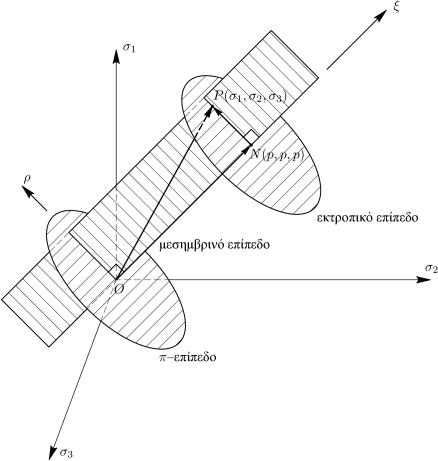
Το διάνυσμα περιγράφει την υδροστατική συνιστώσα της εντατικής κατάστασης και ο άξονας ονομάζεται υδροστατικός άξονας. Για κάθε σημείο που βρίσκεται στον άξονα ισχύει και η συντεταγμένη ορίζεται:
| (6.212) |
Το διάνυσμα ταυτίζεται με την εκτροπική συνιστώσα της εντατικής κατάστασης και είναι κάθετο στον άξονα . Κάθε επίπεδο κάθετο στον υδροστατικό άξονα μπορεί να περιγραφεί από τη σχέση
| (6.213) |
και ονομάζεται εκτροπικό επίπεδο. Το εκτροπικό επίπεδο που περνά από την αρχή των αξόνων, εκείνο δηλαδή για το οποίο ισχύει , ονομάζεται -επίπεδο.
Τέλος, κάθε επίπεδο που περιέχει τον άξονα ονομάζεται μεσημβρινό επίπεδο. Το διάνυσμα βρίσκεται εντός ενός μεσημβρινού επιπέδου για το οποίο ορίζεται η συντεταγμένη :
| (6.214) |
όπου οι ιδιοτιμές του εκτροπικού τανυστή των τάσεων και η δεύτερη αναλλοίωτή του (βλ. και Ενότητα 6.2).
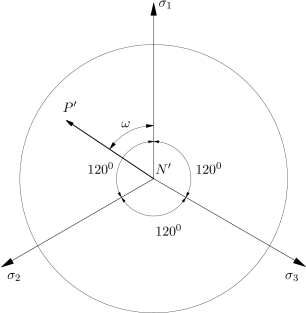
Η προβολή του διανύσματος και των αξόνων σε ένα εκτροπικό επίπεδο φαίνεται στο επόμενο σχήμα (Σχήμα 6.11). Η προβολή του διανύσματος σχηματίζει τη γωνία του Lode (βλ. και Ενότητα 6.2), η οποία ορίζεται ως:
| (6.215) |
Οι μεταβλητές ορίζουν ένα κυλινδρικό σύστημα συντεταγμένων, το οποίο συνδέεται με τις κύριες τάσεις ως:
| (6.216) | ||||
| (6.217) |
Ένα άλλο επίπεδο στο οποίο δίνεται συνήθως γραφικά η απεικόνιση των κριτηρίων διαρροής είναι το επίπεδο - (), στο οποίο περιγράφεται η καταστατική συμπεριφορά σε συνθήκες επίπεδης έντασης.
Τέλος, ενδιαφέρον παρουσιάζει στο πλαίσιο της γεωτεχνικής μηχανικής η παράσταση των κριτηρίων σε άξονες διατμητικής τάσης-ορθής τάσης -.
Έχοντας επομένως πέντε διαφορετικούς τρόπους γραφικής απεικόνισης των κριτηρίων διαρροής (χώρος --, εκτροπικό επίπεδο, μεσημβρινό επίπεδο, επίπεδο - και άξονες -), στις επόμενες ενότητες εξετάζονται δύο χαρακτηριστικές περιπτώσεις κριτηρίων που συναντώνται στη γεωτεχνική μηχανική.
6.10 Το κριτήριο διαρροής Tresca
Το κριτήριο διαρροής Tresca είναι ένα από τα πρώτα και πιο σημαντικά κριτήρια διαρροής [4]. Προτάθηκε το 1864 από τον γάλλο μηχανικό Henri Édouard Tresca, ο οποίος έπειτα από μια σειρά εργαστηριακών δοκιμών κατέληξε στο συμπέρασμα ότι ένα δοκίμιο διαρρέει όταν η μέγιστη διατμητική τάση ισούται με μία κρίσιμη τιμή.
6.10.1 Περιγραφή
Σύμφωνα με το κριτήριο Tresca, ένα υλικό διαρρέει όταν η μέγιστη εφαρμοζόμενη διατμητική τάση ισούται με τη διατμητική αντοχή , δηλαδή όταν ισχύει:
| (6.218) |
Η μέγιστη διατμητική τάση δίνεται κατά τα γνωστά ως:
| (6.219) |
όπου
| (6.220) | ||||
| (6.221) |
και επομένως η (6.218) γράφεται ως:
| (6.222) |
Από την παραπάνω εξίσωση εύκολα προκύπτει ότι η αντοχή σε μονοαξονική θλίψη/εφελκυσμό () ισούται με
| (6.223) |
και επομένως το κριτήριο διαρροής Tresca μπορεί να επαναδιατυπωθεί ως:
| (6.224) |
ή με τη μορφή συνάρτηση διαρροής:
| (6.225) |
Η συνάρτηση (6.225) περιγράφεται αναλυτικότερα από τις ακόλουθες έξι συναρτήσεις διαρροής:
| (6.226) | ||||
| (6.227) | ||||
| (6.228) | ||||
| (6.229) | ||||
| (6.230) | ||||
| (6.231) |
και είναι υποδιαφορίσιμη στον χώρο των κυρίων τάσεων. Για σταθερή τιμή του ορίζει την παρακάτω κυρτή ελαστική περιοχή,
| (6.232) |
ή οποία δίνεται στο Σχήμα 6.12. Τέλος, με τη βοήθεια των τασικών αναλλοίωτων και για , η συνάρτηση διαρροής μπορεί να διατυπωθεί ως:
| (6.233) |
6.10.2 Αριθμητική επίλυση
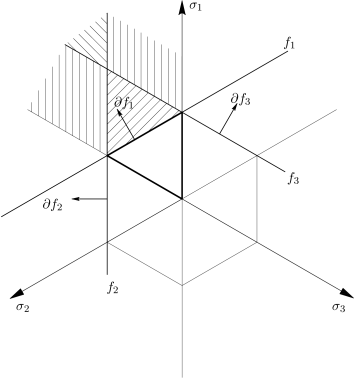
Θεωρώντας ότι οι παρακάτω συναρτήσεις αρκούν για την πλήρη περιγραφή του κριτηρίου:
| (6.234) | ||||
| (6.235) | ||||
| (6.236) |
ορίζοντας το εκτοκύκλιο που φαίνεται στο Σχήμα 6.13.
Εφόσον πρόκειται για γραμμικές συναρτήσεις, οι πρώτες παράγωγοι προκύπτουν σταθερές:
| (6.237) | ||||
| (6.238) | ||||
| (6.239) |
και οι δεύτερες παράγωγοι μηδενικές:
| (6.240) |
6.11 Το κριτήριο διαρροής Mohr-Coulomb
Το κριτήριο διαρροής Mohr-Coulomb αποτελεί ίσως το πιο διαδεδομένο κριτήριο για την περιγραφή της συμπεριφοράς ψαθυρών υλικών και βρίσκει εφαρμογή σε ένα ευρύ φάσμα προβλημάτων της εδαφομηχανικής, της βραχομηχανικής ή της μηχανικής του οπλισμένου σκυροδέματος.
Οι πρώτες έρευνες στο πεδίο της μέγιστης διατμητικής αντοχής αποδίδονται στον Charles-Augustin de Coulomb (1736-1806). Στην έκθεσή του, που παρουσιάστηκε στη Γαλλική Ακαδημία στις 10 Μαρτίου/2 Απριλίου 1773 και κατόπιν δημοσιεύτηκε στο Παρίσι το 1776, περιγράφεται η πειραματική εργασία σε εδαφικά υλικά και αναφέρεται μεταξύ άλλων το πρόβλημα ευστάθειας των τοίχων αντιστήριξης. Ο Coulomb θεώρησε ότι η θραύση επέρχεται λόγω της ολίσθησης κατά μήκος ενός επιπέδου και πρότεινε ότι πρέπει να λαμβάνονται υπόψη τόσο η συνοχή κατά μήκος του επιπέδου θραύσης όσο και η τριβή λόγω της κάθετης στο επίπεδο δύναμης.
Ο γερμανός μηχανικός Karl Culmann (1821-1881) ήταν ο πρώτος που εισήγαγε τη γραφική αναπαράσταση των τάσεων με τη μορφή τασικών κύκλων, όρισε τον πόλο του κύκλου και ανακάλυψε τις ιδιότητές του. Ο επίσης γερμανός μηχανικός Christian Otto Mohr (1835-1918) ήταν όμως αυτός που χρησιμοποίησε συστηματικά τους κύκλους τάσεων για προβλήματα δύο και τριών διαστάσεων και πρότεινε ένα κριτήριο αστοχίας βασιζόμενο στην περιβάλλουσα κύκλων που αντιστοιχούν σε διάφορες περιπτώσεις αστοχίας.
Το προτεινόμενο από τον Mohr κριτήριο αποτελεί στην ουσία μια γενίκευση της θεωρίας του Coulomb και για αυτό τον λόγο αναφέρεται και ως κριτήριο διαρροής Mohr-Coulomb.
6.11.1 Περιγραφή
Σύμφωνα με την κλασική διατύπωση του κριτηρίου Mohr-Coulomb, η αστοχία επέρχεται όταν η διατμητική τάση και η ορθή τάση ικανοποιούν την παρακάτω σχέση:
| (6.241) |
όπου η συνοχή, η γωνία τριβής και η τάση θεωρείται θετική όταν είναι εφελκυστική.
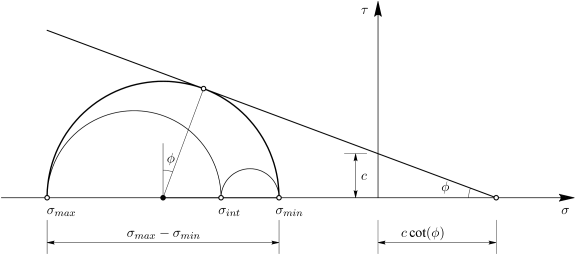
Από τη γραφική απεικόνιση του κριτηρίου (Σχήμα 6.14), η σχέση (6.241) μπορεί να επαναδιατυπωθεί συναρτήσει της μέγιστης και της ελάχιστης κύριας τάσης ως:
| (6.242) |
και επομένως προκύπτει:
| (6.243) |
ή με τη μορφή συνάρτησης διαρροής:
| (6.244) |
Η συνάρτηση (6.244) είναι υποδιαφορίσιμη στον χώρο των κυρίων τάσεων -- και ορίζει την ακόλουθη κυρτή ελαστική περιοχή
| (6.245) |
Μπορεί να διατυπωθεί αναλυτικά συναρτήσει των -- ως:
| (6.246) | ||||
| (6.247) | ||||
| (6.248) | ||||
| (6.249) | ||||
| (6.250) | ||||
| (6.251) |
ή με τη βοήθεια των τασικών αναλλοίωτων και για ,
| (6.252) |
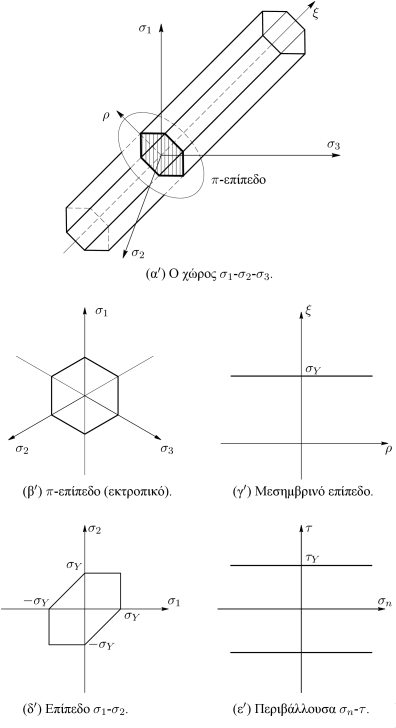
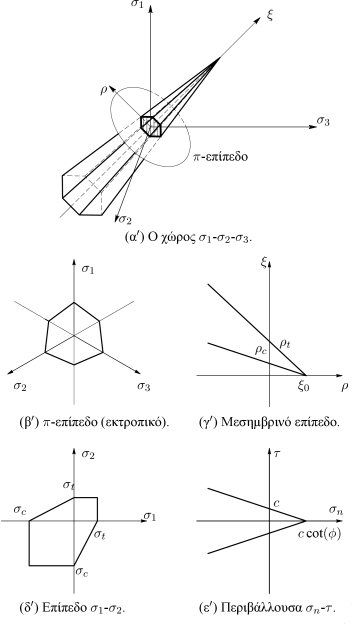
Η γραφική απεικόνιση του κριτηρίου Mohr-Coulomb δίνεται στο Σχήμα 6.15. Η ελαστική περιοχή στον χώρο -- περικλείεται από έξι γραμμικές επιφάνειες που σχηματίζουν έναν μη κανονικό εξαγωνικό κώνο [Σχήμα 6.15(α)], ο οποίος, όπως φαίνεται στο Σχήμα 6.15(β), σχηματίζει ένα μη κανονικό εξάγωνο στο -επίπεδο.
Στο επίπεδο - [Σχήμα 6.15(γ)] αποτελείται από δύο ευθείες που τέμνουν τον άξονα στο σημείο
| (6.253) |
και τον άξονα στα σημεία
| (6.254) | ||||
| (6.255) |
όπου ο δείκτης αναφέρεται στον εφελκυσμό και ο δείκτης στη θλίψη.
Στο επίπεδο - [Σχήμα 6.15(δ)] η προβολή του κριτηρίου τέμνει τους άξονες στα σημεία και αντίστοιχα, όπου
| (6.256) | ||||
| (6.257) |
Τέλος, σε άξονες - [Σχήμα 6.14 και Σχήμα 6.15(ε)] το κριτήριο περιγράφεται από την περιβάλλουσα η οποία τέμνει τον άξονα των ορθών τάσεων στην τιμή και τον άξονα των διατμητικών τάσεων στην τιμή .
6.11.2 Αριθμητική επίλυση
Θεωρώντας ότι οι παρακάτω συναρτήσεις αρκούν για την πλήρη περιγραφή του κριτηρίου:
| (6.258) | ||||
| (6.259) | ||||
| (6.260) |
ορίζοντας το εκτοκύκλιο που φαίνεται στο Σχήμα 6.16.
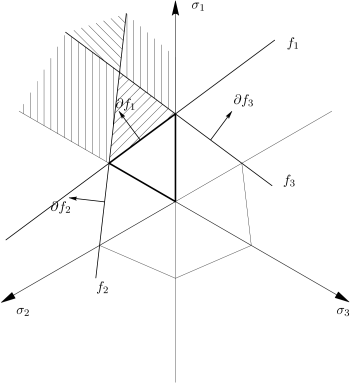
Εφόσον πρόκειται για γραμμικές συναρτήσεις στον χώρο των κυρίων τάσεων, οι πρώτες παράγωγοι προκύπτουν σταθερές,
| (6.261) | ||||
| (6.262) | ||||
| (6.263) |
και οι δεύτερες παράγωγοι μηδενικές:
| (6.264) |
Χρησιμοποιώντας τις σχέσεις (6.258-6.264), o αλγόριθμος που παρουσιάστηκε στην προηγούμενη ενότητα εφαρμόζεται χωρίς καμία τροποποίηση.
Για την περίπτωση μη συζευγμένου κανόνα ροής, χρησιμοποιείται η γωνία διαστολής αντί της γωνίας τριβής και οι παράγωγοι των συναρτήσεων του πλαστικού δυναμικού ορίζονται αντίστοιχα [2].
6.12 Βιβλιογραφία
- 1 F. Armero and A. Perez-Foguet. On the formulation of closest-point projection algorithms in elastoplasticity – Part I: The variational structure. International Journal for Numerical Methods in Engineering, 53(2): 297-329, 2002.
- 2 E. de Souza Neto, D. Perić and D. R. J. Owen. Computational methods for plasticity: Theory and applications. John Wiley & Sons Inc, 2008.
- 3 E. Hairer, S. P. Nørsett and G. Wanner. Solving ordinary differential equations I – Nonstiff problems, 1987.
- 4 R. Hill. The mathematical theory of plasticity. Oxford University Press, Oxford, UK, 1950.
- 5 Fotios E, Karaoulanis. Implicit numerical integration of nonsmooth multisurface yield criteria in the principal stress space. Archives of Computational Methods in Engineering, 20(3): 263-308, 2013.
- 6 W. T. Koiter. General theorems for elastic-plastic solids. In I.N. Sneddon and R. Hill, editors, Progress in Solid Mechanics, volume 6, pp. 167-221. North-Holland Publishing Company, Amsterdam, 1960.
- 7 H. O. Kreiss and J. Lorenz. Initial-boundary value problems and the Navier-Stokes equations. Academic Press, 1989.
- 8 J. Lemaitre and J. L. Chaboche. Mechanics of solids materials. Cambridge University Press, 1990.
- 9 J. Mandel. Contribution théorique à l’ étude de l’ écroissage et des lois de l’ écoulement plastique. In 11th International Congress on Applied Mechanics, pp. 502-509, 1964.
- 10 J. Nocedal and S. J. Wright. Numerical optimization. Springer Verlag, 1999.
- 11 N. S. Ottosen and M. Ristinmaa. The mechanics of constitutive modeling. Elsevier Science Ltd, 2005.
- 12 J. C. Simo and T. J. R. Hughes. Computational inelasticity. Interdisciplinary Applied Mathematics, New York, 1998.
- 13 J. C. Simo. Nonlinear stability of the time-discrete variational problem of evolution in nonlinear heat conduction, plasticity and viscoplasticity. Computer Methods in Applied Mechanics and Engineering, 88(1): 111-131, 1991.
- 14 J. C. Simo, J. G. Kennedy and S. Govindjee. Non-smooth multisurface plasticity and viscoplasticity. Loading/unloading conditions and numerical algorithms. International Journal for Numerical Methods in Engineering, 26(10): 2161-2185, 1988.