Κεφάλαιο 5 Περιπτώσεις συνοριακών συνθηκών σε προβλήματα γεωτεχνικής μηχανικής
Στο παρόν κεφάλαιο παρουσιάζονται οι περιπτώσεις συνοριακών συνθηκών οι οποίες συναντώνται σε προβλήματα γεωτεχνικής μηχανικής.
Αρχικά εξετάζονται οι βασικές και φυσικές συνοριακές συνθήκες (Ενότητα 5.1) και αναλύονται ιδιαίτερα οι βασικές συνοριακές συνθήκες (Ενότητα 5.1.1).
Στη συνέχεια παρουσιάζονται τα φορτία που εφαρμόζονται στο σύνορο του προσομοιώματος (Ενότητα 5.2) και δίνονται ο υπολογισμός φορτίων ανά κόμβο (Ενότητα 5.2.1) και ο υπολογισμός φορτίων ανά στοιχείο (Ενότητα 5.2.2). Τέλος δίνεται και ο ενεργειακά συνεπής υπολογισμός των φορτίων (Ενότητα 5.2.3).
Ακολουθεί η παρουσίαση των φορτίων που εμφανίζονται σε προβλήματα που χαρακτηρίζονται από την αφαίρεση ή την προσθήκη εδαφικού υλικού (Ενότητα 5.3) και τέλος των φορτίων που οφείλονται στην παρουσία μαζικών δυνάμεων (Ενότητα 5.4).
Στο τέλος του κεφαλαίου παρατίθεται η σχετική βιβλιογραφία (Ενότητα 5.5).
5.1 Βασικές και φυσικές συνοριακές συνθήκες
Ένα σημαντικό χαρακτηριστικό της μεθόδου των πεπερασμένων στοιχείων είναι ότι μπορεί να εφαρμοστεί σχετικά εύκολα σε προβλήματα των οποίων η εξεταζόμενη περιοχή χαρακτηρίζεται από πολύπλοκα όρια ή/και διεπιφάνειες.
Στο πλαίσιο της εφαρμογής της μεθόδου των πεπερασμένων στοιχείων, οι συνοριακές συνθήκες χαρακτηρίζονται από τον τρόπο με τον οποίο επιδρούν στην τελική μορφή του προβλήματος, δηλαδή στη μητρωική σχέση:
| (5.1) |
Έτσι έχουμε:
-
1.
Τις βασικές (ή Neumann) συνοριακές συνθήκες. Επιδρούν με άμεσο τρόπο στους βαθμούς ελευθερίας που βρίσκονται στο διάνυσμα , το οποίο αποτελεί το αριστερό μέλος της εξίσωσης (5.1).
-
2.
Τις φυσικές (ή Dirichlet) συνοριακές συνθήκες. Επιδρούν με έμμεσο τρόπο στους βαθμούς ελευθερίας του διανύσματος , αφού εφαρμόζονται στο διάνυσμα που βρίσκεται στο δεξί μέλος της εξίσωσης (5.1).
5.1.1 Βασικές συνοριακές συνθήκες
Οι βασικές συνοριακές συνθήκες στα προβλήματα γεωτεχνικής μηχανικής που εξετάζονται στο παρόν σύγγραμμα είναι οι μετακινήσεις.
Οι βασικές συνοριακές συνθήκες συνήθως εμπίπτουν σε μία από τις ακόλουθες κατηγορίες [1]:
-
1.
Συνθήκες στήριξης, οι οποίες απαγορεύουν από την εξεταζόμενη περιοχή τις κινήσεις στερεού σώματος (μετακινήσεις και περιστροφές).
Αν δεν παρέχονται οι κατάλληλες συνθήκες στήριξης, τότε αυτό σημαίνει για το μεν φυσικό πρόβλημα ότι μπορεί να ακολουθήσει τις κινήσεις στερεού σώματος, για το δε μαθηματικό προσομοίωμα ότι το μητρώο δυσκαμψίας έχει περισσότερες της μίας μηδενικές ιδιομορφές και επομένως δεν μπορεί να αντιστραφεί.
-
2.
Συνθήκες συμμετρίας, οι οποίες εφαρμόζονται ώστε να δημιουργηθούν τα σημεία, ευθείες ή επίπεδα συμμετρίας (ή αντισυμμετρίας) που χαρακτηρίζουν το αρχικό πρόβλημα.
Με τον τρόπο αυτό προσομοιώνεται μόνο ένα τμήμα αντί του συνόλου του φυσικού προβλήματος, μειώνοντας τον αριθμό των αγνώστων και κατ’ επέκταση τον αριθμό των εξισώσεων και τις υπολογιστικές απαιτήσεις του αντίστοιχου μαθηματικού προβλήματος.
-
3.
Συνθήκες σύνδεσης, οι οποίες περιγράφουν τη σύνδεση μεταξύ διαφορετικών τμημάτων μίας κατασκευής ή σχέσεις μεταξύ διαφορετικών βαθμών ελευθερίας. Σε αρκετές περιπτώσεις οι συνθήκες αυτές ονομάζονται και πολλαπλοί περιορισμοί.
-
4.
Αδιάφορες συνθήκες, οι οποίες μπορούν να παραλείπονται από το μαθηματικό προσομοίωμα, γιατί δεν σχετίζονται με αυτό.
5.2 Φορτία που εφαρμόζονται στο σύνορο του προσομοιώματος
Εξετάζεται ο υπολογισμός φορτίων ανά κόμβο (Ενότητα 5.2.1) και ο υπολογισμός φορτίων ανά στοιχείο (Ενότητα 5.2.2). Τέλος δίνεται και ο ενεργειακά συνεπής υπολογισμός των φορτίων (Ενότητα 5.2.3).
5.2.1 Υπολογισμός φορτίων ανά κόμβο
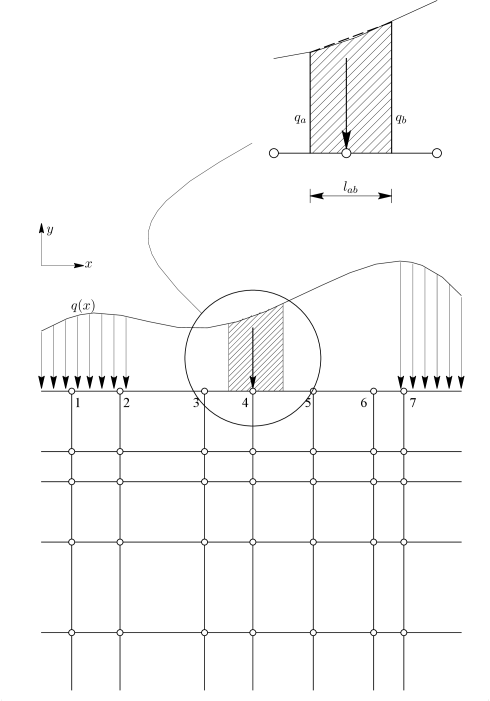
Η μέθοδος υπολογισμού των φορτίων που εφαρμόζονται στο σύνορο του προσομοιώματος ανά κόμβο περιγράφεται γραφικά στο Σχήμα 5.1. Στο παράδειγμα του σχήματος δίνεται ένα φορτίο το οποίο δρα κάθετα σε ένα δισδιάστατο προσομοίωμα πεπερασμένων στοιχείων. Το πάχος θεωρείται μοναδιαίο, ώστε το υπόψη φορτίο να μετατρέπεται αυτομάτως σε γραμμικό φορτίο με μονάδες δύναμης ανά μονάδα μήκους.
Με τη μέθοδο υπολογισμού του φορτίου ανά κόμβο, θεωρείται ότι το φορτίο στον κόμβο 4 ισούται με το ολοκλήρωμα της φόρτισης σε μια περιοχή εκατέρωθεν του κόμβου 4 και τυπικά ίση με το μισό των αποστάσεων 3-4 και 4-5, δηλαδή
| (5.2) |
Συνήθως θεωρείται ότι η συνάρτηση είναι γραμμική στο συγκεκριμένο τμήμα, οπότε η παραπάνω σχέση απλοποιείται και ταυτίζεται με τον τύπο υπολογισμού του εμβαδού τραπεζίου,
| (5.3) |
όπου:
-
, οι τιμές του φορτίου στα άκρα του γραμμοσκιασμένου τμήματος του Σχήματος 5.1 και
-
το μήκος του υπόψη τμήματος.
Το πλεονέκτημα αυτής της μεθόδου είναι η ευκολία άμεσου υπολογισμού των επικόμβιων φορτίων και για αυτό τον λόγο χρησιμοποιείται αρκετά συχνά. Θα πρέπει να αποφεύγεται όμως στις περιπτώσεις που το φορτίο αλλάζει πολύ γρήγορα σε σχέση με το μήκος του στοιχείου ή το στοιχείο ορίζεται από συναρτήσεις ανώτερου βαθμού [1].
5.2.2 Υπολογισμός φορτίων ανά στοιχείο
Με τη μέθοδο υπολογισμού των φορτίων ανά στοιχείο, το κατανεμημένο φορτίο διαμοιράζεται στα στοιχεία στα οποία δρα, όπως φαίνεται και στο Σχήμα 5.2. Στη συνέχεια επιμερίζεται στους κόμβους της πλευράς του στοιχείου στην οποία αναφέρεται.
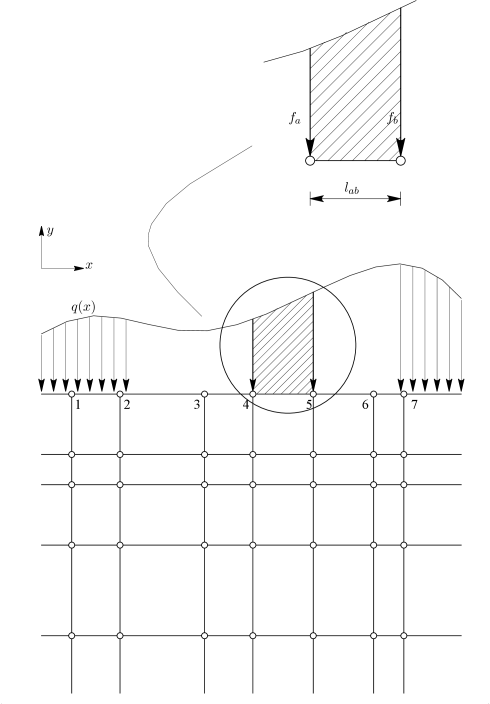
Για τον υπολογισμό των επιμέρους φορτίων και υπολογίζεται καταρχήν το συνολικό φορτίο της γραμμοσκιασμένης περιοχής του Σχήματος 5.2 στο γεωμετρικό της κέντρο και στη συνέχεια μεταφέρεται στους αντίστοιχους κόμβους.
Στην περίπτωση που και εδώ θεωρήσουμε γραμμική μεταβολή του φορτίου επί της πλευράς του στοιχείου, προκύπτει:
| (5.4) | ||||
| (5.5) |
Η συγκεκριμένη μέθοδος είναι πιο ακριβής από την προηγούμενη (υπολογισμός φορτίων ανά κόμβο). Στην περίπτωση που τα υπόψη στοιχεία δεν έχουν ενδιάμεσους κόμβους, ταυτίζεται με την ενεργειακά συνεπή μέθοδο που θα εξεταστεί στη συνέχεια [1].
Σε αντίθεση με την προηγούμενη μέθοδο, η ακρίβεια αυτής της μεθόδου δεν επηρεάζεται σημαντικά στις περιπτώσεις που το φορτίο αλλάζει γρήγορα σε σχέση με το μήκος του στοιχείου.
5.2.3 Ενεργειακά συνεπής υπολογισμός φορτίων
Αυτή η μέθοδος εφαρμόζεται κυρίως όταν τα στοιχεία στα οποία εφαρμόζεται η φόρτιση είναι ανώτερου βαθμού και περιέχουν και ενδιάμεσους κόμβους, όπως φαίνεται στο Σχήμα 5.3.
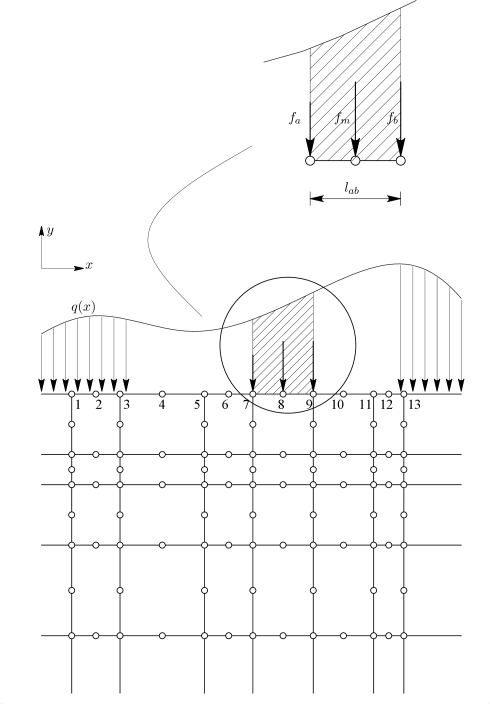
Για τον υπολογισμό με αυτήν τη μέθοδο μπορεί να εφαρμοστεί η αρχή των δυνατών έργων [1].
Το εξωτερικό δυνατό έργο της ορίζεται ως:
| (5.6) |
Αντίστοιχα, το εσωτερικό δυνατό έργο ορίζεται ως:
| (5.7) |
Εξισώνοντας τις παραπάνω σχέσεις, προκύπτει
| (5.8) | ||||
| (5.9) | ||||
| (5.10) |
όπου το μητρώο των συναρτήσεων μορφής.
5.3 Φορτία λόγω της αφαίρεσης ή της προσθήκης εδαφικού υλικού
Συχνά στα γεωτεχνικά έργα αντιμετωπίζονται προβλήματα στα οποία οι φορτίσεις οφείλονται στην αφαίρεση ή στην προσθήκη εδαφικού υλικού.
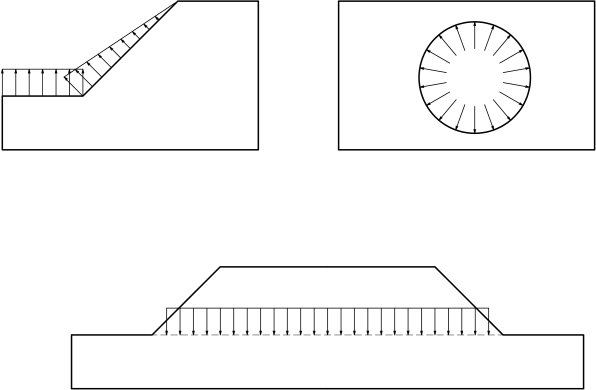
Τυπικές περιπτώσεις τέτοιων προβλημάτων είναι οι περιπτώσεις εκσκαφών, διάνοιξης σηράγγων ή κατασκευής επιχωμάτων, όπως δίνονται στο Σχήμα 5.3.
Σε αυτές τις περιπτώσεις υπολογίζονται συχνά τα κατανεμημένα φορτία και εφαρμόζονται στο προσομοίωμα με έναν από τους τρόπους που αναφέρθηκαν στις προηγούμενες ενότητες.
5.4 Φορτία που οφείλονται στην παρουσία μαζικών δυνάμεων
Φορτία που οφείλονται στην παρουσία μαζικών δυνάμεων, όπως τα φορτία βαρύτητας, είναι αρκετά συνηθισμένα σε προβλήματα γεωτεχνικής μηχανικής. Η μετατροπή των φορτίων αυτών σε επικόμβια γίνεται με ολοκλήρωση σε επίπεδο στοιχείου, σύμφωνα με τη σχέση:
| (5.11) |
όπου
-
η πυκνότητα του υλικού,
-
το μητρώο των συναρτήσεων σχήματος και
-
η περιοχή του στοιχείου.
5.5 Βιβλιογραφία
- 1 Carlos A. Felippa. Lecture notes in introduction to finite element methods, 2013.