Κεφάλαιο 7 Τυπικά προβλήματα γεωτεχνικής μηχανικής
Στο παρόν κεφάλαιο παρουσιάζεται η διαδικασία της προσομοίωσης του φυσικού προβλήματος ως σύνθεση των εννοιών που αναπτύχθηκαν στα προηγούμενα κεφάλαια και εξετάζονται χαρακτηριστικά προβλήματα της γεωτεχνικής μηχανικής.
Πιο συγκεκριμένα, στην Ενότητα 7.1 εξετάζεται το πρόβλημα μίας πεδιλοδοκού επί ελαστικού εδάφους, στην Ενότητα 7.2 παρουσιάζεται η περίπτωση ενός μεμονωμένου πασσάλου υπό οριζόντια φόρτιση, ενώ στην Ενότητα 7.3 προσομοιώνεται το πρόβλημα ενός επιμήκους πεδίλου επί ελαστικού εδάφους. Τα τρία αυτά προβλήματα επιλύονται θεωρώντας ελαστικά γραμμικό υλικό, ενώ το λογισμικό για την επίλυσή τους έχει αναπτυχθεί και είναι διαθέσιμο από το Εργαστήριο Εδαφομηχανικής, Θεμελιώσεων και Τεχνικής Σεισμολογίας του ΑΠΘ.
Στη συνέχεια εξετάζονται δύο πιο περίπλοκα προβλήματα γεωτεχνικής μηχανικής, στα οποία γίνεται επιπλέον η θεώρηση της μη γραμμικής συμπεριφοράς των εδαφικών υλικών. Το πρώτο πρόβλημα αφορά την περίπτωση της φέρουσας ικανότητας ενός θεμελίου (Ενότητα 7.4), θεωρώντας είτε αστράγγιστες (Ενότητα 7.4.1) είτε στραγγιζόμενες συνθήκες φόρτισης (Ενότητα 7.4.2). Το δεύτερο πρόβλημα που παρουσιάζεται αφορά την αστοχία μίας ανυποστήρικτης εκσκαφής (Ενότητα 7.5). Τα παραπάνω προβλήματα έχουν προσομοιωθεί με το λογισμικό nemesis, που επίσης αναπτύχθηκε στο Εργαστήριο Εδαφομηχανικής, Θεμελιώσεων και Τεχνικής Σεισμολογίας του ΑΠΘ.
Τέλος, παρουσιάζεται στην Ενότητα 7.6 η προσομοίωση τυπικών εργαστηριακών δοκιμών στο πλαίσιο της μεθόδου των πεπερασμένων στοιχείων. Παρόμοιες διαδικασίες κρίνονται απαραίτητες κατά την αξιολόγηση των δυνατοτήτων λογισμικών πεπερασμένων στοιχείων, όταν πρόκειται να χρησιμοποιηθούν σε προβλήματα γεωτεχνικής μηχανικής. Στο παρόν σύγγραμμα εξετάζεται η προσομοίωση της δοκιμής ανεμπόδιστης θλίψης/εφελκυσμού (Ενότητα 7.6.1) και της δοκιμής απλής διάτμησης (Ενότητα 7.6.2). Τα παραπάνω προβλήματα έχουν προσομοιωθεί επίσης με το λογισμικό nemesis που αναφέρθηκε προηγουμένως.
Στο τέλος του κεφαλαίου παρατίθεται η σχετική βιβλιογραφία (Ενότητα 7.7).
7.1 Πεδιλοδοκός επί ελαστικού εδάφους
H θεμελίωση με πεδιλοδοκούς αποτελεί ίσως την πλέον συνηθισμένη λύση επιφανειακής θεμελίωσης. Οι πεδιλοδοκοί συνδέουν δύο ή και περισσότερα ευθυγραμμισμένα υποστυλώματα, έτσι ώστε η θεμελίωσή τους να γίνεται κοινή [1].
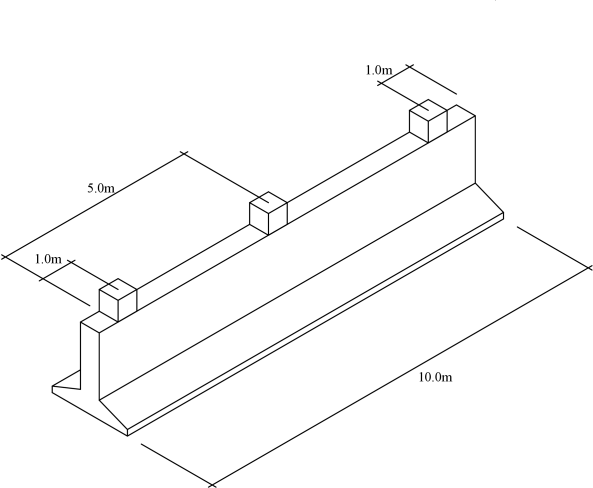
Στο παράδειγμα που εξετάζεται στη συνέχεια δίνεται πεδιλοδοκός μήκους =10.0m στην οποία καταλήγουν τρία κατακόρυφα υποστυλώματα, όπως φαίνεται στο Σχήμα 7.1. Τα δύο υποστυλώματα καταλήγουν σε απόσταση 1.0m από τα άκρα της πεδιλοδοκού μεταφέροντας κατακόρυφο φορτίο = = 1000kN, και ροπή = = 1500kNm αντίστοιχα και ένα στο μέσο της που μεταφέρει μόνο κατακόρυφο φορτίο =2000kN. Το βάθος θεμελίωσης βρίσκεται στα 2.0m. Η πεδιλοδοκός είναι τυπικής τραπεζοειδούς διατομής, με διαστάσεις m, m, m, m και m (βλέπε Σχήμα 7.2). Το μέτρο ελαστικότητας του υλικού της πεδιλοδοκού είναι kN/m και το ειδικό του βάρος 25kN/m. Τέλος, όσον αφορά το έδαφος, η τιμή της ελατηριακής του σταθεράς θεωρείται σταθερή και ίση με =10000kN/m, ενώ το ειδικό βάρος του εδάφους είναι ίσο με 20kN/m . Συγκεντρωτικά τα δεδομένα παρατίθενται στον Πίνακα 7.1.

| Παράμετρος | Τιμή |
|---|---|
| Μήκος πεδιλοδοκού | 10.0m |
| Πλάτος δοκού | 0.5m |
| Πλάτος πέλματος | 2.0m |
| Ύψος πέλματος | 0.5m |
| Ύψος κεκλιμένου τμήματος | 0.5m |
| Ελεύθερο ύψος δοκού | 0.5m |
| Συνολικό ύψος | 1.5m |
| Μέτρο ελαστικότητας (σκυρόδεμα) | 30.MPa |
| Λόγος του Poisson (σκυρόδεμα) | 0.20 |
| Κατακόρυφο φορτίο στο m, | 1000kN |
| Ροπή στο m, | 1500kN |
| Κατακόρυφο φορτίο στο m, | 2000kN |
| Κατακόρυφο φορτίο στο m, | 1000kN |
| Ροπή στο m, | 1500kN |
Για την προσομοίωση του προβλήματος, η πεδιλοδοκός ανάγεται σε γραμμική δοκό επί ελαστικού φορέα και χωρίζεται σε 40 στοιχεία μήκους 0.25m (βλ. Σχήμα 7.3).
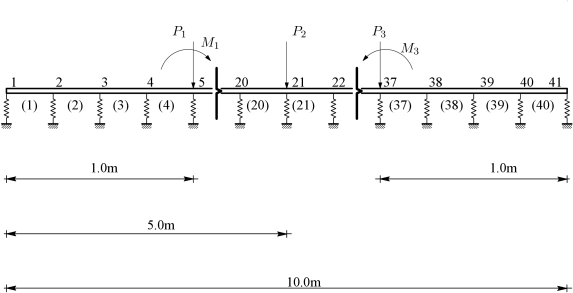
Τα αποτελέσματα της επίλυσης δίνονται στο Σχήμα 7.4.
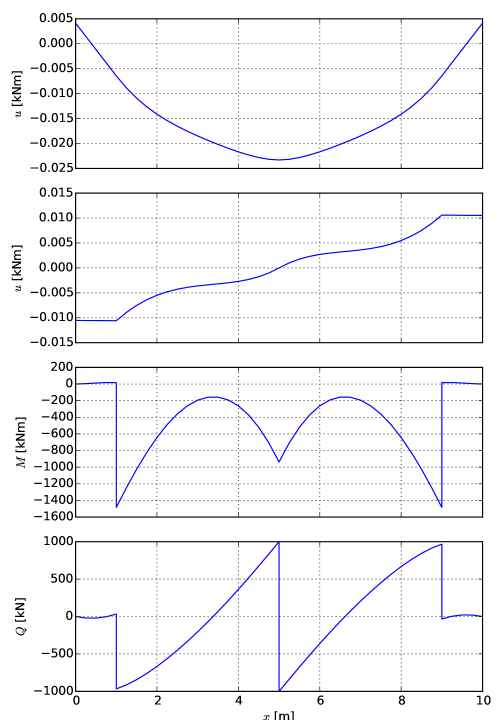
7.2 Μεμονωμένος πάσσαλος υπό οριζόντια φόρτιση
Η θεμελίωση με πασσάλους αποτελεί τον συνηθέστερο τρόπο βαθιάς θεμελιώσεως. Ως πάσσαλοι θεωρούνται τα μεμονωμένα εκείνα στοιχεία με σχετικά μικρή διάμετρο (0.30m έως και κατ’ εξαίρεση 3.00m) και αρκετά υψηλό λόγο όπου το μήκος τους, που μεταφέρουν τα φορτία της ανωδομής στα βαθύτερα στρώματα του εδάφους.
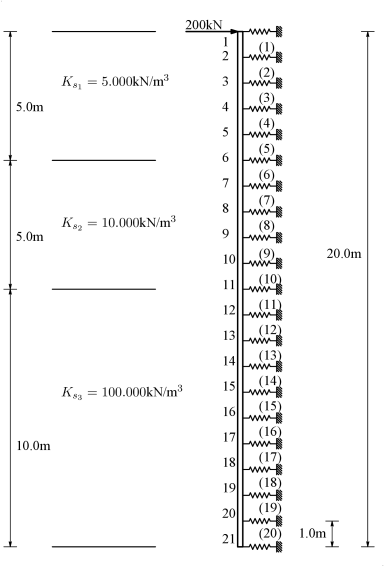
Στο παράδειγμα που εξετάζεται δίνεται πάσσαλος διαμέτρου 0.5m και μήκους 20.0m, ο οποίος φορτίζεται με οριζόντιο φορτίο στην κεφαλή ίσο με kN, όπως φαίνεται και στο Σχήμα 7.5.
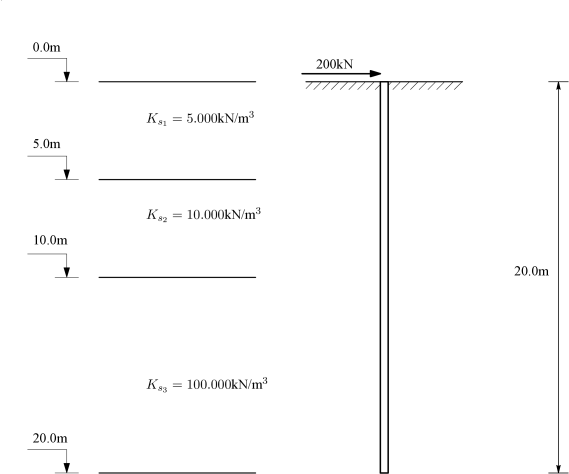
Ο πάσσαλος έχει κατασκευαστεί σε έδαφος για το οποίο δίνονται οι τιμές για την ελατηριακή σταθερά ως:
| (7.1) |
Συγκεντρωτικά τα δεδομένα παρατίθενται στον Πίνακα 7.2.
| Παράμετρος | Τιμή |
|---|---|
| Μήκος πασσάλου | 20.0m |
| Διάμετρος πασσάλου | 0.5m |
| Μέτρο ελαστικότητας (σκυρόδεμα) | 30.MPa |
| Λόγος του Poisson (σκυρόδεμα) | 0.20 |
| Οριζόντιο φορτίο στο m, | 200kN |
| Ελατηριακή σταθερά για 0m¡¡5m | 5000kN/m |
| Ελατηριακή σταθερά για 5m¡¡10m | 10000kN/m |
| Ελατηριακή σταθερά για 10m¡¡20m | 100000kN/m |
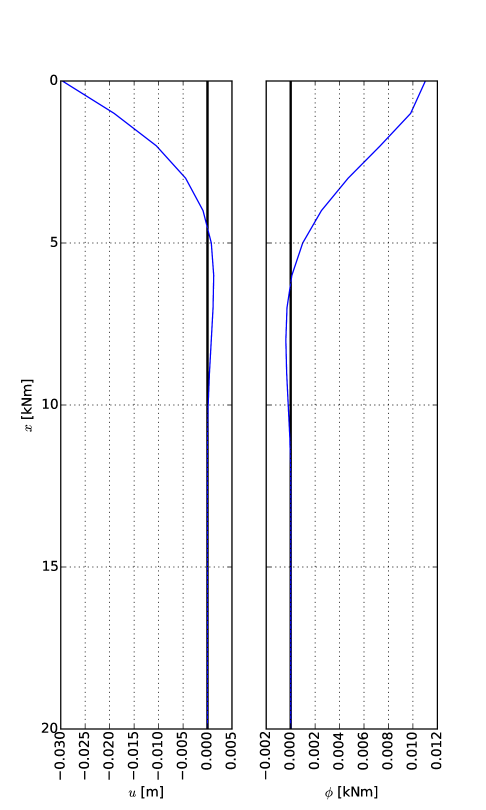
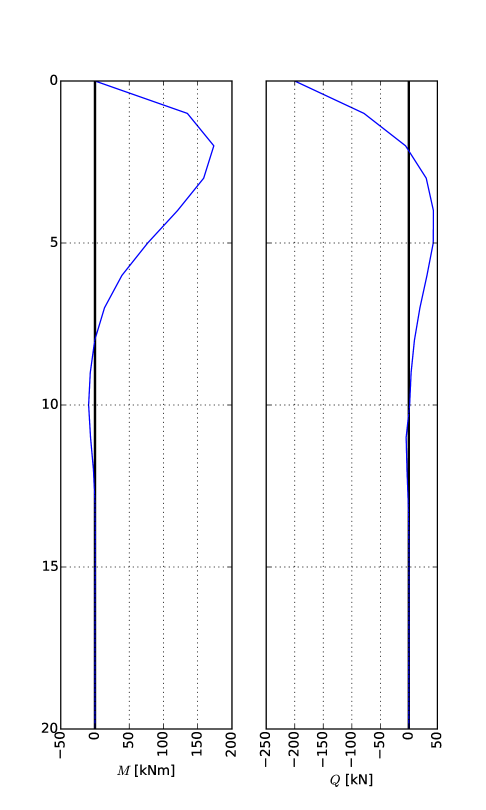
Για την προσομοίωση του προβλήματος, ο πάσσαλος ανάγεται σε γραμμική δοκό επί ελαστικού φορέα και χωρίζεται σε 20 στοιχεία μήκους 1.00m, όπως φαίνεται στο Σχήμα 7.6.
7.3 Επίμηκες πέδιλο επί ελαστικού εδάφους
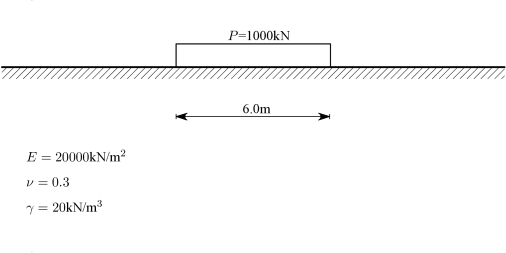
Στη συνέχεια εξετάζεται ένα επίμηκες θεμέλιο με πλάτος 6.0m στην επιφάνεια ενός εδαφικού υλικού που θεωρείται γραμμικά ελαστικό και χαρακτηρίζεται από μέτρο ελαστικότητας kN/m, ειδικό βάρος kN/m και λόγο Poisson (βλ. Σχήμα 7.9.) Το θεμέλιο, που θεωρείται εύκαμπτο, μεταφέρει στο έδαφος κατανεμημένο φορτίο ίσο με kN/m. Κατά την προσομοίωση του φορέα εξετάζονται η περιοχή επιρροής, η συμμετρία, η διακριτοποίηση, οι συνοριακές συνθήκες και το ιδίο βάρος.
Θεωρούμε ότι λόγω του θεμελίου επηρεάζεται μία περιοχή πλάτους . Η περιοχή που λαμβάνεται υπόψη προτείνεται να είναι της τάξης των ή και μεγαλύτερη, όπου το πλάτος του θεμελίου. Λόγω του εκπαιδευτικού χαρακτήρα του συγκεκριμένου παραδείγματος, η περιοχή αυτή λαμβάνεται μικρότερη.
Λόγω της συμμετρίας της κατασκευής αλλά και της φόρτισης, θα μελετηθεί μόνο η μισή από την περιοχή που προαναφέρθηκε.
Η περιοχή μελέτης χωρίζεται με τη βοήθεια τετραγωνικού δικτύου πεπερασμένων στοιχείων, που περιγράφεται από 20 κόμβους και 12 τετράκομβα στοιχεία επίπεδης παραμόρφωσης και μοναδιαίου πλάτους. Σε κάθε κόμβο θεωρούνται δύο βαθμοί ελευθερίας (β.ε.), ένας για την οριζόντια και ένας για την κατακόρυφη μετακίνηση (βλ. Σχήμα 7.10).
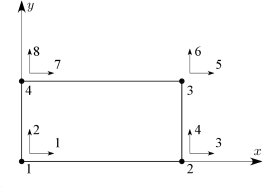
Όπως αναφέρθηκε και προηγουμένως, λόγω του εκπαιδευτικού χαρακτήρα του συγκεκριμένου παραδείγματος, η διακριτοποίηση είναι αρκετά αραιή. Στην πράξη προτιμάται πυκνότερη διακριτοποίηση, ιδίως στις περιοχές όπου αναμένονται μεγάλες διαφοροποιήσεις στα πεδία τάσεων, παραμορφώσεων και μετακινήσεων, όπως αναμένεται να συμβεί στην άκρη του θεμελίου για το συγκεκριμένο παράδειγμα.
Σε βάθος 9.0m, εκεί δηλαδή όπου θεωρούμε ότι πρακτικά σταματά η επιρροή του θεμελίου, παγιώνονται και οι δύο βαθμοί ελευθερίας, δηλαδή στους αντίστοιχους κόμβους θα τοποθετηθούν αρθρώσεις. Αντίστοιχα, στα κατακόρυφα όρια της περιοχής, επιλέγονται κυλίσεις ως στηρίξεις στους αντίστοιχους κόμβους, γιατί εκεί η κατακόρυφη μετακίνηση αναμένεται να είναι μη μηδενική.
Οι συνοριακές συνθήκες δίνονται στους γενικούς βαθμούς ελευθερίας. Οι τοπικοί βαθμοί ελευθερίας συνδέονται με τους γενικούς μέσω των σχέσεων (βλ. και Σχήμα 7.10):
-
για τον βαθμό ελευθερίας κατά τη διεύθυνση και
-
για τον βαθμό ελευθερίας κατά τη διεύθυνση
όπου ο αντίστοιχος κόμβος.
Το ιδίο βάρος υπολογίζεται από το ειδικό βάρος του υλικού της θεμελίωσης. Τα φορτία μετατρέπονται από επιφανειακά σε επικόµβια. Έτσι, για την περιοχή που μελετούμε και για μοναδιαίο πλάτος, έχουμε:
| (7.2) |
σε κάθε κόμβο. Αυτό το φορτίο θα πρέπει να εφαρμοστεί στον αντίστοιχο βαθμό ελευθερίας.
Η προσομοίωση του προβλήματος σύμφωνα με τα παραπάνω δίνεται στο Σχήμα 7.11.
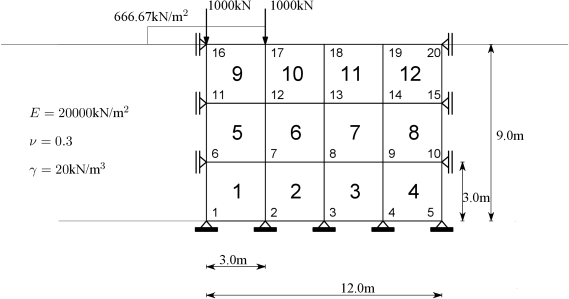
Για το προσομοίωμα του Σχήματος 7.11, ένα τυπικό αρχείο εισόδου για ένα πρόγραμμα πεπερασμένων στοιχείων δίνεται στη συνέχεια.
| 1 | 20,12,16,2,1,2,1. |
| 2 | 0., 0. |
| 3 | 3., 0. |
| 4 | 6., 0. |
| 5 | 9., 0. |
| 6 | 12., 0. |
| 7 | 0., 3. |
| 8 | 3., 3. |
| 9 | 6., 3. |
| 10 | 9., 3. |
| 11 | 12., 3. |
| 12 | 0., 6. |
| 13 | 3., 6. |
| 14 | 6., 6. |
| 15 | 9., 6. |
| 16 | 12., 6. |
| 17 | 0., 9. |
| 18 | 3., 9. |
| 19 | 6., 9. |
| 20 | 9., 9. |
| 21 | 12., 9. |
| 22 | 1, 2, 7, 6, 1 |
| 23 | 2, 3, 8, 7, 1 |
| 24 | 3, 4, 9, 8, 1 |
| 25 | 4, 5,10, 9, 1 |
| 26 | 6, 7,12,11, 1 |
| 27 | 7, 8,13,12, 1 |
| 28 | 8, 9,14,13, 1 |
| 29 | 9,10,15,14, 1 |
| 30 | 11,12,17,16, 1 |
| 31 | 12,13,18,17, 1 |
| 32 | 13,14,19,18, 1 |
| 33 | 14,15,20,19, 1 |
| 34 | 1,0. |
| 35 | 2,0. |
| 36 | 3,0. |
| 37 | 4,0. |
| 38 | 5,0. |
| 39 | 6,0. |
| 40 | 7,0. |
| 41 | 8,0. |
| 42 | 9,0. |
| 43 | 10,0. |
| 44 | 11,0. |
| 45 | 19,0. |
| 46 | 21,0. |
| 47 | 29,0. |
| 48 | 31,0. |
| 49 | 39,0. |
| 50 | 32,-1000. |
| 51 | 34,-1000. |
| 52 | 20000,0.3,20. |
Η παραπάνω δομή του αρχείου εισόδου αφορά το εκπαιδευτικό λογισμικό FEM.EDU του εργαστηρίου. Πιο συγκεκριμένα, στο υπόψη αρχείο δίνονται:
-
•
Στην πρώτη γραμμή nn, ne, nd, nl, nm, at, th όπου:
-
nn
Ο αριθμός των κόμβων.
-
ne
Ο αριθμός των στοιχείων.
-
nd
Ο αριθμός των προκαθορισμένων μετακινήσεων.
-
nl
Ο αριθμός των φορτίων.
-
nm
Ο αριθμός των υλικών.
-
at
Ο τύπος του προβλήματος. Παίρνει τιμές:
-
1
για την περίπτωση της επίπεδης έντασης.
-
2
για την περίπτωση της επίπεδης παραμόρφωσης.
-
3
για την περίπτωση της αξονοσυµµετρίας.
-
1
-
th
Το πάχος του προβλήματος (για την περίπτωση της αξονοσυµµετρίας αφορά τη γωνία μετρημένη σε rad).
-
nn
-
•
Στις επόμενες nn γραμμές οι συντεταγμένες και του κάθε κόμβου.
-
•
Στις επόμενες ne γραμμές οι κόμβοι που αποτελούν το στοιχείο και το υλικό του στοιχείου.
-
•
Στις επόμενες nd γραμμές οι βαθμοί ελευθερίας με προκαθορισμένη μετακίνηση και η τιμή της μετακίνησης.
-
•
Στις επόμενες nl γραμμές οι βαθμοί ελευθερίας με προκαθορισμένο φορτίο και η τιμή του φορτίου.
-
•
Τέλος, στις επόμενες nm γραμμές τα υλικά και οι παράμετροί τους.
Στο Σχήμα 7.12 δίνονται χαρακτηριστικά αποτελέσματα της επίλυσης του συγκεκριμένου παραδείγματος.
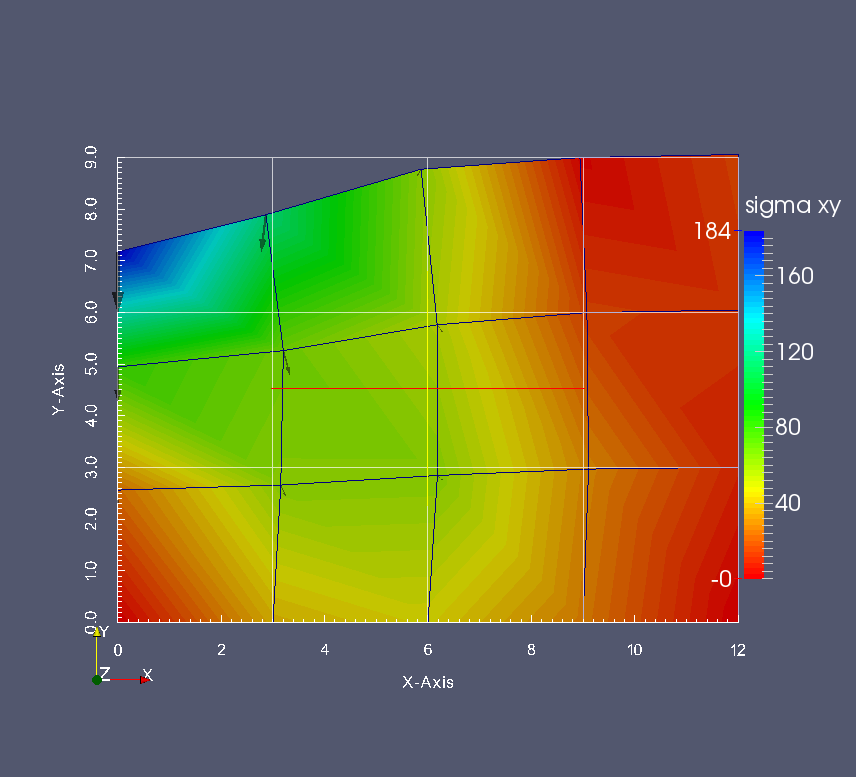
7.4 Φέρουσα ικανότητα θεμελίου
Η φέρουσα ικανότητα ενός θεμελίου αποτελεί ένα από τα θεμελιώδη προβλήματα της γεωτεχνικής μηχανικής και συναντάται τόσο στη σχετική βιβλιογραφία όσο και στις αντίστοιχες κανονιστικές διατάξεις. Χαρακτηριστικά αναφέρονται οι εργασίες των Prandtl [17], Hencky [10], Terzaghi & Peck [22], Meyerhof [15], Hansen [9] και Vesic [24] αλλά και οι κανονισμοί DIN 4017 [7] και ο Ευρωκώδικας 7 [6].
Στη συνέχεια εξετάζονται οι περιπτώσεις φόρτισης υπό αστράγγιστες και υπό πλήρως στραγγιζόμενες συνθήκες και οι λύσεις συγκρίνονται με τις αντίστοιχες θεωρητικές λύσεις ή με τις αντίστοιχες κανονιστικές διατάξεις.
7.4.1 Φόρτιση υπό αστράγγιστες συνθήκες
Το έδαφος θεωρείται ισότροπο, αβαρές, σχεδόν ασυμπίεστο () και υποβάλλεται σε κεντρική κατακόρυφη φόρτιση υπό αστράγγιστες συνθήκες.
Σύμφωνα με τη θεωρία, η αστοχία επέρχεται για τιμή του οριακού φορτίου ίση με:
| (7.3) |
Αν η αστράγγιστη διατμητική αντοχή θεωρηθεί μοναδιαία, τότε σύμφωνα με την παραπάνω σχέση ισχύει και για την περίπτωση ενός επιμήκους θεμελίου σύμφωνα με τον Prandtl [17] ισχύει:
| (7.4) |
ενώ για την περίπτωση κυκλικού θεμελίου σύμφωνα με τους Cox et al. [5] ισχύει:
| (7.5) |
θεωρώντας λεία ή τραχιά διεπιφάνεια μεταξύ εδάφους και θεμελίωσης αντίστοιχα.
Τέλος, για την περίπτωση ενός τετραγωνικού θεμελίου δεν υπάρχει ακριβής λύση για τον υπολογισμό της φέρουσας ικανότητας. Σύμφωνα με τον Levin [13], η λύση αναμένεται ανάμεσα στις δύο προηγούμενες. Οι Shield και Drucker [20] πρότειναν το 1953 μία λύση άνω ορίου ίση με:
| (7.6) |
οι Michalowski και Dawson [16] το 2002 μία λύση με τη μέθοδο των πεπερασμένων διαφορών ίση με
| (7.7) |
και οι Gourvenec et al. [8] το 2006 μία λύση με τη μέθοδο των πεπερασμένων στοιχείων ίση με: ίση με
| (7.8) |
Για την προσομοίωση του προβλήματος υπό συνθήκες επίπεδης έντασης ή αξονοσυμμετρίας επιλέγεται το δίκτυο πεπερασμένων στοιχείων του Σχήματος 7.13 το οποίο στηρίζεται στο δίκτυο SRF3 που χρησιμοποιείται κατά τις πρότυπες επιλύσεις των Sloan & Randolph [21] και αποτελείται από 324 κόμβους και 289 τετράπλευρα στοιχεία. Για τις ανάγκες του τρισδιάστατου προσομοιώματος χρησιμοποιείται το αντίστοιχο δίκτυο το οποίο αποτελείται από 5832 κόμβους και 4913 εξαεδρικά στοιχεία (Σχήμα 7.14). Για την αποφυγή του έντονου κλειδώματος (locking) που χαρακτηρίζει τη συμπεριφορά των τυπικών στοιχείων σε καταστάσεις ασυμπιεστότητας, χρησιμοποιούνται τετράπλευρα και εξαεδρικά B-Bar στοιχεία [11] αντίστοιχα. Η απομείωση του εύρους της ζώνης του συνολικού μητρώου του προβλήματος πραγματοποιείται με την εφαρμογή του αλγορίθμου των Cuthill & McKee, ενώ για την επίλυση του μη γραμμικού προβλήματος χρησιμοποιείται η μέθοδος των Broyden-Fletcher-Goldfarb-Shanno (BFGS, βλ. π.χ. [2]), η οποία επιταχύνεται με τον αλγόριθμο line search [14]. Τέλος, η επίλυση του γραμμικού συστήματος εξισώσεων γίνεται με τη βοήθεια της βιβλιοθήκης LAPACK και η σύγκλιση θεωρείται ότι επιτυγχάνεται όταν οι τιμές της απόλυτης, της σχετικής και της ενεργειακής νόρμας είναι αντίστοιχα μικρότερες από , και .
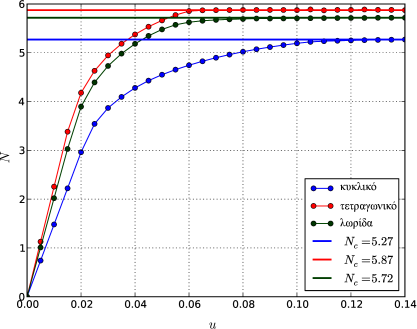
Τα δεδομένα του προβλήματος δίνονται στον Πίνακα 7.3 ενώ τα αποτελέσματα των επιλύσεων φαίνονται στο Σχήμα 7.15.
| Παράμετρος | Τιμή |
|---|---|
| 1 | |
| 100 | |
| 0.499995 |
7.4.2 Φόρτιση υπό πλήρως στραγγιζόμενες συνθήκες
Η πλήρης εξίσωση της φέρουσας ικανότητας του εδάφους για την περίπτωση πεδίλου λωρίδας όπως προτάθηκε αρχικά από τους Buisman [4] και Terzaghi [22] δίνεται από την παρακάτω σχέση:
| (7.9) |
Σε επίπεδο κανονισμών χρησιμοποιείται η επόμενη σχέση, η οποία στην Αμερική συνήθως αποδίδεται στον Meyerhof [15] ενώ στην Ευρώπη αντίστοιχα στον Hansen [9]:
| (7.10) |
όπου:
-
•
, και συντελεστές σχήματος,
-
•
, και συντελεστές βάθους,
-
•
, και συντελεστές κλίσης εδάφους και
-
•
, και συντελεστές κλίσης της βάσης θεμελίωσης.
Σημειώνεται ότι δεν προβλέπεται το σύνολο των συντελεστών σε όλους τους κανονισμούς. Στην παραπάνω σχέση είναι το πλάτος του θεμελίου, η ενεργός συνοχή, η υπερκείμενη τάση, το ενεργό βάρος και , και οι συντελεστές της φέρουσας ικανότητας.
Για τους συντελεστές και σε επίπεδο κανονισμών είναι αποδεκτός ο υπολογισμός τους σύμφωνα με τις προτάσεις των Reissner [19] και Prandtl [18] αντίστοιχα, σε όρους της γωνίας τριβής :
| (7.11) | ||||
| (7.12) |
Για τον συντελεστή όμως υπάρχουν διάφορες προτάσεις τόσο στη βιβλιογραφία όσο και στους κανονισμούς. Στην Ευρώπη κατά τον σχεδιασμό γεωτεχνικών έργων χρησιμοποιείται συνήθως η σχέση του Hansen [9]:
| (7.13) |
ενώ στην Αμερική η σχέση του Meyerhof [15]:
| (7.14) |
Κατά τον σχεδιασμό υπεράκτιων έργων προτείνεται η χρήση της σχέσης του Vesic [23]:
| (7.15) |
για την οποία πρόσφατες δημοσιεύσεις θεωρούν ότι υπερεκτιμά την τιμή του . Τέλος, υπάρχει και η σχέση του Chen:
| (7.16) |
η οποία συμπεριλαμβάνεται στο παράρτημα του Ευρωκώδικα 7 [6].
Για τις ανάγκες του παραδείγματος πραγματοποιήθηκε μια ανάλυση επίπεδης παραμόρφωσης χρησιμοποιώντας το δίκτυο του Σχήματος 7.13 με τα δεδομένα που παρατίθενται στον Πίνακα 7.4.
| Παράμετρος | Τιμή |
|---|---|
| 0.20 |
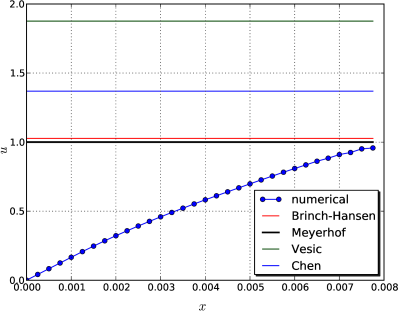
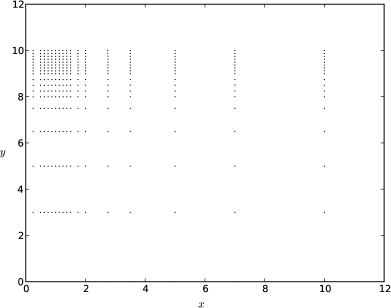
Τα αποτελέσματα της ανάλυσης παρατίθενται στο Σχήμα 7.16 και συγκρίνονται με τις παραπάνω προτάσεις. Στο Σχήμα 7.17 παρατίθενται επίσης οι διαφορές μεταξύ των δύο τελευταίων διαδοχικών βημάτων φόρτισης.
 |
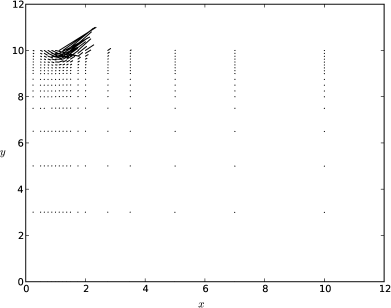 |
7.5 Αστοχία ανυποστήρικτης εκσκαφής
Σύμφωνα με τη θεωρία του Coulomb (βλ. π.χ. [3]), μία εδαφική μάζα πίσω από έναν κατακόρυφο τοίχο αντιστήριξης βρίσκεται σε κατάσταση οριακής ισορροπίας και τείνει να ολισθήσει κατά μήκος ενός επιπέδου κεκλιμένου ως προς το οριζόντιο κατά γωνία , όπου η γωνία τριβής (βλ. Σχήμα 7.18).
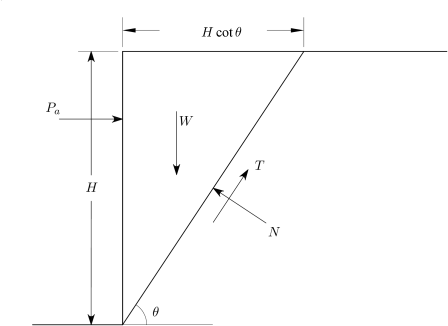
Αν θεωρηθεί ότι , εύκολα προκύπτει από μεθόδους οριακής ισορροπίας το κρίσιμο βάθος , που ορίζεται ως εκείνο το βάθος για το οποίο η εκσκαφή μπορεί να παραμείνει ανυποστήρικτη. Στην περίπτωση πλήρους κορεσμένου εδάφους, το κρίσιμο βάθος ισούται με:
| (7.17) |
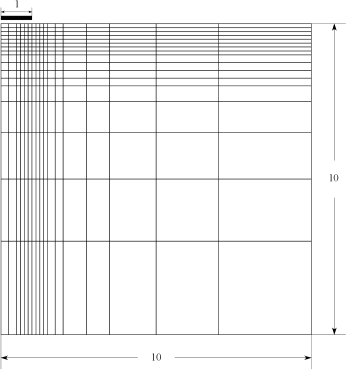
Για την προσομοίωση του προβλήματος επιλέγεται περιοχή ενώ το ημιπλάτος της εκσκαφής θεωρείται ίσο με (Σχήμα 7.19). Η περιοχή διακριτοποιείται σε ένα δίκτυο τυπικών τετράκομβων τετράπλευρων πεπερασμένων στοιχείων.
| Παράμετρος | Τιμή |
|---|---|
| Μέτρο ελαστικότητας | 40000kPa |
| Λόγος του Poisson | 0.20 |
| Συνοχή | 13.23771kPa |
| Γωνία τριβής | |
| Ειδικό βάρος | 20.kN/m |
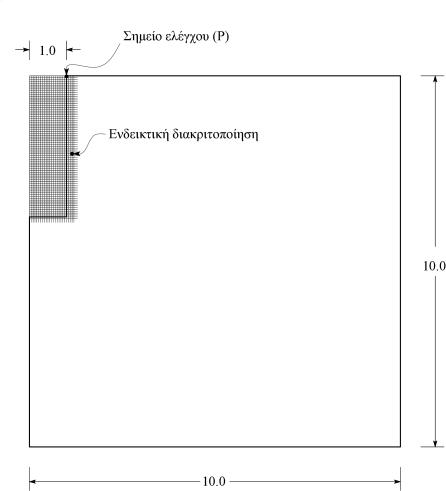
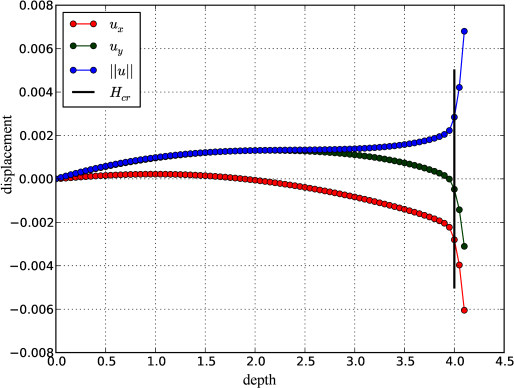
Η επίλυση αφορά ένα έδαφος με χαρακτηριστικά που δίνονται στον Πίνακα 7.5, από τα οποία σύμφωνα με την (7.17) προκύπτει κρίσιμο ύψος ίσο με . Κατά την επίλυση υπολογίζονται αρχικά οι γεωστατικές τάσεις θεωρώντας συντελεστή ωθήσεων σε ηρεμία . Στη συνέχεια αυξάνεται διαρκώς το βάθος της εκσκαφής αφαιρώντας διαδοχικά σε κάθε βήμα μία στρώση ύψους μέχρι τη δημιουργία πλαστικού μηχανισμού αστοχίας.
Η απομείωση του εύρους της ζώνης του συνολικού μητρώου του προβλήματος πραγματοποιείται με την εφαρμογή του αλγορίθμου των Cuthill & McKee, ενώ για την επίλυση του μη γραμμικού προβλήματος χρησιμοποιείται η μέθοδος των Broyden-Fletcher-Goldfarb-Shanno (BFGS), η οποία επιταχύνεται με τον αλγόριθμο line search. Τέλος, η επίλυση του γραμμικού συστήματος εξισώσεων γίνεται με τη βοήθεια της βιβλιοθήκης LAPACK και η σύγκλιση θεωρείται ότι επιτυγχάνεται όταν οι τιμές της απόλυτης, της σχετικής και της ενεργειακής νόρμας είναι αντίστοιχα μικρότερες από , και .
Ο μηχανισμός αστοχίας σχηματίζεται τελικά για βάθος εκσκαφής , σε πλήρη συμφωνία με τη θεωρία. Οι οριζόντιες, κατακόρυφες και συνολικές μετακινήσεις δίνονται στο Σχήμα 7.20.
7.6 Αριθμητική προσομοίωση εργαστηριακών δοκιμών
Τέλος εξετάζεται η προσομοίωση μιας σειράς αριθμητικών δοκιμών που περιγράφουν χαρακτηριστικές καταστάσεις φόρτισης. Παρόμοιες προσομοιώσεις θεωρούνται εξαιρετικά χρήσιμες κατά τον έλεγχο και την αξιολόγηση των καταστατικών μοντέλων που παρέχονται από εμπορικά προγράμματα αριθμητικής ανάλυσης.
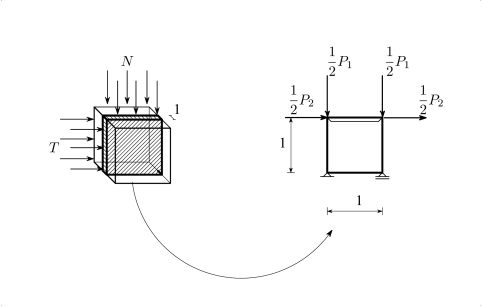
Για τις ανάγκες των δοκιμών που ακολουθούν εισάγονται τα δύο αριθμητικά προσομοιώματα που φαίνονται στα επόμενα σχήματα (Σχήμα 7.21 και Σχήμα 7.22). Το πρώτο προσομοίωμα (Σχήμα 7.21) αφορά τριαξονική φόρτιση υπό συνθήκες αξονοσυμμετρίας, ενώ με το δεύτερο (Σχήμα 7.22) προσομοιώνεται η δοκιμή απλής διάτμησης σε συνθήκες επίπεδης παραμόρφωσης. Και στις δύο περιπτώσεις το προσομοίωμα πεπερασμένων στοιχείων αποτελείται τελικά από ένα μοναδικό τυπικό τετράπλευρο, τετράκομβο στοιχείο αξονοσυμμετρίας ή επίπεδης παραμόρφωσης αντίστοιχα. Επιπροσθέτως, επιβάλλεται με τη μέθοδο της ποινής στην τελευταία περίπτωση ίδια οριζόντια και κατακόρυφη μετακίνηση στους ελεύθερους κόμβους.
Ο έλεγχος της βηματικής φόρτισης εξαρτάται από τη φύση του εκάστοτε προβλήματος και πραγματοποιείται είτε ελέγχοντας το φορτίο είτε ελέγχοντας τις μετακινήσεις. Σε όλες τις αριθμητικές δοκιμές θεωρείται ότι το υλικό είναι ισότροπο και αβαρές. Για την επίλυση του μη γραμμικού προβλήματος χρησιμοποιείται η τροποποιημένη μέθοδος Newton-Raphson και η σύγκλιση θεωρείται ότι επιτυγχάνεται όταν οι τιμές της απόλυτης, της σχετικής και της ενεργειακής νόρμας είναι αντίστοιχα μικρότερες από , και .
Στα αποτελέσματα των αριθμητικών δοκιμών που παρατίθενται στη συνέχεια, ακολουθείται η σύμβαση προσήμου της εδαφομηχανικής, σύμφωνα με την οποία θετικές τάσεις θεωρούνται οι θλιπτικές.
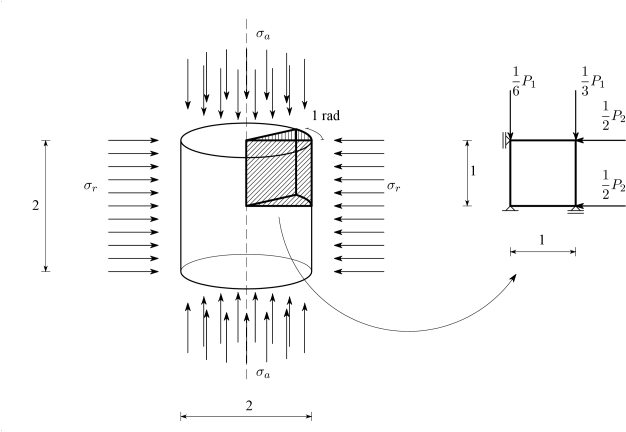
7.6.1 Δοκιμή ανεμπόδιστης θλίψης/εφελκυσμού
Εξετάζεται η δοκιμή ανεμπόδιστης θλίψης/εφελκυσμού όπως προκύπτει από το προσομοίωμα του Σχήματος 7.21, θεωρώντας και ή για τη θλίψη ή τον εφελκυσμό αντίστοιχα. Το υλικό θεωρείται ότι διαρρέει σύμφωνα με τα κριτήρια Mohr-Coulomb και Tresca και οι τιμές των αντίστοιχων παραμέτρων δίνονται στον Πίνακα 7.6. Η επίλυση γίνεται με έλεγχο των μετακινήσεων θεωρώντας βήμα αύξησης των μετακινήσεων ίσο με και εξετάζοντας συνολικά 60 βήματα φόρτισης.
| Παράμετρος | Τιμή |
|---|---|
| Μέτρο ελαστικότητας | 1000. |
| Λόγος του Poisson | 0.25 |
| Συνοχή | 15. |
| Γωνία τριβής | |
| Γωνία διαστολής | |
| Αστράγγιστη διατμητική αντοχή |
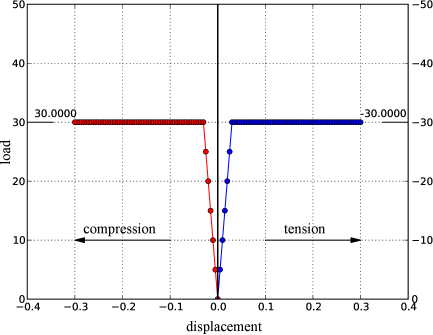
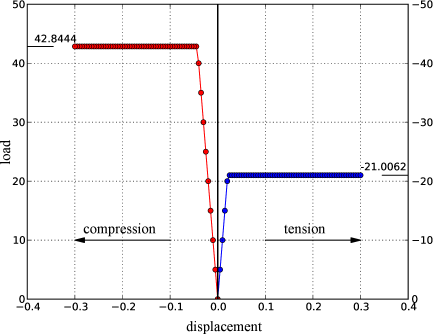
Και στις δύο περιπτώσεις οι τάσεις οδηγούνται υποχρεωτικά στην τομή δύο ενεργών επιφανειών ( για την περίπτωση του εφελκυσμού και για την περίπτωση της θλίψης αντίστοιχα). Τα αποτελέσματα της αριθμητικής επίλυσης δίνονται στα Σχήματα 7.23 και 7.24 και αποδεικνύεται εύκολα ότι ταυτίζονται με τη θεωρία.
7.6.2 Δοκιμή απλής διάτμησης
Στο παράδειγμα που ακολουθεί εξετάζεται η συμπεριφορά σε μια δοκιμή απλής διάτμησης ενός υλικού που διαρρέει σύμφωνα με το κριτήριο Mohr-Coulomb. Στο συγκεκριμένο παράδειγμα εξετάζεται η εφαρμογή του μη συζευγμένου κανόνα ροής, ο οποίος στο υπόψη κριτήριο περιγράφεται από τη γωνία διαστολής .
| Παράμετρος | Τιμή |
|---|---|
| Μέτρο ελαστικότητας | 1000. |
| Λόγος του Poisson | 0.25 |
| Συνοχή | 15. |
| Γωνία τριβής | |
| Γωνία διαστολής |
Για την αριθμητική προσομοίωση του προβλήματος χρησιμοποιείται το προσομοίωμα του Σχήματος 7.22. Η φόρτιση που επιβάλλεται περιλαμβάνει δύο στάδια:
-
1.
Την εφαρμογή μιας κατακόρυφης δύναμης ίσης με .
-
2.
Την εφαρμογή μιας οριζόντιας δύναμης το μέγεθος της οποίας καθορίζεται από τον έλεγχο μετακινήσεων, ώστε σε κάθε βήμα η αύξηση της οριζόντιας μετακίνησης να ισούται με . Η επίλυση πραγματοποιείται για 50 βήματα.
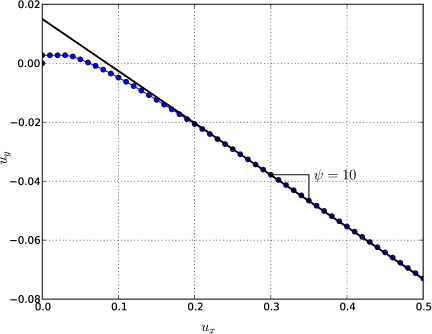
Τα αποτελέσματα της επίλυσης δίνονται στο Σχήμα 7.25, όπου κατά την εφαρμογή της οριζόντιας φόρτισης διακρίνονται αρχικά οι ελαστικές παραμορφώσεις () και στη συνέχεια οι πλαστικές ογκομετρικές παραμορφώσεις που περιγράφονται από τη γωνία διαστολής .
7.7 Βιβλιογραφία
- 1 Joseph E. Bowles. Foundation analysis and design. 1988.
- 2 C. G. Broyden. The convergence of a class of double-rank minimization algorithms – 1. General considerations. IMA Journal of Applied Mathematics, 6(1): 76, 1970.
- 3 M. Budhu. Soil mechanics and foundations. John Wiley & Son, 2009.
- 4 A. S. K. Buisman. Grondmechanica. Walman, Delft, 281, 1940.
- 5 A. D. Cox. Axially-symmetric plastic deformation in soils – II. Indentation of ponderable soils. International Journal of Mechanical Sciences, 4(5): 371-380, 1962.
- 6 Comité Europeen de Normalisation. Eurocode 7: Geotechnical design. European Prestandard ENV, 1, 1997.
- 7 Deutsches Institut für Normung. DIN 4017:2006-03 Baugrund - Berechnung des Grundbruchwiderstands von Flachgründungen, 2006.
- 8 S. Gourvenec, M. Randolph and O. Kingsnorth. Undrained bearing capacity of square and rectangular footings. International Journal of Geomechanics, 6: 147, 2006.
- 9 J. B. Hansen. A Revised and Extended Formula for Bearing Capacity. Danish Geotechnical Institute Bulletin, 28: 5-11, 1970.
- 10 H. Hencky. Über Einige Statisch Bestimmte Fälle des Gleichgewichts in Plastischen Körpern. ZAMM-Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik, 3(4): 241-251, 1923.
- 11 T. J. R. Hughes. Generalization of selective integration procedures to anisotropic and nonlinear media. International Journal for Numerical Methods in Engineering, 15(9): 1413-1418, 1980.
- 12 Fotios E. Karaoulanis. nemesis. an experimental finite element code. http://www.nemesis-project.org. [Online; accessed 20-October-2015].
- 13 E. Levin. Indentation pressure of a smooth circular punch. Quarterly of Applied Mathematics, 13: 133-137, 1955.
- 14 H. Matthies and G. Strang. The Solution of Nonlinear Finite Element Equations. International Journal for Numerical Methods in Engineering, 14(11): 1613-1626, 1979.
- 15 G. G. Meyerhof. Some recent research on the bearing capacity of foundations. Canadian Geotechnical Journal, 1(1): 16-26, 1964.
- 16 R. L. Michalowski. Upper-bound load estimates on square and rectangular footings. Géotechnique, 51(9): 787-798, 2001.
- 17 L. Prandtl. Uber die Harte Plastischer Korper. Nachrichten von der Gesellschaft der Wissenschaften zu Gottingen, Mathematisch Phisicalische Klasse, page 74, 1920.
- 18 L. Prandtl. Über die Eindringungsfestigkeit (Härte) Plastische Baustoffe und die Festigkeit von Schneiden. Z. Angew. Math. Mech, 1(1): 15-20, 1921.
- 19 H. Reissner. Zum Erddruckproblem. In Proc. First Intem. Congress of Applied Mechanics, pp. 295-311, 1924.
- 20 R. T. Shield and D. C. Drucker. The Application of Limit Analysis to Punch-Indentation Problems. Journal of Applied Mechanics, 20(4), 1953.
- 21 S. W. Sloan and M. F. Randolph. Numerical Prediction of Collapse Loads Using Finite Element Methods. International Journal for Numerical and Analytical Methods in Geomechanics, 6(1): 47-76, 1982.
- 22 K. Terzaghi and R. B. Peck. Soil mechanics. Wiley, New York, 1943.
- 23 A. S. Vesic. Analysis of ultimate loads of shallow foundations. Journal of the Soil Mechanics and Foundations Division, 99(1): 45-73, 1973.
- 24 A. S. Vesic. Bearing capacity of shallow foundations. Foundation Engineering Handbook, 2: 121-147, 1975.