Κεφάλαιο 4 Μόρφωση του συστήματος εξισώσεων. Επίλυση και επεξεργασία των αποτελεσμάτων
Στο παρόν κεφάλαιο περιγράφεται η διαδικασία με την οποία γίνεται η μεταφορά από το τοπικό στο συνολικό μητρώο δυσκαμψίας, η μόρφωση και η επίλυση του συστήματος εξισώσεων και η επεξεργασία των αποτελεσμάτων.
Πιο συγκεκριμένα, στην Ενότητα 4.1 εξετάζεται η αντιστοίχιση των βαθμών ελευθερίας από το τοπικό στο συνολικό μητρώο δυσκαμψίας.
Στη συνέχεια εξετάζονται αλγόριθμοι επαναρίθμησης των βαθμών ελευθερίας και αναδιάταξης του συνολικού μητρώου δυσκαμψίας με σκοπό τη μείωση των απαιτήσεων σε αποθηκευτικό χώρο στη μνήμη του υπολογιστή (Ενότητα 4.2) και εξετάζεται σε συντομία η αντίστροφη μέθοδος Cuthill-Mckee (Ενότητα 4.2.1).
Ακολουθεί η παρουσίαση των μεθόδων αποθήκευσης των συντελεστών του συνολικού μητρώου δυσκαμψίας (Ενότητα 4.3): Η αποθήκευση του μητρώου σε πλήρη μορφή (Ενότητα 4.3.1), σε συμμετρική μορφή (Ενότητα 4.3.2), σε ταινιωτή μορφή ή μορφή λωρίδας (Ενότητα 4.3.3), σε μορφή προφίλ ή κορυφογραμμής (Ενότητα 4.3.4) και σε αραιή μορφή (Ενότητα 4.3.5).
Στη συνέχεια δίνονται τρόποι επίλυσης του συστήματος εξισώσεων, τόσο άμεσοι όσο και επαναληπτικοί (Ενότητα 4.4). Παρουσιάζονται η μέθοδος απαλοιφής Gauss (Ενότητα 4.4.1), η μέθοδος Cholesky (Ενότητα 4.4.2) και η μέθοδος της συζυγούς διανυσματικής κλίσης (Ενότητα 4.4.3).
Ακολουθεί η επεξεργασία και τρόποι απεικόνισης των αποτελεσμάτων (Ενότητα 4.5), όπως αυτή πραγματοποιείται είτε στους κόμβους των στοιχείων (Ενότητα 4.5.1) είτε στα σημεία ολοκλήρωσης (Ενότητα 4.5.2).
Στο τέλος του κεφαλαίου παρατίθεται η σχετική βιβλιογραφία (Ενότητα 4.6).
4.1 Το συνολικό μητρώο δυσκαμψίας
Για τη μόρφωση του συνολικού συστήματος συνήθως ακολουθείται η εξής διαδικασία:
-
1.
Οι τοπικοί βαθμοί ελευθερίας ορίζονται σε κάθε κόμβο και αριθμούνται επί του συνόλου σύμφωνα με κάποιο σχήμα αρίθμησης. Το σχήμα αυτό μπορεί είτε να ακολουθεί μια συνεχόμενη αρίθμηση στους βαθμούς ελευθερίας, ανάλογα με τον κόμβο στον οποίο βρίσκονται, είτε κάποια εντελώς τυχαία διαδικασία. Η αρίθμηση των βαθμών ελευθερίας αποθηκεύεται για κάθε κόμβο, σε ένα διάνυσμα, έστω (Freedom Fable).
-
2.
Για κάθε στοιχείο δημιουργείται το αντίστοιχο διάνυσμα , παραθέτοντας τα επιμέρους αντίστοιχα διανύσματα των κόμβων του στοιχείου, όπως αυτοί έχουν προκύψει από την αρίθμηση του βήματος 1.
-
3.
Οι θέσεις των στο γενικό μητρώο βρίσκονται πλέον με τη βοήθεια της σχέσης:
(4.1) όπως σχηματικά δίνεται και στο Σχήμα 4.1.

4.2 Αλγόριθμοι επαναρίθμησης
Η μόρφωση του μητρώου δυσκαμψίας οδηγεί συχνά σε δομές μητρώων οι οποίες δεν είναι οι βέλτιστες ούτε όσον αφορά την αποθήκευση του μητρώου αλλά ούτε και στην επίλυση του συστήματος.
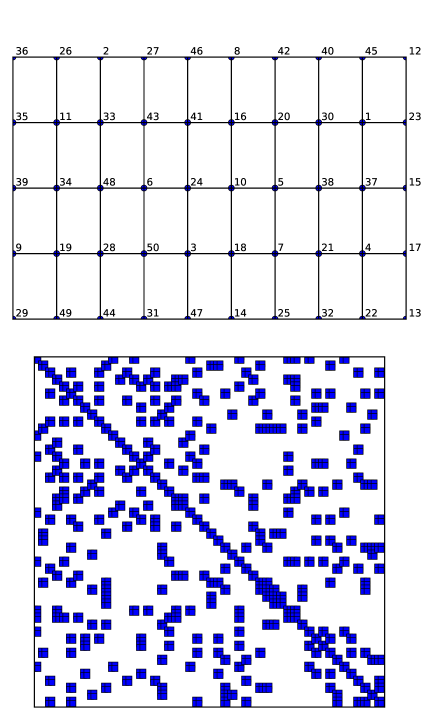
Χαρακτηριστικές δομές μητρώων δυσκαμψίας για διάφορες περιπτώσεις μόρφωσης του μητρώου για το ίδιο πρόβλημα δίνονται στα επόμενα σχήματα. Πιο συγκεκριμένα, στο Σχήμα 4.2 δίνεται το πρόβλημα (ορθογωνικό δίκτυο πεπερασμένων στοιχείων), η αρίθμηση των κόμβων (κατά γραμμές) και η αντίστοιχη δομή του μητρώου, όπου με μπλε τετράγωνα σχεδιάζονται οι μη μηδενικοί όροι. Για το ίδιο πρόβλημα και αρίθμηση των κόμβων κατά στήλες, το αντίστοιχο διάγραμμα δίνεται στο Σχήμα 4.2, ενώ τέλος για τυχαία αρίθμηση των κόμβων το αντίστοιχο διάγραμμα δίνεται στο Σχήμα 4.4.
Διαπιστώνεται ότι:
-
•
Τα μητρώα δυσκαμψίας αποτελούνται πρωτίστως από μηδενικούς όρους.
-
•
Η αρίθμηση των κόμβων και κατ’ επέκταση των βαθμών ελευθερίας επηρεάζει σε σημαντικό βαθμό τη δομή του μητρώου δυσκαμψίας και κατ’ επέκταση τη μορφή των εξισώσεων του προβλήματος.
Υπάρχουν στη βιβλιογραφία αρκετοί αλγόριθμοι επαναρίθμησης, οι οποίοι επιδιώκουν να μειώσουν το πλάτος λωρίδας του παραγόμενου μητρώου του συστήματος (όπως π.χ. οι αλγόριθμοι Cuthill-McKee, King) είτε το προφίλ του μητρώου (Sloan), είτε ακόμα τον επιπλέον χώρο που μπορεί να χρειαστεί κατά την επίλυσή του (αρίθμηση ελάχιστου βαθμού). Στη συνέχεια δίνεται συνοπτικά η αντίστροφη μέθοδος Cuthill-Mckee.


4.2.1 Η αντίστροφη μέθοδος Cuthill-Mckee
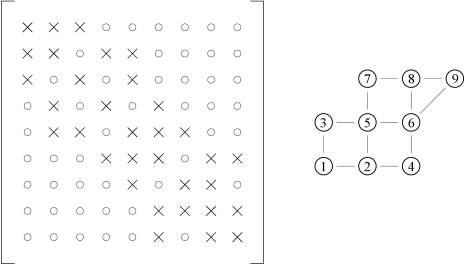
Η αντίστροφη μέθοδος Cuthill-Mckee [2] στηρίζεται στη θεωρία των γραφημάτων για να μειώσει το εύρος ενός μητρώου. Θεωρώντας ένα συμμετρικό μητρώο αρχικά δημιουργείται το γράφημα που αντιστοιχεί στο υπόψη μητρώο και στη συνέχεια γίνεται η επαναρίθμηση του γραφήματος ώστε το μητρώο να έχει το ελάχιστο εύρος.
Έστω για παράδειγμα το μητρώο και το γράφημα του Σχήματος 4.5.

Αν επαναπαριθμηθούν οι κορυφές του γραφήματος χωρίς να τροποποιηθεί ο τρόπος με τον οποίο αυτές συνδέονται, όπως φαίνεται στο Σχήμα 4.6, προκύπτει ένα μητρώο με μειωμένο εύρος.
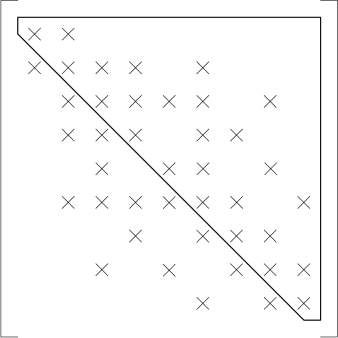
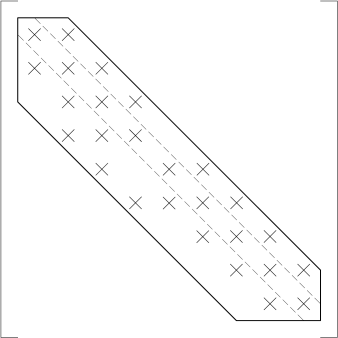
Εφαρμόζοντας την αντίστροφη μέθοδος Cuthill-Mckee στα παραδείγματα που εξετάστηκαν στην προηγούμενη ενότητα, προκύπτουν τώρα τα τροποποιημένα μητρώα για την περίπτωση της αρίθμησης των κόμβων κατά γραμμές (βλ. Σχήμα 4.7), της αρίθμησης των κόμβων κατά στήλες (βλ. Σχήμα 4.8) και της τυχαίας αρίθμησης των κόμβων (βλ. Σχήμα 4.9).
Διαπιστώνεται ότι η εφαρμογή του αλγορίθμου δεν είναι πάντα επιτυχής, καθώς δεν οδηγεί απαραίτητα στο βέλτιστο αποτέλεσμα, όπως φαίνεται και στο Σχήμα 4.8.



4.3 Αποθήκευση του μητρώου
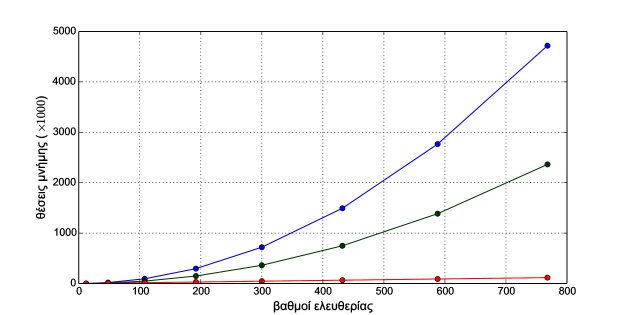
Το μέγεθος του συστήματος καθιστά πολλές φορές απαγορευτική την αποθήκευσή του ή ακόμα και τη χρήση του. Επιπλέον, η μέθοδος των πεπερασμένων στοιχείων χαρακτηρίζεται από συστήματα γραμμικών εξισώσεων στα οποία ο μεγαλύτερος αριθμός των συντελεστών είναι μηδενικοί.
Για αυτό τις περισσότερες φορές δεν αποθηκεύεται εξ ολοκλήρου το συνολικό μητρώο του προβλήματος, αλλά ένα τμήμα του μητρώου το οποίο αποτελείται από τους μη μηδενικούς όρους. Εκτός από την αποθήκευση σε πλήρη μορφή επομένως, επιλέγονται συχνά οι ακόλουθες μέθοδοι αποθήκευσης του μητρώου:
-
•
Σε συμμετρική μορφή.
-
•
Σε ταινιωτή μορφή.
-
•
Σε μορφή προφίλ.
-
•
Σε αραιή μορφή.
Οι μέθοδοι αυτές, μαζί με την αποθήκευση σε πλήρη μορφή, εξετάζονται στη συνέχεια.
4.3.1 Αποθήκευση του μητρώου σε πλήρη μορφή
Στην περίπτωση αυτή που φαίνεται στο Σχήμα 4.10, αποθηκεύεται το σύνολο των στοιχείων του μητρώου δυσκαμψίας, ακόμα και στην περίπτωση που αυτά είναι μηδενικά. Ο απαιτούμενος χώρος αποθήκευσης ισούται με , όπου το μέγεθος του τετραγωνικού πίνακα .

Για παράδειγμα, για τον και έχουμε:
| (4.2) |
Όταν αποθηκεύονται οι παραπάνω όροι κατά γραμμή, σε συμπαγή μορφή ως μονοδιάστατος πίνακας, τότε προκύπτει:
| (4.3) |
Αντίστοιχα κατά στήλη προκύπτει:
| (4.4) |
4.3.2 Αποθήκευση του μητρώου σε συμμετρική μορφή
Στην περίπτωση που το μητρώο των εξισώσεων είναι συμμετρικό (βλ. Σχήμα 4.11), μπορούμε να εκμεταλλευτούμε τη συμμετρία αποθηκεύοντας μόνο το άνω τριγωνικό (U) ή κάτω τριγωνικό (L) τμήμα του πίνακα [1]. Ο απαιτούμενος χώρος αποθήκευσης σε αυτή την περίπτωση ισούται με , όπου το μέγεθος του τετραγωνικού πίνακα .
Για παράδειγμα, για τον και για το άνω τριγωνικό τμήμα (U) του πίνακα έχουμε:
| (4.5) |
Όταν αποθηκεύονται οι παραπάνω όροι κατά γραμμή, σε συμπαγή μορφή ως μονοδιάστατος πίνακας, τότε προκύπτει:
| (4.6) |
Αντίστοιχα κατά στήλη προκύπτει:
| (4.7) |
Για το κάτω τριγωνικό τμήμα (L) αντίστοιχα,
| (4.8) |
Ομοίως, όταν αποθηκεύονται οι παραπάνω όροι κατά γραμμή, σε συμπαγή μορφή ως μονοδιάστατος πίνακας, τότε προκύπτει:
| (4.9) |
Αντίστοιχα κατά στήλη προκύπτει:
| (4.10) |
4.3.3 Αποθήκευση του μητρώου σε ταινιωτή μορφή ή μορφή λωρίδας
Μητρώο ταινιωτής μορφής ή μορφής λωρίδας ονομάζεται το μητρώο εκείνο που έχει τους μη μηδενικούς του όρους συγκεντρωμένους σε μία διαγώνια λωρίδα που περιλαμβάνει
-
•
την κύρια διαγώνιο του μητρώου και
-
•
άλλες διαγώνιες από τη μία ή και από τις δύο πλευρές της κύριας διαγωνίου.
Ένα παράδειγμα μητρώου ταινιωτής μορφής δίνεται στο Σχήμα 4.12.
Ο αριθμός των διαγωνίων που βρίσκονται κάτω από την κύρια διαγώνιο () και ο αριθμός των διαγωνίων που βρίσκονται πάνω από την κύρια διαγώνιο () ορίζουν το εύρος του πίνακα () σύμφωνα με τη σχέση:
| (4.11) |
Η αποθήκευση ενός μη συμμετρικού, τετραγωνικού μητρώου (έστω ) ταινιωτής μορφής ακολουθεί το παρακάτω πρότυπο [1]:
| (4.12) |
Όταν αποθηκεύονται οι παραπάνω όροι κατά γραμμή, σε συμπαγή μορφή ως μονοδιάστατος πίνακας, τότε προκύπτει:
| (4.13) |
Αντίστοιχα κατά στήλη προκύπτει:
| (4.14) |
4.3.4 Αποθήκευση του μητρώου σε μορφή προφίλ ή κορυφογραμμής
Μια ακόμη μέθοδος που συναντάται συχνά κατά την αποθήκευση των εξισώσεων της μεθόδου των πεπερασμένων στοιχείων είναι η αποθήκευση σε μορφή προφίλ ή κορυφογραμμής, όπως δίνεται στο Σχήμα 4.13.
Σε αντίθεση με τη μέθοδο της λωρίδας, κατά την οποία αποθηκεύονται όλοι οι όροι του μητρώου από την κύρια διαγώνιο έως μία σταθερή απόσταση (το άνω ή το κάτω ημιεύρος), στη μέθοδο αποθήκευσης της κορυφογραμμής αποθηκεύονται ανά στήλη του μητρώου μόνο οι όροι που βρίσκονται μεταξύ του πρώτου και του τελευταίου μη μηδενικού όρου [3]. Αυτή η προσέγγιση οδηγεί σε ακόμα μικρότερες απαιτήσεις διαθέσιμου χώρου μνήμης, σε σύγκριση με τη μέθοδο της λωρίδας.
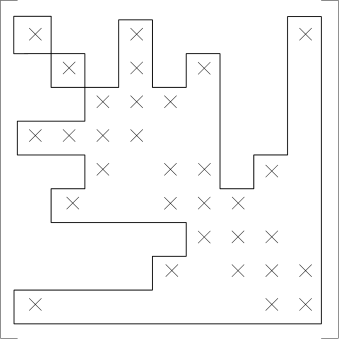
Έστω για παράδειγμα το τετραγωνικό, συμμετρικό μητρώο με , το οποίο δίνεται ως:
| (4.15) |
Ορίζουμε τώρα την περιβάλλουσα του μητρώου ως εξής. Από κάθε διαγώνιο στοιχείο του μητρώου μετακινούμαστε προς τα πάνω έως ότου συναντήσουμε το τελευταίο μη μηδενικό στοιχείο. Το σύνολο των μη μηδενικών στοιχείων αποτελεί την κορυφογραμμή του μητρώου, η οποία μπορεί και συνήθως περιέχει και μηδενικά στοιχεία. Οι μηδενικοί αυτοί όροι ονομάζονται όροι πλήρωσης (fill-in) επειδή κατά την παραγοντοποίηση του πίνακα παίρνουν μη μηδενικές τιμές.
Τα μηδενικά στοιχεία που βρίσκονται άνω της κορυφογραμμής μπορούμε τώρα να τα απορρίψουμε, οπότε έχουμε:
| (4.16) |
Μόνο οι παραπάνω όροι αποθηκεύονται σε αυτή την περίπτωση.
4.3.5 Αποθήκευση του μητρώου σε αραιή μορφή
Σποραδικό ή αραιό ονομάζεται ένα μητρώο το οποίο έχει ένα σχετικά μικρό ποσοστό μη μηδενικών στοιχείων (βλ. π.χ. το Σχήμα 4.14). Ο απαιτούμενος αριθμός των μηδενικών στοιχείων ενός μητρώου ώστε αυτό να αποκαλείται αραιό εξαρτάται από το μέγεθος, τη δομή και χρήση του μητρώου [5].

Υπάρχουν πολλοί τρόποι αποθήκευσης των αραιών μητρώων, με τους πιο συνηθισμένους να είναι:
-
•
Λίστα από λίστες (list of lists).
Με αυτήν τη μέθοδο αποθηκεύεται μία λίστα ανά γραμμή. Κάθε στοιχείο αυτής της λίστας περιέχει τη στήλη και την τιμή του μη μηδενικού στοιχείου. Συνήθως τα στοιχεία της κάθε λίστας είναι ταξινομημένα ως προς τη στήλη για γρηγορότερες αναζητήσεις. -
•
Συντεταγμένη λίστα (coordinate list – COO).
Με αυτήν τη μέθοδο κάθε μη μηδενικό στοιχείο αποθηκεύεται ως τριάδα (γραμμή, στήλη, τιμή). Και σε αυτή την περίπτωση οι τριάδες είναι συνήθως ταξινομημένες ως προς γραμμή και στήλη για γρηγορότερες αναζητήσεις. -
•
Πεπιεσμένη αποθήκευση κατά γραμμές (compressed row storage). Με αυτήν τη μέθοδο τα μη μηδενικά στοιχεία του μητρώου τοποθετούνται καταρχήν σε διαδοχικές θέσεις μνήμης (διάνυσμα , από αριστερά προς τα δεξιά και από πάνω προς τα κάτω). Επιπλέον δημιουργούνται δύο διανύσματα στα οποία αποθηκεύονται:
-
–
ένα διάνυσμα που αποθηκεύει τους δείκτες των στηλών των στοιχείων του διανύσματος και
-
–
ένα διάνυσμα που αποθηκεύει για κάθε στήλη τη θέση στο διάνυσμα που αντιστοιχεί στο πρώτο μη μηδενικό στοιχείο του.
-
–
-
•
Πεπιεσμένη αποθήκευση κατά στήλες (compressed column storage). Η μέθοδος αυτή είναι παρόμοια με τη μέθοδο της πεπιεσμένης αποθήκευσης κατά γραμμές.
Η επιλογή μίας από τις διαθέσιμες μεθόδους εξαρτάται από πολλούς παράγοντες, όπως:
-
•
Τα χαρακτηριστικά και την αραιότητα του μητρώου.
-
•
Τις διαθέσιμες μεθόδους επίλυσης και την απόδοσή τους.
-
•
Την απαίτηση να υποστηρίζεται η αποτελεσματική τροποποίηση των στοιχείων του πίνακα ή
-
•
την απαίτηση να υποστηρίζεται η αποτελεσματική εισαγωγή νέων στοιχείων ή τέλος
-
•
την απαίτηση να υποστηρίζονται αποτελεσματικά τελεστές και πράξεις επί των μητρώων.

4.4 Επίλυση του συστήματος εξισώσεων
Οι μέθοδοι που χρησιμοποιούνται για την επίλυση του συστήματος εξισώσεων ανήκουν σε μία από τις ακόλουθες κατηγορίες:
- Άμεσες μέθοδοι
-
Οι πιο συνηθισμένες είναι οι μέθοδοι απαλοιφής του Gauss και του Cholesky. Θεωρητικά αυτές οι μέθοδοι δίνουν την ακριβή λύση του συστήματος των εξισώσεων.
- Επαναληπτικές μέθοδοι
-
Όταν η τάξη του συστήματος είναι πολύ μεγάλη, τότε οι παραπάνω μέθοδοι εμφανίζονται πρακτικά ασύμφορες και συνήθως χρησιμοποιούνται μέθοδοι όπως οι Gauss-Seidel ή πιο συχνά η μέθοδος της συζυγούς κλίσης (conjugate gradient), οι οποίες μέσω επαναλήψεων δίνουν μια προσεγγιστική λύση στα όρια της επιθυμητής ακρίβειας.
Σε σπάνιες περιπτώσεις εξαιρετικά μεγάλων συστημάτων επιχειρείται ακόμα και η διάσπαση του συνολικού μητρώου (domain decomposition) και η επίλυση μικρότερων συστημάτων, που επανασυντιθέμενα τελικά μας δίνουν τη συνολική λύση.
Στη συνέχεια παρουσιάζονται οι πιο σημαντικές άμεσες και επαναληπτικές μέθοδοι.
4.4.1 Η μέθοδος απαλοιφής Gauss
Έστω το σύστημα γραμμικών εξισώσεων
| (4.17) |
ή σε πλήρη μορφή:
| (4.18) |
Κατασκευάζουμε τώρα τον επαυξημένο πίνακα του συστήματος, προσαρτώντας στο μητρώο το διάνυσμα , ως:
| (4.19) |
Στη συνέχεια με στοιχειώδεις διαδικασίες γραμμών προσπαθούμε να φέρουμε το σύστημα στην ακόλουθη μορφή, άνω τριγωνικού μητρώου [7]:
| (4.20) |
Οι στοιχειώδεις διαδικασίες γραμμών αφορούν τις ακόλουθες διαδικασίες:
-
1.
Εναλλαγή δύο γραμμών.
-
2.
Πολλαπλασιασμό μίας γραμμής ή μίας στήλης με έναν μη μηδενικό αριθμό.
-
3.
Πρόσθεση σε μία γραμμή το πολλαπλάσιο μίας άλλης γραμμής.
Από το άνω τριγωνικό μητρώο (4.20) εύκολα μπορεί πλέον να βρεθεί η λύση του συστήματος. Πιο συγκεκριμένα, επιλύεται η -ιοστή γραμμή ως προς προς , το αποτέλεσμά της αντικαθίσταται στην , η οποία επιλύεται ως προς κ.ο.κ. Η παραπάνω διαδικασία περιγράφεται από τον τύπο:
| (4.21) |
4.4.2 Η μέθοδος Cholesky
Η μέθοδος παραγοντοποίησης Cholesky αποτελεί μια παραλλαγή της μεθόδου απαλοιφής Gauss. Είναι μια μέθοδος με την οποία παραγοντοποιείται ένα συμμετρικό, θετικά ορισμένο μητρώο σε ένα κάτω τριγωνικό μητρώο και το ανάστροφό του σύμφωνα με τη σχέση [4]:
| (4.22) |
Η μέθοδος αυτή αναπτύσσεται στη συνέχεια. Έστω λοιπόν το μητρώο ,
| (4.23) |
Μπορούμε να υπολογίσουμε το μητρώο , όπως αυτό ορίζεται από τη σχέση (4.22), ως:
| (4.24) | ||||
| (4.25) | ||||
| (4.26) |
Παρατηρούμε ότι τα διαγώνια στοιχεία του μητρώου μπορούν να υπολογιστούν από τις σχέσεις:
| (4.27) | ||||
| (4.28) | ||||
| (4.29) |
Στη γενική περίπτωση για τα διαγώνια στοιχεία του μητρώου της παραγοντοποίησης ισχύει:
| (4.30) |
Για τα στοιχεία που βρίσκονται κάτω από την κύρια διαγώνιο, δηλαδή τα στοιχεία
| (4.31) |
παρατηρούμε ότι
| (4.32) | ||||
| (4.33) | ||||
| (4.34) |
το οποίο οδηγεί στη γενική σχέση:
| (4.35) |
Αν το μητρώο είναι μη συμμετρικό, τότε εφαρμόζεται μια παραλλαγή της μεθόδου, που έχει τη μορφή
| (4.36) |
όπου ένα κάτω τριγωνικό και ένα άνω τριγωνικό μητρώο αντίστοιχα. Από τα μητρώα και η μέθοδος αυτή ονομάζεται LU παραγοντοποίηση.
Μια πιο ευρέως χρησιμοποιούμενη παραλλαγή της μεθόδου Chοlesky είναι η παραγοντοποίηση κατά Crout, στην οποία το μητρώο παραγοντοποιείται ως:
| (4.37) |
όπου ένα διαγώνιο μητρώο.
4.4.3 Η μέθοδος της συζυγούς διανυσματικής κλίσης
Η μέθοδος της συζυγούς διανυσματικής κλίσης περιγράφεται από τον αλγόριθμο που παρουσιάζεται στη συνέχεια:
| (4.38) | ||||
| (4.39) | ||||
| (4.40) | ||||
| επανάληψη | (4.41) | |||
| (4.42) | ||||
| (4.43) | ||||
| (4.44) | ||||
| (4.45) | ||||
| (4.46) | ||||
| (4.47) | ||||
| (4.48) |
Ο παραπάνω αλγόριθμος αναφέρεται σε ένα σύστημα της μορφής:
| (4.49) |
και ξεκινάει με μια αρχική θεώρηση της λύσης .
Σε περιβάλλον ιδεατής αριθμητικής ακρίβειας, για την ακριβή λύση απαιτούνται το πολύ επαναλήψεις, όπου ο αριθμός των αγνώστων [6]. Στην πραγματικότητα, όμως, τα αριθμητικά σφάλματα στρογγύλευσης επηρεάζουν την ταχύτητα σύγκλισης.
4.5 Επεξεργασία των αποτελεσμάτων
Η επεξεργασία των αποτελεσμάτων ακολουθεί την κύρια επεξεργασία που είναι η μόρφωση και επίλυση του συστήματος και για αυτό αναφέρεται συχνά και ως μετα-επεξεργασία. Αφορά:
-
•
Τον υπολογισμό των επιμέρους αγνώστων, όπως είναι τα εντατικά μεγέθη.
-
•
Τη γραφική απεικόνιση του συνόλου των μεγεθών που έχουν υπολογιστεί.
Στη συνέχεια θα ασχοληθούμε με την επεξεργασία των αποτελεσμάτων που αναφέρονται είτε στους κόμβους των στοιχείων είτε στα σημεία ολοκλήρωσης, όπως αυτά ορίστηκαν στην Ενότητα 3.5.1.
Τα αποτελέσματα χωρίζονται σε δύο κατηγορίες:
-
•
Στα πρωτεύοντα, όπως είναι οι μετακινήσεις για τα προβλήματα που κυρίως εξετάζονται στο παρόν βιβλίο.
-
•
Στα δευτερεύοντα, όπως οι τάσεις και οι παραμορφώσεις.
Σε γενικές γραμμές αναμένεται τα δευτερεύοντα αποτελέσματα να μην χαρακτηρίζονται από την ακρίβεια των πρωτευόντων.
4.5.1 Αποτελέσματα στους κόμβους των στοιχείων
Για τα προβλήματα που εξετάζονται στο παρόν βιβλίο, οι άγνωστοι στους κόμβους είναι οι μετακινήσεις. Κατ’ επέκταση, τα αντίστοιχα αποτελέσματα της επίλυσης αφορούν πρωτίστως τις μετακινήσεις των κόμβων. Μια τυπική απεικόνιση αποτελεσμάτων, όπου οι μετακινήσεις στους κόμβους σχεδιάζονται ως διανύσματα, δίνεται στο Σχήμα 4.17, που αφορά τα αποτελέσματα προσομοίωσης μίας σήραγγας και της επένδυσής της.

Σε γενικές γραμμές η οπτικοποίηση των αποτελεσμάτων που είναι γνωστά στους κόμβους των στοιχείων δεν παρουσιάζει ιδιαίτερες δυσκολίες. Δυσκολίες μπορεί να υπάρχουν κατά την οπτικοποίηση των αποτελεσμάτων που είναι γνωστά εντός του στοιχείου (π.χ. στα σημεία ολοκλήρωσης), όπως θα δούμε στην επόμενη ενότητα.
4.5.2 Αποτελέσματα στα σημεία ολοκλήρωσης
Αν το υλικό που χαρακτηρίζει το πρόβλημα θεωρηθεί ελαστικό, οι τάσεις σχετίζονται άμεσα με τις παραμορφώσεις σε κάθε σημείο μέσω των γνωστών σχέσεων τάσεων-παραμορφώσεων:
| (4.50) |
Επομένως, κατά τη διαδικασία υπολογισμού των τάσεων υπολογίζονται καταρχήν οι παραμορφώσεις και η ακρίβεια των πρώτων εξαρτάται από την ακρίβεια των τελευταίων. Οι παραμορφώσεις υπολογίζονται κατά τα γνωστά από τις μετακινήσεις μέσω των κινηματικών εξισώσεων.
Στη συνέχεια θα περιγραφεί ο τρόπος υπολογισμού των τάσεων για ένα τυπικό δισδιάστατο ισοπαραμετρικό στοιχείο και πιο συγκεκριμένα το τετράπλευρο/τετράκομβο ισοπαραμετρικό στοιχείο που παρουσιάστηκε αναλυτικά στην Ενότητα 3.6.
Έστω ότι έχει επιλυθεί το σύστημα των εξισώσεων των πεπερασμένων στοιχείων
| (4.51) |
για τις επικόμβιες μετακινήσεις .
Για τον υπολογισμό των τάσεων και των παραμορφώσεων υπολογίζεται καταρχήν σε κάθε στοιχείο του προσομοιώματος, έστω , το διάνυσμα των επικόμβιων μετακινήσεων του στοιχείου . Για τη συγκεκριμένη περίπτωση του τετράκομβου τετράπλευρου στοιχείου, αυτό θα είναι ένα διάνυσμα της μορφής:
| (4.52) |
Με γνωστό το διάνυσμα , μπορούν πλέον να υπολογιστούν οι παραμορφώσεις μέσω των κινηματικών εξισώσεων του στοιχείου, δηλαδή,
| (4.53) |
όπου το γνωστό μητρώο μετακινήσεων-παραμορφώσεων.
Επομένως, οι τάσεις υπολογίζονται εντός του στοιχείου ως:
| (4.54) |
Μια σημαντική παρατήρηση στο σημείο αυτό είναι ότι οι τάσεις που υπολογίζονται στους ίδιους κόμβους από γειτονικά στοιχεία δεν θα είναι ίδιες γενικά δεδομένου ότι οι τάσεις, σε αντίθεση με τις παραμορφώσεις, δεν απαιτείται να είναι συνεχείς από στοιχείο σε στοιχείο. Για αυτό τον λόγο απαιτούνται τεχνικές εξομάλυνσης των τάσεων που προκύπτουν από γειτονικά στοιχεία.
Για τον υπολογισμό τώρα των τάσεων στους κόμβους του στοιχείου υπάρχουν γενικά δύο προσεγγίσεις:
-
1.
Υπολογισμός των τάσεων απευθείας από την (4.54) χρησιμοποιώντας τις συναρτήσεις μορφής και τις αντίστοιχες συντεταγμένες των κόμβων.
-
2.
Υπολογισμός των τάσεων στα σημεία ολοκλήρωσης Gauss και στη συνέχεια η παρεκβολή τους στους κόμβους του στοιχείου.
H μέθοδος που ακολουθείται συχνότερα είναι η δεύτερη, καθώς θεωρείται ότι δίνει καλύτερα αποτελέσματα από τον απευθείας υπολογισμό των τάσεων στους κόμβους, και αναλύεται στη συνέχεια [3].
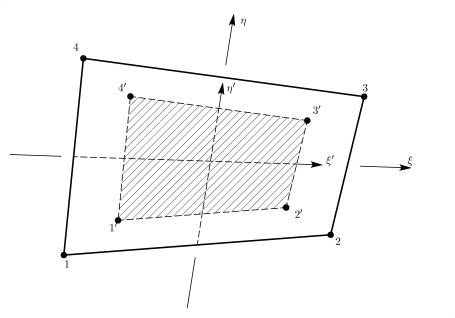
Έστω το τετράκομβο/τετράπλευρο στοιχείο του Σχήματος 4.18 στο οποίο έχει γίνει ολοκλήρωση των εξισώσεων του στοιχείου με τη μέθοδο Gauss και κανόνα . Οι τάσεις υπολογίζονται στα σημεία Gauss, τα οποία δίνονται ως , , και στο Σχήμα 4.18. Τα σημεία Gauss ακολουθούν την αρίθμηση των κόμβων του στοιχείου, με το σημείο π.χ. να είναι το πλησιέστερο στον κόμβο 1 του στοιχείου. Οι συντεταγμένες των σημείων Gauss στο σύστημα του στοιχείου δίνονται στον Πίνακα 4.1.
| Σημείο Gauss | ||
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
Έστω τώρα ένα στοιχείο που έχει ως συντεταγμένες κόμβων τις συντεταγμένες των σημείων Gauss , , και , όπως δίνεται από τη γραμμοσκιασμένη περιοχή του Σχήματος 4.18. Εφόσον γνωρίσουμε ένα μέγεθος στα σημεία αυτά, μπορούμε να το παρεκβάλουμε στα σημεία , , και που μας ενδιαφέρουν.
Η παρεκβολή αυτή γίνεται υπολογίζοντας τις συντεταγμένες στα σημεία , , και στο σύστημα και που ορίζεται από το καινούργιο στοιχείο. Τα δύο συστήματα συνδέονται με τις παρακάτω σχέσεις:
| (4.55) | ||||
| (4.56) | ||||
| (4.57) | ||||
| (4.58) |
και οι συντεταγμένες των κόμβων του στοιχείου δίνονται στο σύστημα του στοιχείου που ορίζεται από τα σημεία Gauss, σύμφωνα με τα όσα αναφέρονται στον Πίνακα 4.2.
| Κόμβος στοιχείου | ||
|---|---|---|
Έστω τώρα ένα βαθμωτό πεδίο του οποίου οι τιμές είναι γνωστές στα σημεία Gauss. Αυτές μπορούν να παρεμβληθούν με τις τυπικές διγραμμικές εξισώσεις παρεμβολής, οι οποίες όμως τώρα δίνονται σε όρους και ως:
| (4.59) |
όπου
| (4.60) | ||||
| (4.61) | ||||
| (4.62) | ||||
| (4.63) |
Για την παρεκβολή του μεγέθους αντικαθιστούμε στις παραπάνω εξισώσεις τις αντίστοιχες συντεταγμένες. Π.χ. για τον κόμβο 1 προκύπτει:
Εφαρμόζοντας την παραπάνω διαδικασία για όλους τους κόμβους, προκύπτει:
| (4.64) |
Όπως αναφέρθηκε προηγουμένως, οι τάσεις ή άλλα μεγέθη που υπολογίζονται ανά στοιχείο δεν είναι απαραίτητα ίσα μεταξύ τους στους κοινούς κόμβους των στοιχείων.
Για τον λόγο αυτό στη συνέχεια εξισώνονται και εξομαλύνονται, είτε βρίσκοντας τον μέσο όρο (μη σταθμισμένο) όλων των τιμών που αναφέρονται σε έναν κόμβο είτε χρησιμοποιούνται για τη στάθμιση των επιμέρους τιμών συντελεστές βαρύτητας των συνεισφορών κάθε στοιχείου.
Στην πράξη ακολουθείται τις περισσότερες φορές ο πρώτος και πιο απλός τρόπος.
4.6 Βιβλιογραφία
- 1 E. Anderson, Z. Bai and C. Bischof. LAPACK Users’ guide. Society for Industrial Mathematics, 1999.
- 2 E. Cuthill and J. McKee. Reducing the Bandwidth of Sparse Symmetric Matrices. In Proceedings of the 1969 24th National Conference, pp. 157-172. ACM, 1969.
- 3 Carlos A. Felippa. Lecture notes in introduction to finite element methods, 2013.
- 4 Gene H. Golub and Charles F. Van Loan. Matrix computations, volume 3. JHU Press, 2012.
- 5 Sergio Pissanetzky. Sparse matrix technology – electronic edition. Academic Press, 1984.
- 6 Jonathan Richard Shewchuk. An introduction to the conjugate gradient method without the agonizing pain, School of Computer Science, Carnegie Mellon University, 1994.
- 7 Endre Süli and David F. Mayers. An introduction to numerical analysis. Cambridge University Press, 2003.