2 Η μέθοδος των πεπερασμένων στοιχείων 4 Μόρφωση του συστήματος εξισώσεων. Επίλυση και επεξεργασία των αποτελεσμάτων

Κεφάλαιο 3 Μόρφωση πεπερασμένων στοιχείων

Στο παρόν κεφάλαιο μορφώνονται τυπικά πεπερασμένα στοιχεία που χρησιμοποιούνται ευρέως στη γεωτεχνική μηχανική.

Αρχικά εξετάζονται τα γραμμικά στοιχεία, όπως το στοιχείο ράβδου (Ενότητα 3.1) και το στοιχείο δοκού (Ενότητα 3.2).

Για το στοιχείο ράβδου (Ενότητα 3.1), δίνεται καταρχήν η διατύπωσή του σε όρους δυσκαμψίας (Ενότητα 3.1.1). Στη συνέχεια επαναδιατυπώνονται οι εξισώσεις του στοιχείου με τη χρήση συναρτήσεων μορφής (Ενότητα 3.1.2). Πιο συγκεκριμένα, δίνονται οι συναρτήσεις μορφής (Ενότητα 3.1.2), το μητρώο παραμόρφωσης (Ενότητα 3.1.2), το μητρώο ελαστικότητας (Ενότητα 3.1.2) και το μητρώο δυσκαμψίας στο τοπικό σύστημα συντεταγμένων (Ενότητα 3.1.2). Στη συνέχεια εξετάζεται ο μετασχηματισμός του μητρώου δυσκαμψίας και δίνεται το καθολικό μητρώο δυσκαμψίας (Ενότητα 3.1.3). Τέλος συζητείται η χρήση του στοιχείου σε προβλήματα γεωτεχνικής μηχανικής (Ενότητα 3.1.4).

Για το στοιχείο δοκού (Ενότητα 3.2), δίνονται αντίστοιχα οι συναρτήσεις σχήματος (Ενότητα 3.2.1), οι σχέσεις παραμορφώσεων-μετακινήσεων (Ενότητα 3.2.2) και το μητρώο δυσκαμψίας (Ενότητα 3.2.3). Τέλος συζητείται η χρήση του στοιχείου σε προβλήματα γεωτεχνικής μηχανικής (Ενότητα 3.2.4).

Στη συνέχεια παρουσιάζεται ένα πιο εξειδικευμένο στοιχείο δοκού, που αφορά ένα στοιχείο δοκού που εδράζεται επί του εδάφους (Ενότητα 3.3). Δίνεται το μητρώο δυσκαμψίας του στοιχείου (Ενότητα 3.3.1), ενώ παρουσιάζεται και ο προγραμματισμός του (Ενότητα 3.3.2).

Ακολουθεί η παρουσίαση των επίπεδων στοιχείων, ξεκινώντας από το τριγωνικό στοιχείο τριών κόμβων σταθερής παραμόρφωσης (Ενότητα 3.4). Δίνονται το μητρώο συναρτήσεων μορφής (Ενότητα 3.4.1), το μητρώο συναρτήσεων παραμορφώσεων-μετακινήσεων (Ενότητα 3.4.2), το μητρώο ελαστικότητας (Ενότητα 3.4.3) και τέλος το μητρώο δυσκαμψίας (Ενότητα 3.4.4).

Στη συνέχεια αναπτύσσεται η ισοπαραμετρική αναπαράσταση και δίνονται οι μέθοδοι αριθμητικής ολοκλήρωσης (Ενότητα 3.5). Πιο συγκεκριμένα, παρουσιάζεται η ισοπαραμετρική θεώρηση (Ενότητα 3.5.1), δίνεται η περιγραφή της γεωμετρίας (Ενότητα 3.5.1) και περιγράφεται το φυσικό σύστημα συντεταγμένων (Ενότητα 3.5.1). Τέλος αναπτύσσεται η αριθμητική ολοκλήρωση (Ενότητα 3.5.1).

Από τα ισοπαραμετρικά επίπεδα στοιχεία εξετάζονται το τετράκομβο τετράπλευρο στοιχείο (Ενότητα 3.6) και το αντίστοιχο στοιχείο διεπιφάνειας (Ενότητα 3.7) σε συνθήκες επίπεδης παραμόρφωσης.

Για το τετράκομβο στοιχείο (Ενότητα 3.6) δίνονται το μητρώο συναρτήσεων μορφής (Ενότητα 3.6.1), το μητρώο συναρτήσεων παραμορφώσεων-μετακινήσεων (Ενότητα 3.6.2), το μητρώο ελαστικότητας (Ενότητα 3.6.3) και τέλος το μητρώο δυσκαμψίας (Ενότητα 3.6.4), όπως προκύπτει από την αριθμητική ολοκλήρωση (Ενότητα 3.6.5).

Για το στοιχείο διεπιφάνειας (Ενότητα 3.7) δίνονται ομοίως το μητρώο συναρτήσεων μορφής (Ενότητα 3.7.1), το μητρώο ελαστικότητας (Ενότητα 3.7.2), το μητρώο συναρτήσεων παραμορφώσεων-μετακινήσεων (Ενότητα 3.7.3) και τέλος το μητρώο δυσκαμψίας (Ενότητα 3.7.4).

Τέλος παρουσιάζονται οι εξισώσεις του εξάπλευρου, οκτάκομβου τριγραμμικού τρισδιάστατου στοιχείου (Ενότητα 3.8).

Στο τέλος του κεφαλαίου παρατίθεται η σχετική βιβλιογραφία (Ενότητα 3.9).

3.1 Το στοιχείο ράβδου

Το στοιχείο ράβδου (ή στοιχείο δικτυώματος) αποτελεί ίσως το πιο απλό στοιχείο που χρησιμοποιείται κατά την εφαρμογή της μεθόδου των πεπερασμένων στοιχείων. Το στοιχείο ράβδου περιγράφεται συνήθως από δύο ή τρεις κόμβους και μπορεί να χρησιμοποιηθεί σε προβλήματα μίας, δύο ή τριών διαστάσεων.

3.1.1 Διατύπωση σε όρους δυσκαμψίας

Έστω το στοιχείο ράβδου του Σχήματος 3.1, μήκους $L$ , διατομής $A$ και μέτρου ελαστικότητας $E$ .

Σχήμα 3.1: Στοιχείο ράβδου. Φυσικό πρόβλημα (α), ελατηριακό ανάλογο (β) και προσομοίωμα (γ).

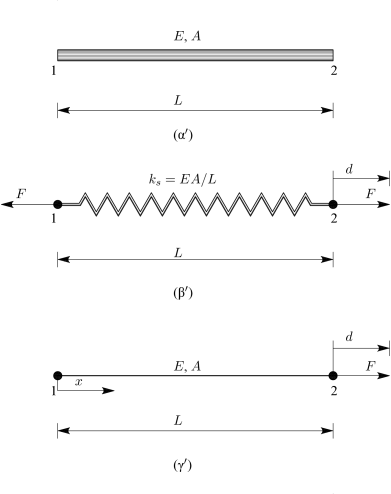
Οι δυνάμεις συνδέονται με τις μετακινήσεις μέσω του μητρώου δυσκαμψίας $\bar{\mathbf{K}}^{e}$ , σύμφωνα με τη σχέση:

\bar{\boldsymbol{f}}^{e}=\bar{\mathbf{K}}^{e}\bar{\boldsymbol{u}}^{e}

(3.1)

η οποία αναλυτικά δίνεται ως:

\left[\begin{array}[]{c}\bar{f}_{1}\\ \bar{f}_{2}\\ \end{array}\right]=\left[\begin{array}[]{cc}\bar{K}_{11}&\bar{K}_{12}\\ \bar{K}_{21}&\bar{K}_{22}\\ \end{array}\right]\left[\begin{array}[]{c}\bar{u}_{1}\\ \bar{u}_{2}\\ \end{array}\right]

(3.2)

Τα διανύσματα $\bar{\boldsymbol{f}}^{e}$ και $\bar{\boldsymbol{u}}^{e}$ ονομάζονται διανύσματα επικόμβιων φορτίσεων και επικόμβιων μετακινήσεων αντίστοιχα.

Υπάρχουν αρκετοί διαφορετικοί τρόποι για να μορφωθεί ο πίνακας $\bar{\mathbf{K}}^{e}$ . Αρχικά εξετάζεται ίσως ο πιο απλός, σύμφωνα με τον οποίο το στοιχείο ράβδου αντικαθίσταται από ένα γραμμικό ελατήριο με δυσκαμψία $k_{s}$ , όπως φαίνεται στο Σχήμα 3.1 [3]. Αν οι ιδιότητες του στοιχείου είναι σταθερές σε όλο το μήκος του, τότε ισχύει:

k_{s}=\dfrac{EA}{L}

(3.3)

Επομένως η σχέση δυνάμεων-μετακινήσεων δίνεται ως

F=k_{s}d=\dfrac{EA}{L}d

(3.4)

όπου $F$ είναι η αξονική δύναμη και $d$ η σχετική αξονική μετακίνηση που αντιστοιχεί στην αλλαγή του μήκους του στοιχείου.

Σε όρους επικόμβιων δυνάμεων και μετακινήσεων προκύπτει:

	$\displaystyle F$	$\displaystyle=\bar{f}_{2}=-\bar{f}_{1}$		(3.5)
	$\displaystyle d$	$\displaystyle=\bar{u}_{2}-\bar{u}_{1}$		(3.6)

Οι παραπάνω εξισώσεις αντιστοιχούν στην ισορροπία των δυνάμεων και στο συμβιβαστό των μετακινήσεων αντίστοιχα.

Συνδυάζοντας την (3.2) με τις (3.5)-(3.6) προκύπτει

\bar{\boldsymbol{f}}^{e}=\left[\begin{array}[]{c}\bar{f}_{1}\\ \bar{f}_{2}\\ \end{array}\right]=\dfrac{EA}{L}\left[\begin{array}[]{cc}1&-1\\ -1&1\\ \end{array}\right]\left[\begin{array}[]{c}\bar{u}_{1}\\ \bar{u}_{2}\\ \end{array}\right]=\bar{\mathbf{K}}^{e}\bar{\boldsymbol{u}}^{e}

(3.7)

όπου το μητρώο δυσκαμψίας στο τοπικό σύστημα συντεταγμένων δίνεται ως:

\bar{\mathbf{K}}^{e}=\dfrac{EA}{L}\left[\begin{array}[]{cc}1&-1\\ -1&1\\ \end{array}\right]

(3.8)

3.1.2 Διατύπωση με τη χρήση συναρτήσεων μορφής

Η παραπάνω διαδικασία είναι εφικτή μόνο σε πολύ απλές περιπτώσεις. Στη συνέχεια εξετάζεται η μόρφωση του μητρώου δυσκαμψίας σύμφωνα με τη γενική σχέση,

\bar{\mathbf{K}}^{e}=\int_{\Omega}\mathbf{B}^{T}\mathbf{C}\mathbf{B}d\Omega

(3.9)

όπως προέκυψε από τη μέθοδο των πεπερασμένων στοιχείων που εξετάστηκε στο προηγούμενο κεφάλαιο.

Συναρτήσεις μορφής

Αν υποθέσουμε ότι η κατανομή των μετακινήσεων εντός του στοιχείου είναι γραμμική, τότε οι μετακινήσεις μπορεί να εκφραστούν με τη βοήθεια της σχέσης:

u=a_{1}+a_{2}x

(3.10)

H (3.10) ονομάζεται πολυώνυμο παρεμβολής, που στην προκειμένη περίπτωση λόγω της γραμμικής θεώρησης των μετακινήσεων είναι πρώτου βαθμού ως προς το $u$ .

Σε μητρωική μορφή η (3.10) γράφεται ως:

u=\left[\begin{array}[]{cc}1&x\\ \end{array}\right]\left[\begin{array}[]{c}a_{1}\\ a_{2}\\ \end{array}\right]

(3.11)

Οι συντελεστές $a_{1}$ και $a_{2}$ του πολυωνύμου παρεμβολής συνδέονται με τις επικόμβιες μετακινήσεις μέσω των συνοριακών συνθηκών του στοιχείου:

	$\displaystyle u=u_{1}$	όταν	$\displaystyle x=0$		(3.12)
	$\displaystyle u=u_{2}$	όταν	$\displaystyle x=L$		(3.13)

Αντικαθιστώντας τις (3.12)-(3.13) στην (3.11), προκύπτει:

	$\displaystyle\left[\begin{array}[]{cc}u_{1}\\ u_{2}\end{array}\right]$	$\displaystyle=\left[\begin{array}[]{cc}1&0\\ 1&L\\ \end{array}\right]\left[\begin{array}[]{c}a_{1}\\ a_{2}\\ \end{array}\right]$		(3.14)
	$\displaystyle\boldsymbol{u}$	$\displaystyle=\mathbf{A}\boldsymbol{a}$		(3.15)

Επομένως οι συντελεστές του $\boldsymbol{a}$ πολυωνύμου παρεμβολής μπορούν να υπολογιστούν επιλύοντας το παραπάνω $2\times 2$ γραμμικό σύστημα. Για την περίπτωση που εξετάζεται, η επίλυση μπορεί να γίνει με την αντιστροφή του μητρώου $\mathbf{A}$ ως:

	$\displaystyle\boldsymbol{a}$	$\displaystyle=\mathbf{A}^{-1}\boldsymbol{u}$		(3.16)
	$\displaystyle\left[\begin{array}[]{cc}a_{1}\\ a_{2}\end{array}\right]$	$\displaystyle=\left[\begin{array}[]{cc}1&0\\ -\dfrac{1}{L}&\dfrac{1}{L}\\ \end{array}\right]\left[\begin{array}[]{c}u_{1}\\ u_{2}\\ \end{array}\right]$		(3.17)

Αντικαθιστώντας την (3.17) στην (3.11), προκύπτει:

$\displaystyle u$	$\displaystyle=\left[\begin{array}[]{cc}1&x\\ \end{array}\right]\left[\begin{array}[]{c}a_{1}\\ a_{2}\\ \end{array}\right]$
	$\displaystyle=\left[\begin{array}[]{cc}1&x\\ \end{array}\right]\left[\begin{array}[]{cc}1&0\\ -\dfrac{1}{L}&\dfrac{1}{L}\\ \end{array}\right]\left[\begin{array}[]{c}u_{1}\\ u_{2}\\ \end{array}\right]$
	$\displaystyle=\underbrace{\left[\begin{array}[]{cc}1-\dfrac{x}{L}&\dfrac{x}{L}% \\ \end{array}\right]}_{\mathbf{N}}\left[\begin{array}[]{c}u_{1}\\ u_{2}\\ \end{array}\right]$	(3.18)
$\displaystyle u$	$\displaystyle=\mathbf{N}\boldsymbol{u}$	(3.19)

Το μητρώο $\mathbf{N}$ αποτελεί το μητρώο συναρτήσεων σχήματος του στοιχείου.

Αναλυτικά η παραπάνω σχέση μπορεί να γραφτεί ως:

u=N_{1}u_{1}+N_{2}u_{2}

(3.20)

όπου οι συναρτήσεις $N_{i}$ για $i=1,2$ ορίζονται ως

	$\displaystyle N_{1}$	$\displaystyle=1-\dfrac{x}{L}$		(3.21)
	$\displaystyle N_{2}$	$\displaystyle=\dfrac{x}{L}$		(3.22)

και απεικονίζονται στο Σχήμα 3.2.

Σχήμα 3.2: Συναρτήσεις σχήματος του στοιχείου ράβδου.

Μητρώο παραμορφώσεων-μετακινήσεων

Το μητρώο παραμόρφωσης συνδέει την ανηγμένη παραμόρφωση με τις επικόμβιες μετακινήσεις του στοιχείου για την περίπτωση του στοιχείου ράβδου μέσω της σχέσης

\varepsilon_{x}=\dfrac{du}{dx}

(3.23)

Αντικαθιστώντας στην παραπάνω σχέση την (3.20), προκύπτει:

\varepsilon_{x}=\dfrac{dN_{1}}{dx}u_{1}+\dfrac{dN_{2}}{dx}u_{2}=N_{1,x}u1+N_{2% ,x}u_{2}

(3.24)

όπου οι παράγωγοι των συναρτήσεων μορφής δίνονται ως:

$\displaystyle N_{1,x}$	$\displaystyle=-\dfrac{1}{L}$	(3.25)
και
$\displaystyle N_{2,x}$	$\displaystyle=\dfrac{1}{L}$	(3.26)

Επομένως η (3.23) μπορεί να επαναδιατυπωθεί σε μητρωική μορφή ως:

	$\displaystyle\varepsilon_{x}$	$\displaystyle=\left[\begin{array}[]{cc}-\dfrac{1}{L}&\dfrac{1}{L}\\ \end{array}\right]\left[\begin{array}[]{c}u_{1}\\ u_{2}\\ \end{array}\right]$		(3.27)
	$\displaystyle\varepsilon_{x}$	$\displaystyle=\mathbf{B}\boldsymbol{u}$		(3.28)

όπου

\mathbf{B}=\left[\begin{array}[]{cc}-\dfrac{1}{L}&\dfrac{1}{L}\\ \end{array}\right]

(3.29)

το μητρώο παραμορφώσεων-μετακινήσεων.

Μητρώο ελαστικότητας

Για την περίπτωση του στοιχείου ράβδου, το μητρώο ελαστικότητας που συνδέει τις τάσεις με τις παραμορφώσεις ως

\sigma=E\varepsilon

(3.30)

ορίζεται ως το ακόλουθο $1\times 1$ μητρώο:

\mathbf{C}=[E]

(3.31)

Μητρώο δυσκαμψίας

Το μητρώο δυσκαμψίας προκύπτει από τη σχέση

\bar{\mathbf{K}}^{e}=\int_{\Omega}\mathbf{B}^{T}\mathbf{C}\mathbf{B}d\Omega

(3.32)

αντικαθιστώντας τα αντίστοιχα μητρώα παραμορφώσεων-μετακινήσεων $\mathbf{B}$ (3.29) και τάσεων-παραμορφώσεων $\mathbf{C}$ (3.31) και ολοκληρώνοντας στο μήκος του στοιχείου, δηλαδή στο διάστημα $[0,L]$ , οπότε προκύπτει:

$\displaystyle\bar{\mathbf{K}}^{e}$	$\displaystyle=\int_{\Omega}\underbrace{\mathbf{B}^{T}}_{(2\times 1)}% \underbrace{\mathbf{C}}_{(1\times 1)}\underbrace{\mathbf{B}}_{(1\times 2)}d\Omega$
	$\displaystyle=\int_{\Omega}\left[\begin{array}[]{c}-\dfrac{1}{L}\\ \dfrac{1}{L}\end{array}\right][E]\left[\begin{array}[]{cc}-\dfrac{1}{L}&\dfrac% {1}{L}\\ \end{array}\right]d\Omega$
	$\displaystyle=\int_{0}^{L}\int_{A}\left[\begin{array}[]{c}-\dfrac{1}{L}\\ \dfrac{1}{L}\end{array}\right][E]\left[\begin{array}[]{cc}-\dfrac{1}{L}&\dfrac% {1}{L}\\ \end{array}\right]dAdx$
	$\displaystyle=\dfrac{EA}{L^{2}}\int_{0}^{L}\left[\begin{array}[]{cc}1&-1\\ -1&1\\ \end{array}\right]dx$
$\displaystyle\bar{\mathbf{K}}^{e}$	$\displaystyle=\dfrac{EA}{L}\left[\begin{array}[]{cc}1&-1\\ -1&1\\ \end{array}\right]$	(3.33)

Συγκρίνοντας τις (3.8) και (3.33) παρατηρούμε ότι τα μητρώα δυσκαμψίας που προκύπτουν ταυτίζονται.

3.1.3 Μετασχηματισμός του μητρώου δυσκαμψίας. Το καθολικό μητρώο δυσκαμψίας

Το μητρώο δυσκαμψίας του στοιχείου δικτυώματος, όπως αυτό περιγράφεται από τις (3.8) και (3.33), αναφέρεται στο τοπικό σύστημα συντεταγμένων του στοιχείου. Στη συνέχεια εξετάζεται πώς μπορεί να επαναδιατυπωθεί το μητρώο $\bar{\mathbf{K}}^{e}$ από το τοπικό σύστημα συντεταγμένων στο σύστημα συντεταγμένων του συνολικού προβλήματος, που στη συνέχεια θα αναφέρεται ως γενικό σύστημα συντεταγμένων. Η επαναδιατύπωση του μητρώου γίνεται με τον μετασχηματισμό του από το ένα σύστημα συντεταγμένων στο άλλο με τη βοήθεια των μητρώων μετασχηματισμού.

Η περίπτωση που εξετάζεται αναφέρεται σε ένα δισδιάστατο γενικό σύστημα συντεταγμένων, ενώ η αντίστοιχη περίπτωση του τρισδιάστατου γενικού συστήματος συντεταγμένων αφήνεται ως άσκηση για τον αναγνώστη.

Αρχικά επαναδιατυπώνεται το μητρώο δυσκαμψίας στο τοπικό σύστημα συντεταγμένων, λαμβάνοντας υπόψη και τον άξονα $\bar{y}$ . Εύκολα διαπιστώνεται ότι το μητρώο $\bar{\mathbf{K}}^{e}$ όπως δίνεται π.χ. στην (3.33)

\bar{\mathbf{K}}^{e}=\dfrac{EA}{L}\left[\begin{array}[]{cc}1&-1\\ -1&1\\ \end{array}\right]

(3.34)

μπορεί ισοδύναμα να διατυπωθεί και ως:

\bar{\mathbf{K}}^{e}=\dfrac{EA}{L}\left[\begin{array}[]{cccc}1&0&-1&0\\ 0&0&0&0\\ -1&0&1&0\\ 0&0&0&0\\ \end{array}\right]

(3.35)

Σχήμα 3.3: Μετασχηματισμός των δυνάμεων και των μετακινήσεων.

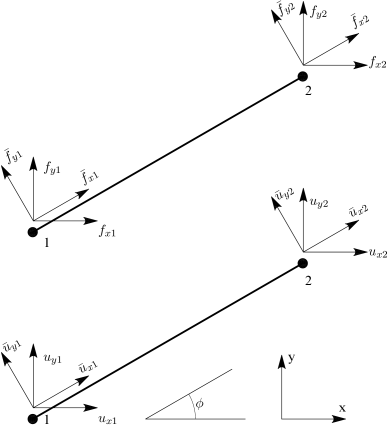
Οι μετασχηματισμοί που απαιτούνται προκύπτουν εύκολα εξετάζοντας το Σχήμα 3.3. Για τις μετακινήσεις του κόμβου 1 ισχύει:

	$\displaystyle\bar{u}_{x_{1}}$	$\displaystyle=u_{x_{1}}\cos\phi+u_{y_{1}}\sin\phi$		(3.36)
	$\displaystyle\bar{u}_{y_{1}}$	$\displaystyle=-u_{x_{1}}\sin\phi+u_{y_{1}}\cos\phi$		(3.37)

ενώ αντίστοιχες είναι οι σχέσεις και για τις μετακινήσεις του κόμβου 2:

	$\displaystyle\bar{u}_{x_{2}}$	$\displaystyle=u_{x_{2}}\cos\phi+u_{y_{2}}\sin\phi$		(3.38)
	$\displaystyle\bar{u}_{y_{2}}$	$\displaystyle=-u_{x_{2}}\sin\phi+u_{y_{2}}\cos\phi$		(3.39)

Έστω τώρα $c=\cos\phi$ και $s=\sin\phi$ , όπου $\phi$ η γωνία μεταξύ του γενικού ( $\boldsymbol{x}$ ) και του τοπικού ( $\bar{\boldsymbol{x}}$ ) συστήματος συντεταγμένων, μετρούμενη από το $\boldsymbol{x}$ στο $\bar{\boldsymbol{x}}$ με αντι-ωρολογιακή φορά. Διατυπώνοντας τις παραπάνω σχέσεις σε μητρωική μορφή, προκύπτει το μητρώο μετασχηματισμού των μετακινήσεων από το γενικό σύστημα συντεταγμένων ( $\boldsymbol{x}$ ) στο τοπικό ( $\bar{\boldsymbol{x}}$ ):

\left[\begin{array}[]{c}\bar{u}_{x_{1}}\\ \bar{u}_{y_{1}}\\ \bar{u}_{x_{2}}\\ \bar{u}_{y_{2}}\\ \end{array}\right]=\left[\begin{array}[]{cccc}c&s&0&0\\ -s&c&0&0\\ 0&0&c&s\\ 0&0&-s&c\\ \end{array}\right]\left[\begin{array}[]{c}u_{x_{1}}\\ u_{y_{1}}\\ u_{x_{2}}\\ u_{y_{2}}\\ \end{array}\right]

(3.40)

ή σε συμπαγή μορφή:

\bar{\boldsymbol{u}}^{e}=\mathbf{T}\boldsymbol{u}^{e}

(3.41)

Το μητρώο $4\times 4$ που προκύπτει ονομάζεται μητρώο μετασχηματισμού και συμβολίζεται με $\mathbf{T}$ .

Ακολουθώντας παρόμοια διαδικασία, προκύπτει για τον μετασχηματισμό των δυνάμεων από το τοπικό ( $\bar{\boldsymbol{x}}$ ) στο γενικό σύστημα συντεταγμένων ( $\boldsymbol{x}$ ) ότι:

\left[\begin{array}[]{c}f_{x_{1}}\\ f_{y_{1}}\\ f_{x_{2}}\\ f_{y_{2}}\\ \end{array}\right]=\left[\begin{array}[]{cccc}c&-s&0&0\\ s&c&0&0\\ 0&0&c&-s\\ 0&0&s&c\\ \end{array}\right]\left[\begin{array}[]{c}\bar{f}_{x_{1}}\\ \bar{f}_{y_{1}}\\ \bar{f}_{x_{2}}\\ \bar{f}_{y_{2}}\\ \end{array}\right]

(3.42)

ή σε συμπαγή μορφή:

\boldsymbol{f}^{e}=\mathbf{T}^{T}\bar{\boldsymbol{f}}^{e}

(3.43)

Εύκολα διαπιστώνεται ότι το μητρώο που προκύπτει από τον μετασχηματισμό των δυνάμεων ισούται με τον ανάστροφο του $\mathbf{T}$ , δηλαδή $\mathbf{T}^{T}$ . Η σχέση αυτή μπορεί να αποδειχτεί ότι ισχύει γενικά.

Αξίζει επίσης να σημειωθεί ότι στην (3.40) το τοπικό σύστημα συντεταγμένων ( $\bar{\boldsymbol{x}}$ ) εμφανίζεται στο αριστερό σκέλος της εξίσωσης ενώ στην (3.42) στο δεξί. Στην πραγματικότητα οι εξισώσεις (3.40) και (3.42) αποτελούν τη διακριτή διατύπωση του συναλλοίωτου και του ανταλλοίωτου μετασχηματισμού, όπως αποκαλούνται στη μηχανική του συνεχούς μέσου, περιγράφουν δηλαδή τον κανόνα που προσδιορίζει πώς συγκεκριμένες γεωμετρικές οντότητες (τανυστές, διανύσματα) συμπεριφέρονται στην αλλαγή της βάσης τους. Στη συνεχή τους διατύπωση οι εξισώσεις (3.40) και (3.42) αποκαλούνται συμπληρωματικές. Σε κάθε περίπτωση (διακριτή ή συνεχής) οι εξισώσεις (3.40) και (3.42) αναφέρονται στην έννοια της δυϊκότητας.

Σημειώνεται επίσης ότι, για τη συγκεκριμένη περίπτωση στοιχείου, ο πίνακας μετασχηματισμού είναι τετραγωνικός και ορθογωνικός, ισχύει δηλαδή ότι $T^{T}=T^{-1}$ . Αλλά αυτή η ιδιότητα δεν ισχύει απαραίτητα σε πιο περίπλοκα στοιχεία. Στη γενική περίπτωση ο πίνακας μετασχηματισμού $T$ δεν είναι τετραγωνικός, οπότε και δεν μπορεί να οριστεί ο αντίστροφός του.

Επιστρέφοντας στη διατύπωση των εξισώσεων του στοιχείου δικτυώματος στο γενικό σύστημα συντεταγμένων, αυτές δίνονται σε μητρωική μορφή ως:

\mathbf{K}^{e}\boldsymbol{u}^{e}=\boldsymbol{f}^{e}

(3.44)

ενώ στο τοπικό σύστημα συντεταγμένων ως:

\bar{\mathbf{K}}^{e}\bar{\boldsymbol{u}}^{e}=\bar{\boldsymbol{f}}^{e}

(3.45)

Αντικαθιστώντας στην τελευταία σχέση τις (3.41) και (3.43), δηλαδή:

\bar{\boldsymbol{u}}^{e}=\mathbf{T}\boldsymbol{u}^{e},\quad\boldsymbol{f}^{e}=% \mathbf{T}^{T}\bar{\boldsymbol{f}}^{e}

(3.46)

προκύπτει ότι το μητρώο δυσκαμψίας στο γενικό σύστημα συντεταγμένων ορίζεται συναρτήσει του αντίστοιχου μητρώου στο τοπικό σύστημα συντεταγμένων μέσω του ακόλουθου μετασχηματισμού:

\boxed@math{\mathbf{K}^{e}=\left(\mathbf{T}^{e}\right)^{Τ}\bar{\mathbf{K}}^{e}% \mathbf{T}^{e}}

(3.47)

H σχέση (3.47) δίνεται αναλυτικά ως:

\mathbf{K}^{e}=\dfrac{E^{e}A^{e}}{L^{e}}\left[\begin{array}[]{cccc}c^{2}&sc&-c% ^{2}&-sc\\ sc&s^{2}&-sc&-s^{2}\\ -c^{2}&-sc&c^{2}&sc\\ -sc&-s^{2}&sc&s^{2}\\ \end{array}\right]

(3.48)

όπου σύμφωνα και με τα όσα αναφέρθηκαν προηγουμένως $s=\sin\phi^{e}$ και $c=\cos\phi^{e}$ .

Στη συνέχεια δίνεται ενδεικτικά κώδικας σε γλώσσα προγραμματισμού Python, για τον υπολογισμό του μητρώου δυσκαμψίας.

1	def get_K(self):
2	dx = self.nodes[1].x[0] - self.nodes[0].x[0]
3	dy = self.nodes[1].x[1] - self.nodes[0].x[1]
4	L = math.sqrt(dx * dx + dy * dy)
5	s = dy / L
6	c = dx / L
7	K = numpy.array([
8	[ c * c, s * c, -c * c, -s * c],
9	[ s * c, s * s, s * c, -s * s],
10	[ c * c, -s * c, c * c, s * c],
11	[-s * c, -s * s, s * c, s * s]])
12	K = self.E self.A / L
13	return K

3.1.4 Χρήση του στοιχείου στη γεωτεχνική μηχανική

Το στοιχείο δικτυώματος χρησιμοποιείται στη γεωτεχνική μηχανική για την προσομοίωση αγκυρώσεων, αντηρίδων και γενικά ραβδωτών κατασκευών για τις οποίες η αντίσταση σε ροπή θεωρείται αμελητέα. Για αυτές τις περιπτώσεις χρησιμοποιείται το στοιχείο δοκού, που περιγράφεται στη συνέχεια.

3.2 Το στοιχείο δοκού

Οι δοκοί αποτελούν τον συνηθέστερο τύπο δομικού στοιχείου στην περιγραφή και ανάλυση προβλημάτων κυρίως της δομοστατικής μηχανικής.

Από μηχανικής άποψης, ένα στοιχείο δοκού διαφέρει από ένα στοιχείο δικτυώματος, όπως αυτό περιγράφηκε στην προηγούμενη ενότητα (Ενότητα 3.1), στο γεγονός ότι το στοιχείο δοκού μπορεί να παραλάβει φόρτιση και σε μια εγκάρσια διεύθυνση στον άξονά της.

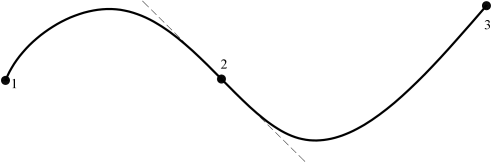
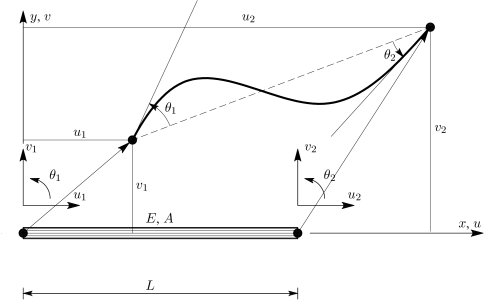
Από μαθηματικής άποψης, η διαφορά της δοκού που εξετάζεται στη συνέχεια με το στοιχείο του δικτυώματος οφείλεται ακριβώς στο γεγονός ότι θα πρέπει να περιγραφούν επιπλέον οι εγκάρσιες μετακινήσεις. Οι εγκάρσιες μετακινήσεις για να θεωρηθούν επιτρεπτές θα πρέπει να περιγράφονται από συναρτήσεις οι οποίες είναι μεν συνεχείς αλλά και οι πρώτες παράγωγοί τους είναι συνεχείς, έτσι ώστε να ισχύει το συμβιβαστό των μετακινήσεων στα άκρα των δοκών και για τις μετακινήσεις όσο και για τις κλίσεις (στροφές στο πλαίσιο των μικρών μετακινήσεων), όπως δίνεται σχηματικά στο Σχήμα 3.4.

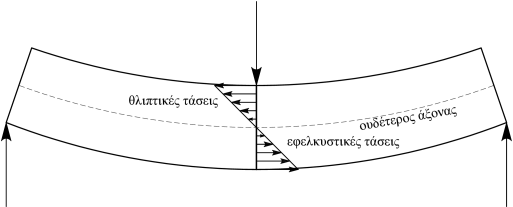
Σχήμα 3.4: Οι συναρτήσεις που μπορούν να χρησιμοποιηθούν στην περιγραφή των εγκάρσιων μετακινήσεων του στοιχείου της δοκού θα πρέπει να μπορούν να περιγράψουν σωστά και τις κλίσεις στα άκρα της.

Η δοκός παραλαμβάνει τα εγκάρσια φορτία πρωτίστως μέσω της καμπτικής λειτουργίας της, η οποία δημιουργεί περιοχές θλιπτικών και εφελκυστικών τάσεων. Οι περιοχές αυτές διαχωρίζονται από τον ουδέτερο άξονα (ή επίπεδο) στον οποίο οι τάσεις είναι μηδενικές. Σε επίπεδο διατομής της δοκού, ο συνδυασμός θλιπτικών και εφελκυστικών τάσεων δημιουργεί μία ροπή, η οποία μεταφέρει τη φόρτιση στις στηρίξεις, όπως περιγράφεται και στο Σχήμα 3.5.

Σχήμα 3.5: Παραλαβή της εξωτερικής φόρτισης από μία δοκό.

Στην ευρύτερη οικογένεια των στοιχείων δοκών ανήκουν διάφοροι τύποι στοιχείων. Με τον όρο γενική δοκός συνήθως αναφερόμαστε σε εκείνον τον τύπο γραμμικών στοιχείων τα οποία μπορούν να παραλάβουν έναν συνδυασμό δράσεων, όπως π.χ. διαξονική κάμψη, διάτμηση και στρέψη. Στην περίπτωση που φορτίζεται κατά τη διαμήκη διεύθυνσή της με θλιπτικό φορτίο, το στοιχείο της δοκού θα πρέπει να μπορεί να περιγράψει και το φαινόμενο του λυγισμού.

Στην περίπτωση που υποβάλλεται κυρίως σε αξονικά και καμπτικά φορτία, τότε αναφέρεται και ως δοκός-υποστύλωμα.

Αν υποβάλλεται κυρίως σε καμπτικά φορτία, τότε αναφέρεται απλά ως δοκός. Μία δοκός συνήθως είναι ευθύγραμμη και η διατομή της είναι πρισματική και σταθερή σε όλο το μήκος της.

Μία χωρική δοκός μπορεί να παραλάβει εγκάρσια φόρτιση σε τυχαία διεύθυνση στο επίπεδο της διατομής της. Αντίθετα, μία επίπεδη δοκός μπορεί να παραλάβει εγκάρσια φόρτιση μόνο σε μία διεύθυνση η οποία βρίσκεται εντός ενός δεδομένου επιπέδου. Στη συνέχεια του παρόντος κεφαλαίου θα ασχοληθούμε μόνο με αυτή την περίπτωση δοκού.

Από μαθηματικής άποψης, τα απλούστερα και πιο διαδεδομένα μαθηματικά προσομοιώματα δοκών στηρίζονται στη θεωρία των Bernoulli-Euler (η οποία ονομάζεται επίσης και κλασική θεωρία των Δοκών) και στη θεωρία του Timoshenko. Η θεωρία των Bernoulli-Euler οδηγεί στα επονομαζόμενα Hermitian στοιχεία δοκού (ή αλλιώς στοιχεία $C^{1}$ ) λόγω των απαιτήσεων συνέχειας των συναρτήσεων σχήματος που χρησιμοποιούνται.

Η θεωρία των Bernoulli-Euler στηρίζεται στις ακόλουθες παραδοχές:

1.

Επίπεδη συμμετρία. Ο διαμήκης άξονας της δοκού είναι ευθύγραμμος και η διατομή της δοκού έχει ένα επίπεδο συμμετρίας. Η συνισταμένη των εγκάρσιων φορτίων και οι στηρίξεις της δοκού βρίσκονται σε αυτό το επίπεδο.
2.

Μεταβλητή διατομή. Η διατομή είτε είναι σταθερή σε όλο το μήκος της δοκού είτε μεταβάλλεται ομαλά.
3.

Επιπεδότητα. Διατομές οι οποίες αρχικά (στην απαραμόρφωτη κατάσταση) ήταν επίπεδες στον διαμήκη άξονα της δοκού παραμένουν επίπεδες και μετά την επιβολή του εξωτερικού φορτίου.
4.

Ενέργεια παραμόρφωσης. Η εσωτερική ενέργεια λόγω των παραμορφώσεων αντιστοιχεί μόνο στις καμπτικές παραμορφώσεις. Η συνεισφορά των υπόλοιπων παραμορφώσεων (αξονικές και διατμητικές) αγνοείται.
5.

Μικρές μετακινήσεις. Οι εγκάρσιες μετακινήσεις και στροφές θεωρούνται πολύ μικρές ώστε να γίνεται δεκτή η παραδοχή των μικρών μετακινήσεων.
6.

Υλικό. Το υλικό θεωρείται ελαστικό και ισότροπο.

3.2.1 Συναρτήσεις σχήματος

Το πεδίο των μετακινήσεων του στοιχείου της δοκού ορίζεται από την αξονική μετακίνηση $u$ και την εγκάρσια μετακίνηση $v$ . Για την πρώτη επιλέγεται μία γραμμική συνάρτηση κατά μήκος του στοιχείου, αντίστοιχη με με εκείνη που χρησιμοποιήθηκε στο στοιχείο του δικτυώματος, ενώ η εγκάρσια μετακίνηση $v$ εκφράζεται με μία συνάρτηση τρίτου βαθμού.

Σχήμα 3.6: Στοιχείο δοκού στο επίπεδο (αρχική/παραμορφωμένη κατάσταση).

Επομένως μπορούμε να γράψουμε:

	$\displaystyle u$	$\displaystyle=\alpha_{1}+\alpha_{2}x$		(3.49)
	$\displaystyle v$	$\displaystyle=\alpha_{3}+\alpha_{2}x+\alpha_{2}x^{2}+\alpha_{2}x^{3}$		(3.50)

ή σε μητρωική μορφή:

	$\displaystyle u$	$\displaystyle=\left[\begin{array}[]{cc}1&x\\ \end{array}\right]\left[\begin{array}[]{c}\alpha_{1}\\ \alpha_{2}\\ \end{array}\right]$		(3.51)
	$\displaystyle v$	$\displaystyle=\left[\begin{array}[]{cccc}1&x&x^{2}&x^{3}\\ \end{array}\right]\left[\begin{array}[]{c}\alpha_{3}\\ \alpha_{4}\\ \alpha_{5}\\ \alpha_{6}\\ \end{array}\right]$		(3.52)

Ο υπολογισμός των παραμέτρων $\alpha_{1}$ και $\alpha_{2}$ γίνεται ακολουθώντας παρόμοια διαδικασία με αυτή που ακολουθήθηκε στο στοιχείο δικτυώματος, οπότε και προκύπτει:

u=N_{1}u_{1}+N_{2}u_{2}

(3.53)

όπου οι συναρτήσεις $N_{i}$ για $i=1,2$ ορίζονται ως

	$\displaystyle N_{1}$	$\displaystyle=1-\dfrac{x}{L}$		(3.54)
	$\displaystyle N_{2}$	$\displaystyle=\dfrac{x}{L}$		(3.55)

και απεικονίζονται στο Σχήμα 3.2.

Ο υπολογισμός των παραμέτρων $\alpha_{3}$ - $\alpha_{6}$ γίνεται συνδέοντας τις παραμέτρους με τις συνοριακές συνθήκες του στοιχείου,

	$\displaystyle u=u_{1},\;\dfrac{du}{dx}=\theta_{1}$	όταν	$\displaystyle x=0$		(3.56)
	$\displaystyle u=u_{2},\;\dfrac{du}{dx}=\theta_{1}$	όταν	$\displaystyle x=L$		(3.57)

Αντικαθιστώντας τις παραπάνω σχέσεις (3.56)-(3.57) στην (3.52), προκύπτει:

\left[\begin{array}[]{c}u_{1}\\ \theta_{1}\\ u_{2}\\ \theta_{2}\\ \end{array}\right]=\left[\begin{array}[]{cccc}1&0&0&0\\ 0&1&0&0\\ 1&L&L^{2}&L^{3}\\ 0&1&2L&3L^{2}\\ \end{array}\right]\left[\begin{array}[]{c}\alpha_{1}\\ \alpha_{2}\\ \alpha_{3}\\ \alpha_{4}\\ \end{array}\right]

(3.58)

ή σε συντετμημένη μορφή:

\boldsymbol{d}_{b}=\mathbf{A}_{b}\boldsymbol{a}_{b}

(3.59)

όπου ο δείκτης $b$ αναφέρεται στα καμπτικά μεγέθη του στοιχείου.

Από την επίλυση της παραπάνω σχέσης με αντιστροφή του πίνακα $\mathbf{A}_{b}$ προκύπτει:

\boldsymbol{a}_{b}=\mathbf{A}_{b}^{-1}\boldsymbol{d}_{b}

(3.60)

ή αναλυτικά

\left[\begin{array}[]{c}\alpha_{1}\\ \alpha_{2}\\ \alpha_{3}\\ \alpha_{4}\\ \end{array}\right]=\left[\begin{array}[]{cccc}1&0&0&0\\ 0&1&0&0\\ -\dfrac{3}{L^{2}}&-\dfrac{2}{L}&\dfrac{3}{L^{2}}&-\dfrac{1}{L}\\ \dfrac{2}{L^{3}}&\dfrac{1}{L^{2}}&-\dfrac{2}{L^{3}}&-\dfrac{1}{L^{2}}\\ \end{array}\right]\left[\begin{array}[]{c}u_{1}\\ \theta_{1}\\ u_{2}\\ \theta_{2}\\ \end{array}\right]

(3.61)

Αντικαθιστώντας την (3.52) στην (3.61), προκύπτει

	$\displaystyle v$	$\displaystyle=\left[\begin{array}[]{cccc}1&x&x^{2}&x^{3}\\ \end{array}\right]\left[\begin{array}[]{c}\alpha_{3}\\ \alpha_{4}\\ \alpha_{5}\\ \alpha_{6}\\ \end{array}\right]$
		$\displaystyle=\left[\begin{array}[]{cccc}1&x&x^{2}&x^{3}\\ \end{array}\right]\left[\begin{array}[]{cccc}1&0&0&0\\ 0&1&0&0\\ -\dfrac{3}{L^{2}}&-\dfrac{2}{L}&\dfrac{3}{L^{2}}&-\dfrac{1}{L}\\ \dfrac{2}{L^{3}}&\dfrac{1}{L^{2}}&-\dfrac{2}{L^{3}}&-\dfrac{1}{L^{2}}\\ \end{array}\right]\left[\begin{array}[]{c}u_{1}\\ \theta_{1}\\ u_{2}\\ \theta_{2}\\ \end{array}\right]$		(3.62)

ή αλλιώς

v=\mathbf{N}_{b}\boldsymbol{d}_{b}

(3.63)

όπου

	$\displaystyle\mathbf{N}_{b}$	$\displaystyle=\left[\begin{array}[]{cccc}1&x&x^{2}&x^{3}\\ \end{array}\right]\left[\begin{array}[]{cccc}1&0&0&0\\ 0&1&0&0\\ -\dfrac{3}{L^{2}}&-\dfrac{2}{L}&\dfrac{3}{L^{2}}&-\dfrac{1}{L}\\ \dfrac{2}{L^{3}}&\dfrac{1}{L^{2}}&-\dfrac{2}{L^{3}}&-\dfrac{1}{L^{2}}\\ \end{array}\right]$
		$\displaystyle=\left[\begin{array}[]{cccc}1-\dfrac{3x^{2}}{L^{2}}+\dfrac{2x^{3}% }{L^{3}}&x-\dfrac{2x^{2}}{L^{2}}+\dfrac{x^{3}}{L^{3}}&\dfrac{3x^{2}}{L^{2}}-% \dfrac{2x^{3}}{L^{3}}&-\dfrac{x^{2}}{L^{2}}+\dfrac{x^{3}}{L^{3}}\end{array}\right]$		(3.64)

Επομένως η (3.63) μπορεί τώρα να γραφτεί ως

v=N_{3}v_{1}+N_{4}\theta_{1}+N_{5}v_{2}+N_{6}\theta_{2}

(3.65)

όπου οι συναρτήσεις $N_{3}$ , $N_{4}$ , $N_{5}$ και $N_{6}$ γράφονται αναλυτικά ως

$\displaystyle N_{3}$	$\displaystyle=1-\dfrac{3x^{2}}{L^{2}}+\dfrac{2x^{3}}{L^{3}}$	(3.66)
$\displaystyle N_{4}$	$\displaystyle=x-\dfrac{2x^{2}}{L^{2}}+\dfrac{x^{3}}{L^{3}}$	(3.67)
$\displaystyle N_{5}$	$\displaystyle=\dfrac{3x^{2}}{L^{2}}-\dfrac{2x^{3}}{L^{3}}$	(3.68)
$\displaystyle N_{6}$	$\displaystyle=-\dfrac{x^{2}}{L^{2}}+\dfrac{x^{3}}{L^{3}}$	(3.69)

και δίνονται στο Σχήμα 3.7.

Σχήμα 3.7: Κυβικές συναρτήσεις σχήματος για το στοιχείο επίπεδης δοκού.

Συνδυάζοντας την (3.53) και την (3.65), μπορούμε τώρα να γράψουμε:

\left[\begin{array}[]{c}u\\ v\\ \end{array}\right]=\left[\begin{array}[]{cccccc}N_{1}&0&0&N_{2}&0&0\\ 0&N_{3}&N_{4}&0&N_{5}&N_{6}\\ \end{array}\right]\left[\begin{array}[]{c}u_{1}\\ v_{1}\\ \theta_{1}\\ u_{2}\\ v_{2}\\ \theta_{2}\\ \end{array}\right]

(3.70)

Η παραπάνω σχέση εκφράζει το πεδίο των μετακινήσεων του στοιχείου της επίπεδης δοκού συναρτήσει των επικόμβιων μετακινήσεων της $u_{1}$ , $v_{1}$ , $\theta_{1}$ , $u_{2}$ , $v_{2}$ και $\theta_{2}$ .

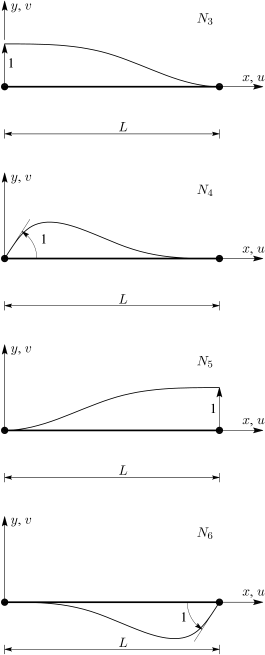
3.2.2 Σχέσεις παραμορφώσεων-μετακινήσεων

Για τον υπολογισμό του μητρώου παραμορφώσεων-μετακινήσεων $\mathbf{B}$ του στοιχείου, διατυπώνονται στη συνέχεια οι αντίστοιχες σχέσεις παραμορφώσεων-μετακινήσεων.

Σύμφωνα με τη θεωρία των Euler-Bernoulli που εξετάζεται, προκύπτει ότι οι μετακινήσεις ενός εγκάρσιου επιπέδου της δοκού δίνονται από τις σχέσεις (βλ. και Σχήμα 3.8):

	$\displaystyle u$	$\displaystyle=u(x)-y\theta(x)$		(3.71)
	$\displaystyle v$	$\displaystyle=v(x)$		(3.72)

Σχήμα 3.8: Κινηματική μίας δοκού που περιγράφεται από τη θεωρία Euler-Bernoulli.

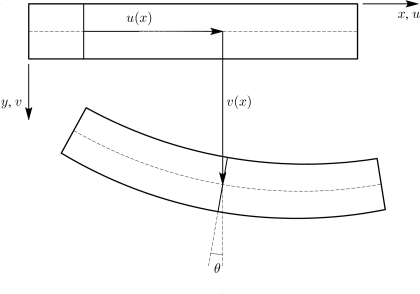
Σύμφωνα με τη θεωρία των Euler-Bernoulli οι διατμητικές παραμορφώσεις $\varepsilon_{xy}$ που ορίζονται ως

\varepsilon_{xy}=\dfrac{1}{2}\left(\dfrac{\partial u}{\partial y}+\dfrac{% \partial v}{\partial x}\right)

(3.73)

είναι μηδενικές, ενώ η ανηγμένη παραμόρφωση της δοκού $\varepsilon_{x}$ δίνεται από τη σχέση:

\varepsilon_{x}=\dfrac{du}{dx}

(3.74)

Αντικαθιστώντας την (3.71) στην (3.74), τελικά προκύπτει σχέση παραμορφώσεων-μετακινήσεων για τη δοκό που στηρίζεται στη θεωρία των Euler-Bernoulli:

\varepsilon_{x}=\dfrac{du}{dx}-y\dfrac{du^{2}}{dx^{2}}

(3.75)

Το μητρώο παραμόρφωσης $\mathbf{B}$ προκύπτει από τις (3.53), (3.65) και (3.75).

Από την (3.53), η οποία περιγράφει την παρεμβολή των αξονικών μετακινήσεων,

u=N_{1}u_{1}+N_{2}u_{2}

(3.76)

προκύπτει η παράγωγος $\dfrac{du}{dx}$ ,

$\displaystyle\dfrac{du}{dx}$	$\displaystyle=\dfrac{d\left(N_{1}u_{1}+N_{2}u_{2}\right)}{dx}$
	$\displaystyle=\dfrac{d\left(N_{1}u_{1}\right)}{dx}+\dfrac{d\left(N_{2}u_{2}% \right)}{dx}$
	$\displaystyle=\dfrac{d\left(N_{1}\right)}{dx}u_{1}+\dfrac{d\left(N_{2}\right)}% {dx}u_{2}$
	$\displaystyle=N_{1,x}u_{1}+N_{2,x}u_{2},$	(3.77)

ή σε μητρωική μορφή:

\dfrac{du}{dx}=\left[\begin{array}[]{cc}N_{1,x}&N_{2,x}\end{array}\right]\left% [\begin{array}[]{c}u_{1}\\ u_{2}\end{array}\right]

(3.78)

Ομοίως, από την (3.65), η οποία περιγράφει την παρεμβολή των εγκάρσιων μετακινήσεων και στροφών,

v=N_{3}v_{1}+N_{4}\theta_{1}+N_{5}v_{2}+N_{6}\theta_{2}

(3.79)

προκύπτει η παράγωγος $\dfrac{d^{2}v}{dx^{2}}$ ,

	$\displaystyle\dfrac{d^{2}v}{dx^{2}}$	$\displaystyle=\dfrac{d^{2}N_{3}}{dx^{2}}v_{1}+\dfrac{d^{2}N_{4}}{dx^{2}}\theta% _{1}+\dfrac{d^{2}N_{5}}{dx^{2}}v_{2}+\dfrac{d^{2}N_{6}}{dx^{2}}\theta_{2}$
		$\displaystyle=N_{3,xx}v_{1}+N_{4,xx}\theta_{1}+N_{5,xx}v_{2}+N_{6,xx}\theta_{2}$		(3.80)

ή σε μητρωική μορφή:

\dfrac{du}{dx}=\left[\begin{array}[]{cccc}N_{3,xx}&N_{4,xx}&N_{5,xx}&N_{6,xx}% \end{array}\right]\left[\begin{array}[]{c}v_{1}\\ \theta_{1}\\ v_{2}\\ \theta_{2}\end{array}\right]

(3.81)

Η ανηγμένη παραμόρφωση $\varepsilon_{x}$ , όπως δίνεται από την (3.75),

\varepsilon_{x}=\dfrac{du}{dx}-y\dfrac{du^{2}}{dx^{2}}

(3.82)

μπορεί πλέον να γραφτεί σύμφωνα με τα παραπάνω ως:

\varepsilon_{x}=\left[\begin{array}[]{cccccc}N_{1,x}&-yN_{3,xx}&-yN_{4,xx}&N_{% 2,x}&-yN_{5,xx}&-yN_{6,xx}\end{array}\right]\left[\begin{array}[]{c}u_{1}\\ v_{1}\\ \theta_{1}\\ u_{2}\\ v_{2}\\ \theta_{2}\end{array}\right]

(3.83)

ή σε μητρωική μορφή:

\varepsilon_{x}=\mathbf{B}\boldsymbol{d}

(3.84)

όπου οι όροι του μητρώου παραμορφώσεων-μετακινήσεων δίνονται ως:

$\displaystyle B_{1}$	$\displaystyle=-\dfrac{1}{L}$	(3.85)
$\displaystyle B_{2}$	$\displaystyle=-y\left[-\dfrac{6}{L^{2}}\left(1-\dfrac{2x}{L}\right)\right]$	(3.86)
$\displaystyle B_{3}$	$\displaystyle=-y\left[-\dfrac{2}{L}\left(3-\dfrac{3x}{L}\right)\right]$	(3.87)
$\displaystyle B_{4}$	$\displaystyle=-\dfrac{1}{L}$	(3.88)
$\displaystyle B_{5}$	$\displaystyle=-y\left[-\dfrac{6}{L^{2}}\left(1-\dfrac{2x}{L}\right)\right]$	(3.89)
$\displaystyle B_{6}$	$\displaystyle=-y\left[-\dfrac{2}{L}\left(1-\dfrac{3x}{L}\right)\right]$	(3.90)

3.2.3 Το μητρώο δυσκαμψίας

Με γνωστό το μητρώο παραμορφώσεων-μετακινήσεων $\mathbf{B}$ , το μητρώο δυσκαμψίας $\mathbf{Κ}$ , εύκολα πλέον προκύπτει από τη γενική σχέση

\mathbf{Κ}_{(6\times 6)}=\int_{\Omega}\mathbf{B}^{T}_{(6\times 1)}\mathbf{C}_{% (1\times 1)}\mathbf{B}_{(1\times 6)}d\Omega

(3.91)

Το μητρώο ελαστικότητας για τη συγκεκριμένη περίπτωση ταυτίζεται με το μέτρο του Young, $E$ , δηλαδή

\mathbf{C}=\left[E\right].

(3.92)

Θεωρώντας ότι οι άξονες που περιγράφουν τη διατομή του στοιχείου είναι κύριοι και κεντροβαρικοί και ότι η δοκός είναι πρισματική, σταθερής διατομής, προκύπτει το μητρώο δυσκαμψίας ως:

\mathbf{K}^{e}=\left[\begin{array}[]{cccccc}\dfrac{AE}{L}&0&0&-\dfrac{AE}{L}&0% &0\\ 0&12\dfrac{EI}{L^{3}}&6\dfrac{EI}{L^{2}}&0&-12\dfrac{EI}{L^{3}}&6\dfrac{EI}{L^% {2}}\\ 0&6\dfrac{EI}{L^{2}}&4\dfrac{EI}{L}&0&-6\dfrac{EI}{L^{2}}&2\dfrac{EI}{L}\\ \dfrac{AE}{L}&0&0&\dfrac{AE}{L}&0&0\\ 0&-12\dfrac{EI}{L^{3}}&-6\dfrac{EI}{L^{2}}&0&12\dfrac{EI}{L^{3}}&-6\dfrac{EI}{% L^{2}}\\ 0&6\dfrac{EI}{L^{2}}&2\dfrac{EI}{L}&0&-6\dfrac{EI}{L^{2}}&4\dfrac{EI}{L}\\ \end{array}\right]

(3.93)

3.2.4 Χρήση του στοιχείου στη γεωτεχνική μηχανική

Το στοιχείο της δοκού χρησιμοποιείται στην προσομοίωση προβλημάτων της γεωτεχνικής μηχανικής για την προσομοίωση δοκών, πεδιλοδοκών και γενικά επιφανειακών θεμελιώσεων, πασσάλων, διαφραγματικών τοίχων αντιστήριξης και γενικά όλων εκείνων των στοιχείων στα οποία η καμπτική λειτουργία τους είναι επικρατούσα.

3.3 Το στοιχείο δοκού επί εδάφους

Σε γεωτεχνικά κυρίως προβλήματα υπάρχει συχνά η ανάγκη προσομοίωσης οριζόντιων ή κατακόρυφων δοκών οι οποίες να υποστηρίζονται ελαστικά κατά το μήκος τους και στις οποίες η χρήση ενός απλού στοιχείου δοκού επί επιφανειακών ή χωρικών στοιχείων, τα οποία θα αναπτυχθούν στις επόμενες ενότητες, κρίνεται συχνά υπερβολική. Στις περιπτώσεις αυτές χρησιμοποιείται το στοιχείο δοκού επί ελαστικού εδάφους [3].

Οι πιο συνηθισμένες εφαρμογές των στοιχείων δοκού επί ελαστικού εδάφους αφορούν:

1.

την προσομοίωση πεδιλοδοκών (δοκών θεμελίωσης επί του εδάφους) και
2.

την προσομοίωση πασσάλων.

Μια συνηθισμένη απλοποιητική παραδοχή που εφαρμόζεται στα παραπάνω προβλήματα είναι το προσομοίωμα ελαστικής στήριξης Winkler. Πρόκειται για μια προσέγγιση της συμπεριφοράς του εδάφους κατά την οποία:

•

το έδαφος προσομοιώνεται ως συνεχή ελαστικά ελατήρια,
•

αγνοείται η επίδραση της πολυδιάστατης ελαστικότητας και
•

αγνοείται η επίδραση της τριβής.

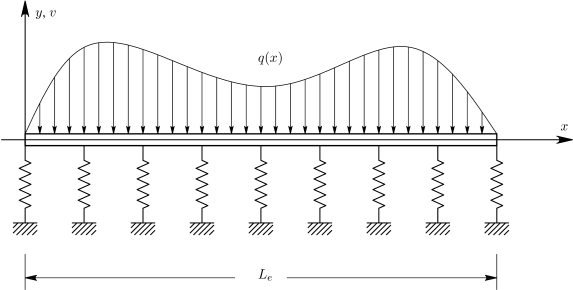
Σχήμα 3.9: Το στοιχείο δοκού επί εδάφους.

3.3.1 Το μητρώο δυσκαμψίας

Έστω μία πρισματική δοκός σταθερής διατομής επί ελαστικού εδάφους το οποίο θεωρείται ότι προσεγγίζεται με το προσομοίωμα ελαστικής στήριξης Winkler, όπως δίνεται στο Σχήμα 3.9. Η ελατηριακή σταθερά που περιγράφει το προσομοίωμα ελαστικής στήριξης Winkler συμβολίζεται με $k_{F}$ , όπου $k_{F}>0$ .

Η εξίσωση που περιγράφει την ισορροπία της δοκού δίνεται ως:

EI\dfrac{d^{4}v}{dx^{4}}+k_{F}v=q(x)

(3.94)

όπου:

$E$ Το μέτρο ελαστικότητας του υλικού της δοκού.
$I$ Η ροπή αδράνειας της διατομής της δοκού.
$q(x)$ Το κατανεμημένο φορτίο κατά μήκος της δοκού (βλ. και Σχήμα 3.9).

Η γενική, ομογενής λύση της παραπάνω εξίσωσης για ένα μήκος ίσο με $l$ , από $x=0$ έως $x=l$ , δίνεται ως:

v(x)=e^{\zeta}(c_{1}\sin\zeta+c_{2}\cos\zeta)+e^{-\zeta}(c_{3}\sin\zeta+c_{4}% \cos\zeta)

(3.95)

όπου

\zeta=\dfrac{\lambda x}{l}

(3.96)

και

\lambda=\sqrt[4]{\dfrac{k_{f}}{4EI}}

(3.97)

Οι συντελεστές $c_{1}$ , $c_{2}$ , $c_{3}$ και $c_{4}$ στην (3.95) καθορίζονται από τις συνοριακές συνθήκες. Στη συνέχεια οι συντελεστές $c_{1}$ , $c_{2}$ , $c_{3}$ και $c_{4}$ θεωρούνται ως οι γενικευμένες συντεταγμένες:

\boldsymbol{c}=\left[\begin{array}[]{c}c_{1}\\ c_{2}\\ c_{3}\\ c_{4}\\ \end{array}\right]

(3.98)

Το συναρτησιακό της συνολικής δυναμικής ενέργειας του συστήματος ορίζεται ως προς τις γενικευμένες συντεταγμένες σύμφωνα με τη σχέση:

	$\displaystyle\Pi_{c}^{e}$	$\displaystyle=\int_{0}^{l}\left(\dfrac{1}{2}EI(v^{\prime\prime})^{2}+\dfrac{1}% {2}k_{f}v^{2}-q_{0}v\right)dx$
		$\displaystyle=\dfrac{1}{2}\boldsymbol{c}^{T}\left(\mathbf{K}_{cB}+\mathbf{K}_{% cF}\right)\boldsymbol{c}-\boldsymbol{c}^{T}\mathbf{f}_{c}$		(3.99)

Από την παραπάνω εξίσωση ορίζονται τα μητρώα $\mathbf{K}_{cB}$ και $\mathbf{K}_{cF}$ ως τα γενικευμένα μητρώα δυσκαμψίας που αναφέρονται στην κάμψη της δοκού και στο ελατηριακό προσομοίωμα του εδάφους αντίστοιχα.

Το διάνυσμα $\mathbf{f}_{c}$ είναι το γενικευμένο διάνυσμα φόρτισης λόγω ενός κατανεμημένου φορτίου $q(x)$ .

Οι επικόμβιοι βαθμοί ελευθερίας σχετίζονται με τις γενικευμένες μετακινήσεις μέσω της σχέσης:

\left[\begin{array}[]{c}v_{1}\\ \theta_{1}\\ v_{2}\\ \theta_{2}\\ \end{array}\right]=\left[\begin{array}[]{cccc}0&1&0&1\\ \dfrac{\lambda}{l}&\dfrac{\lambda}{l}&\dfrac{\lambda}{l}&\dfrac{\lambda}{l}\\ e^{\lambda}\sin\lambda&e^{\lambda}\cos\lambda&e^{-\lambda}\sin\lambda&e^{-% \lambda}\cos\lambda\\ \dfrac{\lambda e^{\lambda}(\cos\lambda+\sin\lambda)}{l}&\dfrac{\lambda e^{% \lambda}(\cos\lambda-\sin\lambda)}{l}&\dfrac{\lambda e^{-\lambda}(\cos\lambda-% \sin\lambda)}{l}&\dfrac{-\lambda e^{-\lambda}(\cos\lambda+\sin\lambda)}{l}\\ \end{array}\right]\left[\begin{array}[]{c}c_{1}\\ c_{2}\\ c_{3}\\ c_{4}\\ \end{array}\right]

(3.100)

ή αλλιώς σε συνεπτυγμένη μορφή:

\boldsymbol{u}^{e}=\mathbf{G}_{F}\boldsymbol{c}.

(3.101)

Αντιστρέφοντας την παραπάνω σχέση, προκύπτει:

\boldsymbol{c}=\mathbf{H}_{F}\boldsymbol{u}^{e}

(3.102)

όπου

\mathbf{H}_{F}=\mathbf{G}_{F}^{-1}

(3.103)

Η δυσκαμψία του στοιχείου προκύπτει τελικά ως το άθροισμα των επιμέρους δυσκαμψιών

\mathbf{Κ}^{e}=\mathbf{Κ}_{B}^{e}+\mathbf{Κ}_{F}^{e}

(3.104)

όπου

\mathbf{Κ}_{B}^{e}=\mathbf{H}_{F}^{T}\mathbf{Κ}_{cB}\mathbf{H}_{F}

(3.105)

και

\mathbf{Κ}_{F}^{e}=\mathbf{H}_{F}^{T}\mathbf{Κ}_{cF}\mathbf{H}_{F}.

(3.106)

Αντίστοιχα το διάνυσμα της φόρτισης προκύπτει ίσο με:

\mathbf{f}^{e}=\mathbf{H}_{F}^{T}\mathbf{f}_{c}.

(3.107)

Κάνοντας τις παραπάνω πράξεις, προκύπτει:

$\displaystyle\mathbf{K}_{B}^{e}$	$\displaystyle=\begin{bmatrix}B_{1}&B_{2}&B_{5}&-B_{4}\\ &B_{3}&B_{4}&B_{6}\\ &&B_{1}&-B_{2}\\ \omit\span\omit\text{symm}&&B_{3}\end{bmatrix}$	(3.108)
$\displaystyle\mathbf{K}_{F}^{e}$	$\displaystyle=\begin{bmatrix}F_{1}&F_{2}&F_{5}&-F_{4}\\ &F_{3}&F_{4}&F_{6}\\ &&F_{1}&-F_{2}\\ \omit\span\omit\text{symm}&&F_{3}\end{bmatrix}$	(3.109)
$\displaystyle\mathbf{f}^{e}$	$\displaystyle=\dfrac{q_{0}l}{\lambda^{2}g}\begin{bmatrix}f_{1}\\ f_{2}\\ f_{1}\\ -f_{2}\end{bmatrix}$	(3.110)

Οι όροι του μητρώου $\mathbf{K}^{e}_{B}$ δίνονται ως:

$\displaystyle B_{1}$	$\displaystyle=2\lambda^{2}-4\sin(2\lambda)+\sin(4\lambda)+4\sin\lambda(\cos% \lambda\cosh(2\lambda)+8\lambda\sin\lambda\sinh^{2}\lambda)$
	$\displaystyle+2\cos(2\lambda)-2)\sinh(2\lambda)+\sinh(4\lambda)$	(3.111)
$\displaystyle B_{2}$	$\displaystyle=2l_{e}\lambda(4\cos(2\lambda)-\cos(4\lambda)-4\cosh(2\lambda)+% \cosh(4\lambda)$
	$\displaystyle-8\lambda\sin(2\lambda)\sinh\lambda\sinh\lambda+8\lambda\sin% \lambda\sin\lambda\sinh(2\lambda))$	(3.112)
$\displaystyle B_{3}$	$\displaystyle=-(l_{e}l_{e}(8\lambda\cos(2\lambda)-12\sin(2\lambda)+\cosh(2% \lambda)(6\sin(2\lambda)-8\lambda)$
	$\displaystyle+3\sin(4\lambda)+2(6-3\cos(2\lambda)+4\lambda\sin(2\lambda))% \sinh(2*\lambda)-3\sinh(4\lambda)))$	(3.113)
$\displaystyle B_{4}$	$\displaystyle=-4l_{e}\lambda(\lambda\cosh(3\lambda)\sin\lambda-\lambda\cosh% \lambda(-2\sin\lambda+\sin(3\lambda))+(\lambda(\cos\lambda+\cos(3\lambda))$
	$\displaystyle+\cosh(2\lambda)(-2\lambda\cos\lambda+4\sin\lambda)+2(-5\sin% \lambda+\sin(3\lambda)))\sinh\lambda)$	(3.114)
$\displaystyle B_{5}$	$\displaystyle=-4\lambda\lambda(2\cos\lambda(-2+\cos(2\lambda)+\cosh(2\lambda))\sinh\lambda$
	$\displaystyle+\sin(3\lambda)(\cosh\lambda-2\lambda\sinh\lambda)+\sin\lambda(-4% \cosh\lambda+\cosh(3\lambda)+2\lambda\sinh(3\lambda)))$	(3.115)
$\displaystyle B_{6}$	$\displaystyle=2l_{e}^{2}(\cosh(3\lambda)(-2\lambda\cos\lambda+3\sin\lambda)+% \cosh\lambda(2\lambda\cos(3\lambda)+3(\sin(3\lambda)-4\sin\lambda))$
	$\displaystyle+(9\cos\lambda-3\cos(3\lambda)-6\cos\lambda\cosh(2\lambda)+16% \lambda\sin\lambda)\sinh\lambda)$	(3.116)

Αντίστοιχα οι όροι του μητρώου $\mathbf{K}^{e}_{F}$ δίνονται ως:

$\displaystyle F_{1}$	$\displaystyle=2\lambda\lambda(-32\lambda\sin\lambda\sin\lambda\sinh\lambda% \sinh\lambda+6(-2+\cos(2\lambda))(\sin(2\lambda)+\sinh(2\lambda))$
	$\displaystyle+6\cosh(2\lambda)(\sin(2\lambda)+\sinh(2\lambda)))$	(3.117)
$\displaystyle F_{2}$	$\displaystyle=2l_{e}\lambda(4\cos(2\lambda)-\cos(4\lambda)-4\cosh(2\lambda)$
	$\displaystyle+\cosh(4\lambda)+8\lambda\sin(2\lambda)\sinh\lambda\sinh\lambda-8% \lambda\sin\lambda\sin\lambda\sinh(2\lambda))$	(3.118)
$\displaystyle F_{3}$	$\displaystyle=l_{e}l_{e}(8\lambda\cos(2\lambda)+4\sin(2\lambda)-2\cosh(2% \lambda)(4\lambda+\sin(2\lambda))$
	$\displaystyle-\sin(4\lambda)+2(\cos(2\lambda)+4\lambda\sin(2\lambda)-2)\sinh(2% \lambda)+\sinh(4\lambda))$	(3.119)
$\displaystyle F_{4}$	$\displaystyle=4l_{e}\lambda(\lambda\cosh(3\lambda)\sin\lambda-\lambda\cosh% \lambda(-2\sin\lambda+\sin(3\lambda))$
	$\displaystyle+(\lambda\cos\lambda+\lambda\cos(3\lambda)+10\sin\lambda-2\cosh(2% \lambda)(\lambda\cos\lambda+2\sin\lambda)-2\sin(3\lambda))\sinh\lambda)$	(3.120)
$\displaystyle F_{5}$	$\displaystyle=-4\lambda\lambda(6\cos\lambda(-2+\cos(2\lambda)+\cosh(2\lambda))\sinh\lambda$
	$\displaystyle+\sin(3\lambda)(3\cosh\lambda+2\lambda\sinh\lambda)+\sin\lambda(-% 12\cosh\lambda+3\cosh(3\lambda)-2\lambda\sinh(3\lambda)))$	(3.121)
$\displaystyle F_{6}$	$\displaystyle=-2l_{e}l_{e}(-(\cosh(3\lambda)(2\lambda\cos\lambda+\sin\lambda))$
	$\displaystyle+\cosh\lambda(2\lambda\cos(3\lambda)+4\sin\lambda-\sin(3\lambda))$	(3.122)
	$\displaystyle+(\cos(3\lambda)+\cos\lambda(2\cosh(2\lambda)-3)+16\lambda\sin% \lambda)\sinh\lambda)$	(3.123)

Τέλος, οι όροι του διανύσματος $\mathbf{F}^{e}$ δίνονται ως:

	$\displaystyle f_{1}$	$\displaystyle=2l\left(\cosh\lambda-\cos\lambda\right)\left(\sin\lambda-\sinh% \lambda\right)$		(3.124)
	$\displaystyle f_{2}$	$\displaystyle=-\left(l_{e}\left(\sin\lambda-\sinh\lambda\right)\left(\sin% \lambda-\sinh\lambda\right)\right)$		(3.125)

Στα παραπάνω ισχύει:

$\displaystyle\lambda$	$\displaystyle=l_{e}\sqrt[4]{\dfrac{k_{f}}{4EI}}$	(3.126)
και
$\displaystyle g$	$\displaystyle=2-\cos(2\lambda)-cosh(2\lambda)$	(3.127)

3.3.2 Προγραμματισμός του στοιχείου

Με βάση τα παραπάνω δίνεται στη συνέχεια ενδεικτικά ο προγραμματισμός του στοιχείου στη γλώσσα προγραμματισμού Python.

Πιο συγκεκριμένα, το μητρώο $\mathbf{K}^{e}_{B}$ δίνεται ως:

1	def get_KeB(self):
2	l = self.le * ((self.kf/(4 * self.E * self.I))**(0.25))
3	g = 2 - math.cos(2 * l) - math.cosh(2 * l)
4	B1 = 2 * l * l * (
5	-4 * math.sin(2 * l)
6	+ math.sin(4 * l)
7	+ 4 * math.sin(l) * (
8	math.cos(l) * math.cosh(2 * l)
9	+ 8 * l * math.sin(l) * math.sinh(l) * math.sinh(l)
10	) + 2 * (math.cos(2 * l) -2) * math.sinh(2 * l)
11	+ math.sinh(4 * l)
12	)
13	B2 = 2 * self.le * l * (
14	4 * math.cos(2 * l)
15	- math.cos(4 * l)
16	- 4 * math.cosh(2 * l)
17	+ math.cosh(4 * l)
18	- 8 * l * math.sin(2 * l) * math.sinh(l) * math.sinh(l)
19	+ 8 * l * math.sin(l) * math.sin(l) * math.sinh(2 * l)
20	)
21	B3 = -(
22	self.le * self.le * (
23	8 * l * math.cos(2 * l)
24	- 12 * math.sin(2 * l)
25	+ math.cosh(2 * l) * (
26	6 * math.sin(2 * l)
27	- 8 * l
28	)
29	+ 3 * math.sin(4 * l)
30	+ 2 *(
31	6
32	- 3 * math.cos(2 * l)
33	+ 4 * l * math.sin(2 * l)
34	)* math.sinh(2*l)
35	- 3 * math.sinh(4 * l)
36	)
37	)
38	B4 = - 4 * self.le * l * (
39	l * math.cosh(3 * l) * math.sin(l)
40	- l * math.cosh(l) * (-2 * math.sin(l) + math.sin(3 * l))
41	+ (l * (math.cos(l) + math.cos(3 * l))
42	+ math.cosh(2 * l) * (-2 * l * math.cos(l) + 4 * math.sin(l))
43	+ 2 * (-5 * math.sin(l) + math.sin(3 * l))) * math.sinh(l))
44	B5 = -4 * l * l * (
45	2 * math.cos(l) * (
46	-2 + math.cos(2 * l)
47	+ math.cosh(2 * l)
48	) * math.sinh(l) + math.sin(3 * l) * (
49	math.cosh(l) - 2 * l * math.sinh(l)
50	) + math.sin(l) * (
51	-4 * math.cosh(l)
52	+ math.cosh(3 * l)
53	+ 2 * l * math.sinh(3 * l)
54	)
55	)
56	B6 = 2 * self.le * self.le * (
57	math.cosh(3 * l) * (
58	-2 * l * math.cos(l)
59	+ 3 * math.sin(l)
60	) + math.cosh(l) * (
61	2 * l * math.cos(3 * l)
62	+ 3 * (math.sin(3 * l)
63	- 4 * math.sin(l))
64	) + (
65	9 * math.cos(l)
66	- 3 * math.cos(3 * l)
67	- 6 * math.cos(l) * math.cosh(2 * l)
68	+ 16 * l * math.sin(l)
69	) * math.sinh(l)
70	)
71	facB = (self.E * self.I * l / self.le * self.le * self.le)/(4 * g * g)
72	KeB = facB * np.array([
73	[ B1, B2, B5, -B4],
74	[ B2, B3, B4, B6],
75	[ B5, B4, B1, -B2],
76	[-B4, B6, -B2, B3]
77	])
78	return KeB

Το μητρώο $\mathbf{K}^{e}_{F}$ δίνεται ως:

1	def get_KeF(self):
2	l = self.le * ((self.kf/(4 * self.E * self.I))**(0.25))
3	g = 2 - math.cos(2 * l) - math.cosh(2 * l)
4	F1 = 2 * l * l *(
5	-32 * l * math.sin(l) * math.sin(l) * math.sinh(l) * math.sinh(l)
6	+ 6 * (
7	-2 + math.cos(2 * l)) * (math.sin(2 * l)
8	+ math.sinh(2 * l)
9	)
10	+ 6 * math.cosh(2 * l) * (
11	math.sin(2 * l)
12	+ math.sinh(2 * l)
13	)
14	)
15	F2 = 2 * self.le * l * (
16	4 * math.cos(2 * l)
17	- math.cos(4 * l)
18	- 4 * math.cosh(2 * l)
19	+ math.cosh(4 * l)
20	+ 8 * l * math.sin(2 * l) * math.sinh(l) * math.sinh(l)
21	- 8 * l * math.sin(l) * math.sin(l) * math.sinh(2 * l)
22	)
23	F3 = self.le * self.le * (
24	8 * l * math.cos(2 * l)
25	+ 4 * math.sin(2 * l)
26	- 2 * math.cosh(2 * l) * (
27	4 * l
28	+ math.sin(2 * l)
29	) - math.sin(4 * l)
30	+ 2 * (
31	math.cos(2 * l) + 4 * l * math.sin(2 * l) - 2
32	) * math.sinh(2 * l)
33	+ math.sinh(4 * l)
34	)
35	F4 =4 * self.le * l *(
36	l * math.cosh(3 * l) * math.sin(l)
37	- l * math.cosh(l) * (
38	- 2 * math.sin(l)
39	+ math.sin(3 * l)
40	) + (
41	l * math.cos(l)
42	+ l * math.cos(3 * l)
43	+ 10 * math.sin(l)
44	- 2 * math.cosh(2 * l) * (
45	l * math.cos(l)
46	+ 2 * math.sin(l)
47	) -2 * math.sin(3 * l)
48	) * math.sinh(l)
49	)
50	F5 = -4 * l * l * (
51	6 * math.cos(l) * (
52	- 2
53	+ math.cos(2 * l)
54	+ math.cosh(2 * l)
55	) * math.sinh(l)
56	+ math.sin(3 * l) * (
57	3 * math.cosh(l)
58	+ 2 * l * math.sinh(l)
59	) + math.sin(l) * (
60	- 12 * math.cosh(l)
61	+ 3 * math.cosh(3 * l)
62	- 2 * l * math.sinh(3 * l)
63	)
64	)
65	F6 = -2 * self.le * self.le *(
66	-(
67	math.cosh(3 * l) * (
68	2 * l * math.cos(l)
69	+ math.sin(l)
70	)
71	) + math.cosh(l) * (
72	2 * l * math.cos(3 * l)
73	+ 4 * math.sin(l)
74	- math.sin(3 * l)
75	) + (
76	math.cos(3 * l)
77	+ math.cos(l) * (
78	2 * math.cosh(2 * l)
79	- 3
80	) + 16 * l * math.sin(l)
81	) * math.sinh(l)
82	)
83	facF = (self.kf * self.le)/(16 * l * l * l * g * g)
84	KeF = facF * np.array([
85	[ F1, F2, F5, -F4],
86	[ F2, F3, F4, F6],
87	[ F5, F4, F1, -F2],
88	[ -F4, F6, -F2, F3]])
89	return KeF

Το συνολικό μητρώο $\mathbf{K}^{e}$ επομένως προκύπτει ως:

1	def get_Ke(self):
2	KeB = self.get_KeB()
3	KeF = self.get_KeF()
4	ke = KeB + KeF
5	return ke

Τέλος, το αντίστοιχο διάνυσμα της φόρτισης δίνεται ως:

1	def get_Fe(self, q0):
2	l = self.le * ((self.kf/(4 * self.E * self.I))**(0.25))
3	f1 = 2 * l *(
4	math.cosh(l)
5	- math.cos(l)
6	) *(math.sin(l) - math.sinh(l)
7	)
8	f2 =-(
9	le * (
10	math.sin(l)
11	- math.sinh(l)
12	) * (
13	math.sin(l)
14	- math.sinh(l)
15	)
16	)
17	facf = (q0 * le) / (l * l * g )
18	fe = facf * np.array([
19	f1,
20	f2,
21	f1,
22	-f2]
23	)
24	return fe

3.4 Το τριγωνικό στοιχείο

Στη συνέχεια εξετάζεται η μόρφωση επίπεδων στοιχείων δισδιάστατης ελαστικότητας ξεκινώντας από το κλασικό τριγωνικό στοιχείο [5], του οποίου οι εξισώσεις θα διατυπωθούν στο καρτεσιανό σύστημα συντεταγμένων $x$ - $y$ .

3.4.1 Το μητρώο συναρτήσεων μορφής

Έστω το τριγωνικό στοιχείο του Σχήματος 3.10 με συντεταγμένες $(x_{1},y_{1})$ , $(x_{2},y_{2})$ , $(x_{3},y_{3})$ στους κόμβους 1, 2, 3 αντίστοιχα.

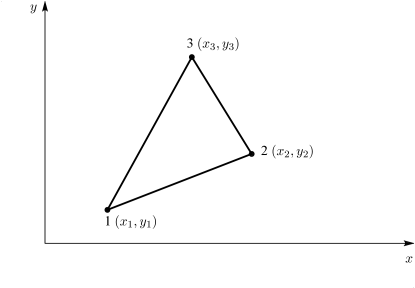
Σχήμα 3.10: Το τριγωνικό στοιχείο στο καρτεσιανό σύστημα συντεταγμένων.

Αν θεωρηθεί ότι η συνάρτηση μορφής είναι διγραμμική, δηλαδή γραμμική και κατά $x$ και κατά $y$ , τότε ένα μέγεθος $\phi$ μπορεί να περιγραφεί από σχέσεις της μορφής:

\phi=a_{1}+a_{2}x+a_{3}y=\left[1\quad x\quad y\right]\left[\begin{array}[]{c}a% _{1}\\ a_{2}\\ a_{3}\\ \end{array}\right]=\boldsymbol{a}{c}.

(3.128)

Οι σταθερές $a_{1}$ , $c_{2}$ και $a_{3}$ υπολογίζονται από τις συντεταγμένες των κόμβων και τις τιμές $\phi_{i}$ της συνάρτησης $\phi$ στους κόμβους, δηλαδή:

$\displaystyle\phi_{1}$	$\displaystyle=a_{1}+a_{2}x_{1}+a_{3}y_{1},$	(3.129)
$\displaystyle\phi_{2}$	$\displaystyle=a_{1}+a_{2}x_{2}+a_{3}y_{2},$	(3.130)
$\displaystyle\phi_{3}$	$\displaystyle=a_{1}+a_{2}x_{3}+a_{3}y_{3},$	(3.131)

Οι παραπάνω εξισώσεις μπορούν να γραφούν σε μητρωική μορφή,

\left[\begin{array}[]{c}\phi_{1}\\ \phi_{2}\\ \phi_{3}\\ \end{array}\right]=\left[\begin{array}[]{ccc}1&x_{1}&y_{1}\\ 1&x_{2}&y_{2}\\ 1&x_{3}&y_{3}\\ \end{array}\right]\left[\begin{array}[]{c}a_{1}\\ a_{2}\\ a_{3}\\ \end{array}\right]\Rightarrow\boldsymbol{\phi}=\mathbf{A}\boldsymbol{a}.

(3.132)

Λύνοντας ως προς $\boldsymbol{a}$ ,

\boldsymbol{a}=\mathbf{A}^{-1}\boldsymbol{\phi},

(3.133)

και αντικαθιστώντας στην (3.128), προκύπτει:

\phi=\boldsymbol{a}\mathbf{A}^{-1}\boldsymbol{\phi}.

(3.134)

Επομένως, οι συναρτήσεις μορφής δίνονται ως:

\mathbf{N}=\boldsymbol{a}\mathbf{A}^{-1}.

(3.135)

Προκύπτει ότι

$\displaystyle N_{1}$	$\displaystyle=$	$\displaystyle[(x_{2}y_{3}-x_{3}y_{2})+x(y_{2}-y_{3})+y(x_{3}-x_{2})]/2A,$	(3.136)
$\displaystyle N_{2}$	$\displaystyle=$	$\displaystyle[(x_{3}y_{1}-x_{1}y_{3})+x(y_{3}-y_{1})+y(x_{1}-x_{3})]/2A,$	(3.137)
$\displaystyle N_{3}$	$\displaystyle=$	$\displaystyle[(x_{1}y_{2}-x_{2}y_{1})+x(y_{1}-y_{2})+y(x_{2}-x_{1})]/2A,$	(3.138)

όπου $A$ το εμβαδό του τριγωνικού στοιχείου.

Η διακριτοποίηση των μετακινήσεων σε επίπεδο στοιχείου με τη βοήθεια των συναρτήσεων μορφής οδηγεί στις σχέσεις:

	$\displaystyle u_{x}$	$\displaystyle=$	$\displaystyle N_{1}u_{1_{x}}+N_{2}u_{2_{x}}+N_{3}u_{3_{x}},$		(3.139)
	$\displaystyle u_{y}$	$\displaystyle=$	$\displaystyle N_{1}u_{1_{y}}+N_{2}u_{2_{y}}+N_{3}u_{3_{y}},$		(3.140)

ή σε μητρωική μορφή:

\left[\begin{array}[]{c}u_{x}\\ u_{y}\\ \end{array}\right]=\left[\begin{array}[]{cccccc}N_{1}&0&N_{2}&0&N_{3}&0\\ 0&N_{1}&0&N_{2}&0&N_{3}\\ \end{array}\right]\left[\begin{array}[]{c}u_{1_{x}}\\ u_{1_{y}}\\ u_{2_{x}}\\ u_{2_{y}}\\ u_{3_{x}}\\ u_{3_{y}}\\ \end{array}\right]

(3.141)

όπου $N_{1}$ , $N_{2}$ και $N_{3}$ οι συναρτήσεις μορφής για το τριγωνικό στοιχείο όπως δίνονται από τις (3.136)-(3.138). Επομένως μπορεί να οριστεί το μητρώο $\mathbf{N}$ των συναρτήσεων μορφής του στοιχείου σύμφωνα με τη (3.135) ως:

\mathbf{N}=\left[\begin{array}[]{cccccc}N_{1}&0&N_{2}&0&N_{3}&0\\ 0&N_{1}&0&N_{2}&0&N_{3}\\ \end{array}\right].

(3.142)

3.4.2 Το μητρώο συναρτήσεων παραμορφώσεων-μετακινήσεων

Το μητρώο παραμορφώσεων-μετακινήσεων $\mathbf{B}$ προκύπτει ως:

$\displaystyle\mathbf{B}$	$\displaystyle=\mathbf{L}\mathbf{N}$	(3.143)
	$\displaystyle=\left[\begin{array}[]{cc}\dfrac{\partial}{\partial x}&0\\ 0&\dfrac{\partial}{\partial y}\\ \dfrac{\partial}{\partial y}&\dfrac{\partial}{\partial x}\\ \end{array}\right]\left[\begin{array}[]{cccccc}N_{1}&0&N_{2}&0&N_{3}&0\\ 0&N_{1}&0&N_{2}&0&N_{3}\\ \end{array}\right]$	(3.144)
	$\displaystyle=\left[\begin{array}[]{cccccc}\dfrac{\partial N_{1}}{\partial x}&% 0&\dfrac{\partial N_{2}}{\partial x}&0&\dfrac{\partial N_{3}}{\partial x}&0\\ 0&\dfrac{\partial N_{1}}{\partial y}&0&\dfrac{\partial N_{2}}{\partial y}&0&% \dfrac{\partial N_{3}}{\partial y}\\ \dfrac{\partial N_{1}}{\partial y}&\dfrac{\partial N_{1}}{\partial x}&\dfrac{% \partial N_{2}}{\partial y}&\dfrac{\partial N_{2}}{\partial x}&\dfrac{\partial N% _{3}}{\partial y}&\dfrac{\partial N_{3}}{\partial x}\\ \end{array}\right]$	(3.145)
	$\displaystyle=\left[\begin{array}[]{cccccc}y_{2}-y_{3}&0&y_{3}-y_{1}&0&y_{1}-y% _{2}&0\\ 0&x_{3}-x_{2}&0&x_{1}-x_{3}&0&x_{2}-x_{1}\\ x_{3}-x_{2}&y_{2}-y_{3}&x_{1}-x_{3}&y_{3}-y_{1}&x_{2}-x_{1}&y_{1}-y_{2}\\ \end{array}\right]/2A$	(3.146)

όπου $A$ το εμβαδό του τριγωνικού στοιχείου, όπως δίνεται από τη σχέση:

$\displaystyle A$	$\displaystyle=\dfrac{1}{2}\left\|\textrm{det}\left(\begin{array}[]{ccc}1&x_{1}&% y_{1}\\ 1&x_{2}&y_{2}\\ 1&x_{3}&y_{3}\\ \end{array}\right)\right\|$
	$\displaystyle=\dfrac{1}{2}\left[(x_{2}y_{3}-y_{2}x_{3})-(x_{1}y_{3}-y_{1}x_{3}% )+(x_{1}y_{2}-y_{1}x_{2})\right]$
	$\displaystyle=\dfrac{1}{2}\left\|x_{2}y_{3}-y_{2}x_{3}-x_{1}y_{3}+y_{1}x_{3}+x_% {1}y_{2}-y_{1}x_{2}\right\|$	(3.147)

3.4.3 Το μητρώο ελαστικότητας

Το μητρώο υλικού $\mathbf{C}$ για συνθήκες επίπεδης παραμόρφωσης δίνεται από την παρακάτω σχέση:

\mathbf{C}=\dfrac{E(1-\nu)}{(1+\nu)(1-2\nu)}\left[\begin{array}[]{ccc}1&\dfrac% {\nu}{1-\nu}&0\\ \dfrac{\nu}{1-\nu}&1&0\\ 0&0&\dfrac{1-2\nu}{2(1-\nu)}\\ \end{array}\right].

(3.148)

3.4.4 Το μητρώο δυσκαμψίας

Τέλος, το μητρώο δυσκαμψίας $\mathbf{Κ}$ , εφόσον είναι γνωστά τα μητρώα $\mathbf{B}$ (3.148) και $\mathbf{C}$ (3.146), προκύπτει από τη γενική σχέση ως:

$\displaystyle\mathbf{K}^{e}$	$\displaystyle=\int_{\Omega}\mathbf{B}^{T}\mathbf{C}\mathbf{B}d\Omega$	(3.149)
	$\displaystyle=t\int_{x}\int_{y}\mathbf{B}^{T}\mathbf{C}\mathbf{B}dxdy$	(3.150)
	$\displaystyle=t\mathbf{B}^{T}\mathbf{C}\mathbf{B},\int_{x}\int_{y}dxdy$	(3.151)
	$\displaystyle=t\mathbf{B}^{T}\mathbf{C}\mathbf{B}A$	(3.152)

όπου $t$ το πάχος του στοιχείου.

3.5 Ισοπαραμετρική διατύπωση και αριθμητική ολοκλήρωση

Η διαδικασία που ακολουθήθηκε στις προηγούμενες ενότητες για τη μόρφωση του μητρώου δυσκαμψίας του στοιχείου ράβδου ή του διγραμμικού τριγώνου θα μπορούσε θεωρητικά να εφαρμοστεί και στην περίπτωση τετράπλευρων στοιχείων ή γενικά στοιχείων με συναρτήσεις μορφής ανώτερου βαθμού. Μια τέτοια προσέγγιση όμως θα συναντούσε τις ακόλουθες δυσκολίες:

1.

Οι συναρτήσεις μορφής στοιχείων ανώτερου βαθμού ορίζονται από εξαιρετικά πολύπλοκες σχέσεις όταν ορίζονται στο καρτεσιανό σύστημα συντεταγμένων.
2.

Η ολοκλήρωση των παραπάνω σχέσεων για τη μόρφωση του μητρώου δυσκαμψίας και του αντίστοιχου διανύσματος φόρτισης δεν μπορεί να γίνει πλέον αναλυτικά.

Για την επίλυση των δύο παραπάνω προβλημάτων εισάγονται οι έννοιες της ισοπαραμετρικής διατύπωσης και της αριθμητικής ολοκλήρωσης αντίστοιχα, οι οποίες αποτελούν βασικά χαρακτηριστικά της εφαρμογής της μεθόδου των πεπερασμένων στοιχείων [6].

3.5.1 Ισοπαραμετρική θεώρηση

Η ισοπαραμετρική θεώρηση στηρίζεται στη διατύπωση της περιγραφής της γεωμετρίας και του πεδίου μετατοπίσεων με τις ίδιες συναρτήσεις μορφής σε ένα νέο σύστημα συντεταγμένων που, σε αντίθεση με το πραγματικό σύστημα συντεταγμένων (συνήθως το καρτεσιανό), ονομάζεται φυσικό σύστημα συντεταγμένων.

Περιγραφή της γεωμετρίας/μετατοπίσεων

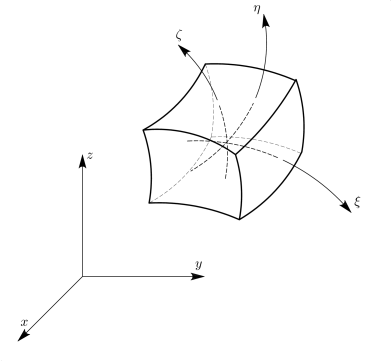
Για την κατανόηση της ισοπαραμετρικής θεώρησης εξετάζεται η γενική περίπτωση ενός τρισδιάστατου στοιχείου, όπως αυτό που απεικονίζεται στο Σχήμα 3.11.

Καταρχήν θεωρείται ότι τόσο η γεωμετρία του στοιχείου ( $x$ , $y$ και $z$ ) όσο και το αντίστοιχο πεδίο μετατοπίσεων ( $u_{x}$ , $u_{y}$ και $u_{z}$ ) περιγράφονται από τις ίδιες συναρτήσεις μορφής. Η θεώρηση αυτή δίνεται σε μητρωική μορφή ως:

\left[\begin{array}[]{c}1\\ x\\ y\\ z\\ u_{x}\\ u_{y}\\ u_{z}\\ \end{array}\right]=\left[\begin{array}[]{cccc}1&1&\ldots&1\\ x_{1}&x_{2}&\ldots&x_{n}\\ y_{1}&x_{2}&\ldots&y_{n}\\ z_{1}&x_{2}&\ldots&z_{n}\\ u_{x1}&u_{x2}&\ldots&u_{xn}\\ u_{y1}&u_{y2}&\ldots&u_{yn}\\ u_{z1}&u_{z2}&\ldots&u_{zn}\\ \end{array}\right]\left[\begin{array}[]{c}N_{1}\\ N_{2}\\ \vdots\\ N_{n}\\ \end{array}\right]

(3.153)

όπου $x_{i}$ , $y_{i}$ , $z_{i}$ $(i=1,\ldots n)$ οι συντεταγμένες των $n$ κόμβων του στοιχείου στο πραγματικό σύστημα συντεταγμένων, $u_{x_{i}}$ , $u_{y_{i}}$ , $u_{z_{i}}$ οι επικόμβιες μετατοπίσεις και $N_{i}$ οι αντίστοιχες συναρτήσεις σχήματος.

Αναλυτικά η (3.153) μπορεί να γραφτεί ως:

$\displaystyle 1$	$\displaystyle=\sum_{i=1}^{n}N_{i}=N_{1}+N_{2}+\ldots+N_{n}$	(3.154)
$\displaystyle x$	$\displaystyle=\sum_{i=1}^{n}N_{i}x_{i}=N_{1}x_{1}+N_{2}x_{2}+\ldots+N_{n}x_{n}$	(3.155)
$\displaystyle y$	$\displaystyle=\sum_{i=1}^{n}N_{i}y_{i}=N_{1}y_{1}+N_{2}y_{2}+\ldots+N_{n}y_{n}$	(3.156)
$\displaystyle z$	$\displaystyle=\sum_{i=1}^{n}N_{i}z_{i}=N_{1}z_{1}+N_{2}z_{2}+\ldots+N_{n}z_{n}$	(3.157)
$\displaystyle u_{x}$	$\displaystyle=\sum_{i=1}^{n}N_{i}u_{xi}=N_{1}u_{x_{1}}+N_{2}u_{x_{2}}+\ldots+N% _{n}u_{x_{n}}$	(3.158)
$\displaystyle u_{y}$	$\displaystyle=\sum_{i=1}^{n}N_{i}u_{yi}=N_{1}u_{y_{1}}+N_{2}u_{y_{2}}+\ldots+N% _{n}u_{y_{n}}$	(3.159)
$\displaystyle u_{z}$	$\displaystyle=\sum_{i=1}^{n}N_{i}u_{zi}=N_{1}u_{z_{1}}+N_{2}u_{z_{2}}+\ldots+N% _{n}u_{z_{n}}$	(3.160)

Σχήμα 3.11: Πραγματικό (καρτεσιανό) σύστημα συντεταγμένων.

Σχήμα 3.12: Φυσικό σύστημα συντεταγμένων.

Το φυσικό σύστημα συντεταγμένων

Η ορθή απεικόνιση των πραγματικών συντεταγμένων $x$ , $y$ και $z$ συναρτήσει των φυσικών συντεταγμένων $\xi$ , $\eta$ και $\zeta$ ορίζεται ως:

$\displaystyle x$	$\displaystyle=x(\xi,\eta,\zeta)$	(3.161)
$\displaystyle y$	$\displaystyle=y(\xi,\eta,\zeta)$	(3.162)
$\displaystyle z$	$\displaystyle=z(\xi,\eta,\zeta)$	(3.163)

Ομοίως η αντίστροφη απεικόνιση των φυσικών συντεταγμένων $\xi$ , $\eta$ και $\zeta$ συναρτήσει των πραγματικών συντεταγμένων $x$ , $y$ και $z$ δίνεται ως:

$\displaystyle\xi$	$\displaystyle=\xi(x,y,z)$	(3.164)
$\displaystyle\eta$	$\displaystyle=\eta(x,y,z)$	(3.165)
$\displaystyle\zeta$	$\displaystyle=\zeta(x,y,z)$	(3.166)

Η απεικόνιση μεταξύ των δύο συστημάτων πρέπει να είναι αμφιμονοσήμαντη, έτσι ώστε κάθε σημείο με συντεταγμένες $(x,y,z)$ να έχει αντίστοιχες μοναδικά ορισμένες συντεταγμένες $(\xi,\eta,\zeta)$ και το αντίστροφο.

Ο μετασχηματισμός από το πραγματικό σύστημα συντεταγμένων στο φυσικό σύστημα συντεταγμένων περιγράφεται από το Ιακωβιανό μητρώο, το οποίο ορίζεται ως:

\mathbf{J}=\dfrac{\partial(x,y,z)}{\partial(\xi,\eta,\zeta)}=\left[\begin{% array}[]{cccc}\dfrac{\partial x}{\partial\xi}&\dfrac{\partial x}{\partial\eta}% &\dfrac{\partial x}{\partial\zeta}\\ \dfrac{\partial y}{\partial\xi}&\dfrac{\partial y}{\partial\eta}&\dfrac{% \partial y}{\partial\zeta}\\ \dfrac{\partial z}{\partial\xi}&\dfrac{\partial z}{\partial\eta}&\dfrac{% \partial z}{\partial\zeta}\\ \end{array}\right]

(3.168)

Αριθμητική ολοκλήρωση

Η αριθμητική ολοκλήρωση είναι τις περισσότερες φορές απαραίτητη για τον υπολογισμό των ολοκληρωμάτων που περιγράφουν τα μητρώα και τα διανύσματα ενός ισοπαραμετρικού στοιχείου. Στη συνέχεια εξετάζεται η αριθμητική ολοκλήρωση, ξεκινώντας από το (μονοδιάστατο) ολοκλήρωμα

I:=\int_{a}^{b}f(x)dx

(3.169)

όπου $f$ μία πραγματική συνάρτηση μίας μεταβλητής $x$ , και $a$ , $b$ τα όρια ολοκλήρωσης. Το διάστημα ολοκλήρωσης $(a,b)$ μπορεί να μετασχηματιστεί στο διάστημα $(-1,1)$ συναρτήσει μίας νέας μεταβλητής $\xi$ θέτοντας:

x=\dfrac{1}{2}(a+b)+\dfrac{1}{2}(b-a)\xi

(3.170)

Ο παραπάνω μετασχηματισμός είναι αμφιμονοσήμαντος όταν ισχύει $a\neq b$ . Εύκολα αποδεικνύεται ότι ισχύει:

	$\displaystyle x=a$	$\displaystyle\quad\text{αν}\quad\xi=-1$		(3.171)
	$\displaystyle x=b$	$\displaystyle\quad\text{αν}\quad\xi=+1$		(3.172)

Το ολοκλήρωμα (3.169) μπορεί τώρα να διατυπωθεί ως:

I:=\int_{a}^{b}f(x)dx=\int_{-1}^{1}f(\dfrac{1}{2}(a+b)+\dfrac{1}{2}(b-a)\xi)d% \xi:=\int_{-1}^{1}g(\xi)d\xi

(3.173)

Η αριθμητική ολοκλήρωση του μετασχηματισμένου πλέον ολοκληρώματος (3.173) ορίζεται συνήθως ως ένα άθροισμα:

I:=\int_{-1}^{1}f(\dfrac{1}{2}(a+b)+\dfrac{1}{2}(b-a)\xi)d\xi\approx\sum_{k=1}% ^{n}w_{k}g(\xi_{k})

(3.174)

όπου $\xi_{k}$ είναι οι συντεταγμένες των (δειγματοληπτικών) σημείων ολοκλήρωσης και $w_{k}$ τα αντίστοιχα βάρη ολοκλήρωσης.

Από τις πιο γνωστές μεθόδους ολοκλήρωσης είναι:

•

Ο κανόνας του τραπεζίου, όπου $n=2$ , $w_{1}=w_{2}=1$ , $\xi_{1}=-1$ και $\xi_{2}=1$ . Με τον κανόνα του τραπεζίου επιτυγχάνεται ακριβής ολοκλήρωση για πολυώνυμα μέχρι πρώτου βαθμού ( $q=1$ ).
•

Ο κανόνας Simpson, όπου $n=3$ , $w_{1}=w_{3}=\dfrac{1}{3}$ , $w_{2}=\dfrac{4}{3}$ $\xi_{1}=-1$ , $\xi_{2}=0$ και $\xi_{3}=1$ . Με τον κανόνα Simpson επιτυγχάνεται ακριβής ολοκλήρωση για πολυώνυμα μέχρι τρίτου βαθμού ( $q=3$ ).
•

Η μέθοδος των Newton-Cotes, κατά την οποία τα $n$ σημεία ολοκλήρωσης ορίζονται σε ίσες αποστάσεις στο διάστημα $(-1,1)$ . Η μέθοδος αυτή ενδέχεται να παρουσιάσει μειωμένη ακρίβεια για μεγάλο αριθμό σημείων $n$ . Ο κανόνας του τραπεζίου και ο κανόνας Simpson αποτελούν υποπεριπτώσεις των κλειστών σχέσεων Newton-Cotes.
•

Η μέθοδος ολοκλήρωσης Gauss, στην οποία τα σημεία ολοκλήρωσης σε βελτιστοποιημένες, μη ισαπέχουσες θέσεις, όπως αυτά προκύπτουν από τις λύσεις των πολυωνύμων Legendre. Στον Πίνακα 3.1 δίνονται οι θέσεις $xi_{i}$ και τα βάρη $w_{i}$ για $n=1-5$ .

Η συνήθης πρακτική είναι να γίνεται ολοκλήρωση με τη μέθοδο Gauss, χρησιμοποιώντας τον ελάχιστο αριθμό σημείων ώστε να επιτυγχάνεται η απαραίτητη ακρίβεια.

$n$	$\xi_{i}$	$w_{i}$
1	$0$	$2$
2	$\pm 1/\sqrt{3}$	$1$
3	$0$	$\dfrac{8}{9}$
	$\pm\sqrt{3}/\sqrt{5}$	$\dfrac{5}{9}$
4	$\pm\dfrac{1}{35}\sqrt{525-70\sqrt{30}}$	$\dfrac{1}{36}\left(18+\sqrt{30}\right)$
	$\pm\dfrac{1}{35}\sqrt{525+70\sqrt{30}}$	$\dfrac{1}{36}\left(18-\sqrt{30}\right)$
5	$0$	$\dfrac{128}{225}$
	$\pm\dfrac{1}{21}\sqrt{245-14\sqrt{70}}$	$\dfrac{1}{900}\left(322+13\sqrt{70}\right)$
	$\pm\dfrac{1}{21}\sqrt{245+14\sqrt{70}}$	$\dfrac{1}{900}\left(322-13\sqrt{70}\right)$

Πίνακας 3.1: Θέσεις και βάρη των σημείων Gauss.

3.6 Το τετράκομβο τετράπλευρο στοιχείο

Στη συνέχεια εξετάζεται το δισδιάστατο, ισοπαραμετρικό, τετράκομβο, τετράπλευρο στοιχείο, που αποτελεί ένα από τα πλέον συνήθη στοιχεία που χρησιμοποιούνται στην επίλυση προβλημάτων με τη μέθοδο των πεπερασμένων στοιχείων [4]. Η γεωμετρία του στοιχείου περιγράφεται στο Σχήμα 3.13.

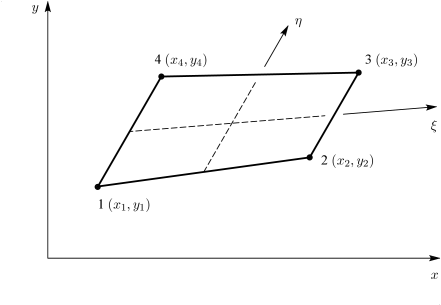
Σχήμα 3.13: Το τετράκομβο τετράπλευρο στοιχείο.

3.6.1 Το μητρώο συναρτήσεων μορφής

	$\displaystyle u_{x}$	$\displaystyle=$	$\displaystyle N_{1}u_{1_{x}}+N_{2}u_{2_{x}}+N_{3}u_{3_{x}}+N_{4}u_{4_{x}}$		(3.175)
	$\displaystyle u_{y}$	$\displaystyle=$	$\displaystyle N_{1}u_{1_{y}}+N_{2}u_{2_{y}}+N_{3}u_{3_{y}}+N_{4}u_{4_{y}}$		(3.176)

ή σε μητρωική μορφή:

\left[\begin{array}[]{c}u_{x}\\ u_{y}\\ \end{array}\right]=\left[\begin{array}[]{cccccccc}N_{1}&0&N_{2}&0&N_{3}&0&N_{4% }&0\\ 0&N_{1}&0&N_{2}&0&N_{3}&0&N_{4}\\ \end{array}\right]\left[\begin{array}[]{c}u_{1_{x}}\\ u_{1_{y}}\\ u_{2_{x}}\\ u_{2_{y}}\\ u_{3_{x}}\\ u_{3_{y}}\\ u_{4_{x}}\\ u_{4_{y}}\\ \end{array}\right]

(3.177)

όπου $N_{1}$ , $N_{2}$ , $N_{3}$ και $N_{3}$ οι συναρτήσεις μορφής για το τετράκομβο στοιχείο.

Μπορεί επομένως να οριστεί το μητρώο $\mathbf{N}$ των συναρτήσεων μορφής του ως:

\mathbf{N}=\left[\begin{array}[]{cccccccc}N_{1}&0&N_{2}&0&N_{3}&0&N_{4}&0\\ 0&N_{1}&0&N_{2}&0&N_{3}&0&N_{4}\\ \end{array}\right].

(3.178)

3.6.2 Το μητρώο παραμορφώσεων-μετακινήσεων

Το μητρώο παραμορφώσεων-μετακινήσεων $\mathbf{B}$ προκύπτει από την κινηματική εξίσωση που συνδέει τις τάσεις με τις παραμορφώσεις,

\varepsilon_{ij}=\dfrac{1}{2}\left(\dfrac{\partial u_{i}}{\partial x_{j}}+% \dfrac{\partial u_{j}}{\partial x_{i}}\right)

(3.179)

όπου για τη συγκεκριμένη περίπτωση $i=1,2$ .

Προκύπτει επομένως για $k=1,\dots,n$ :

$\displaystyle\varepsilon_{11}=\varepsilon_{xx}$	$\displaystyle=\dfrac{1}{2}\left(\dfrac{\partial u_{x_{k}}}{\partial x}+\dfrac{% \partial u_{x_{k}}}{\partial x}\right)=\dfrac{\partial u_{x_{k}}}{\partial x}=% \dfrac{\partial(N_{k}u_{x_{k}})}{\partial x}=\dfrac{\partial N_{k}}{\partial x% }u_{x_{k}}$	(3.180)
$\displaystyle\varepsilon_{22}=\varepsilon_{yy}$	$\displaystyle=\dfrac{1}{2}\left(\dfrac{\partial u_{y_{k}}}{\partial y}+\dfrac{% \partial u_{y_{k}}}{\partial y}\right)=\dfrac{\partial u_{x}}{\partial y}=% \dfrac{\partial(N_{k}u_{y_{k}})}{\partial y}=\dfrac{\partial N_{k}}{\partial y% }u_{y_{k}}$	(3.181)
$\displaystyle 2\varepsilon_{12}=2\varepsilon_{21}=2\varepsilon_{xy}$	$\displaystyle=\dfrac{\partial u_{x}}{\partial y}+\dfrac{\partial u_{y}}{% \partial x}=\dfrac{\partial(N_{k}u_{x_{k}})}{\partial y}+\dfrac{\partial(N_{k}% u_{y_{k}})}{\partial x}=\dfrac{\partial N_{k}}{\partial y}u_{x_{k}}+\dfrac{% \partial N_{k}}{\partial x}u_{y_{k}}$	(3.182)

Οι παραπάνω σχέσεις μπορούν να διατυπωθούν σε μητρωική μορφή ως:

\boldsymbol{\varepsilon}=\mathbf{B}\boldsymbol{u}

(3.183)

όπου το μητρώο $\mathbf{B}$ , γνωστό και ως μητρώο παραμορφώσεων-μετακινήσεων, ορίζεται ως:

$\displaystyle\mathbf{B}$	$\displaystyle=\mathbf{L}\mathbf{N}$	(3.184)
	$\displaystyle=\left[\begin{array}[]{cc}\dfrac{\partial}{\partial x}&0\\ 0&\dfrac{\partial}{\partial y}\\ \dfrac{\partial}{\partial y}&\dfrac{\partial}{\partial x}\\ \end{array}\right]\left[\begin{array}[]{cccccccc}N_{1}&0&N_{2}&0&N_{3}&0&N_{4}% &0\\ 0&N_{1}&0&N_{2}&0&N_{3}&0&N_{4}\\ \end{array}\right]$	(3.185)
	$\displaystyle=\left[\begin{array}[]{cccccccc}\dfrac{\partial N_{1}}{\partial x% }&0&\dfrac{\partial N_{2}}{\partial x}&0&\dfrac{\partial N_{3}}{\partial x}&0&% \dfrac{\partial N_{4}}{\partial x}&0\\ 0&\dfrac{\partial N_{1}}{\partial y}&0&\dfrac{\partial N_{2}}{\partial y}&0&% \dfrac{\partial N_{3}}{\partial y}&0&\dfrac{\partial N_{4}}{\partial y}\\ \dfrac{\partial N_{1}}{\partial y}&\dfrac{\partial N_{1}}{\partial x}&\dfrac{% \partial N_{2}}{\partial y}&\dfrac{\partial N_{2}}{\partial x}&\dfrac{\partial N% _{3}}{\partial y}&\dfrac{\partial N_{3}}{\partial x}&\dfrac{\partial N_{4}}{% \partial y}&\dfrac{\partial N_{4}}{\partial x}\\ \end{array}\right].$	(3.186)

Οι παράγωγοι των συναρτήσεων $Ν_{i}$ , όπου $i=1,2,3,4$ ως προς $x$ και $y$ , προκύπτουν από τον κανόνα της αλυσίδας:

$\displaystyle\dfrac{\partial N_{1}}{\partial x}$	$\displaystyle=\dfrac{\partial N_{1}}{\partial\xi}\dfrac{\partial\xi}{\partial x% }+\dfrac{\partial N_{1}}{\partial\eta}\dfrac{\partial\eta}{\partial x}=\dfrac{% 1}{4}\left[(-1+\eta)\dfrac{\partial\xi}{\partial x}+(-1+\xi)\dfrac{\partial% \eta}{\partial x}\right]$	(3.187)
$\displaystyle\dfrac{\partial N_{1}}{\partial y}$	$\displaystyle=\dfrac{\partial N_{1}}{\partial\xi}\dfrac{\partial\xi}{\partial y% }+\dfrac{\partial N_{1}}{\partial\eta}\dfrac{\partial\eta}{\partial y}=\dfrac{% 1}{4}\left[(-1+\eta)\dfrac{\partial\xi}{\partial y}+(-1+\xi)\dfrac{\partial% \eta}{\partial y}\right]$	(3.188)
$\displaystyle\dfrac{\partial N_{2}}{\partial x}$	$\displaystyle=\dfrac{\partial N_{2}}{\partial\xi}\dfrac{\partial\xi}{\partial x% }+\dfrac{\partial N_{2}}{\partial\eta}\dfrac{\partial\eta}{\partial x}=\dfrac{% 1}{4}\left[(1-\eta)\dfrac{\partial\xi}{\partial x}+(-1-\xi)\dfrac{\partial\eta% }{\partial x}\right]$	(3.189)
$\displaystyle\dfrac{\partial N_{2}}{\partial y}$	$\displaystyle=\dfrac{\partial N_{2}}{\partial\xi}\dfrac{\partial\xi}{\partial y% }+\dfrac{\partial N_{2}}{\partial\eta}\dfrac{\partial\eta}{\partial y}=\dfrac{% 1}{4}\left[(1-\eta)\dfrac{\partial\xi}{\partial y}+(-1-\xi)\dfrac{\partial\eta% }{\partial y}\right]$	(3.190)
$\displaystyle\dfrac{\partial N_{3}}{\partial x}$	$\displaystyle=\dfrac{\partial N_{3}}{\partial\xi}\dfrac{\partial\xi}{\partial x% }+\dfrac{\partial N_{3}}{\partial\eta}\dfrac{\partial\eta}{\partial x}=\dfrac{% 1}{4}\left[(1+\eta)\dfrac{\partial\xi}{\partial x}+(1+\xi)\dfrac{\partial\eta}% {\partial x}\right]$	(3.191)
$\displaystyle\dfrac{\partial N_{3}}{\partial y}$	$\displaystyle=\dfrac{\partial N_{3}}{\partial\xi}\dfrac{\partial\xi}{\partial y% }+\dfrac{\partial N_{3}}{\partial\eta}\dfrac{\partial\eta}{\partial y}=\dfrac{% 1}{4}\left[(1+\eta)\dfrac{\partial\xi}{\partial y}+(1+\xi)\dfrac{\partial\eta}% {\partial y}\right]$	(3.192)
$\displaystyle\dfrac{\partial N_{4}}{\partial x}$	$\displaystyle=\dfrac{\partial N_{4}}{\partial\xi}\dfrac{\partial\xi}{\partial x% }+\dfrac{\partial N_{4}}{\partial\eta}\dfrac{\partial\eta}{\partial x}=\dfrac{% 1}{4}\left[(-1-\eta)\dfrac{\partial\xi}{\partial x}+(1-\xi)\dfrac{\partial\eta% }{\partial x}\right]$	(3.193)
$\displaystyle\dfrac{\partial N_{4}}{\partial y}$	$\displaystyle=\dfrac{\partial N_{4}}{\partial\xi}\dfrac{\partial\xi}{\partial y% }+\dfrac{\partial N_{4}}{\partial\eta}\dfrac{\partial\eta}{\partial y}=\dfrac{% 1}{4}\left[(-1-\eta)\dfrac{\partial\xi}{\partial y}+(1-\xi)\dfrac{\partial\eta% }{\partial y}\right]$	(3.194)

Ο υπολογισμός των $\dfrac{\partial\xi}{\partial x}$ , $\dfrac{\partial\xi}{\partial y}$ , $\dfrac{\partial\eta}{\partial x}$ και $\dfrac{\partial\eta}{\partial y}$ γίνεται με τη βοήθεια του αντίστροφου μητρώου της Ιακωβιανής (3.168), δηλαδή

$\displaystyle\dfrac{\partial\xi}{\partial x}$	$\displaystyle=\dfrac{1}{\textrm{det}(\mathbf{J})}J_{22}=\dfrac{1}{\textrm{det}% (\mathbf{J})}\dfrac{\partial y}{\partial\eta},$	(3.195)
$\displaystyle\dfrac{\partial\xi}{\partial y}$	$\displaystyle=-\dfrac{1}{\textrm{det}(\mathbf{J})}J_{12}=-\dfrac{1}{\textrm{% det}(\mathbf{J})}\dfrac{\partial y}{\partial\xi},$	(3.196)
$\displaystyle\dfrac{\partial\eta}{\partial x}$	$\displaystyle=-\dfrac{1}{\textrm{det}(\mathbf{J})}J_{21}=-\dfrac{1}{\textrm{% det}(\mathbf{J})}\dfrac{\partial x}{\partial\eta},$	(3.197)
$\displaystyle\dfrac{\partial\eta}{\partial y}$	$\displaystyle=\dfrac{1}{\textrm{det}(\mathbf{J})}J_{11}=\dfrac{1}{\textrm{det}% (\mathbf{J})}\dfrac{\partial x}{\partial\xi},$	(3.198)

όπου $\dfrac{\partial x}{\partial\xi}$ , $\dfrac{\partial x}{\partial\eta}$ , $\dfrac{\partial y}{\partial\xi}$ και $\dfrac{\partial y}{\partial\eta}$ μπορούν να προκύψουν εύκολα από την παραγώγιση των $x$ και $y$ :

$\displaystyle\dfrac{\partial x}{\partial\xi}$	$\displaystyle=-\dfrac{1}{4}(1-\eta)x_{1}+\dfrac{1}{4}(1-\eta)x_{2}+\dfrac{1}{4% }(1+\eta)x_{3}-\dfrac{1}{4}(1+\eta)x_{4},$	(3.199)
$\displaystyle\dfrac{\partial y}{\partial\xi}$	$\displaystyle=-\dfrac{1}{4}(1-\eta)y_{1}+\dfrac{1}{4}(1-\eta)y_{2}+\dfrac{1}{4% }(1+\eta)y_{3}-\dfrac{1}{4}(1+\eta)y_{4},$	(3.200)
$\displaystyle\dfrac{\partial x}{\partial\eta}$	$\displaystyle=-\dfrac{1}{4}(1-\xi)x_{1}-\dfrac{1}{4}(1+\xi)x_{2}+\dfrac{1}{4}(% 1+\xi)x_{3}+\dfrac{1}{4}(1-\xi)x_{4},$	(3.201)
$\displaystyle\dfrac{\partial y}{\partial\eta}$	$\displaystyle=-\dfrac{1}{4}(1-\xi)y_{1}-\dfrac{1}{4}(1+\xi)y_{2}+\dfrac{1}{4}(% 1+\xi)y_{3}+\dfrac{1}{4}(1-\xi)y_{4}.$	(3.202)

Με βάση τα παραπάνω ορίζεται πλήρως το μητρώο $\mathbf{B}$ .

3.6.3 Το μητρώο ελαστικότητας

Το μητρώο υλικού $\mathbf{C}$ για συνθήκες επίπεδης παραμόρφωσης ταυτίζεται με αυτό της (3.148):

\mathbf{C}=\dfrac{E(1-\nu)}{(1+\nu)(1-2\nu)}\left[\begin{array}[]{ccc}1&\dfrac% {\nu}{1-\nu}&0\\ \dfrac{\nu}{1-\nu}&1&0\\ 0&0&\dfrac{1-2\nu}{2(1-\nu)}\\ \end{array}\right]

(3.203)

3.6.4 Το μητρώο δυσκαμψίας

Τέλος, το μητρώο δυσκαμψίας $\mathbf{Κ}^{e}$ προκύπτει ως:

\mathbf{K}^{e}=\int_{\Omega}\mathbf{B}^{T}\mathbf{C}\mathbf{B}d\Omega

(3.204)

όπου $\mathbf{B}$ και $\mathbf{C}$ όπως δίνονται από τις (3.186) και (3.203) αντίστοιχα.

3.6.5 Αριθμητική ολοκλήρωση

Για τον υπολογισμό του μητρώου $\mathbf{K}^{e}$ η ολοκλήρωση γίνεται αριθμητικά, ακολουθώντας τη μέθοδο του Gauss. Σύμφωνα με τη μέθοδο αυτή ο υπολογισμός ενός διπλού ολοκληρώματος της μορφής

I=\int_{-1}^{1}\int_{-1}^{1}f(\xi,\eta)d\xi d\eta

(3.205)

ανάγεται σε άθροισμα της μορφής

Ι\approx\sum_{i=1}^{n}\sum_{j=1}^{n}w_{i}w_{j}f(\xi_{i},\eta_{j})

(3.206)

όπου $w_{i}$ τα βάρη και $\xi_{i}$ οι θέσεις των σημείων Gauss όπως αυτά δίνονται στην Ενότητα 3.5.1.

Για το μητρώο $\mathbf{K}^{e}$ επομένως μπορούμε να γράψουμε:

\mathbf{K}^{e}=\int_{\Omega}\mathbf{B}^{T}\mathbf{C}\mathbf{B}d\Omega=t\int_{-% 1}^{1}\int_{-1}^{1}\mathbf{B}^{T}\mathbf{C}\mathbf{B}\textrm{det}\mathbf{J}d% \xi d\eta,

(3.207)

όπου $t$ το πάχος, το οποίο λαμβάνεται ανεξάρτητο των $\xi,\eta$ στη συγκεκριμένη περίπτωση.

Έστω $f(\xi,\eta)$ η συνάρτηση προς ολοκλήρωση,

f(\xi,\eta)=t\mathbf{B}^{T}(\xi,\eta)\mathbf{C}\mathbf{B}(\xi,\eta)det(\mathbf% {J}(\xi,\eta)),

(3.208)

και $K^{e}_{ij}$ το $(i,j)$ στοιχείο του μητρώου $\mathbf{K}$ .

Τότε από την (3.207) και για κανόνα ολοκλήρωσης $2\times 2$ προκύπτει:

K^{e}_{ij}=w_{1}^{2}f(\xi_{1},\eta_{1})+w_{1}w_{2}f(\xi_{1},\eta_{2})+w_{2}w_{% 1}f(\xi_{2},\eta_{1})+w_{2}^{2}f(\xi_{2},\eta_{2}).

(3.209)

Στη συνέχεια δίνεται ενδεικτικά κώδικας σε γλώσσα προγραμματισμού Python για τον υπολογισμό των συναρτήσεων μορφής και της Ιακωβιανής του τετράκομβου, τετράπλευρου γραμμικού στοιχείου.

1	def shape41(nodes, gps):
2	N = np.zeros((4, 3, 4))
3	detJ = np.zeros(4)
4
5	for k, gp in enumerate(gps):
6	m1 = 1 - gp.xi
7	p1 = 1 + gp.xi
8	m2 = 1 - gp.eta
9	p2 = 1 + gp.eta
10
11	N[0, 0, k] = 0.25 * m1 * m2
12	N[1, 0, k] = 0.25 * p1 * m2
13	N[2, 0, k] = 0.25 * p1 * p2
14	N[3, 0, k] = 0.25 * m1 * p2
15	N[0, 1, k] = -0.25 * m2
16	N[1, 1, k] = +0.25 * m2
17	N[2, 1, k] = +0.25 * p2
18	N[3, 1, k] = -0.25 * p2
19	N[0, 2, k] = -0.25 * m1
20	N[1, 2, k] = -0.25 * p1
21	N[2, 2, k] = +0.25 * p1
22	N[3, 2, k] = +0.25 * m1
23
24	J = np.zeros((2, 2))
25	for i in range(4):
26	J[0, 0] += N[i][1][k] * nodes[i].x[0]
27	J[1, 0] += N[i][2][k] * nodes[i].x[0]
28	J[0, 1] += N[i][1][k] * nodes[i].x[1]
29	J[1, 1] += N[i][2][k] * nodes[i].x[1]
30	detJ[k] = J[0, 0]J[1, 1] - J[0, 1]J[1, 0]
31	if detJ[k] < 0.:
32	print ’Negative derivative at element %i.’%self.id
33	print ’Nodes:’, [n.id for n in nodes]
34	exit(-1.)
35
36	for i in range(4):
37	d1 = N[i, 1, k] * ( J[1, 1] / detJ[k])
38	+ N[i, 2, k] * (-J[0, 1] / detJ[k])
39	d2 = N[i, 1, k] * (-J[1, 0] / detJ[k])
40	+ N[i, 2, k] * ( J[0, 0] / detJ[k])
41	N[i, 1, k] = d1
42	N[i, 2, k] = d2
43
44	return N, detJ

3.7 Το στοιχείο διεπιφάνειας

Τα στοιχεία διεπιφάνειας χρησιμοποιούνται σε προβλήματα πεπερασμένων στοιχείων για να προσομοιώσουν τις διεπιφάνειες μεταξύ γειτονικών σωμάτων που βρίσκονται σε επαφή και έχουν σημαντικά διαφορετικά μεταξύ τους χαρακτηριστικά [1]. Τυπικό παράδειγμα προσομοίωσης με στοιχείο διεπιφάνειας αποτελεί η προσομοίωση της επαφής μεταξύ ενός τοίχου αντιστήριξης και της εδαφικής μάζας.

Ένα τυπικό στοιχείο διεπιφάνειας τεσσάρων κόμβων δίνεται στο Σχήμα 3.14.

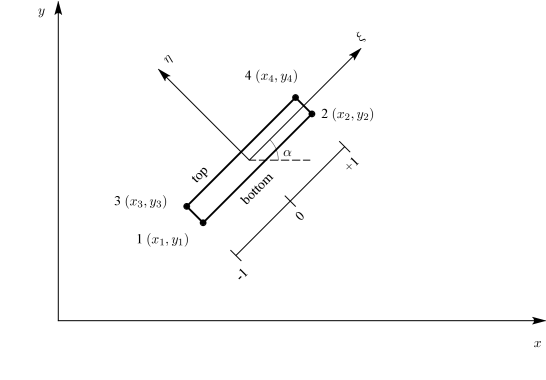
Σχήμα 3.14: Στοιχείο διεπιφάνειας 4 κόμβων.

3.7.1 Συναρτήσεις μορφής

Για το στοιχείο του Σχήματος 3.14 επιλέγονται γραμμικές συναρτήσεις για την περιγραφή της γεωμετρίας και των μετακινήσεων, οι οποίες δίνονται από τις ακόλουθες σχέσεις:

	$\displaystyle N_{1}=N_{3}$	$\displaystyle=\dfrac{1}{2}(1-\xi)$		(3.210)
	$\displaystyle N_{2}=N_{4}$	$\displaystyle=\dfrac{1}{2}(1+\xi)$		(3.211)

Οι μετακινήσεις του στοιχείου ορίζονται επομένως με τη βοήθεια των συναρτήσεων μορφής ως:

$\displaystyle u^{bottom}$	$\displaystyle=N_{1}u_{1}+N_{2}u_{2}$	(3.212)
$\displaystyle v^{bottom}$	$\displaystyle=N_{1}v_{1}+N_{2}v_{2}$	(3.213)
$\displaystyle u^{top}$	$\displaystyle=N_{1}u_{3}+N_{2}u_{4}$	(3.214)
$\displaystyle v^{top}$	$\displaystyle=N_{1}v_{3}+N_{2}v_{4}$	(3.215)

όπου bottom και top η βάση και η κορυφή του στοιχείου αντίστοιχα, όπως διακρίνονται στο Σχήμα 3.14.

3.7.2 Μητρώο ελαστικότητας

Οι παραμορφώσεις ορίζονται βάσει των σχετικών μετακινήσεων της κορυφής (top) ως προς τη βάση (bottom), όπως φαίνεται στο Σχήμα 3.14:

	$\displaystyle\gamma$	$\displaystyle=u^{top}-u^{bottom}$		(3.216)
	$\displaystyle\varepsilon$	$\displaystyle=v^{top}-v^{bottom}$		(3.217)

Η διατμητική και η ορθή τάση δίνονται αντίστοιχα από τις σχέσεις:

	$\displaystyle\tau$	$\displaystyle=K_{s}\gamma$		(3.218)
	$\displaystyle\sigma$	$\displaystyle=K_{n}\varepsilon$		(3.219)

όπου $K_{s}$ και $K_{n}$ η διατμητική και η ορθή δυσκαμψία αντίστοιχα. Συνδέονται με το μέτρο ελαστικότητας $E$ και το μέτρο διάτμησης του υλικού της διεπιφάνειας, σύμφωνα με τις παρακάτω σχέσεις:

	$\displaystyle K_{s}$	$\displaystyle=\dfrac{G}{t}$		(3.220)
	$\displaystyle K_{n}$	$\displaystyle=\dfrac{E}{t}$		(3.221)

όπου $t$ το πάχος του στοιχείου.

Θα πρέπει στο σημείο αυτό να σημειωθεί ότι επιλέγοντας χαμηλές τιμές για τα μέτρα δυσκαμψίας $K_{s}$ και $K_{n}$ μπορεί να προκύψουν εξαιρετικά μεγάλες μετακινήσεις. Στην περίπτωση όμως που επιλεγούν πολύ υψηλές τιμές, τότε μπορεί να δημιουργηθούν αριθμητικά προβλήματα κατά την επίλυση.

Με βάση τα παραπάνω, το μητρώο ελαστικότητας για το στοιχείο διεπιφάνειας ορίζεται ως:

\mathbf{C}=\left[\begin{array}[]{cc}K_{s}&0\\ 0&K_{n}\\ \end{array}\right]

(3.222)

3.7.3 Το μητρώο παραμορφώσεων-μετακινήσεων

Το μητρώο παραμορφώσεων-μετακινήσεων προκύπτει από τις (3.216) και (3.217).

Αντικαθιστώντας στις (3.216) και (3.217) τις (3.212)-(3.212) και λαμβάνοντας υπόψη τον μετασχηματισμό από το τοπικό στο γενικό σύστημα συντεταγμένων, ο οποίος δίνεται ως:

	$\displaystyle u^{\prime}$	$\displaystyle=v\sin a+u\cos a$		(3.223)
	$\displaystyle v^{\prime}$	$\displaystyle=u\cos a-u\sin a$		(3.224)

ή σε μητρωική μορφή:

\left[\begin{array}[]{c}u^{\prime}\\ v^{\prime}\\ \end{array}\right]=\left[\begin{array}[]{cc}\cos a&\sin a\\ -\sin a&\cos a\\ \end{array}\right]\left[\begin{array}[]{c}u\\ v\\ \end{array}\right]

(3.225)

προκύπτει το μητρώο παραμορφώσεων-μετακινήσεων,

\mathbf{B}=\left[\begin{array}[]{cccc}-\mathbf{T}\mathbf{B}_{1}&-\mathbf{T}% \mathbf{B}_{2}&\mathbf{T}\mathbf{B}_{1}&\mathbf{T}\mathbf{B}_{2}\\ \end{array}\right]

(3.226)

για το οποίο ισχύει:

\left[\begin{array}[]{c}\gamma\\ \varepsilon\\ \end{array}\right]=\mathbf{B}\boldsymbol{u}

(3.227)

θεωρώντας

\mathbf{B}_{i}=N_{i}\mathbf{I}_{2\times 2}.

(3.228)

και

\boldsymbol{u}=\left[\begin{array}[]{cccccccc}u_{1}&v_{1}&u_{2}&v_{2}&u_{3}&v_% {3}&u_{4}&v_{4}\\ \end{array}\right]^{T}.

(3.229)

3.7.4 Το μητρώο δυσκαμψίας

Το μητρώο δυσκαμψίας προκύπτει εύκολα από τη γενική σχέση:

\mathbf{K}=\int_{-1}^{1}\mathbf{B}^{T}\mathbf{C}\mathbf{B}\|\mathbf{J}\|d\xi

(3.230)

Στην παραπάνω σχέση, η ορίζουσα $\|\mathbf{J}\|$ δίνεται ως:

\|\mathbf{J}\|=\sqrt{\left[\left(\dfrac{dx}{d\xi}\right)^{2}+\left(\dfrac{dy}{% d\xi}\right)^{2}\right]}

(3.231)

3.8 Το εξάπλευρο, οκτάκομβο τριγραμμικό τρισδιάστατο στοιχείο

Τέλος εξετάζεται το εξάπλευρο, οκτάκομβο, τριγραμμικό τρισδιάστατο στοιχείο με την αρίθμηση των κόμβων που απεικονίζεται στο Σχήμα 3.15.

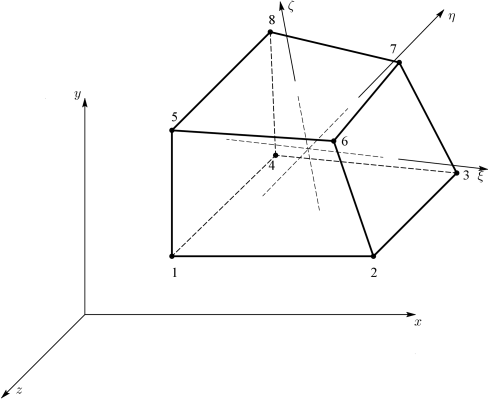
Σχήμα 3.15: Το εξάπλευρο, οκτάκομβο τριγραμμικό τρισδιάστατο στοιχείο.

Οι συναρτήσεις μορφής για αυτό το στοιχείο ορίζονται από τις ακόλουθες σχέσεις:

$\displaystyle N_{1}$	$\displaystyle=\dfrac{1}{8}(1-\xi)(1-\eta)(1-\zeta)$	(3.232)
$\displaystyle N_{2}$	$\displaystyle=\dfrac{1}{8}(1+\xi)(1-\eta)(1-\zeta)$	(3.233)
$\displaystyle N_{3}$	$\displaystyle=\dfrac{1}{8}(1+\xi)(1+\eta)(1-\zeta)$	(3.234)
$\displaystyle N_{4}$	$\displaystyle=\dfrac{1}{8}(1-\xi)(1+\eta)(1-\zeta)$	(3.235)
$\displaystyle N_{5}$	$\displaystyle=\dfrac{1}{8}(1-\xi)(1-\eta)(1+\zeta)$	(3.236)
$\displaystyle N_{6}$	$\displaystyle=\dfrac{1}{8}(1+\xi)(1-\eta)(1+\zeta)$	(3.237)
$\displaystyle N_{7}$	$\displaystyle=\dfrac{1}{8}(1+\xi)(1+\eta)(1+\zeta)$	(3.238)
$\displaystyle N_{8}$	$\displaystyle=\dfrac{1}{8}(1-\xi)(1+\eta)(1+\zeta)$	(3.239)

Οι παράγωγοι των παραπάνω συναρτήσεων μορφής δίνονται με τον κανόνα της αλυσίδας:

$\displaystyle\dfrac{\partial N_{i}}{\partial x}$	$\displaystyle=\dfrac{\partial N_{i}}{\partial\xi}\dfrac{\partial\xi}{\partial x% }+\dfrac{\partial N_{i}}{\partial\eta}\dfrac{\partial\eta}{\partial x}+\dfrac{% \partial N_{i}}{\partial\zeta}\dfrac{\partial\zeta}{\partial x}$	(3.240)
$\displaystyle\dfrac{\partial N_{i}}{\partial y}$	$\displaystyle=\dfrac{\partial N_{i}}{\partial\xi}\dfrac{\partial\xi}{\partial y% }+\dfrac{\partial N_{i}}{\partial\eta}\dfrac{\partial\eta}{\partial y}+\dfrac{% \partial N_{i}}{\partial\zeta}\dfrac{\partial\zeta}{\partial y}$	(3.241)
$\displaystyle\dfrac{\partial N_{i}}{\partial z}$	$\displaystyle=\dfrac{\partial N_{i}}{\partial\xi}\dfrac{\partial\xi}{\partial z% }+\dfrac{\partial N_{i}}{\partial\eta}\dfrac{\partial\eta}{\partial z}+\dfrac{% \partial N_{i}}{\partial\zeta}\dfrac{\partial\zeta}{\partial z}$	(3.242)

ή σε μητρωική μορφή:

\left[\begin{array}[]{c}\dfrac{\partial N_{i}}{\partial x}\\ \dfrac{\partial N_{i}}{\partial y}\\ \dfrac{\partial N_{i}}{\partial z}\end{array}\right]=\left[\begin{array}[]{ccc% }\dfrac{\partial\xi}{\partial x}&\dfrac{\partial\eta}{\partial x}&\dfrac{% \partial\zeta}{\partial x}\\ \dfrac{\partial\xi}{\partial y}&\dfrac{\partial\eta}{\partial y}&\dfrac{% \partial\zeta}{\partial y}\\ \dfrac{\partial\xi}{\partial z}&\dfrac{\partial\eta}{\partial z}&\dfrac{% \partial\zeta}{\partial z}\\ \end{array}\right]\left[\begin{array}[]{c}\dfrac{\partial N_{i}}{\partial\xi}% \\ \dfrac{\partial N_{i}}{\partial\eta}\\ \dfrac{\partial N_{i}}{\partial\zeta}\end{array}\right]

(3.243)

O $3\times 3$ πίνακας που εμφανίζεται στην προηγούμενη εξίσωση είναι ο $\mathbf{J}^{-1}$ , ο ανάστροφος δηλαδή του

\mathbf{J}=\dfrac{\partial(x,y,z)}{\partial(\xi,\eta,\zeta)}=\left[\begin{% array}[]{ccc}\dfrac{\partial x}{\partial\xi}&\dfrac{\partial x}{\partial\xi}&% \dfrac{\partial x}{\partial\xi}\\ \dfrac{\partial y}{\partial\eta}&\dfrac{\partial y}{\partial\eta}&\dfrac{% \partial y}{\partial\eta}\\ \dfrac{\partial x}{\partial\zeta}&\dfrac{\partial x}{\partial\zeta}&\dfrac{% \partial x}{\partial\zeta}\\ \end{array}\right]

(3.244)

Με βάση τα παραπάνω μπορεί να μορφωθεί το μητρώο παραμορφώσεων-μετακινήσεων και το μητρώο δυσκαμψίας, σύμφωνα με τη μεθοδολογία που ακολουθήθηκε στα προηγούμενα στοιχεία [2].

Στη συνέχεια δίνεται ενδεικτικά κώδικας σε γλώσσα προγραμματισμού Python για τον υπολογισμό των συναρτήσεων μορφής και της Ιακωβιανής του εξάπλευρου γραμμικού στοιχείου.

1	def shape(self):
2	N = zeros((8, 4, 8))
3	detJ = zeros(8)
4
5	for k, gp in enumerate(self.gps):
6	m1 = 1. - gp.xi # 1 - xi
7	p1 = 1. + gp.xi # 1 + xi
8	m2 = 1. - gp.eta # 1 - eta
9	p2 = 1. + gp.eta # 1 + eta
10	m3 = 1. - gp.zeta # 1 - zeta
11	p3 = 1. + gp.zeta # 1 + zeta
12
13	N[0][0][k] = 0.125 * m1 * m2 * m3 # N1
14	N[1][0][k] = 0.125 * p1 * m2 * m3 # N2
15	N[2][0][k] = 0.125 * p1 * p2 * m3 # N3
16	N[3][0][k] = 0.125 * m1 * p2 * m3 # N4
17	N[4][0][k] = 0.125 * m1 * m2 * p3 # N5
18	N[5][0][k] = 0.125 * p1 * m2 * p3 # N6
19	N[6][0][k] = 0.125 * p1 * p2 * p3 # N7
20	N[7][0][k] = 0.125 * m1 * p2 * p3 # N8
21
22	N[0][1][k] = -0.125 * m2 * m3 # N1, xi
23	N[1][1][k] = +0.125 * m2 * m3 # N2, xi
24	N[2][1][k] = +0.125 * p2 * m3 # N3, xi
25	N[3][1][k] = -0.125 * p2 * m3 # N4, xi
26	N[4][1][k] = -0.125 * m2 * p3 # N5, xi
27	N[5][1][k] = +0.125 * m2 * p3 # N6, xi
28	N[6][1][k] = +0.125 * p2 * p3 # N7, xi
29	N[7][1][k] = -0.125 * p2 * p3 # N8, xi
30
31	N[0][2][k] = -0.125 * m1 * m3 # N1, eta
32	N[1][2][k] = -0.125 * p1 * m3 # N2, eta
33	N[2][2][k] = +0.125 * p1 * m3 # N3, eta
34	N[3][2][k] = +0.125 * m1 * m3 # N4, eta
35	N[4][2][k] = -0.125 * m1 * p3 # N5, eta
36	N[5][2][k] = -0.125 * p1 * p3 # N6, eta
37	N[6][2][k] = +0.125 * p1 * p3 # N7, eta
38	N[7][2][k] = +0.125 * m1 * p3 # N8, eta
39
40	N[0][3][k] = -0.125 * m1 * m2 # N1, zeta
41	N[1][3][k] = -0.125 * p1 * m2 # N2, zeta
42	N[2][3][k] = -0.125 * p1 * p2 # N3, zeta
43	N[3][3][k] = -0.125 * m1 * p2 # N4, zeta
44	N[4][3][k] = +0.125 * m1 * m2 # N5, zeta
45	N[5][3][k] = +0.125 * p1 * m2 # N6, zeta
46	N[6][3][k] = +0.125 * p1 * p2 # N7, zeta
47	N[7][3][k] = +0.125 * m1 * p2 # N8, zeta
48
49	# Jacobian
50	J = zeros((3, 3))
51	for i in range(3):
52	J[0][i] = 0.;
53	J[1][i] = 0.;
54	J[2][i] = 0.;
55	for j in range(8):
56	J[0][i] += N[j][1][k] * self.nodes[j].x[i]
57	J[1][i] += N[j][2][k] * self.nodes[j].x[i]
58	J[2][i] += N[j][3][k] * self.nodes[j].x[i]
59	detJ[k] = linalg.det(J)
60	if detJ[k] < 0.:
61	print ’Negative derivative at element %i.’%self.id
62	print ’Nodes:’, [n.id for n in self.nodes]
63	exit(-100.)
64	J = linalg.inv(J)
65
66	# dNdx
67	for i in range(8):
68	d1 = N[i][1][k] * J[0][0] \
69	+ N[i][2][k] * J[0][1] \
70	+ N[i][3][k] * J[0][2]
71	d2 = N[i][1][k] * J[1][0] \
72	+ N[i][2][k] * J[1][1] \
73	+ N[i][3][k] * J[1][2]
74	d3 = N[i][1][k] * J[2][0] \
75	+ N[i][2][k] * J[2][1] \
76	+ N[i][3][k] * J[2][2]
77	N[i][1][k] = d1
78	N[i][2][k] = d2
79	N[i][3][k] = d3
80
81	return N, detJ

3.9 Βιβλιογραφία

1 G. Bear. An isoparametric joint/interface element for finite element analysis. International journal for numerical methods in engineering, 21(4): 585-600, 1985.
2 Guido Dhondt. The finite element method for three-dimensional thermomechanical applications. John Wiley & Sons, 2004.
3 Carlos A. Felippa. Lecture notes in introduction to finite element methods, 2013.
4 T. J. R. Hughes. The finite element method. Pentice-Hall, Englewood-Cliffs, New Jersey, 1987.
5 W. Lewis Roland, Perumal Nithiarasu and Kankanhalli Seetharamu. Fundamentals of the finite element method for heat and fluid flow, Wiley, 2004.
6 O. C. Zienkiewicz and R. L. Taylor. The finite element method for solid and structural mechanics. Butterworth-Heinemann, 2005.