Κεφάλαιο 2 Η μέθοδος των πεπερασμένων στοιχείων
Στο παρόν κεφάλαιο παρουσιάζεται η μέθοδος των πεπερασμένων στοιχείων.
Η προσέγγιση που προκρίνεται για την περιγραφή της μεθόδου των πεπερασμένων στοιχείων στο παρόν βιβλίο είναι αυτή των σταθμισμένων καταλοίπων. Τα βασικά βήματα της μεθόδου των πεπερασμένων στοιχείων με τη μέθοδο των σταθμισμένων καταλοίπων είναι:
-
1.
Ορισμός της ισχυρής μορφής του προβλήματος.
-
2.
Ορισμός της ασθενούς μορφής του προβλήματος.
-
3.
Επιλογή προσεγγιστικών συναρτήσεων για τις άγνωστες εξισώσεις.
-
4.
Επίλυση του συστήματος.
Το παρόν κεφάλαιο επομένως διαρθρώνεται με τρόπο που να αντιστοιχεί στα παραπάνω βήματα.
Αρχικά ορίζεται το πρόβλημα με τη βοήθεια της κλασικής εξίσωσης Poisson (Ενότητα 2.1). Πιο συγκεκριμένα, εξετάζεται το πρόβλημα ροής που περιγράφεται από την εξίσωση Poisson και δίνονται οι εξισώσεις πεδίου (Ενότητα 2.1.1) και οι συνοριακές συνθήκες (Ενότητα 2.1.2). Η σύνοψη των εξισώσεων σε διάφορες μορφές που συναντώνται στη βιβλιογραφία παρουσιάζονται στην Ενότητα 2.1.3.
Στη συνέχεια εξετάζεται η ασθενής διατύπωση του προβλήματος και συγκρίνεται με την αντίστοιχη ισχυρή μορφή (Ενότητα 2.2).
Ακολουθεί η προσέγγιση της άγνωστης συνάρτησης που αποτελεί τη λύση των εξισώσεων του προβλήματος (Ενότητα 2.3). Εξηγείται η έννοια της προσεγγιστικής συνάρτησης στη μέθοδο των πεπερασμένων στοιχείων (Ενότητα 2.3.1), οι συναρτήσεις βάσης (Ενότητα 2.3.2) και πώς τα παραπάνω εφαρμόζονται στην ασθενή διατύπωση του προβλήματος (Ενότητα 2.3.3).
Στη συνέχεια εξετάζεται η αντικατάσταση της συνάρτησης βάρους και επαναδιατυπώνεται η ασθενής μορφή του προβλήματος (Ενότητα 2.4).
Ακολουθεί η σύγκριση της μεθόδου των πεπερασμένων στοιχείων με την εξίσου διαδεδομένη μέθοδο των πεπερασμένων διαφορών (Ενότητα 2.5), όπου επισημαίνονται οι κύριες διαφορές τους.
Τέλος δίνεται η εφαρμογή της μεθόδου στις εξισώσεις της ελαστοστατικής (Ενότητα 2.6), όπου εξετάζεται συνοπτικά το πρόβλημα της δισδιάστατης ελαστικότητας (Ενότητα 2.6.1). Για λόγους πληρότητας διατυπώνονται οι χαρακτηριστικές εξισώσεις και με την σρχή των δυνατών έργων (Ενότητα 2.6.2).
Στο τέλος του κεφαλαίου παρατίθεται η σχετική βιβλιογραφία (Ενότητα 2.7).
2.1 Ορισμός του προβλήματος. Η εξίσωση Poisson
Για την καλύτερη κατανόηση της μεθόδου των πεπερασμένων στοιχείων εξετάζεται στη συνέχεια με ένα τυπικό πρόβλημα υπόγειας ροής [1], όπως δίνεται στο Σχήμα 2.1. Στο υπόψη σχήμα περιγράφεται η ροή του νερού ενός αδιαπέρατου φράγματος μέσω μίας διαπερατής εδαφικής στρώσης στη βάση του ταμιευτήρα.

Για ένα τυπικό στοιχείο μοναδιαίου πάχους και διαστάσεων και (βλ. Σχήμα 2.2) που βρίσκεται εντός της διαπερατής εδαφικής στρώσης του Σχήματος 2.1, η αρχή διατήρησης της μάζας ορίζει ότι θα πρέπει η συνολική ροή που εισέρχεται να είναι ίση με τη ροή που εξέρχεται.
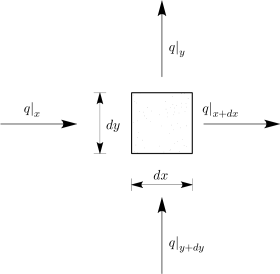
Επομένως ισχύει ότι:
| (2.1) |
όπου η ροή και ένας όρος που αναφέρεται στην ύπαρξη επιπρόσθετης εισροής εκροής εντός του στοιχειώδους τμήματος που εξετάζεται.
Η παραπάνω εξίσωση μπορεί να γραφτεί και ως:
| (2.2) |
Ο Νόμος του Darcy ορίζει τη ροή ως συνάρτηση μιας συνάρτησης δυναμικού ως
| (2.3) | ||||
| (2.4) |
Αντικαθιστώντας τις παραπάνω εξισώσεις στην (2.2), προκύπτει
| (2.5) | ||||
| (2.6) |
Η (2.6) μπορεί να γραφτεί και ως
| (2.7) |
όπου η κλίση (div) μίας πραγματικής συνάρτησης πεδίου
| (2.8) |
και η απόκλιση (grad) μίας διανυσματικής συνάρτησης
| (2.9) |
αντίστοιχα.
Η (2.7) αποτελεί μια εξίσωση που χρησιμοποιείται εκτεταμένα για την περιγραφή προβλημάτων δυναμικού και είναι γνωστή και ως γενικευμένη εξίσωση Poisson.
Η διαπερατότητα και η συνάρτηση μπορεί να είναι μεταβαλλόμενες χωρικά, δηλαδή μπορεί να ισχύει:
| (2.10) | ||||
| (2.11) |
Στην περίπτωση που η διαπερατότητα είναι σταθερή, τότε η (2.7) μπορεί να γραφτεί ως:
| (2.12) |
η οποία αποτελεί την έκφραση της κλασικής εξίσωσης Poisson.
Στην παραπάνω εξίσωση
| (2.13) |
είναι ο τελεστής του Laplace.
Στην περίπτωση που και ο όρος φόρτισης είναι μηδενικός, τότε η (2.12) απλοποιείται ακόμη περισσότερο και τελικώς εκφράζεται σύμφωνα με τα παραπάνω ως:
| (2.14) |
Η εξίσωση αυτή είναι γνωστή ως εξίσωση του Laplace. Οι λύσεις της εξίσωσης Laplace καλούνται αρμονικές συναρτήσεις.
2.1.1 Εξισώσεις πεδίου
Η απόκλιση της συνάρτησης δυναμικού είναι ένα διάνυσμα , το οποίο, για την περίπτωση της δισδιάστατης ροής που εξετάζεται, δίνεται αναλυτικά ως:
| (2.15) |
Το διάνυσμα της ροής δίνεται από τον καταστατικό νόμο
| (2.16) |
ή αναλυτικά
| (2.17) |
ο οποίος αποτελεί έκφραση του νόμου του Darcy για ένα ισότροπο μέσο.
Η ροή ως προς μία κατεύθυνση που ορίζεται από το μοναδιαίο διάνυσμα δίνεται ως:
| (2.18) |
Η ροή είναι ένα βαθμωτό μέγεθος και χαρακτηρίζει τη μεταφορά του ρευστού προς τη δεδομένη κατεύθυνση.
Στην ειδική περίπτωση που το διάνυσμα είναι το κάθετο διάνυσμα στο σύνορο , τότε γράφεται:
| (2.19) |
Τέλος, η εξίσωση ισορροπίας, όπως αναφέρθηκε προηγουμένως, δίνεται ως:
| (2.20) |
ή
| (2.21) |
2.1.2 Συνοριακές συνθήκες
Οι τυπικές συνοριακές συνθήκες για το πρόβλημα Poisson ανήκουν σε μία από τις επόμενες κατηγορίες:
-
1.
Η τιμή της συνάρτησης του δυναμικού είναι γνωστή και ίση με σε ένα τμήμα του συνόρου , δηλαδή
(2.22) -
2.
Η ροή κάθετα στο υπόλοιπο τμήμα του συνόρου , που συμβολίζεται με , είναι γνωστή, είναι δηλαδή γνωστό το διάνυσμα:
(2.23)
2.1.3 Σύνοψη των εξισώσεων
Η κινηματική εξίσωση (2.15), η καταστατική εξίσωση (2.16), η εξίσωση ισορροπίας (2.21) και οι συνοριακές συνθήκες (2.22) και (2.23) αποτελούν τις εξισώσεις που περιγράφουν το μαθηματικό προσομοίωμα του φυσικού προβλήματος. Το συγκεκριμένο πρόβλημα, όπως διατυπώνεται μέσω του μαθηματικού του προσομοιώματος, ανήκει σε μια κατηγορία προβλημάτων που ονομάζονται προβλήματα συνοριακών τιμών.
Συνοψίζοντας τα παραπάνω, θεωρείται χρήσιμο να διατυπωθούν οι εξισώσεις του προβλήματος με διαφορετικούς συμβολισμούς, όπως συχνά συναντώνται στη βιβλιογραφία [3].
-
1.
Σε μορφή πινάκων/διανυσμάτων:
(2.24) Ή ισοδύναμα:
(2.25) -
2.
Σε μορφή δεικτών:
(2.26) -
3.
Και τέλος σε πλήρη μορφή:
(2.27)
2.2 Ασθενής διατύπωση
Η παραπάνω μορφή του προβλήματος, δηλαδή:
| (2.28) |
αποτελεί την επονομαζόμενη ισχυρή διατύπωση του προβλήματος Poisson, που είναι ένα πρόβλημα μερικών διαφορικών εξισώσεων.
Ελάχιστα προβλήματα μερικών διαφορικών εξισώσεων που διατυπώνονται σε ισχυρή μορφή έχουν λύσεις κλειστού τύπου και για αυτό τον λόγο συνήθως επιχειρείται η προσεγγιστική επίλυσή τους μέσω της επαναδιατύπωσής τους σε ασθενή μορφή.
Ως ασθενής μορφή (ή αλλιώς ασθενής διατύπωση) του προβλήματος ορίζεται η διατύπωση εκείνη του ίδιου προβλήματος που αντιστοιχεί και είναι ισοδύναμη με την ισχυρή του προβλήματος και δεν ισχύει σε κάθε σημείο αλλά στο σύνολο της εξεταζόμενης περιοχής.
Η ασθενής διατύπωση του προβλήματος πραγματοποιείται ακολουθώντας τα παρακάτω τέσσερα βήματα [6]:
-
1.
Πολλαπλασιάζεται η μερική διαφορική εξίσωση με μία τυχαία μεν, αλλά αποδεκτή συνάρτηση , η οποία ικανοποιεί τις συνοριακές συνθήκες στο .
Η συνάρτηση επιλέγεται καταρχήν έτσι ώστε το αρχικό πρόβλημα να μετατρέπεται από διανυσματικό σε βαθμωτό, π.χ. για το πρόβλημα ροής που εξετάζεται, επιλέγεται , έτσι ώστε
(2.29) -
2.
Ολοκληρώνεται το παραπάνω γινόμενο στο σύνολο της εξεταζόμενης περιοχής του προβλήματος . Αυτό έχει ως αποτέλεσμα να προκύψει μια διαφορική εξίσωση δεύτερης τάξης για το πρόβλημα Poisson που εξετάζεται στο παρόν κεφάλαιο.
-
3.
Στη συνέχεια απομειώνεται ο βαθμός της διαφορικής εξίσωσης εφαρμόζοντας το θεώρημα ολοκλήρωσης του Green. Στη συγκεκριμένη περίπτωση το φυσικό πρόβλημα περιγράφεται πλέον από μία διαφορική εξίσωση πρώτης τάξης.
-
4.
Αντικαθίστανται τέλος οι συνοριακές συνθήκες.
Επομένως η ασθενής διατύπωση του συγκεκριμένου προβλήματος οδηγεί σε μία βαθμωτή διανυσματική εξίσωση πρώτου βαθμού.
Αναλυτικά εφαρμόζοντας τα παραπάνω βήματα και ξεκινώντας από την (2.28), η οποία δίνεται ως εξής,
| (2.30) |
την πολλαπλασιάζουμε με την αποδεκτή συνάρτηση , οπότε προκύπτει
| (2.31) |
Θεωρούμε τώρα το ολοκλήρωμα στην περιοχή του προβλήματος
| (2.32) |
το οποίο γράφεται και ως:
| (2.33) |
Με ολοκλήρωση κατά Green του πρώτου όρου προκύπτει:
| (2.34) |
ή αντικαθιστώντας τη συνθήκη στο σύνορο του προβλήματος και η οποία σύμφωνα με τα όσα περιγράφηκαν παραπάνω δίνεται από τη σχέση :
| (2.35) |
Ο συνοριακός όρος μπορεί να αναλυθεί ως
| (2.36) |
Επειδή όμως έχουμε θεωρήσει ότι για την τυχαία συνάρτηση ισχύει ότι στο , έχουμε
| (2.37) |
και επομένως:
| (2.38) |
Παρατηρούμε ότι η παραπάνω διατύπωση περιλαμβάνει μόνο πρώτες παραγώγους αντί για τις δεύτερες παραγώγους του αρχικού προβλήματος. Αυτό οδηγεί σε ασθενέστερους περιορισμούς κατά την επιλογή των συναρτήσεων που αποτελούν πιθανές λύσεις του προβλήματος και για αυτό τον λόγο η παραπάνω διατύπωση ονομάζεται ασθενής.
Συνοψίζοντας επομένως για το πρόβλημα, έχουμε την ισχυρή του διατύπωση:
| (2.39) |
και την ασθενή του διατύπωση:
| (2.40) |
οι οποίες θεωρούνται ισοδύναμες.
2.3 Προσέγγιση της άγνωστης συνάρτησης
Στη μέθοδο των πεπερασμένων στοιχείων, η περιοχή του εξεταζόμενου προβλήματος χωρίζεται σε έναν πεπερασμένο αριθμό επιμέρους τμημάτων (ή αλλιώς και συνηθέστερα στοιχείων) και η προσέγγιση της άγνωστης συνάρτησης, που στη συγκεκριμένη περίπτωση είναι η συνάρτηση του δυναμικού , επιχειρείται καταρχήν ανά στοιχείο [5]. Στη συνέχεια, η συνολική λύση του προβλήματος προκύπτει ως η σύνθεση των επιμέρους προσεγγιστικών λύσεων επί του πεπερασμένου αριθμού των στοιχείων στα οποία υποδιαιρείται η συνολική περιοχή του αρχικού προβλήματος.
Επομένως η συνολική λύση του προβλήματος προκύπτει από την προσέγγιση της λύσης ανά στοιχείο, σε ένα σύνολο πεπερασμένου αριθμού στοιχείων που προσεγγίζουν την αρχική περιοχή.
Στη διαδικασία αυτή οφείλεται και το όνομα της μεθόδου.
2.3.1 Η έννοια της προσεγγιστικής συνάρτησης στη μέθοδο των πεπερασμένων στοιχείων
Αρχικά ας εξετάσουμε τις προσεγγίσεις των συναρτήσεων στο πλαίσιο της μεθόδου των πεπερασμένων στοιχείων. Έστω η συνάρτηση (συνεχής γραμμή) του Σχήματος 2.3 η οποία είναι συνεχής στο διάστημα . Αν είναι γνωστές οι τιμές της συνάρτησης στα σημεία που ισαπέχουν μεταξύ τους, τότε μπορούμε να προσεγγίσουμε την αρχική συνάρτηση με την (διακεκομμένη γραμμή). Η προσεγγιστική συνάρτηση εμφανίζει τα ακόλουθα χαρακτηριστικά:
-
1.
Είναι γραμμική κατά τμήματα.
-
2.
Οι τιμές της προσεγγιστικής συνάρτησης ταυτίζονται με τις τιμές της άγνωστης συνεχούς συνάρτησης στα σημεία .
-
3.
Εντός των επιμέρους τμημάτων που ορίζονται από τα σημεία η αποτελεί μία γραμμική προσέγγιση της άγνωστης συνάρτησης .
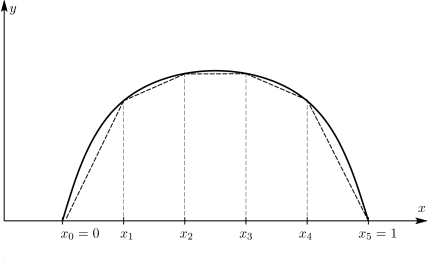
Αν τώρα η περιοριστεί σε ένα μόνο τμήμα, έστω , τότε μπορούμε να ορίσουμε την αντίστοιχη γραμμική συνάρτηση ως:
| (2.41) |
Τα και μπορεί να είναι διαφορετικά σε καθένα από τα πέντε τμήματα στα οποία υποδιαιρείται το διάστημα αλλά είναι σταθερά εντός των αντίστοιχων τμημάτων.
2.3.2 Συναρτήσεις βάσης
Στο Σχήμα 2.3 θεωρήσαμε 6 σημεία τα οποία ισαπέχουν μεταξύ τους και ορίζουν τα αντίστοιχα 5 ίσα τμήματα. Γνωρίζουμε ότι στα άκρα του διαστήματος ( και ) ισχύει ότι ενώ στα ενδιάμεσα σημεία .
Ορίζουμε τώρα τέσσερις συναρτήσεις , για τα ενδιάμεσα σημεία (, , , ), τα οποία στη μέθοδο των πεπερασμένων στοιχείων αποκαλούνται κόμβοι. Αντίστοιχα, τα τμήματα μεταξύ των σημείων και θα τα ονομάζουμε στη συνέχεια στοιχεία, όπως αναφέρθηκε και προηγουμένως.
Ένα χαρακτηριστικό των συναρτήσεων που θέλουμε να έχουν οι συναρτήσεις που ορίζουμε περιγράφεται από την ακόλουθη εξίσωση:
| (2.42) |
όπου το Δέλτα του Kronecker, για το οποίο ισχύει:
| (2.43) |
Θέλουμε δηλαδή για τις συναρτήσεις να είναι ίσες με τη μονάδα μόνο στον αντίστοιχο κόμβο που αναφέρονται και μηδέν σε όλους τους υπόλοιπους. Π.χ. για τη συνάρτηση που αντιστοιχεί στον κόμβο θέλουμε να ισχύει:
| (2.44) |
Από τα παραπάνω προκύπτει και ένα άλλο κύριο χαρακτηριστικό της γραμμικής συνάρτησης , ότι δηλαδή η είναι μη μηδενική μόνο στα τμήματα και , στα τμήματα δηλαδή που έχουν κοινό τον κόμβο .
Οι συναρτήσεις , όπως περιγράφηκαν παραπάνω, δίνονται στο Σχήμα 2.4.
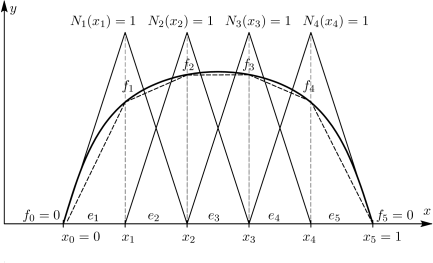
Τώρα που έχουν οριστεί οι συναρτήσεις , ας δοκιμάσουμε να προσεγγίσουμε την αρχική συνάρτηση . Παρατηρώντας το Σχήμα 2.4, διακρίνουμε ότι σε κάθε τμήμα στοιχείο αντιστοιχούν δύο συναρτήσεις . Πιο συγκεκριμένα, για το στοιχείο ( στο Σχήμα 2.4), έχουμε τις συναρτήσεις και . Οι δύο αυτές συναρτήσεις μπορούν να παραστήσουν κάθε γραμμική συνάρτηση εντός του στοιχείου .
Η γραμμική προσέγγιση μπορεί να γραφτεί ως ο γραμμικός συνδυασμός των συναρτήσεων ως εξής:
| (2.45) |
Για τα σημεία , προκύπτει από την παραπάνω σχέση:
| (2.46) |
Από την παραπάνω εξίσωση συμπεραίνεται ότι η τιμή της προσεγγιστικής συνάρτησης στους κόμβους με συντεταγμένες , όπου , ισούται με την τιμή του συντελεστή (σημειώνεται ότι και ).
Αν γνωρίζουμε τις τιμές των συντελεστών στους κόμβους , τότε μπορούμε να προσεγγίσουμε με την την .
2.3.3 Επιστροφή στην ασθενή διατύπωση του προβλήματος
Επιστρέφουμε τώρα στην ασθενή διατύπωση του προβλήματος (2.40), δηλαδή,
| (2.48) |
Σύμφωνα με τα όσα αναφέρθηκαν στην προηγούμενη ενότητα, χωρίζουμε την περιοχή του προβλήματος σε υποπεριοχές (στοιχεία) ως:
| (2.49) |
όπου είναι η περιοχή στην οποία αναζητούμε την προσεγγιστική λύση της συνάρτησης του δυναμικού την οποία υποδιαιρούμε σε έναν αριθμό πεπερασμένων στοιχείων. είναι η επιμέρους περιοχή που καταλαμβάνει το στοιχείο .
Τα ολοκληρώματα επί των στοιχείων μπορούν να αθροιστούν, επομένως μπορούμε να γράψουμε:
| (2.50) |
Η ασθενής μορφή του προβλήματος μπορεί να επαναδιατυπωθεί προσεγγιστικά τώρα ως:
| (2.51) |
Για να είναι σωστά ορισμένο το παραπάνω πρόβλημα, τα ολοκληρώματα μεταξύ δύο γειτονικών στοιχείων θα πρέπει να αλληλοακυρώνονται. Αυτό συμβαίνει όταν οι συναρτήσεις και είναι συνεχείς στην εξεταζόμενη περιοχή .
Στο σημείο αυτό σημειώνεται ότι δεν τίθεται κάποιος περιορισμός για τις παραγώγους των και , οι οποίες μπορεί να είναι και ασυνεχείς στο . Οι συναρτήσεις που είναι συνεχείς σε ένα διάστημα αλλά έχουν ασυνεχείς παραγώγους ονομάζονται συναρτήσεις.
Τώρα θεωρούμε τις συναρτήσεις με τις οποίες προσπαθούμε να προσεγγίσουμε την άγνωστη συνάρτηση δυναμικού . Σύμφωνα με τα όσα προαναφέρθηκαν:
| (2.52) |
Αντικαθιστώντας στην παραπάνω σχέση, προκύπτει:
| (2.53) | ||||
| (2.54) |
Και εφόσον οι τιμές είναι σταθερές, η παραπάνω σχέση γράφεται ως:
| (2.55) |
2.4 Αντικατάσταση της συνάρτησης βάρους
Αν τώρα θεωρήσουμε ότι οι συναρτήσεις βάρους ταυτίζονται με τις συναρτήσεις βάσης, ισχύει δηλαδή ότι:
| (2.56) |
όπου τυχαίες παράμετροι, τότε μπορούμε να γράψουμε:
| (2.57) | ||||
| (2.58) |
Ομοίως, επειδή το είναι σταθερό, μπορεί να βγει ως κοινός παράγοντας, οπότε έχουμε:
| (2.59) |
Επαναδιατυπώνοντας την παραπάνω σχέση προκύπτει:
| (2.60) |
που αποτελεί και την έκφραση της μεθόδου των πεπερασμένων στοιχείων.
Πιο συγκεκριμένα, αντικαθιστώντας
| (2.61) | ||||
| (2.62) | ||||
| (2.63) |
προκύπτει το ακόλουθο γραμμικό σύστημα
| (2.64) |
η επίλυση του οποίου οδηγεί στον προσδιορισμό των άγνωστων τιμών της συνάρτησης δυναμικού στους κόμβους των στοιχείων.
2.5 Σύγκριση με τη μέθοδο των πεπερασμένων διαφορών
Η επίσης γνωστή μέθοδος των πεπερασμένων διαφορών θα μπορούσε να χρησιμοποιηθεί για την επίλυση της εξίσωσης του προβλήματος (2.28), δηλαδή:
| (2.65) |
ή αναλυτικότερα
| (2.66) |
Σε αντίθεση με τη μέθοδο των πεπερασμένων στοιχείων, η οποία προσπαθεί να προσεγγίσει τη λύση του προβλήματος, η μέθοδος των πεπερασμένων διαφορών προσπαθεί να προσεγγίσει τις παραγώγους της διαφορικής εξίσωσης.
Η προσέγγιση που χρησιμοποιείται στη μέθοδο των πεπερασμένων διαφορών στηρίζεται στα αναπτύγματα Taylor [2], το οποίο για την περίπτωση μίας συνάρτησης δύο μεταβλητών μπορεί να γραφτεί ως:
| (2.67) |
όπου
| (2.68) |
Στις παραπάνω σχέσεις, και είναι το μήκος του βήματος στις διευθύνσεις και αντίστοιχα.
Έστω τώρα για λόγους απλοποίησης ότι
| (2.69) |
και
| (2.70) |
Τότε προκύπτει
| (2.71) |
Στην παραπάνω εξίσωση θεωρείται ότι ο δείκτης υποδηλώνει μερική παραγώγιση ως προς , δηλαδή:
| (2.72) |
Επιπροσθέτως με συμβολίζονται οι μεγαλύτεροι του όροι.
Αντίστοιχα τώρα γράφεται:
| (2.73) | ||||
| (2.74) | ||||
| (2.75) |
Αν τώρα θεωρήσουμε ότι
| (2.76) |
και
| (2.77) |
από τα παραπάνω προκύπτει για τη διεύθυνση :
| (2.78) | ||||
| (2.79) |
Ομοίως κατά τη διεύθυνση προκύπτει:
| (2.81) | ||||
| (2.82) |
Αν τώρα θεωρηθεί ότι:
| (2.83) |
τότε προκύπτει κατά τη διεύθυνση και αντίστοιχα η κεντρική μέθοδος, η οποία διατυπώνεται ως:
| (2.84) | ||||
| (2.85) |
Χωρίς να χάνεται η γενικότητα, η εξίσωση Poisson που εξετάζεται,
| (2.87) |
για = σταθερό και (εξίσωση Laplace), μπορεί πλέον γραφτεί ως:
| (2.88) | ||||
| (2.89) |
Η τελευταία εξίσωση είναι γνωστή και ως ο κανόνας των πέντε σημείων, ο οποίος γραφικά δίνεται στο Σχήμα 2.5.

Από τα όσα αναπτύχθηκαν γίνεται φανερό ότι η μέθοδος των πεπερασμένων διαφορών απαιτεί έναν σχετικά ορθοκανονικό κάναβο. Αυτός ο περιορισμός δεν υπάρχει στη μέθοδο των πεπερασμένων στοιχείων.
2.6 Εφαρμογή στις εξισώσεις της ελαστοστατικής
Στη συνέχεια δίνεται συνοπτικά η εφαρμογή της μεθόδου των πεπερασμένων στοιχείων και στις εξισώσεις της (ελαστο)-στατικής.
Για ιστορικούς λόγους και για λόγους συχνής αναφοράς στη βιβλιογραφία [4] εξετάζεται η μέθοδος των πεπερασμένων στοιχείων όπως ισοδύναμα προκύπτει από την αρχή των δυνατών έργων.
2.6.1 Εξισώσεις του προβλήματος
Έστω η περιοχή του Σχήματος 2.6 με σύνορο , το οποίο αποτελείται από το , στο οποίο είναι γνωστές οι μετακινήσεις, και το , στο οποίο είναι γνωστές οι τάσεις, με .

Από τη θεωρία της δισδιάστατης ελαστικότητας γνωρίζουμε ότι ισχύουν οι εξής τρεις ομάδες εξισώσεων πεδίου:
-
1.
Εξισώσεις ισορροπίας.
(2.90) (2.91) όπου , είναι οι μαζικές δυνάμεις (π.χ. το βάρος) ανά μονάδα όγκου. Σε μητρωική μορφή, η παραπάνω εξίσωση γράφεται:
(2.92) (2.93) -
2.
Ο καταστατικός νόμος (σχέσεις τάσεων-παραμορφώσεων).
(2.94) (2.95) όπου το μητρώο υλικού, διαφορετικό για τις περιπτώσεις επίπεδης έντασης, επίπεδης παραμόρφωσης και αξονοσυμμετρίας.
-
3.
Οι κινηματικές εξισώσεις (σχέσεις παραμορφώσεων-μετακινήσεων).
(2.96) (2.97) (2.98) Σε μητρωική μορφή, οι παραπάνω εξισώσεις γράφονται:
(2.99) (2.100)
Οι εξισώσεις (2.93), (2.95) και (2.100) μαζί με τις συνοριακές συνθήκες στο ,
| (2.101) |
και στο ,
| (2.102) |
αποτελούν το γνωστό πρόβλημα συνοριακών τιμών, το οποίο αντίστοιχα σε μητρωική μορφή μπορεί να διατυπωθεί ως εξής:
| (2.103) |
2.6.2 Διατύπωση των χαρακτηριστικών εξισώσεων με την αρχή των δυνατών έργων
Η δυναμική ενέργεια δίνεται ως η διαφορά της εσωτερικής ενέργειας μείον το έργο των εξωτερικών δυνάμεων που δρουν στο σώμα .
| (2.104) |
Όπου:
| (2.105) | ||||
| (2.106) |
Σύμφωνα με την αρχή της ελάχιστης δυναμικής ενέργειας, η δυναμική ενέργεια θα πρέπει να είναι η ελάχιστη (εφόσον το μητρώο είναι θετικά ορισμένο). Το ελάχιστο βρίσκεται εκεί που το διαφορικό της (2.104) ισούται με το μηδέν, δηλαδή:
| (2.107) |
Διαφορίζοντας επομένως τις (2.105) και (2.106) ως προς , προκύπτει:
| (2.108) |
που είναι γνωστή και ως η αρχή των δυνατών έργων.
2.7 Βιβλιογραφία
- 1 Klaus-Jürgen Bathe. Finite element procedures. Klaus-Jurgen Bathe, 2006.
- 2 Richard L. Burden, J. Douglas Faires and Annette M. Burden. Numerical analysis. Nelson Education, 2015.
- 3 Carlos A. Felippa. Lecture notes in introduction to finite element methods, 2013.
- 4 G. P. Nikishkov. Introduction to the finite element method, 2004.
- 5 Gagandeep Singh. Short introduction to finite element method, 2015.
- 6 R. L. Taylor. FEAP – A Finite Element Analysis Program, Version 7.5 User Manual. University of California at Berkeley, Berkeley, CA, 2005.