Κεφάλαιο 1 Βασικές έννοιες
Στο παρόν κεφάλαιο παρουσιάζεται και εξετάζεται το πλαίσιο στο οποίο ορίζεται το πρόβλημα της συνοριακής τιμής στη γραμμική ελαστικότητα.
Αρχικά παρουσιάζεται ο τανυστής των τάσεων (Ενότητα 1.1): Η έννοια της τάσης (Ενότητα 1.1.1), ο τανυστικός χαρακτήρας της τάσης (Ενότητα 1.1.2), οι μετασχηματισμοί των τάσεων (Ενότητα 1.1.3), οι κύριες τάσεις (Ενότητα 1.1.4), o εκτροπικός τανυστής των τάσεων (Ενότητα 1.1.5) και ο κύκλος του Mohr (Ενότητα 1.1.6).
Ακολουθεί η παρουσίαση του τανυστή των παραμορφώσεων, όπου περιγράφονται η έννοια της παραμόρφωσης, η γεωμετρική ερμηνεία της παραμόρφωσης και οι συνθήκες συμβιβαστού (Ενότητα 1.2).
Στη συνέχεια δίνονται οι σχέσεις τάσεων-παραμορφώσεων (Ενότητα 1.3): Εξετάζεται η γενική περίπτωση του Νόμου του Hooke (Ενότητα 1.3.1), ο μετασχηματισμός του τανυστή της ελαστικότητας (Ενότητα 1.3.2) και οι ιδιαίτερες περιπτώσεις ελαστικής ανισοτροπίας που αφορούν εγκαρσίως ισότροπα ελαστικά υλικά (Ενότητα 1.3.3) και ορθότροπα ελαστικά υλικά (Ενότητα 1.3.4). Τέλος παρουσιάζονται τα ισότροπα ελαστικά υλικά (Ενότητα 1.3.5).
Οι περιπτώσεις της επίπεδης συμμετρίας (Ενότητα 1.4) και της αξονοσυμμετρίας (Ενότητα 1.5) εξετάζονται στη συνέχεια. Ειδικά για την περίπτωση της αξονοσυμμετρίας δίνεται το σύστημα συντεταγμένων (Ενότητα 1.5.1), οι μετακινήσεις, οι παραμορφώσεις και τάσεις (Ενότητα 1.5.2), οι κινηματικές εξισώσεις (Ενότητα 1.5.3), οι καταστατικές εξισώσεις (Ενότητα 1.5.4) και οι εξισώσεις ισορροπίας (Ενότητα 1.5.5).
Στο τέλος του κεφαλαίου παρατίθεται η σχετική βιβλιογραφία (Ενότητα 1.6).
1.1 Τάσεις
Ο τανυστής τάσεων του Cauchy, που χρησιμοποιείται για την περιγραφή της εντατικής κατάστασης που αναπτύσσεται σε σώματα που υπόκεινται σε μικρές παραμορφώσεις, περιγράφεται στη συνέχεια.
1.1.1 Ορισμός
Έστω ένα σώμα που ορίζεται από το κλειστό και φραγμένο σύνορό του . Σε ένα τμήμα του συνόρου, που συμβολίζεται με , είναι γνωστές οι μετακινήσεις .
Θεωρείται ότι στο σώμα δρουν επιφανειακά φορτία , σημειακά φορτία και μαζικά φορτία , όπως φαίνεται στο Σχήμα 1.1.
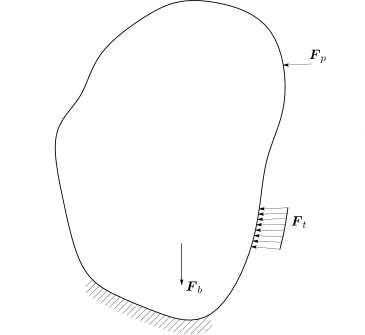
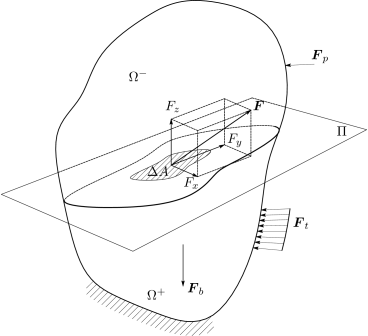
Έστω τώρα ένα τυχαίο επίπεδο που χωρίζει το σώμα σε δύο τμήματα, και . Θεωρώντας ένα καρτεσιανό σύστημα συντεταγμένων, η δύναμη που ασκείται στην περιοχή του επιπέδου μπορεί να οριστεί ως [2]:
| (1.1) |
όπου , και τα μοναδιαία διανύσματα του συστήματος αναφοράς, όπως αυτά περιγράφονται στο Σχήμα 1.2).
Η δύναμη μπορεί επίσης να αναλυθεί ως προς ένα διάνυσμα κάθετο στο επίπεδο και σε ένα διάνυσμα παράλληλο ως προς αυτό, όπως φαίνεται στο Σχήμα 1.3. Σε αυτή την περίπτωση οι συνιστώσες και ονομάζονται ορθή και διατμητική δύναμη στην περιοχή αντίστοιχα.

Το διάνυσμα της τάσης σε ένα σημείο ορίζεται θεωρώντας ότι το γίνεται απειροστό,
| (1.2) |
ή σε μορφή δεικτών
| (1.3) |
Αντίστοιχα, η ορθή τάση και η διατμητική τάση ορίζονται αντίστοιχα ως:
| (1.4) | ||||
| και | ||||
| (1.5) |
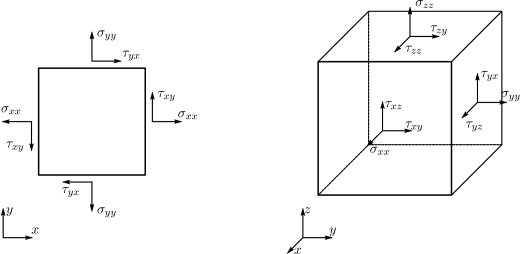
Σύμφωνα με τη σύμβαση προσήμου που ακολουθείται στην κλασική μηχανική, ως θετική ορθή τάση θεωρείται η εφελκυστική, ενώ η θετική διατμητική τάση έχει θετική φορά στο επίπεδο του οποίου το κάθετο διάνυσμα με κατεύθυνση προς τα έξω είναι επίσης θετικό, όπως αυτές δίνονται στο Σχήμα 1.4.
Στην κλασική γεωτεχνική μηχανική ακολουθείται συνήθως η αντίθετη σύμβαση προσήμου, όπως σημειώνεται στο Σχήμα 1.5. Έτσι, οι αρχικές τάσεις, οι οποίες είναι συνήθως θλιπτικές, ορίζονται ως θετικές.

Στο παρόν βιβλίο ακολουθείται η σύμβαση προσήμου της κλασικής μηχανικής για λόγους συμβατότητας με τη βιβλιογραφία και τις τυπικές εφαρμογές της μεθόδου των πεπερασμένων στοιχείων.
1.1.2 Ο τανυστής των τάσεων του Cauchy
Σύμφωνα με τη θεώρηση του Cauchy, οι τάσεις είναι ίδιες για όλες τις επιφάνειες που περνούν από το σημείο και έχουν το ίδιο κάθετο μοναδιαίο διάνυσμα στο , έχουν δηλαδή κοινή εφαπτομένη στο σημείο . Πρακτικά αυτό σημαίνει ότι ο τανυστής των τάσεων είναι συνάρτηση μόνο του κάθετου μοναδιαίου διανύσματος σε ένα σημείο.
Συνέπεια της παραπάνω θεώρησης αποτελεί το γνωστό και ως θεμελιώδες λήμμα του Cauchy, που αναφέρει ότι τα διανύσματα των τάσεων που δρουν στις αντίθετες πλευρές της ίδιας επιφάνειας είναι ίσα όσον αφορά το μέγεθος και αντίθετα όσον αφορά την κατεύθυνση.
Το θεμελιώδες λήμμα του Cauchy που εκφράζεται ως
| (1.6) |
μπορεί να θεωρηθεί και ως μια ισοδύναμη διατύπωση του Τρίτου Νόμου του Νεύτωνα που αναφέρεται στη δράση και την αντίδραση.

Το θεώρημα των τάσεων του Cauchy ορίζει τον τανυστή των τάσεων του Cauchy σε μια επιφάνεια κάθετη στο ως:
| (1.7) |
ή σε μορφή δεικτών
| (1.8) |
Θεωρούμε τώρα ένα στοιχειώδες σώμα με επίπεδα κάθετα στο καρτεσιανό σύστημα συντεταγμένων, όπως αυτό περιγράφεται στο Σχήμα 1.6. Τα διανύσματα τάσεων για κάθε επίπεδο (, , ) μπορούν να αναλυθούν σε μία ορθή και δύο διατμητικές τάσεις κατά τις διευθύνσεις των αξόνων του συστήματος συντεταγμένων. Στην περίπτωση ενός επιπέδου με κάθετο διάνυσμα στην κατεύθυνση του άξονα, η ορθή τάση ορίζεται ως και οι δύο διατμητικές ως και αντίστοιχα.
Με βάση τα παραπάνω αποδεικνύεται εύκολα ότι:
| (1.9) | ||||
| (1.10) | ||||
| (1.11) |
ή αλλιώς
| (1.12) |
Οι εννέα συνιστώσες των διανυσμάτων τάσεων αποτελούν τις συνιστώσες του τανυστή τάσεων του Cauchy, με τον οποίο περιγράφεται πλήρως η εντατική κατάσταση σε ένα σημείο ως:
| (1.13) |
ή ισοδύναμα στο σύστημα --
| (1.14) |
όπου (), () και () οι ορθές τάσεις και (), (), (), (), () και () οι διατμητικές τάσεις αντίστοιχα.
Λαμβάνοντας υπόψη τη συμμετρία του τανυστή των τάσεων, μπορούμε να τον απεικονίσουμε ως διάνυσμα της μορφής
| (1.15) |
η οποία ονομάζεται σύμβαση Voigt. Πιο συνηθισμένη είναι η ακόλουθη διατύπωση:
| (1.16) |
η οποία και θα χρησιμοποιηθεί στη συνέχεια.
Για την περίπτωση δύο διαστάσεων ισχύει
| (1.17) |
ενώ τέλος για την περίπτωση ενός προβλήματος μιας διάστασης γράφουμε απλά
| (1.18) |
1.1.3 Μετασχηματισμός των τάσεων
Ο μετασχηματισμός του τανυστή των τάσεων ακολουθεί τους κανόνες μετασχηματισμού των τανυστών δευτέρου βαθμού. Επομένως για τον μετασχηματισμό από ένα σύστημα συντεταγμένων σε ένα σύστημα , οι συνιστώσες του αρχικού συστήματος μετασχηματίζονται στις συνιστώσες του τελικού συστήματος σύμφωνα με την ακόλουθη σχέση:
| (1.19) |
ή σε μητρωική μορφή:
| (1.20) |
όπου είναι ένα μητρώο μετασχηματισμού με συνιστώσες .
Αναλυτικά, η παραπάνω σχέση δίνεται ως:
| (1.21) |
1.1.4 Κύριες τάσεις
Κύριες τάσεις ονομάζονται οι ορθές τάσεις οι οποίες δρουν σε επίπεδα στα οποία οι αντίστοιχες διατμητικές τάσεις είναι μηδενικές. Οι τιμές των κυρίων τάσεων είναι ανεξάρτητες του συστήματος συντεταγμένων αναφοράς, οι διευθύνσεις τους όμως εξαρτώνται από αυτό. Σε δισδιάστατα προβλήματα, οι κύριες τάσεις αποτελούν τη συνολικά ελάχιστη και τη μέγιστη κατά μέγεθος τάση που δρουν σε κάθε επίπεδο.
Στη γενική περίπτωση οι κύριες τάσεις προκύπτουν από την επίλυση του ιδιοπροβλήματος [9]:
| (1.22) |
Από την παραπάνω ορίζουσα προκύπτει η χαρακτηριστική εξίσωση:
| (1.23) |
όπου:
| (1.24) | ||||
| (1.25) | ||||
| (1.26) | ||||
| (1.27) | ||||
| (1.28) | ||||
| (1.29) | ||||
| (1.30) | ||||
| (1.31) | ||||
| (1.32) | ||||
| (1.33) |
Επειδή ο τανυστής των τάσεων είναι συμμετρικός, η χαρακτηριστική εξίσωση έχει τρεις πραγματικές λύσεις . Οι κύριες τάσεις ορίζονται ως:
| (1.35) | ||||
| (1.36) | ||||
| και | ||||
| (1.37) |
Από την αναλυτική επίλυση του προβλήματος προκύπτει για τη γενική, τρισδιάστατη περίπτωση:
| (1.38) | ||||
| (1.39) | ||||
| (1.40) |
όπου
| (1.41) |
Αντίστοιχα για την περίπτωση δισδιάστατου προβλήματος, προκύπτει:
| (1.42) | ||||
| (1.43) |
1.1.5 Ο εκτροπικός τανυστής των τάσεων
Η χαρακτηριστική εξίσωση για τον εκτροπικό τανυστή των τάσεων αντίστοιχα είναι:
| (1.44) |
όπου , και είναι η πρώτη, η δεύτερη και η τρίτη αναλλοίωτη αντίστοιχα.
| (1.45) | ||||
| (1.46) | ||||
| (1.47) | ||||
| (1.48) | ||||
| (1.49) | ||||
| (1.50) | ||||
| (1.51) | ||||
| (1.52) | ||||
| (1.53) | ||||
| (1.54) | ||||
| (1.55) | ||||
| (1.56) | ||||
| (1.57) | ||||
| (1.58) |
1.1.6 Ο κύκλος του Mohr
Ο κύκλος του Mohr, όπως ονομάστηκε προς τιμήν του Christian Otto Mohr, αποτελεί μια δισδιάστατη γραφική απεικόνιση του μετασχηματισμού του τανυστή των τάσεων του Cauchy [5] (βλ. π.χ. τον κύκλο του Mohr για μια τρισδιάστατη εντατική κατάσταση στο Σχήμα 1.7).
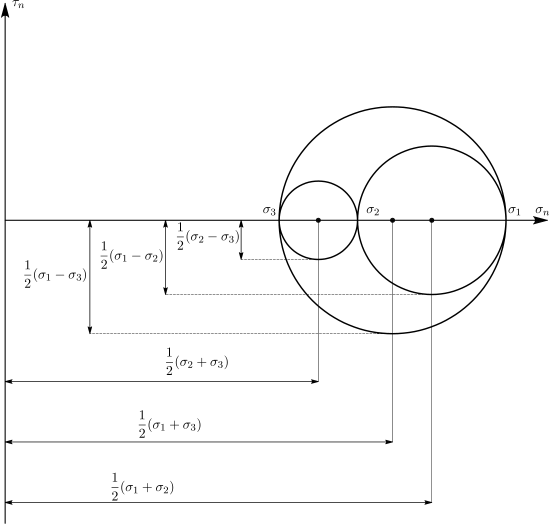
Από την ισορροπία των δυνάμεων, η ορθή τάση και η αντίστοιχη διατμητική προκύπτουν ως:
| (1.59) | ||||
| (1.60) |
1.2 Παραμορφώσεις
Όταν σε ένα σώμα ασκείται μία δύναμη, τότε το σώμα παραμορφώνεται ή μετακινείται. Αν το σώμα δεν είναι επαρκώς περιορισμένο, τότε οι εκτός ισορροπίας δυνάμεις το αναγκάζουν σε περιστροφή ή κίνηση στερεού σώματος. Αν στο σώμα υπάρχουν περιορισμοί στην κίνησή του, τότε το σώμα παραμορφώνεται υπό την επήρεια των δυνάμεων που ασκούνται σε αυτό [11].
Έστω για παράδειγμα ένα εδαφικό δείγμα υπό καθεστώς μονοαξονικής θλίψης. Στην περίπτωση αυτή ένα φορτίο ασκείται στη μία άκρη του δείγματος ενώ στην άλλη δεν επιτρέπονται οι μετακινήσεις. Αν είναι ένα τμήμα του δοκιμίου και η αλλαγή του τμήματος, τότε η απειροστική ανηγμένη παραμόρφωση ορίζεται ως:
| (1.61) |
Ο παραπάνω ορισμός αντιστοιχεί στην ορθή παραμόρφωση και αναφέρεται στην περίπτωση που αυτή συμβαίνει κατά μιας ευθείας γραμμής. Αντίστοιχα, διατμητική παραμόρφωση παρατηρείται όταν η γωνία μεταξύ δύο αρχικά ευθειών γραμμών αλλάζει.

Στο Σχήμα 1.8 δίνεται ένα στοιχειώδες ορθογώνιο ενός επίπεδου σώματος πριν από και μετά την παραμόρφωση στο οποίο οι μετατοπίσεις και θεωρούνται συναρτήσεις των συντεταγμένων και , ισχύει δηλαδή:
| (1.62) | ||||
| (1.63) |
Με την παραδοχή των μικρών παραμορφώσεων, η ανοιγμένη παραμόρφωση κατά τη διεύθυνση δίνεται από τη σχέση
| (1.64) |
και αντίστοιχα κατά τη διεύθυνση :
| (1.65) |
Η διατμητική ανηγμένη παραμόρφωση ορίζεται ως η αλλαγή της ορθής γωνίας του στοιχειώδους παραλληλογράμμου -. Με την παραδοχή των μικρών παραμορφώσεων (, ), προκύπτει:
| (1.66) |
Στη γενική περίπτωση ισχύει:
| (1.67) | ||||
| (1.68) | ||||
| (1.69) | ||||
| (1.70) | ||||
| (1.71) | ||||
| (1.72) |
Οι παραπάνω σχέσεις μπορούν να γραφτούν σε μητρωική μορφή ως:
| (1.73) |
ή συνεπτυγμένα
| (1.74) |
1.3 Σχέσεις τάσεων-ανηγμένων παραμορφώσεων
Οι τάσεις και οι ανηγμένες παραμορφώσεις συνδέονται μεταξύ τους με τις σχέσεις τάσεων-ανηγμένων παραμορφώσεων.
1.3.1 Περιπτώσεις ανισοτροπίας
Στη γενική του μορφή ο Νόμος του Hooke [10] δίνεται ως:
| (1.75) |
όπου και είναι τανυστές δεύτερης τάξης και ένας τανυστής τέταρτης τάξης.
Λόγω της συμμετρίας του τανυστή των τάσεων του Cauchy,
| (1.76) |
μπορεί να αποδειχτεί ότι:
| (1.77) |
Παρομοίως, λόγω της συμμετρίας του τανυστή των ανηγμένων παραμορφώσεων,
| (1.78) |
ισχύει:
| (1.79) |
Επομένως ο αριθμός των σταθερών που περιγράφουν των τανυστή μειώνεται από 81 σε 36. Σε μητρωική μορφή (σύμβαση Voigt) ο Νόμος του Hooke πλέον μπορεί να γραφτεί ως:
| (1.80) |
Αν τώρα θεωρήσουμε ένα υπερελαστικό υλικό, τότε οι τάσεις θεωρούνται ότι προκύπτουν από μια συνάρτηση δυναμικού ως εξής:
| (1.81) |
Η παραπάνω εξίσωση οδηγεί στον ακόλουθο ορισμό για τον τανυστή ελαστικότητας:
| (1.82) |
Επειδή δεν έχει σημασία η σειρά των παραγωγίσεων, προκύπτει επιπλέον ότι ισχύει:
| (1.83) |
Επομένως ο αριθμός των σταθερών που περιγράφουν τον τανυστή μειώνεται από 36 σε 21. Σε μητρωική μορφή μπορούμε τώρα να γράψουμε:
| (1.84) |
1.3.2 Μετασχηματισμός του ελαστικού τανυστή
Ο μετασχηματισμός του τανυστή ακολουθεί τους κανόνες μετασχηματισμού των τανυστών τετάρτης τάξης [1]. Πιο συγκεκριμένα, ορίζεται το μητρώο μετασχηματισμού ως:
| (1.85) |
Στο παραπάνω πίνακα , το συμβολίζει το συνημίτονο της γωνίας μεταξύ του αρχικού συστήματος συντεταγμένων και του τελικού συστήματος συντεταγμένων.
| (1.86) |
Σημειώνεται ότι, λόγω της ορθοκανονικότητας των συνημίτονων κατεύθυνσης, ισχύει:
| (1.87) |
όπου το ονομάζεται και δέλτα του Kronecker.
Βάσει των παραπάνω θα οριστούν στη συνέχεια τα εγκαρσίως ισότροπα και τα ορθότροπα ελαστικά υλικά, που εμφανίζουν ιδιαίτερο ενδιαφέρον στη γεωτεχνική μηχανική.
1.3.3 Eγκαρσίως ισότροπα ελαστικά υλικά
Μια πρώτη ειδική περίπτωση ενός ανισότροπου υλικού είναι αυτή κατά την οποία το υλικό περιέχει ένα επίπεδο ισοτροπίας, όπως συχνά παρατηρείται στην περίπτωση ιζηματογενών πετρωμάτων. Κάθε στρώση έχει περίπου τις ίδιες ελαστικές ιδιότητες εντός του επιπέδου της αλλά οι ιδιότητες του υλικού διαφοροποιούνται με το βάθος. Το επίπεδο κάθε στρώσης αποτελεί το επίπεδο ισοτροπίας και ο κάθετος σε αυτό άξονας τον αντίστοιχο άξονα συμμετρίας [3]. Άλλες περιπτώσεις εγκαρσίως ισότροπων ελαστικών υλικών δίνονται στο Σχήμα 1.9.
Αυτή η παραδοχή έχει ως αποτέλεσμα να μπορούμε να περιστρέψουμε το στερεό σώμα γύρω από έναν άξονα συμμετρίας, ο οποίος ορίζεται ως ο κάθετος άξονας στο ισότροπο επίπεδο, χωρίς να μεταβάλλεται η ελαστική συμπεριφορά του υλικού.

Στη συνέχεια περιγράφεται η διαδικασία εύρεσης του ελαστικού μητρώου για τα εγκαρσίως ισότροπα ελαστικά υλικά, θεωρώντας ότι ο άξονας (βλ. Σχήμα 1.10) είναι ο άξονας συμμετρίας, δηλαδή κάθετος στο επίπεδο ισοτροπίας του υλικού.
Περιστροφή κατά 90
Ο πίνακας μετασχηματισμού σε αυτή την περίπτωση δίνεται ως:
| (1.88) |
Επομένως το μετασχηματισμένο ελαστικό μητρώο προκύπτει σύμφωνα με τον μετασχηματισμό:
| (1.89) |
Λόγω των παραδοχών που διέπουν τα εγκαρσίως ισότροπα υλικά, θα πρέπει να ισχύει:
| (1.90) |
Επομένως:
| (1.91) | ||||
| (1.92) | ||||
| (1.93) | ||||
| (1.94) | ||||
| (1.95) | ||||
| (1.96) | ||||
| (1.97) | ||||
| (1.98) | ||||
| (1.99) | ||||
| (1.100) | ||||
| (1.101) | ||||
| (1.102) | ||||
| (1.103) | ||||
| (1.104) | ||||
| (1.105) | ||||
| (1.106) | ||||
| (1.107) | ||||
| (1.108) |
Σύμφωνα με τα παραπάνω, το μητρώο ελαστικότητας ενός εγκαρσίως ισότροπου υλικού μπορεί να περιγραφεί ως:
| (1.109) |
Περιστροφή κατά 180
Θεωρείται τώρα μια δεύτερη περιστροφή κατά 180. Το αντίστοιχο μητρώο μετασχηματισμού σε αυτή την περίπτωση δίνεται ως:
| (1.110) |
Ο μετασχηματισμένος τανυστής της ελαστικότητας δίνεται τώρα σύμφωνα με τον μετασχηματισμό:
| (1.111) |
Και τώρα θα πρέπει να ισχύει:
| (1.112) |
Επομένως:
| (1.113) | ||||
| (1.114) | ||||
| (1.115) | ||||
| (1.116) |
Σύμφωνα με τα παραπάνω, το μητρώο ελαστικότητας ενός εγκαρσίως ισότροπου υλικού μπορεί να περιγραφεί ως:
| (1.117) |
Περιστροφή κατά 45
Τέλος θεωρείται μια περιστροφή κατά 45. Το αντίστοιχο μητρώο μετασχηματισμού σε αυτή την περίπτωση δίνεται ως:
| (1.118) |
Ο μετασχηματισμένος τανυστής της ελαστικότητας δίνεται τώρα σύμφωνα με τον μετασχηματισμό:
| (1.119) |
Θα πρέπει επίσης να ισχύει:
| (1.120) |
Και επομένως:
| (1.121) | ||||
| (1.122) | ||||
| (1.123) | ||||
| (1.124) |
Σύμφωνα με τα παραπάνω, το μητρώο ελαστικότητας ενός εγκαρσίως ισότροπου υλικού μπορεί τελικά να περιγραφεί ως:
| (1.126) |
Περιστροφή κατά 135
Μπορεί να αποδειχτεί ότι κάθε επιπλέον περιστροφή αφήνει το μητρώο ελαστικότητας ανεπηρέαστο. Π.χ. το μητρώο μετασχηματισμού για μια γωνία ίση με 135 δίνεται ως:
| (1.127) |
Εύκολα διακρίνεται ότι ο μετασχηματισμένος τανυστής της ελαστικότητας,
| (1.128) |
παραμένει ανεπηρέαστος.
Τελική διατύπωση
Από τα παραπάνω καταλήγουμε στο συμπέρασμα ότι ο ελαστικός τανυστής για την περίπτωση εγκαρσίως ισότροπων υλικών δίνεται ως:
| (1.129) |
Για τον ορισμό του απαιτούνται πέντε ανεξάρτητες σταθερές, οι , , , και αντίστοιχα.
1.3.4 Ορθότροπα υλικά
Ένα ορθότροπο υλικό έχει τουλάχιστον δύο επίπεδα συμμετρίας ορθογώνια μεταξύ τους, όπου οι ιδιότητες του υλικού είναι ανεξάρτητες από τη διεύθυνση εντός των επιπέδων αυτών [6]. Η παραδοχή αυτή χρησιμοποιείται στη συνέχεια για τον προσδιορισμό του αντίστοιχου μητρώου ελαστικότητας. Οι άξονες του συστήματος συντεταγμένων που χρησιμοποιείται στη συνέχεια θεωρείται ότι ταυτίζονται με τα τρία επίπεδα συμμετρίας του υλικού.
Αντανάκλαση ως προς το επίπεδο 2-3
Ας θεωρήσουμε αρχικά μια αντανάκλαση ως προς το επίπεδο 2-3. Το αντίστοιχο μητρώο μετασχηματισμού σε αυτή την περίπτωση δίνεται από την ακόλουθη εξίσωση:
| (1.130) |
Ο μετασχηματισμένος τανυστής της ελαστικότητας δίνεται τώρα σύμφωνα με τη σχέση:
| (1.131) |
Βάσει των παραδοχών για τα ορθότροπα ελαστικά υλικά, ισχύει:
| (1.132) |
Επομένως:
| (1.133) |
Η παραπάνω απαίτηση μπορεί να ικανοποιηθεί μόνο όταν:
| (1.134) | ||||
| (1.135) | ||||
| (1.136) | ||||
| (1.137) | ||||
| (1.138) | ||||
| (1.139) | ||||
| (1.140) | ||||
| (1.141) |
Επομένως, ο τανυστής της ελαστικότητας ισούται με:
| (1.142) |
Αντανάκλαση ως προς το επίπεδο 3-1
Ας θεωρήσουμε τώρα μια αντανάκλαση ως προς το επίπεδο 3-1. Το αντίστοιχο μητρώο μετασχηματισμού σε αυτή την περίπτωση δίνεται από την ακόλουθη εξίσωση:
| (1.143) |
Ο μετασχηματισμένος τανυστής της ελαστικότητας δίνεται τώρα σύμφωνα με τη σχέση:
| (1.144) |
Βάσει των παραδοχών για τα ορθότροπα ελαστικά υλικά, ισχύει:
| (1.145) |
Επομένως:
| (1.146) |
Η παραπάνω απαίτηση μπορεί να ικανοποιηθεί μόνο όταν:
| (1.147) | ||||
| (1.148) | ||||
| (1.149) | ||||
| (1.150) |
Επομένως, ο τανυστής της ελαστικότητας μπορεί να γραφτεί ως:
| (1.151) |
Αντανάκλαση ως προς το επίπεδο 1-2
Μπορεί να αποδειχτεί ότι κάθε επιπλέον μετασχηματισμός αφήνει το μητρώο ελαστικότητας ανεπηρέαστο. Έστω π.χ. μια αντανάκλαση ως προς το επίπεδο 1-2. Τότε το μητρώο μετασχηματισμού γράφεται ως:
| (1.152) |
Ο μετασχηματισμένος τανυστής της ελαστικότητας δίνεται τώρα σύμφωνα με τη σχέση:
| (1.153) |
ο οποίος είναι ίδιος με τον προηγούμενο.
Τελική διατύπωση
Από τα παραπάνω καταλήγουμε στο συμπέρασμα ότι ο ελαστικός τανυστής για την περίπτωση ορθότροπων υλικών δίνεται ως:
| (1.154) |
και για τον ορισμό του απαιτούνται εννέα ανεξάρτητες ελαστικές σταθερές, δηλαδή οι , , , , , , και .
1.3.5 Ισότροπα υλικά
Ισότροπα υλικά θεωρούνται τα υλικά εκείνα των οποίων οι μηχανικές τους ιδιότητες σε κάθε σημείο τους είναι ίδιες ως προς κάθε διεύθυνση [8]. Επομένως το μητρώο ελαστικότητας των ισότροπων υλικών θα πρέπει να παραμένει ανεπηρέαστο, ανεξαρτήτως του μετασχηματισμού που μπορεί να εφαρμόσουμε σε αυτό.
Για τη μελέτη των ισότροπων υλικών αρχικά ορίζουμε τον τανυστή των παραμορφώσεων ως:
| (1.155) |
όπου το του Dirac, το οποίο ορίζεται ως:
| (1.156) |
Ο τανυστής των παραμορφώσεων (1.155) επομένως ορίζεται ως το άθροισμα,
-
•
ενός σταθερού τανυστή, , ο οποίος και ονομάζεται και ογκομετρικός τανυστής των παραμορφώσεων, ή ,
-
•
και ενός συμμετρικού τανυστή με μηδενικό ίχνος, , ο οποίος και ονομάζεται και αποκλίνων τανυστής των παραμορφώσεων, ή .
Η (1.155) τώρα μπορεί να γραφτεί και ως:
| (1.157) | ||||
| (1.158) | ||||
| (1.159) |
Στην πιο γενική του μορφή ο Νόμος του Hooke ορίζει για τα ελαστικά, ισότροπα υλικά τη σχέση των τάσεων παραμορφώσεων ως έναν γραμμικό συνδυασμό του ογκομετρικού και του αποκλίνοντα τανυστή των παραμορφώσεων, σύμφωνα με τη σχέση:
| (1.160) |
όπου:
-
είναι το μέτρο διόγκωσης και
-
το μέτρο διάτμησης.
Χρησιμοποιώντας τις σχέσεις μεταξύ των ελαστικών σταθερών, όπως αυτές παρουσιάζονται στον Πίνακα 1.1, η (1.160) μπορεί να γραφτεί με διάφορους τρόπους.
Χρησιμοποιώντας τις σταθερές του Lamé, και , η (1.160) δίνεται ως:
| (1.161) |
όπου το μοναδιαίο μητρώο και ο τανυστής της ελαστικότητας,
| (1.162) |
Στην παραπάνω σχέση το είναι το συμμετρικό τμήμα του μοναδιαίου τανυστή τετάρτης τάξης. Σε μορφή δεικτών η (1.161) δίνεται ως:
| (1.163) |
όπου
| (1.164) |
Χρησιμοποιώντας το μέτρο του Young και τον λόγο του Poisson , ο Νόμος του Hooke μπορεί να γραφτεί σε μορφή δεικτών:
| (1.165) |
η οποία μπορεί να αναπτυχθεί ως:
| (1.166) | ||||
| (1.167) | ||||
| (1.168) | ||||
| (1.169) | ||||
| (1.170) | ||||
| (1.171) |
Σε μητρωική μορφή, ο Νόμος του Hooke για ισότροπα υλικά δίνεται ως:
| (1.172) |
όπου, σύμφωνα και με όσα προαναφέρθηκαν:
| (1.173) |
Η αντίστροφη σχέση τώρα δίνεται ως:
| (1.174) |
ή με τη χρήση των σταθερών του Lamé:
| (1.175) |
| () | |||||
|---|---|---|---|---|---|
| , | |||||
| , | |||||
| , | |||||
| , | |||||
| , | |||||
| , |
1.4 Επίπεδη παραμόρφωση
H εντατική κατάσταση της επίπεδης παραμόρφωσης αποτελεί μια αρκετά συνηθισμένη εντατική κατάσταση σε προβλήματα γεωτεχνικής μηχανικής. Αναφέρεται σε περιπτώσεις κατά τις οποίες οι παραμορφώσεις οι σχετικές με ένα επίπεδο, κατά σύμβαση το επίπεδο κάθετα στον άξονα , είναι μηδενικές ή σχεδόν μηδενικές [7], ισχύει δηλαδή:
| (1.176) |
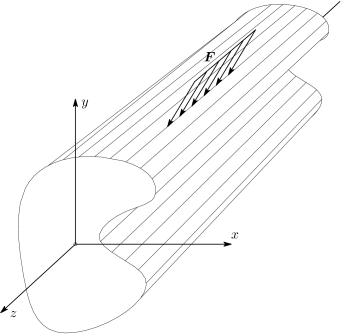
Συνθήκες επίπεδης παραμόρφωσης θεωρούμε ότι επικρατούν σε σώματα στα οποία δεν μεταβάλλεται ούτε η γεωμετρία αλλά ούτε και η φόρτιση κατά μήκος του άξονα , όπως φαίνεται στο Σχήμα 1.11, και:
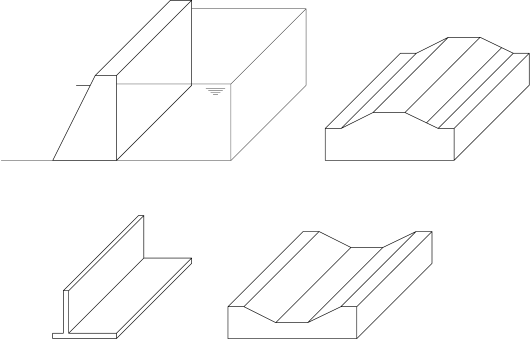
Στη δεύτερη περίπτωση ανήκουν πολλά προβλήματα της γεωτεχνικής μηχανικής, όπως φράγματα, επιχώματα, ορύγματα, τοίχοι αντιστήριξης κ.ά. (βλ. και Σχήμα 1.12).
Οι σχέσεις τάσεων παραμορφώσεων προκύπτουν από το τρισδιάστατο μητρώο ελαστικότητας μηδενίζοντας τους αντίστοιχους όρους που ορίζονται στην (1.176). Για την περίπτωση της ισότροπης ελαστικότητας π.χ. ισχύει:
| (1.177) |
και αντικαθιστώντας την (1.176) προκύπτει:
| (1.178) |
Από την παραπάνω σχέση εύκολα προκύπτει ότι
| (1.179) | ||||
| (1.180) |
και
| (1.181) |
Επομένως οι σχέσεις τάσεων παραμορφώσεων μπορούν πλέον να περιγραφούν από την ακόλουθη σχέση:
| (1.182) |
1.5 Αξονοσυμμετρία
Αντίστοιχη εντατική κατάσταση είναι και η κατάσταση της αξονοσυμμετρίας που αφορά σώματα που εμφανίζουν περιστροφική συμμετρία, τόσο όσον αφορά τη γεωμετρία αλλά και όσον αφορά και τη φόρτιση γύρω από έναν άξονα [4] (βλ. π.χ. Σχήμα 1.13.)

Και αυτή η εντατική κατάσταση συναντάται συχνά στη γεωτεχνική μηχανική, όπως π.χ. σε περιπτώσεις θεμελίων ή πασσάλων κυκλικής διατομής, ή κυκλικών κατασκευών γενικότερα (π.χ. σιλό, δεξαμενές).
1.5.1 Το σύστημα συντεταγμένων
Για τον προσδιορισμό των καταστατικών εξισώσεων του αξονοσυμμετρικού προβλήματος, χρησιμοποιείται ένα κυλινδρικό σύστημα συντεταγμένων , όπου:
-
η ακτινική συντεταγμένη,
-
η συντεταγμένη κατά τον άξονα συμμετρίας και
-
η περιμετρική συντεταγμένη.
Σημειώνεται ότι το αποτελεί ένα δεξιόστροφο καρτεσιανό σύστημα συντεταγμένων για τα επίπεδα όπου , ενώ για τα επίπεδα όπου ισχύει σχηματίζεται το πολικό σύστημα συντεταγμένων .
Το παραπάνω σύστημα συντεταγμένων δίνεται στο Σχήμα 1.5.
1.5.2 Μετακινήσεις, παραμορφώσεις και τάσεις
Το πεδίο μετακινήσεων είναι μια συνάρτηση μόνο της ακτινικής συντεταγμένης και της συντεταγμένης κατά τον άξονα συμμετρίας και ορίζεται ως:
| (1.183) |
Ο τανυστής των απειροστών παραμορφώσεων στο κυλινδρικό σύστημα συντεταγμένων δίνεται από το :
| (1.184) |
Το παραπάνω μητρώο είναι συμμετρικό, ισχύει δηλαδή ότι:
| (1.185) |
Λόγω των παραδοχών της αξονοσυμμετρικής κατάστασης, ισχύει:
| (1.186) | ||||
| (1.187) |
και επομένως ο τανυστής των παραμορφώσεων ξαναγράφεται ως:
| (1.188) |
Εύκολα διαπιστώνεται ότι οι όροι του μητρώου είναι συναρτήσεις μόνο των συντεταγμένων και .
Όπως και στις προηγούμενες ενότητες, παραλείποντας τους μηδενικούς όρους το παραπάνω μητρώο επαναδιατυπώνεται ως ένα διάνυσμα :
| (1.189) |
Συχνά στη βιβλιογραφία συναντούμε το παραπάνω διάνυσμα και ως:
| (1.190) |
όπου
| (1.191) |
Στην περίπτωση αυτή χρήζει ιδιαίτερης προσοχής ο ορισμός του μητρώου ελαστικότητας.
Ο τανυστής των τάσεων σε κυλινδρικές συντεταγμένες δίνεται αντίστοιχα από το συμμετρικό μητρώο:
| (1.192) |
Και σε αυτή την περίπτωση, λόγω των παραδοχών της αξονοσυμμετρικής κατάστασης, ισχύει:
| (1.193) | ||||
| (1.194) |
και επομένως ο τανυστής των τάσεων ξαναγράφεται ως:
| (1.195) |
Αντίστοιχα με τον τανυστή των παραμορφώσεων, ο τανυστής των τάσεων επαναδιατυπώνεται ως ένα διάνυσμα , του οποίου οι όροι είναι συναρτήσεις μόνο των συντεταγμένων και :
| (1.196) |
1.5.3 Κινηματικές εξισώσεις
Συνεχίζουμε με τον προσδιορισμό των κινηματικών εξισώσεων την αξονοσυμμετρική κατάσταση. Οι σχέσεις μετακινήσεων-παραμορφώσεων για το πρόβλημα δίνονται ως:
| (1.197) | ||||
| (1.198) | ||||
| (1.199) | ||||
| (1.200) |
Οι παραπάνω εξισώσεις δίνονται σε μητρωική μορφή ως:
| (1.201) |
ή αλλιώς σε συνεπτυγμένη μορφή,
| (1.202) |
όπου το μητρώο που ορίζεται ως
| (1.203) |
είναι ένας διαφορικός τελεστής που συνδέει τις μετακινήσεις με τις παραμορφώσεις.
1.5.4 Καταστατικές εξισώσεις
Οι καταστατικές εξισώσεις, οι σχέσεις τάσεων-παραμορφώσεων δηλαδή, δίνονται από τη σχέση
| (1.204) |
ή αλλιώς σε συνεπτυγμένη μορφή,
| (1.205) |
όπου το μητρώο του τανυστή της ελαστικότητας
| (1.206) |
Λόγω της παραδοχής της αξονοσυμμετρίας, οι περιμετρικές τάσεις δεν θα πρέπει να συνδέονται με τις διατμητικές παραμορφώσεις . Θα πρέπει δηλαδή να ισχύει
| (1.207) |
μόνο.
Επομένως μπορούμε να ξαναγράψουμε το μητρώο του τανυστή της ελαστικότητας ως:
| (1.208) |
γιατί εξαιτίας της συμμετρίας θα πρέπει να ισχύει:
| (1.209) |
Θεωρώντας τώρα ένα ομογενές και ισότροπο υλικό με μέτρο του Young και λόγο του Poisson , το μητρώο του τανυστή της ελαστικότητας για την περίπτωση της αξονοσυμμετρίας δίνεται ως:
| (1.210) |
1.5.5 Εξισώσεις ισορροπίας
Τέλος δίνονται οι γενικές (τρισδιάστατες) μερικές διαφορικές εξισώσεις ισορροπίας σε κυλινδρικές συντεταγμένες, οι οποίες ορίζονται ως:
| (1.211) | ||||
| (1.212) | ||||
| (1.213) |
όπου , , , τα στοιχεία του διανύσματος των μαζικών δυνάμεων
| (1.214) |
κατά τις διευθύνσεις , και αντίστοιχα.
Για το αξονοσυμμετρικό πρόβλημα οι παραπάνω εξισώσεις (1.211) γράφονται ως:
| (1.215) | ||||
| (1.216) |
Η τρίτη εξίσωση από τη σχέση (1.211) ισχύει ταυτοτικά αν . Αν , το πρόβλημα δεν μπορεί να θεωρηθεί αξονοσυμμετρικό.
1.6 Βιβλιογραφία
- 1 R. D. Cook, D. S. Malkus, M. E. Plesha and R. J. Witt. Concepts and applications of finite element analysis. John Wiley & Sons, 1989.
- 2 Debasis Deb. Finite element methods: concepts and applications in geomechanics. PHI Learning Pvt. Ltd., 2006.
- 3 Haojiang Ding, Weiqiu Chen and Liangchi Zhang. Elasticity of transversely isotropic materials, volume 126. Springer Science & Business Media, 2006.
- 4 Carlos A. Felippa. Lecture notes in advanced finite element methods, 2013.
- 5 J. C. Jaeger, N. G. W. Cook and R. W. Zimmerman. Fundamentals of rock mechanics. Wiley-Blackwell, 2007.
- 6 Robert M. Jones. Mechanics of composite materials, volume 1. McGraw-Hill New York, 1975.
- 7 Marc A. Meyers and Krishan Kumar Chawla. Mechanical behavior of materials, volume 2. Cambridge University Press, 2009.
- 8 Graeme W. Milton. The theory of composites, volume 6. Cambridge University Press, 2002.
- 9 Eugenio Oñate and Roger Owen. Computational plasticity, volume 7. Springer, 2007.
- 10 Ivan Stephen Sokolnikoff and Robert Dickerson Specht. Mathematical theory of elasticity. McGraw-Hill New York, 1956.
- 11 Μ. Παπαδρακάκης. Ανάλυση φορέων με τη μέθοδο των πεπερασμένων στοιχείων. Παπασωτηρίου, 2001.