1.3 Σειρές Fourier
Όπως είδαμε στις προηγούμενες παραγράφους, μπορούμε να αναπαραστήσουμε τη λύση ορισμένων διαφορικών εξισώσεων, όπως π.χ. την εξίσωση της θερμότητας, χρησιμοποιώντας συγκλίνουσες σειρές τριγωνομετρικών συναρτήσεων. Μια κατηγορία τριγωνομετρικών σειρών συναρτήσεων είναι οι σειρές Fourier, τις οποίες θα παρουσιάσουμε εν συντομία σε αυτή την παράγραφο.
Γνωρίζουμε ότι μπορούμε να χρησιμοποιήσουμε πολυώνυμα για να προσεγγίσουμε μία αρκετά ομαλή συνάρτηση κοντά σε ένα δοσμένο σημείο του πεδιού ορισμού της, π.χ. αν είναι μια φορές συνεχώς παραγωγίσιμη συνάρτηση κοντά στο , τότε
Ένας άλλος τρόπος για την προσέγγιση μιας συνάρτησης είναι η χρήση τριγωνομετρικών συναρτήσεων με το ανάπτυγμα σε σειρές Fourier της . Σε αυτή την περίπτωση αντί να χρησιμοποιήσουμε πολυώνυμα, δηλαδή δυνάμεις του ως βασικές συναρτήσεις, χρησιμοποιούμε τριγωνομετρικές συναρτήσεις π.χ., και , για
Ορισμός 1.1.
Το ανάπτυγμα σε σειρά Fourier μιας συνάρτησης με περίοδο , , δίνεται ως
| (1.54) |
όπου
Παράδειγμα 1.5.
Αν θέλουμε να βρούμε το ανάπτυγμα σε σειρά Fourier της περιοδικής συνάρτησης , με περίοδο , η οποία στο ορίζεται ως , τότε για έχουμε
και
Ακόμα
Επομένως, το ανάπτυγμα σε σειρά Fourier της είναι
Αν θεωρήσουμε τα πεπερασμένα αθροίσματα, , αυτής της σειράς,
μπορούμε να δούμε ότι, καθώς αυξάνει το , το γράφημα τους πλησιάζει αυτό της , όπως φαίνεται και από το Σχήμα 1.6.
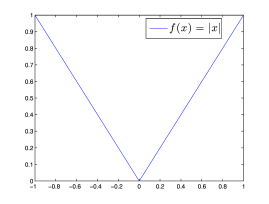 |
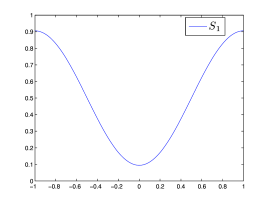 |
 |
 |
΄Ενα προφανές ερώτημα που προκύπτει είναι αν η είναι ίση με την αντίστοιχη τιμή του ανάπτυγματος Fourier της . Μια απάντηση σε αυτό δίνεται στο παρακάτω θεώρημα.
Θεώρημα 1.5.
΄Εστω ότι μια συνάρτηση και η παράγωγος της‚ , είναι φραγμένες και συνεχείς παντού στο , εκτός, ίσως, από ένα πεπερασμένο πλήθος σημείων. Τότε
σε όλα τα σημεία συνέχειας της .
Μια βασική ιδιότητα που έχουν οι τριγωνομετρικές συναρτήσεις του αναπτύγματος (1.54) είναι ότι είναι ορθογώνιες μεταξύ τους, αν τις ολοκληρώσουμε στο διάστημα , δηλαδή
| (1.55) | ||||
| (1.56) | ||||
| (1.57) |
Επίσης, μπορούμε να δούμε και ότι αν η συνάρτηση είναι άρτια στο , δηλ. , τότε επειδή η είναι περιττή στο , οι συντελεστές στην (1.54) θα μηδενίζονται. Επομένως, το ανάπτυγμα σε σειρά Fourier μιας άρτιας συνάρτησης έχει μόνο όρους συνημιτόνων, δηλαδή είναι της μορφής
και μάλιστα
| (1.58) |
΄Ομοια για μια περιοδική περιττή συνάρτηση μπορούμε να δούμε ότι , Επομένως, το ανάπτυγμά της σε σειρά Fourier έχει μόνο όρους ημιτόνων, δηλαδή είναι της μορφής
| (1.59) |
με
| (1.60) |
΄Εστω τώρα ότι έχουμε μια συνεχή συνάρτηση στο . H μπορεί να επεκταθεί στο ως άρτια ή ως περιττή συνάρτηση. Επομένως, το ανάπτυγμα της σε σειρά Fourier μπορεί να γραφεί είτε ως σειρά συνημιτόνων είτε ως σειρά ημιτόνων, αντίστοιχα.
Παράδειγμα 1.6.
΄Εστω , . Μπορούμε να επεκτείνουμε την στο ως μια άρτια συνάρτηση. Έτσι
Συνεπώς, η μπορεί να γραφεί ως σειρά συνημιτόνων και, υπολογίζοντας τους αντίστοιχους συντελεστές της (1.58), έχουμε