Κεφάλαιο 10
Ομογενείς χώροι - Γεωμετρία κατά Klein
Σύνοψη
Σύμφωνα με τον F. Klein η γεωμετρία είναι η μελέτη εκείνων των ιδιοτήτων ενός χώρου οι οποίες παραμένουν
αναλλοίωτες από τη δράση μιας ομάδας μετασχηματισμών. Σε σύχγρονη γλώσσα, ο χώρος είναι μια λεία
πολλαπλότητα και η ομάδα είναι μια ομάδα Lie, η οποία δρα στην πολλαπλότητα μεταβατικά. Διαφορετικές ομάδες
Lie ορίζουν, μέσω των δράσεών τους, διαφορετικές γεωμετρίες σε μια πολλαπλότητα. Στο κεφάλαιο
αυτό παρουσιάζουμε τα γενικά χαρακτηριστικά της θεωρίας των ομογενών χώρων, με έμφαση στους
αναγωγικούς ομογενείς χώρους. Για έναν τέτοιο ομογενή χώρο δίνουμε τύπους για τη συνοχή Levi-Civita,
τανυστή καμπυλότητας, καμπυλότητα Ricci και βαθμωτή καμπυλότητα. Τέλος, κάνουμε εφαρμογή σε
ενδεικτικά παραδείγματα. Οι αναφορές μας με αύξοντα βαθμό δυσκολίας είναι τα βιβλία [1], [2], [5],
[6], [9], [11], [3], [12], [16], [10], [7], καθώς και οι καλογραμμένες διπλωματικές εργασίες [15] και
[18].
Προαπαιτούμενη γνώση
Εισαγωγή στις Πολλαπλότητες, Εισαγωγή στις Ομάδες Lie, Γραμμική Άλγεβρα, Στοιχειώδης Θεωρία
Αναπαραστάσεων.
΄Ενας ομογενής χώρος είναι μια λεία πολλαπλότητα M στην οποία δρα μεταβατικά μια ομάδα Lie G. Οι
ομογενείς χώροι αποτελούν μια φυσική επέκταση των ομάδων Lie και η βασική τους ιδιότητα είναι ότι, αν
γνωρίζουμε την τιμή κάποιου γεωμετρικού αντικειμένου (π.χ. καμπυλότητα) σε ένα σημείο του χώρου, τότε
χρησιμοποιώντας απεικονίσεις μεταφοράς, μπορούμε να υπολογίσουμε την τιμή του σε οποιοδήποτε σημείο του
χώρου. Μια κλάση ομογενών χώρων είναι οι αναγωγικοί ομογενείς χώροι τους οποίους θα μελετήσουμε στη
συνέχεια του κεφαλαίου.
Οι ομογενείς χώροι είναι το μοντέλο της γεωμετρίας του Klein, σύμφωνα με το οποίο η γεωμετρία είναι η
μελέτη εκείνων των γεωμετρικών αντικειμένων που παραμένουν αναλλοίωτα μέσω της δράσης μιας ομάδας σε ένα
χώρο. Η ομάδα αυτή είναι γνωστή ως ομάδα μετασχηματισμών (transformation group). Θεωρώντας
διαφορετικές ομάδες κάθε φορά, οδηγούμαστε σε διαφορετικές γεωμετρίες. Τέλος, να αναφέρουμε ότι η
θεωρία των ομογενών χώρων χρησιμοποιείται ευρέως στη μαθηματική φυσική, όπου μαζί με την
θεωρία συνοχών αποτελούν σημαντικό εργαλείο για την έρευνα στη σύγχρονη θεωρία στοιχειωδών
σωματιδίων.
10.1 Δράσεις ομάδων
Θα ξεκινήσουμε την ενότητα με τον ορισμό της δράσης μιας τοπολογικής ομάδας ή μιας ομάδας Lie σε ένα σύνολο,
το οποίο μπορεί να είναι τοπολογικός χώρος, λεία πολλαπλότητα ή και διανυσματικός χώρος. Στη συνέχεια, θα
δώσουμε μερικούς ορισμούς σχετικά με την έννοια της δράσης, για παράδειγμα θα δούμε πότε η δράση λέγεται
μεταβατική και τέλος θα αναφέρουμε μερικά παραδείγματα.
Ορισμός 10.1: ΄Εστω G μια τοπολογική ομάδα (αντίστ. ομάδα Lie) και M ένας τοπολογικός χώρος (αντίστ.
λεία πολλαπλότητα). Μια αριστερή δράση (left action) της G στη M είναι μια συνεχής (αντίστ. λεία)
απεικόνιση
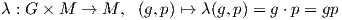
η οποία για κάθε g1,g2 ∈ G και p ∈ M ικανοποιεί τις παρακάτω συνθήκες:
- (α) λ(e,p) = ep = p και
- (β) λ(g1g2,p) = (g1g2)p = g1(g2p) = λ(g1,λ(g2,p))
Παρόμοια, μπορούμε να ορίσουμε τη δεξιά δράση της G στη M, μέσω μιας συνεχούς (αντίστ. λείας)
απεικόνισης ϕ : M × G → M, όπου κάθε ζεύγος (p,g) ∈ M × G απεικονίζεται στο σημείο p ⋅ g = pg το οποίο
ανήκει στην M και ικανοποιεί τις ανάλογες συνθήκες:
- (α') ϕ(p,e) = pe = p και
- (β') ϕ(p,g1g2) = p(g1g2) = (pg1)g2 = ϕ(ϕ(p,g1),g2)
για κάθε g1,g2 ∈ G και p ∈ M. Πολλές φορές ο χώρος M με τη δράση της G καλείται G-χώρος (G-space), ενώ η
ομάδα G αναφέρεται και ως ομάδα μετασχηματισμών (transformation group) της M.
Στο βιβλίο αυτό η G θα είναι μια ομάδα Lie και η M μια λεία πολλαπλότητα ενώ, επειδή κάθε αριστερή δράση
μπορεί να γίνει δεξιά θέτοντας το g ⋅ p να είναι p ⋅ g-1 και αντιστρόφως, θα ασχοληθούμε μόνο με τις αριστερές
δράσεις.
Αν λ είναι μια αριστερή δράση της G στην M, τότε για κάθε g ∈ G η απεικόνιση
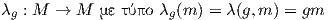
είναι μια αμφιδιαφόριση της M. Πράγματι, παρατηρούμε ότι
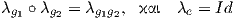
κατά συνέπεια για κάθε g ∈ G, η αντίστροφη απεικόνιση της λg είναι η λεία απεικόνιση λg-1 = (λg)-1. Οπότε,
μέσω των αριστερών δράσεων (αντίστ. δεξιών) μπορούμε να αναπαραστήσουμε την ομάδα G ως μια υποομάδα της
ομάδας των αμφιδιαφορίσεων της πολλπαπλότητας M. Ας δούμε τώρα κάποιους ορισμούς σχετικά με μια δράση.
΄Εστω M ένας G-χώρος.
- Μια δράση λέγεται μεταβατική (transitive), αν για κάθε ζεύγος σημείων p,q ∈ M υπάρχει g ∈ G
τέτοιο ώστε q = gp.
- Για κάθε m ∈ M, η ομάδα ισοτροπίας (isotropy group) του m, είναι το σύνολο εκείνων των στοιχείων
της ομάδας, που διατηρούν το m σταθερό, δηλαδή είναι το σύνολο το οποίο συμβολίζουμε με Gm,
όπου
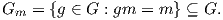
- Για κάθε m ∈ M, η τροχιά (orbit) του m, είναι το σύνολο
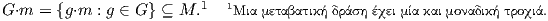
- Μια δράση καλείται αποτελεσματική (effective), αν το e ∈ G είναι το μοναδικό στοιχείο που ορίζει
την τετριμμένη δράση, δηλαδή αν gm = m για όλα τα m ∈ M, τότε g = e.
- Μια δράση καλείται ελεύθερη (free), αν η σχέση gm = m για κάποιο m ∈ M συνεπάγεται ότι g = e.
Δηλαδή η δράση είναι ελεύθερη αν Gm = {e}.
Παρατηρήσεις.
1. Εύκολα προκύπτει ότι η ομάδα ισοτροπίας Gm του m ∈ M είναι μια υποομάδα Lie της G. Πράγματι,
παρατηρούμε ότι για κάθε g1,g2 ∈ Gm είναι (g1g2) ⋅ m = g1 ⋅ (g2 ⋅ m) = g1 ⋅ m = m, δηλαδή g1g2 ∈ Gm,
οπότε το σύνολο Gm είναι κλειστό ως προς τον πολλαπλασιασμό της G. Το ουδέτερο στοιχείο e ∈ G
ανήκει στην ομάδα ισοτροπίας του m, αφού e ⋅ m = m. Τέλος, για κάθε g ∈ Gm έχουμε g-1 ∈ Gm,
διότι m = e ⋅ m = (g-1g) ⋅ m = g-1 ⋅ (gm) = g-1 ⋅ m. ΄Αρα το Gm είναι υποομάδα της G. Για να
δείξουμε ότι είναι υποομάδα Lie της G, αρκεί να δείξουμε ότι είναι κλειστό (τοπολογικά) υποσύνολο της
G. Παρατηρούμε ότι το Gm είναι η αντίστροφη εικόνα της συνεχούς απεικόνισης fm : G → M, με
τιμή fm(g) = gm. Συνεπώς, η ομάδα ισοτροπίας του σημείου m ∈ M είναι μια υποομάδα Lie της
G.
2. Αν M είναι ένας G-χώρος, τότε για m1,m2 ∈ M ορίζουμε
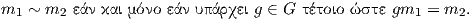
Τότε η σχέση ῾῾~᾿᾿ είναι μια σχέση ισοδυναμίας. Πράγματι, για κάθε m ∈ M έχουμε em = m, άρα m ~ m. ΄Εστω
m1 ~ m2, δηλαδή gm1 = m2 για κάποιο g ∈ G. Τότε
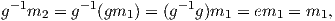
άρα m2 ~ m1. Τέλος αν m1 ~ m2 και m2 ~ m3 τότε g1m1 = m2 και g2m2 = m3, για κάποια
g1,g2 ∈ G. ΄Αρα (g2g1)m1 = g2(g1m1) = g2m2 = m3, δηλαδή m1 ~ m3. Οι κλάσεις ισοδυναμίας της
~ είναι ακριβώς οι τροχιές της δράσεις της ομάδας G. Κατά συνέπεια, οι τροχιές διαμερίζουν την
πολλαπλότητα M. Με αυτόν τον τρόπο δημιουργείται ο χώρος πηλίκο M∕G (χώρος τροχιών – orbit
space).
3. Για κάθε g ∈ G ισχύει ότι Gg⋅x = gGxg-1. Πράγματι, αν h ∈ Gg⋅x, τότε h ⋅ (g ⋅ x) = g ⋅ x. Πολλαπλασιάζουμε
την προηγούμενη σχέση με το g-1 από αριστερά και έχουμε
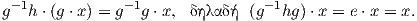
΄Αρα g-1hg ∈ Gx, ή h ∈ g-1Gxg. Επομένως, δείξαμε ότι Gg⋅x ⊆ g-1Gxg. Μένει να δείξουμε ότι g-1Gxg ⊆ Gg⋅x.
΄Εστω h ∈ g-1Gxg. Τότε το g-1hg ανήκει στο σύνολο Gx, δηλαδή (g-1hg) ⋅ x = x. Πολλαπλασιάζοντας την
τελευταία σχέση από αριστερά με g, θα πάρουμε g(g-1hg) ⋅ x = g ⋅ x, ή eh(g ⋅ x) = g ⋅ x, δηλαδή h ∈ Gg⋅x. Αυτό
μας λέει ότι, στην περίπτωση που δύο στοιχεία x,gx ≡ m ∈ M ανήκουν στην ίδια τροχιά, τότε οι ομάδες
ισοτροπίας τους διαφέρουν μόνο κατά τον εσωτερικό αυτομορφισμό Ig : G → G, Ig(α) = g-1αg, ή ότι οι ομάδες
ισοτροπίας είναι συζυγείς.
Παραδείγματα.
1. ΄Εχουμε δει στο Κεφάλαιο 8 ότι κάθε αναπαράσταση ϕ : G → Aut(V ) ορίζει μια δράση της ομάδας G στον
διανυσματικό χώρο V με τον εξής τρόπο:
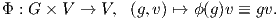
Τότε ισχύει
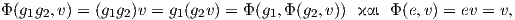
δηλαδή η απεικόνιση Φ είναι πράγματι μια δράση.
2. Η φυσική δράση της GLnℝ στον χώρο ℝn.
Θεωρούμε έναν πίνακα A = [αij] ∈ GLnℝ και ένα διάνυσμα-στήλη u = (ui) ∈ ℝn. Τότε η απεικόνιση
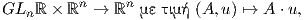
είναι μια αριστερή δράση της γενικής γραμμικής ομάδας στον Ευκλείδειο χώρο ℝn. Πράγματι, παρατηρούμε ότι για
κάθε u ∈ ℝn και A,B ∈ GLnℝ έχουμε In ⋅u = u και (AB) ⋅u = A⋅ (B ⋅u). Επίσης, η παραπάνω απεικόνιση είναι
λεία, διότι τα στοιχεία του πίνακα A ⋅ u είναι οι λείες συναρτήσεις, A ⋅ u = ∑
j[αij]uj.
Η δράση αυτή δεν είναι μεταβατική, επειδή για κάθε A ∈ GLnℝ ισχύει ότι A⋅ 0 = 0. Η μεταβατικότητα ισχύει στην
περίπτωση που η γενική γραμμική ομάδα δρά στον ℝn\{0}. Για παράδειγμα, όταν n = 2, τότε θεωρούμε ένα μη
μηδενικό διάνυσμα υ = 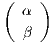 ∈ ℝ2, και ζητάμε έναν πίνακα A ∈ GL2ℝ, τέτοιον ώστε A
∈ ℝ2, και ζητάμε έναν πίνακα A ∈ GL2ℝ, τέτοιον ώστε A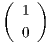 = υ. Στην
περίπτωση που έχουμε α≠0, θεωρούμε τον πίνακα A =
= υ. Στην
περίπτωση που έχουμε α≠0, θεωρούμε τον πίνακα A = 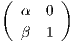 , ενώ αν β≠0 τότε θεωρούμε τον πίνακα
B =
, ενώ αν β≠0 τότε θεωρούμε τον πίνακα
B = 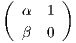 . Παρατηρούμε ότι οι πίνακες A,B ανήκουν στη γενική γραμμική ομάδα και ο καθένας στέλνει το
διάνυσμα
. Παρατηρούμε ότι οι πίνακες A,B ανήκουν στη γενική γραμμική ομάδα και ο καθένας στέλνει το
διάνυσμα 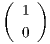 στο υ. Με το ίδιο σκεπτικό ορίζεται η μεταβατική δράση των υποομάδων της GLnℝ στον
Ευκλείδειο χώρο ℝn\{0}.
στο υ. Με το ίδιο σκεπτικό ορίζεται η μεταβατική δράση των υποομάδων της GLnℝ στον
Ευκλείδειο χώρο ℝn\{0}.
3. Κάθε ομάδα Lie G μπορεί να θεωρηθεί ως G-χώρος, αφού η G δρά στον ευατό της μέσω της
απεικόνισης
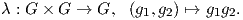
Επίσης, αν H είναι μια υποομάδα της G τότε η G είναι ένας H-χώρος μέσω της δράσης H × G → G,
(h,g)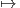 hg. Η απεικόνιση Ih : G → G με τιμή Ih(g) = hgh-1 για κάθε h ∈ H, ορίζει μια λεία δράση της
υποομάδας H στην G. Πράγματι, για κάθε h1,h2 ∈ H και g ∈ G είναι Ie = ege-1 = g και
Ih1h2(g) = h1h2g(h1h2)-1 = h1(h2gh2-1)h1-1 = Ih1(Ih2(g)).
hg. Η απεικόνιση Ih : G → G με τιμή Ih(g) = hgh-1 για κάθε h ∈ H, ορίζει μια λεία δράση της
υποομάδας H στην G. Πράγματι, για κάθε h1,h2 ∈ H και g ∈ G είναι Ie = ege-1 = g και
Ih1h2(g) = h1h2g(h1h2)-1 = h1(h2gh2-1)h1-1 = Ih1(Ih2(g)).
10.2 Πολλαπλότητες πηλίκο
΄Εστω G μια ομάδα Lie και K μια υποομάδα της G. Το σύνολο όλων των αριστερών συμπλόκων {gK : g ∈ G}
της K στην G συμβολίζεται με G∕K. Το σύνολο αυτό εφοδιασμένο με την τοπολογία πηλίκο (που
ορίζεται μέσω της κανονικής προβολής π : G → G∕K, π(g) = gK), ονομάζεται χώρος πηλίκο (coset
space).
Γενικά, αν X είναι ένας τοπολογικός χώρος και ~ είναι μια σχέση ισοδυναμίας στον X, τότε ο χώρος πηλίκο
X∕ ~ είναι το σύνολο όλων των κλάσεων ισοδυναμίας, δηλαδή
![X∕ ~ = {[x] : x ∈ X } = {{y ∈ X : y ~ x } : x ∈ X }.](02_chapter_1018x.png) Ο
χώρος αυτός εφοδιάζεται με την εξής τοπολογία. ΄Εστω π : X → X∕ ~, x
Ο
χώρος αυτός εφοδιάζεται με την εξής τοπολογία. ΄Εστω π : X → X∕ ~, x [x] η κανονική προβολή (συμβολίζεται
και αυτή με το ίδιο γράμμα). Τότε το U ⊂ X∕ ~ ονομάζεται ανοικτό εάν και μόνο εάν το π-1(U) είναι ανοικτό στο
X.
[x] η κανονική προβολή (συμβολίζεται
και αυτή με το ίδιο γράμμα). Τότε το U ⊂ X∕ ~ ονομάζεται ανοικτό εάν και μόνο εάν το π-1(U) είναι ανοικτό στο
X.
Προκειμένου ο χώρος πηλίκο να αποκτήσει δομή λείας πολλαπλότητας, η υποομάδα K απαιτείται να είναι
κλειστή. Για την απόδειξη της παρακάτω πρότασης παραπέμπουμε στα βιβλία [7], [11], [16].
Θεώρημα 10.1: ΄Εστω G μια ομάδα Lie και K μια κλειστή υποομάδα της G. Τότε ο χώρος πηλίκο G∕K
επιδέχεται μία και μοναδική δομή λείας πολλαπλότητας, τέτοια ώστε η προβολή π : G → G∕K να είναι μια
υπεμβάπτιση, δηλαδή το διαφορικό dπg της π να είναι επί για κάθε g ∈ G.
ϒπάρχουν πολλές περιπτώσεις κατά τις οποίες η υποομάδα K μπορεί να είναι κλειστή. Για παράδειγμα, εάν η G
είναι συνεκτική και απλά συνεκτική και η K είναι συνεκτική με ημιαπλή άλγεβρα Lie, τότε η K είναι κλειστή. Για
περισσότερες πληροφορίες επί αυτού παραπέμπουμε στο βιβλίο [10].
Η λεία πολλαπλότητα G∕K, που κατασκευάζεται σύμφωνα με το Θεώρημα 10.1, ονομάζεται
πολλαπλότητα πηλίκο (coset manifold) ή ομογενής χώρος (homogeneous space). Επιπλέον, ισχύει ότι
dim(G∕K) = dim G - dim K.
Αν G∕K είναι ένας ομογενής χώρος, τότε η απεικόνιση
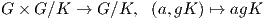
είναι μια δράση και ονομάζεται φυσική δράση της G στον G∕K. Η δράση αυτή είναι μεταβατική.
Για κάθε α ∈ G ορίζουμε την απεικόνιση τa : G∕K → G∕K με τa(gK) = agK, η οποία ονομάζεται αριστερή
μεταφορά (left translation) στον G∕K. Αν a,b ∈ G και La η αριστερή μεταφορά της ομάδας Lie G, τότε έχουμε
ότι
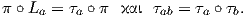
Η απεικόνιση τa είναι μια αμφιδιαφόριση του G∕K, αφού είναι λεία και έχει αντίστροφη τη λεία απεικόνιση
τa-1 = (τa)-1.
Θα δούμε τώρα ότι κάθε μεταβατική δράση μπορεί να περιγραφεί με αυτόν τον τρόπο. Συγκεκριμένα, αν έχουμε
μια μεταβατική δράση μιας ομάδας Lie G σε μια πολλαπλότητα M, τότε η M είναι ένας ομογενής χώρος.
Συγκεκριμένα, ισχύει το εξής:
Θεώρημα 10.2: ΄Εστω G×M → M μια μεταβατική δράση της ομάδας Lie G στη λεία πολλαπλότητα M και έστω
K = Gm η ομάδα ισοτροπίας του σημείου m ∈ M. Τότε
- (α) Η ομάδα ισοτροπίας K είναι μια κλειστή υποομάδα της G.
- (β) Η φυσική απεικόνιση j : G∕K → M με τιμή j(gK) = g⋅m είναι μια G-ισοαναλλοίωτη αμφιδιαφόριση.
- (γ) Η τροχιά G ⋅ m είναι αμφιδιαφορική με τον ομογενή χώρο G∕K.
Για την απόδειξη του θεωρήματος αυτού θα χρειαστούμε κάποια αποτελέσματα, για τις αποδείξεις των οποίων
παραπέμπουμε στο βιβλίο [11].
Πρόταση 10.1: ΄Εστω M,N δύο λείες πολλαπλότητες και π : M → N μια υπεμβάπτιση. ΄Εστω P μια
λεία πολλαπλότητα και F : M → P λεία απεικόνιση, η οποία είναι σταθερή, όταν περιοριστεί στην
υποπολλαπλότητα π-1(p) για κάθε p ∈ N. Τότε υπάρχει μοναδική λεία απεικόνιση 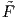 : N → P, τέτοια
ώστε
: N → P, τέτοια
ώστε 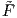 ∘ π = F.
∘ π = F.
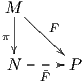
Επειδή η απεικόνιση π στο παραπάνω θεώρημα είναι καταβύθιση, τότε για κάθε p ∈ N το σύνολο π-1(p)
(κανονικό σύνολο στάθμης) είναι μια υποπολλαπλότητα της M διάστασης dimM - dimN.
Θυμίζουμε ότι (βλ. Κεφάλαιο 8), όταν έχουμε δύο G-χώρους V και W, τότε μια απεικόνιση A : V → W
λέγεται ισοαναλλοίωτη, αν για κάθε g ∈ G και υ ∈ V ισχύει A(g ⋅υ) = g ⋅A(υ). Στην περίπτωση που η δράση της
ομάδας G στο χώρο V είναι μεταβατική, τότε η τάξη της απεικόνισης A είναι σταθερή. Συγκεκριμένα ισχύει το
εξής:
Πρόταση 10.2: ΄Εστω M και N δύο λείες πολλαπλότητες και έστω G μια ομάδα Lie. ϒποθέτουμε ότι η
λεία απεικόνιση F : M → N είναι ισοαναλλοίωτη ως προς μια μεταβατική δράση της G στη πολλαπλότητα
M και ως προς οποιαδήποτε δράση της G στη N. Τότε η απεικόνιση F έχει σταθερή τάξη.
Απόδειξη. (του Θεωρήματος 10.2)
(α) Θεωρούμε τη λεία απεικόνιση F : G → M με τιμή F(g) = g⋅m. Τότε παρατηρούμε ότι K = F-1({m}),
δηλαδή η K είναι ένα κλειστό υποσύνολο της G ως αντίστροφη εικόνα του κλειστού συνόλου {m}⊆ M.
Επομένως, σύμφωνα με το Θεώρημα 7.1 η ομάδα ισοτροπίας του σημείου m ∈ M είναι μια κλειστή υποομάδα
Lie της G.
(β) Θα δείξουμε πρώτα ότι η j είναι καλώς ορισμένη. ϒποθέτουμε ότι g1K = g2K, δηλαδή g1-1g2 ∈ K.
Θέτουμε g1-1g2 = k. Τότε είναι:
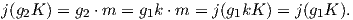
Η τέταρτη ισότητα ισχύει, διότι το k ∈ K. Στη συνέχεια, θα δείξουμε ότι η απεικόνιση j είναι
G-ισοαναλλοίωτη. Πράγματι, είναι
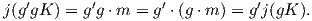
Επίσης, η j είναι λεία, διότι, αν περιορίσουμε την απεικόνιση F στην ομάδα ισοτροπίας K, δηλαδή
F : K → M, τότε είναι σταθερή, αφού για κάθε k ∈ K έχουμε
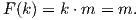
Επομένως, από την Πρόταση 10.1 και επειδή ισχύει ότι π-1(m) = K, θα υπάρχει μοναδική λεία απεικόνιση
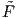 , τέτοια ώστε
, τέτοια ώστε 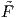 ∘ π = F. Στη συγκεκριμένη περίπτωση η
∘ π = F. Στη συγκεκριμένη περίπτωση η 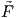 είναι η απεικόνιση j : G∕K → M.
είναι η απεικόνιση j : G∕K → M.
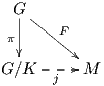
΄Αρα, αφού η j είναι λεία και ισοαναλλοίωτη, από την Πρόταση 10.2 θα έχει σταθερή τάξη. Για να είναι
αμφιδιαφόριση, αρκεί να δείξουμε ότι η j είναι 1 - 1 (άσκηση, βλ. και []). Για το επί, έστω q ∈ M. Τότε
υπάρχει κάποιο στοιχείο g ∈ G, τέτοιο ώστε j(gK) = g⋅m = q. Η τελευταία ισότητα ισχύει, επειδή η δράση
της G στην πολλαπλότητα M είναι μεταβατική. Τέλος, η απεικόνιση j είναι 1-1, αφού, αν j(g1K) = j(g2K),
τότε g1 ⋅ m = g2 ⋅ m, δηλαδή g1-1g2 ⋅ m = m κατ′ επέκταση g1-1g2 ∈ K, οπότε g1K = g2K. Το (γ) είναι
άμεσο. ▄
Από το Θεώρημα 10.2 οδηγούμαστε στον παρακάτω ορισμό:
Ορισμός 10.2: ΄Ενας ομογενής χώρος είναι μια λεία πολλαπλότητα M στην οποία δρά μεταβατικά μια ομάδα
Lie G. Ισοδύναμα, είναι μια λεία πολλαπλότητα της μορφής G∕K, όπου G είναι μια ομάδα Lie και K μια
κλειστή υποομάδα της G.
Αν (M,g) είναι μια πολλαπλότητα Riemann, τότε το σύνολο των ισομετριών I(M) είναι ομάδα
με πράξη τη σύνθεση συναρτήσεων. ΄Ενα θεώρημα των Myers-Steenrod αναφέρει ότι το σύνολο
I(M) είναι ομάδα Lie. Επίσης, η ομάδα I(M) δρά μεταβατικά στην πολλαπλότητα Riemann M ως
εξής:
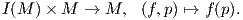
Η μεταβατικότητα σημαίνει ότι, για κάθε δύο σημεία p,q ∈ M υπάρχει μια ισομετρία f ∈ I(M), τέτοια ώστε
f(p) = q. Σε αυτή την περίπτωση η M ονομάζεται omogen�c pollapl�thta Riemann. Επιπλέον, ισχυει το
εξής:
Πρόταση 10.3: Αν η M είναι μια ομογενής πολλαπλότητα Riemann, τότε η ομάδα ισοτροπίας σε κάποιο
σημείο της είναι συμπαγής υποομάδα της I(M). Επιπλέον, η I(M) είναι συμπαγής εάν και μόνο εάν η M
είναι συμπαγής.
Ορισμός 10.3: Μια γεωμετρία Klein είναι ένα ζεύγος (G,K) όπου G είναι μια ομάδα Lie και K μια κλειστη
υποομάδα της G.
Περισσότερα για τις γεωμετρίες Klein και για τη μετάβαση στη γεωμετρία κατά Cartan (μελέτη μιας
συνοχής σε μια κύρια G-δέσμη), παραπέμπουμε στο βιβλίο [14].
Σε μια πολλαπλότητα ενδέχεται να δρούν μεταβατικά περισσότερες από μία ομάδες Lie, έτσι η
ίδια πολλαπλότητα θα είναι αμφιδιαφορική με διαφορετικούς ομογενείς χώρους. Ενα χαρακτηριστικό
παράδειγμα, όπως θα δούμε στη συνέχεια είναι η σφαίρα Sn. Η εύρεση όλων ομάδων Lie, οι οποίες
δρουν μεταβατικά σε μια πολλαπλότητα, αποτελεί ένα δύσκολο πρόβλημα της γεωμετρίας. Επίσης,
πρέπει να αναφέρουμε ότι τα παραδείγματα που θα μελετήσουμε στη συνέχεια είναι όλα παραδείγματα
ομογενών πολλαπλότητων Riemann. Το χαρακτηριστικό στοιχείο σε αυτά τα παραδείγματα είναι
ότι δεν απαιτείται να δρά ολόκληρη η ομάδα των ισομετρίων της πολλαπλότητας, αλλά μια υποομάδα
αυτής.
Παραδείγματα.
1. ΄Εστω G μια ομάδα Lie. Τότε η G εκφράζεται ως ομογενής χώρος με τους εξής δύο τρόπους:
G = G∕{e} = (G × G)∕G. Στην πρώτη περίπτωση η G δρα μεταβατικά στον ευατό της μέσω της αριστερής
μεταφοράς La : G → G, για κάθε a ∈ G. Στη δεύτερη περίπτωση η ομάδα G × G δρά στην G μέσω των
αριστερών και δεξιών μεταφορών. Η ομάδα ισοτροπίας στη δεύτερη περίπτωση είναι η G, η οποία εμφυτεύεται
στην G × G κατά διαγώνιο τρόπο.
2. ΄Εστω G μια ομάδα Lie διάστασης n και έστω 𝔤 η άλγεβρα Lie της G. Θεωρούμε το σύνολο 𝔐 όλων των
εσωτερικών γινομένων της άλγεβρας 𝔤. Θα αποδείξουμε ότι το σύνολο
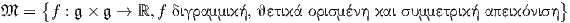
είναι αμφιδιαφορικό με τον ομογενή χώρο GLnℝ∕O(n). Συγκεκριμένα, θα δείξουμε ότι η γενική γραμμική ομάδα
GLnℝ δρά μεταβατικά στο 𝔐. ΄Εστω
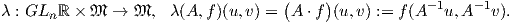 | (10.1) |
Η απεικόνιση (10.1) είναι μια δράση διότι, για κάθε (u,υ) ∈𝔤 ×𝔤 έχουμε
Επίσης, ισχύει ότι Από τις παραπάνω ισότητες προκύπτει ότι λ(AB,f)(u,υ) = λ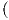 A,λ(B,f)
A,λ(B,f)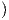 (u,υ). Στη συνέχεια, θα δείξουμε ότι η
δράση είναι μεταβατική, δηλαδή ότι για κάθε δύο εσωτερικά γινόμενα f,f′∈𝔐 υπάρχει πίνακας
g ∈ GLnℝ τέτοιος ώστε g ⋅ f = f′. Πράγματι, έστω f′ : 𝔤 ×𝔤 → ℝ ένα εσωτερικό γινόμενο του οποίου ο
πίνακας D ως προς μια τυχαία βάση του χώρου 𝔤 είναι διαγώνιος και έστω f : 𝔤 ×𝔤 → ℝ ένα άλλο
εσωτερικό γινόμενο. Επειδή η απεικόνιση f είναι συμμετρική, υπάρχει ένας ορθογώνιος πίνακας P τέτοιος
ώστε
(u,υ). Στη συνέχεια, θα δείξουμε ότι η
δράση είναι μεταβατική, δηλαδή ότι για κάθε δύο εσωτερικά γινόμενα f,f′∈𝔐 υπάρχει πίνακας
g ∈ GLnℝ τέτοιος ώστε g ⋅ f = f′. Πράγματι, έστω f′ : 𝔤 ×𝔤 → ℝ ένα εσωτερικό γινόμενο του οποίου ο
πίνακας D ως προς μια τυχαία βάση του χώρου 𝔤 είναι διαγώνιος και έστω f : 𝔤 ×𝔤 → ℝ ένα άλλο
εσωτερικό γινόμενο. Επειδή η απεικόνιση f είναι συμμετρική, υπάρχει ένας ορθογώνιος πίνακας P τέτοιος
ώστε
![- 1 t t -1 - 1
P [f]P = P [f]P = D, ισοδύναμα [f ] = (P ) DP ,](02_chapter_1039x.png)
όπου [f] είναι ο πίνακας της απεικόνισης f ως προς μια βάση του χώρου 𝔤. Επομένως, αν επιλέξουμε τον πίνακα
g = P ∈ O(n) ⊂ GLnℝ, τότε θα έχουμε
![P ⋅D = (P -1)tDP -1 = (Pt)-1DP - 1 = [f].](02_chapter_1040x.png)
Πρέπει να σημειώσουμε ότι η δράση που ορίσαμε μέσω της απεικόνισης (10.1) με μορφή πινάκων, γράφεται ως
A ⋅ [f] = (A-1)t[f]A-1. Τέλος, θα υπολογίσουμε την ομάδα ισοτροπίας του εσωτερικού γινομένου h ∈𝔐 ως
προς το οποίο η βάση της άλγεβρας Lie 𝔤 είναι ορθοκανονική, δηλαδή πρέπει να προσδιορίσουμε το
σύνολο
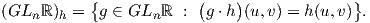
Γνωρίζουμε ότι κάθε πίνακας A ∈ GLnℝ ικανοποιεί την σχέση 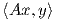 =
= 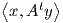 , οπότε αν υποθέσουμε ότι
A ∈ O(n), τότε θα έχουμε
, οπότε αν υποθέσουμε ότι
A ∈ O(n), τότε θα έχουμε 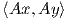 =
= 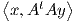 =
= 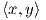 , δηλαδή οι ορθογώνιοι πίνακες αφήνουν αναλλοίωτο
το εσωτερικό γινόμενο. Επομένως, για την ομάδα ισοτροπίας (GLnℝ)h, αν επιλέξουμε g ∈ O(n), τότε θα
είναι
, δηλαδή οι ορθογώνιοι πίνακες αφήνουν αναλλοίωτο
το εσωτερικό γινόμενο. Επομένως, για την ομάδα ισοτροπίας (GLnℝ)h, αν επιλέξουμε g ∈ O(n), τότε θα
είναι
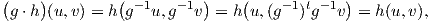
άρα (GLnℝ)h = O(n). Από το Θεώρημα 10.2 η απεικόνιση
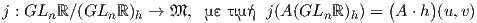
είναι αμφιδιαφόριση, οπότε
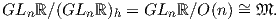 Τέλος, η διάσταση του 𝔐 είναι
Τέλος, η διάσταση του 𝔐 είναι
3. ΄Εστω Sn = 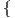 (x1,…,xn+1) ∈ ℝn+1 : ∑
ixi2 = 1
(x1,…,xn+1) ∈ ℝn+1 : ∑
ixi2 = 1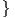 η μοναδιαία σφαίρα στον ℝn+1. Αν
η μοναδιαία σφαίρα στον ℝn+1. Αν 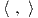 είναι το κανονικό
εσωτερικό γινόμενο του ℝn+1, τότε το σύνολο αυτό εκφράζεται και ως
είναι το κανονικό
εσωτερικό γινόμενο του ℝn+1, τότε το σύνολο αυτό εκφράζεται και ως
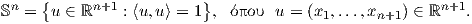
Θα δείξουμε ότι η σφαίρα Sn είναι αμφιδιαφορική με τον ομογενή χώρο O(n + 1)∕O(n). Θα πρέπει δηλαδή να
ορίσουμε μια μεταβατική δράση της ορθογώνιας ομάδας O(n + 1) στην Sn και στη συνέχεια να υπολογίσουμε την
ομάδα ισοτροπίας σε κάποιο σημείο της σφαίρας. Για το πρώτο γνωρίζουμε ότι η GLn+1ℝ δρά με φυσικό τρόπο
στον Ευκλείδειο χώρο ℝn+1 μέσω του πολλαπλασιασμού πινάκων. Στην περίπτωση που A ∈ O(n + 1), δηλαδή
AtA = I, τότε είναι
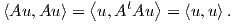
Η πρώτη ισότητα ισχύει, διότι για κάθε πίνακα A ∈ GLnℝn+1 το εσωτερικό γινόμενο ικανοποιεί
την σχέση 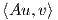 =
= 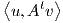 . Η παραπάνω σχέση μας λέει ότι κάθε ορθογώνιος πίνακας διατηρεί
τα μέτρα των διανυσμάτων του ℝn+1. Επομένως, μπορούμε να περιορίσουμε τη φυσική δράση της
ειδικής γραμμικής ομάδας στον ℝn+1, στη δράση της ομάδας O(n + 1) στη μοναδιαία σφαίρα Sn ως
εξής:
. Η παραπάνω σχέση μας λέει ότι κάθε ορθογώνιος πίνακας διατηρεί
τα μέτρα των διανυσμάτων του ℝn+1. Επομένως, μπορούμε να περιορίσουμε τη φυσική δράση της
ειδικής γραμμικής ομάδας στον ℝn+1, στη δράση της ομάδας O(n + 1) στη μοναδιαία σφαίρα Sn ως
εξής:
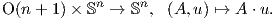
Θα αποδείξουμε ότι η δράση αυτή είναι μεταβατική. Πράγματι, αν e1 =  t ∈ Sn και υ ∈ Sn ένα άλλο
μοναδιαίο διάνυσμα, αναζητάμε πίνακα A ∈ O(n + 1) τέτοιον ώστε Ae1 = υ. Αρκεί να επιλέξουμε A = (υ υ1…υn),
όπου {υ,υ1,…,υn} είναι μια ορθοκανονική βάση του ℝn+1. Στη συνέχεια, θα υπολογίσουμε την ομάδα ισοτροπίας
του σημείου e1 ∈ Sn, δηλαδή θα πρέπει να βρούμε το σύνολο
t ∈ Sn και υ ∈ Sn ένα άλλο
μοναδιαίο διάνυσμα, αναζητάμε πίνακα A ∈ O(n + 1) τέτοιον ώστε Ae1 = υ. Αρκεί να επιλέξουμε A = (υ υ1…υn),
όπου {υ,υ1,…,υn} είναι μια ορθοκανονική βάση του ℝn+1. Στη συνέχεια, θα υπολογίσουμε την ομάδα ισοτροπίας
του σημείου e1 ∈ Sn, δηλαδή θα πρέπει να βρούμε το σύνολο
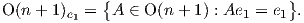
Αν επιλέξουμε A = 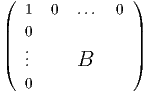 , τότε Ae1 = e1. Θα πρέπει όμως ο A να ανήκει στην ορθογώνια ομάδα
O(n + 1), δηλαδή detA = ±1, άρα αρκεί να πάρουμε B ∈ O(n). Επομένως, η ομάδα ισοτροπίας θα περιέχει πίνακες
της παραπάνω μορφής. Λόγω της εμβύθισης
, τότε Ae1 = e1. Θα πρέπει όμως ο A να ανήκει στην ορθογώνια ομάδα
O(n + 1), δηλαδή detA = ±1, άρα αρκεί να πάρουμε B ∈ O(n). Επομένως, η ομάδα ισοτροπίας θα περιέχει πίνακες
της παραπάνω μορφής. Λόγω της εμβύθισης
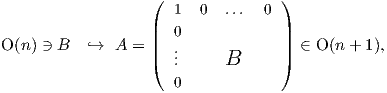
μπορούμε να ταυτίσουμε όλους τους πίνακες της ορθογώνιας ομάδας O(n) με πίνακες της O(n + 1), οπότε η ομάδα
ισοτροπίας του σημείου e1 ∈ Sn είναι
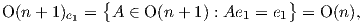
δηλαδή μια κλειστή υποομάδα της O(n + 1). Σύμφωνα με το Θεώρημα 10.2 η απεικόνιση
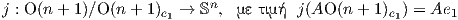
είναι αμφιδιαφόριση, επομένως
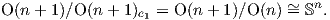
Στην περίπτωση που θεωρήσουμε την δράση της ειδικής ορθογώνιας ομάδας SO(n + 1) στη σφαίρα Sn τότε θα
έχουμε
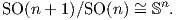 Σε αυτή την περίπτωση το μόνο που θα αλλάξει είναι ότι η ορθοκανονική βάση {υ,υ1,
Σε αυτή την περίπτωση το μόνο που θα αλλάξει είναι ότι η ορθοκανονική βάση {υ,υ1, ,υn} του
ℝn+1 είναι προσανατολισμένη, δηλαδή ο ορθογώνιος πίνακας A ικανοποιεί την σχέση detA = 1, οπότε
A ∈ SO(n).
,υn} του
ℝn+1 είναι προσανατολισμένη, δηλαδή ο ορθογώνιος πίνακας A ικανοποιεί την σχέση detA = 1, οπότε
A ∈ SO(n).
4. Το μιγαδικό ανάλογο του προηγούμενου παραδείγματος προέρχεται από τη φυσική δράση της GLn+1ℂ στον
μιγαδικό χώρο ℂn+1. Σε αυτή την περίπτωση θα είναι
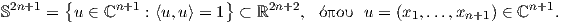
Το εσωτερικό γινόμενο ορίζεται ως 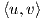 = ∑
i=1uiυi. Θα δείξουμε ότι η σφαίρα είναι αμφιδιαφορική με τον
ομογενή χώρο U(n + 1)∕U(n). Ενας ερμητιανός πίνακας A ∈ U(n + 1) διατηρεί τα μέτρα των διανυσμάτων του
χώρου ℂn+1. Πράγματι,
= ∑
i=1uiυi. Θα δείξουμε ότι η σφαίρα είναι αμφιδιαφορική με τον
ομογενή χώρο U(n + 1)∕U(n). Ενας ερμητιανός πίνακας A ∈ U(n + 1) διατηρεί τα μέτρα των διανυσμάτων του
χώρου ℂn+1. Πράγματι,
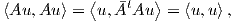
όπου η πρώτη ισότητα ισχύει από την ιδιότητα του εσωτερικού γινομένου στον ℂn+1, ενώ στη δεύτερη ισότητα
χρησιμοποιήσαμε το γεγονός ότι A ∈ U(n + 1), δηλαδή AtA = I. Συνεπώς, περιορίζοντας τη δράση της GLn+1ℂ
στη δράση της μοναδιαίας ομάδας U(n + 1) στην σφαίρα Sn, δηλαδή
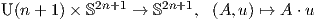
και εργαζόμενοι όπως στο Παράδειγμα 3, προκύπτει ότι η δράση είναι μεταβατική. Επιπλέον, η ομάδα ισοτροπίας
σε κάποιο σημείο της σφαίρας είναι η κλειστή υποομάδα U(n) της U(n + 1). ΄Αρα η μοναδιαία σφαίρα S2n+1 θα είναι
αμφιδιαφορική με τον ομογενή χώρο U(n + 1)∕U(n). Τέλος, λαμβάνοντας υπόψη τον προσανατολισμό
των βάσεων στον ℂn+1, η S2n+1 θα είναι αμφιδιαφορική με τον ομογενή χώρο SU(n + 1)∕SU(n),
άρα
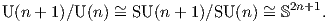
Επίσης, υπάρχει και το υπερμιγαδικό ανάλογο του παραδείγματος αυτού, δηλαδή
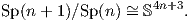
Μάλιστα, από τα παραπάνω προκύπτει ότι S0 O(1), S1
O(1), S1 U(1)
U(1) SO(2) και S3
SO(2) και S3 SU(2)
SU(2) Sp(1) (και
όπως έχουμε αναφέρει στο Κεφάλαιο 7 αυτές είναι οι μόνες σφαίρες που επιδέχονται δομή ομάδας
Lie).
Sp(1) (και
όπως έχουμε αναφέρει στο Κεφάλαιο 7 αυτές είναι οι μόνες σφαίρες που επιδέχονται δομή ομάδας
Lie).
5. Ο πραγματικός προβολικός χώρος ℝPn είναι αμφιδιαφορικός με τον ομογενή χώρο
SO(n + 1)∕O(n) O(n + 1)∕O(n) × O(1). Για την πρώτη περίπτωση θεωρούμε τη δράση της SO(n + 1) στον
ℝn+1\{0} μέσω του πολλαπλασιασμού πινάκων και την περιορίζουμε στον υπόχωρο ℝPn ⊂ ℝn+1\{0},
δηλαδή
O(n + 1)∕O(n) × O(1). Για την πρώτη περίπτωση θεωρούμε τη δράση της SO(n + 1) στον
ℝn+1\{0} μέσω του πολλαπλασιασμού πινάκων και την περιορίζουμε στον υπόχωρο ℝPn ⊂ ℝn+1\{0},
δηλαδή
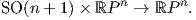
Η δράση αυτή είναι μεταβατική, ενώ η ομάδα ισοτροπίας είναι η O(n), η οποία είναι μια κλειστή υποομάδα της
SO(n + 1), οπότε ℝPn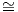 SO(n + 1)∕O(n). Στη δεύτερη περίπτωση θεωρούμε τη λεία δράση της ορθογώνιας
ομάδας O(n + 1) στον ℝPn. Αποδεικνύεται ότι η δράση είναι μεταβατική, ενώ η ομάδα ισοτροπίας σε κάποιο σημείο
του προβολικού χώρου αποτελείται από τους πίνακες
SO(n + 1)∕O(n). Στη δεύτερη περίπτωση θεωρούμε τη λεία δράση της ορθογώνιας
ομάδας O(n + 1) στον ℝPn. Αποδεικνύεται ότι η δράση είναι μεταβατική, ενώ η ομάδα ισοτροπίας σε κάποιο σημείο
του προβολικού χώρου αποτελείται από τους πίνακες
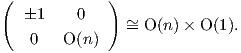
Θα ισχύουν τα ίδια και για τον μιγαδικό προβολικό χώρο ℂPn, ο οποίος θα είναι αμφιδιαφορικός με τους
ομογενείς χώρους SU(n + 1)∕U(n) = U(n + 1)∕U(n) × U(1).
6. Οι πολλαπλότητες Grassmann Grkℝn.
Μία πολλαπλότητα Grassmann αποτελείται από το σύνολο όλων των k-διάστατων υποχώρων του ℝn.
Αποδεικνύεται ότι το σύνολο αυτο έχει δομή μιας λείας πολλαπλότητας (βλ. [4], [13]). ΄Ενας k-διάστατος
υπόχωρος W ∈ Grkℝn είναι δυνατόν να παράγεται από k ορθοκανονικά διανύσματα του ℝn, δηλαδή
W = span{x1,…,xk}≡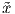 , όπου k ≤ n. Θεωρώντας τα xi, i = 1,…,k ως διανύσματα-στήλη, μπορούμε να
γράψουμε το
, όπου k ≤ n. Θεωρώντας τα xi, i = 1,…,k ως διανύσματα-στήλη, μπορούμε να
γράψουμε το 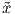 ως έναν n × k πίνακα ως
ως έναν n × k πίνακα ως 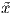 = (x1,…,xk). Θα δείξουμε ότι η πολλαπλότητα Grkℝn είναι
αμφιδιαφορική με τον ομογενή χώρο
= (x1,…,xk). Θα δείξουμε ότι η πολλαπλότητα Grkℝn είναι
αμφιδιαφορική με τον ομογενή χώρο
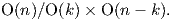
Από το Παράδειγμα 2 γνωρίζουμε ότι ένας ορθογώνιος πίνακας A ∈ O(n) διατηρεί τα μέτρα των διανυσμάτων του
ℝn, οπότε το σύνολο
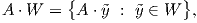
(όπου A⋅ỹ είναι πολλαπλασιασμός πινάκων), θα είναι ένας k-διάστατος υπόχωρος του ℝn. Επομένως, η δράση της
ορθογώνιας ομάδας O(n) στην πολλαπλότητα Grassmann μπορεί να οριστεί ως εξής:
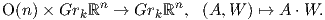
Θα αποδείξουμε ότι η δράση είναι μεταβατική. ΄Εστω V ένας k-διάστατος υπόχωρος του ℝn, ο οποίος παράγεται
από τα πρώτα k διανύσματα της κανονικής βάσης του ℝn, ας τη συμβολίζουμε με B = {e1,…,ek,ek+1,…,en} και
έστω W ∈ Grkℝn ένας άλλος k-διάστατος υπόχωρος, ο οποίος παράγεται από k ορθοκανονικά διανύσματα
u1,…,uk του ℝn. Από την γραμμική άλγεβρα γνωρίζουμε ότι μπορούμε να βρούμε διανύσματα uk+1,…,un τέτοια
ώστε το σύνολο B′ = {u1,…,uk,uk+1,…,un} να είναι μια ορθοκανονική βάση του ℝn. Επίσης, γνωρίζουμε ότι ο
πίνακας μετάβασης από μια ορθοκανονική βάση σε μία άλλη είναι ορθογώνιος, οπότε στην περίπτωσή μας αρκεί να
πάρουμε τον πίνακα μετάβασης από τη βάση B′ στην B, δηλαδή A = (u1,…,un), όπου τα ui, i = 1,…,n είναι τα
διανύσματα-στήλες του ℝn. Τότε θα είναι Aei = ui, i = 1,…,n. Για παράδειγμα, αν υποθέσουμε ότι κάθε
ui εκφράζεται ως ui = 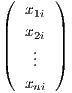 , τότε A =
, τότε A =  . Οπότε, για παράδειγμα
έχουμε:
. Οπότε, για παράδειγμα
έχουμε:
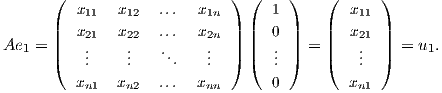
Τέλος, αν θέσουμε ẽ = (e1…,ek) και ũ = (u1,…,uk) ως τους n × k πίνακες που αποτελούνται από τα
διανύσματα-στήλες του ℝn τα οποία παράγουν τους υποχώρους V και W αντίστοιχα, τότε θα είναι
Aẽ = (u1,…,uk) = ũ, δηλαδή A⋅V = W. Επομένως, η δράση είναι μεταβατική. Η ομάδα ισοτροπίας του υπόχωρου
V είναι το σύνολο το οποίο περιέχει πίνακες της μορφής
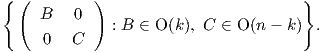
Αυτό είναι μια κλειστή υποομάδα της O(n) και είναι ισόμορφο με την ομάδα O(k) × O(n - k). Επομένως, η
απεικόνιση
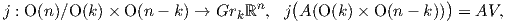
είναι αμφιδιαφόριση, άρα Grkℝn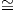 O(n)∕O(k) × O(n - k). Στην περίπτωση που λάβουμε υπόψην τον
προσανατολισμό των βάσεων και διαλέξουμε προσανατολισμένους υπόχωρους του Ευκλείδειου χώρου, τότε
οδηγούμαστε σε μια μεταβατική δράση της SO(n) στην πολλαπλότητα Grassmann, οπότε με παρόμοιο σκεπτικό η
πολλαπλότητα Grkℝn είναι αμφιδιαφορική με τον ομογενή χώρο SO(n)∕SO(k) × SO(n - k). Τέλος, αξίζει να
σημειώσουμε ότι η διάσταση της πολλαπλότητας Grassmann είναι:
O(n)∕O(k) × O(n - k). Στην περίπτωση που λάβουμε υπόψην τον
προσανατολισμό των βάσεων και διαλέξουμε προσανατολισμένους υπόχωρους του Ευκλείδειου χώρου, τότε
οδηγούμαστε σε μια μεταβατική δράση της SO(n) στην πολλαπλότητα Grassmann, οπότε με παρόμοιο σκεπτικό η
πολλαπλότητα Grkℝn είναι αμφιδιαφορική με τον ομογενή χώρο SO(n)∕SO(k) × SO(n - k). Τέλος, αξίζει να
σημειώσουμε ότι η διάσταση της πολλαπλότητας Grassmann είναι:
Παρόμοια, ορίζονται και οι μιγαδικές πολλαπλότητες Grassmann
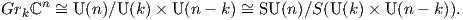
7. Οι πολλαπλότητες Stiefel V kℝn.
Οι πολλαπλότητες Stiefel V kℝn είναι το σύνολο όλων των ορθοκανονικών k-διάστατων πλαισίων
(orthonormal k-frames) ũ = (u1,…,uk), k ≤ n, όπου ui, i = 1,…,k είναι ορθοκανονικά διανύσματα του ℝn.
Αποδεικνύεται ότι το σύνολο αυτό έχει δομή λείας πολλαπλότητας (βλ. [4], [13]). ΄Οπως και στο προηγούμενο
παράδειγμα, αν θεωρήσουμε τα διανύσματα του ℝn ως διανύσματα-στήλες, τότε κάθε τέτοιο πλαίσιο μπορεί
να εκφραστεί ως ένας n × k πίνακας. Θα αποδείξουμε ότι ο χώρος V kℝn είναι αμφιδιαφορικός με
τον ομογενή χώρο O(n)∕O(n - k). Πρώτα θα ορίσουμε μια δράση της ορθογώνιας ομάδας στην
πολλαπλότητα V kℝn. Επειδή η ομάδα O(n) όταν δράσει στον χώρο ℝn διατηρεί τα μήκη των διανυσμάτων,
θα έχουμε ότι το A ⋅ũ (όπου ũ είναι n × k πίνακας), είναι ένα ορθοκανονικό πλαίσιο, αφού ισχύει
ότι
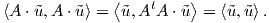
Συνεπώς, ορίζουμε την δράση της O(n) στην πολλαπλότητα V kℝn, ως εξής:
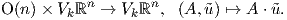
Θα αποδείξουμε ότι η δράση αυτή είναι μεταβατική. ΄Εστω ένα τυχαίο στοιχείο ũ = (u1,…,uk) ∈ V kℝn. Τότε ως
γνωστόν μπορούμε να βρούμε διανύσματα uk+1,…,un του ℝn, έτσι ώστε το σύνολο {u1,…,uk,uk+1,…,un} να είναι
μια ορθοκανονική βάση του ℝn. Θεωρώντας κάθε ui,(i = 1,…,n) ως διάνυσμα-στήλη, ορίζουμε τον n×n πίνακα
A = (u1 … un). Προφανώς ο πίνακας A ανήκει στην O(n) και ικανοποιεί τη σχέση
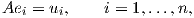
όπου {e1 = (1,…,0),…,en = (0,…,1)} είναι η κανονική βάση του ℝn. ΄Αρα, αν θέσουμε ẽ = (e1,…,ek), θα έχουμε
A ⋅ẽ = ũ, επομένως η δράση είναι μεταβατική. Η ομάδα ισοτροπίας του ẽ = (e1,…,ek) είναι το σύνολο το οποίο
αποτελείται από πίνακες της μορφής
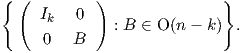
Το σύνολο αυτό αποτελεί κλειστή υποομάδα της O(n) και είναι ισόμορφο με την ομάδα O(n - k). ΄Αρα η
απεικόνιση
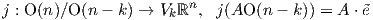
είναι μια αμφιδιαφόριση, οπότε V kℝn O(n)∕O(n - k). Στην περίπτωση που επιλέξουμε A ∈ SO(n), τότε με
παρόμοιο τρόπο προκύπτει ότι
O(n)∕O(n - k). Στην περίπτωση που επιλέξουμε A ∈ SO(n), τότε με
παρόμοιο τρόπο προκύπτει ότι
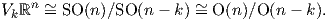
Τέλος, η διάσταση της πολλαπλότητας V kℝn είναι:
Σημειώνουμε ότι ανάλογα ορίζονται οι μιγαδικές πολλαπλότητες Stiefel. Στην περίπτωση αυτή έχουμε
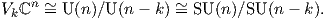
10.3 Αναγωγικοί ομογενείς χώροι
Προκειμένου να μελετήσουμε τη γεωμετρία ενός ομογενούς χώρου G∕K, θα επιθυμούσαμε μια αποτελεσματική
περιγραφή του εφαπτόμενου χώρου To(G∕K), όπου o = eK = K είναι το ουδέτερο σύμπλοκο του χώρου
πηλίκο G∕K. Μια τέτοια περίπτωση συμβαίνει όταν ο ομογενής χώρος είναι αναγωγικός. Επειδή η
κανονική προβολή π : G → G∕K είναι υπεμβάπτιση, τότε To(G∕K)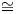 𝔤∕𝔨, όπου με o συμβολίζουμε το
ουδέτερο σύμπλοκο eK = K του ομογενούς χώρου G∕K. Στους αναγωγικούς ομογενείς χώρους,
που θα παρουσιάσουμε στη συνέχεια, θα δούμε ότι ο πρηγούμενος ισομορφισμός γίνεται πολύ πιο
απλός.
𝔤∕𝔨, όπου με o συμβολίζουμε το
ουδέτερο σύμπλοκο eK = K του ομογενούς χώρου G∕K. Στους αναγωγικούς ομογενείς χώρους,
που θα παρουσιάσουμε στη συνέχεια, θα δούμε ότι ο πρηγούμενος ισομορφισμός γίνεται πολύ πιο
απλός.
Ορισμός 10.4: ΄Ενας ομογενής χώρος ονομάζεται αναγωγικός (reductive), εάν υπάρχει ένας υπόχωρος 𝔪
της άλγεβρας Lie 𝔤, τέτοιος ώστε 𝔤 = 𝔨 ⊕𝔪 με την ιδιότητα Ad(k)𝔪 ⊂ 𝔪 για κάθε k ∈ K, δηλαδή ο
υπόχωρος 𝔪 είναι Ad(K)-αναλλοίωτος.
Αν ισχύει Ad(k)𝔪 ⊂𝔪, τότε προκύπτει ότι [𝔨,𝔪] ⊂𝔪. Το αντίστροφο ισχύει μόνο στην περίπτωση που η
ομάδα K είναι συνεκτική.
Μια περίπτωση όπου ο ομογενής χώρος G∕K είναι αναγωγικός, είναι αυτή κατά την οποία η ομάδα Lie G
είναι συμπαγής και ημιαπλή. Πράγματι, τότε αρκεί να πάρουμε ως υπόχωρο 𝔪 = 𝔨⊥, το ορθογώνιο
συμπλήρωμα της 𝔨 στην άλγεβρα Lie 𝔤 ως πρός το -B, την αρνητική τιμή της μορφής Killing της 𝔤
(γενικότερα μπορούμε να πάρουμε ένα οποιοδήποτε Ad(K)-αναλλοίωτο εσωτερικό γινόμενο της 𝔤).
΄Αλλες περιπτώσεις κατά τις οποίες ένας ομογενής χώρος G∕K αναγωγικός, είναι οι εξής (βλ. [10]):
- Η K να είναι συμπαγής.
- Η K να είναι συνεκτική και ημιαπλή.
- Η K να είναι διακριτή υποομάδα της G. Τότε έχουμε την τετριμμένη περίπτωση 𝔨 = 0 και 𝔪 = 𝔤.
Πρόταση 10.4: ΄Εστω G∕K ένας αναγωγικός ομογενής χώρος και 𝔤, 𝔨 οι αντίστοιχες άλγεβρες Lie.
Τότε το ορθογώνιο συμπλήρωμα 𝔨⊥ της 𝔨 ως προς ένα Ad(K)-αναλλοίωτο εσωτερικό γινόμενο είναι ένας
Ad(K)-αναλλοίωτος υπόχωρος της άλγεβρας Lie 𝔤.
Απόδειξη. Θα δείξουμε ότι για κάθε k ∈ K είναι Ad(k)𝔨⊥ = {Ad(k)X : X ∈𝔨⊥}⊆𝔨⊥. ΄Εστω X ∈𝔨⊥ και Y ∈𝔨,
οπότε 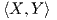 = 0. Για κάθε h ∈ K θα έχουμε:
= 0. Για κάθε h ∈ K θα έχουμε:
Επομένως, αφού για κάθε
k ∈ K ισχύει
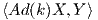 = 0,
= 0, αυτό σημαίνει ότι το
Ad(k)X είναι ορθογώνιο σε κάθε
Y ∈𝔨, άρα είναι ορθογώνιο στον υπόχωρο
𝔨. Οπότε για κάθε
X ∈𝔨⊥ και
k ∈ K, έχουμε
Ad(h)X ∈𝔨⊥, δηλαδή ο
υπόχωρος
𝔨⊥ είναι
Ad(K)-αναλλοίωτος. ▄
Θεωρούμε τώρα την κανονική προβολή π : G → G∕K, π(g) = gK και υποθέτουμε ότι ο G∕K είναι ένας
αναγωγικός ομογενής χώρος. Τότε το διαφορικό (dπ)e : 𝔤 → To(G∕K) επάγει έναν γραμμικό ισομορφισμό μεταξύ
του 𝔪 και To(G∕K). Για να το αποδείξουμε, χρειαζόμαστε την παρακάτω πρόταση.
Πρόταση 10.5: ΄Εστω M,N λείες πολλαπλότητες, f : M → N λεία απεικόνιση, y ∈ N μια κανονική τιμή της
f και Z = f-1(y) η υποπολλαπλότητα της M διάστασης dimM - dimN. Τότε ο πυρήνας του διαφορικού
dfx : TxM → TyN σε κάθε σημείο x ∈ Z ισούται με τον εφαπτόμενο χώρο της υποπολλαπλότητας Z,
δηλαδή Kerdfx = TxZ.
Απόδειξη. Η απεικόνιση f είναι σταθερή στο σύνολο Z = f-1(y) ⊂ M, οπότε το διαφορικό της θα είναι μηδέν
στον TxZ ⊂ TxM, για κάθε x ∈ Z. ΄Αρα ο TxZ είναι υπόχωρος του Kerdfx = {A ∈ TxM : dfxA = 0}.
Επίσης, έχουμε ότι για κάθε σημείο x ∈ Z η απεικόνιση dfx : TxM → TyN είναι επί. Επομένως,
Η τέταρτη ισότητα ισχύει από υπόθεση. Οπότε, αφού
dimKerdfx = dim(Z) = dim(KerTxZ) και
επειδή ο
TxZ είναι υπόχωρος του πυρήνα
Kerdfx, θα έχουμε το ζητούμενο, δηλαδή
Kerdfx = TxZ.
▄
Ο ισομορφισμός 𝔪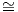 To(G∕K) προκύπτει τώρα ως εξής: Η π είναι υπεμβάπτιση οπότε το διαφορικό της είναι
επί σε κάθε σημείο της G, άρα και στο ουδέτερο e. Το σημείο o = eK = K ∈ G∕K είναι μια κανονική τιμή της
προβολής π και π-1(o) = K. Τότε, ο πυρήνας του διαφορικού (dπ)e, σύμφωνα με την προηγούμενη πρόταση, θα
είναι ο εφαπτόμενος χώρος της υποπολλαπλότητας K = π-1(o), δηλαδή Ker(dπ)e = TeK = 𝔨. Συνεπώς
έχουμε
To(G∕K) προκύπτει τώρα ως εξής: Η π είναι υπεμβάπτιση οπότε το διαφορικό της είναι
επί σε κάθε σημείο της G, άρα και στο ουδέτερο e. Το σημείο o = eK = K ∈ G∕K είναι μια κανονική τιμή της
προβολής π και π-1(o) = K. Τότε, ο πυρήνας του διαφορικού (dπ)e, σύμφωνα με την προηγούμενη πρόταση, θα
είναι ο εφαπτόμενος χώρος της υποπολλαπλότητας K = π-1(o), δηλαδή Ker(dπ)e = TeK = 𝔨. Συνεπώς
έχουμε
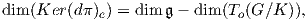
και επειδή ο ομογενής χώρος G∕K είναι αναγωγικός, δηλαδή 𝔤 = 𝔨 ⊕𝔪, η παραπάνω ισότητα γράφεται
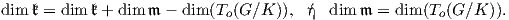
Επειδή το διαφορικό (dπ)e είναι μια γραμμική και επί απεικόνιση, παίρνουμε τον κανονικό ισομορφισμό
𝔪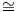 To(G∕K). Στην περίπτωση που ο ομογενής χώρος G∕K δεν είναι αναγωγικός, ο παραπάνω ισομορφισμός είναι
μόνο μεταξύ των 𝔤∕𝔨 και To(G∕K).
To(G∕K). Στην περίπτωση που ο ομογενής χώρος G∕K δεν είναι αναγωγικός, ο παραπάνω ισομορφισμός είναι
μόνο μεταξύ των 𝔤∕𝔨 και To(G∕K).
΄Εστω G∕K ένας αναγωγικός ομογενής χώρος και 𝔤 = 𝔨 ⊕𝔪 η αντίστοιχη αναγωγική ανάλυση της
άλγεβρας Lie 𝔤. Αν X ∈𝔤 και exptX η αντίστοιχη μονοπαραμετρική υποομάδα που παράγεται από το X
τότε
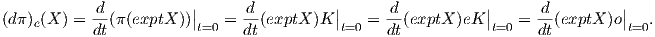 Το
εφαπτόμενο διάνυσμα (dπ)e(X) ∈ To(G∕K) θα το συμβολίζουμε με Xo*, δηλαδή
Το
εφαπτόμενο διάνυσμα (dπ)e(X) ∈ To(G∕K) θα το συμβολίζουμε με Xo*, δηλαδή
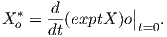 Αν
𝔤 = 𝔨 ⊕𝔪 τότε για κάθε X ∈𝔤 γράφουμε X = X𝔨 + X𝔪. Επειδή Ker(dπ)e = 𝔨 τότε θα είναι (dπ)e(X𝔨) = 0 για
κάθε X𝔨 ∈𝔨, οπότε
Αν
𝔤 = 𝔨 ⊕𝔪 τότε για κάθε X ∈𝔤 γράφουμε X = X𝔨 + X𝔪. Επειδή Ker(dπ)e = 𝔨 τότε θα είναι (dπ)e(X𝔨) = 0 για
κάθε X𝔨 ∈𝔨, οπότε
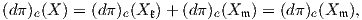
δηλαδή (dπ)e(X) = (dπ)e(X𝔪) = Xo*. Γενικά, για κάθε αριστερά αναλλοίωτο διανυσματικό πεδίο X ∈𝔤 ορίζουμε
το διανυσματικό πεδίο X* στον ομογενή χώρο G∕K μέσω της σχέσης
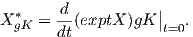
Για την καλύτερη κατανόηση των παραπάνω εννοιών θα δώσουμε στη συνέχεια, ένα παράδειγμα υπολογισμού της
αναγωγικής ανάλυσης ενός ομογενούς χώρου.
Παράδειγμα. Θα βρούμε την αναγωγική ανάλυση του ομογενούς χώρου SU(3)∕S(U(1) × U(1) × U(1)) = SU(3)∕T,
όπου T ο μεγιστικός δακτύλιος της SU(3). Ο συγκεκριμένος χώρος ονομάζεται πολλαπλότητα σημαιών (flag manifold)
και
έχει διάσταση dimSU(3) - dimT = 32 - 1 - (3 - 1) = 6. Η άλγεβρα Lie της SU(3) είναι το σύνολο
Η διάσταση της SU(3) είναι 8. Αντίστοιχα, για την άλγεβρα Lie της S(U(1) × U(1) × U(1)) έχουμε
Προφανώς η διάσταση της S(U(1)×U(1)×U(1)) είναι 2. Για την εύρεση ενός Ad(S(U(1)×U(1)×U(1)))-αναλλοίωτου
υποχώρου 𝔪, έτσι ώστε να ισχύει
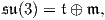
θα χρησιμοποιήσουμε τη μορφή Killing της SU(3), η οποία δίνεται από την σχέση B(X,Y ) = 6tr(XY ). Επειδή η
SU(3) είναι συμπαγής και ηπιαπλή, ένα εσωτερικό γινόμενο που ορίζεται στην άλγεβρα Lie 𝔰𝔲(3) είναι το
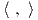 = -B( , ), οπότε ως προς αυτό το γινόμενο θα έχουμε
= -B( , ), οπότε ως προς αυτό το γινόμενο θα έχουμε
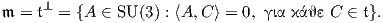
Για να προσδιορίσουμε το παραπάνω σύνολο παίρνουμε για C τους πίνακες e1,e2 και για A τον πίνακα που
δίνεται από την έκφραση (10.2) και θα πρέπει 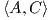 = -tr(AC) = 0 για κάθε C ∈{e1,e2}. ΄Εχουμε
= -tr(AC) = 0 για κάθε C ∈{e1,e2}. ΄Εχουμε
άρα 0 = 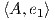 = -tr(Ae1) = -a + c, δηλαδή a = c. Τέλος, με όμοιο τρόπο είναι Επομένως 0 =
= -tr(Ae1) = -a + c, δηλαδή a = c. Τέλος, με όμοιο τρόπο είναι Επομένως 0 = 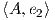 = -tr(Ae2) = -b + c, δηλαδή b = c. ΄Ομως a + b + c = 0, οπότε c = 0 δηλαδή a = b = 0.
΄Αρα ο υπόχωρος 𝔪 θα έχει τη μορφή Επίσης, βλέπουμε ότι dim𝔪 = 6, άρα 𝔰𝔲(3) = 𝔱 ⊕𝔪. Τέλος, θα πρέπει να δείξουμε ότι υπόχωρος 𝔪 είναι
Ad(S(U(1) × U(1) × U(1)))-αναλλοίωτος. Επειδή η ομάδα U(1) είναι συνεκτική, το ίδιο ισχύει και το καρτεσιανό
γινόμενο U(1) × U(1) × U(1), άρα η S(U(1) × U(1) × U(1)) θα είναι συνεκτική, οπότε αρκεί να δείξουμε
ότι
= -tr(Ae2) = -b + c, δηλαδή b = c. ΄Ομως a + b + c = 0, οπότε c = 0 δηλαδή a = b = 0.
΄Αρα ο υπόχωρος 𝔪 θα έχει τη μορφή Επίσης, βλέπουμε ότι dim𝔪 = 6, άρα 𝔰𝔲(3) = 𝔱 ⊕𝔪. Τέλος, θα πρέπει να δείξουμε ότι υπόχωρος 𝔪 είναι
Ad(S(U(1) × U(1) × U(1)))-αναλλοίωτος. Επειδή η ομάδα U(1) είναι συνεκτική, το ίδιο ισχύει και το καρτεσιανό
γινόμενο U(1) × U(1) × U(1), άρα η S(U(1) × U(1) × U(1)) θα είναι συνεκτική, οπότε αρκεί να δείξουμε
ότι
![[𝔱,𝔪] ⊂ 𝔪, ή ισοδύ να μα [X, Y] ∈ 𝔪 για κάθε X ∈ 𝔱, Y ∈ 𝔪.](02_chapter_10131x.png)
Παίρνουμε για X και Y τους πίνακες
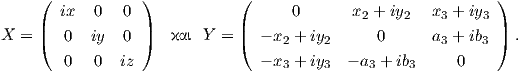
Τότε μετά από πράξεις θα καταλήξουμε στο εξής:
![( )
| 0 A + iB Γ + iΔ |
[X, Y] = XY - YX = ( - A + iB 0 K + iΛ ) , δηλα δή [X,Y ] ∈ 𝔪.
- Γ + iΔ - K + iΛ 0](02_chapter_10133x.png)
Συνεπώς, έχουμε βρεί μια αναγωγική ανάλυση του ομογενούς χώρου SU(3)∕S(U(1) × U(1) × U(1)) = SU(3)∕T.
10.4 Η ισοτροπική αναπαράσταση
Σε προηγούμενο κεφάλαιο ορίσαμε τη συζυγή αναπαράσταση Ad ≡ AdG : G → Aut(𝔤) μιας ομάδας Lie G ως το
διαφορικό του εσωτερικού αυτομορφισμού Ig : G → G, με Ig(x) = gxg-1 στο ουδέτερο σημείο της ομάδας
G, δηλαδή Ad(g) ≡ AdG(g) = (dIg)e. Θα γενικεύσουμε τώρα αυτήν την έννοια για τους ομογενείς
χώρους.
΄Εστω M μια λεία πολλαπλότητα και G μια ομάδα Lie η οποία δρά από τα αριστερά στην M μέσω της
απεικόνισης a : G × M → M, (g,m) gm. Θεωρούμε την αμφιδιαφόριση ag : M → M και έστω
H = {g ∈ G : gp = p}⊆ G η ομάδα ισοτροπίας του σημείου p ∈ M. Τότε η ισοτροπική αναπαράσταση (isotropy
representation) της H στο p ορίζεται ως
gm. Θεωρούμε την αμφιδιαφόριση ag : M → M και έστω
H = {g ∈ G : gp = p}⊆ G η ομάδα ισοτροπίας του σημείου p ∈ M. Τότε η ισοτροπική αναπαράσταση (isotropy
representation) της H στο p ορίζεται ως
Στην παραπάνω σχέση το διαφορικό της απεικόνισης ag αποτελεί έναν αυτομορφισμό του εφαπτόμενου χώρου
TpM, διότι για κάθε h ∈ H έχουμε ag(h) = gh = h. Στη συνέχεια θα ορίσουμε την ισοτροπική αναπαράσταση του
ομογενούς χώρου M = G∕K, όπου G μια ομάδα Lie και K η ομάδα ισοτροπίας σε κάποιο σημείο της M.
Θυμίζουμε ότι για κάθε α ∈ G η απεικόνιση
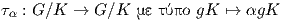
είναι μια αμφιδιαφόριση. Επίσης, παρατηρούμε ότι για κάθε k ∈ K έχουμε τk(o) = τk(eK) = keK = ekK = eK = o.
Συνεπώς, για κάθε k ∈ K το διαφορικό της απεικόνισης τk αποτελεί έναν αυτομορφισμό του χώρου
To(G∕K) 𝔤∕𝔨. Επομένως, για την ισοτροπική αναπαράσταση δίνουμε τον εξής ορισμό.
𝔤∕𝔨. Επομένως, για την ισοτροπική αναπαράσταση δίνουμε τον εξής ορισμό.
Ορισμός 10.5: Η ισοτροπική αναπαράσταση (isotropy representation) ενός ομογενούς χώρου G∕K είναι ο
ομομορφισμός
Δηλαδή για κάθε
X ∈ To(G∕K) έχουμε
AdG∕K(k)(X) = (dτk)o(X).
Στην περίπτωση που ο ομογενής χώρος G∕K είναι αναγωγικός, δηλαδή υπάρχει ένας AdG(K)-αναλλοίωτος
υπόχωρος 𝔪 τέτοιος ώστε 𝔤 = 𝔨 ⊕𝔪, τότε είναι δυνατόν να δοθεί μια ακριβής σχέση ανάμεσα στην ισοτροπική
αναπαράσταση του ομογενούς χώρου G∕K και της συζυγούς αναπαράστασης AdG της ομάδας Lie G. Αρχικά θα
συνοψίσουμε τις αναπαραστάσεις που έχουμε ορίσει μέχρι στιγμής
Περιορίζοντας τη συζυγή αναπαράσταση AdG της G στην υποομάδα Lie K, θα πάρουμε την αναπαράσταση
AdG K : K → Aut(𝔤), k
K : K → Aut(𝔤), k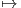 AdG
AdG K(k) : 𝔤 →𝔤, δηλαδή AdK(k) = AdG(k)
K(k) : 𝔤 →𝔤, δηλαδή AdK(k) = AdG(k)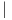 𝔨. Ας έρθουμε τώρα στην σχέση
μεταξύ της ισοτροπικής και της συζυγούς αναπαράστασης.
𝔨. Ας έρθουμε τώρα στην σχέση
μεταξύ της ισοτροπικής και της συζυγούς αναπαράστασης.
Πρόταση 10.6: ΄Εστω G∕K ένας αναγωγικός ομογενής χώρος και 𝔤 = 𝔨 ⊕𝔪 η αναγωγική ανάλυση της 𝔤. Τότε
για κάθε k ∈ K και X = X𝔨 ⊕ X𝔪 ∈𝔤, όπου X𝔨 ∈𝔨 και X𝔪 ∈𝔪 ισχύει:
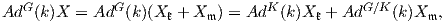 | (10.3) |
δηλαδή, AdG K = AdK ⊕ AdG∕K.
K = AdK ⊕ AdG∕K.
Απόδειξη. Επειδή έχουμε ευθύ άθροισμα, αρκεί να αποδείξουμε την σχέση (10.3) για τις περιπτώσεις X𝔨 = 0
και X𝔪 = 0. Στη δεύτερη περίπτωση, δηλαδή X𝔪 = 0, η (10.3) ισοδυναμεί με την AdG(k)X𝔨 = AdK(k)X𝔨.
Αυτό πράγματι ισχύει, διότι, αν θεωρήσουμε τον περιορισμό της AdG στην K, AdG K : K → Aut(𝔤), τότε
για κάθε k ∈ K έχουμε AdK(k) = AdG(k)
K : K → Aut(𝔤), τότε
για κάθε k ∈ K έχουμε AdK(k) = AdG(k)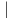 𝔨, αφού η K είναι υποομάδα Lie της G.
𝔨, αφού η K είναι υποομάδα Lie της G.
Στην πρώτη περίπτωση αρκεί να δείξουμε ότι AdG(k)X𝔪 = AdG∕K(k)X𝔪, ή ισοδύναμα
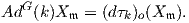
Δηλαδή θα πρέπει να αποδείξουμε ότι η ισοτροπική αναπαράσταση του χώρου G∕K είναι ισοδύναμη με
την συζυγή αναπαράσταση AdG K στο χώρο 𝔪. Επομένως αρκεί να αποδειχθεί ότι το παρακάτω διάγραμμα
είναι αντιμεταθετικό:
K στο χώρο 𝔪. Επομένως αρκεί να αποδειχθεί ότι το παρακάτω διάγραμμα
είναι αντιμεταθετικό:
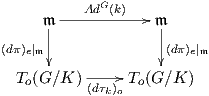
Πριν προχωρήσουμε στην απόδειξη, διευκρινίζουμε τα εξής: Η πρώτη οριζόντια απεικόνιση του διαγράμματος
προέρχεται από τον περιορισμό της AdG(k) στον υπόχωρο 𝔪 και από το γεγονός ότι AdG(k)𝔪 ⊂𝔪. Οι κάθετες
απεικονίσεις είναι ισομορφισμοί και προέρχονται από τον περιορισμό της (dπ)e : 𝔤 → To(G∕K) στον 𝔪. ΄Εστω
λοιπόν k ∈ K και X𝔪 ∈𝔪. Θα δείξουμε ότι (dπ)e(AdG(k)X𝔪) = (dτk)o((dπ)e(X𝔪)). ΄Εχουμε:
Στην τέταρτη ισότητα χρησιμοποιήσαμε ότι
exp(Ad(g)X) = gexp(tX)g-1 και στην πέμπτη ότι για κάθε
k ∈ K
ισχύει
k-1K = K. ▄
Από την παραπάνω απόδειξη προκύπτει το εξής:
Πόρισμα 10.1: Αν ο ομογενής χώρος είναι αναγωγικός, τότε η ισοτροπική αναπαράσταση του G∕K είναι
ισοδύναμη με τη συζυγή αναπαράσταση AdG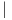 K στον υπόχωρο 𝔪.
K στον υπόχωρο 𝔪.
Στην περίπτωση που ο G∕K δεν είναι αναγωγικός, το προηγούμενο πόρισμα ισχύει αν αντικαταστήσουμε τον 𝔪 με
τον 𝔤∕𝔨.
Ορισμός 10.6: ΄Ενας ομογενής χώρος G∕K καλείται ισοτροπικά μη αναγώγιμος (isotropy irreducible), αν η
ισοτροπική αναπαράσταση AdG∕K είναι μη αναγώγιμη .
Παρατήρηση. ΄Εστω G∕K ένας ομογενής χώρος και 𝔤 = 𝔨 ⊕𝔪 η αναγωγική ανάλυση της άλγεβρας Lie 𝔤. Τότε
συνδυάζοντας τα όσα έχουμε αναφέρει μέχρι στιγμής καταλήγουμε στα ακόλουθα συμπεράσματα:
- Αν η ισοτροπική αναπαράσταση AdG∕K : K → Aut(𝔪) είναι μη αναγώγιμη (δηλαδή οι μοναδικοί
AdG∕K-αναλλοίωτοι υπόχωροι του 𝔪 είναι ο τετριμμένος {0} και ο 𝔪), τότε ο εφαπτόμενος χώρος
𝔪
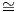 To(G∕K) δεν διασπάται σε μικρότερης διάστασης υποχώρους.
To(G∕K) δεν διασπάται σε μικρότερης διάστασης υποχώρους.
- Στην περίπτωση που η ισοτροπική αναπαράσταση AdG∕K : K → Aut(𝔪) είναι αναγώγιμη, (δηλαδή
υπάρχουν AdG∕K-αναλλοίωτοι υπόχωροι 𝔪i του 𝔪
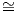 To(G∕K)), τότε η ισοτροπική αναπαράσταση
μπορεί να γραφεί ως ευθύ άθροισμα μη αναγώγιμων αναπαραστάσεων (ισοδύναμων ή μη ισοδύναμων)
φi : K → Aut(𝔪i), i = 1,2…l και l ≤ dim(𝔪) ως εξής:
To(G∕K)), τότε η ισοτροπική αναπαράσταση
μπορεί να γραφεί ως ευθύ άθροισμα μη αναγώγιμων αναπαραστάσεων (ισοδύναμων ή μη ισοδύναμων)
φi : K → Aut(𝔪i), i = 1,2…l και l ≤ dim(𝔪) ως εξής:
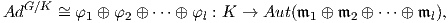
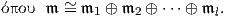
Παραδείγματα.
1. Θα υπολογίσουμε την ισοτροπική αναπαράσταση του ομογενούς χώρου SO(4)∕SO(2) (πολλαπλότητα
Stiefel διάστασης 5). ΄Εστω λ4 : SO(4) → Aut(ℝ4) και AdSO(4) = ∧2λ4 η συνήθης αναπαράσταση
και η συζυγής αναπαράσταση αντίστοιχα, της SO(4). Γνωρίζουμε ότι η ισοτροπική αναπαράσταση
AdSO(4)∕SO(2) : SO(2) → Aut(𝔪) του ομογενούς χώρου SO(4)∕SO(2) συνδέεται με τη συζυγή αναπαράσταση της
SO(4) μέσω της σχέσης
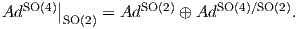
Τότε θα έχουμε:
Στη δεύτερη ισότητα συμβολίζουμε με 2 το ευθύ άθροισμα 2 = 1 ⊕ 1, όπου 1 η τετριμμένη αναπαράσταση, και στην
τρίτη ισότητα χρησιμοποίησαμε την αλγεβρική ταυτότητα
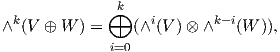
όπου V,W είναι διανυσματικοί χώροι πεπερασμένης διάστασης. Βλέπουμε ότι ο πρώτος όρος στην τελική έκφραση
της περιορισμένης αναπαράστασης AdSO(4)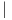 SO(2) είναι η συζυγής αναπαράσταση της SO(2), οπότε η ισοτροπική
αναπαράσταση του ομογενούς χώρου είναι η
SO(2) είναι η συζυγής αναπαράσταση της SO(2), οπότε η ισοτροπική
αναπαράσταση του ομογενούς χώρου είναι η
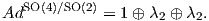 | (10.4) |
Παρατηρούμε ότι η ισοτροπική αναπαράσταση εκφράζεται ως ευθύ άθροισμα τριών μη αναγώγιμων
αναπαραστάσεων διαστάσεων 1,2 και 2 αντίστοιχα. Το παραπάνω άθροισμα επάγει έναν
ισομορφισμό του εφαπτόμενου χώρου 𝔪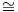 To(G∕K) με το ευθύ άθροισμα τριών πραγματικών
υποχώρων
διαστάσεων 1,2 και 2 αντίστοιχα, δηλαδή
To(G∕K) με το ευθύ άθροισμα τριών πραγματικών
υποχώρων
διαστάσεων 1,2 και 2 αντίστοιχα, δηλαδή
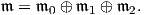
Πρέπει να σημειώσουμε εδώ ότι, επειδή στην σχέση (10.4) οι δύο τελευταίες αναπαραστάσεις είναι ισοδύναμες, η
διάσπαση του 𝔪 δεν είναι μοναδική.
2. ΄Εστω ο ομογενής χώρος G∕K = U(3)∕U(1) × U(1) × U(1) (πολλαπλότητα σημαιών διάστασης 6). Θα
υπολογίσουμε την ισοτροπική αναπαράσταση του χώρου G∕K. Επειδή οι ομάδες Lie περιέχουν μιγαδικά στοιχεία,
είναι πιο εύχρηστο να υπολογίσουμε τη μιγαδοποιημένη ισοτροπική αναπαράσταση. ΄Εστω μ3 : U(3) → Aut(ℂ3)
και μ1 : U(1) → Aut(ℂ) οι κανονικές αναπαραστάσεις των U(3) και U(1) αντίστοιχα. Για τη μιγαδοποίηση της
συζυγούς αναπαράστασης της U(n) ισχύει ότι AdU(n) ⊗ ℂ = μn ⊗ℂμn. ΄Εστω σi : U(1) × U(1) × U(1) → U(1),
i = 1,2,3, η προβολή στην i-συνιστώσα. Τότε η σύνθεση
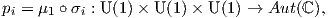
είναι η κανονική αναπαράσταση της i-συνιστώσας του καρτεσιανού γινομένου K = U(1) × U(1) × U(1)
(i = 1,2,3). ΄Εχουμε:
όπου με pipj συμβολίζουμε το τανυστικό γινόμενο pi ⊗pj. Το πρώτο μέλος του παραπάνω αθροίσματος είναι η
μιγαδοποιημένη συζυγής αναπαράσταση της K = U(1) × U(1) × U(1). ΄Ετσι, από την Πρόταση 10.3,
συμπεραίνουμε ότι η μιγαδοποιημένη ισοτροπική αναπαράσταση του ομογενούς χώρου G∕K είναι
η
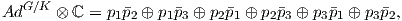
Η παραπάνω αναπαράσταση είναι αναγώγιμη και εκφράζεται ως ευθύ άθροισμα έξι μη ισοδύναμων και μη
αναγώγιμων μιγαδικών αναπαραστάσεων. Κάθε μία από αυτές είναι μονοδιάστατη. Γι΄ αυτό, ο μιγαδοποιημένος
εφαπτόμενος χώρος 𝔪ℂ της G∕K είναι ισόμορφος με το ευθύ άθροισμα έξι μονοδιάστατων μιγαδικών
υποχώρων
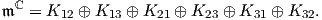
Σημειώνουμε ότι αυτή η διάσπαση επάγει μια διάσπαση του 𝔪 σε τρεις δισδιάστατους πραγματικούς
υποχώρους,
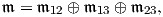
όπου 𝔪ijℂ = Kij ⊕ Kji.
Ο ομογενής χώρος G′∕K′ = SU(3)∕S(U(1) × U(1) × U(1)) έχει διάσταση 6 και είναι ισόμορφος με
τον G∕K, συνεπώς ο μιγαδοποιημένος εφαπτόμενος χώρος του G′∕K′ (τον οποίο θα συμβολίζουμε
επίσης με 𝔪ℂ), είναι ισόμορφος με το παραπάνω ευθύ άθροισμα των έξι μονοδιάστατων υποχώρων
Kij.
10.5 G-αναλλοίωτες μετρικές και η συνοχή Levi-Civita
Ορισμός 10.7: ΄Εστω M = G∕K ένας ομογενής χώρος. Μια μετρική Riemann g στην M καλείται
G-αναλλοίωτη (G-invariant), εάν για κάθε a ∈ G,p ∈ M η αμφιδιαφόριση τa : G∕K → G∕K τa(p) = ap
είναι μια ισομετρία, δηλαδή
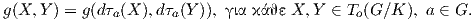
Θα δώσουμε τώρα μια περιγραφή των G-αναλλοίωτων μετρικών σε έναν αναγωγικό ομογενή χώρο.
Πρόταση 10.7: Αν το διαφορικό (dπ)e : 𝔤 → To(G∕K) είναι μια ισομετρία, τότε υπάρχει μια 1 - 1 αντιστοιχία
μεταξύ:
- G-αναλλοίωτων μετρικών g στον ομογενή χώρο G∕K και
- AdG∕K ≡ AdG(K)-αναλλοίωτων εσωτερικών γινομένων
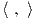 στον 𝔪,
στον 𝔪,
δηλαδή για κάθε X,Y ∈𝔪, k ∈ K, ισχύει ⟨AdG∕K(k)X,AdG∕K(k)Y ⟩ = 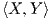 .
.
Απόδειξη. ΄Εστω g μια G-αναλλοίωτη μετρική στον ομογενή χώρο G∕K. Ορίζουμε στον 𝔪 ένα εσωτερικό
γινόμενο 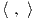 o με περιορισμό της μετρικής στον εφαπτόμενο χώρο To(G∕K)
o με περιορισμό της μετρικής στον εφαπτόμενο χώρο To(G∕K)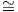 𝔪, δηλαδή
𝔪, δηλαδή
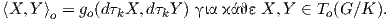
Επειδή η μετρική είναι G-αναλλοίωτη, η προηγούμενη σχέση γράφεται και ως 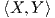 o = go(X,Y ). Το εσωτερικό
αυτό γινόμενο είναι AdG∕K-αναλλοίωτο. Πράγματι, είναι
o = go(X,Y ). Το εσωτερικό
αυτό γινόμενο είναι AdG∕K-αναλλοίωτο. Πράγματι, είναι
Στην πρώτη ισότητα χρησιμοποιήσαμε το γεγονός ότι η προβολή
π είναι ισομετρία. Η τρίτη ισότητα ισχύει, διότι το
διάγραμμα της Πρότασης
10.6 είναι αντιμεταθετικό και η τελευταία ισότητα ισχύει από τον ορισμό του εσωτερικού
γινομένου, αφού για κάθε
X ∈ To(G∕K) έχουμε ότι
AdG∕K(k)X ∈ To(G∕K).
Αντίστροφα, έστω 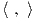 o ένα AdG∕K-αναλλοίωτο εσωτερικό γινόμενο στο χώρο 𝔪. Επεκτείνουμε αυτό το
γινόμενο σε ολόκληρο τον ομογενή χώρο G∕K, δηλαδή για κάθε σημείο gK ∈ G∕K θέτουμε
o ένα AdG∕K-αναλλοίωτο εσωτερικό γινόμενο στο χώρο 𝔪. Επεκτείνουμε αυτό το
γινόμενο σε ολόκληρο τον ομογενή χώρο G∕K, δηλαδή για κάθε σημείο gK ∈ G∕K θέτουμε
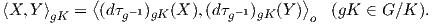 | (10.5) |
Λόγω του AdG∕K-αναλλοίωτου, αυτό το εσωτερικό γινόμενο δεν εξαρτάται από την επιλογή του αντιπροσώπου
(άσκηση). Επίσης από την σχέση (10.5) προκύπτει ότι η dτk : 𝔪 →𝔪 είναι ισομετρία, επομένως η μετρική στον
ομογενή χώρο είναι G-αναλλοίωτη. ▄
Κάθε εσωτερικό γινόμενο στον υπόχωρο 𝔪 που ικανοποιεί τη Συνθήκη 2 της προηγούμενης πρότασης
καλείται Ad(K)-αναλλοίωτο.
Αν K = {e}, τότε ο ομογενής χώρος G∕K είναι ουσιαστικά η ομάδα Lie G και σε αυτή την περίπτωση ο
ισομορφισμός 𝔪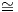 To(G∕K) γενικεύει τον ισομορφισμό 𝔤
To(G∕K) γενικεύει τον ισομορφισμό 𝔤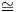 TeG. Τότε οι G-αναλλοίωτες μετρικές στον
ομογενή χώρο G∕K αποτελούν τη γενίκευση των αριστερά αναλλοίωτων μετρικών στην ομάδα G. Η
έννοια της αμφιαναλλοίωτης μετρικής σε μια ομάδα Lie G στους ομογενείς χώρους γενικεύται ως
εξής:
TeG. Τότε οι G-αναλλοίωτες μετρικές στον
ομογενή χώρο G∕K αποτελούν τη γενίκευση των αριστερά αναλλοίωτων μετρικών στην ομάδα G. Η
έννοια της αμφιαναλλοίωτης μετρικής σε μια ομάδα Lie G στους ομογενείς χώρους γενικεύται ως
εξής:
Ορισμός 10.8: ΄Εστω G∕K ένας αναγωγικός ομογενής χώρος εφοδιασμένος με μια G-αναλλοίωτη μετρική. Ο G∕K
ονομάζεται φυσικά αναγωγικός (naturally reductive), αν το αντίστοιχο εσωτερικό γινόμενο στον χώρο 𝔪
ικανοποιεί την σχέση
για κάθε
X,Y,Z ∈𝔪.
Επειδή ο ομογενής χώρος G∕K είναι αναγωγικός, η άλγεβρα Lie 𝔤 της ομάδας G θα γράφεται ως 𝔤 = 𝔨 ⊕𝔪,
οπότε στην παραπάνω σχέση συμβολίζουμε με [X,Y ]𝔪 τη συνιστώσα του [X,Y ] στον υπόχωρο 𝔪. Γενικά ισχύει
[X,Y ] = [X,Y ]𝔨 + [X,Y ]𝔪. ΄Ενα παράδειγμα φυσικά αναγωγικού ομογενούς χώρου είναι η σφαίρα
Sn SO(n + 1)∕SO(n).
SO(n + 1)∕SO(n).
΄Εστω G∕K ένας ομογενής χώρος με την G να είναι συμπαγής και ημιαπλή ομάδα Lie. Επειδή η
G είναι συμπαγής, θα επιδέχεται μια αμφιαναλλοίωτη μετρική. Αυτή επάγει ένα Ad(G)-αναλλοίωτο
εσωτερικό γινόμενο στην άλγεβρα Lie 𝔤, το οποίο θα συμβολίζουμε με Q = Q(⋅,⋅). Ως προς αυτό το
εσωτερικό γινόμενο θεωρούμε την αναγωγική ανάλυση 𝔤 = 𝔨 ⊕𝔪 της 𝔤, όπου ο υπόχωρος 𝔪 είναι το
ορθογώνιο συμπλήρωμα ως προς το Q του 𝔨, δηλαδή 𝔪 = 𝔨⊥ και Q(𝔪,𝔨) = 0. Ο περιορισμός του
εσωτερικού γινομένου Q στον υπόχωρο 𝔪 επάγει στον ομογενή χώρο G∕K μια G-αναλλοίωτη μετρική
g = Q|𝔪, η οποία λέγεται φυσική μετρική (normal homogeneous Riemannian metric). Μια τέτοια
μετρική είναι φυσικά αναγωγική. Μια ειδική κατηγορία αυτών των μετρικών δίνεται από τον παρακάτω
ορισμό,
Ορισμός 10.9: Η φυσική μετρική στον ομογενή χώρο G∕K, η οποία επάγεται από το εσωτερικό γινόμενο
-B(⋅,⋅), όπου B η μορφή Killing της 𝔤, δηλαδή
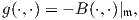
λέγεται κανονική μετρική (standard homogeneous Riemannian metric).
Ο καθορισμός όλων των G-αναλλοίωτων μετρικών στον ομογενή χώρο ή ισοδύναμα όλων των
AdG∕K-αναλλοίωτων εσωτερικών γινομένων στον υπόχωρο 𝔪 εξαρτάται από την ισοτροπική αναπαράσταση
AdG∕K : K → Aut(𝔪) του ομογενούς χώρου. Συγκεκριμένα, διακρίνουμε τις εξής δύο περιπτώσεις:
- * Η ισοτροπική αναπαράσταση είναι μη αναγώγιμη. Τότε υπάρχει μοναδικό (αγνοώντας πολλαπλασιασμό
με θετικές σταθερές) ισοτροπικά αναλλοίωτο εσωτερικό γινόμενο στον χώρο 𝔪, οπότε από την
Πρόταση 10.7 η G-αναλλοίωτη μετρική στον ομογενή χώρο θα είναι μοναδική. Επιπλέον η μετρική
αυτή είναι Einstein.
Πράγματι, επειδή η ομάδα Lie είναι συμπαγής και ημιαπλή, επιδέχεται μια αμφιαναλλοίωτη μετρική και κατ′ επέκταση θα
υπάρχει ένα Ad(G)-αναλλοίωτο εσωτερικό γινόμενο στην 𝔤. Συγκεκριμένα, επειδή η ομάδα G είναι ημιαπλή, η
μορφή Killing B θα είναι αρνητικά ορισμένη, οπότε μπορούμε να επιλέξουμε 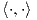 = -B(⋅,⋅). Οταν το περιορίσουμε
στον υπόχωρο 𝔪, θα πάρουμε την κανονική μετρική g = -B(⋅,⋅)|𝔪 στον ομογενή χώρο. Η μετρική αυτή είναι
μοναδική, διότι η ισοτροπική αναπαράσταση είναι μη αναγώγιμη, άρα από το Θεώρημα 8.8 θα έχουμε ότι, αν
= -B(⋅,⋅). Οταν το περιορίσουμε
στον υπόχωρο 𝔪, θα πάρουμε την κανονική μετρική g = -B(⋅,⋅)|𝔪 στον ομογενή χώρο. Η μετρική αυτή είναι
μοναδική, διότι η ισοτροπική αναπαράσταση είναι μη αναγώγιμη, άρα από το Θεώρημα 8.8 θα έχουμε ότι, αν 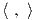 ′
είναι ένα άλλο AdG∕K-αναλλοίωτο εσωτερικό γινόμενο στον 𝔪, τότε θα υπάρχει σταθερά λ ∈ ℝ+, τέτοια
ώστε
′
είναι ένα άλλο AdG∕K-αναλλοίωτο εσωτερικό γινόμενο στον 𝔪, τότε θα υπάρχει σταθερά λ ∈ ℝ+, τέτοια
ώστε 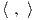 = λ
= λ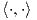 ′. Επιπλέον, επειδή ο τανυστής Ricci είναι μια AdG∕K-αναλλοίωτη συμμετρική
διγραμμική μορφή, θα πρέπει με το ίδιο σκεπτικό να ισούται με κάποιο πολλαπλάσιο της μετρικής,
δηλαδή Ric = cg, c ∈ ℝ+, επομένως η κανονική μετρική του ομογενούς χώρου G∕K είναι μετρική
Einstein.
′. Επιπλέον, επειδή ο τανυστής Ricci είναι μια AdG∕K-αναλλοίωτη συμμετρική
διγραμμική μορφή, θα πρέπει με το ίδιο σκεπτικό να ισούται με κάποιο πολλαπλάσιο της μετρικής,
δηλαδή Ric = cg, c ∈ ℝ+, επομένως η κανονική μετρική του ομογενούς χώρου G∕K είναι μετρική
Einstein.
- ** Η ισοτροπική αναπαράσταση είναι αναγώγιμη, δηλαδή υπάρχουν AdG∕K-αναλλοίωτοι υπόχωροι 𝔪i του
𝔪. Τότε η AdG∕K : K → Aut(𝔪) θα γράφεται ως ευθύ άθροισμα μη αναγώγιμων υποαναπαραστάσεων
φi : K → Aut(𝔪i), δηλαδή
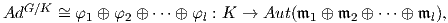
όπου 𝔪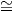 𝔪1 ⊕𝔪2 ⊕
𝔪1 ⊕𝔪2 ⊕ ⊕𝔪l και κάθε 𝔪i είναι AdG∕K-αναλλοίωτος υπόχωρος.
⊕𝔪l και κάθε 𝔪i είναι AdG∕K-αναλλοίωτος υπόχωρος.
Επειδή κάθε φi είναι μια μη αναγώγιμη αναπαράσταση, τότε σε κάθε υπόχωρο 𝔪i θα υπάρχει μοναδικό
Ad(K)-αναλλοίωτο εσωτερικό γινόμενο, δηλαδή ερχόμαστε στην πρώτη περίπτωση που περιγράψαμε
προηγουμένως. ΄Οταν οι αναπαραστάσεις φi είναι ανά δύο μη ισοδύναμες, τότε η διάσπαση 𝔪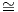 𝔪1 ⊕𝔪2 ⊕
𝔪1 ⊕𝔪2 ⊕ ⊕𝔪l
θα είναι μοναδική και επιπλέον οι υπόχωροι 𝔪i, i = 1,…,l θα είναι κάθετοι μεταξύ τους. Σε αυτή την περίπτωση το
ισοτροπικά αναλλοίωτο εσωτερικό γινόμενο στον 𝔪 θα γράφεται ως
⊕𝔪l
θα είναι μοναδική και επιπλέον οι υπόχωροι 𝔪i, i = 1,…,l θα είναι κάθετοι μεταξύ τους. Σε αυτή την περίπτωση το
ισοτροπικά αναλλοίωτο εσωτερικό γινόμενο στον 𝔪 θα γράφεται ως
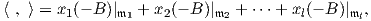
όπου xi ∈ ℝ+ για κάθε i = 1,2,…,l. ΄Αρα όλες οι G-αναλλοίωτες μετρικές στον ομογενή χώρο G∕K θα
δίνονται από το παραπάνω εσωτερικό γινόμενο. Οι μετρικές αυτές ονομάζονται διαγώνιες (diagonal
metrics).
Στην περίπτωση όμως που κάποιες από τις αναπαραστάσεις φi είναι ισοδύναμες, τότε η διάσπαση του 𝔪 δεν
είναι μοναδική και επίσης ενδέχεται κάποιοι από τους υποχώρους 𝔪i να μην είναι κάθετοι μεταξύ τους, οπότε εδώ οι
διαγώνιες μετρικές θα αποτελούν ένα υποσύνολο όλων των G-αναλλοίωτων μετρικών του ομογενούς χώρου G∕K.
Η πλήρης περιγραφή όλων των G-αναλλοίωτων μετρικών στον G∕K είναι αρκετά πιο δύσκολη. ΄Ενα παράδειγμα
αυτής της περίπτωσης αποτελούν οι πολλαπλότητες Stiefel V kℝn. Για παράδειγμα, έχουμε δει ότι η ισοτροπική
αναπαράσταση της V 1ℝ4 SO(4)∕SO(2) είναι AdSO(4)∕SO(2) = 1 ⊕ λ2 ⊕ λ2, όπου οι δύο τελευταίες
υποαναπαραστάσεις είναι ισοδύναμες.
SO(4)∕SO(2) είναι AdSO(4)∕SO(2) = 1 ⊕ λ2 ⊕ λ2, όπου οι δύο τελευταίες
υποαναπαραστάσεις είναι ισοδύναμες.
Στη συνέχεια, θα ορίσουμε τη συνοχή Levi-Civita σε έναν αναγωγικό ομογενή χώρο G∕K εφοδιασμένον με
μια G-αναλλοίωτη μετρική. ΄Εστω 𝔤 = 𝔨 ⊕𝔪 η αναγωγική ανάλυση της άλγεβρας Lie 𝔤. Για κάθε X ∈𝔤 ορίζουμε
το διανυσματικό πεδίο X* στον ομογενή χώρο G∕K από την σχέση
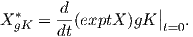
Επειδή ο χώρος είναι αναγωγικός, μπορούμε να ταυτίσουμε τον 𝔪 με τον εφαπτόμενο χώρο To(G∕K) μέσω της
απεικόνισης
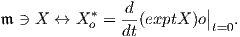
Το διανυσματικό πεδίο X* είναι ένα πεδίο Killing (βλ. Κεφάλαιο 6, ΄Ασκηση 8) και για κάθε X*,Y *∈𝔛(G∕K) ισχύει
η σχέση
![[X*,Y *] = - [X, Y ]*.](02_chapter_10197x.png) | (10.7) |
Θα χρειαστούμε λοιπόν το εξής:
Πρόταση 10.8: ΄Εστω (M,g) μια πολλαπλότητα Riemann εφοδιασμένη με τη συνοχή Levi-Civita. Αν X,Y,Z είναι
διανυσματικά πεδία Killing, τότε ισχύει
![2g(∇X Y,Z ) = g([X, Y],Z) + g([X, Z],Y )+ g([Y, Z],X ).](02_chapter_10198x.png) | (10.8) |
Απόδειξη. Η συνοχή Levi-Civita χαρακτηρίζεται από την ταυτότητα Koszul:
Επειδή τα
X,Y,Z είναι διανυσματικά πεδία
Killing, θα ισχύουν οι σχέσεις
Αντικαθιστώντας τις σχέσεις αυτές στην ταυτότητα
Koszul, θα πάρουμε τη ζητούμενη σχέση. ▄
Μπορούμε τώρα να ορίσουμε τη συνοχή Levi-Civita σε έναν ομογενή χώρο G∕K.
Θεώρημα 10.3: ΄Εστω G∕K ένας αναγωγικός ομογενής χώρος με αναγωγική διάσπαση 𝔤 = 𝔨 ⊕𝔪. ΄Εστω g μια
G-αναλλοίωτη μετρική στον G∕K με 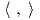 το αντίστοιχο AdG∕K-αναλλοίωτο εσωτερικό γινόμενο στον 𝔪. Τότε,
για κάθε X,Y,Z ∈𝔪
το αντίστοιχο AdG∕K-αναλλοίωτο εσωτερικό γινόμενο στον 𝔪. Τότε,
για κάθε X,Y,Z ∈𝔪 To(G∕K), ισχύει
To(G∕K), ισχύει
![1
(∇X *Y *)o = - -[X,Y ]𝔪 + U (X, Y),
2](02_chapter_10203x.png) | (10.9) |
όπου η απεικόνιση U : 𝔪 ×𝔪 →𝔪 ορίζεται από την σχέση
![2⟨U (X, Y ),Z⟩ = ⟨[Z, X]𝔪,Y ⟩+ ⟨X, [Z, Y]𝔪⟩.](02_chapter_10204x.png) | (10.10) |
Απόδειξη. ΄Εστω X,Y,Z ∈𝔪 με X*,Y *,Z* τα αντίστοιχα διανυσματικά πεδία Killing. Από τις σχέσεις (10.8) και
(10.7) παίρνουμε
Επίσης, επειδή
X,Y,Z ∈𝔪 έχουμε ότι
απ΄ όπου προκύπτει η ζητούμενη σχέση. ▄
Παρατήρηση. Στην περίπτωση που έχουμε U ≡ 0, δηλαδή ⟨[Z,X]𝔪,Y ⟩ = -⟨X,[Z,Y ]𝔪⟩, τότε επειδή το γινόμενο
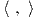 είναι AdG∕K-αναλλοίωτο, από την Πρόταση 9.2 θα ισχύει
είναι AdG∕K-αναλλοίωτο, από την Πρόταση 9.2 θα ισχύει ![⟨[X, Y] ,Z ⟩
𝔪](02_chapter_10208x.png) = -
= -![⟨Y,[X, Z] ⟩
𝔪](02_chapter_10209x.png) για κάθε
X,Y,Z ∈𝔪. Συνδυάζοντας τις δύο προηγούμενες σχέσεις παίρνουμε ότι
για κάθε
X,Y,Z ∈𝔪. Συνδυάζοντας τις δύο προηγούμενες σχέσεις παίρνουμε ότι
![⟨[X, Y ]𝔪, Z⟩ = - ⟨X, [Z,Y ]𝔪 ⟩ = ⟨X, [Y, Z]𝔪⟩,](02_chapter_10210x.png)
δηλαδή ο ομογενής χώρος είναι φυσικά αναγωγικός.
10.6 Καμπυλότητα
Θα παρουσιάσουμε τύπους για τις διάφορες καμπυλότητες για μια G-αναλλοίωτη μετρική σε έναν αναγωγικό
ομογενή χώρο. Επειδή οι αποδείξεις τους είναι αρκετά τεχνικές, δεν θα τις δώσουμε εδώ, αλλά παραπέμπουμε στα
βιβλία [1] και [3], στις διπλωματικές εργασίες [15] και [18], καθώς και στην εργασία [17]. Θα δούμε όμως εφαρμογές
σε μερικά παραδείγματα.
Θεώρημα 10.4: ΄Εστω G∕K ένας αναγωγικός ομογενής χώρος εφοδιασμένος με μια G-αναλλοίωτη μετρική g και
𝔤 = 𝔨 ⊕𝔪 η αναγωγική ανάλυση της άλγεβρας Lie 𝔤. Τότε, για κάθε X,Y ∈𝔪 ο τανυστής καμπυλότητας
ικανοποιεί την σχέση
Εάν 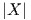 =
= 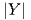 = 1 και
= 1 και 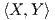 = 0, τότε η παραπάνω σχέση μας δίνει την καμπυλότητα τομής του επιπέδου
που παράγεται από τα X,Y ∈ To(G∕K)
= 0, τότε η παραπάνω σχέση μας δίνει την καμπυλότητα τομής του επιπέδου
που παράγεται από τα X,Y ∈ To(G∕K)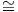 𝔪.
𝔪.
Στη συνέχεια θα περιγράψουμε την καμπυλότητα Ricci σε έναν αναγωγικό ομογενή χώρο G∕K. Θεωρούμε μια
ορθοκανονική βάση {Xi} του 𝔪 ως προς το AdG∕K-αναλλοίωτο εσωτερικό γινόμενο 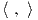 . Για να απλοποιήσουμε
τον τύπο της καμπυλότητας Ricci, θέτουμε Z = ∑
iU(Xi,Xi).
. Για να απλοποιήσουμε
τον τύπο της καμπυλότητας Ricci, θέτουμε Z = ∑
iU(Xi,Xi).
Λήμμα 10.1: Το Z = ∑
iU(Xi,Xi) είναι το μοναδικό εφαπτόμενο διάνυσμα στον χώρο 𝔪, το οποίο για
κάθε X ∈𝔪 ικανοποιεί την σχέση
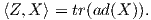
Εδώ με tr συμβολίζουμε το ίχνος του ενδομορφισμού ad(X) : 𝔤 →𝔤.
Απόδειξη. Επειδή ο υπόχωρος 𝔪 είναι AdG∕K-αναλλοίωτος, θα ισχύει [𝔪,𝔨] ⊂𝔪, οπότε για κάθε X ∈𝔪
θα είναι [X,𝔨] ⊂𝔪. Συνεπώς, είναι
![∑ ∑
tr(ad(X )) = ⟨ad(X )Xi,Xi ⟩ = ⟨[X, Xi]𝔪,Xi⟩ = ⟨Z,X ⟩.
i i](02_chapter_10218x.png)
▄
Πρόταση 10.9: Η καμπυλότητα Ricci ενός αναγωγικού ομογενούς χώρου G∕K δίνεται από την σχέση
όπου
{Xi} μια ορθοκανονική βάση του
𝔪 και
Z το μοναδικό εφαπτόμενο διάνυσμα που ορίσαμε παραπάνω.
Ο προηγούμενος τύπος απλουστεύεται σημαντικά με την χρήση της μορφής Killing της 𝔤.
Πρόταση 10.10: Η καμπυλότητα Ricci για τον αναγωγικό ομογενή χώρο G∕K δίνεται από την σχέση
Τέλος, για τη βαθμωτή καμπυλότητα του αναγωγικού ομογενούς χώρου έχουμε το εξής:
Πρόταση 10.11: Η βαθμωτή καμπυλότητα δίνεται από την σχέση:
![1∑ 1 ∑
S = - -- |[Xi,Xj ]𝔪 |2 - -- B (Xi, Xi)- |Z |2.
2 i,j 2 i](02_chapter_10221x.png)
Ας δούμε τώρα την περίπτωση που ο ομογενής χώρος G∕K είναι φυσικά αναγωγικός. Τότε για την
απεικόνιση U : 𝔪 ×𝔪 →𝔪 θα έχουμε U ≡ 0, επομένως η συνοχή Levi-Civita θα δίνεται από τον
τύπο
![(∇X *Y *)o = - 1[X, Y]𝔪.
2](02_chapter_10222x.png)
Συνεπώς σε αυτή την περίπτωση οι τύποι για την καμπυλότητα του ομογενούς χώρου θα απλοποιούνται
αρκετά.
Πρόταση 10.12: ΄Εστω G∕K ένας φυσικά αναγωγικός ομογενής χώρος. Τότε ο τανυστής καμπυλότητας
δίνεται από τον τύπο
![1- 2
⟨R (X, Y)X, Y⟩ = 4|[X,Y ]𝔪| + ⟨[[X, Y]𝔨,X ]𝔪,Y ⟩.](02_chapter_10223x.png)
΄Οταν η μετρική στον φυσικά αναγωγικό ομογενή χώρο G∕K είναι η φυσική μετρική, δηλαδή g(⋅,⋅) = Q(⋅,⋅)|𝔪
για την οποία ισχύει Q(𝔨,𝔪) = 0, τότε ο τανυστής καμπυλότητας και η καμπυλότητα Ricci δίνονται αντίστοιχα απο
τους παρακάτω τύπους:
όπου X,Y ∈𝔪 και {V i} είναι μια Q-ορθοκανονική βάση του 𝔪. Τέλος, αν η μετρική είναι η κανονική μετρική,
δηλαδή g(⋅,⋅) = -B(⋅,⋅)|𝔪, τότε οι παραπάνω τύποι παίρνουν τη μορφή
Παραδείγματα.
1. Θα μελετήσουμε την καμπυλότητα της σφαίρας S3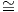 SO(4)∕SO(3) ως προς την κανονική μετρική. Προτρέπουμε
τον αναγνώστη να γενικεύσει το παράδειγμα αυτό για την σφαίρα Sn
SO(4)∕SO(3) ως προς την κανονική μετρική. Προτρέπουμε
τον αναγνώστη να γενικεύσει το παράδειγμα αυτό για την σφαίρα Sn SO(n + 1)∕SO(n).
SO(n + 1)∕SO(n).
Η άλγεβρα Lie 𝔰𝔬(4) της ομάδας Lie SO(4) αποτελείται από όλους τους 4 × 4 αντισυμμετρικούς πραγματικούς
πίνακες, ΄Εστω eij ο 4 × 4 πίνακας ο οποίος έχει 1 στην (i,j)-θέση, -1 στην (j,i)-θέση και στις υπόλοιπες
θέσεις 0. Τότε 𝔰𝔬(4) = span{eij : 1 ≤ i < j ≤ 4}. Για την εύρεση ενός Ad(SO(3))-αναλλοίωτου
υποχώρου 𝔪, έτσι ώστε να ισχύει 𝔰𝔬(4) = 𝔰𝔬(3) ⊕𝔪, θα χρησιμοποιήσουμε τη μορφή Killing της
SO(4), η οποία δίνεται από τη σχέση B(X,Y ) = 2tr(XY ), X,Y ∈𝔰𝔬(4). Επειδή η ομάδα Lie SO(4)
είναι συμπαγής και ημιαπλή, η μορφή Killing είναι αρνητικά ορισμένη, οπότε θεωρούμε το εσωτερικό
γινόμενο
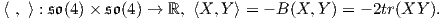
Ως προς το εσωτερικό γινόμενο αυτό ο υπόχωρος 𝔪 θα είναι το ορθογώνιο συμπλήρωμα της 𝔰𝔬(3),
δηλαδή
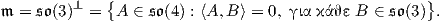
Εμβυθίζουμε τα στοιχεία του συνόλου 𝔰𝔬(3) μέσα στο σύνολο 𝔰𝔬(4) ως εξής:
Για να υπολογίσουμε τον 𝔪 = 𝔰𝔬(3)⊥ θα πρέπει να ισχύει 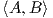 = -2tr(AB) = 0, για κάθε B ∈{e12,e13,e23}
και A ∈𝔰𝔬(4). Με έναν εύκολο υπολογισμό προκύπτει ότι ο υπόχωρος 𝔪 θα έχει τη μορφή
𝔪 = span{e14,e24,e34}. Πρατηρούμε ότι dim𝔪 = 3, επομένως επειδή η διάσταση της 𝔰𝔬(3) είναι 3, θα
έχουμε πράγματι 𝔰𝔬(4) = 𝔰𝔬(3) ⊕𝔪. Απομένει να δείξουμε ότι ο παραπάνω υπόχωρος της 𝔰𝔬(4) είναι
AdSO(3)-αναλλοίωτος, δηλαδή ότι για κάθε x ∈ SO(3) ισχύει Ad(x)𝔪 ⊂𝔪. Επειδή η ομάδα SO(3)
είναι συνεκτική, αυτό ισοδυναμεί με το ότι [𝔰𝔬(3),𝔪] ⊂𝔪, ή ισοδύναμα ότι [X,Y ] ∈𝔪 για κάθε
X ∈𝔰𝔬(3),Y ∈𝔪. Παίρνουμε ένα τυχαίο στοιχείο X της 𝔰𝔬(3) και το εμβυθίζουμε στην 𝔰𝔬(4) ως
΄Εστω Τότε, μετά από πράξεις προκύπτει ότι άρα ο υπόχωρος 𝔪 είναι Ad(SO(3))-αναλλοίωτος. Επειδή επιπλέον είναι 𝔰𝔬(4) = 𝔰𝔬(3) ⊕𝔪, η διάσπαση αυτή
αποτελεί πράγματι μια αναγωγική διάσπαση του ομογενούς χώρου SO(4)∕SO(3).
= -2tr(AB) = 0, για κάθε B ∈{e12,e13,e23}
και A ∈𝔰𝔬(4). Με έναν εύκολο υπολογισμό προκύπτει ότι ο υπόχωρος 𝔪 θα έχει τη μορφή
𝔪 = span{e14,e24,e34}. Πρατηρούμε ότι dim𝔪 = 3, επομένως επειδή η διάσταση της 𝔰𝔬(3) είναι 3, θα
έχουμε πράγματι 𝔰𝔬(4) = 𝔰𝔬(3) ⊕𝔪. Απομένει να δείξουμε ότι ο παραπάνω υπόχωρος της 𝔰𝔬(4) είναι
AdSO(3)-αναλλοίωτος, δηλαδή ότι για κάθε x ∈ SO(3) ισχύει Ad(x)𝔪 ⊂𝔪. Επειδή η ομάδα SO(3)
είναι συνεκτική, αυτό ισοδυναμεί με το ότι [𝔰𝔬(3),𝔪] ⊂𝔪, ή ισοδύναμα ότι [X,Y ] ∈𝔪 για κάθε
X ∈𝔰𝔬(3),Y ∈𝔪. Παίρνουμε ένα τυχαίο στοιχείο X της 𝔰𝔬(3) και το εμβυθίζουμε στην 𝔰𝔬(4) ως
΄Εστω Τότε, μετά από πράξεις προκύπτει ότι άρα ο υπόχωρος 𝔪 είναι Ad(SO(3))-αναλλοίωτος. Επειδή επιπλέον είναι 𝔰𝔬(4) = 𝔰𝔬(3) ⊕𝔪, η διάσπαση αυτή
αποτελεί πράγματι μια αναγωγική διάσπαση του ομογενούς χώρου SO(4)∕SO(3).
Θα υπολογίσουμε στη συνέχεια την ισοτροπική αναπαράσταση AdSO(4)∕SO(3) : SO(3) → Aut(𝔪) του ομογενούς
χώρου SO(4)∕SO(3), η οποία όπως γνωρίζουμε χαρακτηρίζεται από την ισότητα
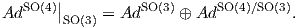
Θυμίζουμε ότι AdSO(4) = ∧2λ4 και λ4 : SO(4) → Aut(ℝ4) είναι αντίστοιχα η συζυγής και η συνήθης
αναπαράσταση της ομάδας SO(4), οπότε έχουμε
Παρατηρούμε ότι ο πρώτος προσθετέος στην τελευταία ισότητα είναι η συζυγής αναπαράσταση της SO(3), οπότε η
ισοτροπική αναπαράσταση του ομογενούς χώρου είναι η
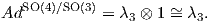
Αυτή είναι η συνήθης αναπαράσταση της SO(3) η οποία είναι μη αναγώγιμη,
επειδή οι μοναδικοί αναλλοίωτοι υπόχωροι του ℝ3 κάτω από την δράση της ομάδας
SO(3)
είναι οι {0} και ℝ3. Επομένως, υπάρχει μοναδικό (αγνοώντας πολλαπλασιασμό με θετικές σταθερές)
AdSO(3)-αναλλοίωτο εσωτερικό γινόμενο στον χώρο 𝔪, συνεπώς η SO(4)-αναλλοίωτη μετρική στον ομογενή χώρο
SO(4)∕SO(3) θα είναι μοναδική. Θεωρούμε την κανονική μετρική
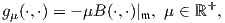
όπου B η μορφή Killing της 𝔰𝔬(4) η οποία δίνεται από την σχέση B(X,Y ) = 2tr(XY ).
Τέλος, θα υπολογίσουμε την καμπυλότητα τομής του αναγωγικού ομογενούς χώρου SO(4)∕SO(3) ως προς την
κανονική μετρική gμ(X,Y ) = -2μtr(XY ). Παρατηρούμε ότι η βάση {e14,e24,e34} του χώρου 𝔪 δεν είναι
ορθοκανονική ως προς την gμ, οπότε θέτουμε
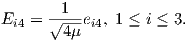
Θα χρειαστούμε τα παρακάτω γινόμενα Lie:
![( )
0 - 14μ 0 0
|| 1- 0 0 0 || 1
[E14,E24] = E14E24 - E24E14 = | 4μ | = - --e12,
( 0 0 0 0 ) 4μ
0 0 0 0](02_chapter_10240x.png)
![( )
0 0 - 41μ 0
|| 0 0 0 0 || -1-
[E14,E34] = E14E34 - E34E14 = |( 1- 0 0 0 |) = - 4μe13,
4μ
0 0 0 0](02_chapter_10241x.png)
![( )
0 0 0 0
| -1 |
[E24,E34] = E24E34 - E34E24 = || 0 01 - 4μ 0 || = - -1e23.
( 0 4μ 0 0 ) 4μ
0 0 0 0](02_chapter_10242x.png)
Λόγω της ισότητας 𝔰𝔬(4) = 𝔰𝔬(3) ⊕𝔪 θα είναι [X,Y ] = [X,Y ]𝔰𝔬(3) + [X,Y ]𝔪, για κάθε X,Y ∈𝔰𝔬(4). Από τους
προηγούμενους υπολογισμούς βλέπουμε ότι για κάθε X,Y ∈𝔪 είναι [X,Y ]𝔪 = 0. ΄Αρα η απεικόνιση
U : 𝔪 ×𝔪 →𝔪 που ορίζεται από την σχέση (10.10) θα είναι η μηδενική, άρα ο ομογενής χώρος SO(4)∕SO(3) είναι
φυσικά αναγωγικός. Συνεπώς, για την καμπυλότητα τομής μπορούμε να χρησιμοποιήσουμε τον τύπο (10.11) και
παίρνουμε:
Παρατηρούμε ότι η καμπυλότητα τομής της σφαίρας S3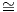 SO(4)∕SO(3), είναι σταθερή και μονίμως θετική.
Επίσης, για μ =
SO(4)∕SO(3), είναι σταθερή και μονίμως θετική.
Επίσης, για μ = 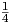 η καμπυλότητα τομής ισούται με 1. Στην περίπτωση αυτή, η κανονική μετρική της
S3
η καμπυλότητα τομής ισούται με 1. Στην περίπτωση αυτή, η κανονική μετρική της
S3 SO(4)∕SO(3) συμπίπτει με το συνηθισμένο εσωτερικό γινόμενο στην S3 που επάγεται από τον
ℝ4.
SO(4)∕SO(3) συμπίπτει με το συνηθισμένο εσωτερικό γινόμενο στην S3 που επάγεται από τον
ℝ4.
Με τον ίδιο τρόπο βρίσκουμε ότι
Επίσης, από τον τύπο (10.12) η καμπυλότητα Ricci του ομογενούς χώρου SO(4)∕SO(3) είναι Μπορούμε εύκολα να δούμε ότι η κανονική μετρική gμ(⋅,⋅) = -μB(⋅,⋅)|𝔪 είναι μια μετρική Einstein, δηλαδή ικανοποιεί
την εξίσωση Ric(X,X) = cg(X,X),c ∈ ℝ. Πράγματι, έστω X = λ1E14 +λ2E24 +λ3E34 ∈𝔪 = span{E14,E24,E34},
λi ∈ ℝ*, i = 1,2,3. Τότε Επίσης, ισχύει ότι συνεπώς, ικανοποιείται η εξίσωση Einstein Ric(X,X) = (-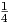 +
+ 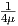 )gμ(X,X), όπου c = -
)gμ(X,X), όπου c = -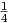 +
+ 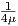 .
.
2. Θα μελετήσουμε την καμπυλότητα της σφαίρας S5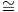 SU(3)∕SU(2). Προτρέπουμε τον αναγνώστη να επεκτείνει
τους υπολογισμούς στην σφαίρα S2n+1
SU(3)∕SU(2). Προτρέπουμε τον αναγνώστη να επεκτείνει
τους υπολογισμούς στην σφαίρα S2n+1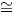 SU(n + 1)∕SU(n).
SU(n + 1)∕SU(n).
Επειδή η ομάδα SU(2) είναι συμπαγής, ο ομογενής χώρος SU(3)∕SU(2) θα είναι αναγωγικός. ΄Εστω
𝔰𝔲(3) = 𝔰𝔲(2) ⊕𝔪 μια αναγωγική ανάλυση της άλγεβρας Lie 𝔰𝔲(3). Θα προσδιορίσουμε τον υπόχωρο 𝔪. Η
άλγεβρα Lie της ομάδας SU(3) έχει διάσταση 8 και αποτελείται από όλους τους 3 × 3 αντιερμητιανούς πίνακες
Αντίστοιχα, η άλγεβρα Lie της SU(2) έχει διάσταση 3 και δίνεται ως Για την εύρεση ενός Ad(SU(2))-αναλλοίωτου υποχώρου 𝔪, έτσι ώστε να ισχύει 𝔰𝔲(3) = 𝔰𝔲(2) ⊕𝔪, θα
χρησιμοποιήσουμε τη μορφή Killing της SU(3), η οποία δίνεται από τον τύπο B(X,Y ) = 6tr(XY ). Επειδή η
ομάδα SU(3) είναι συμπαγής και ημιαπλή, η B : 𝔰𝔲(3) ×𝔰𝔲(3) → ℝ θα είναι αρνητικά ορισμένη, οπότε θεωρούμε το
εσωτερικό γινόμενο 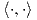 = -B(⋅,⋅). Ο υπόχωρος 𝔪 ως προς αυτό το γινόμενο θα είναι το ορθογώνιο συμπλήρωμα
της άλγεβρας Lie 𝔰𝔲(2), δηλαδή
= -B(⋅,⋅). Ο υπόχωρος 𝔪 ως προς αυτό το γινόμενο θα είναι το ορθογώνιο συμπλήρωμα
της άλγεβρας Lie 𝔰𝔲(2), δηλαδή
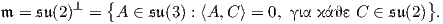
Για να κάνουμε πράξεις, θα πρέπει να δούμε τα στοιχεία της 𝔰𝔲(2) ως στοιχεία της 𝔰𝔲(3), μέσω της
εμβύθισης 𝔰𝔲(2)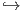 𝔰𝔲(3). Πρέπει να σημειώσουμε ότι ο υπόχωρος 𝔪 εξαρτάται από τον τρόπο που θα
επιλέξουμε να εμβυθίσουμε τη βάση της 𝔰𝔲(2) μέσα στην 𝔰𝔲(3). Διαλέγουμε την εξής εμβύθιση
𝔰𝔲(3). Πρέπει να σημειώσουμε ότι ο υπόχωρος 𝔪 εξαρτάται από τον τρόπο που θα
επιλέξουμε να εμβυθίσουμε τη βάση της 𝔰𝔲(2) μέσα στην 𝔰𝔲(3). Διαλέγουμε την εξής εμβύθιση
Επομένως, για την εύρεση του 𝔪 = 𝔰𝔲(2)⊥ θα πρέπει να ισχύει 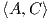 = 0 για κάθε C ∈{υ6,υ7,υ8}.
Επιλέγουμε ως C να είναι οι πίνακες υi, i = 6,7,8 και για A παίρνουμε έναν πίνακα της 𝔰𝔲(3) της μορφής
(*). ΄Ενας υπολογισμός δίνει ότι ο υπόχωρος 𝔪 θα αποτελείται από όλους τους πίνακες της μορφής
Επειδή dim𝔪 = 5 και dim𝔰𝔲(2) = 3, θα είναι πράγματι 𝔰𝔲(3) = 𝔰𝔲(2) ⊕𝔪. Αφήνουμε ως άσκηση ότι ο 𝔪 είναι ένας
Ad(SU(2))-αναλλοίωτος υπόχωρος του 𝔰𝔲(3).
= 0 για κάθε C ∈{υ6,υ7,υ8}.
Επιλέγουμε ως C να είναι οι πίνακες υi, i = 6,7,8 και για A παίρνουμε έναν πίνακα της 𝔰𝔲(3) της μορφής
(*). ΄Ενας υπολογισμός δίνει ότι ο υπόχωρος 𝔪 θα αποτελείται από όλους τους πίνακες της μορφής
Επειδή dim𝔪 = 5 και dim𝔰𝔲(2) = 3, θα είναι πράγματι 𝔰𝔲(3) = 𝔰𝔲(2) ⊕𝔪. Αφήνουμε ως άσκηση ότι ο 𝔪 είναι ένας
Ad(SU(2))-αναλλοίωτος υπόχωρος του 𝔰𝔲(3).
Σχετικά με την ισοτροπική αναπαράσταση του SU(3)∕SU(2), επειδή SU(3)∕SU(2) U(3)∕U(2), είναι πιο
εύχρηστο να υπολογιστεί η μιγαδοποιημένη ισοτροπική αναπαράσταση AdU(3)∕U(2) ⊗ ℂ : U(2) → Aut(𝔪).
Αφήνουμε ως άσκηση ότι αυτή ισούται με
U(3)∕U(2), είναι πιο
εύχρηστο να υπολογιστεί η μιγαδοποιημένη ισοτροπική αναπαράσταση AdU(3)∕U(2) ⊗ ℂ : U(2) → Aut(𝔪).
Αφήνουμε ως άσκηση ότι αυτή ισούται με
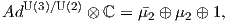
η οποία είναι αναγώγιμη και εκφράζεται ως ευθύ άθροισμα τριών μη αναγώγιμων και μη ισοδύναμων
υποαναπαραστάσεων διαστάσεων 2, 2 και 1 αντίστοιχα. Συνεπώς, ο μιγαδοποιήμενος εφαπτόμενος χώρος 𝔪ℂ του
ομογενούς χώρου U(3)∕U(2) θα εκφράζεται ως ευθύ άθροισμα τριών μιγαδικών υποχώρων διαστάσεων 2, 2 και 1,
δηλαδή
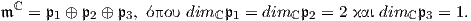
Επομένως, ο πραγματικός εφαπτόμενος χώρος 𝔪 θα γράφεται ως ευθύ άθροισμα δύο πραγματικών
Ad(U(2))-αναλλοίωτων υποχώρων διαστάσεων 4 και 1, δηλαδή θα είναι
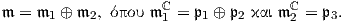
Επειδή U(3)∕U(2)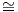 SU(3)∕SU(2), ο εφαπτόμενος χώρος του SU(3)∕SU(2) (τον οποίο συμβολίζουμε
επίσης με 𝔪) θα είναι ισόμορφος με το παραπάνω ευθύ άθροισμα των δύο Ad(SU(2))-αναλλοίωτων
υπόχωρων 𝔪1 και 𝔪2. Επιπλέον, επειδή για τους υποχώρους 𝔪1 και 𝔪2 θα πρέπει να ισχύουν οι σχέσεις
[𝔰𝔲(2),𝔪1] ⊂𝔪1 και [𝔰𝔲(2),𝔪2] ⊂𝔪2, θα έχουμε 𝔪1 = span
SU(3)∕SU(2), ο εφαπτόμενος χώρος του SU(3)∕SU(2) (τον οποίο συμβολίζουμε
επίσης με 𝔪) θα είναι ισόμορφος με το παραπάνω ευθύ άθροισμα των δύο Ad(SU(2))-αναλλοίωτων
υπόχωρων 𝔪1 και 𝔪2. Επιπλέον, επειδή για τους υποχώρους 𝔪1 και 𝔪2 θα πρέπει να ισχύουν οι σχέσεις
[𝔰𝔲(2),𝔪1] ⊂𝔪1 και [𝔰𝔲(2),𝔪2] ⊂𝔪2, θα έχουμε 𝔪1 = span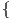 υ2,υ3,υ4,υ5
υ2,υ3,υ4,υ5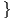 και 𝔪2 = span
και 𝔪2 = span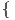 υ1
υ1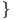 .
Επομένως, επειδή η ισοτροπική αναπαράσταση εκφράζεται ως ευθύ άθροισμα μη αναγώγιμων και μη
ισοδύναμων υποαναπαραστάσεων, κάθε Ad(SU(2))-αναλλοίωτο εσωτερικό γινόμενο στον 𝔪 θα δίνεται
ως
.
Επομένως, επειδή η ισοτροπική αναπαράσταση εκφράζεται ως ευθύ άθροισμα μη αναγώγιμων και μη
ισοδύναμων υποαναπαραστάσεων, κάθε Ad(SU(2))-αναλλοίωτο εσωτερικό γινόμενο στον 𝔪 θα δίνεται
ως
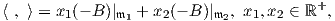
όπου B : 𝔰𝔲(3) ×𝔰𝔲(3) → ℝ, (X,Y ) 6tr(XY ). Συνεπώς, κάθε SU(3)-αναλλοίωτη μετρική στον SU(3)∕SU(2)
περιγράφεται από το παραπάνω εσωτερικό γινόμενο.
6tr(XY ). Συνεπώς, κάθε SU(3)-αναλλοίωτη μετρική στον SU(3)∕SU(2)
περιγράφεται από το παραπάνω εσωτερικό γινόμενο.
Θεωρούμε τη διαγώνια μετρική
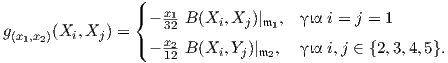
Για ευκολία στις πράξεις πολλαπλασιάζουμε την παραπάνω μετρική με 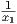 και θέτουμε λ =
και θέτουμε λ = 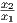 , τότε θα προκύψει
μια νέα μετρική με μία παράμετρο, δηλαδή
, τότε θα προκύψει
μια νέα μετρική με μία παράμετρο, δηλαδή
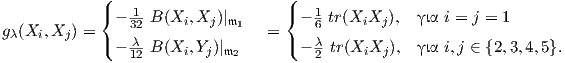
Με βάση την παραπάνω μετρική θα υπολογίσουμε την καμπυλότητα τομής του ομογενούς χώρου
SU(3)∕SU(2) S5, χρησιμοποιώντας το Θεώρημα 10.4. Λόγω της συμπεριφοράς της καμπυλότητας τομής ως προς
ομοιοθεσίες (βλ. τέλος του Κεφαλαίου 6), η καμπυλότητα ως προς τη μετρική g(x1,x2) θα δίνεται ως
Kg(x
1,x2) =
S5, χρησιμοποιώντας το Θεώρημα 10.4. Λόγω της συμπεριφοράς της καμπυλότητας τομής ως προς
ομοιοθεσίες (βλ. τέλος του Κεφαλαίου 6), η καμπυλότητα ως προς τη μετρική g(x1,x2) θα δίνεται ως
Kg(x
1,x2) = 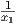 Kgλ. Παρατηρούμε ότι η βάση
Kgλ. Παρατηρούμε ότι η βάση 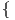 υ1,υ2,υ3,υ4,υ5
υ1,υ2,υ3,υ4,υ5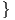 του χώρου 𝔪 δεν είναι ορθοκανονική ως προς την
μετρική gλ, οπότε θέτουμε
του χώρου 𝔪 δεν είναι ορθοκανονική ως προς την
μετρική gλ, οπότε θέτουμε
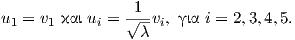
Θα χρειαστούμε τα γινόμενα Lie [ui,uj], τα οποία μετά από υπολογισμό είναι τα εξής:
Η απεικόνιση U : 𝔪 ×𝔪 →𝔪 η οποία ορίζεται από την σχέση (10.10) δίνεται ως εξής: U(u2,u3) = U(u2,u4) = U(u2,u5) = U(u3,u4) = U(u3,u5) = U(u4,u5) = 0.
Επομένως, επειδή τα εφαπτόμενα διανύσματα ui, i = 1,2,…,5 είναι ορθοκανονικά ως προς τη μετρική gλ, η
καμπυλότητα τομής του επιπέδου που παράγεται από τα δύο διανύσματα ui,uj (i≠j), θα δίνεται από την σχέση
K(ui,uj) = gλ(R(ui,uj)ui,uj), όπου ο τανυστής καμπυλότητας R καθορίζεται από το Θεώρημα 10.4. ΄Εχουμε ότι
Στη συνέχεια, θα υπολογίσουμε την καμπυλότητα Ricci του χώρου SU(3)∕SU(2) και θα διερευνήσουμε κατά
πόσον η διαγώνια μετρική gλ είναι μετρική Einstein. ΄Εχουμε
Θεωρούμε ένα τυχαίο στοιχείο X = ∑
i=15μiui ∈𝔪, μi ∈ ℝ \{0}. Για να είναι η μετρική gλ Einstein, θα πρέπει
Ric(X,X) = cgλ(X,X), c ∈ ℝ, ή ισοδύναμα εάν ισχύει
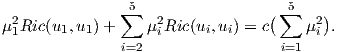
Επομένως, θα πρέπει
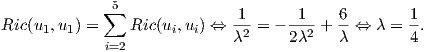
Από την παραπάνω διαδικασία συμπεραίνουμε ότι η διαγώνια μετρική του ομογενούς χώρου SU(3)∕SU(2) είναι
μετρική Einstein μόνο στην περίπτωση που η καμπυλότητα είναι σταθερή. Το αποτέλεσμα αυτό είχε αποδειχθεί
στις εργασίες [8] και [19].
Επίσης, παρατηρούμε ότι για λ = 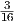 προκύπτει K(u2,u3) = K(u4,u5) = 0, ενώ για 0 < λ <
προκύπτει K(u2,u3) = K(u4,u5) = 0, ενώ για 0 < λ < 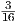 παίρνουμε
K(u2,u3), K(u4,u5) < 0. Τέλος, αν λ >
παίρνουμε
K(u2,u3), K(u4,u5) < 0. Τέλος, αν λ > 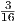 η καμπυλότητα του ομογενούς χώρου SU(3)∕SU(2)
η καμπυλότητα του ομογενούς χώρου SU(3)∕SU(2)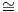 S5 είναι
παντού θετική. Στην περίπτωση όμως που η σφαίρα S5 είναι αμφιδιαφορική με τον ομογενή χώρο SO(6)∕SO(5),
τότε η καμπυλότητα θα είναι πάντα θετική. Βλέπουμε δηλαδή ότι η γεωμετρία της σφαίρας Sn εξαρτάται κάθε φορά
από την ομάδα που δρα μεταβατικά σε αυτήν.
S5 είναι
παντού θετική. Στην περίπτωση όμως που η σφαίρα S5 είναι αμφιδιαφορική με τον ομογενή χώρο SO(6)∕SO(5),
τότε η καμπυλότητα θα είναι πάντα θετική. Βλέπουμε δηλαδή ότι η γεωμετρία της σφαίρας Sn εξαρτάται κάθε φορά
από την ομάδα που δρα μεταβατικά σε αυτήν.
10.7 Ασκήσεις
1. Αποδείξτε ότι το σύνολο Gr2ℝ4 όλων των δισδιάστατων υποχώρων του ℝ4 αποτελεί μια λεία πολλαπλότητα
διάστασης 6.
2. Η Ευκλείδεια ομάδα
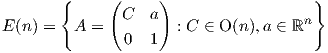 είναι
μια κλειστή υποομάδα της GLn+1ℝ (άρα μια ομάδα Lie) και δρα στον ℝn μέσω της σχέσης A⋅x = Cx + a, όπου
το x είναι διάνυσμα-στήλη. Αποδείξτε ότι η δράση είναι μεταβατική και ότι η ομάδα ισοτροπίας του σημείου
(0,0,…,0) ∈ ℝn είναι η ομάδα O(n), συνεπώς ℝn
είναι
μια κλειστή υποομάδα της GLn+1ℝ (άρα μια ομάδα Lie) και δρα στον ℝn μέσω της σχέσης A⋅x = Cx + a, όπου
το x είναι διάνυσμα-στήλη. Αποδείξτε ότι η δράση είναι μεταβατική και ότι η ομάδα ισοτροπίας του σημείου
(0,0,…,0) ∈ ℝn είναι η ομάδα O(n), συνεπώς ℝn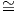 E(n)∕O(n).
E(n)∕O(n).
3. Θεωρούμε την ομάδα Lie SL2ℝ = {A ∈ GL2ℝ : detA = 1} και το υπερβολικό επίπεδο M = {z ∈ ℂ : Imz > 0}.
Αποδείξτε ότι η σχέση
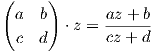 ορίζει
μια μεταβατική δράση. Στη συνέχεια, αποδείξτε ότι η ομάδα ισοτροπίας του σημείου i ∈ M είναι ισόμορφη με την
SO(2), συνεπώς M = SL2ℝ∕SO(2).
ορίζει
μια μεταβατική δράση. Στη συνέχεια, αποδείξτε ότι η ομάδα ισοτροπίας του σημείου i ∈ M είναι ισόμορφη με την
SO(2), συνεπώς M = SL2ℝ∕SO(2).
4. Αποδείξτε ότι η ομάδα GLn+1ℝ δρα μεταβατικά στον προβολικό χώρο ℝPn και βρείτε την ομάδα ισοτροπίας στο
σημείο [e1], e1 = (1,0,…,0) ∈ ℝn+1.
5. Βρείτε μια αναγωγική διάσπαση 𝔤 = 𝔨 ⊕𝔪 των εξής ομογενών χώρων G∕K: S3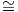 SO(4)∕SO(3), S5
SO(4)∕SO(3), S5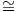 SU(3)∕SU(2),
του προβολικού χώρου ℝP2
SU(3)∕SU(2),
του προβολικού χώρου ℝP2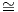 SO(3)∕O(2), της πολλαπλότητας Grassmann Gr2ℝ4
SO(3)∕O(2), της πολλαπλότητας Grassmann Gr2ℝ4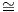 SO(4)∕SO(2) × SO(2) και
της πολλαπλότητας Stiefel V 2ℝ4
SO(4)∕SO(2) × SO(2) και
της πολλαπλότητας Stiefel V 2ℝ4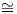 SO(4)∕SO(2).
SO(4)∕SO(2).
6. Αποδείξτε ότι η ισοτροπική αναπαράσταση της σφαίρας Sn = SO(n + 1)∕SO(n) είναι μη αναγώγιμη.
7. Αποδείξτε ότι η μιγαδοποιημένη ισοτροπική αναπαράσταση του ομογενούς χώρου SO(2n)∕U(n) είναι μη
αναγώγιμη. Συγκεκριμένα, αποδείξτε ότι AdSO(2n)∕U(n) ⊗ ℂ = ∧2μn ⊕∧2μn.
8. Αποδείξτε αναλυτικά το αντίστροφο της Πρότασης 10.7. Συγκεκριμένα, αποδείξτε ότι αν gK = hK (g,h ∈ G)
τότε το εσωτερικό γινόμενο (10.5) ικανοποιεί την σχέση ⟨X,Y ⟩hK = ⟨X,Y ⟩gK.
9. Βρείτε μια αναγωγική διάσπαση της πολλαπλότητας Stiefel V 2ℝ4 SO(4)∕SO(2) ως προς το εσωτερικό
γινόμενο ⟨X,Y ⟩ = -B(X,Y ) = -2tr(XY ) της 𝔰𝔬(4). Χρησιμοποιείστε τον τύπο (10.12) για να υπολογίσετε την
καμπυλότητα Ricci για την κανονική μετρική gB = -B|𝔪.
SO(4)∕SO(2) ως προς το εσωτερικό
γινόμενο ⟨X,Y ⟩ = -B(X,Y ) = -2tr(XY ) της 𝔰𝔬(4). Χρησιμοποιείστε τον τύπο (10.12) για να υπολογίσετε την
καμπυλότητα Ricci για την κανονική μετρική gB = -B|𝔪.
10. ΄Ενας ομογενής χώρος ονομάζεται συμμετρικός (symmetric space) εάν επιδέχεται μια αναγωγική διάσπαση
𝔤 = 𝔨 ⊕𝔪, τέτοια ώστε να ισχύουν οι σχέσεις
![[𝔨,𝔨] ⊂ 𝔨, [𝔨,𝔪 ] ⊂ 𝔪, [𝔪,𝔪 ] ⊂ 𝔨.](02_chapter_10306x.png) (α)
Αποδείξτε ότι για κάθε G-αναλλοίωτη μετρική ο G∕K ειναι φυσικά αναγωγικός.
(α)
Αποδείξτε ότι για κάθε G-αναλλοίωτη μετρική ο G∕K ειναι φυσικά αναγωγικός.
(β) Αποδείξτε ότι για κάθε X,Y ∈𝔪 ο τανυστής καμπυλότητας και η καμπυλότητα Ricci δίνονται αντίστοιχα από
τις σχέσεις
Βιβλιογραφία
[1] A. Arvanitoyeorgos, An Introduction to Lie Groups and the Geometry of Homogeneous Spaces,
American Mathematical Society, 2003.
[2] Α. Αρβανιτογεώργος, Ομάδες Lie, Ομογενείς Χώροι και Διαφορική Γεωμετρία, Εκδόσεις
Τροχαλία, Αθήνα 1999.
[3] A. L. Besse, Einstein Manifolds, Springer-Verlag, Berlin, 1986.
[4] F. Brickell and R.S. Clark, Differentiable Manifolds, Von Nostrand Reinhold, London, 1970.
[5] J. Cheeger and D.G. Ebin, Comparison Theorems in Riemannian Geometry, AMS Chelsea
Publishing Company, Providence, RI 1975.
[6] S. Gallot, D. Hulin and J. Lafontaine, Riemannian Geometry, Third Edition, Springer-Verlag,
New York, 2004.
[7] S. Helgason, Differential Geometry, Lie Groups and Symmetric Spaces, Academic Press, New
York 1978.
[8] G.R. Jensen, Einstein metrics on principal fibre bundles, J. Diff. Geom. 8 (1973) 599–614.
[9] J. Jost, Riemannian Geometry and Geometric Analysis, Third Edition, Springer-Verlag,
Berlin, 2002.
[10] S. Kobayashi and K. Nomizu, Foundations of Differential Geometry Vol II, Wiley - Interscience,
New York, 1969.
[11] J. M. Lee, Introduction to Smooth Manifolds, Springer-Verlag, New York, 2003.
[12] M. Nakahara, Geometry, Topology and Physics, Second Edition, Institute of Physics
Publishing, Bristol-Philadelphia, 2005.
[13] I. R. Porteous, Topological Geometry, Von Nostrand Reinhold, London, 1969.
[14] R.W Sharpe, Differential Geometry: Cartan’s Generalization of Klein’s Erlangen Programm,
Springer-Verlag New York, 1997.
[15] Μ. Σταθά, Μελέτη Γεωμετρίας Σφαιρών και Πολλαπλοτήτων Stiefel, Διπλωματική Εργασία για
Μ.Δ.Ε., Πανεπιστήμιο Πατρών, 2013.
[16] F. W. Warner: Foundations of Differentiable Manifolds and Lie Groups, Springer-Verlag New
York, 1983.
[17] N. R. Wallach, Compact homogeneous Riemannian manifolds with strictly positive sectional
curvature, Ann. of Math. 96 (1972) 277–295.
[18] Ι. Χρυσικός, Η Γεωμετρία των Ομογενών Χώρων και Πολλαπλότητες Σημαιών, Διπλωματική
Εργασία για Μ.Δ.Ε., Πανεπιστήμιο Πατρών, 2007.
[19] W. Ziller, Homogeneous Einstein metrics on spheres and projective spaces, Math. Ann. 259
(1982) 351–358.
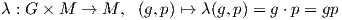
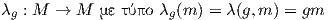
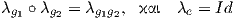
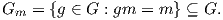
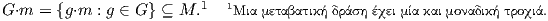
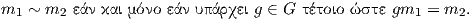
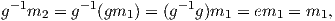
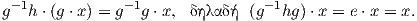
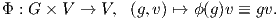
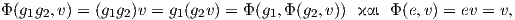
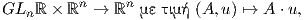
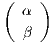
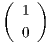
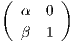
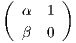
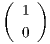 στο
στο 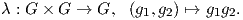
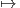
![X∕ ~ = {[x] : x ∈ X } = {{y ∈ X : y ~ x } : x ∈ X }.](02_chapter_1018x.png)

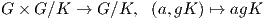
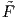
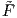
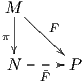
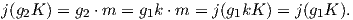
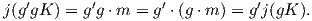
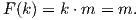
 , τέτοια ώστε
, τέτοια ώστε 
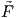 είναι η απεικόνιση
είναι η απεικόνιση 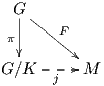
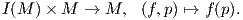
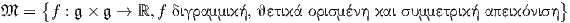
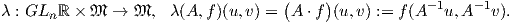
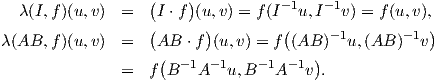
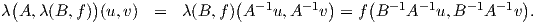
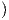
![- 1 t t -1 - 1
P [f]P = P [f]P = D, ισοδύναμα [f ] = (P ) DP ,](02_chapter_1039x.png)
![P ⋅D = (P -1)tDP -1 = (Pt)-1DP - 1 = [f].](02_chapter_1040x.png)
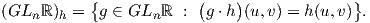
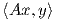
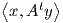
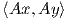
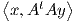
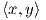
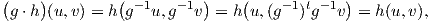
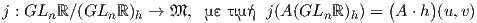
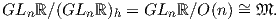
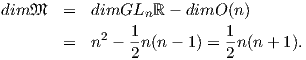
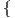
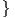
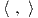 είναι το κανονικό
εσωτερικό γινόμενο του
είναι το κανονικό
εσωτερικό γινόμενο του 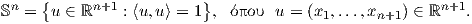
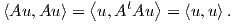
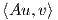
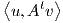
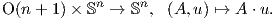

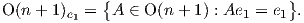
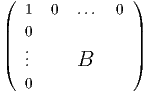
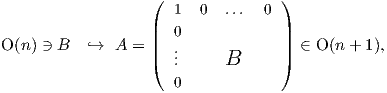
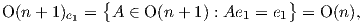
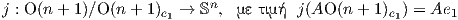
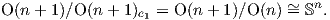
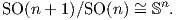

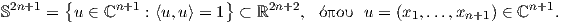
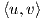
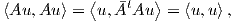
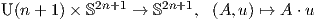
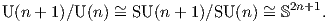
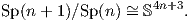






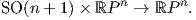
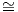
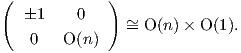
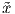 , όπου
, όπου 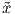 ως έναν
ως έναν 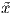
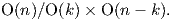
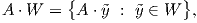
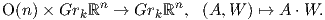
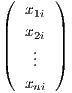 , τότε
, τότε 
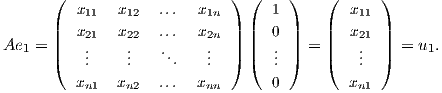
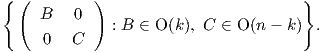
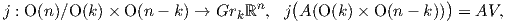
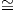
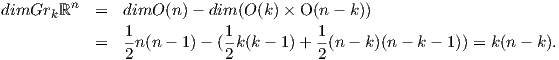
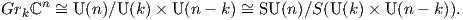
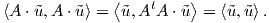
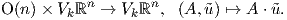
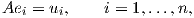
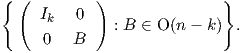
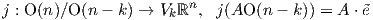

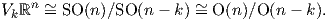
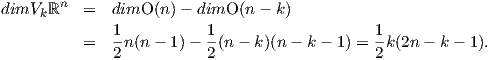
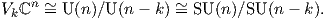
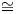
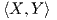
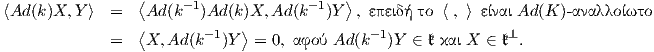
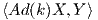
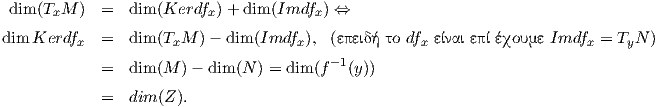
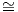
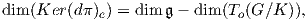
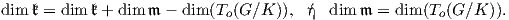
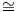
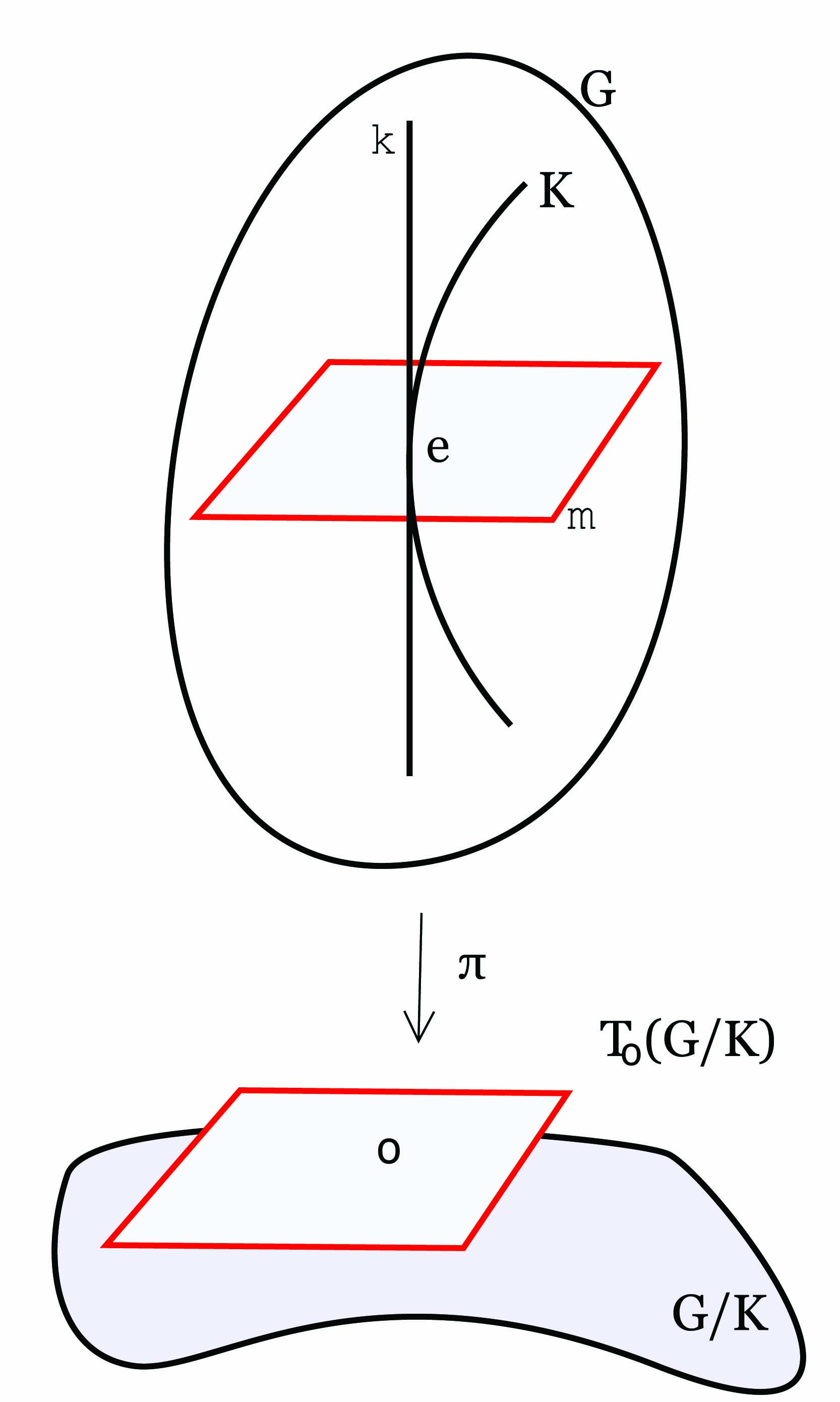
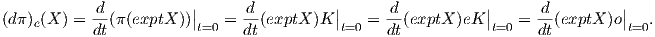
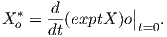
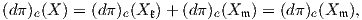
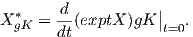
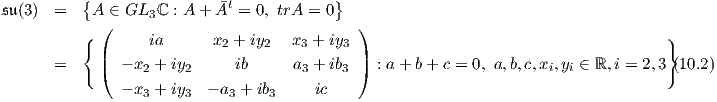
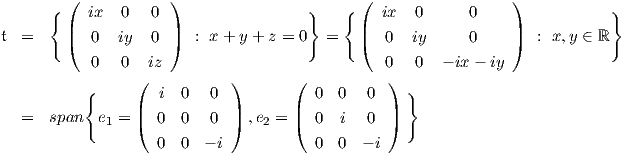
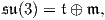
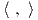
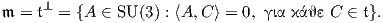
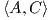
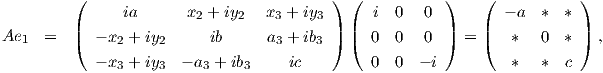
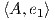
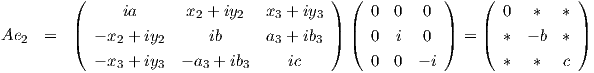
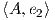
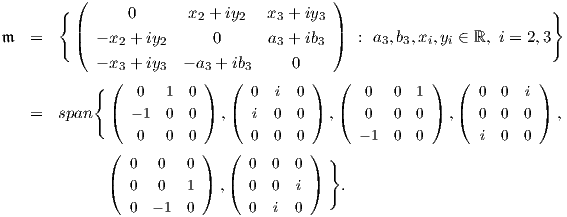
![[𝔱,𝔪] ⊂ 𝔪, ή ισοδύ να μα [X, Y] ∈ 𝔪 για κάθε X ∈ 𝔱, Y ∈ 𝔪.](02_chapter_10131x.png)
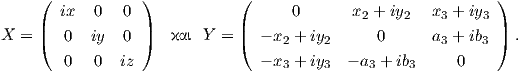
![( )
| 0 A + iB Γ + iΔ |
[X, Y] = XY - YX = ( - A + iB 0 K + iΛ ) , δηλα δή [X,Y ] ∈ 𝔪.
- Γ + iΔ - K + iΛ 0](02_chapter_10133x.png)

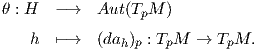
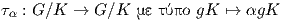

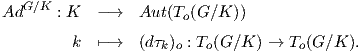
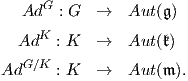

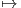

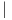
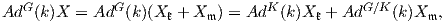


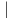

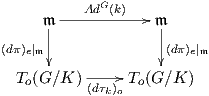
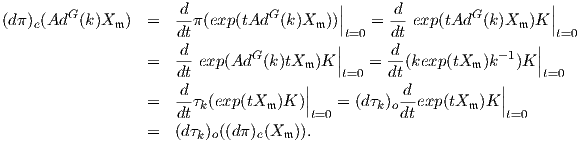
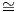
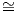
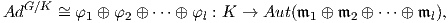
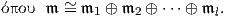
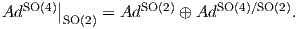
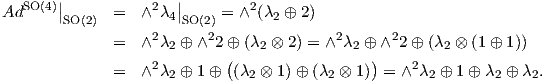
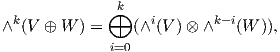
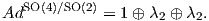
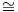
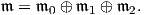
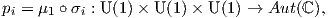
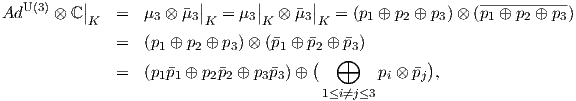
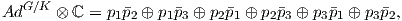
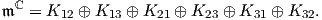
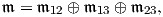
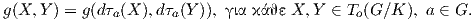
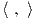 στον
στον 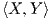
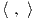 o με περιορισμό της μετρικής στον εφαπτόμενο χώρο
o με περιορισμό της μετρικής στον εφαπτόμενο χώρο 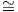
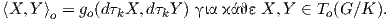
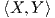 o
o 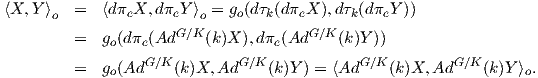
 o ένα
o ένα 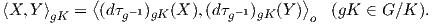
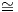
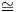
![⟨[X, Y ]𝔪,Z ⟩ = ⟨X, [Y, Z]𝔪⟩ (10.6)](02_chapter_10181x.png)

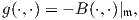
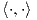
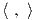
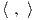
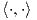
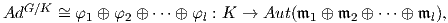
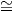

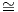

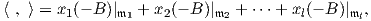

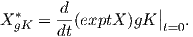
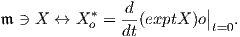
![[X*,Y *] = - [X, Y ]*.](02_chapter_10197x.png)
![2g(∇X Y,Z ) = g([X, Y],Z) + g([X, Z],Y )+ g([Y, Z],X ).](02_chapter_10198x.png)
![2g(∇X Y, Z) = Xg (Y,Z )+ Y g(Z,X )- Zg(X, Y)
+ g([X,Y ],Z )- g([Y,Z ],X )+ g([Z,X ],Y).](02_chapter_10199x.png)
![Xg (Y,Z ) = g([X,Y ],Z )+ g(Y, [X, Z]),
Y g(Z,X ) = g([Y,Z],X )+ g(Z,[Y,X ]),
Zg (X,Y ) = g([Z,X ],Y )+ g(X, [Z,Y ]).](02_chapter_10200x.png)
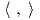 το αντίστοιχο
το αντίστοιχο 
![1
(∇X *Y *)o = - -[X,Y ]𝔪 + U (X, Y),
2](02_chapter_10203x.png)
![2⟨U (X, Y ),Z⟩ = ⟨[Z, X]𝔪,Y ⟩+ ⟨X, [Z, Y]𝔪⟩.](02_chapter_10204x.png)
![2g(∇X *Y *,Z *) = g([X*,Y *],Z *)+ g([X *,Z *],Y *)+ g([Y*,Z *],X *)
= - g([X, Y ]*,Z *) - g([X, Z ]*,Y *)- g([Y, Z]*,X *).](02_chapter_10205x.png)
![2⟨(∇X *Y *)o,Z⟩ = - ⟨[X,Y ]𝔪, Z⟩ - ⟨[X, Z]𝔪,Y ⟩- ⟨X, [Y,Z ]𝔪⟩ ⇔
* 1
2⟨(∇X *Y )o + 2[X,Y ]𝔪, Z⟩ = ⟨[Z,X ]𝔪,Y ⟩+ ⟨X,[Z,Y ]𝔪⟩
= 2⟨U (X, Y),Z ⟩,](02_chapter_10206x.png)
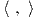 είναι
είναι ![⟨[X, Y] ,Z ⟩
𝔪](02_chapter_10208x.png)
![⟨Y,[X, Z] ⟩
𝔪](02_chapter_10209x.png) για κάθε
για κάθε
![⟨[X, Y ]𝔪, Z⟩ = - ⟨X, [Z,Y ]𝔪 ⟩ = ⟨X, [Y, Z]𝔪⟩,](02_chapter_10210x.png)
![3- 2 1- 1-
⟨R(X, Y )Y, X ⟩ = - 4|[X, Y]𝔪| - 2⟨[X, [X,Y ]𝔪 ]𝔪, Y⟩- 2⟨[Y, [Y, X]𝔪]𝔪,X ⟩
+|U (X, Y )|2 - ⟨U(X, X ),U (Y,Y )⟩+ ⟨Y,[[X, Y] ,X ]⟩.
𝔨 𝔪](02_chapter_10211x.png)
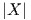
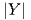
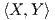
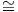
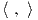
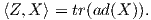
![∑ ∑
tr(ad(X )) = ⟨ad(X )Xi,Xi ⟩ = ⟨[X, Xi]𝔪,Xi⟩ = ⟨Z,X ⟩.
i i](02_chapter_10218x.png)
![1∑ 1
Ric(X, X ) = - -- |[X, Xi]𝔪|2 - -⟨[X, [X, Xi]𝔪]𝔪,Xi⟩
2 i 2
∑ 1∑ 2
- ⟨[X, [X,Xi ]𝔨]𝔪,Xi⟩+ 4 ⟨[Xi,Xj ]𝔪,X ⟩ - ⟨[Z,X ]𝔪,X ⟩,
i i,j](02_chapter_10219x.png)
![∑
Ric(X,X ) = - 1 |[X,Xi ]𝔪 |2 - 1B (X,X )
2 i 2
1 ∑
+-- ⟨[Xi, Xj]𝔪,X ⟩2 - ⟨[Z,X ]𝔪,X ⟩.
4 i,j](02_chapter_10220x.png)
![1∑ 1 ∑
S = - -- |[Xi,Xj ]𝔪 |2 - -- B (Xi, Xi)- |Z |2.
2 i,j 2 i](02_chapter_10221x.png)
![(∇X *Y *)o = - 1[X, Y]𝔪.
2](02_chapter_10222x.png)
![1- 2
⟨R (X, Y)X, Y⟩ = 4|[X,Y ]𝔪| + ⟨[[X, Y]𝔨,X ]𝔪,Y ⟩.](02_chapter_10223x.png)
![1
⟨R (X, Y )Y,X ⟩ = 4⟨[X,Y ]𝔪,[X,Y ]𝔪 ⟩+ Q ([X, Y ]𝔨,[X, Y ]𝔨),
1 1∑
Ric(X, X ) = - -B (X,X )+ -- Q([X,Vi]𝔨,[X, Vi]𝔨),
4 2 i](02_chapter_10224x.png)
![1
B (R(X, Y )X, Y ) = -B ([X,Y ]𝔪,[X, Y ]𝔪 )+ B ([X, Y]𝔨,[X, Y]𝔨), (10.11)
4 ∑
Ric(X, X ) = - 1B (X,X )+ 1- B([X, Vi]𝔨,[X, Vi]𝔨). (10.12)
4 2 i](02_chapter_10225x.png)
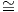

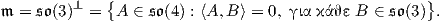
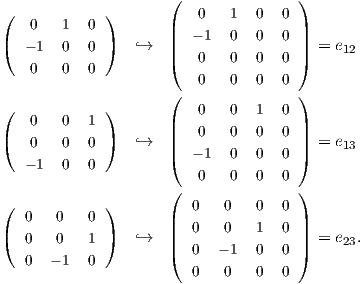
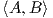
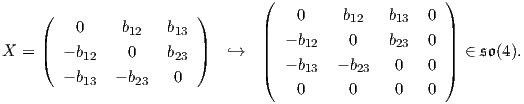
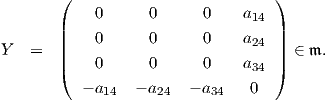
![[(X,Y ] = XY - YX = )
0 0 0 b12a24 + b13a34
|| 0 0 0 - b a + b a ||
|| 12 14 23 34 || ∈ 𝔪,
( 0 0 0 - b13a14 - b23a24 )
- b12a24 - b13a34 b12a14 - b23a34 b13a14 + b23a24 0](02_chapter_10234x.png)
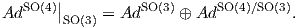
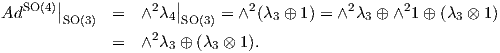
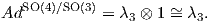
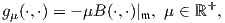
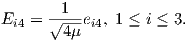
![( )
0 - 14μ 0 0
|| 1- 0 0 0 || 1
[E14,E24] = E14E24 - E24E14 = | 4μ | = - --e12,
( 0 0 0 0 ) 4μ
0 0 0 0](02_chapter_10240x.png)
![( )
0 0 - 41μ 0
|| 0 0 0 0 || -1-
[E14,E34] = E14E34 - E34E14 = |( 1- 0 0 0 |) = - 4μe13,
4μ
0 0 0 0](02_chapter_10241x.png)
![( )
0 0 0 0
| -1 |
[E24,E34] = E24E34 - E34E24 = || 0 01 - 4μ 0 || = - -1e23.
( 0 4μ 0 0 ) 4μ
0 0 0 0](02_chapter_10242x.png)
![K (E14,E24 ) = gμ(R(E14,E24 )E24, E12) = gμ([E14,E24]𝔰𝔬(3),[E14,E24]𝔰𝔬(3))
1 1 1 1
= gμ(--e12,---e12) = ----22μtr(e12e12) =---.
4μ 4μ 16μ 4 μ](02_chapter_10243x.png)
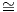
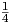 η καμπυλότητα τομής ισούται με 1. Στην περίπτωση αυτή, η κανονική μετρική της
η καμπυλότητα τομής ισούται με 1. Στην περίπτωση αυτή, η κανονική μετρική της

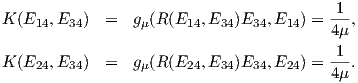
![1
Ric(E14,E14) = ---gμ(E14,E14)+ gμ([E14,E24]𝔰𝔬(3),[E14,E24]𝔰𝔬(3))
4
+g μ([E14,E34 ]𝔰𝔬(3),[E14,E34 ]𝔰𝔬(3))
- 1-+ --1----g (e ,e )+ ---1---g (e ,e ) = - 1-+-1-,
4 2⋅16μ2 μ 12 12 2 ⋅16μ2 μ 13 13 4 4μ
1
Ric(E24,E24) = -4-gμ(E24,E24)+ gμ([E24,E14]𝔰𝔬(3),[E24,E14]𝔰𝔬(3))
1 1
+g μ([E24,E34 ]𝔰𝔬(3),[E24,E34 ]𝔰𝔬(3)) = ---+ ---,
4 4μ
Ric(E34,E34) = gμ(E34,E34)+ gμ([E34,E14]𝔰𝔬(3),[E34,E14]𝔰𝔬(3))
1- -1-
+g μ([E34,E24 ]𝔰𝔬(3),[E34,E24 ]𝔰𝔬(3)) = - 4 + 4μ .](02_chapter_10248x.png)
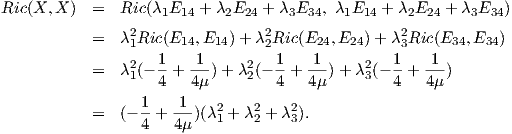
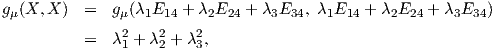
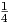
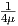
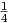
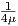
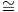
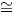
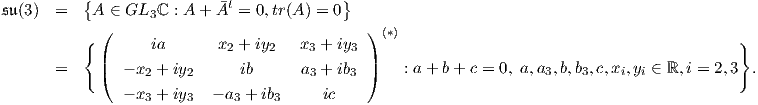
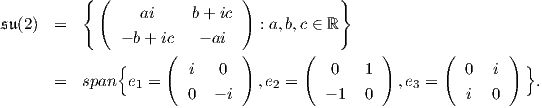
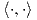
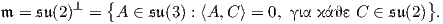
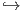
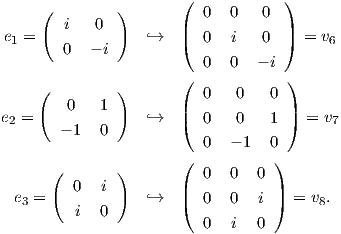
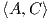
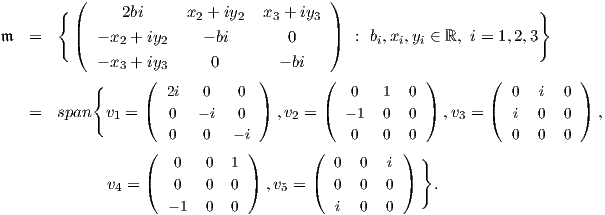

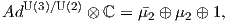
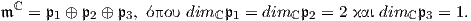
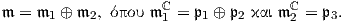
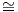
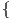
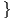
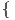
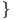
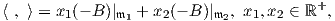

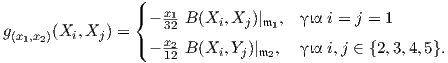
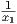 και θέτουμε
και θέτουμε 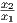
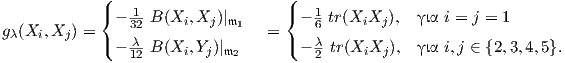

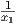
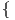
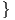
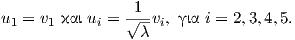
![[u1,u2] = 3u3 ∈ 𝔪, [u1,u3] = - 3u2 ∈ 𝔪, [u1,u4] = 3u5 ∈ 𝔪, [u1,u5] = - 3u4 ∈ 𝔪,
1 1 1
[u2,u3] = -(v1 - v6) ∈ 𝔪 \𝔰𝔲(3), [u2,u4] =-v7 ∈ 𝔰𝔲(3), [u2,u5] = --v8 ∈ 𝔰𝔲(3),
λ λ λ
[u3,u4] = 1v8 ∈ 𝔰𝔲(3 ), [u3,u5] = - 1v7 ∈ 𝔰𝔲(3), [u4,u5] = 1-(v1 + v6) ∈ 𝔪 + 𝔰𝔲 (3),
λ λ λ
[v6,u2] = - u3 ∈ 𝔪, [v7,u2]- u4 ∈ 𝔪.](02_chapter_10285x.png)
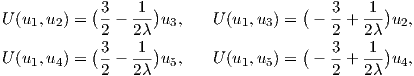
![K(u1,u2) = - 3gλ([u1,u2]𝔪,[u1,u2]𝔪 )- 1-gλ([u1,[u1,u2]𝔪 ]𝔪) - 1gλ([u2,[u2,u1]𝔪]𝔪,u1)
4 2 2
= +gλ(U (u1,u2),U (u1,u2))- gλ(U (u1,u1),U (u2,u2))+ gλ(u2,[[u1,u2]𝔰𝔲(2),u1 ]𝔪)
27- 1- 1- 3- 1--2 -1--
= - 4 - 2gλ([u1,3u3]𝔪,u2) - 2gλ([u2,- 3u3]𝔪,u1) + (2 - 2λ) = 4λ2
3 1 1
K(u2,u3) = - 4gλ([u2,u3]𝔪,[u2,u3]𝔪 )- 2-gλ([u2,[u2,u3]𝔪 ]𝔪) - 2gλ([u3,[u3,u2]𝔪]𝔪,u2)
3 1 1 1
= - --2 - --gλ([u2,u1]𝔪,u3 )+ ---gλ([u3,u1]𝔪,u2)+ gλ(u3,[- -v6,u2]𝔪)
4λ 2λ 2λ λ
= - -3-+ 3--+ -3-+ 1-= - -3--+ -4.
4λ2 2λ 2λ λ 4λ2 λ](02_chapter_10287x.png)
![K (u2,u4 ) = - 3gλ([u2,u4]𝔪,[u2,u4]𝔪)- 1-gλ([u2,[u2,u4]𝔪 ]𝔪 )- 1gλ([u4,[u4,u2 ]𝔪]𝔪,u2)
4 2 2
= gλ(u4,[- 1-v7,u2 ]𝔪) = - 1gλ(u4,- u4) = 1-
λ λ λ](02_chapter_10288x.png)
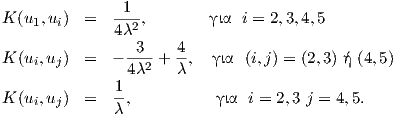
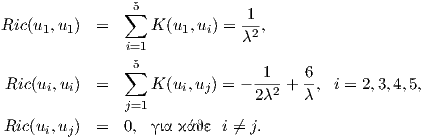
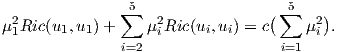
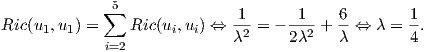
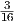 προκύπτει
προκύπτει  παίρνουμε
παίρνουμε
 η καμπυλότητα του ομογενούς χώρου
η καμπυλότητα του ομογενούς χώρου 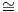
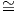
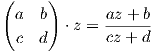
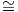
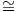
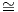
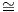
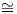

![[𝔨,𝔨] ⊂ 𝔨, [𝔨,𝔪 ] ⊂ 𝔪, [𝔪,𝔪 ] ⊂ 𝔨.](02_chapter_10306x.png)
![⟨R (X,Y )Y,X ⟩ = - ⟨[[X,Y ],Y],X ⟩
1-
Ric (X, Y ) = - 2B (X,Y ).](02_chapter_10307x.png)