Σύνοψη
Ορίζουμε ένα εφαπτόμενο διάνυσμα σε ένα σημείο μιας πολλαπλότητας ως μια παραγώγιση κατά σημείο. Το σύνολο
όλων των εφαπτόμενων διανυσμάτων σε ένα σημείο αποτελεί τον εφαπτόμενο χώρο της πολλαπλότητας στο σημείο
αυτό. Ορίζουμε το διαφορικό μιας λείας απεικόνισης μεταξύ πολλαπλοτήτων και δίνουμε τρόπο υπολογισμού του με
χρήση καμπυλών σε πολλαπλότητες. Ορίζουμε την έννοια της κανονικής υποπολλαπλότητας μιας λείας
πολλαπλότητας. Χρησιμοποιούμε το θεώρημα αντίστροφης συνάρτησης για να αποδείξουμε ότι ένα κανονικό
σύνολο στάθμης μιας πραγματικής λείας συνάρτησης, είναι μια κανονική υποπολλαπλότητα. Οι βασικές μας
αναφορές είναι τα βιβλία [1], [3], [4], [5], [6].
Προαπαιτούμενη γνώση
Διαφορικός Λογισμός μιας και πολλών μεταβλητών, Βασική Γραμμική Άλγεβρα.
Η βασική δυσκολία με τη θεωρία πολλαπλοτήτων είναι ότι αυτή αναπτύσσεται χωρίς να λαμβάνεται υπόψη κάποια πιθανή εμφύτευση της λείας πολλαπλότητας σε έναν ευκλείδειο χώρο. Συνεπώς, έννοιες που αντιμετωπίστηκαν με σχετική ευκολία στη θεωρία επιφανειών (όπως εφαπτόμενος χώρος, καμπυλότητα, κ.λπ.) χρειάζονται διαφορετικό χειρισμό.
΄Εχοντας ορίσει την έννοια της λείας απεικόνισης μεταξύ δύο πολλαπλοτήτων, θα προχωρήσουμε στον ορισμό του διαφορικού μιας λείας απεικόνισης. Για τον σκοπό αυτό θα χρειαστούμε να ορίσουμε τον εφαπτόμενο χώρο TpM μιας πολλαπλότητας M σε ένα σημείο p. Τα εφαπτόμενα διανύσματα θα τα αναγνωρίζουμε ως παραγωγίσεις στο σημείο p. Η γενική αρχή είναι ότι ο εφαπτόμενος χώρος αποτελεί τη βέλτιστη προσέγγιση μιας πολλαπλότητας σε ένα σημείο της και το διαφορικό τη βέλτιστη προσέγγιση μιας λείας συνάρτησης σε ένα σημείο. Στη συνέχεια, θα ορίσουμε την έννοια της υποπολλαπλότητας μιας λείας πολλαπλότητας και ως εφαρμογή του θεωρήματος αντίστροφης απεικόνισης θα δούμε μέθοδο κατασκευής υποπολλαπλοτήτων μέσω συνόλων στάθμης. Η συλλογή όλων των εφαπτόμενων χώρων μιας λείας πολλαπλότητας θα ορίσει την εφαπτομένη δέσμη, η οποία αποτελεί παράδειγμα μιας διανυσματικής δέσμης σε μια πολλαπλότητα. Αυτή θα την εξετάσουμε στο επόμενο κεφάλαιο.
Προκειμένου να προετοιμάσουμε τον επόμενο ορισμό, ας δούμε δύο απλά παραδείγματα.
΄Εστω γ : (-ϵ,ϵ) → ℝn μια λεία καμπύλη. Τότε το εφαπτόμενο διάνυσμα (ταχύτητα) στο σημείο p = γ(0) είναι
το
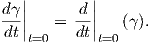
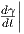 t=0.
t=0. 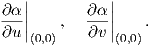
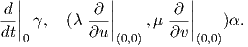
Θεωρούμε λοιπόν το σύνολο Cp∞(M) όλων των σπόρων των πραγματικών συναρτήσεων σε μια περιοχή του σημείου p. Η σημειακή πρόσθεση και πολλαπλασιασμός εφοδιάζουν το σύνολο Cp∞(M) με δομή δακτυλίου. Επιπλέον, με πράξη τον βαθμωτό πολλαπλασιασμό από το σύνολο των πραγματικών αριθμών, το σύνολο Cp∞(M) εφοδιάζεται με δομή μιας πραγματικής άλγεβρας.
Ορισμός 3.1: ΄Εστω M μια λεία πολλαπλότητα και έστω p ∈ M. ΄Ενα εφαπτόμενο διάνυσμα (tangent vector) της M στο p είναι μια απεικόνιση
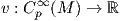
για κάθε f,g ∈ Cp∞(M) και λ,μ ∈ ℝ.
Με άλλα λόγια ένα εφαπτόμενο διάνυσμα είναι μια παραγώγιση κατά σημείο στο σύνολο Cp∞(M). Συμβολίζουμε με TpM το σύνολο όλων των εφαπτόμενων διανυσμάτων της M στο p. Το σύνολο αυτό ονομάζεται ο εφαπτόμενος χώρος (tangent space) της πολλαπλότητας M στο p.
Παρατηρείστε ότι αν U είναι ένα ανοικτό υποσύνολο της M που να περιέχει το σημείο p, τότε επειδή Cp∞(U) = Cp∞(M), θα είναι TpU = TpM.
Παραδείγματα.
1. ΄Εστω M = ℝn εφοδιασμένος με τον κανονικό άτλαντα {(ℝn,Idℝn)}. Τότε οι συναρτήσεις
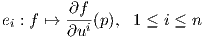
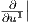 p,…,
p,…,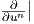 p αποτελούν μια βάση του
Tpℝn, άρα
p αποτελούν μια βάση του
Tpℝn, άρα
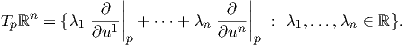
2. ΄Εστω (U,φ) = (U;x1,…,xn) ένας τοπικός χάρτης στο p μιας πολλαπλότητας M, όπου xi = πi ∘φ : U ⊂ M → ℝ. Για κάθε f ∈ Cp∞(U) ορίζουμε
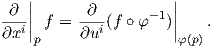
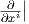 p είναι παραγωγίσεις στο p, άρα εφαπτόμενα διανύσματα της πολλαπλότητας M στο
p.
p είναι παραγωγίσεις στο p, άρα εφαπτόμενα διανύσματα της πολλαπλότητας M στο
p.
΄Εχοντας ορίσει τον εφαπτόμενο χώρο μιας λείας πολλαπλότητας σε ένα σημείο της, μπορούμε να ορίσουμε το διαφορικό μιας λείας απεικόνισης μεταξύ πολλαπλοτήτων.
Ορισμός 3.2: ΄Εστω M και N λείες πολλαπλότητες, F : M → N λεία απεικόνιση και p ∈ M. Το διαφορικό (ή παράγωγος) (differential/derivative) της F στο p είναι η απεικόνιση dFp : TpM → TF(p)N με τιμή
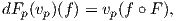
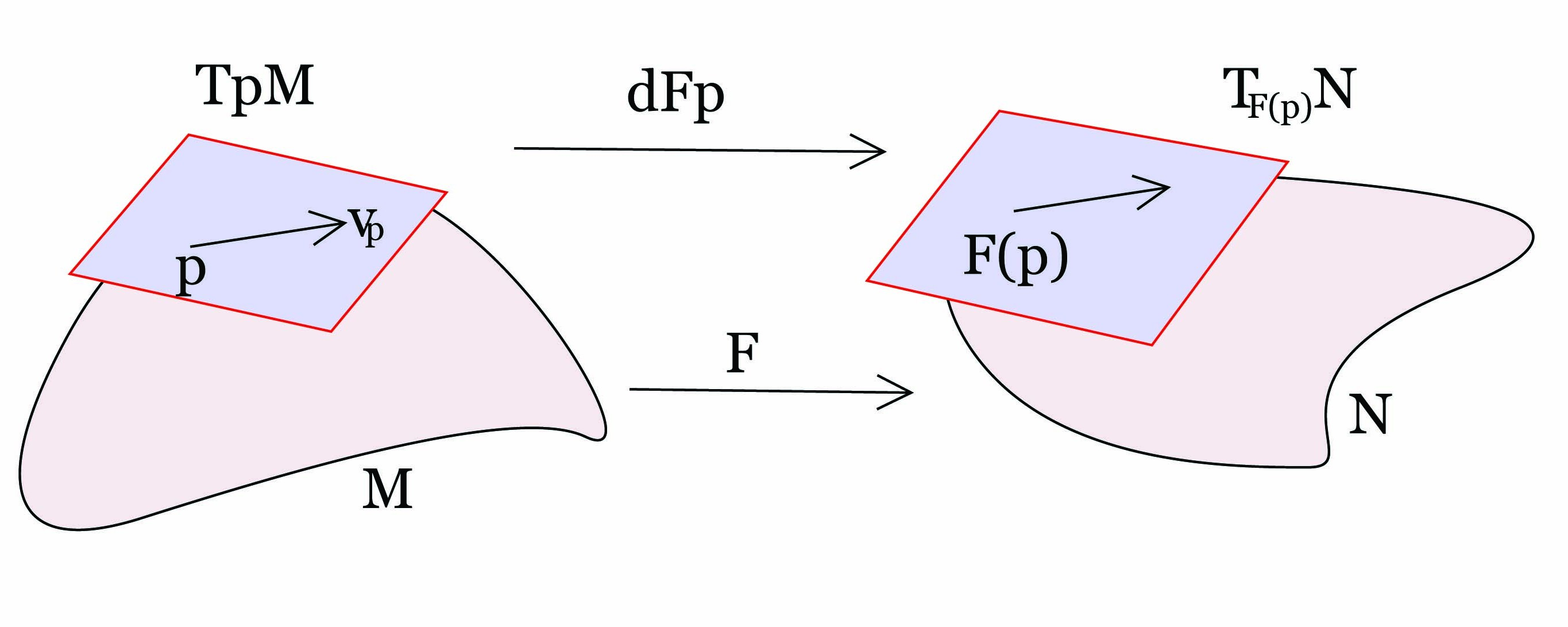
Πολλές φορές παραλείπουμε τον δείκτη του εφαπτόμενου διανύσματος και γράφουμε dfp(υ)(f) = υ(f ∘ F).
Αποδεικνύεται εύκολα ότι dFp(υp) είναι πράγματι μια παραγώγιση στο F(p) και ότι η απεικόνιση dFp : TpM → TF(p)N είναι γραμμική.
Παράδειγμα. ΄Εστω M = ℝn,N = ℝm με συντεταγμένες x1,…,xn και y1,…,ym αντίστοιχα. Θεωρούμε μια λεία
συνάρτηση F : ℝn → ℝm στο σημείο p ∈ ℝn. Θυμίζουμε ότι το σύνολο {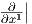 p,…,
p,…,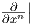 p} αποτελεί μια βάση
του Tpℝn και το σύνολο {
p} αποτελεί μια βάση
του Tpℝn και το σύνολο {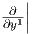 F(p),…,
F(p),…,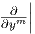 F(p)} μια βάση του TF(p)ℝm. Η γραμμική απεικόνιση
dFp : Tpℝn → TF(p)ℝm καθορίζεται από τον πίνακα (αji) που ορίζεται ως
F(p)} μια βάση του TF(p)ℝm. Η γραμμική απεικόνιση
dFp : Tpℝn → TF(p)ℝm καθορίζεται από τον πίνακα (αji) που ορίζεται ως
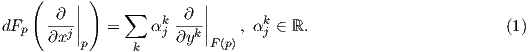
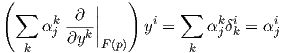
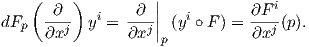
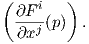
Πρόταση 3.2: (Κανόνας της αλυσίδας). ΄Εστω F : M → N και G : N → P λείες συναρτήσεις μεταξύ πολλαπλοτήτων και έστω p ∈ M. Δείξτε ότι d(G ∘ F)p = dGF(p) ∘ dFp.
Το διαφορικό της ταυτοτικής απεικόνισης IdM : M → M σε κάθε σημείο p ∈ M είναι η ταυτοτική απεικόνιση Id : TpM → TpM. Πράγματι, για κάθε υp ∈ TpM και f ∈ F(M) είναι
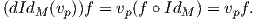
Πόρισμα 3.1: ΄Εστω F : M → N μια αμφιδιαφόριση μεταξύ πολλαπλοτήτων και έστω p ∈ M. Τότε το διαφορικό dFp : TpM → TF(p)N είναι ισομορφισμός διανυσματικών χώρων.
Απόδειξη. Αρκεί να δειχθεί ότι η F έχει μια λεία αντίστροφη G : N → M, τέτοια ώστε G ∘ F = IdM και F ∘ G = IdN. Από τον κανόνα της αλυσίδας προκύπτουν οι σχέσεις d(G ∘ F)p = IdTpM και d(F ∘ G)F(p) = IdTF(p)M, άρα οι απεικονίσεις dFp και dGF(p) είναι ισομορφισμοί. ▄
΄Αμεσο τώρα αποτέλεσμα είναι ότι ο ορισμός της διάστασης μιας λείας πολλαπλότητας είναι καλός.
Πόρισμα 3.2: ΄Εστω U ένα ανοικτό υποσύνολο του ℝn το οποίο είναι αμφιδιαφορικό με το ανοικτό V ⊂ ℝm. Τότε n = m.
Απόδειξη. ΄Εστω F : U → V η αντίστοιχη αμφιδιαφόριση και p ∈ U. Από το προηγούμενο πόρισμα η
απεικόνιση dFp : TpU → TF(p)V είναι ισομορφισμός διανυσματικών χώρων και λόγω των ισομορφισμών
TpU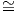 ℝn και TF(p)V
ℝn και TF(p)V  ℝm, προκύπτει ότι n = m. ▄
ℝm, προκύπτει ότι n = m. ▄
Θα βρούμε τώρα μια βάση του εφαπτόμενου χώρου TpM. Θυμίζουμε ότι αν (U,φ) είναι ένας χάρτης σε ένα σημείο p μιας πολλαπλότητας M τότε η απεικόνιση φ : U → ℝn είναι μια αμφιδιαφόριση επί του φ(U), συνεπώς από το Πόρισμα 3.1 το διαφορικό dφp : TpM → Tφ(p)ℝn είναι ισομορφισμός διανυσματικών χώρων. Ειδικότερα, η διάσταση του εφαπτόμενου χώρου TpM ισούται με τη διάσταση n της πολλαπλότητας M.
Πρόταση 3.3: ΄Εστω (U,φ) = (U;x1,…,xn) ένας χάρτης σε ένα σημείο p μια πολλαπλότητας M. Τότε
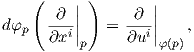
Απόδειξη. ΄Ασκηση.
(ϒπόδειξη: Πάρτε μια f ∈ Cφ(p)∞(ℝn) και χρησιμοποιείστε τον ορισμό του διαφορικού προκειμένου να
δείξετε την ισότητα των δύο εφαπτόμενων διανυσμάτων.) ▄
Πρόταση 3.4: ΄Εστω (U;x1,…,xn) ένας χάρτης σε ένα σημείο p μια πολλαπλότητας M. Τότε το σύνολο
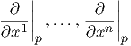
Απόδειξη. ΄Ενας ισομορφισμός διανυσματικών χώρων απεικονίζει βάσεις σε βάσεις. Λόγω της Πρότασης 3.3
ο ισομορφισμός dφp : TpM → Tφ(p)ℝn στέλνει τη βάση 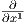 |p,…,
|p,…,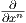 |p στο σύνολο
|p στο σύνολο 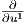 |φ(p),…,
|φ(p),…,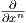 |φ(p),
το οποίο αποτελεί βάση του Tφ(p)ℝn, απ΄ όπου προκύπτει το αποτέλεσμα. ▄
|φ(p),
το οποίο αποτελεί βάση του Tφ(p)ℝn, απ΄ όπου προκύπτει το αποτέλεσμα. ▄
Ας δούμε πώς αλλάζει η παραπάνω βάση στην τομή δύο χαρτών.
Πρόταση 3.5: ΄Εστω (U;x1,…,xn) και (V ;y1,…,yn) δύο χάρτες μιας πολλαπλότητας M. Τότε στην τομή U ∩ V ισχύει
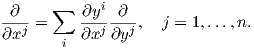
Απόδειξη. Σε κάθε σημείο p ∈ U ∩ V τα σύνολα {∂∕∂xj|p} και {∂∕∂yj|p} είναι και τα δύο βάσεις του εφαπτόμενου χώρου TpM, συνεπώς υπάρχει ένας πραγματικός πίνακας (aji(p)) ώστε στο U ∩V να ισχύει
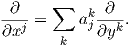
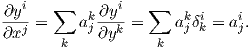
Θα κλείσουμε το τμήμα αυτό με μια τοπική έκφραση του διαφορικού, η οποία γενικεύει γνωστή έκφραση του διαφορικού μιας διαφορίσιμης συνάρτησης μεταξύ Ευκλειδείων χώρων.
Πρόταση 3.6: ΄Εστω F : M → N μια λεία απεικόνιση μεταξύ πολλαπλοτήτων, p ∈ M και έστω
(U;x1,…,xm), (V ;y1,…,yn) τοπικοί χάρτες στα σημεία p ∈ M και F(p) ∈ N αντίστοιχα. Τότε, ως προς τις
βάσεις {∂∕∂xj|p} του TpM και {∂∕∂yi|F(p)} του TF(p)N, το διαφορικό dFp : TpM → TF(p)N παρίσταται
από τον πίνακα 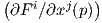 , όπου Fi = yi ∘ F η i-συνιστώσα της F.
, όπου Fi = yi ∘ F η i-συνιστώσα της F.
Απόδειξη. Από τη γραμμική άλγεβρα (π.χ. [2]) γνωρίζουμε ότι το διαφορικό dFp (ως γραμμική απεικόνιση) καθορίζεται πλήρως από τους πραγματικούς αριθμούς aji έτσι ώστε
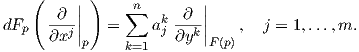
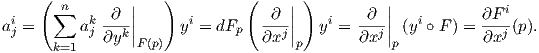
ϒπάρχουν δύο κατηγορίες διαφορίσιμων απεικονίσεων που έχουν ιδιαίτερο ρόλο στη διαφορική γεωμετρία.
Ορισμός 3.3: ΄Εστω F : M → N μια λεία συνάρτηση και έστω p ∈ M.
Η F ονομάζεται εμβάπτιση (αντίστ. υπεμβάπτιση), εάν είναι εμβάπτιση (αντίστ. υπεμβάπτιση), για κάθε p ∈ M.
Παρατήρηση. Εάν οι διάστάσεις των M και N είναι m και n αντίστοιχα, τότε dimTpM = m και dimTF(p) = n. Εάν το διαφορικό dFp : TpM → TF(p)N είναι 1-1 τότε m ≤ n και αντίστοιχα εάν αυτό είναι επί, τότε m ≥ n. Συνεπώς, εάν η F : M → N είναι εμβάπτιση σε ένα σημείο της M, τότε m ≤ n και εάν είναι υπεμβάπτιση σε ένα σημείο της M, τότε m ≥ n.
Παραδείγματα.
1. Για m < n, η ένθεση ι : ℝm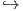 ℝn, ι(x1,…,xm) = (x1,…,xm,0,…,0) είναι μια εμβάπτιση. Για m > n, η προβολή
π : ℝm → ℝn, π(x1,…,xn,xn+1,…,xm) = (x1,…,xn) είναι μια υπεμβάπτιση. Αποδεικνύεται ότι κάθε εμβάπτιση είναι
τοπικά μια ένθεση και κάθε υπεμβάπτιση είναι τοπικά μια προβολή.
ℝn, ι(x1,…,xm) = (x1,…,xm,0,…,0) είναι μια εμβάπτιση. Για m > n, η προβολή
π : ℝm → ℝn, π(x1,…,xn,xn+1,…,xm) = (x1,…,xn) είναι μια υπεμβάπτιση. Αποδεικνύεται ότι κάθε εμβάπτιση είναι
τοπικά μια ένθεση και κάθε υπεμβάπτιση είναι τοπικά μια προβολή.
2. ΄Εστω F : ℝ → ℝ2 με τα εξής ενδεχόμενα: Αν F(t) = (t,t2), τότε η F είναι εμφύτευση. Αν F(t) = (t2,t3), τότε η F δεν είναι εμβάπτιση, αφού F′(0) = 0. Αν F(t) = (t2 - 4,t3 - 4t) τότε η F είναι εμβάπτιση, αλλά όχι εμφύτευση.
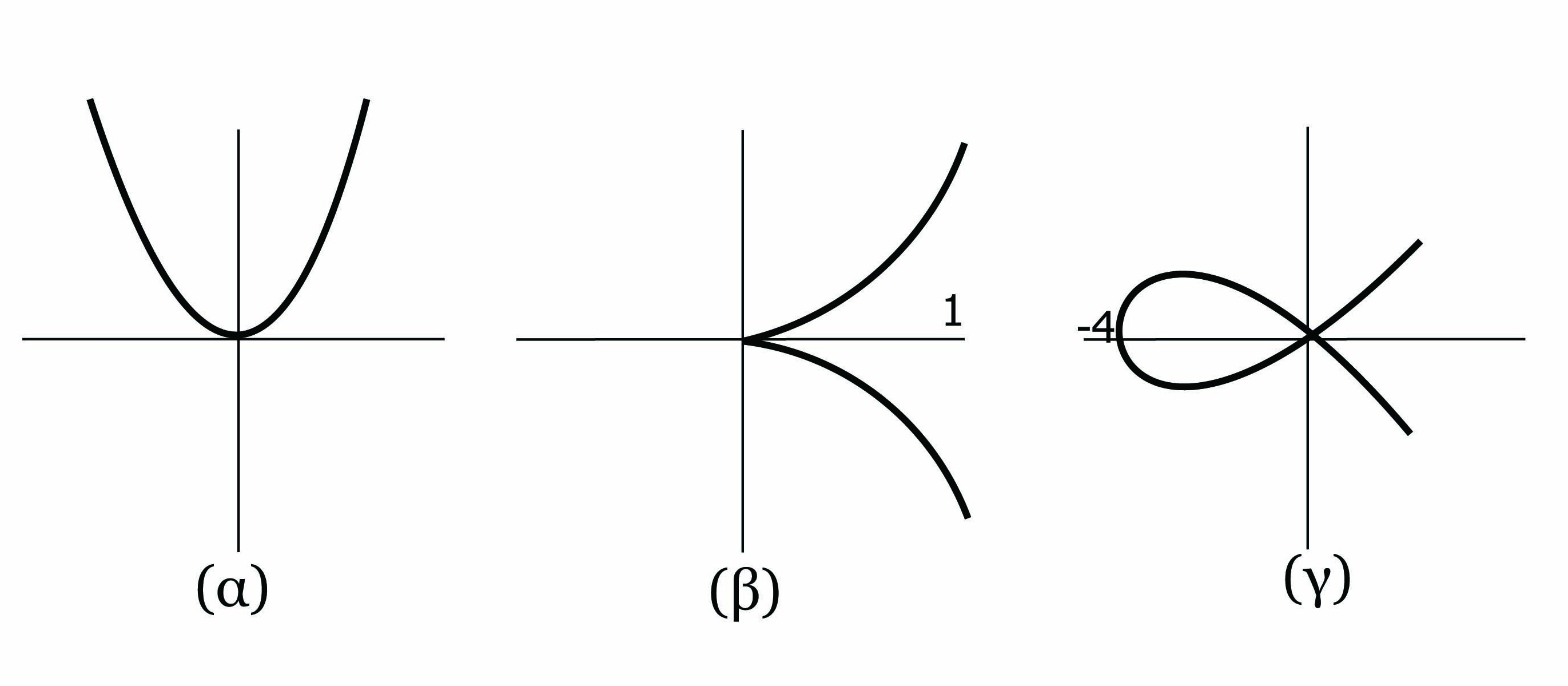
΄Εστω F : M → N μια λεία απεικόνιση. Η τάξη (rank) της F ορίζεται ως η τάξη του διαφορικού
dFp : TpM → TF(p)N. Ως προς τοπικά συστήματα συντεταγμένων (U;x1,…,xm) στο σημείο p και (V ;y1,…,yn)
στο σημείο F(p), η τάξη της F ισούται με την τάξη του Ιακωβιανού πίνακα  .
.
Ορισμός 3.4: ΄Ενα σημείο p ∈ M ονομάζεται κρίσιμο σημείο της F : M → N, εάν το διαφορικό dFp : TpM → TF(p)N δεν είναι επί, διαφορετικά ονομάζεται κανονικό σημείο της F. Με άλλα λόγια, το σημείο p είναι ένα κανονικό σημείο της F εάν και μόνο εάν η F είναι μια υπεμβάπτιση στο p. ΄Ενα σημείο στην πολλαπλότητα N ονομάζεται κρίσιμη τιμή της F, εάν είναι η εικόνα ενός κρίσιμου σημείου, διαφορετικά αυτό ονομάζεται κανονική τιμή.
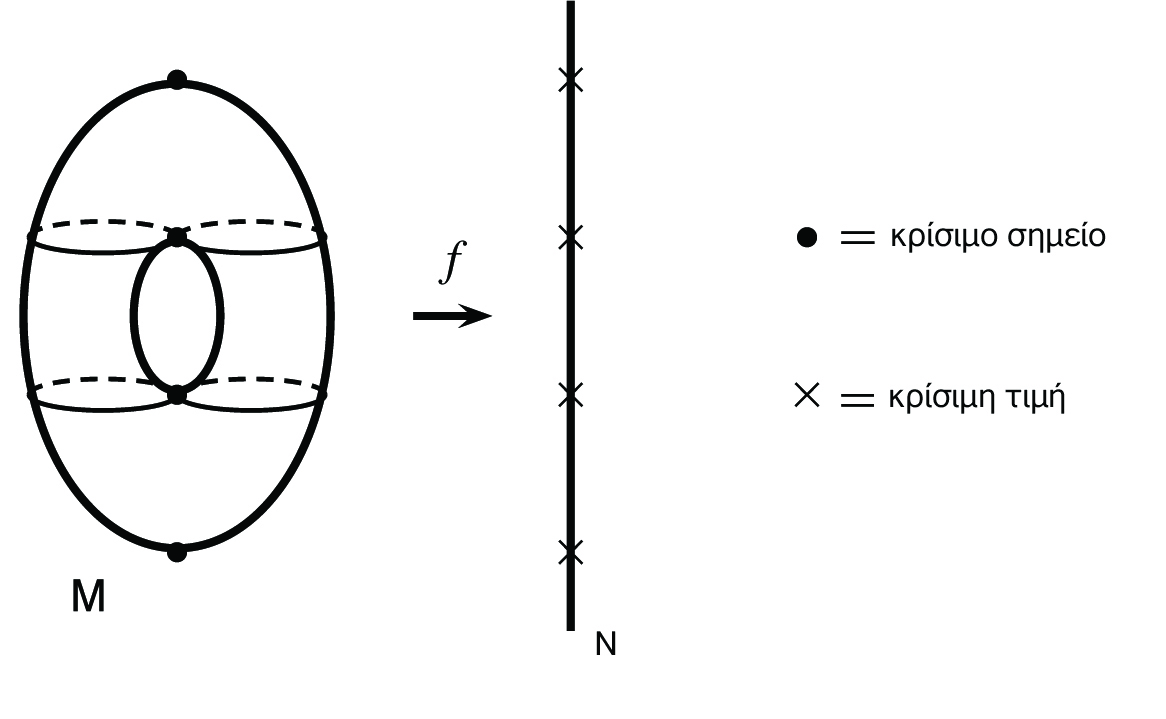
Παρατηρήσεις.
1. Μια κανονική τιμή δεν βρίσκεται απαραίτητα στην εικόνα της F. Κάθε σημείο της N το οποίο δεν ανήκει στην εικόνα της F είναι αυτομάτως μια κανονική τιμή, επειδή αυτό δεν αποτελεί εικόνα ενός κρίσιμου σημείου.
2. ΄Ενα σημείο c της N είναι μια κρίσιμη τιμή, εάν και μόνο εάν υπάρχει ένα σημείο στην αντίστροφη εικόνα F-1({c}) το οποίο είναι κρίσιμο σημείο.
3. ΄Ενα σημείο c στην εικόνα της F είναι μια κανονική τιμή εάν και μόνο εάν κάθε σημείο στην αντίστροφη εικόνα F-1({c}) είναι ένα κανονικό σημείο.
Πρόταση 3.7: ΄Εστω f : M → R. ΄Ενα σημείο p ∈ M είναι κρίσιμο σημείο της f εάν και μόνο εάν ως προς
κάποιον χάρτη (U;x1,…,xn) που περιέχει το p, ισχύει 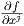 (p) = 0, j = 1,…,n.
(p) = 0, j = 1,…,n.
Απόδειξη. Από την Πρόταση 3.6 το διαφορικό dfp : TpM → Tf(p)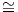 ℝ παρίσταται από τον πίνακα-γραμμή
ℝ παρίσταται από τον πίνακα-γραμμή
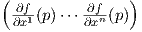 . Η εικόνα του διαφορικού dfp είναι ένας υπόχωρος του ℝ, άρα έχει διάσταση είτε 0
είτε 1, συνεπώς η απεικόνιση dfp είναι είτε η μηδενική απεικόνιση είτε είναι επί. Καταλήγουμε στο ότι το
διαφορικό δεν είναι επί εάν και μόνο έαν όλες οι μερικές παράγωγοι ∂f∕∂xi(p) μηδενίζονται. ▄
. Η εικόνα του διαφορικού dfp είναι ένας υπόχωρος του ℝ, άρα έχει διάσταση είτε 0
είτε 1, συνεπώς η απεικόνιση dfp είναι είτε η μηδενική απεικόνιση είτε είναι επί. Καταλήγουμε στο ότι το
διαφορικό δεν είναι επί εάν και μόνο έαν όλες οι μερικές παράγωγοι ∂f∕∂xi(p) μηδενίζονται. ▄
Θα δούμε στη συνέχεια μία χρήσιμη μέθοδο υπολογισμού του διαφορικού χρησιμοποιώντας καμπύλες σε πολλαπλότητες. Μια λεία καμπύλη σε μια πολλαπλότητα M είναι μια λεία απεικόνιση γ : (a,b) → M, όπου (a,b) ένα ανοικτό διάστημα για το οποίο υποθέτουμε τακτικά ότι περιέχει το μηδέν. Μια καμπύλη γ έχει αρχή το p, εάν γ(0) = p. Το διάνυσμα ταχύτητας γ′(t0) της καμπύλης γ τη χρονική στιγμή t0 ∈ (a,b) (ή στο σημείο γ(t0)) ορίζεται ως
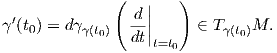
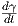 (t0) ή
(t0) ή 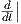 t0γ.
t0γ.
Παρατήρηση. Για την περίπτωση μιας καμπύλης γ : (a,b) → ℝ με τιμές στο σύνολο ℝ, ο συμβολισμός γ′(t) μπορεί
να επιφέρει κάποια σύγχυση. Συμβολίζουμε με t την συντεταγμένη στο πεδίο ορισμού (a,b) και με x την
αντίστοιχη στο πεδίο τιμών ℝ. Σύμφωνα με τον ορισμό μου δώσαμε, το γ′(t) είναι ένα εφαπτόμενο διάνυσμα στο
σημείο γ(t) ∈ ℝ, συνεπώς θα δίνεται ως γ′(t) = λ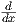 |γ(t), λ ∈ ℝ. Από την άλλη πλευρά, στον απειροστικό λογισμό
συμβολίζουμε με γ′(t) την παράγωγο μιας πραγματικής συνάρτησης, η οποία είναι ένας αριθμός. Οι δύο έννοιες
είναι διαφορετικές, οπότε ας συμβολίσουμε την παράγωγο αυτή με
|γ(t), λ ∈ ℝ. Από την άλλη πλευρά, στον απειροστικό λογισμό
συμβολίζουμε με γ′(t) την παράγωγο μιας πραγματικής συνάρτησης, η οποία είναι ένας αριθμός. Οι δύο έννοιες
είναι διαφορετικές, οπότε ας συμβολίσουμε την παράγωγο αυτή με 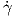 (t). Δείξτε ότι η ακριβής σχέση τους δίνεται
από την ισότητα γ′(t) =
(t). Δείξτε ότι η ακριβής σχέση τους δίνεται
από την ισότητα γ′(t) = 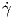 (t)
(t)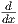 |γ(t).
|γ(t).
Πρόταση 3.8: ΄Εστω γ : (a,b) → ℝ μια λεία καμπύλη και έστω (U;x1,…,xn) ένας τοπικός χάρτης στο σημείο γ(t). Τότε το εφαπτόμενο διάνυσμα γ′(t) εκφράζεται ως
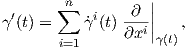
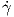 1(t),…,
1(t),…,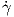 n(t)).
n(t)).
Κάθε λεία καμπύλη γ που διέρχεται από ένα σημείο p μιας πολλαπλότητας M ορίζει ένα εφαπτόμενο διάνυσμα γ′(0) στον εφαπτόμενο χώρο TpM. Θα δούμε τώρα ότι ισχύει και το αντίστροφο.
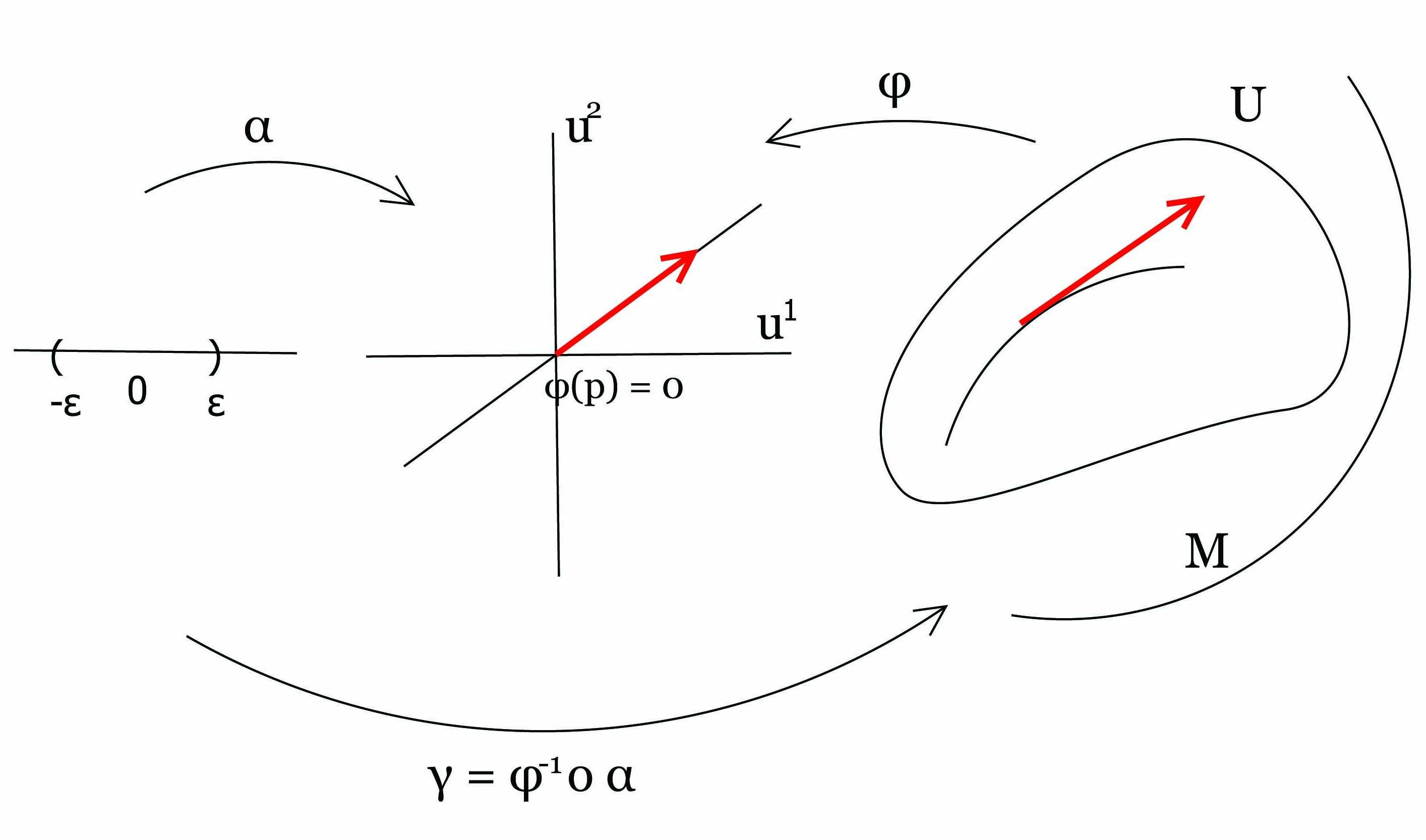
Πρόταση 3.9: ΄Εστω p ένα σημείο μιας πολλαπλότητας M και υp ∈ TpM. Τότε υπάρχουν ε > 0 και μια λεία καμπύλη γ : (-ε,ε) → M, έτσι ώστε γ(0) = p και γ′(0) = υp.
Απόδειξη. Η απόδειξη μπορεί να φανεί λίγο τεχνική, αλλά η ιδέα της είναι απλή: η ζητούμενη καμπύλη
στην πολλαπλότητα θα είναι η αντίστροφη εικόνα, μέσω ενός τοπικού χάρτη, μιας ευθείας στον ℝn.
΄Εστω (U,φ) = (U;x1,…,xn) ένας τοπικός χάρτης στο σημείο p με την ιδιότητα φ(p) = 0 ∈ ℝn (αυτό
είναι εύκολο να το επιτύχουμε κάνοντας μια απλή μεταφορά). ϒποθέτουμε ότι υp = ∑
ai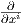 |p και έστω
u1,…,un οι κανονικές συντεταγμένες του ℝn με xi = ui ∘ φ. Θεωρούμε την καμπύλη α(t) = (a1t,…,ant),
t ∈ (-ε,ε) στον ℝn, όπου το ε είναι αρκετά μικρό, ώστε α(t) ∈ φ(U). Ορίζουμε την καμπύλη
γ = φ-1 ∘α : (-ε,ε) → M. Τότε για την καμπύλη αυτή ισχύει γ(0) = φ-1(α(0)) = φ-1(0) = p και λόγω
των Προτάσεων 3.3 και 3.8 προκύπτει ότι
|p και έστω
u1,…,un οι κανονικές συντεταγμένες του ℝn με xi = ui ∘ φ. Θεωρούμε την καμπύλη α(t) = (a1t,…,ant),
t ∈ (-ε,ε) στον ℝn, όπου το ε είναι αρκετά μικρό, ώστε α(t) ∈ φ(U). Ορίζουμε την καμπύλη
γ = φ-1 ∘α : (-ε,ε) → M. Τότε για την καμπύλη αυτή ισχύει γ(0) = φ-1(α(0)) = φ-1(0) = p και λόγω
των Προτάσεων 3.3 και 3.8 προκύπτει ότι
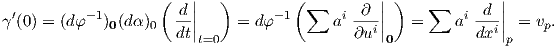
Χρησιμοποιώντας καμπύλες σε μια πολλαπλότητα, μπορούμε να δώσουμε μια ερμηνεία ενός εφαπτόμενου διανύσματος, γνωστή και ως φυσική ερμηνεία των εφαπτόμενων διανυσμάτων.
Πρόταση 3.10: ΄Εστω υp ένα εφαπτόμενο διάνυσμα στο σημείο p μιας πολλαπλότητας M και έστω f ∈ Cp∞(M). Αν γ : (-ε,ε) → M είναι μια λεία καμπύλη που διέρχεται από το σημείο p τέτοια ώστε γ′(0) = υp, τότε
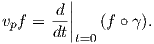
Η επόμενη πρόταση δίνει έναν ιδιαίτερα χρήσιμο τρόπο υπολογισμού του διαφορικού μιας λείας συνάρτησης μεταξύ πολλαπλοτήτων.
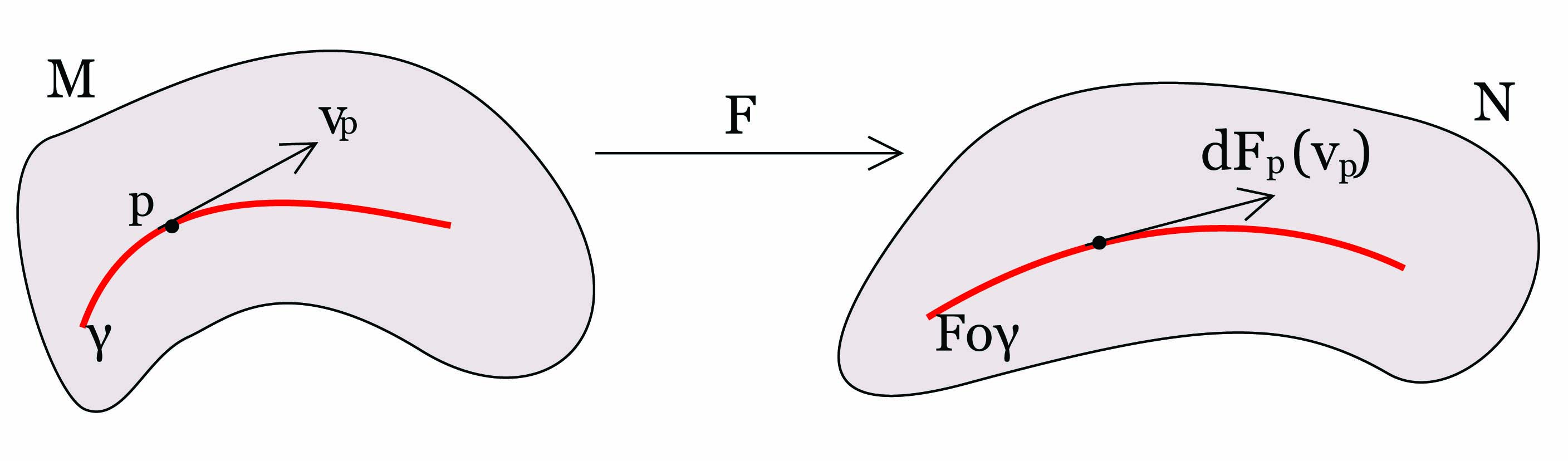
Πρόταση 3.11: ΄Εστω F : M → N μια λεία συνάρτηση μεταξύ πολλαπλοτήτων, p ∈ M και υp ∈ TpM. Αν γ είναι μια λεία καμπύλη με αρχή το σημείο p και με διάνυσμα ταχύτητας υp, τότε ισχύει
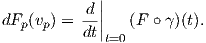
Απόδειξη. Από την υπόθεση έχουμε ότι γ(0) = p και γ′(0) = υp. Τότε χρησιμοποιώντας τους ορισμούς και τον κανόνα της αλυσίδας προκύπτει ότι
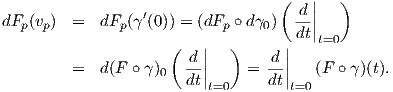
Παράδειγμα. Θεωρούμε τη γενική γραμμική ομάδα Glnℝ και για A ∈ Glnℝ έστω LA : Glnℝ → Glnℝ η αριστερή μεταφορά LA(B) = AB. Επειδή το σύνολο Glnℝ είναι ανοικτό στο Mn(ℝ) (το σύνολο όλων των πραγματικών n × n πινάκων), ο εφαπτόμενος χώρος TA(Glnℝ) ταυτίζεται με το Mn(ℝ). Θα υπολογίσουμε το διαφορικό (dLA)I : TI(Glnℝ) → TI(Glnℝ) της απεικόνισης LA στο ουδέτερο στοιχείο I (ταυτοτικός πίνακας). ΄Εστω X ∈ TI(Glnℝ) = Mn(ℝ) και γ(t) μια καμπύλη στην Glnℝ με γ(0) = I και γ′(0) = X. Τότε η σχέση LA(γ(t)) = Aγ(t) εκφράζει απλώς πολλαπλασιασμό πινάκων, συνεπώς χρησιμοποιώντας την Πρόταση 3.11 προκύπτει ότι
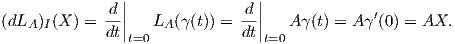
Μια κανονική υποπολλαπλότητα μιας λείας πολλαπλότητας είναι ένα υποσύνολό της το οποίο ορίζεται τοπικά μηδενίζοντας κάποιες από τις συναρτήσεις συντεταγμένων. Η έννοια είναι διαισθητικά απλή, αλλά παρουσιάζει κάποιες τεχνικές δυσκολίες τις οποίες όμως θα παρακάμψουμε. Αυτό συμβαίνει γιατί στην διαφορική γεωμετρία εμφανίζονται και διάφορα άλλα ήδη υποπολλαπλοτήτων. Χρησιμοποιώντας το θεώρημα αντίστοφης απεικόνισης θα διατυπώσουμε ένα κριτήριο που αναφέρει πότε ένα κανονικό σύνολο στάθμης είναι κανονική υποπολλαπλότητα, συνεπώς μια πολλαπλότητα.
Ορισμός 3.5: ΄Εστω M μια πολλαπλότητα διάστασης n και S ένα υποσύνολο της M (με την επαγόμενη τοπολογία). Το S ονομάζεται κανονική υποπολλαπλότητα (regular submanifold) της M διάστασης k εάν ισχύουν τα εξής:
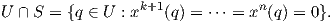
Ο παραπάνω χάρτης ονομάζεται προσαρτημένος χάρτης ως προς S. Συμβολίζουμε με φS : S ∩ U → ℝk την απεικόνιση φS = (x1,…,xk). Δηλαδή η φS προκύπτει με περιορισμό των πρώτων k συντεταγμένων της φ, στο σύνολο U ∩ S.
Παράδειγμα. ΄Εστω M = ℝ2 και S = (-1,1). ΄Ενας προσαρτημένος χάρτης ως προς S είναι το τετράγωνο U = (-1,1) × (-1,1) (ανοικτό σύνολο) με συντεταγμένες x,y. Τότε το S ∩ U είναι ακριβώς το σύνολο μηδενισμού της συντεταγμένης y στο σύνολο U. Παρατηρήστε ότι, για παράδειγμα, το σύνολο V = (-2,0) × (-1,1) δεν είναι ένας προσαρτημένος χάρτης ως προς S, επειδή S ∩ V = (-1,0) στον άξονα x και το σύνολο μηδενισμού της συντεταγμένης y είναι το ανοικτό διάστημα (-2,0) του άξονα x.
Παρατήρηση. Κάποιοι συγγραφείς ορίζουν ‘υποπολλαπλότητα’ ως την εικόνα μιας 1 - 1 εμβάπτισης f : M → N, όπου η εικόνα f(M) είναι εφοδιασμένη, όχι με την επαγόμενη τοπολογία, αλλά με την τοπολογία και τη διαφορική δομή της που κληρονομείται από τη συνάρτηση f. Συγκεκριμένα, ένα υποσύνολο f(U) της f(N) ονομάζεται ανοικτό εάν και μόνο εάν το U είναι ένα ανοικτό υποσύνολο της πολλαπλότητας M. Με την τοπολογία αυτή, η εικόνα f(M) είναι εξ ορισμού ομοιομορφική με τη M και ένα τέτοιο σύνολο ονομάζεται εμβαπτισμένη υποπολλαπλότητα της N. Συνεπώς, μια εμβαπτισμένη υποπολλαπλότητα μπορεί να μην είναι μια πολλαπλότητα υπό την έννοια που την έχουμε ορίσει. Τυπικό παράδειγμα είναι το σχήμα του αριθμού οκτώ, που ορίζεται ως η εικόνα της 1 - 1 εμβάπτισης f(t) = (cost,sin2t), -π∕2 < t < 3π∕2. Το σύνολο αυτό, λόγω της αυτοτομής που παρουσιάζει στην αρχή των αξόνων, δεν είναι κανονική υποπολλαπλότητα του ℝ2.
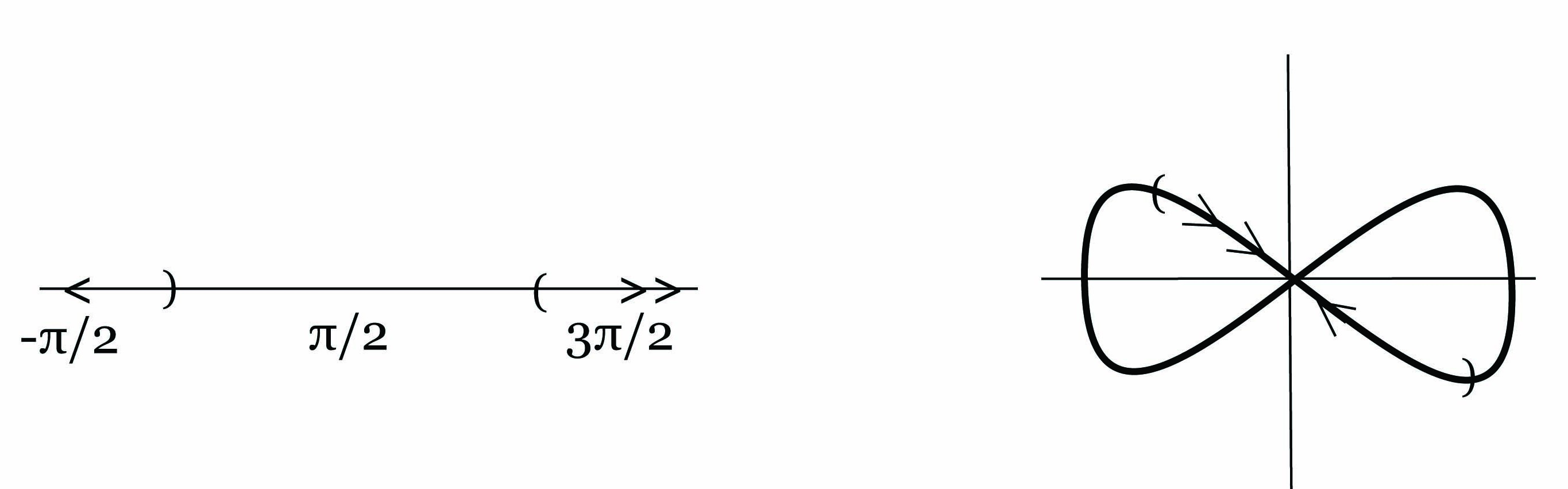
Μια κανονική υποπολλαπλότητα είναι πράγματι μια πολλαπλότητα, όπως φαίνεται στην παρακάτω πρόταση.
Πρόταση 3.12: ΄Εστω S μια κανονική υποπολλαπλότητα της M και έστω A = {(U,φ)} μια συλλογή χαρτών της διαφορικής δομής της M η οποία να καλύπτει την S. Τότε η συλλογή {(S ∩ U,φS)} αποτελεί έναν άτλαντα του συνόλου S. Επιπλέον, εάν η διάσταση της M είναι n και η S ορίζεται τοπικά με μηδενισμό των n - k συναρτήσεων συντεταγμένων, τότε η διάσταση της S είναι k.
Στη συνέχεια, θα δούμε έναν πιο πρακτικό τρόπο απόδειξης ότι ένα υποσύνολο μιας πολλαπλότητας είναι μια κανονική υποπολλαπλότητα, μέσω κανονικών συνόλων στάθμης πραγματικών συναρτήσεων. Η μέθοδος γενικεύεται για σύνολα στάθμης συναρτήσεων μεταξύ πολλαπλοτήτων. Το βασικό εργαλείο είναι το θεώρημα αντίστροφης απεικόνισης.
΄Εστω F : M → N μια συνάρτηση και c ∈ N. Το σύνολο
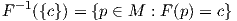
Θυμίζουμε ότι ένα στοιχείο c ∈ N είναι μια κανονική τιμή της F εάν και μόνο εάν, είτε το c δεν ανήκει στην εικόνα της F, είτε για κάθε σημείο p ∈ F-1(c) το διαφορικό dFp : TpM → TF(p) είναι επί. Η αντίστροφη εικόνα F-1(c) μιας κανονικής τιμής c ονομάζεται κανονικό σύνολο στάθμης. Εάν το σύνολο μηδενισμού F-1(0) είναι ένα κανονικό σύνολο στάθμης μιας απεικόνισης F : M → ℝn, τότε αυτό ονομάζεται κανονικό σύνολο μηδενισμού.
Λήμμα 3.1: ΄Εστω g : M → ℝ μια λεία συνάρτηση. Τότε το κανονικό σύνολο στάθμης g-1(c) με στάθμη c, ισούται με το κανονικό σύνολο μηδενισμού f-1(0) της συνάρτησης f = g - c.
Απόδειξη. Για κάθε p ∈ M ισχύει ότι g(p) = c εάν και μόνο εάν f(p) = g(p) - c = 0, συνεπώς g-1(c) = f-1(0) ≡ S. Για κάθε p ∈ M ισχύει ότι dfp = dgp, άρα οι συναρτήσεις f και g έχουν τα ίδια κρίσιμα σημεία. Επειδή η g δεν έχει κανένα κρίσιμο σημείο στο σύνολο S, το ίδιο ισχύει και για την f. ▄
Θεώρημα 3.1: ΄Εστω M μια πολλαπλότητα διάστασης n και έστω g : M → ℝ μια λεία συνάρτηση. Τότε ένα μη κενό κανονικό σύνολο στάθμης S = g-1(c) είναι μια κανονική υποπολλαπλότητα της M διάστασης n - 1.
Απόδειξη. Θεωρούμε τη συνάρτηση f = g - c. Λόγω του προηγούμενου λήμματος είναι S = f-1(0),
το οποίο είναι ένα κανονικό σύνολο στάθμης της συνάρτησης f. ΄Εστω p ∈ S τυχαίο. Επειδή το p είναι
ένα κανονικό σημείο της f, θα υπάρχει κάποιος χάρτης (U;x1,…,xn) στο p ώστε για κάποιο i να ισχύει
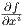 (p)≠0. Αλλάζοντας ενδεχομένως την αρίθμηση των x1,…,xn μπορούμε να υποθέσουμε ότι
(p)≠0. Αλλάζοντας ενδεχομένως την αρίθμηση των x1,…,xn μπορούμε να υποθέσουμε ότι 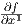 (p)≠0. Ο
Ιακωβιανός πίνακας της λείας συνάρτησης (f,x2,…,xn) : U → ℝn είναι
(p)≠0. Ο
Ιακωβιανός πίνακας της λείας συνάρτησης (f,x2,…,xn) : U → ℝn είναι
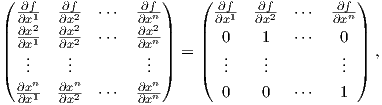
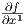 (p)≠0. Από το θεώρημα αντίστροφης απεικόνισης
(συγκεκριμένα Πόρισμα 1.1) υπάρχει μια περιοχή Up του p στην οποία οι συναρτήσεις f,x2,…,xn να
αποτελούν ένα τοπικό σύστημα συντεταγμένων. Θέτοντας την πρώτη συντεταγμένη f του χάρτη (Up;f,x2,…,xn)
ίση με το μηδέν, ορίζεται το σύνολο στάθμης S∩Up, άρα το σύνολο (Up;f,x2,…,xn) είναι ένας προσαρτημένος
χάρτης ως προς S. Επειδή το σημείο p είναι τυχαίο, το σύνολο S αποτελεί μια κανονική υποπολλαπλότητα
της M διάστασης n - 1. ▄
(p)≠0. Από το θεώρημα αντίστροφης απεικόνισης
(συγκεκριμένα Πόρισμα 1.1) υπάρχει μια περιοχή Up του p στην οποία οι συναρτήσεις f,x2,…,xn να
αποτελούν ένα τοπικό σύστημα συντεταγμένων. Θέτοντας την πρώτη συντεταγμένη f του χάρτη (Up;f,x2,…,xn)
ίση με το μηδέν, ορίζεται το σύνολο στάθμης S∩Up, άρα το σύνολο (Up;f,x2,…,xn) είναι ένας προσαρτημένος
χάρτης ως προς S. Επειδή το σημείο p είναι τυχαίο, το σύνολο S αποτελεί μια κανονική υποπολλαπλότητα
της M διάστασης n - 1. ▄
Παράδειγμα. Θα αποδείξουμε ότι η μοναδιαία σφαίρα S2 = {(x,y,z) ∈ ℝ3 : x2 + y2 + z2 = 1} είναι μια πολλαπλότητα διάστασης 2. Θεωρούμε τη λεία συνάρτηση f : ℝ3 → ℝ f(x,y,z) = x2 + y2 + z2 - 1. Τότε S2 = f-1(0). Επίσης, είναι
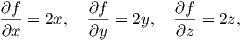
Το Θεώρημα 3.1 γενικεύεται για λείες συναρτήσεις μεταξύ πολλαπλοτήτων στο παρακάτω θεώρημα, το οποίο δεν φαίνεται να έχει μια καθιερωμένη ονομασία στην βιβλιογραφία. Αναφέρεται κατά περίπτωση ως θεώρημα πεπλεγμένης συνάρτησης (για πολλαπλότητες), θεώρημα αντίστροφης εικόνας, ή θεώρημα κανονικού συνόλου στάθμης. Θα ακολουθήσουμε την τελευταία ονομασία.
Θεώρημα 3.2: (Θεώρημα του κανονικού συνόλου στάθμης). ΄Εστω f : M → N μια λεία συνάρτηση μεταξύ πολλαπλοτήτων με dimM = m και dimN = n. Τότε ένα μη κενό κανονικό σύνολο στάθμης f-1(c) (c ∈ N) είναι μια κανονική υποπολλαπλότητα της M διάστασης m - n.
Θεώρημα 3.3: ΄Εστω N μια κανονική υποπολλαπλότητα της πολλαπλότητας M. Τότε η ένθεση ι : N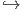 M,
ι(p) = p, είναι μια εμφύτευση.
M,
ι(p) = p, είναι μια εμφύτευση.
Απόδειξη. Επειδή μια κανονική υποπολλαπλότητα έχει την επαγόμενη τοπολογία το ίδιο θα συμβαίνει και
για την εικόνα ι(N), συνεπώς η απεικόνιση ι : N → ι(N) είναι ομοιομορφισμός. Απομένει να δείξουμε
ότι η ι : N → M είναι εμβάπτιση. Πράγματι, έστω p ∈ N. Θεωρούμε έναν προσαρτημένο χάρτη
(V ;y1,…,yn,yn+1,…,ym) της M στο σημείο p, τέτοιον ώστε στο σύνολο N ∩ V να μηδενίζονται οι
συντεταγμένες yn+1,…,ym. Τότε ως προς τους χάρτες (N ∩V ;y1,…,yn) της N και (V ;y1,…,ym) της M,
η ένθεση ι έχει τη μορφή (y1,…,yn)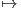 (y1,…,yn,0,…,0), άρα είναι εμβάπτιση. ▄
(y1,…,yn,0,…,0), άρα είναι εμβάπτιση. ▄
Παραδείγματα.
1. ΄Εστω S το υποσύνολο του ℝ3 που αποτελείται από όλα τα σημεία (x,y,z), τα οποία ικανοποιούν το σύστημα των εξισώσεων
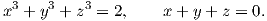
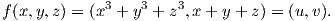
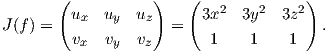
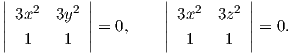 | (3.1) |
(Η τρίτη συνθήκη 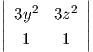 = 0 προκύπτει από τις άλλες δύο). Επιλύοντας το σύστημα (3.1) παίρνουμε ότι
y = ±x, z = ±x. Επειδή στην S ισχύει επιπλέον x + y + z = 0, παίρνουμε τελικά ότι (x,y,z) = (0,0,0), το
οποίο δεν ικανοποιεί την εξίσωση x3 + y3 + z3 = 2, συνεπώς δεν υπάρχουν κρίσιμα σημεία της f στο
σύνολο S. ΄Αρα το S είναι ένα κανονικό σύνολο στάθμης και από το Θεώρημα 3.2 προκύπτει ότι
το S είναι μια κανονική υποπολλαπλότητα του ℝ3 διάστασης 3 - 2 = 1. Συγκρίνετε το παράδειγμα
αυτό με αντίστοιχες εφαρμογές του θεωρήματος πεπλεγμένης συνάρτησης από τον λογισμό πολλών
μεταβλητών.
= 0 προκύπτει από τις άλλες δύο). Επιλύοντας το σύστημα (3.1) παίρνουμε ότι
y = ±x, z = ±x. Επειδή στην S ισχύει επιπλέον x + y + z = 0, παίρνουμε τελικά ότι (x,y,z) = (0,0,0), το
οποίο δεν ικανοποιεί την εξίσωση x3 + y3 + z3 = 2, συνεπώς δεν υπάρχουν κρίσιμα σημεία της f στο
σύνολο S. ΄Αρα το S είναι ένα κανονικό σύνολο στάθμης και από το Θεώρημα 3.2 προκύπτει ότι
το S είναι μια κανονική υποπολλαπλότητα του ℝ3 διάστασης 3 - 2 = 1. Συγκρίνετε το παράδειγμα
αυτό με αντίστοιχες εφαρμογές του θεωρήματος πεπλεγμένης συνάρτησης από τον λογισμό πολλών
μεταβλητών.
2. Θεωρούμε την ειδική γραμμική ομάδα (special linear group) Slnℝ ως το υποσύνολο της Glnℝ που αποτελείται από όλους τους πίνακες με ορίζουσα 1. Το Slnℝ είναι μια υποομάδα της Glnℝ (λόγω της πολλαπλασιαστικής ιδιότητας των οριζουσών και επειδή η ορίζουσα του αντίστροφου ενός πίνακα ισούται με το αντίστροφο της ορίζουσας αυτού). Θα αποδείξουμε ότι το σύνολο Slnℝ είναι μια κανονική υποπολλαπλότητα της Glnℝ.
Εφαρμόζουμε το Θεώρημα 3.2 για τη συνάρτηση ορίζουσας f : Glnℝ → ℝ, f(A) = detA. Επειδή f-1(1) = Slnℝ, θα αποδείξουμε ότι το 1 είναι μια κανονική τιμή της f. Για έναν n×n πίνακα A = (aij) ∈ Mn(ℝ) έστω dij = detSij η ορίζουσα του πίνακα Sij που προκύπτει από τον A διαγράφοντας την i-γραμμή και την j-στήλη (γνωστή και ως ελάσσονα ορίζουσα του A). Από τη γραμμική άλγεβρα γνωρίζουμε ότι το ανάπτυγμα της ορίσουσας κατά την i-γραμμή δίνεται από τη σχέση
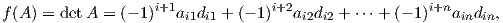
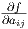 = (-1)i+jdij. Συνεπώς, ο πίνακας A ∈ Glnℝ είναι ένα κρίσιμο σημείο της f εάν και μόνο εάν όλες οι
(n- 1) × (n- 1) ελάσσονες ορίσουσες dij του πίνακα A είναι μηδέν. Λόγω της παραπάνω έκφρασης ένας τέτοιος
πίνακας A θα έχει ορίσουσα μηδέν. Επειδή κάθε πίνακας στην Slnℝ έχει ορίσουσα 1, όλα τα στοιχεία της Slnℝ
είναι κανονικά σημεία της συνάρτησης ορίζουσας. Από το Θεώρημα 3.2 το σύνολο Slnℝ είναι μια κανονική
υποπολλαπλότητα της Glnℝ διάστασης dimSlnℝ = dimGlnℝ - 1 = n2 - 1.
= (-1)i+jdij. Συνεπώς, ο πίνακας A ∈ Glnℝ είναι ένα κρίσιμο σημείο της f εάν και μόνο εάν όλες οι
(n- 1) × (n- 1) ελάσσονες ορίσουσες dij του πίνακα A είναι μηδέν. Λόγω της παραπάνω έκφρασης ένας τέτοιος
πίνακας A θα έχει ορίσουσα μηδέν. Επειδή κάθε πίνακας στην Slnℝ έχει ορίσουσα 1, όλα τα στοιχεία της Slnℝ
είναι κανονικά σημεία της συνάρτησης ορίζουσας. Από το Θεώρημα 3.2 το σύνολο Slnℝ είναι μια κανονική
υποπολλαπλότητα της Glnℝ διάστασης dimSlnℝ = dimGlnℝ - 1 = n2 - 1.
Θα αναφέρουμε μία ακόμα εφαρμογή του θεωρήματος αντίστροφης απεικόνισης, η απόδειξη του οποίου βασίζεται σε ανάλογο αποτέλεσμα της πραγματικής ανάλυσης. Θυμίζουμε ότι η τάξη μιας λείας συνάρτησης f : M → N σε ένα σημείο p ∈ M είναι η τάξη του διαφορικού της στο σημείο p.
Θεώρημα 3.4: (Θεώρημα σταθερής τάξης). ΄Εστω f : M → N μια λεία συνάρτηση μεταξύ πολλαπλοτήτων, dimM = n και έστω c ∈ N. Εάν η συνάρτηση έχει σταθερή τάξη k σε μια περιοχή ενός συνόλου στάθμης f-1(c) ⊂ M, τότε το f-1(c) είναι μια κανονική υποπολλαπλότητα της M διάστασης n - k.
Χρησιμοποιώντας το παραπάνω θεώρημα και το γεγονός ότι κάθε εμβάπτιση εκφράζεται τοπικά όπως η κανονική εμβάπτιση μεταξύ Ευκλειδείων χώρων, προκύπτει ότι, εάν f : M → N είναι μια εμφύτευση, τότε η εικόνα f(M) είναι μια κανονική υποπολλαπλότητα της N, η οποία αναφέρεται ως εμφυτευμένη υποπολλαπλότητα.
΄Ενα φυσικό ερώτημα είναι κατά πόσον μια πολλαπλότητα μπορεί να εμφυτευθεί σε έναν Ευκλείδειο χώρο ℝk για κάποιο k. Η απάντηση βρίσκεται σε διάφορες εκδοχές του θεωρήματος εμφύτευσης του Hassler Whitney, μία από τις οποίες ([7]) αναφέρει ότι κάθε πολλαπλότητα M διάστασης n μπορεί να εμφυτευθεί στον Ευκλείδειο χώρο ℝ2n+1 και να εμβαπτισθεί στον ℝ2n. Μια ισχυρότερη εκδοχή του θεωρήματος, που αποδείχτηκε και αυτή από τον Whitney το 1944 ([8], [9]), αναφέρει ότι η εμφύτευση μπορεί να γίνει στον Ευκλείδειο χώρο ℝ2n. 1
1. Αποδείξτε την Πρόταση 3.2.
2. ΄Εστω f : ℝ2 → ℝ3 με τύπο f(x,y) = (x2y + y2,x - 2y3,yex). ϒπολογίστε το διαφορικό df(x,y) και στη
συνέχεια το διάνυσμα df(0,1)(4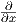 -
-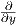 ).
).
3. Δίνεται η καμπύλη γ : ℝ → ℝ3, γ(t) = (t,t2,t3). Εκφράστε το διάνυσμα ταχύτητας γ′(t) ως προς τη βάση {∂∕∂x|γ(t),∂∕∂y|γ(t),∂∕∂z|γ(t)} του εφαπτόμενου χώρου Tγ(t)ℝ3.
4. Συμβολίζουμε με x,y τις κανονικές συντεταγμένες του ℝ2 και έστω ο χάρτης U = ℝ2 \{(x,0) : x ≥ 0}. Στο
ανοικτό σύνολο U ορίζονται οι πολικές συντεταγμένες r,θ από τις σχέσεις x = r cos θ,y = r sin θ
(r > 0,0 < θ < 2π). Εκφράστε τα διανύσματα 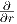 και
και 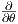 συναρτήσει των διανυσμάτων
συναρτήσει των διανυσμάτων 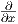 και
και 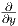 σε ένα
οποιοδήποτε σημείο p = (x,y) ∈ U.
σε ένα
οποιοδήποτε σημείο p = (x,y) ∈ U.
5. ΄Εστω M,N λείες πολλαπλότητες και π1 : M ×N → M, π2 : M ×N → N οι αντίστοιχες προβολές. Αποδείξτε ότι για κάθε (p,q) ∈ M × N η απεικόνιση
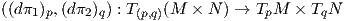
6. Για μια ομάδα Lie G συμβολίζουμε με μ : G × G → G, ι : G → G τις πράξεις του πολλαπλασιασμού και της αντιστροφής αντίστοιχα και με e το ουδέτερο στοιχείο. Αποδείξτε ότι το διαφορικό
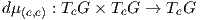
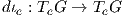
(ϒπόδειξη: Χρησιμοποιήστε την Πρόταση 3.11 και υπολογίστε τα διαφορικά dμ(e,e)(υe,0) και dμ(e,e)(0,we).)
7. ΄Εστω Γ το γράφημα της συνάρτησης f(x) = sin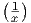 , x ∈ (0,1) και I = {(0,y) ∈ ℝ2 : -1 < y < 1}
(ανοικτό διάστημα). Αποδείξτε ότι το υποσύνολο S = Γ ∪ I δεν είναι κανονική υποπολλαπλότητα του
ℝ2.
, x ∈ (0,1) και I = {(0,y) ∈ ℝ2 : -1 < y < 1}
(ανοικτό διάστημα). Αποδείξτε ότι το υποσύνολο S = Γ ∪ I δεν είναι κανονική υποπολλαπλότητα του
ℝ2.
8. ΄Εστω f : ℝ2 → ℝ, f(x,y) = x3 - 4xy + y2. Για ποιές τιμές του c ∈ ℝ είναι το σύνολο στάθμης f-1(c) μια κανονική υποπολλαπλότητα του ℝ2;
9. ΄Εστω M = {(x,y) ∈ ℝ2 : x2 + y2 < 1}. Ορίζουμε τη λεία απεικόνιση
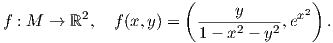
(β) Αποδείξτε ότι η εικόνα f(A) είναι ανοικτό υποσύνολο του ℝ2.
10. ΄Εστω η απεικόνιση f : ℝ3 → ℝ2 με τύπο f(x,y,z) = (x2 + y2 + z2 - 1,2x + 3y + 5z).
(α) Βρείτε τα σημεία στα οποία η f είναι μια υπεμβάπτιση.
(β) Βρείτε το σύνολο f-1(0) και περιγράψτε αυτό γεωμετρικά.
11. Ελέξτε κατά πόσον το σύνολο των λύσεων του συστήματος
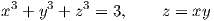
12. Αποδείξτε ότι το σύνολο των λύσεων του συστήματος
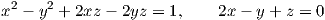
13. ΄Εστω f : ℝ2 → ℝ μια λεία συνάρτηση. Αποδείξτε ότι το γράφημα
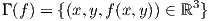
(ϒπόδειξη: Αποδείξτε ότι το σύνολο (ℝ3;x,y,z,-f(x,y)) αποτελεί έναν προσαρτημένο χάρτη του ℝ3 ως προς Γ(f).)
14. Θεωρούμε τον δακτύλιο
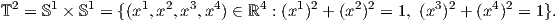
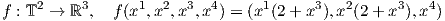
15. Αποδείξτε ότι η απεικόνιση f : ℝP2 S2∕ ~ → ℝ4 με τύπο
S2∕ ~ → ℝ4 με τύπο
![1 2 3 1 2 2 2 1 2 1 3 2 3
f([x ,x ,x ]) = ((x ) - (x ) ,x x ,x x ,x x )](02_chapter_0392x.png)
[1] D. Barden and C. Thomas, An Introduction to Differential Manifolds, Imperial College Press, London, 2003.
[2] S.H. Friedberg, A.J. Insel and L.E. Spence, Linear Algebra, 4th ed. 2002.
[3] J.M. Lee, Introduction to Smooth Manifolds, Springer, New York, 2003.
[4] J.E. Marsden and M.J. Hoffman, Elementary Classical Analysis, 2nd ed., W.H. Freeman, New York, 1993.
[5] J.E. Marsden and A.J. Tromba, Vector Calculus, 6th ed., Macmillan Higher Education, 2011. Μετάφραση 3ης έκδ: Διανυσματικός Λογισμός, Πανεπιστημιακές Εκδόσεις Κρήτης, 1992.
[6] L. Tu, An Introduction to Manifolds, 2nd ed., Springer, New York, 2011.
[7] H. Whitney, Differentiable manifolds, Ann. Math. 37 (1936) 645–680.
[8] H. Whitney, The self-intersections of a smooth n-manifold in 2n-space, Ann. Math. 45 (1944) 220–246.
[9] H. Whitney, The singularities of a smooth n-manifold in 2n - 1-space, Ann. Math. 45 (1944) 247–293.