Ορισμός 1.1: ΄Εστω k ένας μη αρνητικός ακέραιος. Μια πραγματική συνάρτηση f : U → ℝ ονομάζεται κλάσης Ck στο p ∈ U, εάν οι μερικές παράγωγοι
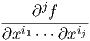
Σύνοψη
Ο Ευκλείδειος χώρος ℝn αποτελεί το βασικό παράδειγμα μιας πολλαπλότητας, συνεπώς απαιτείται μια καλή
κατανόηση της έννοιας της διαφορισιμότητας μιας συνάρτησης στον ℝn, καθώς και αυτής του εφαπτόμενου
διανύσματος. Οι έννοιες αυτές θα επεκταθούν αργότερα στις πολλαπλότητες. Θα μελετήσουμε εφαπτόμενα
διανύσματα και διανυσματικά πεδία στον ℝn ως παραγωγίσεις. Επιπλέον, θα περιγράψουμε τα δυϊκά αντικείμενα των
διανυσματικών πεδίων που είναι οι διαφορικές μορφές. Χρησιμοποιώντας διαφορικές μορφές είναι δυνατόν να δοθεί
μια ενοποιημένη παρουσίαση των θεμελιωδών θεωρημάτων του διανυσματικού λογισμού. Οι βασικές αναφορές μας
είναι τα βιβλία [1], [2], [4], [5], [7] και [8]. Για πιο προχωρημένη άποψη παραπέμπουμε στα βιβλία [3] και
[6].
Προαπαιτούμενη γνώση
Διαφορικός Λογισμός μιας και πολλών μεταβλητών, Βασική Γραμμική Άλγεβρα.
Θεωρούμε τον Ευκλείδειο χώρο ℝn και γράφουμε τις συντεταγμένες του ως x1,…,xn. Για την περίπτωση των ℝ2 και ℝ3 γράφουμε x,y και x,y,z αντίστοιχα. ΄Εστω p = (p1,…,pn) ένα σημείο σε ένα ανοικτό υποσύνολο U του ℝn.
Ορισμός 1.1: ΄Εστω k ένας μη αρνητικός ακέραιος. Μια πραγματική συνάρτηση f : U → ℝ ονομάζεται κλάσης Ck στο p ∈ U, εάν οι μερικές παράγωγοι
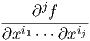
Μια περιοχή ενός σημείου p ∈ ℝn είναι ένα ανοικτό υποσύνολο του ℝn το οποίο περιέχει το σημείο p. Στη μαθηματική ανάλυση συναντάμε και την έννοια της αναλυτικής συνάρτησης σε ένα σημείο p, ως την πραγματική συνάρτηση η οποία σε μια περιοχή του p ισούται με το ανάπτυγμα Taylor αυτής. Μια αναλυτική συνάρτηση είναι κλάσης C∞, αλλά το αντίστοφο δεν ισχύει γενικά. ΄Ενα παράδειγμα είναι η συνάρτηση f : ℝ → ℝ με f(x) = e-1∕x για x > 0 και f(x) = 0 για x ≤ 0. Εμείς θα χρειαστούμε το εξής θεώρημα Taylor με υπόλοιπο για συναρτήσεις κλάσης C∞, για την απόδειξη του οποίου παραπέμπουμε σε βιβλία μαθηματικής ανάλυσης.
΄Ενα υποσύνολο του S του ℝn ονομάζεται αστεροειδές ως προς ένα σημείο p ∈ S, εάν για κάθε x ∈ S το ευθύγραμμο τμήμα από το p στο x βρίσκεται ολόκληρο μέσα στο S.
Πρόταση 1.1: (Θεώρημα Taylor). ΄Εστω U ένα ανοικτό υποσύνολο του ℝn το οποίο είναι αστεροειδές ως προς το σημείο p = (p1,…,pn) και έστω f : U → ℝ μια λεία (δηλ. κλάσης C∞) συνάρτηση. Τότε υπάρχουν συναρτήσεις g1(x),…gn(x) ∈ C∞(U) ώστε να ισχύει
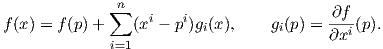
Στην στοιχειώδη διαφορική γεωμετρία ορίζουμε ένα εφαπτόμενο διάνυσμα σε ένα σημείο p μιας επιφάνειας M στον ℝ3 ως ένα σημείο του εφαπτόμενου επιπέδου της M στο p. Το εφαπτόμενο επίπεδο μπορεί να οριστεί διαισθητικά ως εξής: Θεωρούμε όλα τα επίπεδα που διέρχονται από τρία σημεία της επιφάνειας M. Καθώς τα τρία αυτά σημεία πλησιάζουν το σημείο p, εάν τα αντίστοιχα επίπεδα στα οποία βρίσκονται πλησιάζουν σε ένα οριακό επίπεδο έστω Π, τότε το επίπεδο Π ονομάζεται το εφαπτόμενο επίπεδο της M στο p. Ο ορισμός όμως αυτός προϋποθέτει ότι η επιφάνεια βρίσκεται εμφυτευμένη σε έναν Ευκλείδειο χώρο, συνεπώς δεν θα μπορούσε να χρησιμοποιηθεί για περιπτώσεις όπως το προβολικό επίπεδο, το οποίο δεν εμφυτεύεται σε κάποιον χώρο ℝn. Χρειαζόμαστε λοιπόν μια άλλη οπτική για τα εφαπτόμενα διανύσματα του ℝn, προκειμένου αυτά να γενικευθούν σε πολλαπλότητες. Η οπτική αυτή βρίσκεται στην έννοια της παραγώγου κατά κατεύθυνση.
Θεωρούμε τον εφαπτόμενο χώρο Tpℝn σε ένα σημείο p ∈ ℝn, ως τον διανυσματικό χώρο όλων των διανυσμάτων τα οποία έχουν αρχή το σημείο p. Λόγω της αντιστοιχίας μεταξύ διανυσμάτων και στηλών ενός n× 1 ή ενός n× 1 πίνακα, ο διανυσματικός χώρος ℝn μπορεί να ταυτιστεί με τον εφαπτόμενο χώρο Tpℝn. Για να διακρίνουμε μεταξύ σημείων και εφαπτόμενων διανυσμάτων, θα συμβολίζουμε ένα σημείο του ℝn ως p = (p1,…,pn) και ένα διάνυσμα στον εφαπτόμενο χώρο Tpℝn ως
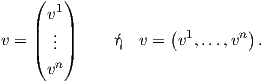
Θεωρούμε την ευθεία στον ℝn η οποία διέρχεται από το σημείο p = (p1,…,pn) και είναι παράλληλη προς το διάνυσμα υ = (υ1,…,υn). Η ευθεία αυτή έχει παραμέτρηση
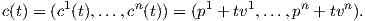
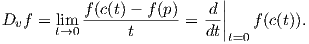
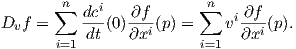 | (1.1) |
Με τον τρόπο αυτό ορίζεται η απεικόνιση
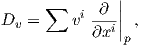
 Dυ, η οποία στέλνει
κάθε εφαπτόμενο διάνυσμα υ στην παράγωγο κατά κατεύθυνση Dυ. Αυτός είναι ο τρόπος με τον
οποίο θα χαρακτηρίσουμε τα εφαπτόμενα διανύσματα, δηλαδή ως συγκεκριμένους τελεστές σε χώρο
συναρτήσεων.
Dυ, η οποία στέλνει
κάθε εφαπτόμενο διάνυσμα υ στην παράγωγο κατά κατεύθυνση Dυ. Αυτός είναι ο τρόπος με τον
οποίο θα χαρακτηρίσουμε τα εφαπτόμενα διανύσματα, δηλαδή ως συγκεκριμένους τελεστές σε χώρο
συναρτήσεων.
Εάν δύο συναρτήσεις παίρνουν τις ίδιες τιμές σε μια περιοχή ενός σημείου p, τότε θα έχουν την ίδια παράγωγο κατά κατεύθυνση στο p. Αυτό μας οδηγεί στο να ορίσουμε μια σχέση ισοδυναμίας στο σύνολο όλων των λείων συναρτήσεων οι οποίες ορίζονται σε μια περιοχή του p. Συγκεκριμένα, έστω το σύνολο όλων των ζευγών (f,U), όπου U μια περιοχή του p και f : U → ℝ μια λεία συνάρτηση. Ορίζουμε την σχέση (f,U) ~ (g,V ), εάν υπάρχει ανοικτό W ⊂ U ∩ V το οποίο να περιέχει το p έτσι ώστε f|W = g|W . Εύκολα προκύπτει ότι η ~ είναι μια σχέση ισοδυναμίας. Η κλάση ισοδυναμίας του (U,f) ονομάζεται σπόρος (germ) της f στο p. Συμβολίζουμε με Cp∞(ℝn) ή απλώς Cp∞ το σύνολο όλων των σπόρων των λείων συναρτήσεων στο p.
Παράδειγμα. Οι συναρτήσεις f(x) = 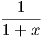 με πεδίο ορισμού το ℝ \{-1} και g(x) = 1 - x + x2 - x3 +
με πεδίο ορισμού το ℝ \{-1} και g(x) = 1 - x + x2 - x3 +  με
πεδίο ορισμού το διάστημα (-1,1) έχουν τον ίδιο σπόρο σε κάθε σημείο p ∈ (-1,1).
με
πεδίο ορισμού το διάστημα (-1,1) έχουν τον ίδιο σπόρο σε κάθε σημείο p ∈ (-1,1).
Οι πράξεις της πρόσθεσης και πολλαπλασιασμού συναρτήσεων εφοδιάζουν το σύνολο Cp∞ με τη δομή μιας (πραγματικής) άλγεβρας (βλ. ΄Ασκηση 2).
Η παράγωγος κατά κατεύθυνση ορίζει μια απεικόνιση Dυ : Cp∞ → ℝ, f Dυf μεταξύ πραγματικών
διανυσματικών χώρων, η οποία είναι γραμμική και λόγω της (1.1) ικανοποιεί τον κανόνα του Leibnitz
Dυf μεταξύ πραγματικών
διανυσματικών χώρων, η οποία είναι γραμμική και λόγω της (1.1) ικανοποιεί τον κανόνα του Leibnitz
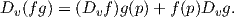 | (1.2) |
Γενικά μια γραμμική απεικόνιση D : Cp∞→ ℝ η οποία ικανοποιεί τον κανόνα του Leibnitz (1.2) ονομάζεται παραγώγιση στο p ή παραγώγιση κατά σημείο στο σύνολο Cp∞. Συμβολίζουμε με Dpℝn το σύνολο όλων των παραγωγίσεων στο p. Το σύνολο αυτό αποτελεί έναν πραγματικό διανυσματικό χώρο (βλ. ΄Ασκηση 2).
΄Εχουμε λοιπόν ορίσει μια απεικόνιση
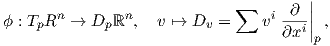 | (1.3) |
η οποία είναι προφανώς γραμμική (λόγω της γραμμικότητας της Dυ ως προς υ).
Λήμμα 1.1: Εάν D είναι μια παραγώγιση κατά σημείο στο σύνολο Cp∞, τότε για κάθε σταθερή συνάρτηση c ισχύει D(c) = 0.
Απόδειξη. Λόγω της γραμμικότητας της D είναι D(c) = D(c ⋅ 1) = cD(1), άρα αρκεί να δείξουμε ότι D(1) = 0. Λόγω της (1.2) είναι
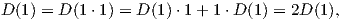
Ορίζουμε το δέλτα του Kronecker ως
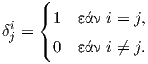
Το βασικό αποτέλεσμα είναι το εξής:
Θεώρημα 1.1: Η γραμμική απεικόνιση ϕ : TpRn → Dpℝn, όπως ορίστηκε στην (1.3), είναι ισομορφισμός διανυσματικών χώρων.
Απόδειξη. Αποδεικνύουμε αρχικά ότι η ϕ είναι 1 - 1. ΄Εστω ότι Dυ = 0 για κάποιο υ ∈ Tpℝn. Τότε παραγωγίζοντας τις συναρτήσεις συντεταγμένων xj (j = 1,…,n) έχουμε ότι
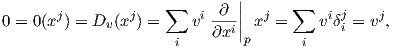
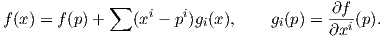
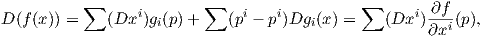
Λόγω του παραπάνω θεωρήματος μπορούμε να ταυτίζουμε τα εφαπτόμενα διανύσματα σε ένα σημείο p με τις
παραγωγίσεις κατά σημείο. Μέσω του ισομορφισμού Tpℝn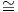 Dpℝn, η κανονική βάση e1,…,en του Tpℝn
αντιστοιχεί στο σύνολο των μερικών παραγώγων
Dpℝn, η κανονική βάση e1,…,en του Tpℝn
αντιστοιχεί στο σύνολο των μερικών παραγώγων 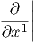 p,…,
p,…,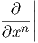 p. Συνεπώς, μπορούμε να γράφουμε ένα
εφαπτόμενο διάνυσμα υ = ∑
υiei ως
p. Συνεπώς, μπορούμε να γράφουμε ένα
εφαπτόμενο διάνυσμα υ = ∑
υiei ως
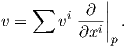 | (1.4) |
΄Ενα διανυσματικό πεδίο X σε ένα ανοικτό υποσύνολο U του ℝn είναι μια συνεχής συνάρτηση η οποία αντιστοιχεί σε κάθε σημείο p ∈ U ένα εφαπτόμενο διάνυσμα Xp ∈ Tpℝn. Λόγω της (1.4) το διάνυσμα αυτό γράφεται ως
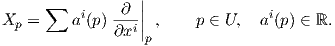
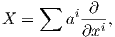
΄Εστω F(U) ο δακτύλιος όλων των λείων συναρτήσεων στο U. Τότε για f ∈ F(U) και X ∈ X(U) ορίζουμε το λείο διανυσματικό πεδίο fX με τιμή
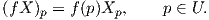
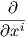 , τότε fX = ∑
(fai)
, τότε fX = ∑
(fai)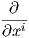 , άρα το σύνολο X(U) δεν είναι απλώς ένας
πραγματικός διανυσματικός χώρος, αλλά ένα αριστερό ℝ-πρότυπο (ℝ-module) επί του δακτυλίου
F(U).2
, άρα το σύνολο X(U) δεν είναι απλώς ένας
πραγματικός διανυσματικός χώρος, αλλά ένα αριστερό ℝ-πρότυπο (ℝ-module) επί του δακτυλίου
F(U).2
Αν X ∈ X(U) και f ∈ F(U) τότε ορίζουμε τη συνάρτηση Xf : U → ℝ με τύπο
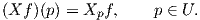
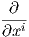 , τότε
, τότε
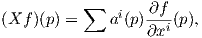
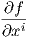 , άρα η Xf είναι λεία. Συνοψίζοντας, δοθέντος ενός λείου διανυσματικού πεδίου X,
ορίζεται η γραμμική απεικόνιση
, άρα η Xf είναι λεία. Συνοψίζοντας, δοθέντος ενός λείου διανυσματικού πεδίου X,
ορίζεται η γραμμική απεικόνιση
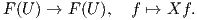
Πρόταση 1.2: (Κανόνας του Leibnitz για διανυσματικά πεδία). Αν X ∈ X(U) και f,g ∈ F(U), τότε ισχύει X(fg) = (Xf)g + f(Xg).
Εάν A είναι μια άλγεβρα επί ενός σώματος K, τότε μια παραγώγιση στην A είναι μια K-γραμμική απεικόνιση D : A → A, τέτοια ώστε για κάθε a,b ∈ A να ισχύει D(ab) = (Da)b + a(Db). Το σύνολο Der(A) όλων των παραγωγίσεων στην A αποτελεί έναν διανυσματικό χώρο, συνεπώς ορίζεται η απεικόνιση
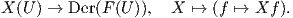
ϒπάρχουν διάφοροι λόγοι (π.χ. η ανάπτυξη μιας θεωρίας ολοκλήρωσης στον ℝn ή σε πολλαπλότητες) για τους οποίους είναι απαραίτητο αντί για τα εφαπτόμενα διανύσματα, να χρησιμοποιούμε τα δυϊκά τους αντικείμενα που είναι οι γραμμικές μορφές σε έναν διανυσματικό χώρο. Στη συνέχεια, μπορούμε εύκολα να τα γεκικεύσουμε και να ορίσουμε τις πολυγραμμικές μορφές. Τέτοια παραδείγματα γνωρίζουμε ήδη και είναι η ορίζουσα ενός πίνακα και το εξωτερικό γινόμενο δύο διανυσμάτων του ℝ3. Τα δύο αυτά παραδείγματα έχουν την επιπλέον ιδιότητα ότι είναι αντισυμμετρικές ή εναλλάσσουσες μορφές. Η σχετική θεωρία αναπτύχθηκε από τον Hermann Grassmann στην προσπάθειά του να γενικεύσει τον διανυσματικό λογισμό του ℝ3 στον χώρο ℝn. Η εργασία του Grassmann αρχικά δεν είχε εκτιμηθεί ιδιαιτέρως, μέχρι που ο Élie Cartan ανέδειξε την αξία της θεωρίας των διαφορικών μορφών, με σημαντικές εφαρμογές στη γεωμετρία και αλγεβρική τοπολογία.
΄Εστω V ένας διανυσματικός χώρος και έστω V * ο δυϊκός χώρος του V . Ο δυϊκός χώρος εποτελείται από όλες τις γραμμικές συναρτήσεις f : V → ℝ (γραμμικές μορφές). ϒποθέτουμε στο εξής ότι ο V είναι πεπερασμένης διάστασης και έστω e1,…,en μια βάση του V . Τότε κάθε υ ∈ V γράφεται κατά μοναδικό τρόπο ως υ = ∑ υiei, υi ∈ ℝ. Ορίζουμε τις γραμμικές μορφές αi : V → ℝ με αi(υ) = υi. Παρατηρούμε ότι
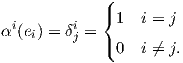 | (1.5) |
Από την γραμμική άλγεβρα είναι γνωστό ότι οι συναρτήσεις α1,…,αn αποτελούν μια βάση του V *, συνεπώς dimV = dimV *.
Παράδειγμα. Κάθε διάνυσμα υ ∈ V μπορεί να γραφτεί κατά μοναδικό τρόπο ως υ = ∑ bi(υ)ei, όπου bi(υ) ∈ ℝ. ΄Εστω α1,…,αn η δυϊκή βάση της e1,…,en. Τότε
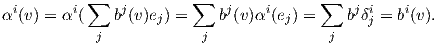
Προτρέπουμε στο σημείο αυτό τον αναγνώστη να κάνει μια σύντομη επανάληψη στην ομάδα μεταθέσεων Sk
(άρτιες, περιττές μεταθέσεις κ.λπ). Θυμίζουμε ότι αν A = {1,…,k} τότε το σύνολο Sk αποτελείται από όλες τις 1-1
και επί απεικονίσεις σ : A → A (μεταθέσεις) σ = 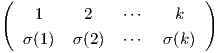 . Το σύνολο Sk αποτελεί ομάδα
με πράξη τσ ≡ τ ∘σ : A → A. Για έναν διανυσματικό χώρο V συμβολίζουμε με V k = V ×V
. Το σύνολο Sk αποτελεί ομάδα
με πράξη τσ ≡ τ ∘σ : A → A. Για έναν διανυσματικό χώρο V συμβολίζουμε με V k = V ×V  ×V το καρτεσιανό
γινόμενο k-φορές.
×V το καρτεσιανό
γινόμενο k-φορές.
Ορισμός 1.2: Μια συνάρτηση f : V k → ℝ ονομάζεται πολυγραμμική μορφή ή k-γραμμική (ή και τανυστής τύπου (0,k)), εάν είναι γραμμική ως προς κάθε μεταβλητή, δηλαδή ισχύει
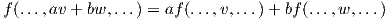
Αν k = 2 ή k = 3, η f ονομάζεται διγραμμική ή τριγραμμική αντίστοιχα. Συμβολίζουμε με Lk(V ) το σύνολο όλων των k-γραμμικών συναρτήσεων.
Παραδείγματα.
1. Το εσωτερικό γινόμενο f = 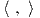 του ℝn με f(υ,w) =
του ℝn με f(υ,w) = 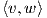 = ∑
υiwi όπου υ = ∑
υiei,w = ∑
wiei ως προς
την κανονική βάση e1,…,en του ℝn είναι μια διγραμμική συνάρτηση.
= ∑
υiwi όπου υ = ∑
υiei,w = ∑
wiei ως προς
την κανονική βάση e1,…,en του ℝn είναι μια διγραμμική συνάρτηση.
2. Η ορίζουσα f(υ1,…,υn) = det(υ1,…,υn) ως συνάρτηση των n διανυσμάτων (στήλες) υ1,…,υn ∈ ℝn είναι μια
πολυγραμμική συνάρτηση.
Ορισμός 1.3: ΄Εστω f : V k → ℝ μια πολυγραμμική συνάρτηση.
Παραδείγματα.
1. Το εσωτερικό γινόμενο f(υ,w) = 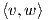 του ℝn είναι συμμετρική συνάρτηση.
του ℝn είναι συμμετρική συνάρτηση.
2. Η ορίζουσα f(υ1,…,υn) = det(υ1,…,υn) του ℝn είναι εναλλάσσουσα.
3. Το εξωτερικό γινόμενο υ × w του ℝ3 είναι εναλλάσσουσα.
4. Αν f,g : V → ℝ γραμμικές μορφές επί του διανυσματικού χώρου V τότε η συνάρτηση f ∧ g : V × V → ℝ με
τύπο (f ∧ g)(u,υ) = f(u)g(υ) - f(υ)g(u) είναι εναλλάσσουσα. Είναι μια ειδική περίπτωση του εξωτερικού
γινομένου που θα ορίσουμε αργότερα.
Συμβολίζουμε με Ak(V ) το σύνολο όλων των εναλλασσουσών πολυγραμμικών συναρτήσεων επί του διανυσματικού χώρου V (k > 0). Για k = 0 ορίζουμε μια 0-πολυγραμμική συνάρτηση να είναι μια σταθερά, άρα A0(V ) = ℝ.
΄Εστω f ∈ Lk(V ) και σ ∈ Sk. Ορίζουμε μια νέα k-γραμμική συνάρτηση σf ως
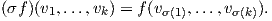
Η απόδειξη αφήνεται ως άσκηση.
Συνεπώς, η ομάδα Sk δρά από τα αριστερά στο σύνολο Lk(V ). Δηλαδή υπάρχει μια απεικόνιση
Sk × Lk(V ) → Lk(V ) (σ,f)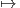 σ ⋅ f η οποία να ικανοποιεί τις ιδιότητες
σ ⋅ f η οποία να ικανοποιεί τις ιδιότητες
(i) 1 ⋅ f = f, για κάθε f ∈ Lk(V ) (όπου 1 η ταυτοτική μετάθεση) και
(ii) σ ⋅ (τ ⋅ f) = (στ) ⋅ f, για κάθε σ,τ ∈ Sk, f ∈ Lk(V ).
΄Εστω τώρα f ∈ Lk(V ). Ορίζουμε τη συμμετρική k-γραμμική συνάρτηση Sf ως
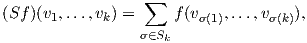
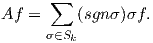
Απόδειξη. Επειδή η f είναι εναλλάσσουσα, θα είναι σf = (sgnσ)f και επειδή sgnσ = ±1, θα έχουμε ότι
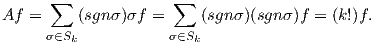
Παράδειγμα. ΄Εστω f ∈ L3(V ) και υ1,υ2,υ3 ∈ V . Τότε
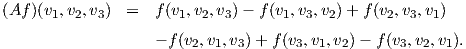
Θα ορίσουμε τώρα μια πρώτη πράξη μεταξύ πολυγραμμικών συναρτήσεων.
Ορισμός 1.4: ΄Εστω f ∈ Lk(V ) και g ∈ Ll(V ). Το τανυστικό γινόμενο f ⊗ g ∈ Lk+l(V ) είναι η (k + l)-πολυγραμμική συνάρτηση
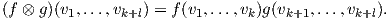
Παράδειγμα. (Διγραμμικές συναρτήσεις) ΄Εστω e1,…,en μια βάση του διανυσματικού χώρου V , α1,…,αn η
αντίστοιχη δυϊκή της βάση του V * και 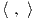 : V ×V → ℝ μια διγραμμική απεικόνιση. Θέτουμε gij =
: V ×V → ℝ μια διγραμμική απεικόνιση. Θέτουμε gij = 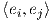 ∈ ℝ
και έστω υ = ∑
υiei,w = ∑
wiei. Τότε είναι υi = αi(υ) και wj = αj(w). Συνεπώς θα έχουμε ότι
∈ ℝ
και έστω υ = ∑
υiei,w = ∑
wiei. Τότε είναι υi = αi(υ) και wj = αj(w). Συνεπώς θα έχουμε ότι
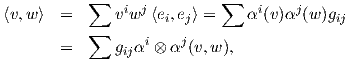
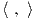 = ∑
gijαi ⊗ αj.
= ∑
gijαi ⊗ αj.
Ο συμβολισμός αυτός χρησιμοποιείται τακτικά στη διαφορική γεωμετρία. Για παράδειγμα, κάντε σύγκριση με την πρώτη θεμελιώδη μορφή
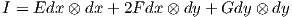
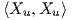 ,F =
,F = 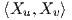 ,G =
,G = 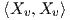 .
.
Η απόδειξη αφήνεται ως άσκηση.
Η επόμενη πράξη μεταξύ δύο πολυγραμμικών συναρτήσεων είναι η πλέον βασική για τη γεωμετρία.
Ορισμός 1.5: ΄Εστω f ∈ Ak(V ),g ∈ Al(V ). Το εξωτερικό γινόμενο (σφηνοειδές) (wedge product) f ∧ g ορίζεται ως
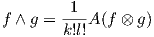
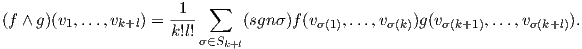
Σημειώστε ότι η f ∧ g είναι πράγματι εναλλάσσουσα, δηλαδή f ∧ g ∈ Ak+l(V ). Αν k = 0, τότε η f ∈ A0(V )
είναι μια σταθερά c άρα c ∧ g = cg(υ1,…,υl). Ο συντελεστής 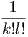 εμφανίζεται προκειμένου να συγκεντρώνονται
διπλοί όροι στο άθροισμα, όπως φαίνεται και στα παρακάτω παραδείγματα.
εμφανίζεται προκειμένου να συγκεντρώνονται
διπλοί όροι στο άθροισμα, όπως φαίνεται και στα παρακάτω παραδείγματα.
Παραδείγματα.
1. ΄Εστω f,g ∈ A1(V ). Τότε f ∧ g ∈ A2(V ) και (f ∧ g)(υ1,υ2) = f(υ1)g(υ2) - f(υ2)g(υ1).
2. ΄Εστω f ∈ A2(V ) και g ∈ A1(V ). Τότε f ∧ g ∈ A3(V ) και έστω υ1,υ2,υ3 ∈ V . Θυμίζουμε ότι
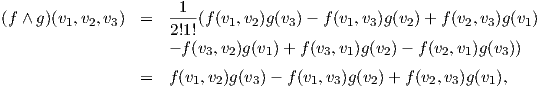
Το εξωτερικό γινόμενο ικανοποιεί τις εξής ιδιότητες:
Συνεπώς, f ∧ g ∧ h = 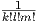 A(f ⊗ g ⊗ h). Πιο γενικά, αν fi ∈ Adi(V ), τότε
A(f ⊗ g ⊗ h). Πιο γενικά, αν fi ∈ Adi(V ), τότε
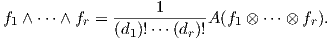
Παράδειγμα. ΄Εστω e1,…,en μια βάση του V και α1,…,αn η αντίστοιχη δυϊκή βάση του V *. Τότε
(α1 ∧ ∧ αn)(e1,…,en) = 1.
∧ αn)(e1,…,en) = 1.
΄Εστω V ένας διανυσματικός χώρος διάστασης n. Το σύνολο A*(V ) = ⊕ k=0nAk(V ) έχει δομή μιας μεταθετικής βαθμωτής άλγεβρας (graded commutative algebra) και ονομάζεται εξωτερική άλγεβρα ή άλγεβρα του Grassmann.
Θα βρούμε τώρα μια βάση του διανυσματικού χώρου Ak(V ).
΄Εστω e1,…,en μια βάση του διανυσματικού χώρου V και α1,…,αn η δυϊκή της βάση στον V *. ΄Εστω
I = (i1,…,ik) και θέτουμε eI = (ei1,…,eik) (πολυδείκτης), αI = αi1 ∧ ∧ αik. Μια k-γραμμική συνάρτηση
f : V k → ℝ καθορίζεται πλήρως από τις τιμές της σε όλα τα στοιχεία της μορφής (ei1,…,eik). Εάν η f είναι
επιπλέον εναλλάσσουσα, τότε καθορίζεται πλήρως από τις τιμές της σε στοιχεία της μορφής (ei1,…,eik) με
1 ≤ i1 <
∧ αik. Μια k-γραμμική συνάρτηση
f : V k → ℝ καθορίζεται πλήρως από τις τιμές της σε όλα τα στοιχεία της μορφής (ei1,…,eik). Εάν η f είναι
επιπλέον εναλλάσσουσα, τότε καθορίζεται πλήρως από τις τιμές της σε στοιχεία της μορφής (ei1,…,eik) με
1 ≤ i1 <  < ik ≤ n.
< ik ≤ n.
Απόδειξη. Λόγω της Πρότασης 1.6 είναι αI(eJ) = det(αi(ej))i∈I,j∈J. Εάν I = J τότε ο πίνακας (αi(ej)) είναι ο ταυτοτικός με ορίζουσα 1. Εάν I≠J τότε υπάρχει κάποιος δείκτης l ώστε i1 = j1,…,il-1 = jl-1,il≠jl. Χωρίς βλάβη της γενικότητας έστω ότι il < jl. Τότε εύκολα προκύπτει ότι ο δείκτης il είναι διαφορετικός από όλους τους δείκτες j1,…,jk, άρα η ł γραμμή του πίνακα (αi(ej)) έχει όλα τα στοιχεία μηδέν, συνεπώς det(αi(ej)) = 0. ▄
Πρόταση 1.7: Οι εναλλάσσουσες k-γραμμικές συναρτήσεις αI,I = (1 ≤ i1 <  < ik ≤ n) αποτελούν
μια βάση του διανυσματικού χώρου Ak(V ). Συνεπώς αν dimV = n, τότε dimAk(V ) =
< ik ≤ n) αποτελούν
μια βάση του διανυσματικού χώρου Ak(V ). Συνεπώς αν dimV = n, τότε dimAk(V ) = 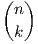 και αν k > n
τότε Ak(V ) = 0.
και αν k > n
τότε Ak(V ) = 0.
Απόδειξη. Αποδεικνύουμε πρώτα την γραμμική ανεξαρτησία. ΄Εστω ότι ∑
cIαI = 0 για κάποια cI ∈ ℝ
για όλους τους γνησίως αύξοντες πολυδείκτες μήκους k. Τότε χρησιμοποιώντας το Λήμμα 1.2 για
J = (j1 <  < jk) και εφαρμόζοντας την παραπάνω ισότητα στο eJ, προκύπτει ότι 0 = ∑
IcIαI(eJ) =
∑
IcIδJI = cJ, άρα τα αI είναι γραμμικώς ανεξάρτητα.
< jk) και εφαρμόζοντας την παραπάνω ισότητα στο eJ, προκύπτει ότι 0 = ∑
IcIαI(eJ) =
∑
IcIδJI = cJ, άρα τα αI είναι γραμμικώς ανεξάρτητα.
Θα δείξουμε τώρα ότι τα αI παράγουν τον Ak(V ). Πράγματι, αν f ∈ Ak(V ) ισχυριζόμαστε ότι
f = ∑
f(eI)αI, όπου το I διατρέχει όλους τους γνησίως αύξοντες πολυδείκτες μήκους k. Για να το
δείξουμε αυτό, έστω g = ∑
f(eI)αI και θα πιστοποιήσουμε την ισότητα των f και g με υπολογισμό σε
κάθε eJ, όπου J = (1 ≤ j1 <  < jk ≤ n) (λόγω της πολυγραμμικότητας και της αντισυμμετρικότητας).
Είναι
< jk ≤ n) (λόγω της πολυγραμμικότητας και της αντισυμμετρικότητας).
Είναι
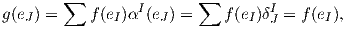
Παράδειγμα. ΄Εστω dimV = 4 και k = 2. ΄Εστω e1,e2,e3,e4 μια βάση του V με αντίστοιχη δυϊκή βάση
α1,α2,α3,α4. Τότε μια βάση του χώρου A2(V ) αποτελείται από τις 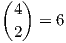 το πλήθος διγραμμικές μορφές
α1 ∧ α2,α1 ∧ α3,α1 ∧ α4,α2 ∧ α3,α2 ∧ α4,α3 ∧ α4. (Αποδείξτε το αυστηρά).
το πλήθος διγραμμικές μορφές
α1 ∧ α2,α1 ∧ α3,α1 ∧ α4,α2 ∧ α3,α2 ∧ α4,α3 ∧ α4. (Αποδείξτε το αυστηρά).
Παρατηρήστε επίσης ότι αν, για παράδειγμα, k = 5 > 4 = dimV , τότε τα στοιχεία της βάσης του A5(V ) θα
περιέχουν μορφές της μορφής
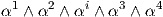
Θα μελετήσουμε τώρα την εξωτερική άλγεβρα του Grassmann για την περίπτωση που ο διανυσματικός χώρος V
είναι ο εφαπτόμενος χώρος Tpℝn. Οι διαφορικές μορφές είναι k-γραμμικές συναρτήσεις, οι οποίες
ορίζονται σε ένα ανοικτό υποσύνολο U του ℝn που περιέχει το σημείο p. Συνεπώς, όπως θα δούμε είναι
δυνατόν να οριστεί έννοια παραγώγισης των διαφορικών μορφών κατά μοναδικό τρόπο, γνωστή ως
εξωτερική παράγωγος. Το ενδιαφέρον γεγονός είναι ότι οι έννοιες αυτές μπορούν να γενικευθούν σε
πολλαπλότητες.
Θα αρχίσουμε με τις 1-μορφές που από μόνες τους έχουν ενδιαφέρον. Συμβολίζουμε τον συνεφαπτόμενο χώρο (Tpℝn)* με Tp*ℝn.
Ορισμός 1.6: ΄Εστω U ⊂ ℝn ανοικτό. Μια διαφορική 1-μορφή (differential 1-form) (ή συναλλοίωτο διανυσματικό πεδίο) είναι μια απεικόνιση ω η οποία σε κάθε p ∈ U αντιστοιχεί ένα διάνυσμα ωp ∈ Tp*ℝn, δηλαδή
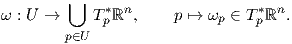
Παρατηρήσεις.
1) Η ένωση ⋃
p∈UTp*ℝn αποτελείται από ξένα μεταξύ τους υποσύνολα.
2) Μια διαφορική 1-μορφή θα ονομάζεται απλώς 1-μορφή.
3) Οι 1-μορφές είναι αντικείμενα δυϊκά των διανυσματικών πεδίων στο U, δεδομένου ότι ένα διανυσματικό πεδίο X
στο U μπορεί να θεωρηθεί ως μια απεικόνιση
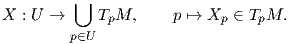
Ορισμός 1.7: ΄Εστω f : U ⊂ ℝn → ℝ λεία. Το διαφορικό της f είναι η 1-μορφή df που ορίζεται ως εξής: ΄Εστω p ∈ U,Xp ∈ TpU. Τότε (df)p(Xp) = Xpf.
Παρατήρηση. Η παράγωγος κατά κατεύθυνση μιας συνάρτησης σε ένα σημείο p ως προς τη διεύθυνση ενός εφαπτόμενου διανύσματος Xp, ορίζει μια διγραμμική απεικόνιση (ζευγάρωμα)
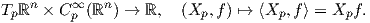
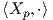 , τότε το διαφορικό
(df)p της f στο p είναι μια συνάρτηση της πρώτης μεταβλητής (df)p =
, τότε το διαφορικό
(df)p της f στο p είναι μια συνάρτηση της πρώτης μεταβλητής (df)p = 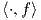 .
.
Πρόταση 1.8: ΄Εστω x1,…,xn οι κανονικές συντεταγμένες του ℝn και p ∈ ℝn. Τότε το σύνολο
{(dx1)p,…,(dxn)p} αποτελεί μια βάση του συνεφαπτόμενου χώρου Tp*ℝn, δυϊκή της βάσης {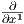
 p,…
p,…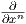
 p}
του Tpℝn.
p}
του Tpℝn.
Λόγω της παραπάνω πρότασης η τιμή μιας 1-μορφής ω σε ένα σημείο p ∈ U ⊂ ℝn είναι
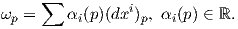
Παράδειγμα. Αν x,y,z είναι οι συντεταγμένες του ℝ3, τότε οι dx,dy,dz είναι οι 1-μορφές στον ℝ3 και κάθε 1-μορφή ω στον ℝ3 γράφεται ως
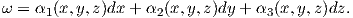
Με την παρακάτω πρόταση θα δούμε ότι μπορούμε να δώσουμε νοήμα σε μια έκφραση του διαφορικού την οποία είχαμε γνωρίσει (συμβολικά) στον λογισμό πολλών μεταβλητών.
Απόδειξη. Λόγω της Πρότασης 1.8, σε κάθε p ∈ U έχουμε ότι (df)p = ∑ αi(p)(dxi)p,αi(p) ∈ ℝ. Συνεπώς,
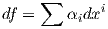 | (1.6) |
για κάποιες πραγματικές συναρτήσεις αi : U → ℝ. Προκειμένου να βρούμε τις αi εφαρμόζουμε και τα δύο μέλη της
(1.6) στο διανυσματικό πεδίο 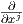 :
:
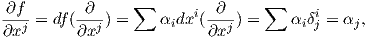
Παράδειγμα. Οι διαφορικές 1-μορφές εμφανίζονται κατά φυσικό τρόπο ακόμα και αν μελετάμε μόνο διανύσματα
Xp ∈ Tpℝn. Πράγματι, αν Xp = ∑
bi(Xp)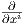
 p, bi(Xp) ∈ ℝ τότε σύμφωνα με το παράδειγμα της σελίδας 7
είναι bi(Xp) = (dxi)p(Xp), συνεπώς, όταν το p μεταβάλλεται, προκύπτει η ισότητα συναρτήσεων
bi = dxi.
p, bi(Xp) ∈ ℝ τότε σύμφωνα με το παράδειγμα της σελίδας 7
είναι bi(Xp) = (dxi)p(Xp), συνεπώς, όταν το p μεταβάλλεται, προκύπτει η ισότητα συναρτήσεων
bi = dxi.
Προχωράμε τώρα στον ορισμό μιας k-μορφής,
Ορισμός 1.8: Μια διαφορική μορφή βαθμού k (ή k-μορφή) ω σε ένα ανοικτό U ⊂ ℝn είναι μια απεικόνιση ω η οποία σε κάθε p ∈ U αντιστοιχεί μια εναλλάσσουσα k-γραμμική συνάρτηση του Tp*ℝn, δηλαδή ωp ∈ Ak(Tpℝn).
Γνωρίζουμε ότι μια βάση του χώρου Ak(Tpℝn) είναι το σύνολο
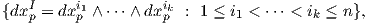
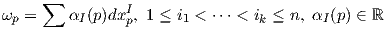
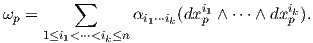
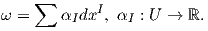
Ορισμός 1.9: ΄Εστω ω ∈ Ωk(U),φ ∈ Ωl(U). Το εξωτερικό γινόμενο (ή σφηνοειδές) (wedge product) ορίζεται σημειακά ως
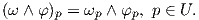
Αν ω = ∑ IαIdxI και φ = ∑ JbJdxJ, τότε
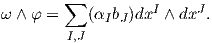
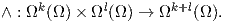
Παραδείγματα.
1. ΄Εστω x,y,z οι συναρτήσεις συντεταγμένων του ℝ3. Η γενική μορφή των λείων 0-μορφών, 1-μορφών, 2-μορφών και 3-μορφών στον ℝ3 είναι η εξής:
όπου f,g,h : ℝ3 → ℝ είναι λείες συναρτήσεις.
2. ΄Εστω x1,x2,x3,x4 οι συναρτήσεις συντεταγμένων του ℝ4. Μια βάση του διανυσματικού χώρου A3(Tpℝ4) είναι το σύνολο
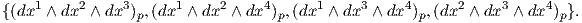
Το σύνολο Ω*(U) = ⊕ k=0∞Ωk(U) αποτελεί μια βαθμωτή, αντιμεταθετική άλγεβρα επί του ℝ και είναι επιπλέον ένα F(U)-πρότυπο.
Μια διαφορική 1-μορφή δρα σε ένα διανυσματικό πεδίο ως εξής:
΄Εστω ω μια λεία 1-μορφή και X ένα λείο διανυσματικό πεδίο στο ανοικτό U ⊂ ℝn. Ορίζουμε τη συνάρτηση ω(X) : U → ℝ με τύπο
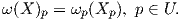
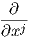 για αi,bj ∈ F(U), τότε
για αi,bj ∈ F(U), τότε
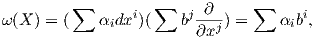
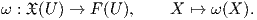
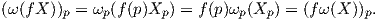
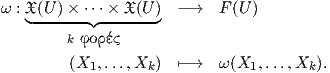
Παραδείγματα.
1. Αν ω ∈ Ω2(ℝ3) και φ ∈ Ω1(ℝ3), τότε ω ∧ φ ∈ Ω3(ℝ3). ΄Αρα για κάθε X,Y,Z ∈ 𝔛(ℝ3) είναι
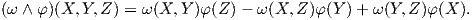
2. ΄Εστω ω = fdx ∧ dy + gdx ∧ dz + hdy ∧ dz ∈ Ω2(ℝ3) και φ = adx + bdy + cdz ∈ Ω1(ℝ3). Τότε
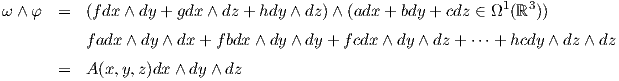
3. ΄Εστω ω = x2dx + exydy + ydz ∈ Ω1(ℝ3) και X = -y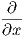 +
+ 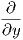 - x2y
- x2y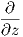 ∈ 𝔛(ℝ3). Τότε
ω(X) = -x2y + exy - x2y2 ∈ F(ℝ3).
∈ 𝔛(ℝ3). Τότε
ω(X) = -x2y + exy - x2y2 ∈ F(ℝ3).
Παρατήρηση. Είναι dxi ∧ dxi = 0, αλλά για ω ∈ Ωk(ℝn) δεν ισχύει γενικά ότι ω ∧ ω = 0 (εκτός εάν k περιττός). Για παράδειγμα, έστω ω = dx1 ∧ dx2 + 2dx3 ∧ dx4 ∈ Ω2(ℝ4). Τότε ω ∧ ω = 4dx1 ∧ dx2 ∧ dx3 ∧ dx4≠0.
΄Εστω ω μια διαφορική k-μορφή σε ένα ανοικτό υποσύνολο U ⊂ ℝn. Θα ορίσουμε μια διαφορική (k + 1)-μορφή dω στο U την οποία θα ονομάσουμε εξωτερική παράγωγο της ω. Πρώτα θα την ορίσουμε για 0-μορφές. Αν f ∈ F(U), ορίζουμε την εξωτερική παράγωγο της f ως το διαφορικό df ∈ Ω1(U)
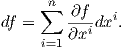
Ορισμός 1.10: ΄Εστω k ≥ 1 και ω = ∑ IαIdxI ∈ Ωk(U). Η εξωτερική παράγωγος (exterior derivative) της ω είναι η (k + 1)-μορφή
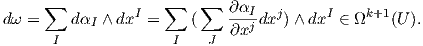
Παραδείγματα.
1. ΄Εστω ω = fdx + gdy ∈ Ω1(ℝ2) όπου f,g λείες συναρτήσεις στο ℝ2. Συμβολίζουμε με fx = 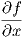 , fy =
, fy = 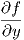 .
Τότε
.
Τότε
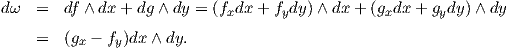
2. ΄Εστω ω = xyzdx + yzdy + (x + z)dz ∈ Ω1(ℝ3). Επιβεβαιώστε ότι
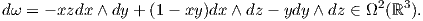
Η εξωτερική παράγωγος είναι μια απεικόνιση της μορφής
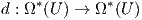
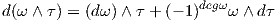
Οι παραπάνω τρεις ιδιότητες χαρακτηρίζουν κατά μοναδικό τρόπο την εξωτερική παράγωγο σε ένα ανοικτό υποσύνολο U του ℝn, όπως φαίνεται στην παρακάτω πρόταση.
Πρόταση 1.10: ΄Εστω D : Ω*(U) → Ω*(U) μια αντιπαραγώγιση βαθμού 1, τέτοια ώστε D2 = 0 και (Df)(X) = Xf για κάθε f ∈ F(U) και X ∈ X(U). Τότε D = d.
Απόδειξη. Επειδή κάθε k-μορφή είναι άθροισμα όρων της μορφης fdxi1∧ ∧dxik, λόγω της γραμμικότητας
αρκεί να δείξουμε την ισότητα D = d για μια τέτοια k-μορφή. Από την υπόθεση, για κάθε λεία συνάρτηση
είναι Df = df και επιπλέον Ddxi = DDxi = 0. Χρησιμοποιώντας το ότι η D είναι αντιπαραγώγιση και
επαγωγή επί του k, προκύπτει ότι για κάθε πολυδείκτη I μήκους k θα είναι D(dxI) = D(dxi1∧
∧dxik, λόγω της γραμμικότητας
αρκεί να δείξουμε την ισότητα D = d για μια τέτοια k-μορφή. Από την υπόθεση, για κάθε λεία συνάρτηση
είναι Df = df και επιπλέον Ddxi = DDxi = 0. Χρησιμοποιώντας το ότι η D είναι αντιπαραγώγιση και
επαγωγή επί του k, προκύπτει ότι για κάθε πολυδείκτη I μήκους k θα είναι D(dxI) = D(dxi1∧ ∧dxik) =
0. Λόγω των ιδιοτήτων του τελεστή D και του ορισμού της εξωτερικής παραγώγου, προκύπτει ότι για κάθε
k-μορφή fdxI ισχύει ότι
∧dxik) =
0. Λόγω των ιδιοτήτων του τελεστή D και του ορισμού της εξωτερικής παραγώγου, προκύπτει ότι για κάθε
k-μορφή fdxI ισχύει ότι
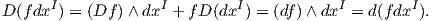
Ορισμός 1.11: Μια k-μορφή ω στο U ονομάζεται κλειστή (closed) εάν dω = 0 και ακριβής (exact) εάν υπάρχει μια (k - 1)-μορφή τ ώστε ω = dτ στο U.
Προφανώς κάθε ακριβής μορφή ω είναι κλειστή, λόγω του ότι d(dτ) = 0. Το αντίστροφο δεν ισχύει πάντα. Πράγματι, η 1-μορφή ω στο ℝ2 \{(0,0)} με τύπο
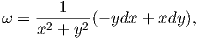
Σημειώνουμε ότι η παραπάνω ορολογία συνδέεται με τις ονομαζόμενες ακριβείς διαφορικές εξισώσεις με τρόπο που αφήνουμε στον αναγνώστη να διερευνήσει.
Ορισμός 1.12: Μια συλλογή διανυσματικών χώρων {V k}k=0∞ μαζί με γραμμικές απεικονίσεις dk : V k → V k+1 ονομάζεται ένα διαφορικό σύμπλεγμα (differential complex) ή και συναλλοίωτο σύμπλεγμα (cochain complex) εάν ισχύει dk+1 ∘ dk = 0.
Από τα παραπάνω προκύπτει ότι για κάθε ανοικτό U ⊂ ℝn η εξωτερική παράγωγος d εφοδιάζει τον διανυσματικό χώρο Ω*(U) των λείων μορφών στο U με δομή διαφορικού συμπλέγματος, το οποίο ονομάζεται σύμπλεγμα του de Rham στο U:
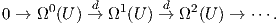
Οι κλειστές μορφές στο U είναι ακριβώς τα στοιχεία του πυρήνα της d και οι ακριβείς μορφές είναι ακριβώς τα στοιχεία της εικόνας της d. Ο χώρος πηλίκο Hk(U) = Kerdk∕Imdk-1 ονομάζεται k-τάξης συνομολογία de Rham του U.
Κλείνουμε το κεφάλαιο αυτό δίνοντας μια ενοποιημένη παρουσίαση των βασικών θεωρημάτων του διανυσματικού λογισμού, χρησιμοποιώντας διαφορικές μορφές. Θυμίζουμε ότι μια διανυσματική συνάρτηση στο ανοικτό U ⊂ ℝn έχει τη μορφή
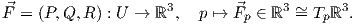
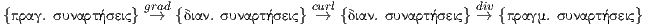
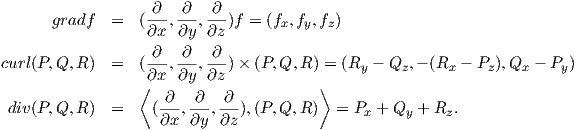
Μπορούμε να ταυτίσουμε τις 1-μορφές στο U με διανυσματικά πεδία στο U μέσω της Pdx + QdyRdz←→(P,Q,R), τις 2-μορφές στο U με διανυσματικά πεδία στο U μέσω της Pdx∧dz + Qdz ∧dx + Rdx∧dy←→(P,Q,R) και τις 3-μορφές στο U με συναρτήσεις στο U μέσω της fdx ∧ dy ∧ dz ↔ f. Οι ταυτίσεις αυτές επάγουν αντίστοιχες ταυτίσεις των εξωτερικών παραγωγίσεων μιας 0-μορφής f, μιας 1-μορφής και μιας 2-μορφής με τους γνωστούς τελεστές ως εξής:
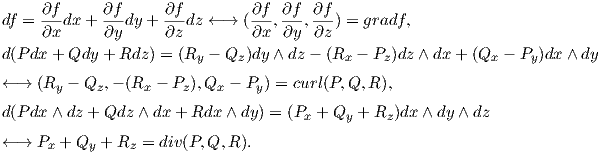
Συνοψίζοντας τα παραπάνω, οι τελεστές grad,curl και div είναι αντίστοιχα η εξωτερική παράγωγος d όταν αυτή δρα σε 0-μορφές, 1-μορφές και 2-μορφές. Το παρακάτω διάγραμμα περιγράφει τις ταυτίσεις αυτές σε ένα ανοικτό υποσύνολο του ℝ3:
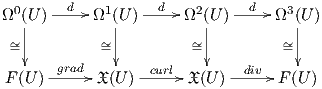
Σύμφωνα με τις ταυτίσεις αυτές, ένα διανυσματικό πεδίο (P,Q,R) του ℝ3 ισούται με την κλίση μιας λείας συνάρτησης f εάν και μόνο εάν η αντίστοιχη 1-μορφή Pdx + Qdy + Rdz ισούται με df.
Από τον διανυσματικό λογισμό γνωρίζουμε τα παρακάτω θεμελιώδη θεωρήματα:
Θεώρημα 1.4: ΄Ενα διανυσματικό πεδίο 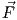 του ℝ3 ισούται με την κλίση κάποιας βαθμωτής συνάρτησης f
(δηλαδή το πεδίο είναι συντηρητικό) εάν και μόνο εάν curl
του ℝ3 ισούται με την κλίση κάποιας βαθμωτής συνάρτησης f
(δηλαδή το πεδίο είναι συντηρητικό) εάν και μόνο εάν curl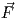 = 0.
= 0.
Τα θεωρήματα αυτά διατυπώνονται σε γλώσσα διαφορικών μορφών ως εξής (άσκηση).
Θεωρήματα 1.2′ και 1.3′. d2 = 0
Θεώρημα 1.4′ Μια 1-μορφή του ℝ3 είναι ακριβής εάν και μόνο εάν είναι κλειστή.
Η γενίκευση του Θεωρήματος 1.4′ για διαφορικές μορφές στον ℝn είναι το παρακάτω σημαντικό αποτέλεσμα.
Θεώρημα 1.5: (Λήμμα του Poincaré.) Για κάθε k ≥ 1, κάθε κλειστή k-μορφή στον ℝn είναι ακριβής, δηλαδή Hk(ℝn) = 0.
Η αιτία της αποτυχίας του αντιστρόφου του Θεωρήματος 1.4′ έγκειται στην τοπολογία του χώρου, όπως φαίνεται στο παρακάτω παράδειγμα:
Παράδειγμα. ΄Εστω U = ℝ3 \{άξονας z} και το διανυσματικό πεδίο του ℝ3, 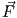 = (-
= (-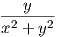 ,
,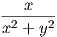 ,0). Τότε
curl
,0). Τότε
curl =
= 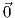 , αλλά το πεδίο
, αλλά το πεδίο 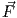 δεν μπορεί να εκφραστεί ως κλίση μιας λείας συνάρτησης f ∈ F(U). Πράγματι,
αν υπήρχε τέτοια συνάρτηση f, τότε από γνωστό θεώρημα των επικαμπύλιων ολοκληρωμάτων θα
είχαμε
δεν μπορεί να εκφραστεί ως κλίση μιας λείας συνάρτησης f ∈ F(U). Πράγματι,
αν υπήρχε τέτοια συνάρτηση f, τότε από γνωστό θεώρημα των επικαμπύλιων ολοκληρωμάτων θα
είχαμε
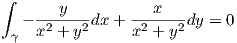
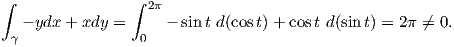
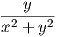 dx +
dx + 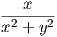 dy είναι κλειστή αλλά όχι ακριβής στο U.
dy είναι κλειστή αλλά όχι ακριβής στο U.
Παρατηρείστε ότι το σύνολο U δεν είναι απλά συνεκτικό3 ενώ ο ℝn είναι απλά συνεκτικός.
1. ΄Εστω το διανυσματικό πεδίο X = x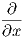 + y2
+ y2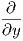 και η συνάρτηση f(x,y,z) = x2 + ey + z2. ϒπολογίστε τη
συνάρτηση Xf και το διανυσματικό πεδίο fX.
και η συνάρτηση f(x,y,z) = x2 + ey + z2. ϒπολογίστε τη
συνάρτηση Xf και το διανυσματικό πεδίο fX.
2. Μια άλγεβρα επί ενός σώματος K είναι ένας διανυσματικός χώρος A επί του K εφοδιασμένος με έναν πολλαπλασιασμό
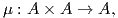
(α) (a ⋅ b) ⋅ c = a ⋅ (b ⋅ c) (προσεταιριστικότητα),
(β) (a + b) ⋅ c = a ⋅ c + b ⋅ c και a ⋅ (b + c) = a ⋅ b + a ⋅ c (επιμεριστικότητα),
(γ) k(a ⋅ b) = (ka) ⋅ b + a ⋅ (kb) (ομογένεια).
Μια άλγεβρα A ονομάζεται μεταθετική εάν για κάθε a,b ∈ A ισχύει a ⋅ b = b ⋅ a.
Ορίστε πράξεις πρόσθεσης, πολλαπλασιασμού και βαθμωτού πολλαπλασιασμού στο σύνολο Cp∞ και αποδείξτε ότι αυτό είναι μια μεταθετική άλγεβρα.
3. Αποδείξτε ότι το σύνολο Dpℝn αποτελεί έναν πραγματικό διανυσματικό χώρο.
4. Αποδείξτε την Πρόταση 1.2.
5. ΄Εστω V ένας διανυσματικός χώρος διάστασης n. Αποδείξτε ότι οι συναρτήσεις α1,…,αn όπως ορίστηκαν στην (1.5) αποτελούν μια βάση του V *
6. Αποδείξτε ότι, αν σ,τ ∈ Sk, f ∈ Lk(V ), τότε τ(σf) = (τσ)f.
7. Αποδείξτε ότι οι Sf, Af είναι συμμετρική και αντισυμμετρική πολυγραμμική συνάρτηση αντίστοιχα.
8. Αποδείξτε τη μεταθετικότητα και την προσεταιριστικότητα του εξωτερικού γινομένου.
9. ΄Εστω f μια k-γραμμική μορφή στον διανυσματικό χώρο V . Αποδείξτε ότι η f είναι εναλλάσσουσα εάν και μόνο εάν ισχύει f(υ1,…,υk) = 0 οποτεδήποτε δύο από τα διανύσματα υ1,…,υk είναι ίσα.
10. ΄Εστω α1,…,αk γραμμικές μορφές σε έναν διανυσματικό χώρο V . Αποδείξτε ότι α1 ∧ ∧αk≠0 εάν και μόνο
εάν τα α1,…,αk είναι γραμμικώς ανεξάρτητα διανύσματα του V *.
∧αk≠0 εάν και μόνο
εάν τα α1,…,αk είναι γραμμικώς ανεξάρτητα διανύσματα του V *.
11. ΄Εστω ω η 1-μορφή z2dx - xdz και X το διανυσματικό πεδίο -y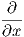 + x
+ x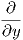 του ℝ3. ϒπολογίστε την
συνάρτηση ω(X) και τη μορφή dω.
του ℝ3. ϒπολογίστε την
συνάρτηση ω(X) και τη μορφή dω.
12. ΄Εστω ω η 1-μορφή xdx-ydy + zdz και X το διανυσματικό πεδίο cos(x + y + z)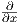 + sin(x + y + z)
+ sin(x + y + z)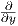 + ey
+ ey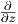 του ℝ3. ϒπολογίστε την τιμή ωp(Xp), όπου p = (1,1,-1).
του ℝ3. ϒπολογίστε την τιμή ωp(Xp), όπου p = (1,1,-1).
13. Συμβολίζουμε τις κανονικές συντεταγμένες του ℝ3 με ρ,ϕ,θ και θέτουμε x = ρsinϕcosθ, y = ρsinϕsinθ και z = ρcosϕ. Εκφράστε τις μορφές dx,dy,dz και dx ∧ dy ∧ dz συναρτήσει των μορφών dρ,dϕ και dθ.
14. Μια συνάρτηση f : ℝ3 → ℝ ονομάζεται ομογενής βαθμού k (k μη αρνητικός ακέραιος) εάν για κάθε (x,y,z) ∈ ℝ3 και για κάθε t ∈ ℝ ισχύει f(tx,ty,tz) = tkf(x,y,z). Αποδείξτε ότι εάν η f : ℝ3 → ℝ είναι ομογενής βαθμού k, τότε ικανοποιεί την ταυτότητα του Euler
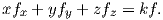
ϒπόδειξη. Παραγωγίστε και τα δύο μέλη της f(tx,ty,tz) = tkf(x,y,z) ως προς t και θέστε t = 1.
15. ΄Εστω V ένας διανυσματικός χώρος διάστασης 3 με {e1,e2,e3} μια βάση του και δυϊκή βάση {α1,α2,α3}. Αντιστοιχούμε στη μορφή α = a1α1 + a2α2 + a3α3 το διάνυσμα υα = (a1,a2,a3) ∈ ℝ3 και στην διγραμμική εναλλάσσουσα συνάρτηση
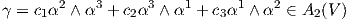
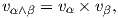
[1] S.S. Chern, W.H. Chen and K.S. Lam, Lectures on Differential Geometry, World Scientific, Singapore, 2000.
[2] M. P. do Carmo, Differential Forms and Applications, Springer, 1994. Μετάφραση: Διαφορικές Μορφές και Εφαρμογές, Leader Books, 2010.
[3] T.A. Ivey and I.M. Landsberg, Cartan for Beginners: Differential Geometry via Moving Frames and Exterior Differential Systems, American Mathematical Society, Rhode Island, 2003.
[4] J.E. Marsden and M.J. Hoffman, Elementary Classical Analysis, 2nd ed., W.H. Freeman, New York, 1993.
[5] J.E. Marsden and A.J. Tromba, Vector Calculus, 6th ed., Macmillan Higher Education, 2011. Μετάφραση 3ης έκδ: Διανυσματικός Λογισμός, Πανεπιστημιακές Εκδόσεις Κρήτης, 1992.
[6] R.W. Sharpe, Differential Geometry. Cartan’s Generalization of Klein’s Erlangen Program, Springer, New York 1997.
[7] M. Spivak, Calculus on Manifolds, W. A. Benjamin, Inc., New York-Amsterdam 1965. Μετάφραση: Λογισμός σε Πολλαπλότητες, Πανεπιστημιακές Εκδόσεις Κρήτης, 1994.
[8] L. Tu, An Introduction to Manifolds, 2nd ed., Springer, New York, 2011.