Chapter

Στο κεφάλαιο αυτό θα δούμε μερικές εφαρμογές των μαρκοβιανών αλυσίδων στις σύγχρονες επιστήμες και στην τεχνολογία. Θα δούμε γιατί η μηχανή αναζήτησης της εταιρείας Google κυριάρχησε στην αγορά, όταν εμφανίστηκε, αξιοποιώντας μια πολύ απλή ιδέα εμπνευσμένη από μαρκοβιανές αλυσίδες. Στη συνέχεια θα δούμε μια αναλογία μεταξύ μαρκοβιανών αλυσίδων και ηλεκτρικών κυκλωμάτων. Θα γνωρίσουμε ακόμα τη μέθοδο MCMC και τον πολύ σημαντικό αλγόριθμο Metropolis-Hastings που έφεραν επανάσταση στην υπολογιστική προσομοίωση. Τέλος θα γνωρίσουμε την τεχνική της προσομοιωμένης ανόπτησης (simulated annealing) και πώς μπορούμε να τη χρησιμοποιήσουμε για να προσεγγίσουμε δύσκολα προβλήματα βελτιστοποίησης, όπως π.χ. το διάσημο πρόβλημα του πλανόδιου πωλητή που προέρχεται από την πληροφορική.

7.2 Μια κατανομή αξίας δισεκατομμυρίων

Οι μεγαλύτεροι σε ηλικία αναγνώστες θα θυμούνται ότι πριν την εμφάνιση της Google οι μηχανές αναζήτησης δεν ήταν τόσο ακριβείς. Στα αποτελέσματα που επέστρεφαν υπήρχαν πολλές σελίδες που δεν είχαν καμία σχέση με την αναζήτηση και έτσι συχνά χρειαζόταν να δει κανείς αρκετές σελίδες αποτελεσμάτων για να βρει σελίδες με χρήσιμο περιεχόμενο. Όταν η Google εμφανίστηκε στην αγορά (1997) και εισήγαγε τη δική της μηχανή αναζήτησης, τα αποτελέσματα ήταν εντυπωσιακά καλύτερα από oτιδήποτε υπήρχε μέχρι τότε. Πολύ σύντομα η συντριπτική πλειονότητα των χρηστών του διαδικτύου χρησιμοποιούσε αυτήν, βάζοντας έτσι τις βάσεις για να γίνει η Google ο κολοσσός που γνωρίζουμε σήμερα.
Το μυστικό της επιτυχίας της συγκεκριμένης μηχανής ήταν ένας αλγόριθμος που χρησιμοποιούσε για να αξιολογεί τις ιστοσελίδες και να προτάσσει στα αποτελέσματα της αναζήτησης εκείνες που αξιολογούνταν ως πιο σημαντικές. O αλγόριθμος αυτός είναι ο PageRank $^{TM}$ και παρά τις τροποποιήσεις που έχει υποστεί από τότε η βασική του ιδέα είναι εξαιρετικά απλή και παραμένει επίκαιρη ακόμα και σήμερα (2015).
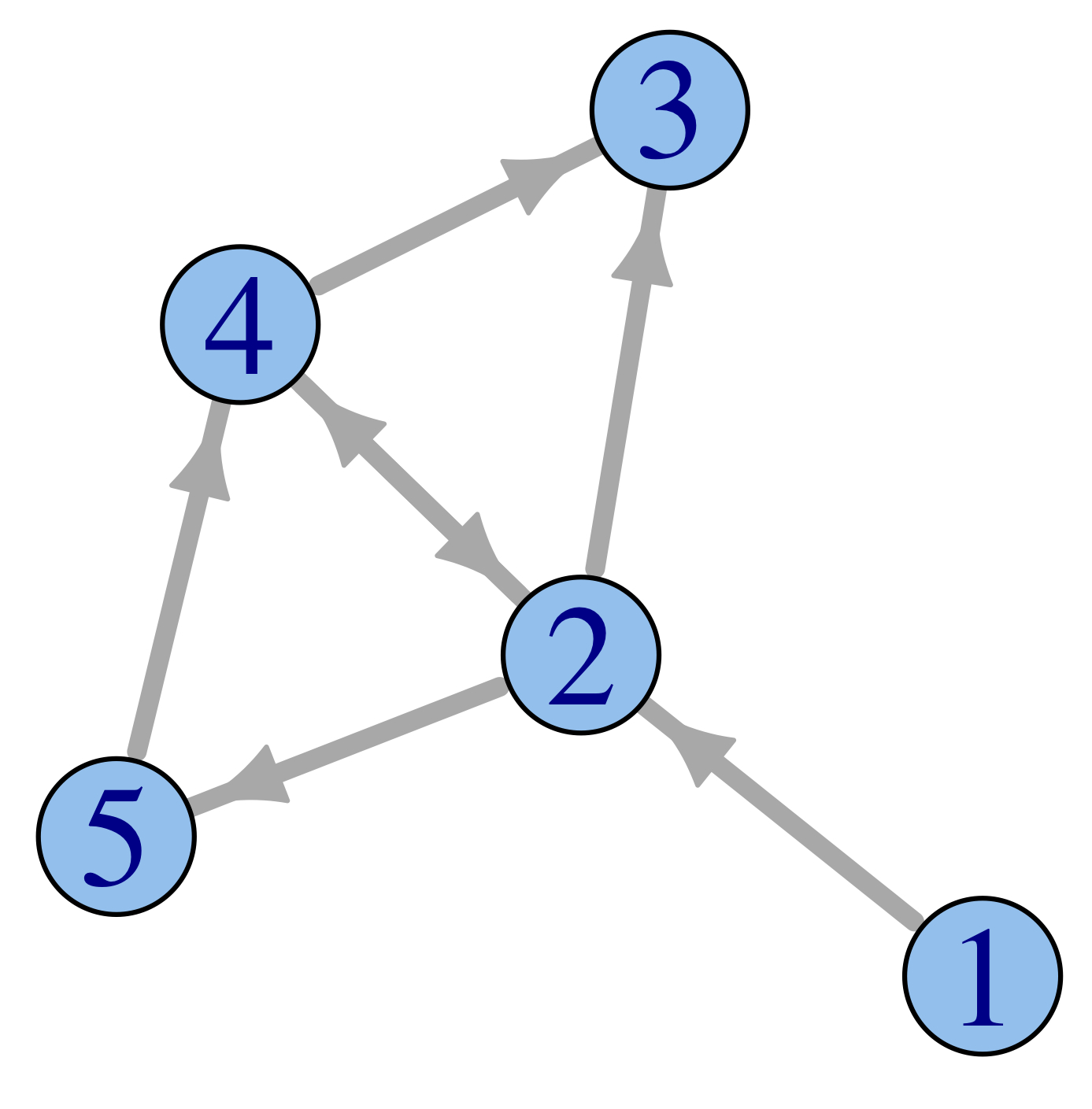
Φανταστείτε έναν περιηγητή του διαδικτύου που σε κάθε του βήμα επιλέγει τυχαία έναν από τους συνδέσμους της σελίδας στην οποία βρίσκεται και μεταβαίνει εκεί. Μπορούμε να φανταστούμε την περιήγηση αυτή ως μια μαρκοβιανή αλυσίδα στο σύνολο $V$ των ιστοσελίδων του διαδικτύου με πιθανότητες μετάβασης

όπου $v_o(x)$ είναι το πλήθος των συνδέσμων από τη σελίδα $x$ προς άλλες σελίδες. Ο χώρος καταστάσεων είναι τεράστιος αλλά πεπερασμένος. Ας υποθέσουμε για λίγο ότι η αλυσίδα αυτή είναι μη υποβιβάσιμη, οπότε θα έχει μοναδική αναλλοίωτη κατανομή $\pi$. Αυτή η υπόθεση είναι ισοδύναμη με το ότι ο περιηγητής μας μπορεί να φτάσει από οποιαδήποτε σελίδα του διαδικτύου σε οποιαδήποτε άλλη μέσα από ένα μονοπάτι διαδοχικών συνδέσμων. Κάτι τέτοιο δεν είναι ρεαλιστικό, αφού λ.χ. υπάρχουν σελίδες χωρίς εξωτερικούς συνδέσμους, θα μας βοηθήσει όμως να καταλάβουμε γιατί το βάρος $\pi(x)$ που αποδίδει στη σελίδα $x$ η αναλλοίωτη κατανομή $\pi$ είναι ένας πολύ καλός δείκτης σημαντικότητας της σελίδας $x$. Στη συνέχεια θα άρουμε τον περιορισμό της μη υποβιβασιμότητας.

Πράγματι, το εργοδικό θεώρημα εξασφαλίζει ότι το ποσοστό του χρόνου θα ξοδεύει ο περιηγητής μας στη σελίδα $x$ είναι ασυμπτωτικά $\pi(x)$. Συγκεκριμένα, αν $N_n(x)$ είναι το πλήθος των επισκέψεων του περιηγητή στη σελίδα $x$ στα πρώτα $n$ βήματά του, τότε

\[ \P\Big[ \lim_{n\to\infty}\frac{N_n(x)}{n}=\pi(x),\quad \forall x\in V\Big]=1. \]

\begin{equation} \sigma(x)=\sum_{y\to x} \frac{\sigma(y)}{v_0(y)},\quad\forall x\in V. \end{equation}

H παραπάνω σχέση μας λέει απλώς ότι η σημαντικότητα της σελίδας $x$ προκύπτει, αν αθροίσουμε τις σημαντικότητες των σελίδων $y$ που παρέχουν συνδέσμους προς τη $x$, με βάρη αντιστρόφως ανάλογα του πλήθους $v_0(y)$ των συνδέσμων τους. Αυτός ο ορισμός της σημαντικότητας είναι αυτοαναφορικός, αφού για να ορίσουμε την σημαντικότητα μιας ιστοσελίδας χρησιμοποιούμε τη σημαντικότητα άλλων σελίδων. Δεν είναι λοιπόν εκ των προτέρων φανερό γιατί οι εξισώσεις (7.1) έχουν λύση. Μπορούμε όμως να ξαναγράψουμε τις εξισώσεις αυτές ως εξής

Αν επιπλέον θελήσουμε να κανονικοποιήσουμε τη συνολική σημαντικότητα όλων των ιστοσελίδων στη μονάδα, δηλαδή

βλέπουμε ότι αυτές είναι ακριβώς οι εξισώσεις που ορίζουν τη μοναδική αναλλοίωτη κατανομή $\pi$ της μαρκοβιανής αλυσίδας μας. Άρα όχι μόνο έχουν λύση, αλλά η λύση αυτή είναι μοναδική και είναι η $\pi$.

Ελπίζω τα παραπάνω επιχειρήματα να σας έχουν πείσει ότι, αν ο τυχαίος περίπατος στο διαδίκτυο που περιγράψαμε αντιστοιχούσε σε μια μη υποβιβάσιμη αλυσίδα, τότε η αναλλοίωτη κατανομή της θα ήταν ένας πολύ καλός δείκτης σημαντικότητας. Όπως προείπαμε όμως, αυτός ο περιορισμός είναι πολύ ισχυρός. Για να τον άρουμε τροποποιούμε την περιήγησή μας ως εξής. Πριν από κάθε μας βήμα στρίβουμε ένα κέρμα που φέρνει κεφαλή με πιθανότητα $\alpha\in(0,1).$ Αν το κέρμα έρθει κεφαλή, τότε όπως και πριν επιλέγουμε τυχαία μία από τις ιστοσελίδες προς τις οποίες υπάρχει σύνδεσμος και μεταβαίνουμε σε αυτήν. Αν το κέρμα έρθει γράμματα, τότε επιλέγουμε τυχαία μία από όλες τις σελίδες του διαδικτύου και μεταβαίνουμε εκεί. Αν $|V|$ είναι το πλήθος των ιστοσελίδων του διαδικτύου, η παραπάνω περιήγηση αντιστοιχεί σε μια μαρκοβιανή αλυσίδα στο $V$ με πιθανότητες μετάβασης

H αλυσίδα αυτή είναι μη υποβιβάσιμη για κάθε $\alpha<1$ και ο δείκτης PageRank $^{TM}$ είναι στην ουσία η αναλλοίωτη κατανομή αυτής της αλυσίδας για την επιλογή $\alpha=0,85$.

7.3 Μαρκοβιανές αλυσίδες και ηλεκτρικά κυκλώματα

Ο Νόμος του Kirchoff ορίζει ότι σε κάθε κόμβο $x$ του κυκλώματος που δεν είναι συνδεδεμένος με την πηγή, το συνολικό ρεύμα που εισέρχεται από άλλους κόμβους είναι μηδέν, δηλαδή

Συνδυάζοντας τις δύο παραπάνω σχέσεις, έχουμε ότι η συνάρτηση που δίνει το δυναμικό $\Phi$ σε κάθε κόμβο λύνει το ΠΣΤ

\begin{equation} \begin{cases}\displaystyle \quad \sum_{y\in \X} c(x,y)\big(\Phi(y)-\Phi(x)\big)=0, & \text{ αν } x\notin A\cup B\\ \quad \Phi(x)=1, &\text{ αν } x\in A\\ \quad \Phi(x)=0, &\text{ αν } x\in B.\end{cases} \end{equation}

Το παραπάνω πρόβλημα μοιάζει με το ΠΣΤ (3.2) που δίνει τις πιθανότητες $\Px{ T_A < T_B }$, με τη διαφορά ότι οι αγωγιμότητες δεν είναι πιθανότητες μετάβασης, αφού δεν αθροίζονται απαραίτητα στη μονάδα. Αυτό όμως μπορούμε να το διορθώσουμε κανονικοποιώντας. Αν ορίσουμε

\begin{equation} p(x,y)=\frac{c(x,y)}{\displaystyle\sum_{y\in\X}c(x,y)}=\frac{c(x,y)}{w(x)}, \end{equation}

τότε τα ΠΣΤ (3.2) και (7.2) ταυτίζονται και μάλιστα αν το κύκλωμα είναι συνεκτικό, αν δηλαδή οποιοιδήποτε δύο κόμβοι επικοινωνούν μέσα από ένα μονοπάτι με θετικές αγωγιμότητες, αυτά τα ΠΣΤ έχουν μοναδική λύση. Επομένως, το δυναμικό στον κόμβο $x \in \X $ ταυτίζεται με την πιθανότητα $\Px{ T_A < T_B } $ για μια μαρκοβιανή αλυσίδα, με πιθανότητες μετάβασης που δίνονται από την (7.3).

Παρατηρήστε ότι οι πιθανότητες μετάβασης αυτής της αλυσίδας βρίσκονται σε ακριβή ισορροπία με τους παράγοντες κανονικοποίησης $w(x)=\sum_{y\in\X} c(x,y)$. Πράγματι, από την (7.3) βλέπουμε ότι

το Λήμμα 5.2 μας δίνει ότι η $\pi$ είναι αναλλοίωτη κατανομή της μαρκοβιανής αλυσίδας με πιθανότητες μετάβασης $\{p(x,y)\}_{x,y\in\X}$, που δίνονται από την (7.3) και η αλυσίδα αυτή είναι χρονικά αντιστρέψιμη. Μάλιστα, αν το κύκλωμα είναι συνεκτικό, η αλυσίδα αυτή είναι μη υποβιβάσιμη και η $\pi$ είναι η μοναδική αναλλοίωτη κατανομή της.

Αντίστροφα, σε κάθε χρονικά αντιστρέψιμη μαρκοβιανή αλυσίδα σ' έναν πεπερασμένο χώρο καταστάσεων $\X$, με πιθανότητες μετάβασης $\{p(x,y)\}_{x,y\in\X}$ και αναλλοίωτη κατανομή $\pi$, μπορούμε να αντιστοιχίσουμε ένα ηλεκτρικό κύκλωμα, θεωρώντας ένα κόμβο σε κάθε κατάσταση του $\X$ και τοποθετώντας αγωγιμότητα

ανάμεσα στους κόμβους που αντιστοιχoύν στις καταστάσεις $x,y$. Αν τώρα ενώσουμε ένα σύνολο κόμβων $A$ αυτού του κυκλώματος με τον θετικό πόλο μιας πηγής κι ένα σύνολο κόμβων $B\ (A\cap B=\emptyset)$ με τον αρνητικό πόλο της πηγής, τότε το δυναμικό $\Phi(x) $ σε κάθε κόμβο $x$ αυτού του κυκλώματος θα ταυτίζεται με την πιθανότητα $\Px{ T_A < T_B } $. Με άλλα λόγια μπορούμε να μετρήσουμε αυτές τις πιθανότητες μ' ένα πολύμετρο.

Η ισχύς που καταναλώνεται σε μια αγωγιμότητα $c(x,y)$ δίνεται σε σχέση με τη διαφορά δυναμικού στα άκρα της από την ποσότητα $c(x,y) \big(\Phi(y)-\Phi(x) \big)^2.$ Το ακόλουθο θεώρημα εξασφαλίζει ότι η κατανομή του δυναμικού σε κάθε κόμβο ενός ηλεκτρικού κυκλώματος γίνεται έτσι ώστε να ελαχιστοποιείται η συνολική ισχύς που καταναλώνεται στο κύκλωμα.

Θεώρημα 7.1 Από όλες τις συναρτήσεις στο σύνολο \[F_{Α,Β}=\{\Psi:\X\to\R:\ \Psi(x)=1 \text{ για κάθε } x\in A,\ \Psi(x)=0 \text{ για κάθε }x\in B\}, \] η λύση του ΠΣΤ (7.2) είναι η μόνη που ελαχιστοποιεί την

\begin{equation} {\cal D}(\Psi)=\frac{1}{2}\sum_{x,y\in\X}c(x,y)\big(\Psi(y)-\Psi(x)\big)^2. \end{equation}

Απόδειξη:> Έστω $\Psi:\X\to\R$ μια συνάρτηση για την οποία $\Psi(x)=1$ για κάθε $x\in A$ και $\Psi(x)=0$ για κάθε $x\in B$. Αν $\Phi$ είναι η λύση του ΠΣΤ (7.2), τότε η $h=\Psi-\Phi$ μηδενίζεται στα $A$ και $B$. Αρκεί λοιπόν να δείξουμε ότι

για κάθε συνάρτηση $h:\X\to\R$ τέτοια ώστε $h(x)=0$ για κάθε $x\in A\cup B.$ Έχουμε όμως ότι \begin{align*} {\cal D}(\Phi+h)&=\frac{1}{2}\sum_{x,y\in\X}c(x,y)\big(\Phi(y)+h(y)-\Phi(x)-h(x)\big)^2\\ &={\cal D}(\Phi)+{\cal D}(h)+\frac{1}{2}\sum_{x,y\in\X}c(x,y)\big(\Phi(y)-\Phi(x)\big)\big(h(y)-h(x)\big)\\ &={\cal D}(\Phi)+{\cal D}(h)+\frac{1}{2}\sum_{x,y\in\X}c(x,y)\big(\Phi(y)-\Phi(x)\big)h(y)-\frac{1}{2}\sum_{x,y\in\X}c(x,y)\big(\Phi(y)-\Phi(x)\big)h(x). \end{align*} Αν εναλλάξουμε τον ρόλο των $x$ και $y$ στο πρώτο άθροισμα της τελευταίας έκφρασης και χρησιμοποιήσουμε ότι η αγωγιμότητα είναι συμμετρική, δηλαδή $c(x,y)=c(y,x)$ για κάθε $x,y\in\X$ παίρνουμε ότι \begin{align*} {\cal D}(\Phi+h)&={\cal D}(\Phi)+{\cal D}(h)-\sum_{x,y\in\X}c(x,y)\big(\Phi(y)-\Phi(x)\big)h(x)\\ &={\cal D}(\Phi)+{\cal D}(h)-\sum_{x\in\X}h(x)\sum_{y\in\X}c(x,y)\big(\Phi(y)-\Phi(x)\big). \end{align*} Από το ΠΣΤ (7.2) που ικανοποιεί η $\Phi$ έχουμε ότι, αν $x\notin A\cup B$, τότε $\sum_{y\in\X}c(x,y)\big(\Phi(y)-\Phi(x)\big)=0$. Επιπλέον, αν $x\in A\cup B$, τότε $h(x)=0$. Σε κάθε περίπτωση ο τελευταίος όρος της παραπάνω σχέσης μηδενίζεται, οπότε

αφού η ${\cal D}(h)$ είναι εξ ορισμού μη αρνητική. Μάλιστα, για να έχουμε ισότητα στην παραπάνω σχέση θα πρέπει ${\cal D}(h)=0$. Εφόσον η ${\cal D}(h)$ είναι άθροισμα μη αρνητικών όρων, αυτό σημαίνει ότι $h(y)=h(x)$, όποτε έχουμε $c(x,y)>0$. Μια και το κύκλωμα είναι συνεκτικό, μπορούμε να συνδέσουμε οποιονδήποτε κόμβο του, $y$, με το $Α$, μέσω ενός μονοπατιού κατά μήκος του οποίου συναντάμε θετικές αγωγιμότητες. Έτσι η $h$ πρέπει να είναι σταθερή στους κόμβους αυτού του μονοπατιού και εφόσον μηδενίζεται στο $A$, έχουμε $h(y)=0$.

Πόρισμα 7.1 ( Αρχή του Rayleigh ) Αν για δύο κυκλώματα με κόμβους $\X$ και αγωγιμότητες $\{c(x,y)\}_{x,y\in\X}$ και $\{\tilde{c}(x,y)\}_{x,y\in\X}$ αντίστοιχα, έχουμε ότι $c(x,y)\le\tilde{c}(x,y)$ για κάθε $x,y\in\X$, τότε η ισχύς που καταναλώνεται στο πρώτο είναι πάντα μικρότερη από την ισχύ που καταναλώνεται στο δεύτερο.

Απόδειξη:Για $\Psi\in F_{A,B}$ ορίζουμε την $\tilde{{\cal D}}(\Psi)$ κατ' αναλογία με την (7.4), χρησιμοποιώντας τις αγωγιμότητες $\tilde{c}(x,y)$. Από την υπόθεση ότι $c(x,y)\le\tilde{c}(x,y)$ για κάθε $x,y\in\X$, έχουμε

Επομένως $\inf_{\Psi\in F_{A,B}}{\cal D}(\Psi)\le \inf_{\Psi\in F_{A,B}} \tilde{{\cal D}}(\Psi).$ Από το Θεώρημα 7.1 όμως, το αριστερό μέλος αυτής της ανίσωσης είναι η ισχύς που καταναλώνεται στο πρώτο κύκλωμα, ενώ το δεξί μέλος είναι η ισχύς που καταναλώνεται στο δεύτερο.

είναι η ισχύς που καταναλώνει ολόκληρο το κύκλωμα όταν συνδέσουμε το σύνολο κόμβων $A$ στον θετικό πόλο και το σύνολο κόμβων $B$ στον αρνητικό πόλο μιας πηγής που δημιουργεί διαφορά δυναμικού 1, αυτή η ποσότητα είναι η ισοδύναμη αγωγιμότητα (ή χωρητικότητα) του κυκλώματος ανάμεσα στο $A$ και στο $B$. Μάλιστα, εύκολα μπορεί να δει κανείς ότι $C(A,B)=C(B,A)$, αφού, αν η $\Phi$ λύνει το ΠΣΤ (7.2), τότε η 1-$\Phi$ λύνει το αντίστοιχο ΠΣΤ με τον ρόλο των $A$ και $B$ εναλλαγμένο, ενώ ${\cal D}(\Phi)={\cal D}(1-\Phi).$

Εντελώς ανάλογα αποτελέσματα με την ίδια ακριβώς απόδειξη έχουμε για μια χρονικά αντιστρέψιμη μαρκοβιανή αλυσίδα. Την αντίστοιχη ποσότητα

ονομάζουμε χωρητικότητα (capacity) ανάμεσα στα σύνολα καταστάσεων $A$ και $B$. Συμβολίζοντας για απλότητα τη συνάρτηση δυναμικού $\Phi_{A,B}$ με $\Phi$, μπορούμε να ξαναγράψουμε τη χωρητικότητα, ως εξής. \begin{align*} C(A,B)&=\frac{1}{2}\sum_{x,y\in\X}\pi(x)p(x,y)\big(\Phi(y)-\Phi(x)\big)\Phi(y)-\frac{1}{2}\sum_{x,y\in\X}\pi(x)p(x,y)\big(\Phi(y)-\Phi(x)\big)\Phi(x). \end{align*} Αν εναλλάξουμε τον ρόλο των $x$ και $y$ στο πρώτο άθροισμα και χρησιμοποιήσουμε τη συνθήκη ακριβούς ισορροπίας, παίρνουμε περαιτέρω \begin{align*} C(A,B)&=\frac{1}{2}\sum_{x,y\in\X}\pi(y)p(y,x)\big(\Phi(x)-\Phi(y)\big)\Phi(x)-\frac{1}{2}\sum_{x,y\in\X}\pi(x)p(x,y)\big(\Phi(y)-\Phi(x)\big)\Phi(x)\\ &=-\sum_{x,y\in\X}\pi(x)p(x,y)\big(\Phi(y)-\Phi(x)\big)\Phi(x)=-\sum_{x\in\X}\pi(x)\Phi(x)L\Phi(x). \end{align*} Όμως από το ΠΣΤ (3.2) που ικανοποιεί η $\Phi$ έχουμε ότι $L\Phi(x)=0$ για $x\notin A\cup B$ και $\Phi(x)=0$ για $x\in B$. Επομένως, στο τελευταίο άθροισμα επιζούν μόνο οι όροι για $x\in A$, για τους οποίους έχουμε $\Phi(x)=1$. Έτσι,

\begin{align} C(A,B) & = - \sum_{ x \in A } \pi (x) L \Phi (x) = \sum_{ x \in A } \pi (x) \sum_{ y \in \X } p(x,y) \big(\Phi (x) - \Phi (y) \big) \nonumber\\ &=\sum_{ x \in A} \pi(x) \sum_{ y \in \X } p(x,y) \big(1- \Phi(y) \big) = \sum_{ x \in A } \pi(x) \sum_{ y \in \X } p(x,y) \P_y \big[ T_B < T_A \big ] \nonumber\\ &=\sum_{ x \in A} \pi(x) \Px{ T_B^+ < T_A^+ }= \sum_{ x \in A } \pi(x) \Px{ T_B < T_A^+}. \end{align}

Στην προτελευταία ισότητα χρησιμοποιήσαμε ανάλυση πρώτου βήματος και τη μαρκοβιανή ιδιότητα και στην τελευταία ότι $A\cap B=\emptyset$. Στην ειδική περίπτωση που $A=\{x\}$ και $B=\{y\}$ έχουμε ότι

Χρησιμοποιώντας τώρα τη συμμετρία της χωρητικότητας, $C(A,B)=C(B,A)$, φτάνουμε στο καθόλου τετριμμένο αποτέλεσμα ότι για οποιεσδήποτε καταστάσεις $x,y\in\X$ μιας χρονικά αντιστρέψιμης μαρκοβιανής αλυσίδας έχουμε

Μπορείτε να διαβάσετε περισσότερα για την αναλογία μαρκοβιανών αλυσίδων και ηλεκτρικών κυκλωμάτων στο εξαιρετικό βιβλίο [Doyle85] . Εκεί μπορείτε να βρείτε και μια απόδειξη πως ο απλός, συμμετρικός τυχαίος περίπατος στο $\Z^d$ είναι επαναληπτικός όταν $d=1$ ή 2 αλλά παροδικός όταν $d>2$, χρησιμοποιώντας αυτή την αναλογία και την Αρχή του Rayleigh.

7.4 O αλγόριθμος Metropolis-Hastings και το μοντέλο Ising

Η κλασική μέθοδος Monte Carlo χρησιμοποιεί τον νόμο τον μεγάλων αριθμών για να υπολογίσει τη μέση τιμή βάσει κάποιας κατανομής $\pi$ ως ένα μέσο όρο ανεξάρτητων δειγμάτων. Συγκεκριμένα, αν $X_1,X_2,\ldots$ είναι ανεξάρτητες, ισόνομες τυχαίες μεταβλητές με κατανομή $\pi$, ο νόμος των μεγάλων αριθμών εξασφαλίζει ότι

Συνηθως χρησιμοποιεί κανείς τη μέθοδο Monte Carlo για να υπολογίσει την αναμενόμενη τιμή $\E^\pi\big[f\big]$ προσομοιώνοντας ανεξάρτητα δείγματα $X_1,X_2,\ldots,X_N$ από την κατανομή $\pi$ και παίρνοντας τον μέσο όρο των $f(X_i)$. Ο νόμος των μεγάλων αριθμών μας εξασφαλίζει ότι με πιθανότητα 1, όταν το $N$ είναι μεγάλο, οι δύο ποσότητες είναι κοντά, ενώ το κεντρικό οριακό θεώρημα μπορεί να μας δώσει εκτιμήσεις για το τυπικό σφάλμα της προσέγγισης.

Σε πολλές ενδιαφέρουσες εφαρμογές το να πάρει κανείς δείγματα από την κατανομή $\pi$ είναι εξαιρετικά δύσκολο. Αυτό μπορεί να συμβεί γιατί ο χώρος $\X$ στον οποίο έχει οριστεί η κατανομή $\pi$ είναι πολύπλοκος και η κατανομή $\pi$ δεν είναι ακριβώς γνωστή. Η μέθοδος Markov Chain Monte Carlo (MCMC) προσομοιώνει την $\pi$ ως την κατανομή ισορροπίας μιας μαρκοβιανής αλυσίδας. Η προσομοίωση της μαρκοβιανής αλυσίδας είναι συνήθως πολύ εύκολη, αφού η δεσμευμένη κατανομή της $X_{n+1}$ δεδομένης της $X_n$ δίνεται από τις πιθανότητες μετάβασης της αλυσίδας. Έχουμε ήδη δει πώς γίνεται αυτό στα αριθμητικά πειράματα. Χρειάζεται όμως να κατασκευάσουμε κατάλληλες πιθανότητες μετάβασης που θα μας εξασφαλίζουν ότι η $\{X_n\}$ έχει κατανομή ισορροπίας την $\pi$. Το πρόβλημα αυτό δεν έχει μοναδική λύση, αλλά μία από τις πιο επιτυχημένες προσεγγίσεις είναι ο αλγόριθμος Metropolis-Hastings.

Ο αλγόριθμος αυτός μπορεί να περιγραφεί ως εξής. Χωρίς βλάβη της γενικότητας μπορούμε να υποθέσουμε ότι $\pi(x)>0$ για κάθε $x\in\X$. Θεωρούμε έναν περίπατο στο $\X$ με πιθανότητες μετάβασης $r(x,y)$ από την κατάσταση $x$ στην κατάσταση $y$. Αν κάποια στιγμή βρισκόμαστε στην κατάσταση $x\in\X$ επιλέγουμε την υποψήφια επόμενη κατάσταση $y$ με πιθανότητα $r(x,y)$. Στη συνέχεια αποφασίζουμε αν θα μεταβούμε στην $y$ με πιθανότητα να το κάνουμε ίση με

Η πιθανότητα μετάβασης από την $x$ στην $y\neq x$ είναι το γινόμενο της πιθανότητας να επιλέξουμε την $y$ ως υποψήφια επόμενη κατάσταση με την πιθανότητα να πραγματοποιήσουμε τη μετάβαση, δεδομένου ότι επιλέξαμε την $y$. Συγκεκριμένα,

\begin{equation} p(x,y)=r(x,y)\left(\frac{\pi(y)r(y,x)}{\pi(x)r(x,y)}\wedge 1\right),\quad y\neq x. \end{equation}

Από την παραπάνω ανισότητα βλέπουμε ότι, αν $r(x,x)>0$ για κάποιο $x\in\X$, τότε η αλυσίδα που κατασκευάσαμε είναι αυτόματα απεριοδική. Ακόμα όμως κι αν επιλέξουμε $r(x,x)=0$ για κάθε $x\in\X$, αν οι πιθανότητες μετάβασης $\{r(x,y)\}_{x,y\in\X}$ δεν είναι σε ακριβή ισορροπία με την $\pi$, τότε υπάρχουν $x,y\in\X$ με $\pi(y)r(y,x)<\pi(x)r(x,y)$. Επομένως,

και πάλι η αλυσίδα με πιθανότητες μετάβασης $\{p(x,y)\}_{x,y\in\X}$ είναι απεριοδική. Η κατανομή $\pi$ που θέλουμε να προσομοιώσουμε και οι πιθανότητες μετάβασης $\{p(x,y)\}_{x,y\in\X}$ βρίσκονται σε ακριβή ισορροπία. Πράγματι, για $x\neq y$ έχουμε

Σύμφωνα με το Λήμμα 1, η $\pi$ είναι αναλλοίωτη κατανομή της αλυσίδας $\{X_n\}$ με πιθανότητες μετάβασης $\{p(x,y)\}_{x,y\in\X}$. Επιπλέον, η $\{X_n\}$ είναι μη υποβιβάσιμη, όταν o περίπατος που ορίζουν οι πιθανότητες μετάβασης $\{r(x,y)\}_{x,y\in\X}$ είναι μη υποβιβάσιμος. Επομένως, όπως είδαμε στο προηγούμενο Κεφάλαιο 6, έχουμε

Μπορούμε λοιπόν να πάρουμε δείγματα από την κατανομή $\pi$, προσομοιώνοντας την $\xn$ για αρκετό χρόνο ώστε να έρθει κοντά στην κατανομή ισορροπίας της.

Ένα κλασικό παράδειγμα κατανομών που παρουσιάζουν μεγάλο ενδιαφέρον και συχνά είναι δύσκολο να προσομοιωθούν είναι οι κατανομές Gibbs. Αυτές εμφανίζονται φυσικά σε συστήματα που βρίσκονται σε κατάσταση θερμοδυναμικής ισορροπίας σε θερμοκρασία $T$, οπότε η πιθανότητα να βρούμε ένα τέτοιο σύστημα σε μια κατάσταση $x$ με ενέργεια $H(x)$ είναι

Στην παραπάνω σχέση $\beta=\frac{1}{KT}$ είναι ο παράγοντας Boltzmann . Η $Ζ(\beta)$, η οποία στη βιβλιογραφία της Φυσικής αναφέρεται ως συνάρτηση επιμερισμού (partition function), είναι μια σταθερά κανονικοποίησης που δίνεται από τη σχέση

Η συνάρτηση επιμερισμού είναι ό,τι θα ήθελε να ξέρει ένας Στατιστικός Φυσικός για το σύστημα που μελετά. Πολλές θερμοδυναμικές παράμετροι του συστήματος, όπως η ελεύθερη ενέργεια, η εντροπία ή η πίεση, μπορούν να υπολογιστούν από την $Z(\cdot)$ και τις παραγώγους της.

Συνήθως όμως είναι δύσκολο να υπολογιστεί το παραπάνω άθροισμα. Σ' ένα απλό μοντέλο μαγνήτισης για παράδειγμα, στις κορυφές ενός τετραγωνικού πλέγματος $L\times L$ τοποθετούμε σωματίδια που έχουν σπιν +1 ή -1. Η κατάσταση του συστήματος $x$ περιγράφεται από το σπιν σε κάθε κορυφή του πλέγματος, επομένως ο χώρος καταστάσεων $\X$ έχει πληθάριθμο $2^{L^2}$. Για ένα πλέγμα $100\times 100$ ατόμων ο $\X$ αριθμεί $2^{10000}\ge 10^{3000}$ καταστάσεις. Αυτός είναι ένας τεράστιος αριθμός. Τα άτομα στο σύμπαν εκτιμάται ότι είναι της τάξης του $10^{80}$. Παρότι λοιπόν η συνάρτηση ενέργειας του συστήματος $Η$ μπορεί να είναι γνωστή, είναι συχνά δύσκολο να πάρει κανείς δείγματα από την κατανομή $\pi$ γιατί δεν μπορεί να υπολογίσει το άθροισμα στον ορισμό της συνάρτησης επιμερισμού.

Με τον αλγόριθμο Metropolis-Hastings έχουμε το πλεονέκτημα ότι δεν χρειάζεται να γνωρίζουμε τη $Z$ για να προσομοιώσουμε την αλυσίδα. Συγκεκριμένα, επιλέγοντας για απλότητα μια συμμετρική $r$, $r(x,y)=r(y,x)$ για κάθε $x,y\in\X$, οι πιθανότητες μετάβασης είναι για $x\neq y$

Μπορούμε να επιλέξουμε τις $r(x,y)$ να είναι 0, εκτός αν οι καταστάσεις $x,y$ διαφέρουν μόνο ως προς το σπιν μίας από τις $L^2$ θέσεις, οπότε $r(x,y)=1/L^2$. Σε αυτή την περίπτωση, ο αλγόριθμος Metropolis-Hastings θα εφαρμοζόταν ως εξής:

Στον κώδικα ising.py υλοποιούμε σε γλώσσα Python τον αλγόριθμο για το μοντέλο Ising, σύμφωνα με το οποίο η ενέργεια του συστήματος στην κατάσταση $x$ δίνεται από τη σχέση

Στην παραπάνω σχέση $x(i),\ x(j)\in\{-1,+1\}$ είναι τα σπιν της κατάστασης $x$ στις θέσεις $i,j$ αντίστοιχα, ενώ ο συμβολισμός $i\sim j$ δείχνει ότι η άθροιση εκτείνεται σε ζευγάρια σωματιδίων που γειτνιάζουν στο πλέγμα. Το πλέγμα που χρησιμοποιούμε στον κώδικα έχει $L=128$, ενώ ο παράγοντας Boltzmann είναι $\beta=1/3.$ Προσέξτε ότι εφόσον $\beta>0$, το μέτρο Gibbs $\pi$ αποδίδει μεγαλύτερη πιθανότητα σε καταστάσεις που έχουν χαμηλή ενέργεια. Στον υπολογισμό της ενέργειας μιας κατάστασης $x$ στο μοντέλο Ising κάθε ζευγάρι γειτονικών σωματιδίων συνεισφέρει -1, αν τα σπιν τους έχουν τον ίδιο προσανατολισμό, και +1, αν έχουν αντίθετο. Άρα καταστάσεις όπου γειτονικά σωματίδια έχουν το ίδιο σπιν είναι πιο πιθανές, γι' αυτό και το μοντέλο Ising είναι ένα μοντέλο σιδηρομαγνητισμού.

Παρατηρήστε ότι, επειδή $r(x,y)\neq 0$ μόνο αν τα σπιν των καταστάσεων $x,y$ διαφέρουν σε μία μόνο θέση, δεν είναι ανάγκη να υπολογίσουμε ολόκληρη τη συνάρτηση ενέργειας στο 2ο βήμα παραπάνω. Συγκέκριμένα, αν η $y$ προκύπτει από τη $x$ αλλάζοντας το σπιν του σωματιδίου που βρίσκεται στη θέση $k$, δηλαδή

Για $\beta\to\infty$, δηλαδή όταν η θερμοκρασία $T\downarrow 0$, η κατανομή $\pi$ τείνει να συγκεντρωθεί στις καταστάσεις με τη μικρότερη δυνατή ενέργεια. Στο μοντέλο Ising αυτές είναι οι δύο καταστάσεις $x_{+}$ και $x_{-}$ όπου όλα τα σπιν έχουν τον ίδιο προσανατολισμό, όλα +1 στην κατάσταση $x_{+}$ ή όλα -1 στην κατάσταση $x_{-}$. Συγκεκριμένα,

Αντίθετα για $\beta=0$ (άπειρη θερμοκρασία) όλες οι καταστάσεις έχουν την ίδια πιθανότητα $\pi(x)=\frac{1}{|\X|}=2^{-L^2}$. Βλέπουμε λοιπόν ότι, καθώς θερμαίνουμε το σύστημα από τη θερμοκρασία $Τ=0$ στη θερμοκρασία $Τ=\infty$, το σύστημα μεταβαίνει από μια κατάσταση πλήρους οργάνωσης (όλα τα σπιν προσανατολισμένα) σε μια κατάσταση πλήρους αταξίας, όπου όλες οι διαμορφώσεις σπιν είναι ισοπίθανες.

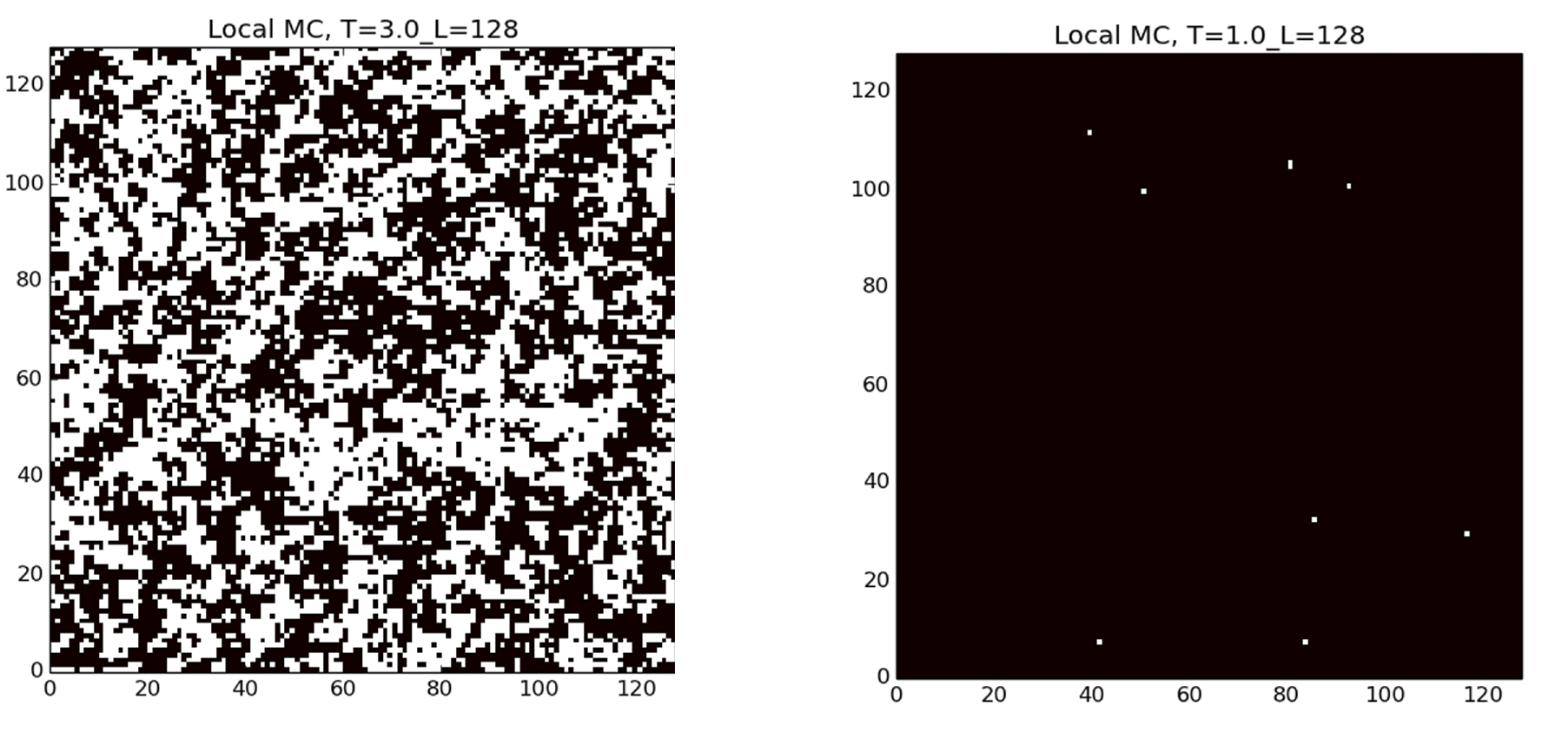
Στο Σχήμα 7.1 βλέπουμε δείγματα από την κατανομή $\pi$ που έχουμε πάρει με τη βοήθεια του αλγορίθμου μας για $\beta=1/3$ (αριστερά) και για $\beta=1$ (δεξιά). Τα μαύρα pixel αντιστοιχούν σε σωματίδια με σπιν +1 ενώ τα άσπρα σε σωματίδια με σπιν -1. Επιβεβαιώνουμε αριθμητικά έτσι ότι σε χαμηλές θερμοκρασίες (δεξιά) τα σπιν τείνουν να είναι σε συμφωνία, ενώ σε υψηλές θερμοκρασίες (αριστερά) τα σπιν φαίνονται τυχαία προσανατολισμένα.

Στα αριθμητικά πειράματα θα εξετάσουμε πώς πραγματοποιείται η μετάβαση από τη μία εικόνα στην άλλη καθώς κατεβάζουμε τη θερμοκρασία και θα δούμε ότι αυτή η μετάβαση συμβαίνει απότομα, όταν η θερμοκρασία πέσει κάτω από μια κρίσιμη τιμή. Περισσότερα για τον αλγόριθμο Metropolis-Hastings και για τη μέθοδο MCMC μπορείτε να διαβάσετε στις αναφορές [Haggstrom02] και [Krauth06] .

7.5 Προσομοιωμένη ανόπτηση (simulated annealing)

Στην προηγούμενη παράγραφο είδαμε ότι καθώς $\beta\to\infty$ (καθώς ψύχουμε το σύστημα), η κατανομή Gibbs $\pi$ τείνει να συγκεντρωθεί στις καταστάσεις εκείνες όπου η ενέργεια του συστήματος ελαχιστοποιείται. Στο μοντέλο Ising οι καταστάσεις που ελαχιστοποιούν την ενέργεια είναι προφανείς. Υπάρχουν όμως παραδείγματα όπου το ελάχιστο της συνάρτησης ενέργειας $H$ είναι εξαιρετικά δύσκολο να υπολογιστεί, όπως για παράδειγμα στο πρόβλημα του πλανόδιου πωλητή που πρέπει να επισκεφτεί μια σειρά από πόλεις και θέλει να βρει την σειρά με την οποία θα τις επισκεφτεί, ώστε να ελαχιστοποιήσει τη συνολική απόσταση που θα διανύσει.

Η μέθοδος της προσομοιωμένης ανόπτησης χρησιμοποιεί αυτή την ιδιότητα των κατανομών Gibbs για να υπολογίσει το ελάχιστο μιας συνάρτησης. H ιδέα οφείλει το όνομά της σε μια τεχνική επεξεργασίας μετάλλων με σταδιακή ψύξη τους (ανόπτηση) και είναι πολύ απλή. Χρησιμοποιούμε τον αλγόριθμο Metropolis-Hastings για κάποιο αρχικό $\beta>0$. Μετά από έναν αριθμό βημάτων ώστε η αλυσίδα μας να έχει προσεγγίσει την κατάσταση ισορροπίας που αντιστοιχεί σε αυτήν τη θερμοκρασία, ανεβάζουμε την τιμή του $\beta$ (ψύχουμε το σύστημα). Συνήθως ρίχνουμε τη θερμοκρασία κατά έναν πολλαπλασιαστικό παράγοντα ψύξης (cooling factor). Στην καινούργια θερμοκρασία αφήνουμε πάλι την αλυσίδα μας να προσεγγίσει την ισορροπία. Η συνάρτηση $r(\cdot,\cdot)$ στον αλγόριθμο Metropolis-Hastings μπορεί να αλλάζει καθώς αλλάζουμε τη θερμοκρασία. Αυτό συνήθως γίνεται επιτρέποντας όλο και πιο εντοπισμένες μεταβάσεις όσο η θερμοκρασία κατεβαίνει, ώστε ο αλγόριθμος να εντοπίζει το ελάχιστο με μεγαλύτερη ακρίβεια. Η επιλογή του παράγοντα ψύξης και της $r$ ονομάζεται πρόγραμμα ψύξης (cooling schedule) και έχει, όπως θα δούμε στις προγραμματιστικές ασκήσεις, μεγάλη σημασία στην αποτελεσματική λειτουργία του αλγορίθμου. Καθώς επαναλαμβάνουμε τη διαδικασία, ανεβάζοντας σταδιακά την τιμή του $\beta$, οι καταστάσεις με χαμηλή ενέργεια γίνονται όλο και πιο πιθανές και στο όριο καθώς $\beta\to\infty$ η αλυσίδα μας θα βρίσκεται με μεγάλη πιθανότητα σε κάποια από τις κατάστασεις με τη χαμηλότερη ενέργεια.

Πιο συγκεκριμένα, ας υποθέσουμε χωρίς βλάβη της γενικότητας (αφού αν μετατοπίσουμε τη συνάρτηση ενέργειας κατά μία σταθερά, το μέτρο $\pi$ δεν αλλάζει) ότι το ελάχιστο της συνάρτησης $H$ στο $\X$ είναι το 0. Ορίζουμε το σταθμικό σύνολο της $H$

Το σύνολο $E_0$ αποτελείται από τα σημεία του $\X$ στα οποία η $H$ λαμβάνει την ελάχιστη τιμή της. Έστω $|E_0|=M$ ο πληθάριθμος του $E_0$. Για $\epsilon>0$ το σύνολο $E_\epsilon^c$ είναι εκείνες οι καταστάσεις με ενέργεια τουλάχιστον $\epsilon$. Μπορούμε να εκτιμήσουμε την $\pi\big[Ε_\epsilon^c\big]$ ως εξής: \begin{align*} \pi\big[E_\epsilon^c\big]&=\frac{\sum_{x\in E_\epsilon^c} e^{-\beta H(x)}}{\sum_{x\in E_\epsilon^c} e^{-\beta H(x)}+\sum_{x\in E_\epsilon} e^{-\beta H(x)}}\le \frac{\sum_{x\in E_\epsilon^c} e^{-\beta H(x)}}{\sum_{x\in E_\epsilon^c} e^{-\beta H(x)}+M}\le \frac{|\X|}{M} e^{-\beta\epsilon}. \end{align*} Βλέπουμε λοιπόν ότι, καθώς $\beta\to\infty$, η $\pi\big[E_\epsilon^c\big]$ τείνει στο 0 και μάλιστα εκθετικά γρήγορα. Επομένως, έχοντας αφήσει την αλυσίδα να ισορροπήσει σε μια χαμηλή θερμοκρασία, με πολύ μεγάλη πιθανότητα αυτή θα βρεθεί σε κάποιο σημείο του $\X$, που δίνει στη συνάρτηση $H$ τιμή κοντά στο ελάχιστό της.

O λόγος που ψύχουμε σταδιακά το σύστημα είναι για να μην παγιδευτούμε σε τοπικά ελάχιστα της συνάρτησης $H$. Αυτός είναι ο κυριότερος λόγος που ο αλγόριθμος της προσομοιωμένης ανόπτησης δουλεύει πολύ καλύτερα από κλασικές μεθόδους κλίσης, στην περίπτωση που τα σταθμικά σύνολα της $H$, $E_t=\{x\in\X: H(x)\le t\}$ έχουν πολύπλοκη γεωγραφία.

Παράδειγμα 7.1 Ας δούμε τώρα τη μέθοδο της προσομοιωμένης ανόπτησης μέσα από ένα εύκολο παράδειγμα που μπορούμε να λύσουμε και αναλυτικά. Η συνάρτηση

\begin{equation} V(x)=\frac{x^4}{4}+\frac{7x^3}{15}-\frac{4x^2}{5}-\frac{4x}{5}+2 \end{equation}

έχει ελάχιστο στο $x=-2$ με $V(-2)=\frac{2}{3}$ και τοπικό ελάχιστο στο $x=+1$ με $V(1)=67/60$. Στο Σχήμα 7.2 φαίνεται η γραφική παράσταση της συνάρτησης $V(\cdot)$. O κώδικας potential_siman.py υλοποιεί σε Python τον αλγόριθμο της προσομοιωμένης ανόπτησης. Η σταθερά gamma στον κώδικα καθορίζει τον παράγοντα ψύξης, αφού όταν κατεβάζουμε την θερμοκρασία η νέα θερμοκρασία $T$ είναι η προηγούμενη πολλαπλασιασμένη με 1- gamma. Το πρόγραμμα επαναλαμβάνει iter φορές τον αλγόριθμο και υπολογίζει το ποσοστό $p$ των φορών που επιτυγχάνει να βρει το ολικό ελάχιστο, δηλαδή το -2.

Στα αριθμητικά πειράματα θα έχετε την ευκαιρία να δείτε ένα κινούμενο σχέδιο σχετικά με το πώς λειτουργεί ο αλγόριθμος της προσομοιωμένης ανόπτησης στο συγκεκριμένο παράδειγμα και πώς επηρεάζεται η αποτελεσματικότητα του αλγορίθμου στο να εντοπίζει το ελάχιστο από το πρόγραμμα ψύξης.
Με αντίστοιχο τρόπο μπορούμε να επιχειρήσουμε να βρούμε το ελάχιστο και στην περίπτωση του προβλήματος του πλανόδιου πωλητή. Με δεδομένες τις θέσεις των πόλεων μπορούμε να πάρουμε ως χώρο των καταστάσεων $\X$ της αλυσίδας μας τις κυκλικές μεταθέσεις των πόλεων που θα παριστάνουν τη σειρά με την οποία ο πωλητής επισκέπτεται τις πόλεις. Σαν ενέργεια μιας τέτοιας κατάστασης μπορούμε να πάρουμε το συνολικό μήκος του μονοπατιού που διανύουμε για επισκεπτούμε τις πόλεις με τη συγκεκριμένη σειρά. Με αυτό το πρόβλημα θα ασχοληθείτε εκτενώς στα αριθμητικά πειράματα. Μπορείτε να βρείτε περισσότερες πληροφορίες για την προσομοιωμένη ανόπτηση στην αναφορά [Krauth06]

7.6 Ασκήσεις

Άσκηση 7.1 Στο δίκτυο του διπλανού σχήματος υπολογίστε τον δείκτη σημαντικότητας που κατασκευάσαμε στην παράγραφο 7.2 για κάθε κορυφή του.

Άσκηση 7.2 Αν διατηρούσατε την σελίδα 1 του διπλανού σχήματος πώς θα μπορούσατε να αυξήσετε τον δείκτη σημαντικότητάς της ώστε να εμφανίζεται πιο ψηλά σε σχετικές αναζητήσεις;

Άσκηση 7.3 Κατασκευάστε μια μαρκοβιανή αλυσίδα στον χώρο $\X=\{A,B,C,D,E,F,G\}$, ώστε να έχει κατανομή ισορροπίας

Άσκηση 7.4 Δείξτε ότι αν $B_1\subset B_2$, τότε $C(A,B_1)\le C(A,B_2)$.

Άσκηση 7.5 Στον αλγόριθμο Metropolis-Hastings παίρνουμε τις προτεινόμενες μεταβάσεις $\{r(x,y)\}_{x,y\in\X}$ ανεξάρτητες από την κατάσταση αφετηρίας, δηλαδή \[ r(x,y)=\rho(y),\quad x,y\in\X, \] όπου η $\rho(\cdot)$ είναι μια σ.μ.π. στον $X$, τέτοια ώστε $\rho(x)>0$ για κάθε $x\in\X$. Ορίζουμε $w(x)=\frac{\rho(x)}{\pi(x)}.$ Με αυτή την επιλογή οι πιθανότητες μετάβασης της αλυσίδας του αλγορίθμου γίνονται \[ p(x,y)=\rho(y)\Big(\frac{w(x)}{w(y)}\wedge 1\Big). \] Αν ταξινομήσουμε τις καταστάσεις του $\X=\{x_1,\ldots,x_N\}$, ώστε \[ w(x_1)\le w(x_2)\le \ldots\le w(x_N), \] δείξτε ότι οι ιδιοτιμές και τα αντίστοιχα ιδιοδιανύσματα του πίνακα πιθανοτήτων μετάβασης $P=\{p(x,y)\}_{x,y\in\X}$ είναι $\lambda_1=1$, $v_1=(1,1,\ldots,1)^T$ και για $k\in\{1,2,\ldots,N-1\}$ \[ \lambda_{k+1}=\sum_{j=k+1}^N\pi(x_j)\big({w(x_j)}-{w(x_k)}\big),\quad v_{k+1}=\big(0,\ldots,0,\sum_{j={k+1}}^N\pi(x_j),-\pi(x_k),\ldots,-\pi(x_k)\big)^T. \] Δείξτε ότι $1=\lambda_1>\lambda_2=1-w(x_1)>\lambda_3>\cdots>\lambda_N$.

7.7 Αριθμητικά πειράματα

Άσκηση 7.6 Στην άσκηση αυτή θα χρησιμοποιήσουμε τον αλγόριθμο Metropolis-Hastings για να κάνουμε δειγματοληψία από την αναλλοίωτη κατανομή $\pi$ του μοντέλου Ising. Καταβάστε και ανοίξτε τον κώδικα ising.py. Στον κώδικά μας θεωρούμε $L=64$, οπότε ο χώρος των δυνατών διαμορφώσεων έχει πληθάριθμο $2^{4096}>10^{1200}$. Καταλαβαίνει κανείς ότι η δειγματοληψία από έναν τόσο μεγάλο χώρο είναι πρακτικά αδύνατη με συμβατικές μεθόδους. Ο κώδικας χρησιμοποιεί τον αλγόριθμο Metropolis-Hastings για να προσομοιώσει μια μαρκοβιανή αλυσίδα στον $\X$ που ξεκινά από μια τυχαία αρχική διαμόρφωση και έχει κατανομή ισορροπίας την $\pi$.

α) Τρέξτε τον κώδικα για τη δοσμένη θερμοκρασία $T=30$ και δείτε τη διαμόρφωση στην οποία καταλήγει ο αλγόριθμος. Επαναλάβετε μερικές φορές.

β) Αλλάξτε τον κώδικα ώστε η αρχική διαμόρφωση των σπιν να είναι +1 παντού. Ξανατρέξτε τον κώδικα μερικές φορές. Αλλάζουν τα ποιοτικά χαρακτηριστικά της διαμόρφωσης που επιστρέφει ο αλγόριθμος;

γ) Αρχίστε τώρα να κατεβάζετε τη θερμοκρασία, θέτοντας διαδοχικά $Τ=10.0, 3.0, 1.0, 0.3, 0.1, 0.03$ και περιγράψτε τι παρατηρείτε.

δ) Εξηγήστε γιατί η γραμμή του κώδικα

if random.uniform(0.0,1.0) < math.exp(-deltaE/Temperature): Spin[k] *=-1

υλοποιεί τον αλγόριθμο Metropolis-Hastings.

ε) Η μαγνήτιση του συστήματος ορίζεται ως ο μέσος όρος των σπιν του πλέγματος $\Lambda$, δηλαδή \[ m(\sigma)=\frac{1}{|\Lambda|}\sum_{k\in\Lambda}\sigma(k). \] Εξετάστε πώς συμπεριφέρεται η $m(\sigma)$ για τις καταστάσεις $\sigma$ που δίνει ο αλγόριθμος καθώς κατεβάζετε τη θερμοκρασία, όπως στο ερώτημα (β).

ε) Για τη θερμοκρασία $Τ=0.03$ αλλάξτε την τιμή της παραμέτρου nsteps. Πώς μοιάζουν τα ενδιάμεσα στάδια από τα οποία περνάει η αλυσίδα μέχρι να καταλήξουμε στην εικόνα που πήραμε για nsteps$=100\times L\times L$;

στ) Η θεωρία προβλέπει ότι υπάρχει μια απότομη μεταβολή φάσης από την παραμαγνητική κατάσταση (υψηλή θερμοκρασία) στη σιδηρομαγνητική (χαμηλή θερμοκρασία) όταν $\beta\simeq 0.44$. Μπορείτε να επιβεβαιώσετε αριθμητικά αυτό το γεγονός;

Άσκηση 7.7 Στην άσκηση αυτή θα χρησιμοποιήσετε τη μέθοδο της προσομοιωμένης ανόπτησης για να βρείτε το ελάχιστο μιας συνάρτησης $V:\R\to\R$. Ο αλγόριθμος έχει ως εξής. Ένα σωματίδιο είναι αρχικά τοποθετημένο τυχαία στο διάστημα (-3.5,+3.5) σε θερμοκρασία $T=128$. Σε κάθε βήμα επιχειρεί μια μετατόπιση που ακολουθεί ομοιόμορφη κατανομή στο διάστημα $(-\delta,+\delta)$ και πραγματοποιεί τη μετατόπιση σύμφωνα με τον αλγόριθμο Metropolis-Hastings. Κάθε 100 βήματα ρίχνουμε τη θερμοκρασία και επαναλαμβάνουμε μέχρι η θερμοκρασία να πέσει κάτω από το $T=0.01$.

Κατεβάστε τον κώδικα sim_annealing.py και μελετήστε τον. Η παράμετρος minima σας επιτρέπει να επιλέξετε αν θα ελαχιστοποιήσετε μια συνάρτηση με 1, 2 ή 3 τοπικά ακρότατα. Η αρχική επιλογή είναι 3. Η παράμετρος gamma σας επιτρέπει να ελέγξετε τον ρυθμό ψύξης. Η αρχική επιλογή είναι να ρίχνουμε τη θερμοκρασία στο μισό κάθε 100 βήματα. Η παράμετρος iterations σας επιτρέπει να επαναλάβετε τη διαδικασία εύρεσης του ελαχίστου όσες φορές θέλετε. Η αρχική επιλογή της είναι 1. Η παράμετρος delta ελέγχει το μέγεθος της επιχειρούμενης μετατόπισης σε κάθε βήμα. Η αρχική της επιλογή είναι 3. Τέλος η λογική παράμετρος animation ελέγχει αν θέλουμε να δούμε μια οπτική αναπαράσταση της προσομοιωμένης ανόπτησης. Η αρχική της επιλογή είναι True.

α) Τρέξτε τον κώδικα. Παρατηρήστε πώς σε μεγάλες θερμοκρασίες το σωματίδιο κινείται σχετικά ελεύθερα στον χώρο και πώς καθώς ψύχουμε το σύστημα το σωματίδιο εντοπίζεται κοντά στο ολικό ελάχιστο της $V$. Αλλάξτε την παράμετρο minima και επαναλάβετε.
β) Αλλάξτε την παράμετρο iterations σε 1000 και την παράμετρο animation σε False ώστε να επιταχύνετε την εκτέλεση του προγράμματος. Για τις διάφορες τιμές της παραμέτρου minima βρείτε σε τι ποσοστό επιτυγχάνει ο αλγόριθμος να εντοπίσει το ελάχιστο της $V$.
γ) Αλλάξτε την τιμή της παραμέτρου delta σε 0.1 και επαναλάβετε το προηγούμενο ερώτημα. Ποιο είναι τώρα το ποσοστό επιτυχούς εύρεσης του ολικού ελαχίστου; Γιατί πιστεύετε ότι συμβαίνει αυτό; Αν θέλετε να έχετε μια εικόνα του τι συμβαίνει, αλλάξτε την παράμετρο iterations σε 1 και την παράμετρο animation σε True για να δείτε πώς κινείται το σωματίδιο και τρέξτε τον κώδικα μέχρι να δείτε το σωματίδιο να καταλήγει κοντά σε ένα τοπικό ελάχιστο, διαφορετικό από το ολικό.
δ) Αλλάξτε τον κώδικα ώστε να βρίσκει το ελάχιστο της συνάρτησης $V$ της (7.7).
ε) Μεταβάλετε το gamma και δείτε πώς συμπεριφέρεται το ποσοστό $p$ των επιτυχημένων προσπαθειών ως συνάρτηση του gamma.

- Επαληθεύστε ότι για σχετικά μεγάλες τιμές του gamma (π.χ. $> 1/2$) o ο αλγόριθμος δεν βρίσκει πάντα το ολικό ελάχιστο.

- Πού τερματίζει ο αλγόριθμος στις περιπτώσεις που δεν βρίσκει το ολικό ελάχιστο; Τι παρατηρείτε;

- Παραστήστε γραφικά την πιθανότητα $p$ ως συνάρτηση του gamma.

- Eπαληθεύστε ότι για πολύ μικρές τιμές του gamma έχουμε $p$ πολύ κοντά στο 1. Δηλαδή για κατάλληλα αργό ρυθμό ανόπτησης ο αλγόριθμος εντοπίζει το ολικό ελάχιστο με πιθανότητα κοντά στο 1.

Άσκηση 7.8 Στην άσκηση αυτή θα χρησιμοποιήσουμε τον αλγόριθμο της προσομοιωμένης ανόπτησης για να λύσουμε το πρόβλημα του πλανόδιου πωλητή. Κατεβάστε το αρχείο eu.csv που περιέχει το γεωργαφικό μήκος και πλάτος 27 ευρωπαϊκών πόλεων. Κατεβάστε τους κώδικες siman_tsp.py και plot_lib.py. Ο πρώτος περιλαμβάνει τη βασική ρουτίνα που θα χρησιμοποιήσουμε, ενώ ο δεύτερος εισάγεται ως βιβλιοθήκη και χρησιμοποιείται για τα διαγράμματα που θα κατασκευάσουμε. Ο κώδικας siman_tsp.py διαβάζει από το αρχείο eu.csv τις πόλεις και τα γεωγραφικά μήκη και πλάτη τους και χρησιμοποιεί τη ρουτίνα geodesic_distance για να υπολογίσει τη γεωδεσιακή τους απόσταση (την απόστασή τους πάνω στη γήινη σφαίρα). Στη συνέχεια χρησιμοποιεί τον αλγόριθμο της προσομοιωμένης ανόπτησης για να υπολογίσει μια προσεγγιστική λύση για το πρόβλημα του πλανόδιου πωλητή, δηλαδή με ποια σειρά πρέπει να επισκεφτεί κανείς αυτές τις πόλεις ώστε να ελαχιστοποιήσει τη συνολική απόσταση που θα διανύσει.

Στην έξοδό του ο κώδικας επιστρέφει τρία διαγράμματα. Το πρώτο έχει ένα μονοπάτι όπου οι επισκέψεις στις πόλεις γίνονται με τυχαία σειρά. Το δεύτερο έχει το βέλτιστο μονοπάτι που υπολογίζει ο αλγόριθμος της προσομοιωμένης ανόπτησης, ενώ το τρίτο δείχνει πώς εξελίσσεται η συνολική απόσταση για το τρέχον μονοπάτι του αλγορίθμου (μπλε γραμμή) και για το βέλτιστο μονοπάτι που έχει βρεθεί μέχρι τότε (κόκκινη γραμμή), καθώς κατεβάζουμε τη θερμοκρασία.

α) Τρέξτε τον κώδικα simulated_annealing_tsp.py και δείτε το μονοπάτι που επιστρέφει ο αλγόριθμος της προσομοιωμένης ανόπτησης και την εξέλιξη της συνολικής απόστασης καθώς ψύχουμε το σύστημα. Τυπώστε αυτά τα διαγράμματα και εξηγήστε την εικόνα που βλέπετε στο δεύτερο.
β) Εντοπίστε στον κώδικα τις εντολές που υλοποιούν τον αλγόριθμο {Metropolis-Hastings} και εξηγήστε πώς ακριβώς αλλάζει το μονοπάτι σε κάθε βήμα του αλγορίθμου.
γ) Αλλάξτε τον κώδικα ώστε να διαβάζει από το αρχείο europe.csv τις συντεταγμένες 35 ευρωπαϊκών πόλεων και λύστε το πρόβλημα του πλανόδιου πωλητή που θέλει να επισκεφτεί και τις 35 αυτές πόλεις. Στο διάγραμμα δεν τυπώνονται τα ονόματα των πόλεων για να είναι πιο ευκρινές το μονοπάτι.
δ) Πόσα είναι τα δυνατά μονοπάτια που περνούν από όλες τις 35 πόλεις μία μόνο φορά; Αν σε έναν υπολογιστή ο χρόνος που απαιτείται για τον υπολογισμό του συνολικού μήκους ενός τέτοιου μονοπατιού ήταν 1μsec, πόσο χρόνο θα χρειαζόμασταν για να βρούμε το βέλτιστο μονοπάτι με έναν εξαντλητικό αλγόριθμο που θα υπολόγιζε τη συνολική απόσταση που θα διανύσει ο πλανόδιος πωλητής κατά μήκος κάθε μονοπατιού και θα επέστρεφε το μονοπάτι με την ελάχιστη συνολική απόσταση;

7.1 Eισαγωγή