Κεφάλαιο 7. Κατηγοριοποίηση Δεδομένων με Δέντρα Απόφασης
7.1 Θεωρητικό υπόβαθρο των αλγορίθμων κατηγοριοποίησης του SQL Server
7.2 Δημιουργία ενός μοντέλου με δέντρα απόφασης
7.3 Αξιολόγηση δέντρων απόφασης
7.4 Ασκήσεις στην παραμετροποίηση του αλγορίθμου δέντρου απόφασης
7.5 Λύσεις ασκήσεων στην παραμετροποίηση του αλγορίθμου δέντρων απόφασης
7.6. Βιβλιογραφία/Αναφορές
Κεφάλαιο
7. Κατηγοριοποίηση Δεδομένων με Δέντρα Απόφασης
Σύνοψη
Σ’ αυτό το κεφάλαιο θα παρουσιάσουμε τα δέντρα αποφάσεων που αποτελούν την πιο δημοφιλή τεχνική εξόρυξης δεδομένων. Διαχωρίζουν τα δεδομένα σε αναδρομικά υποσύνολα, έτσι ώστε το κάθε υποσύνολο που προκύπτει να περιέχει στοιχεία με μεγαλύτερη ή μικρότερη ομοιογένεια σε σχέση με τον τελικό στόχο.
Πίνακας Περιεχομένων /
Περιεχόμενα Κεφαλαίου
7.1. Θεωρητικό υπόβαθρο των αλγορίθμων κατηγοριοποίησης του SQL Server
Με τον όρο
Κατηγοριοποίηση (classification)
προσδιορίζουμε την πράξη της ανάθεσης ενός αντικειμένου σε μία από τις κλάσεις ενός προκαθορισμένου συνόλου κλάσεων.(Νανόπουλος, & Μανωλόπουλος, 2008· Χαλκίδη, & Βεζυργιάννης, 2005) Κάθε αντικείμενο ενός συνόλου δεδομένων διαθέτει έναν αριθμό χαρακτηριστικών (X1,…,Xκ), όπου Π(Χi) είναι το πεδίο ορισμού του χαρακτηριστικού Χi. Επιπλέον, κάθε αντικείμενο έχει ένα χαρακτηριστικό C, το οποίο δηλώνει την κλάση όπου αυτό ανήκει, με Π(C) να συμβολίζει το πεδίο ορισμού του χαρακτηριστικού της κλάσης C. Η κατηγοριοποίηση περιλαμβάνει την εξεύρεση μιας συνάρτησης f: Π(X1) x … x Π(Xκ) -> Π(C), η οποία ονομάζεται μοντέλο κατηγοριοποίησης (classification model). Αν γνωρίζουμε τις τιμές των χαρακτηριστικών X1,…,Xκ ενός αντικειμένου, αλλά όχι την τιμή του χαρακτηριστικού C, τότε εφαρμόζουμε ένα μοντέλο κατηγοριοποίησης και αναθέτουμε το αντικείμενο στην κλάση f(X1,..., Xκ)..
Τα δέντρα απόφασης (decision trees) είναι από τα πιο γνωστά μοντέλα κατηγοριοποίησης. Το δέντρο απόφασης είναι ένας γράφος με την κλασική δενδρική δομή (Νανόπουλος, & Μανωλόπουλος, 2008· Χαλκίδη, & Βεζυργιάννης, 2005), όπου διακρίνουμε: (α) έναν αρχικό κόμβο, τη ρίζα, (β) τους εσωτερικούς κόμβους και (γ) τους εξωτερικούς κόμβους, τα φύλλα. Σε κάθε κόμβο (εσωτερικό ή εξωτερικό) εκτός της ρίζας εισέρχεται μια κατευθυνόμενη ακμή από έναν άλλο κόμβο. Σε κάθε εσωτερικό κόμβο αντιστοιχεί ένα χαρακτηριστικό που χρησιμοποιείται για περαιτέρω διαχωρισμό του δέντρου. Στις ακμές που εξέρχονται από τη ρίζα ή κάθε εσωτερικό κόμβο, αντιστοιχεί μιασυνθήκη ελέγχου με βάση το διαχωριστικό χαρακτηριστικό. Η διαδικασία κατασκευής ενός δέντρου απόφασης είναι επαναληπτική και μπορεί να περιγραφεί συνοπτικά ως ακολούθως: Αρχικά, επιλέγουμε ένα χαρακτηριστικό, το οποίο αναφέρεται στη ρίζα του δέντρου, και, στη συνέχεια, κατασκευάζουμε μιαακμή και έναν κόμβο για καθεμία από τις διακριτές τιμές του χαρακτηριστικού. Αυτά τα δύο βήματα επαναλαμβάνονται συνεχώς, μέχρις ότου όλα τα χαρακτηριστικά να εισαχθούν στους κόμβους του δέντρου.
Τονίζεται ότι στο περιβάλλον του SQL Server, υπάρχει σχετική παράμετρος (Split method), η οποία καθορίζει τη μέθοδο με την οποία θα διαχωρίζονται κάθε φορά οι κόμβοι ενός δέντρου. Ο διαχωρισμός μπορεί να γίνει είτε με δυαδικό τρόπο (binary) είτε με περισσότερες από δύο ακμές (complete). Επιπροσθέτως, για την αντιστοίχιση ενός χαρακτηριστικού με έναν κόμβο του δέντρου, λαμβάνεται υπόψη κάθε φορά η πληροφορία που μεταφέρει ένα χαρακτηριστικό. Συγκεκριμένα, το κριτήριο επιλογής ενός διαχωριστικού χαρακτηριστικού βασίζεται στην ομοιογένεια των κόμβων που αυτό παράγει, ώστε να επιλέγεται αυτό που επιφέρει τη μεγαλύτερη ομοιογένεια (δηλαδή να εμφανίζονται σε ένα κόμβο μόνο αντικείμενα της ίδιας κλάσης) στους νέους κόμβους που δημιουργούνται κάθε φορά. Στο περιβάλλον του SQL Server υπάρχει μια συγκεκριμένη παράμετρος (score_method), η οποία προσδιορίζει ποια μέθοδος επιλογής διαχωριστικού χαρακτηριστικού θα χρησιμοποιηθεί (π.χ. Eντροπία, ή Bayesian with K2 Prior, ή Βayesian Dirichlet Equivalent with Uniform Prior).
Η εντροπία μετράει τον βαθμό αβεβαιότητας (ανομοιογένειας των αντικειμένων που εντάσσονται σε ένα κόμβο) που δημιουργεί ένα διαχωριστικό χαρακτηριστικό.
Για τον υπολογισμό της εντροπίας, χρησιμοποιείται η παρακάτω εξίσωση:
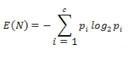
όπου με Ν συμβολίζουμε έναν υπό εξέταση κόμβο, και με c τον αριθμό των υπαρχουσών κλάσεων. Επίσης, pi= ni/ n, όπου ni είναι ο αριθμός των αντικειμένων που ανήκουν τόσο στο κόμβο Ν όσο και στην κλάση i, ενώ n είναι ο συνολικός αριθμός των αντικειμένων που ανήκουν στον κόμβο Ν.
Τέλος, ο SQL Server παρέχει δύο ακόμη μεθόδους επιλογής ενός διαχωριστικού χαρακτηριστικού (Bayesian with K2 Prior, και Bayesian Dirichlet Equivalent with Uniform Prior) που βασίζονται στα Bayesian δίκτυα. Το Bayesian δίκτυο είναι ένας κατευθυνόμενος ακυκλικός γράφος, όπου κάθε κόμβος αναπαριστά ένα χαρακτηριστικό, ενώ κάθε κατευθυνόμενη ακμή αναπαριστά μια εξαρτημένη πιθανότητα μετάβασης από έναν κόμβο σε έναν άλλο. Η μέθοδος Bayesian with K2 Prior (ΒΚ2) προσπαθεί να δώσει απαντήσεις που αφορούν στο ερώτημα ποιος προηγούμενος (prior) κόμβος πρέπει να χρησιμοποιηθεί στον υπολογισμό των πιθανοτήτων μετάβασης για τους επόμενους κόμβους. Η μέθοδος Bayesian Dirichlet Equivalent with Uniform Prior (BDE) βασίζεται στη πολυωνυμική κατανομή Dirichlet, η οποία περιγράφει τη δεσμευμένη πιθανότητα μετάβασης σε ένα κόμβο ενός Bayesian δικτύου βάσει των συνδέσεών του με προηγούμενους κόμβους στο δίκτυο. Ένα κοινό γνώρισμα των δύο παραπάνω μεθόδων είναι ότι όσο πιο κοντά βρίσκεται ένα χαρακτηριστικό στη ρίζα του δέντρου, τόσο πιο σημαντική είναι η πληροφορία σύνδεσής του με το επόμενο χαρακτηριστικό.
Πίνακας Περιεχομένων /
Περιεχόμενα Κεφαλαίου
7.2. Δημιουργία ενός μοντέλου με δέντρα απόφασης
Έστω ότι ένα Video Club, το οποίο τηρεί τη βάση δεδομένων MovieClick
(βλέπε ενότητα 6.1) και για διαφημιστικούς λόγους, θέλει να προβλέψει το
φύλλο των πελατών του με βάση την ηλικία τους, το μορφωτικό τους επίπεδο,
την οικογενειακή τους κατάσταση και τα ενδιαφέροντά τους. Θα εξετάσουμε
αυτό το παράδειγμα με τη χρήση του SQL Server Data Tools του Visual
Studio.
Αναλυτικά βήματα:
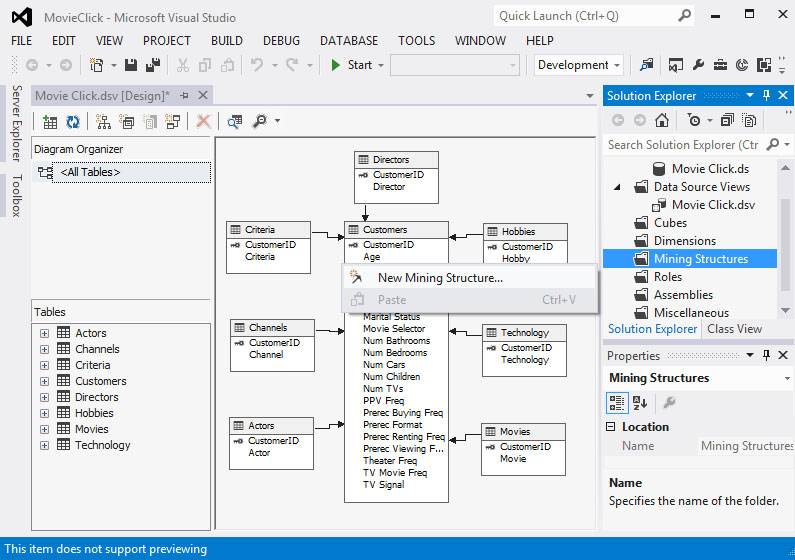
- Στην καρτέλα Solution Explorer κάνουμε δεξί κλικ στο Mining Structure και επιλέγουμε New Mining Structure, όπως φαίνεται στην Εικόνα 7.1.
Εικόνα 7.1
-
Στο παράθυρο καλωσορίσματος του οδηγού Data Mining Wizard, όπως φαίνεται στην Εικόνα 7.2, επιλέγουμε Next>, ώστε να προχωρήσουμε στο επόμενο βήμα.
Εικόνα 7.2
-
Στο παράθυρο που εμφανίζεται, όπως φαίνεται στην Εικόνα 7.3, επιλέγουμε From existing relational database or data warehouse, καθώς τα δεδομένα μας θα εισαχθούν από την σχεσιακή βάση που εισάγαμε προηγουμένως στο project μας. Στη συνέχεια, επιλέγουμε Next>, ώστε να προχωρήσουμε στο επόμενο βήμα.
Εικόνα 7.3
-
Στο νέο παράθυρο, όπως φαίνεται στην Εικόνα 7.4, επιλέγουμε τον αλγόριθμο με τον οποίο θα επεξεργαστούμε τα δεδομένα. Στη συγκεκριμένη περίπτωση επιλέγουμε τον Microsoft Decision Trees, καθώς ασχολούμαστε με τα δέντρα αποφάσεων. Στη συνέχεια, επιλέγουμε Next>, ώστε να προχωρήσουμε στο επόμενο βήμα.
Εικόνα 7.4
-
Στο νέο παράθυρο, όπως φαίνεται στην Εικόνα 7.5, βλέπουμε τα διαθέσιμα source views του project μας. Επιλέγουμε το MovieClick και, στη συνέχεια, Next>, ώστε να προχωρήσουμε στο επόμενο βήμα.
Εικόνα 7.5
-
Σ’ αυτό το στάδιο, όπως φαίνεται στην Εικόνα 7.6, επιλέγουμε ποιος πίνακας θα είναι case και ποιοι πίνακες θα είναι nested. Case είναι ο πίνακας που περιέχει τα δεδομένα που θέλουμε να προβλέψουμε, ενώ Nested είναι οι πίνακες τα δεδομένα των οποίων είναι παράμετροι στον Case. Στη συγκεκριμένη περίπτωση επιλέγουμε τον πίνακα Customers ως Case και τους πίνακες Criteria και Hobbies ως Nested, καθώς θέλουμε να μελετήσουμε κάποια στοιχεία των πελατών σε σχέση με τα Criteria και τα Hobbies.
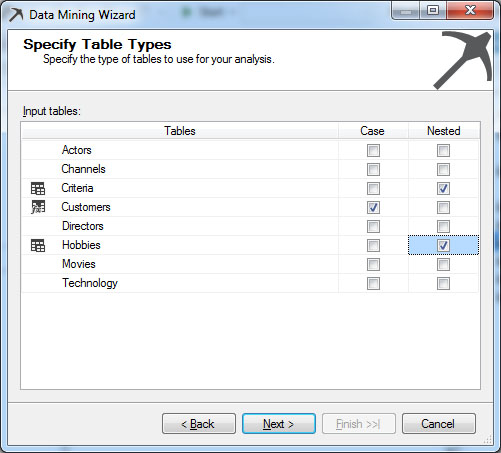
Εικόνα 7.6
-
Σ’ αυτό το στάδιο, όπως φαίνεται στην Εικόνα 7.7, επιλέγουμε ποια δεδομένα των πινάκων που επιλέξαμε στο προηγούμενο βήμα θα είναι είσοδος στο δέντρο απόφασης και ποια δεδομένα θέλουμε να προβλέψουμε με το δέντρο απόφασης. Συγκεκριμένα, κάνουμε τις εξής επιλογές:
- Για κάθε πίνακα επιλέγουμε ένα κλειδί Key. Στη συγκεκριμένη περίπτωση
επιλέγουμε τα CustomerID, Hobby και Criteria.
- Ορίζουμε ως Input τις στήλες των πινάκων που μας ενδιαφέρουν. Στη
συγκεκριμένη περίπτωση επιλέγουμε τα Age, Education Level, Marital
Status, Criteria και Hobby.
- Ορίζουμε ως Predictable τη στήλη που μας ενδιαφέρει να προβλέψουμε. Αυτή θα είναι και η έξοδος του δέντρου. Στη συγκεκριμένη περίπτωση επιλέγουμε το Gender.
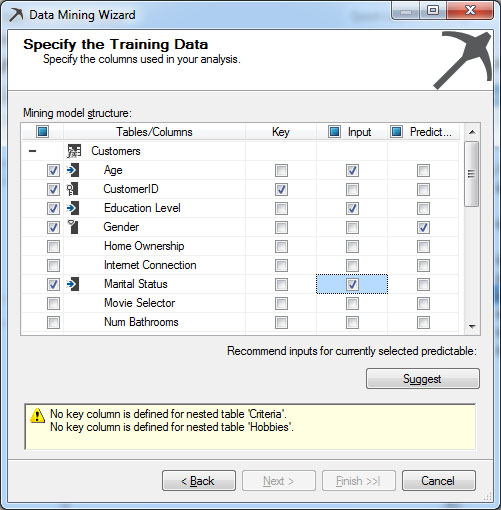
Εικόνα 7.7
-
Αν κάνουμε κλικ στο κουμπί Suggest, εμφανίζεται, όπως φαίνεται στην Εικόνα 7.8, μια εκτίμηση σχετικά με τα πιο σημαντικά χαρακτηριστικά για την πρόβλεψη της Predictable μεταβλητής. Αν επιλέγαμε ΟΚ, τότε όλα τα χαρακτηριστικά που φαίνεται να συσχετίζονται θα συμπεριλημβάνονταν στο Mining Structure που θέλουμε να δημιουργήσουμε. Γι΄ αυτό, εμείς επιλέγουμε Cancel. Στη συνέχεια, επιλέγουμε Next>, ώστε να προχωρήσουμε στο επόμενο βήμα.
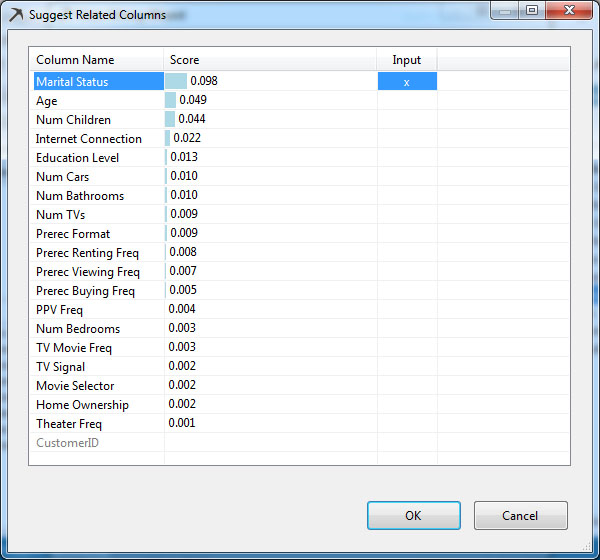
Εικόνα 7.8
-
Στη συνέχεια, όπως φαίνεται στην Εικόνα 7.9, εμφανίζεται μια σύνοψη-επιβεβαίωση του περιεχομένου του Mining Structure. Επιλέγουμε Detect, για να επιλεχθεί ο κατάλληλος τύπος δεδομένων από το σύστημα (είτε continuous ή discrete) που γίνεται ύστερα από δειγματοληψία και ανάλυση των δεδομένων από το σύστημα. Στη συνέχεια, επιλέγουμε Next.
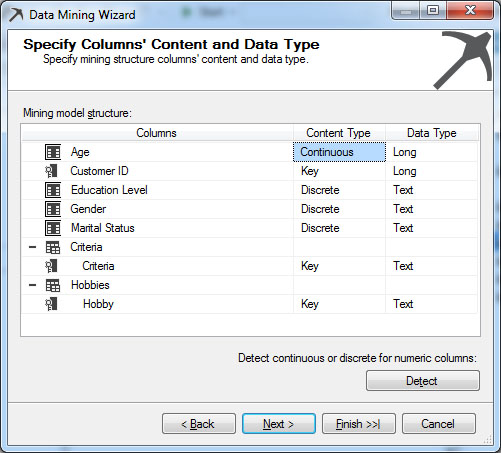
Εικόνα 7.9
-
Στο νέο παράθυρο, όπως φαίνεται στην Εικόνα 7.10, ορίζουμε το ποσοστό των δεδομένων που το μοντέλο θα διατηρήσει για την επαλήθευσή του. Στη συγκεκριμένη περίπτωση δηλώνουμε το ποσοστό 0%, καθώς θέλουμε να χρησιμοποιήσουμε όλο το σύνολο των δεδομένων της βάσης.
Εικόνα 7.10
-
Στη συνέχεια, ορίζουμε όνομα για το Mining Structure και το Mining Model. Στη συγκεκριμένη περίπτωση, όπως φαίνεται στην Εικόνα 7.11, συμπληρώνουμε CustGender στο Mining structure name και Customers_Tree στο Mining model name. Τέλος, επιλέγουμε Allow drill through και κατόπιν Finish, για να ολοκληρωθεί η διαδικασία.
Εικόνα 7.11
-
Στο παράθυρο του Data Source View και στην καρτέλα Mining Structure βλέπουμε το μοντέλο που δημιουργήσαμε, όπως φαίνεται στην Εικόνα 7.12.
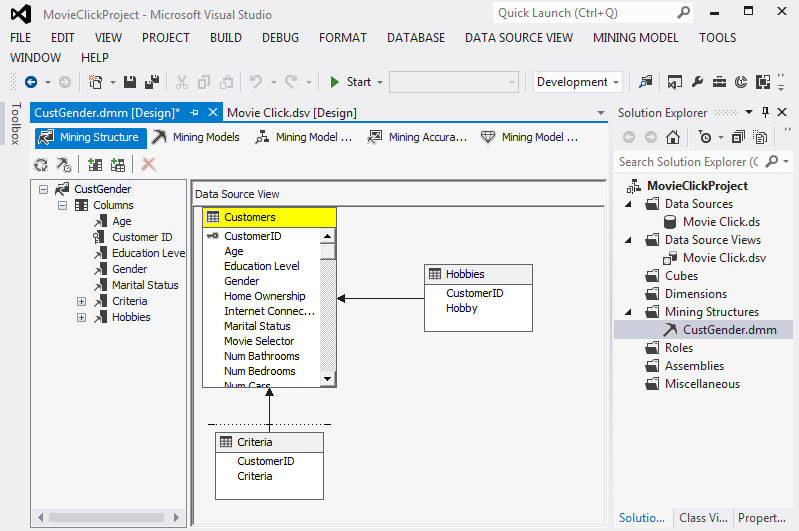
Εικόνα 7.12
-
Στη συνέχεια, επιλέγουμε την καρτέλα Mining Models, ώστε να καθορίσουμε τις παραμέτρους για τα δέντρα που θα μελετήσουμε. Όπως φαίνεται στην Εικόνα 7.13, κάθε δεδομένο έχει οριστεί ως Input, Key, Predict ή PredictOnly. H διαφορά ανάμεσα σε Predict και PredictOnly είναι ότι στο πρώτο τα δεδομένα μπορούμε να τα χρησιμοποιήσουμε ως είσοδο, αλλά και ως έξοδο (πρόβλεψη) στον αλγορίθμου, ενώ στο δεύτερο μπορούμε να τα χρησιμοποιήσουμε μόνο ως έξοδο. Στη συγκεκριμένη περίπτωση θέλουμε να προβλέψουμε το φύλλο των πελατών ανάλογα με την ηλικία, τη μόρφωση, τα hobbies και την οικογενειακή κατάσταση. Επομένως, ορίζουμε τα χαρακτηριστικά ως εξής:
- Age: Input
- Criteria: Ignore
- CustomerID: Key
- Education Level: Input
- Gender: PredictOnly
- Hobies: Input
- Marital Status: Input
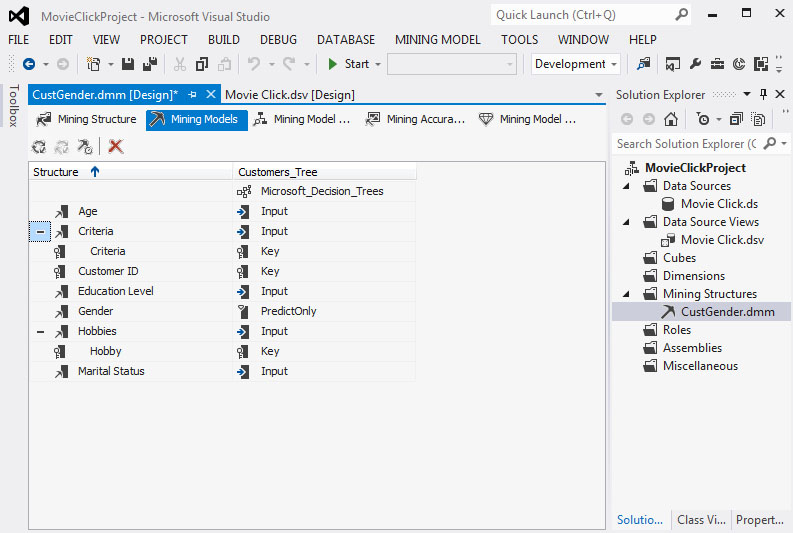
Εικόνα 7.13
-
Στη συνέχεια, θα μελετήσουμε αφενός τις παραμέτρους με τις οποίες κατασκευάζεται το δέντρο απόφασης και αφετέρου τις προεπιλεγμένες τιμές που παίρνουν. Αρχικά, όπως φαίνεται στην Εικόνα 7.14, κάνουμε δεξί κλικ στον αλγόριθμο Microsoft Decision Trees και επιλέγουμε Set Algorithm Parameters.
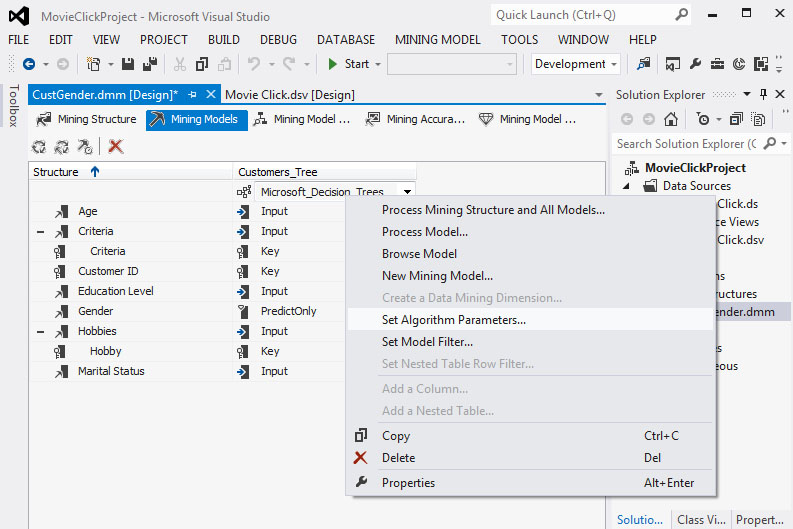
Εικόνα 7.14
-
Στο παράθυρο που εμφανίζεται, όπως φαίνεται στην Εικόνα 7.15, βλέπουμε τις μεταβλητές που μπορούμε να παραμετροποιήσουμε.
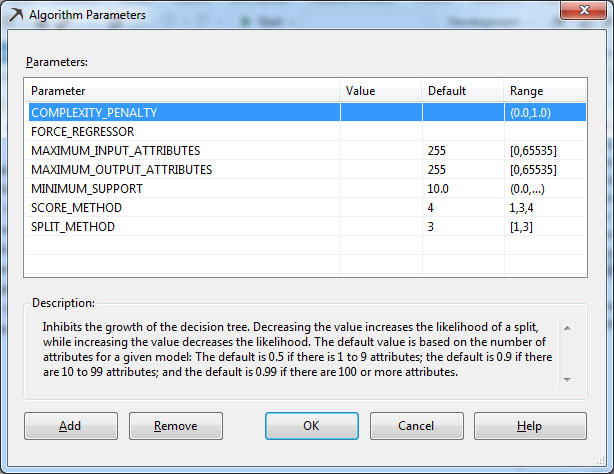
Εικόνα 7.15
Ακολουθεί η αναλυτική περιγραφή της κάθε παραμέτρου του αλγορίθμου
Decision Tree:
- COMPLEXITY_PENALTY: Αυτή η παράμετρος καθορίζει το μέγεθος του δέντρου. Η τιμή της εξαρτάται από το πλήθος των χαρακτηριστικών του μοντέλου και λαμβάνει τιμές [0,1]. Όσο η τιμή τείνει στο 1, τόσο μικρότερο είναι το δέντρο που προκύπτει. Αν τα χαρακτηριστικά είναι λιγότερα από 10, τότε η προεπιλεγμένη τιμή της παραμέτρου είναι 0,5. Αν τα χαρακτηριστικά είναι περισσότερα από 100, τότε η προεπιλεγμένη τιμή είναι 0,9. Τέλος, αν τα χαρακτηριστικά είναι περισσότερα ή ίσα από 100, τότε η προεπιλεγμένη τιμή είναι 0,99. Στη συγκεκριμένη περίπτωση τα χαρακτηριστικά είναι περισσότερα από 10 και λιγότερα από 100, οπότε η προεπιλεγμένη τιμή είναι 0.9.
- FORCE_REGRESSOR: Αυτή η παράμετρος προσδιορίζει τον αριθμό των στιγμιοτύπων που απαιτούνται, προκειμένου ένας κόμβος να διασπαστεί σε δύο ή περισσότερους κόμβους.
- MAXIMUM_INPUT_ATTRIBUTES: Αυτή η παράμετρος καθορίζει τον μέγιστο αριθμό των χαρακτηριστικών εισόδου που ο αλγόριθμος μπορεί να χειριστεί πριν αυτός αρχίσει να επιλέγει χαρακτηριστικά. Η τιμή 0 απενεργοποιεί τη δυνατότητα επιλογής των χαρακτηριστικών εισόδου. Στη συγκεκριμένη περίπτωση αφήνουμε την προεπιλεγμένη τιμή.
- MAXIMUM_OUTPUT_ATTRIBUTES: Η συγκεκριμένη παράμετρος καθορίζει τον μέγιστο αριθμό των χαρακτηριστικών εξόδου που ο αλγόριθμος μπορεί να χειριστεί πριν αυτός αρχίσει να επιλέγει χαρακτηριστικά. Η τιμή 0 απενεργοποιεί την δυνατότητα επιλογής των χαρακτηριστικών εξόδου. Στη συγκεκριμένη περίπτωση αφήνουμε την προεπιλεγμένη τιμή.
- MINIMUM_SUPPORT: Αυτή η παράμετρος προσδιορίζει το ελάχιστο πλήθος των περιπτώσεων στα φύλλα του δέντρου, που απαιτούνται για τη δημιουργία του. Όταν η τιμή αυτή είναι μικρότερη ή ίση με 1, τότε εκφράζει ποσοστό σε σχέση με το πλήθος όλων των περιπτώσεων. Διαφορετικά, όταν η τιμή είναι μεγαλύτερη από 1, εκφράζει πλήθος. Μ’ αυτήν την παράμετρο καθορίζουμε στο σύστημα πότε θα σταματήσει η ανάλυση του δέντρου, δηλαδή καθορίζουμε το μέγεθός του. Στη συγκεκριμένη περίπτωση η προεπιλεγμένη τιμή είναι 10.
- SCORE_METHOD: Αυτή η παράμετρος καθορίζει τη μέθοδο επιλογής διαχωριστικού χαρακτηριστικού για τη δημιουργία ενός δέντρου απόφασης. Μπορεί να πάρει τις τιμές 1, ή 3, ή 4. Η τιμή 1 είναι για την Εντροπία, η τιμή 3 είναι για τα δίκτυα Bayesian with K2 Prior (BK2) και η τιμή 4 είναι για τα δίκτυα Bayesian Dirichlet Equivalent with Uniform Prior (BDE). Στη συγκεκριμένη περίπτωση αφήνουμε την προεπιλεγμένη τιμή 4. Όπως περιγράφηκε στην ενότητα 7.1, η παράμετρος score_method μετράει την βαθμό βεβαιότητας/αβεβαιότητας που δημιουργεί στο μοντέλο ένα χαρακτηριστικό έναντι των υπόλοιπων χαρακτηριστικών. Έτσι, θα μπορούμε να αποφασίσουμε αν αυτό το χαρακτηριστικό θα επιλεγεί ή όχι, για να γίνει κόμβος του δέντρου απόφασης.
- SPLIT_METHOD: Αυτή η παράμετρος καθορίζει τη μέθοδο με την οποία διαχωρίζονται οι κόμβοι του δέντρου. Μπορεί να πάρει τις τιμές [1,3] όπου 1 είναι η τιμή για Binary δέντρο, 2 η τιμή για Complete (multi-way) δέντρο και 3 η τιμή και για τα δύο μαζί.
- Για να προβάλουμε το δέντρο, επιλέγουμε την καρτέλα Mining Model Viewer. Σε περίπτωση που δεν έχουν αποθηκευτεί οι αλλαγές που έχουμε κάνει, θα εμφανιστούν τα παρακάτω μηνύματα στα οποία επιλέγουμε Yes.
Εικόνα 7.16
Εικόνα 7.17
Στη συνέχεια, όπως φαίνεται στην Εικόνα 7.18, εμφανίζονται συγκεντρωμένες οι επιλογές μας. Επιλέγουμε Run, ώστε να δημιουργηθεί το δέντρο και να γίνει deploy.
Εικόνα 7.18
Στο νέο παράθυρο, όπως φαίνεται στην Εικόνα 7.19, παρουσιάζονται οι ενέργειες που έγιναν για τη δημιουργία του δέντρου, συνοδευόμενες από μια παρατήρηση επιτυχούς ολοκλήρωσης. Επιλέγουμε Close, ώστε να ολοκληρώσουμε τη διαδικασία και να προβάλουμε το δέντρο.
Εικόνα 7.19
-
Στη συνέχεια, εμφανίζεται το παράθυρο με το δέντρο που έχει δημιουργηθεί, όπως φαίνεται στην Εικόνα 7.20. Αν επιλέξουμε Size to Fit, εμφανίζεται όλο το δέντρο (με όλα τα επίπεδά του), ώστε να έχουμε μια ολοκληρωμένη εικόνα του.
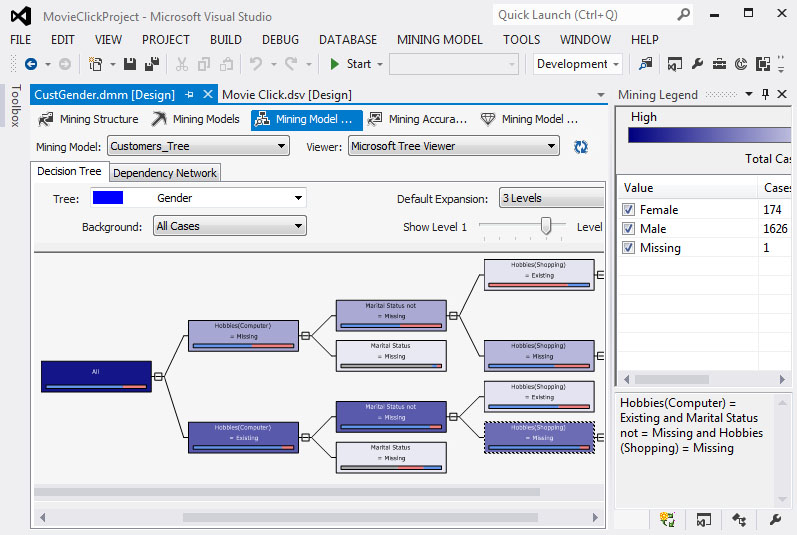
Εικόνα 7.20
Αφήνοντας τον κέρσορα πάνω σε έναν κόμβο, βλέπουμε ότι εμφανίζονται κάποια στατιστικά στοιχεία σχετικά με το σύνολο των περιπτώσεων που ανήκουν σε κάθε κόμβο του δέντρου και σχετικά με την τιμή που έχουν: Male ή Female. επίσης, παρατηρούμε ότι σε κανένα φύλλο του δέντρου η τιμή των συνολικών περιπτώσεων δεν είναι μικρότερη του 10, έτσι όπως είναι καθορισμένη από την παράμετρο MINIMUM_SUPPORT. Τέλος, το σύνολο των περιπτώσεων κάθε κόμβου του δέντρου είναι ίσο με το άθροισμα των περιπτώσεων των παιδιών του, κάτι που ισχύει και για τις τιμές των χαρακτηριστικών.
-
Στη συνέχεια, επιλέγουμε την καρτέλα Dependency Network, όπως φαίνεται στην Εικόνα 7.21, ώστε να μελετήσουμε τη σχέση μεταξύ του χαρακτηριστικού που θέλουμε να προβλέψουμε και των υπολοίπων που σχετίζονται με αυτό και συμμετέχουν στη δημιουργία του δέντρου. Στα αριστερά του γραφήματος υπάρχει μια μπάρα, η μετακίνηση της οποίας παρουσιάζει τον βαθμό εξάρτησης του χαρακτηριστικού που θέλουμε να προβλέψουμε από τα υπόλοιπα χαρακτηριστικά. H διαβάθμιση γίνεται από το χαμηλότερο προς το υψηλότερο επίπεδο της μπάρας, με το χαμηλότερο να δηλώνει τη μεγαλύτερη εξάρτηση και το υψηλότερο τη μικρότερη. Στη συγκεκριμένη περίπτωση, το χαρακτηριστικό που θέλουμε να προβλέψουμε (Gender) επηρεάζεται πρώτα από το χαρακτηριστικό Computer.
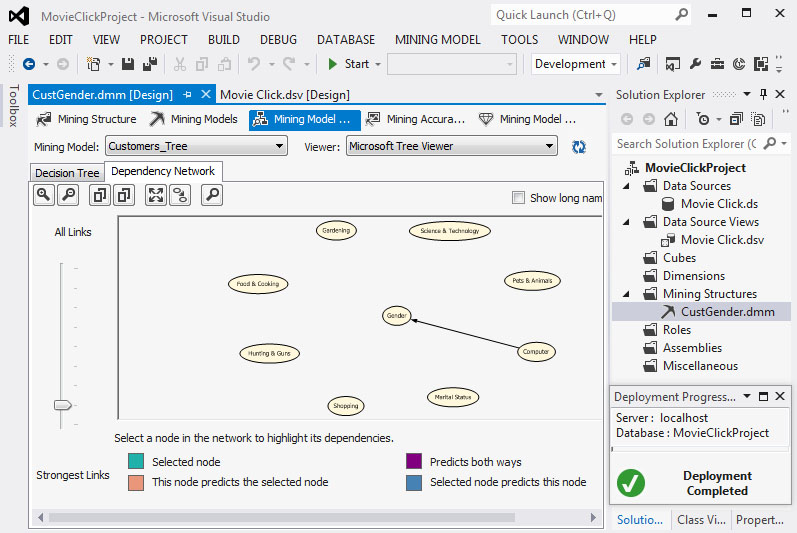
Εικόνα 7.21
Στο δεύτερο επίπεδο εξάρτησης το gender επηρεάζεται από το Computer και το Marital Status, όπως φαίνεται στην Εικόνα 7.22.
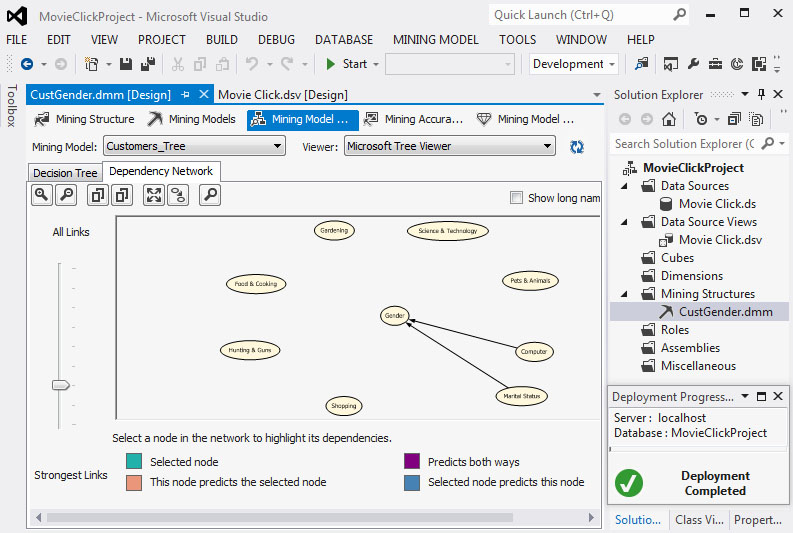
Εικόνα 7.22
Στο τρίτο επίπεδο εξάρτησης το gender επηρεάζεται από το Computer, το Marital Status και το Shopping, όπως φαίνεται στην Εικόνα 7.23.
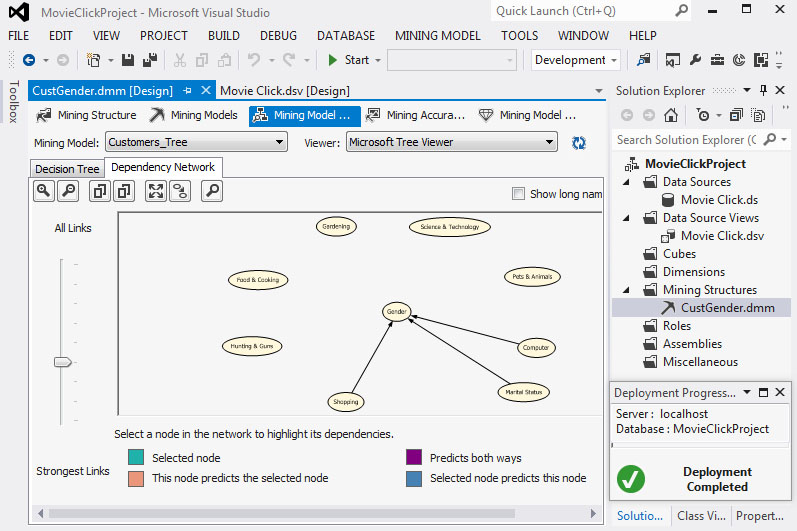
Εικόνα 7.23
Πίνακας Περιεχομένων /
Περιεχόμενα Κεφαλαίου
7.3.
Αξιολόγηση δέντρων απόφασης
Σ’ αυτήν την ενότητα θα παρουσιάσουμε με αναλυτικά βήματα τη μέθοδο με την οποία αξιολογούνται τα δέντρα απόφασης. Πιο συγκεκριμένα, θα εξακριβώσουμε κατά πόσο το δέντρο που έχουμε δημιουργήσει είναι αποτελεσματικό, δηλαδή αν είναι σχετικά ακριβές στα δεδομένα που θέλουμε να προβλέψουμε. Μ’ αυτόν τον τρόπο, θα μπορέσουμε να αξιολογήσουμε το δέντρο απόφασης, αποτυπώνοντας τα αποτελέσματα της ακρίβειας πρόβλεψης είτε με γραφήματα είτε με πίνακες σύγκρισης.
-
Επιλέγουμε την καρτέλα Mining Accuracy Chart και, όπως φαίνεται στην Εικόνα 7.24, στην καρτέλα Input Selection επιλέγουμε Specify a different data set, ώστε να καθορίσουμε το Mining Structure, τον Case πίνακα και τους Nested πίνακες με τους οποίους θα εργαστούμε.
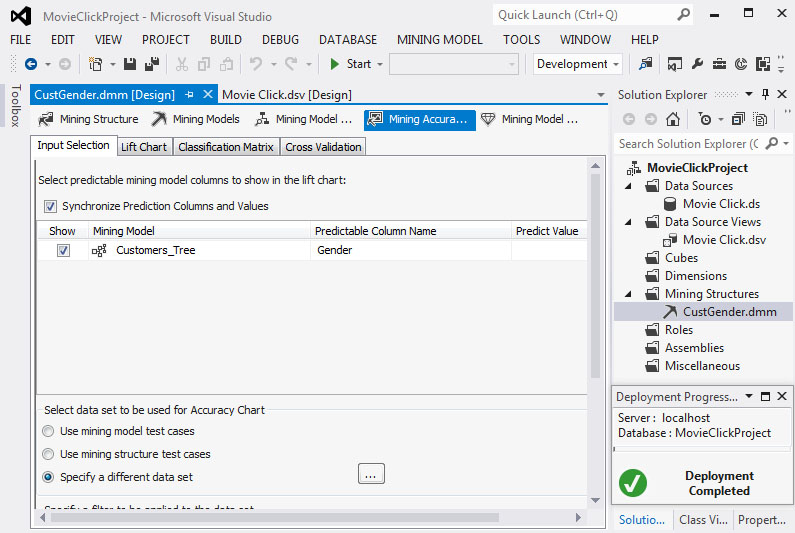
Εικόνα 7.24
-
Στο νέο παράθυρο, όπως φαίνεται στην Εικόνα 7.25, επιλέγουμε Select Structure, ώστε να καθορίσουμε το mining structure με το οποίο θα εργαστούμε.
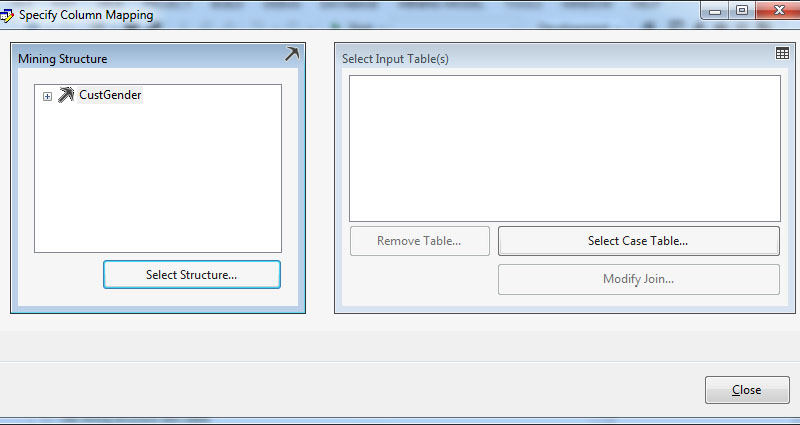
Εικόνα 7.25
-
Εμφανίζεται το παράθυρο επιλογής του mining structure, όπως φαίνεται στην Εικόνα 7.26. Επιλέγουμε το CustGender, που είναι το mining structure με το οποίο εργαζόμαστε, και, στη συνέχεια, επιλέγουμε ΟΚ, ώστε να επιστρέψουμε στο προηγούμενο παράθυρο.
Εικόνα 7.26
-
Στη συνέχεια, επιλέγουμε Select Case Table και, όπως φαίνεται στην Εικόνα 7.27, εμφανίζεται το παράθυρο επιλογής του πίνακα Case, στο οποίο επιλέγουμε τον πίνακα Customers και στη συνέχεια επιλέγουμε ΟΚ ώστε να επιστρέψουμε στο προηγούμενο παράθυρο.
Εικόνα 7.27
-
Στο νέο παράθυρο, όπως φαίνεται στην Εικόνα 7.28, εμφανίζεται συνολικά το Mining Structure με τους πίνακες, όπου βλέπουμε τις σχέσεις που έχουν δημιουργηθεί. Στη συνέχεια, επιλέγουμε Select Nested Table, ώστε να επιλέξουμε τους Nested πίνακες.
Εικόνα 7.28
-
Εμφανίζεται το παράθυρο επιλογής του πίνακα Nested, όπως φαίνεται στην Εικόνα 7.29. Επιλέγουμε τον πίνακα Hobbies, καθώς είναι ο μόνος πίνακας του Data Mining Structure στον οποίο εργαζόμαστε καιδίνει χαρακτηριστικά ως input στον αλγόριθμο που φτιάχνει το δέντρο. Στη συνέχεια, επιλέγουμε ΟΚ, ώστε να επιστρέψουμε στο προηγούμενο παράθυρο.
Εικόνα 7.29
-
Εμφανίζεται ξανά το παράθυρο του Mining Structure με τους πίνακες, όπως φαίνεται στην Εικόνα 7.30, όπου πλέον βλέπουμε όλες τις συσχετίσεις που έχουν δημιουργηθεί. Στη συνέχεια, επιλέγουμε Close, ώστε να αφήσουμε αυτό το παράθυρο.
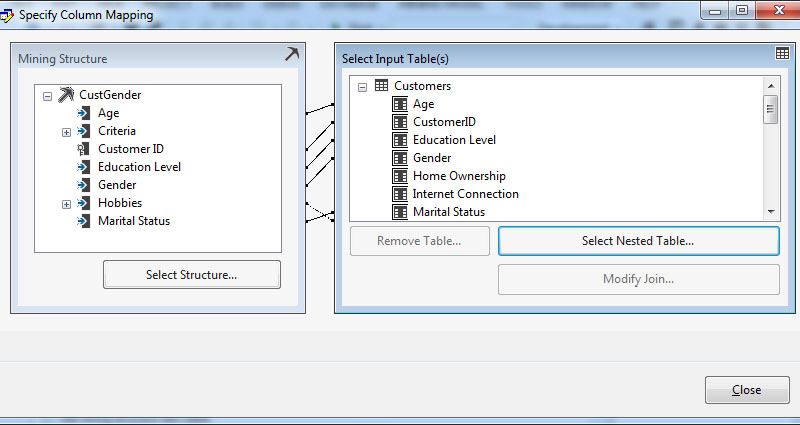
Εικόνα 7.30
-
Επιλέγοντας την καρτέλα Lift Chart, όπως φαίνεται στην Εικόνα 7.31, διαπιστώνουμε πόσο αποτελεσματικό είναι το δέντρο που δημιουργήσαμε, καθώς σ’ αυτό εμφανίζεται το διάγραμμα του ποσοστού του συνολικού πληθυσμού (άξονας Χ) σε σχέση με το ποσοστό του πληθυσμού που έχουμε προβλέψει σωστά (άξονας Υ). Η μπλε γραμμή με κλίση 45ο με τον άξονα Χ απεικονίζει το ιδανικό μοντέλο, ενώ η κόκκινη γραμμή που βρίσκεται κάτω από αυτήν απεικονίζει το δικό μας μοντέλο. Κάνοντας κλικ πάνω στο διάγραμμα εμφανίζεται μια παράλληλη προς τον άξονα Υ ευθεία, καθώς και κάποια στατιστικά στοιχεία που καταγράφονται στο παράθυρο Mining Legend.
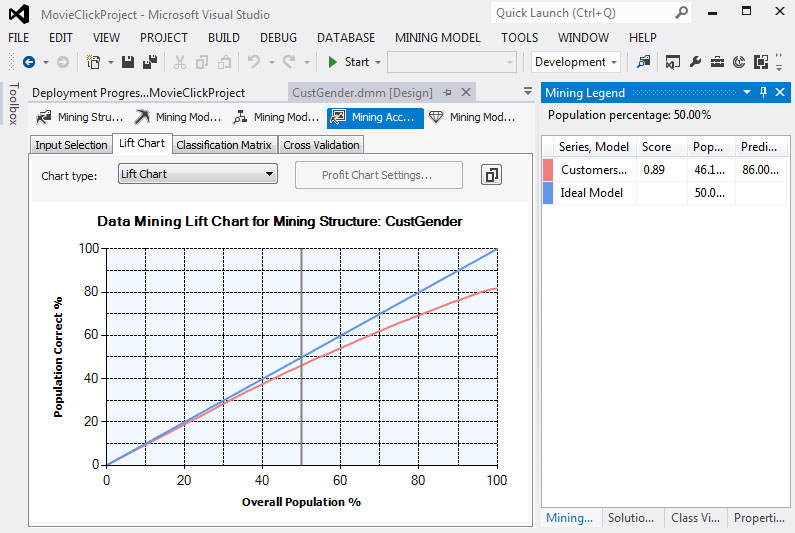
Εικόνα 7.31
Συγκεκριμένα, στο δεξί μέρος της Εικόνας 7.31 βλέπουμε ότι στο 50% του συνολικού πληθυσμού (που είναι το δείγμα) το δέντρο προβλέπει σωστά το 46,1% του δείγματος, ενώ το ιδανικό είναι να προβλέπει σωστά το 50%. Από τη στιγμή που δεν έχει προσδιοριστεί συγκεκριμένη κατάσταση που θέλουμε να προβλέψουμε, η γραμμή του μοντέλου μας θα βρίσκεται πάντα κάτω από την ευθεία του ιδανικού μοντέλου.
- Στη συνέχεια, θα αξιολογήσουμε την αξιοπιστία του μοντέλου μας μ’ έναν άλλο τρόπο. Επιλέγουμε την καρτέλα Classification Matrix. Στον πίνακα που εμφανίζεται, όπως φαίνεται στην Εικόνα 7.32, βλέπουμε ότι στις 34 περιπτώσεις που το φύλλο δεν ήταν καταχωρημένο (Missing), ο αλγόριθμος εσφαλμένα το προέβλεψε 27 φορές ως Male και 7 φορές ως Female. Όσον αφορά τους άνδρες (Male), ο αλγόριθμος τούς προβλέπει πολύ σωστά (2355 σωστές προβλέψεις επί συνόλου 2439 ανδρών) με ποσοστό επιτυχημένης πρόβλεψης 96,5%. Όσον αφορά, όμως, τις γυναίκες (Female), ο αλγόριθμος δεν τις προβλέπει καθόλου σωστά (246 σωστές προβλέψεις επί συνόλου 714) με ποσοστό επιτυχημένης πρόβλεψης 34,5%.
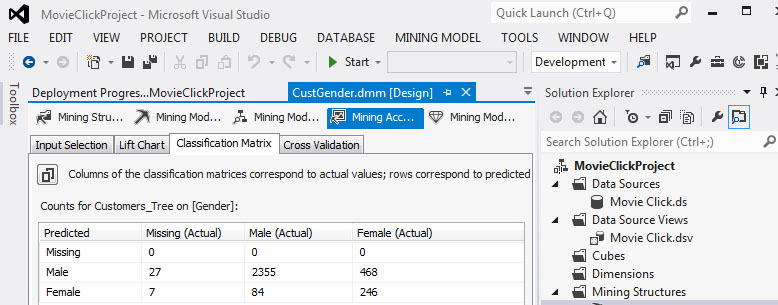
Εικόνα 7.32
-
Στη συνέχεια, θα προσδιορίσουμε μια συγκεκριμένη κατάσταση που θέλουμε να προβλέψουμε. Το χαρακτηριστικό που μας ενδιαφέρει παίρνει μόνο δύο τιμές (Male και Female), οπότε έχουμε μόνο αυτές τις επιλογές. Επιστρέφουμε στην καρτέλα Input Selection, όπως φαίνεται στην Εικόνα 7.33. Στο πεδίο Predictable Column Name επιλέγουμε την τιμή Gender. Στο πεδίο Predict Value επιλέγουμε την τιμή Male.
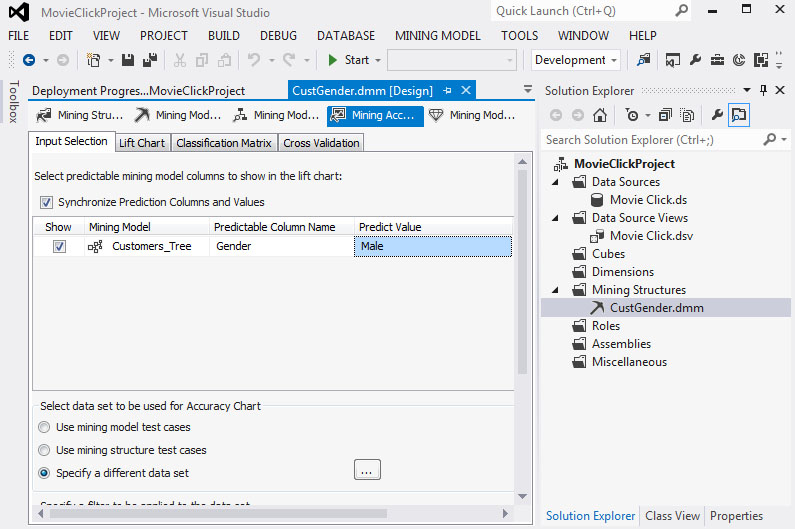
Εικόνα 7.33
-
Τέλος, επιλέγουμε πάλι Lift Chart, ώστε να εμφανιστεί η γραφική απεικόνιση του μοντέλου. Σ’ αυτήν την περίπτωση, όπως φαίνεται στην Εικόνα 7.34, ο άξονας Χ απεικονίζει το ποσοστό του συνολικού πληθυσμού, ενώ ο άξονας Υ το ποσοστό των ανδρών που έχει προβλεφθεί σωστά. Η γραμμή με κλίση 45ο απεικονίζει το τυχαίο μοντέλο, ενώ η γραμμή που βρίσκεται υψηλότερα από τις υπόλοιπες δείχνει το ιδανικό μοντέλο. Η άλλη γραμμή αντιπροσωπεύει το δικό μας μοντέλο. Στη συγκεκριμένη περίπτωση, το ιδανικό μοντέλο πετυχαίνει το 100% των προβλέψεων στο 77% του συνολικού πληθυσμού. Στον πίνακα Mining Legend βλέπουμε ότι το δικό μας μοντέλο έχει Score 0.93 και προβλέπει με ακρίβεια 86,76% (δηλαδή, σχετικά καλά).
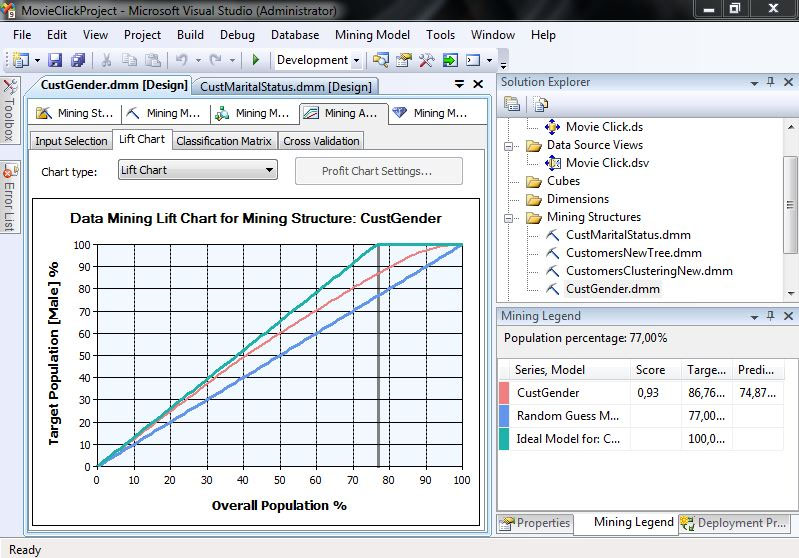
Εικόνα 7.34
Πίνακας Περιεχομένων /
Περιεχόμενα Κεφαλαίου
7.4.
Ασκήσεις στην παραμετροποίηση του αλγορίθμου δέντρου απόφασης
-
Να αλλάξετε στο ήδη δημιουργηθέν μοντέλο (όπως φαίνεται στην Εικόνα 7.13) την τιμή της παραμέτρου COMPLEXITY_PENALTY, ορίζοντας την σε 0.001. Να εμφανίσετε και να σχολιάσετε τα παρακάτω:
- το νέο δέντρο απόφασης που θα δημιουργηθεί,
- το dependency network με τα κύρια χαρακτηριστικά που προσδιορίζουν το φύλο (gender),
- το Lift Chart και το ποσοστό των ανδρών που προβλέπονται σωστά από το νέο μοντέλο,
- το Classification Matrix.
Τέλος, να συγκριθεί το νέο μοντέλο με αυτό που δημιουργούν οι προεπιλεγμένες (default) τιμές του αλγορίθμου Decision Tree.
- Να επαναληφθεί η άσκηση 1, δίνοντας την τιμή 0.999 στην παράμετρο COMPLEXITY_PENALTY του αλγορίθμου Decision Tree.
- Να επαναληφθεί η άσκηση 1, δίνοντας την τιμή 200 στην παράμετρο COMPLEXITY_PENALTY, η οποία υποχρεώνει να βρίσκονται τουλάχιστον διακόσιες κατ’ ελάχιστο περιπτώσεις σε κάθε φύλλο του δέντρου.
- Να επαναληφθεί η άσκηση 1, επιλέγοντας τη δημιουργία ενός μη δυαδικού δέντρου απόφασης (multi-way) και διατηρώντας τις προεπιλεγμένες τιμές στις υπόλοιπες παραμέτρους του αλγορίθμου decision tree.
- Να επαναληφθεί η άσκηση 1, επιλέγοντας τη δημιουργία ενός δέντρου απόφασης, το οποίο θα βασίζεται στο μέτρο της Εντροπίας (τρόπος υπολογισμού της καταλληλότητας ενός πεδίου/ χαρακτηριστικού ως κόμβου του δέντρου).
- Να επαναληφθεί η άσκηση 1, επιλέγοντας τη δημιουργία ενός δέντρου απόφασης, το οποίο θα βασίζεται στο μέτρο της Εντροπίας και θα επιτρέπει πενήντα τουλάχιστον περιπτώσεις στο καθένα από τα φύλλα του.
Πίνακας Περιεχομένων /
Περιεχόμενα Κεφαλαίου
7.5.
Λύσεις ασκήσεων στην παραμετροποίηση του αλγορίθμου δέντρων απόφασης
Άσκηση 1
Να αλλάξετε στο ήδη δημιουργηθέν μοντέλο (όπως φαίνεται στην Εικόνα 7.13) την τιμή της παραμέτρου COMPLEXITY_PENALTY, ορίζοντας την σε 0.001. Να εμφανίσετε και να σχολιάσετε τα παρακάτω:
- το νέο δέντρο απόφασης που θα δημιουργηθεί,
- το dependency network με τα κύρια χαρακτηριστικά που προσδιορίζουν το φύλο (gender),
- το Lift Chart και το ποσοστό των ανδρών που προβλέπονται σωστά από το νέο μοντέλο,
- το Classification Matrix.
Τέλος να συγκριθεί το νέο μοντέλο με αυτό που δημιουργούν οι
προεπιλεγμένες (default) τιμές του αλγορίθμου Desicion Tree.
-
Λύση άσκησης 1 :
+
1. Αλλάζουμε την τιμή της παραμέτρου σε 0.001, όπως
φαίνεται στην Εικόνα 7.35 και κάνουμε run το μοντέλο.
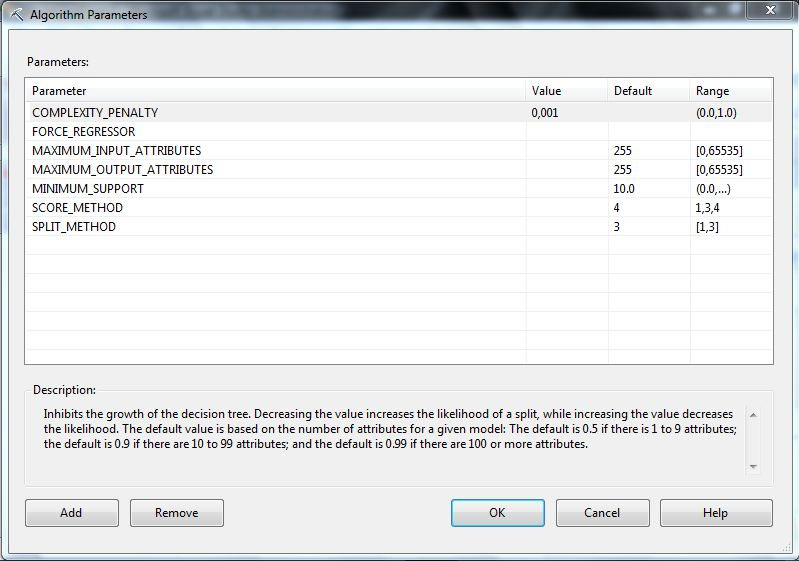
Εικόνα 7.35
2. Στην Εικόνα 7.36 παρατηρούμε ότι το δέντρο είναι πολύ πιο πολύπλοκο σε σχέση μ’ αυτό του προηγούμενου μοντέλου (βλέπε Εικόνα 7.20). Ωστόσο, τα συμπεράσματα στα οποία καταλήγουμε είναι παρόμοια με αυτά του προηγούμενου μοντέλου. Ακόμα και η διάκριση στα πρώτα στάδια δημιουργίας του δέντρου είναι η ίδια.
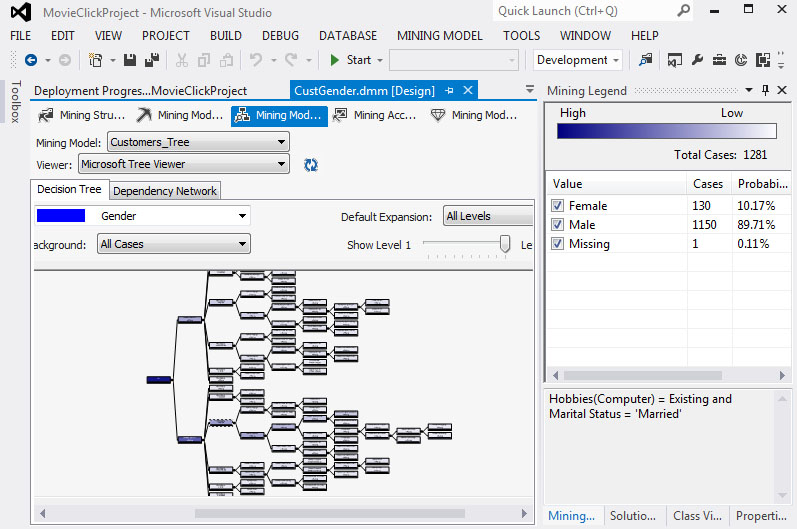
Εικόνα 7.36
3. Οι παράμετροι που καθορίζουν το φύλο έχουν αυξηθεί, όπως φαίνεται στην Εικόνα 7.37, χωρίς αυτό να σημαίνει απαραίτητα ότι η ικανότητα πρόβλεψης του δέντρου έχει βελτιωθεί.
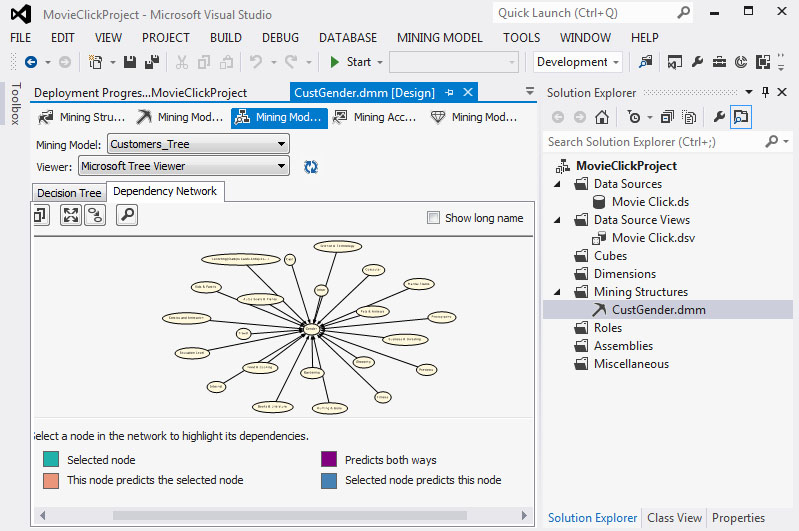
Εικόνα 7.37
4. Στο Lift Chart, όπως φαίνεται στην Εικόνα 7.38, με δείγμα 77% του πληθυσμού μπορούμε να προβλέψουμε σωστά το 87,95% των ανδρών του δείγματος. Το ποσοστό αυτό είναι καλύτερο απ’ αυτό που είχαμε με τιμή 0,9 στην παράμετρο COMPLEXITY_PENALTY (προβλέπαμε σωστά μόνο το 86,76% των ανδρών), αλλά το δέντρο είναι πολύ πιο πολύπλοκο και, συνεπώς, πιο δύσκολα ερμηνεύσιμο. Το Score είναι επίσης καλύτερο (0,94) σε σχέση με το προηγούμενο (0.93) (βλέπε Εικόνα 7.34).
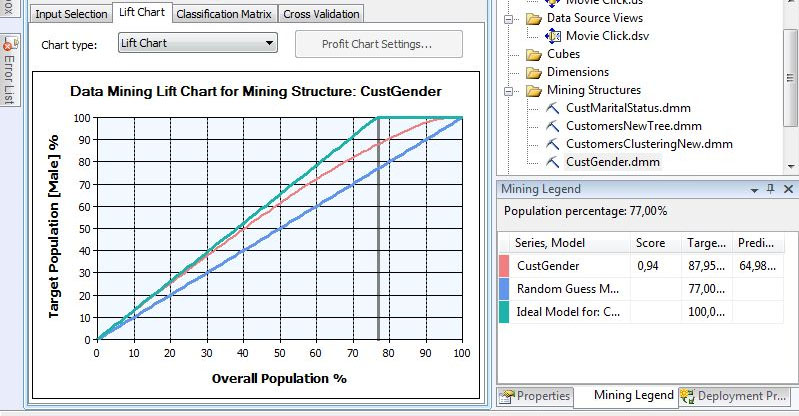
Εικόνα 7.38
5. Στο Classification Matrix, όπως φαίνεται στην Εικόνα 7.39, βλέπουμε να αυξάνονται ελαφρώς τα ποσοστά επιτυχούς πρόβλεψης του φύλου των ανδρών.
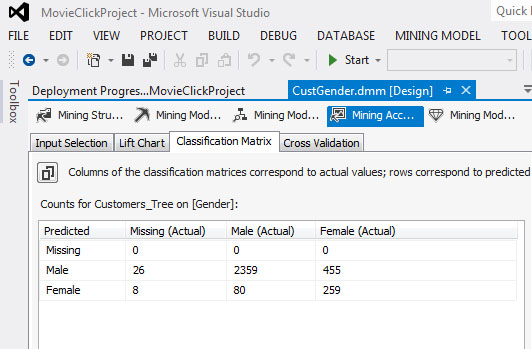
Εικόνα 7.39
6. 6. Συμπερασματικά, το δέντρο μας έχει πλέον μεγαλύτερη ακρίβεια. Πρέπει να τονίσουμε ότι ένα πιο πολύπλοκο δέντρο μπορεί σχεδόν πάντα να εξασφαλίζει ελαφρώς καλύτερη πρόβλεψη. Η αύξηση της πολυπλοκότητάς του, όμως, δεν είναι πάντα ανάλογη της βελτίωσης της πρόβλεψης του δέντρου, γεγονός που το κάνει μη εύκολα ερμηνεύσιμο. Γι’ αυτό, δεν πρέπει να θεωρούμε πάντα ότι τα πολυπλοκότερα δέντρα είναι τα καλύτερα.
Άσκηση 2
Να επαναληφθεί η άσκηση 1 δίνοντας την τιμή 0.999 στην παράμετρο
COMPLEXITY_PENALTY του αλγορίθμου Decision Tree.
Λύση
-
Λύση άσκησης 2 :
+
1. Αλλάζουμε την τιμή της παραμέτρου σε 0.999, όπως φαίνεται στην Εικόνα 7.40, και κάνουμε run το μοντέλο.
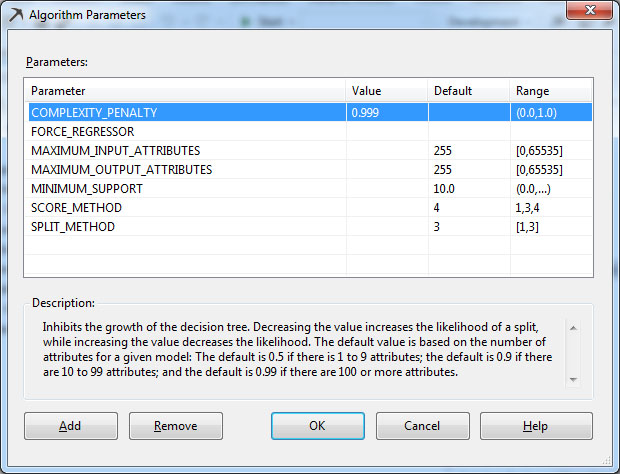
Εικόνα 7.40
2. Όπως φαίνεται στην Εικόνα 7.41, το δέντρο που προκύπτει είναι πολύ πιο απλό, ακόμα και σε σχέση με το αρχικό δέντρο.
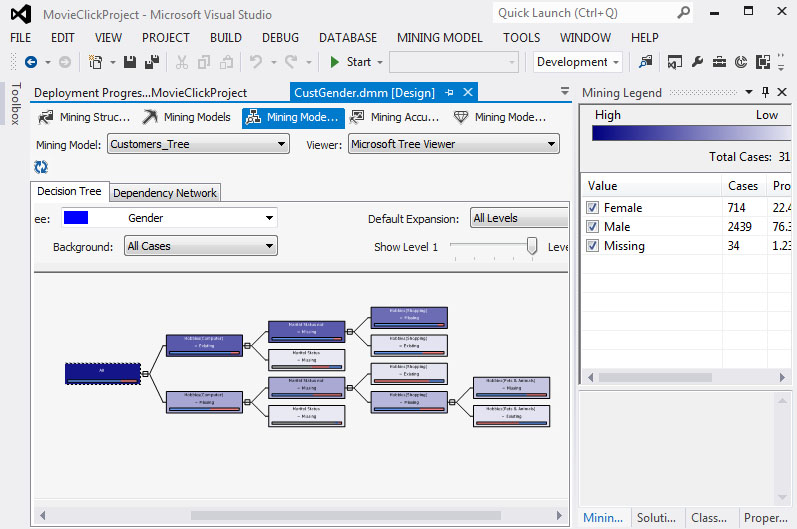
Εικόνα 7.41
3. Μόλις τέσσερα χαρακτηριστικά πλέον χρησιμοποιούνται για την πρόβλεψη του Gender, όπως φαίνεται στην Εικόνα 7.42.
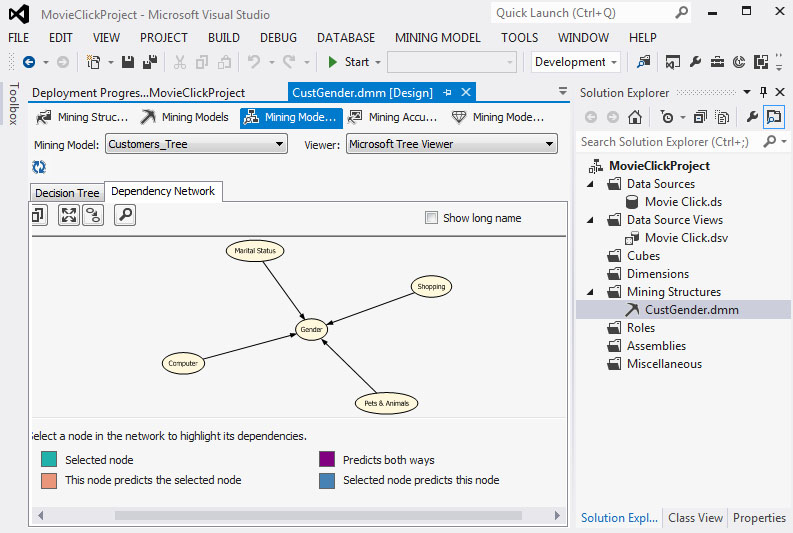
Εικόνα 7.42
4. Στο Lift Chart, όπως φαίνεται στην Εικόνα 7.43, με 77% του πληθυσμού προβλέπουμε σωστά το 85,94% των ανδρών του δείγματος, ποσοστό που είναι μικρότερο απ’ αυτό που έδωσε το δέντρο με τις προεπιλεγμένες τιμές στις παραμέτρους του αλγορίθμου, ενώ το Score είναι 0,91. Τονίζεται ότι με το αρχικό δέντρο απόφασης προβλέπαμε σωστά το 86,76% των ανδρών.
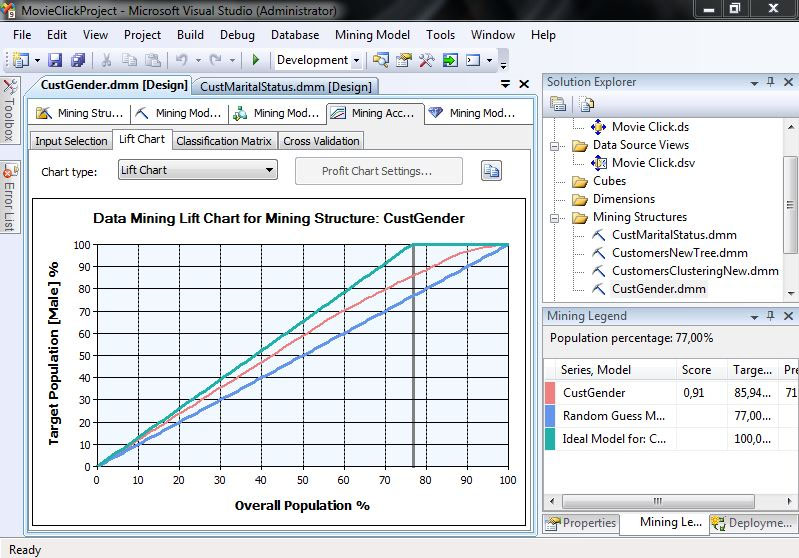
Εικόνα 7.43
5. Στο Classification Matrix, όπως φαίνεται στην Εικόνα 7.44, βλέπουμε ότι τα στατιστικά στοιχεία είναι περίπου στα ίδια επίπεδα.
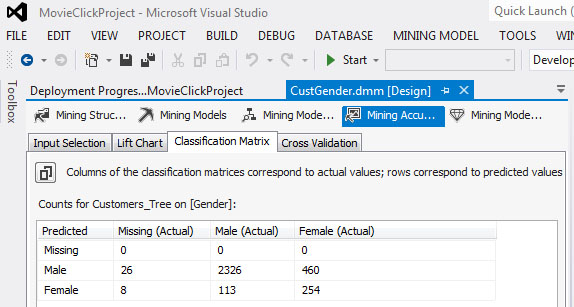
Εικόνα 7.44
6. Συμπερασματικά, όταν ένα δέντρο είναι υπερβολικά μικρό, οι προβλέψεις του δεν είναι πολύ ακριβείς, διότι δεν λαμβάνει υπόψη του όλα τα διαθέσιμα χαρακτηριστικά που πιθανόν να επηρεάζουν την δεσμευμένη μεταβλητή (στην περίπτωση μας, το Φύλο).
Άσκηση 3
Να επαναληφθεί η άσκηση 1, δίνοντας την τιμή 200 στην παράμετρο COMPLEXITY_PENALTY, η οποία υποχρεώνει να βρίσκονται τουλάχιστον διακόσιες κατ’ ελάχιστο περιπτώσεις σε κάθε φύλλο του δέντρου.
-
Λύση άσκησης 3 :
+
1. Αλλάζουμε την τιμή της παραμέτρου σε 200, όπως φαίνεται στην Εικόνα 7.45, και κάνουμε run το μοντέλο.
<
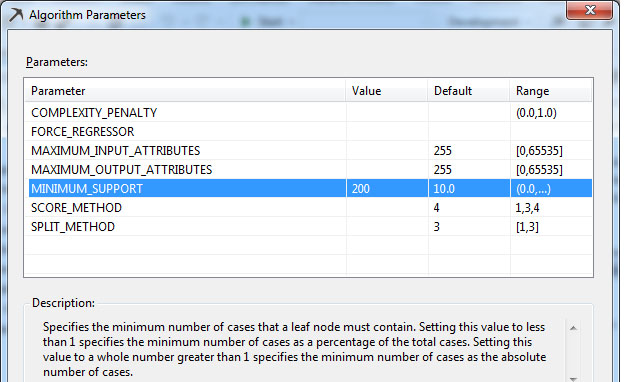
Εικόνα 7.45
2. Παρατηρούμε, όπως φαίνεται στην Εικόνα 7.46, ότι το δέντρο που δημιουργείται είναι απλό και ότι κάθε φύλλο του δέντρου ενσωματώνει περισσότερες από 200 περιπτώσεις (εγγραφές που βρίσκονται στον πίνακα case).
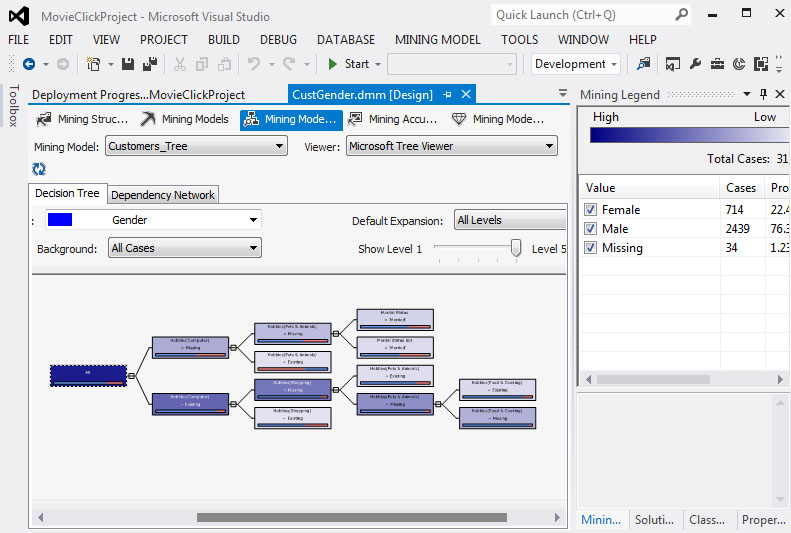
Εικόνα 7.46
3. Ο περιορισμός των διακοσίων περιπτώσεων είχε ως αποτέλεσμα να αλλάξουν τα βασικά κριτήρια με τα οποία γίνεται η διάκριση των πελατών στο δέντρο μας. Πράγματι, όπως φαίνεται στην Εικόνα 7.47, η οικογενειακή κατάσταση δεν θεωρείται τόσο σημαντικό κριτήριο όσο είναι τα κατοικίδια, κάτι που δεν εμφανίστηκε σε προηγούμενη παραμετροποίηση του μοντέλου μας.
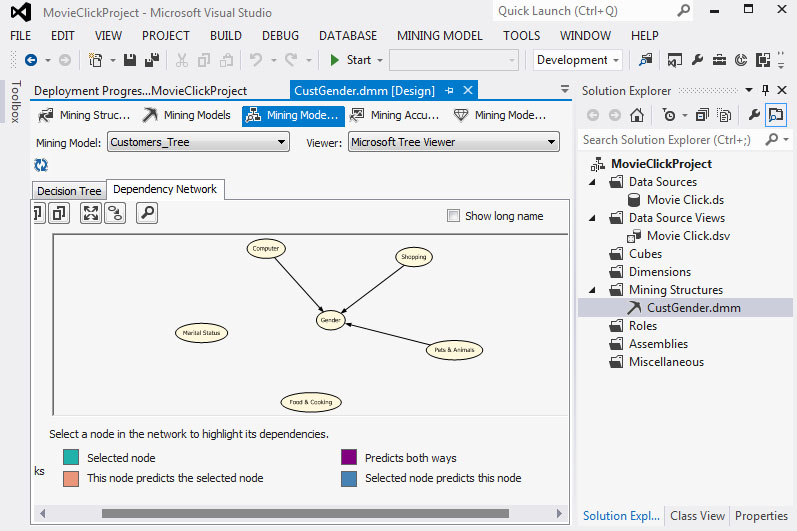
Εικόνα 7.47
4. Στο Lift Chart, όπως φαίνεται στην Εικόνα 7.48, σε δείγμα 50% του συνολικού πληθυσμού, προβλέπεται πλέον σωστά το 45,84% των ανδρών του δείγματος.
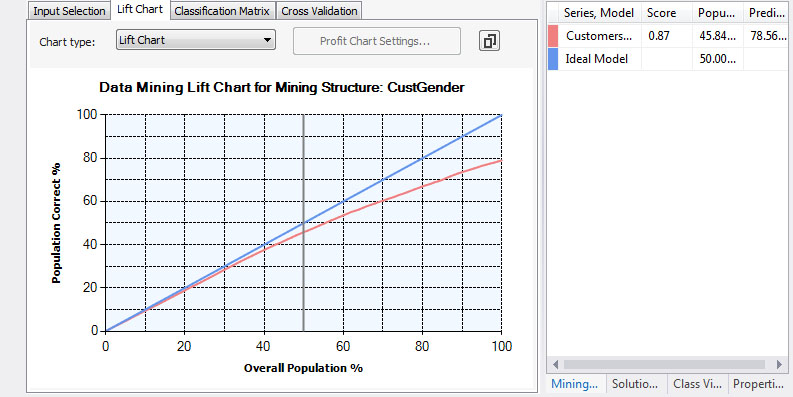
Εικόνα 7.48
5. Στο Classification Matrix, όπως φαίνεται στην Εικόνα 7.49, βλέπουμε ότι τα ποσοστά πρόβλεψης των ανδρών ελαφρώς αυξάνονται έναντι του αρχικού μοντέλου πρόβλεψης. Όσον αφορά όμως τις γυναίκες (Female), τα ποσοστά πρόβλεψης μειώνονται δραματικά (μόνο 158 σωστές προβλέψεις επί συνόλου 714) με ποσοστό επιτυχημένης πρόβλεψης μόλις 22,1%.
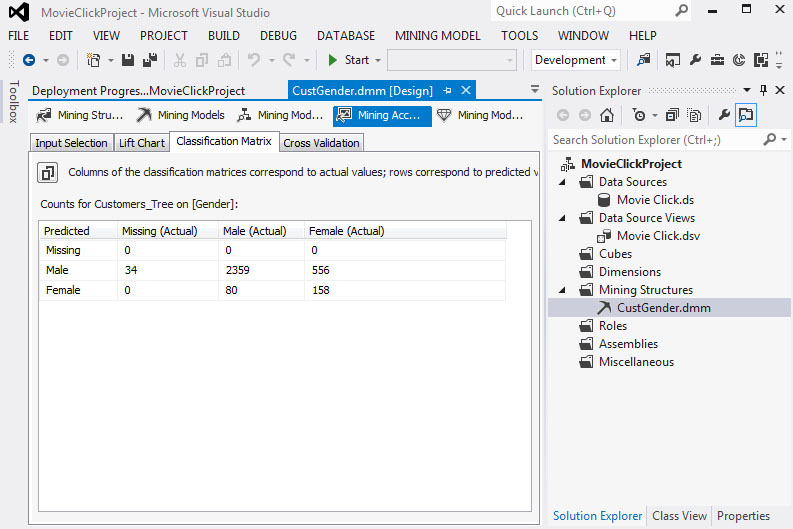
Εικόνα 7.49
6. Συμπερασματικά, αυτή η παράμετρος πρέπει να χρησιμοποιείται μόνο σε περιπτώσεις που το δέντρο αποτελείται από φύλλα με πολύ μικρό αριθμό περιπτώσεων. Σ’ αυτήν την περίπτωση, μπορούμε να δημιουργήσουμε ένα πιο συμπαγές δέντρο που θα βοηθήσει να εξάγουμε πιο σαφή συμπεράσματα.
Άσκηση 4
Να επαναληφθεί η άσκηση 1, επιλέγοντας τη δημιουργία ενός μη δυαδικού δέντρου απόφασης (multi-way) και διατηρώντας τις προεπιλεγμένες τιμές στις υπόλοιπες παραμέτρους του αλγορίθμου decision tree.
-
Λύση άσκησης 4 :
+
1. Επιλέγουμε στην παράμετρο SPLIT_METHOD την τιμή 2, όπως φαίνεται στην Εικόνα 7.50.
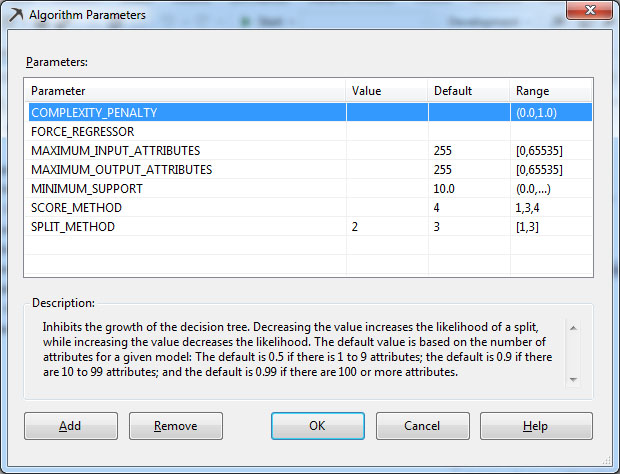
Εικόνα 7.50
2. Παρατηρούμε, όπως φαίνεται στην Εικόνα 7.51, ότι, από τη στιγμή που το δέντρο μας δεν είναι δυαδικό, αφενός η διάκριση των περιπτώσεων δεν γίνεται με σαφήνεια και, αφετέρου, πολλά χαρακτηριστικά επαναλαμβάνονται σε κατώτερα επίπεδα του δέντρου.
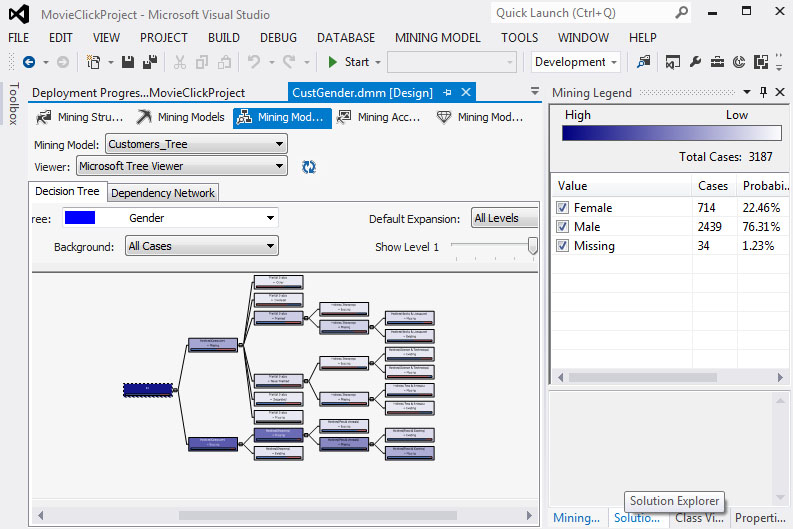
Εικόνα 7.51
3. Τα χαρακτηριστικά που προσδιορίζουν το Gender είναι πλέον περισσότερα απ’ αυτά του δυαδικού δέντρου, όπως φαίνεται στην Εικόνα 7.52.
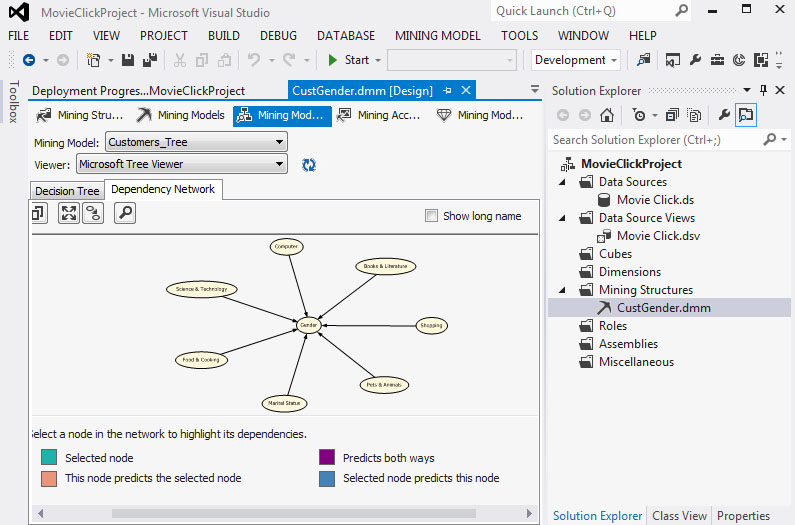
Εικόνα 7.52
4. Στο Lift Chart, όπως φαίνεται στην Εικόνα 7.53, σε δείγμα 77% του πληθυσμού προβλέπεται σωστά το 86,43% των ανδρών του δείγματος.
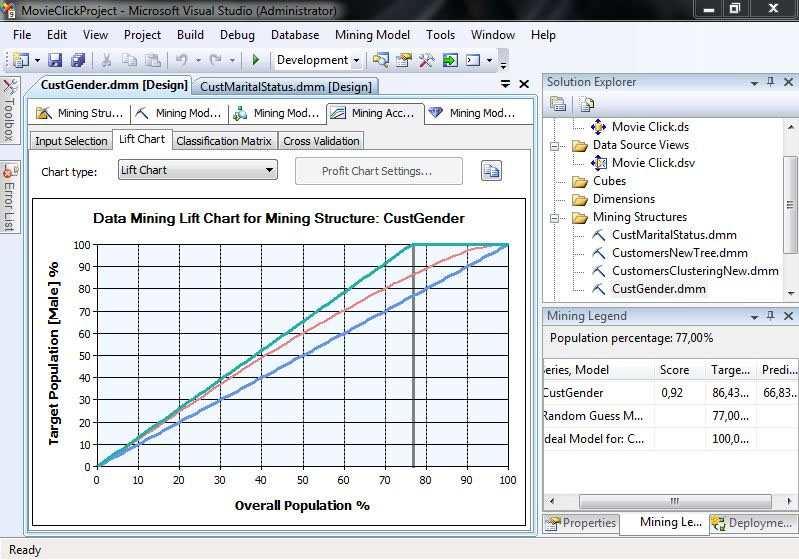
Εικόνα 7.53
5. Τα ποσοστά ακρίβειας είναι περίπου τα ίδια με το αρχικό δέντρο, κάτι που φαίνεται και από το classification matrix της Εικόνας 7.54.
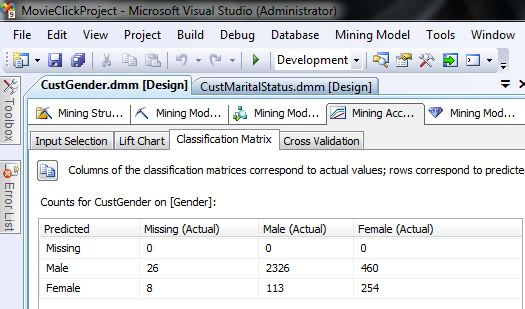
Εικόνα 7.54
6. Συμπερασματικά, στα μη δυαδικά δέντρα απόφασης, η διάκριση των περιπτώσεων δεν γίνεται με σαφήνεια και πολλά χαρακτηριστικά επαναλαμβάνονται σε κατώτερα επίπεδα του δέντρου. Σε γενικές, όμως, γραμμές η ακρίβεια είναι ίδια με τα δυαδικά δέντρα απόφασης.
Άσκηση 5
Να επαναληφθεί η άσκηση 1, επιλέγοντας τη δημιουργία ενός δέντρου απόφασης, το οποίο θα βασίζεται στο μέτρο της Εντροπίας (τρόπος υπολογισμού της καταλληλότητας ενός πεδίου/χαρακτηριστικού ως κόμβου του δέντρου).
Λύση
-
Λύση άσκησης 5 :
+
1. Η εντροπία μετράει τον βαθμό βεβαιότητας/αβεβαιότητας που δημιουργεί στο μοντέλο ένα χαρακτηριστικό έναντι των υπόλοιπων χαρακτηριστικών (ώστε να επιλεχθεί ή όχι να γίνει κόμβος του δέντρου απόφασης). Για να επιλέξουμε την εντροπία ως μέτρο, δίνουμε στην παράμετρο Score_Method την τιμή 1.
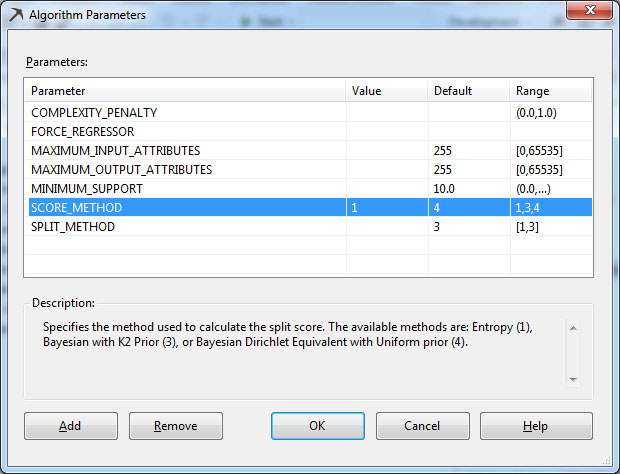
Εικόνα 7.55
2. Στην Εικόνα 7.56 παρατηρούμε ότι το δέντρο που προκύπτει είναι πολύπλοκο και αποτελείται από 14 επίπεδα.
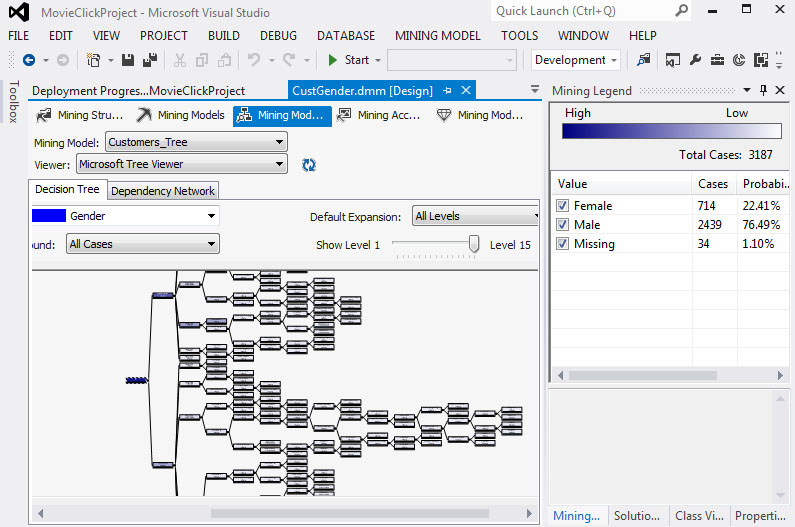
Εικόνα 7.56
3. Η τιμή που θέλουμε να προβλέψουμε εξαρτάται πλέον απ’ όλα, σχεδόν, τα χαρακτηριστικά, όπως φαίνεται στην Εικόνα 7.57.
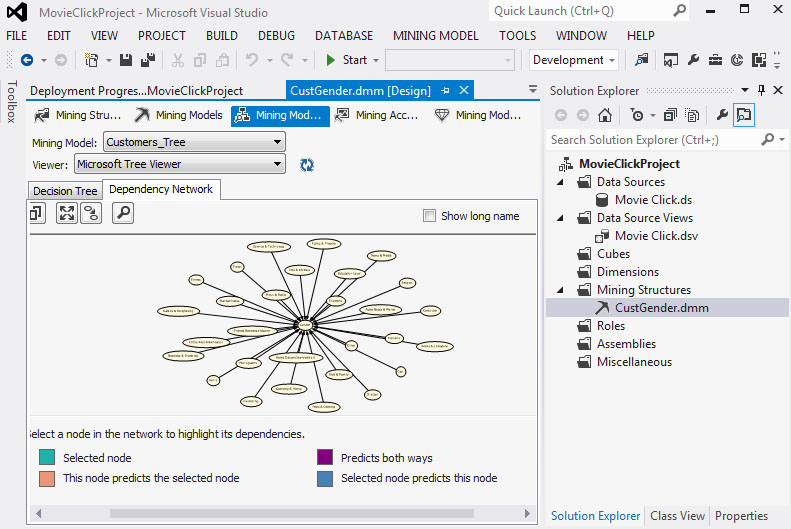
Εικόνα 7.57
4. Στο Lift Chart, όπως φαίνεται στην Εικόνα 7.58, σε δείγμα 77% του πληθυσμού προβλέπεται σωστά το 90,08% των ανδρών με Score 0,94. Αυτό το ποσοστό, που είναι το υψηλότερο που έχει εμφανιστεί στα παραδείγματά μας, αποδεικνύει ότι το δέντρο που παράγεται με την εντροπία μπορεί να προβλέψει με μεγαλύτερη ακρίβεια.
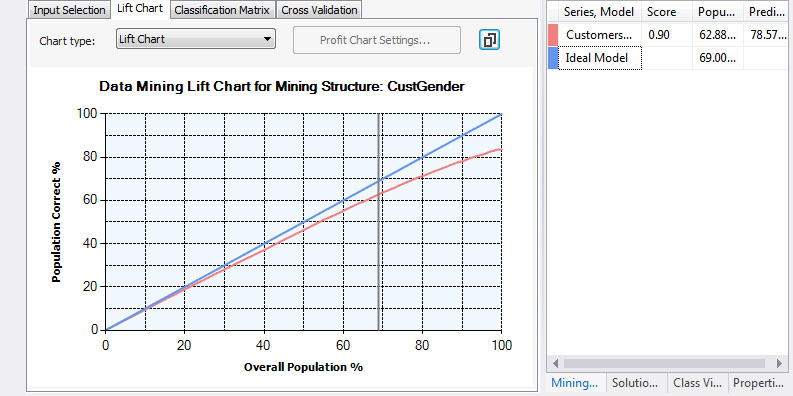
Εικόνα 7.58
5. Στο Classification Matrix, όπως φαίνεται στην Εικόνα 7.59, βλέπουμε ότι τα ποσοστά πρόβλεψης των γυναικών έχουν πλέον βελτιωθεί σημαντικά.
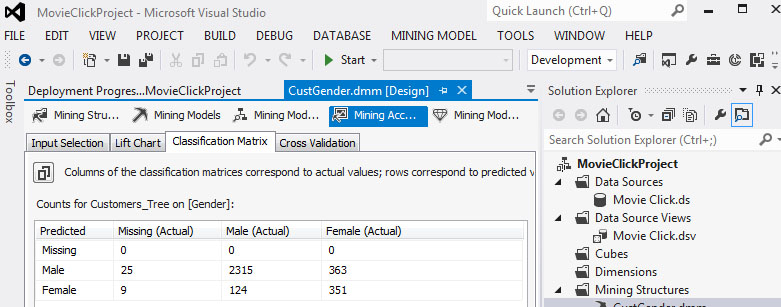
Εικόνα 7.59
6. Συμπερασματικά, στην περίπτωση μας η εντροπία είναι ο πιο αποτελεσματικός τρόπος δημιουργίας ενός δέντρου απόφασης, αφού εξασφαλίζει την πιο ακριβή πρόβλεψη. Αυτό, όμως, δεν σημαίνει ότι είναι πάντα και ο καταλληλότερος τρόπος, καθώς αυξάνει σημαντικά την πολυπλοκότητα ενός δέντρου απόφασης, το οποίο πλέον αποκτά πολλά επίπεδα και κόμβους, με αποτέλεσμα να γίνεται δυσανάγνωστο και δυσερμήνευτο.
Άσκηση 6
Να επαναληφθεί η άσκηση 1, επιλέγοντας τη δημιουργία ενός δέντρου απόφασης, το οποίο θα βασίζεται στο μέτρο της Εντροπίας και θα επιτρέπει πενήντα τουλάχιστον περιπτώσεις σε καθένα από τα φύλλα του.
Λύση
-
Λύση άσκησης 6 :
+
1. Δίνουμε τις παρακάτω τιμές στις παραμέτρους:
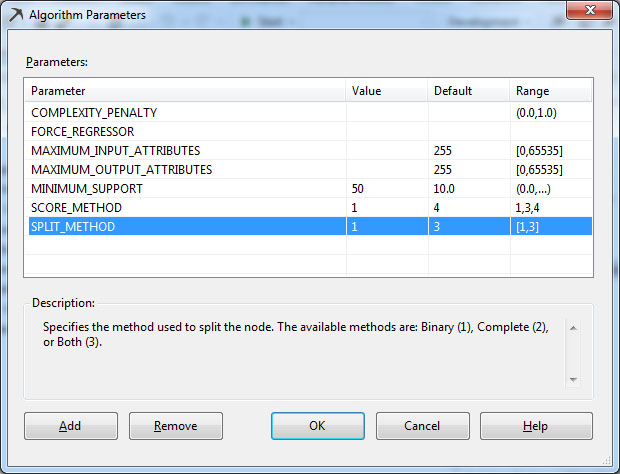
Εικόνα 7.60
2. Το δέντρο έχει την παρακάτω μορφή:
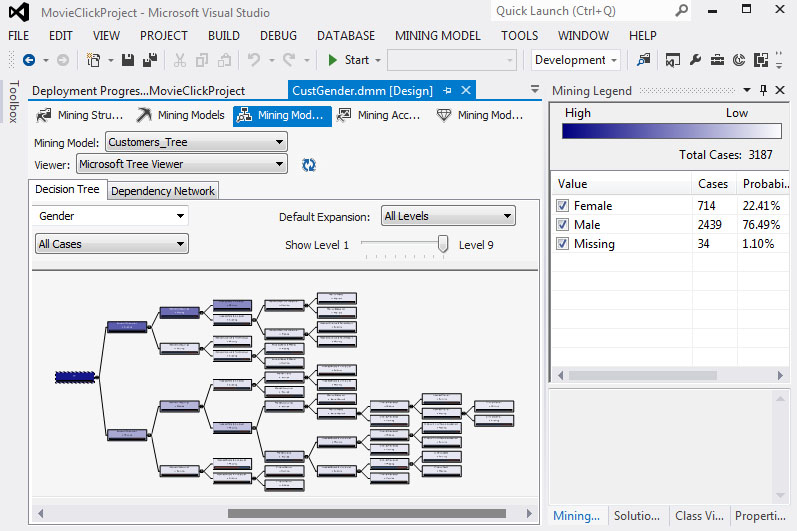
Εικόνα 7.61
3. Τα χαρακτηριστικά από τα οποία εξαρτάται η προβλεπόμενη τιμή είναι τα παρακάτω:
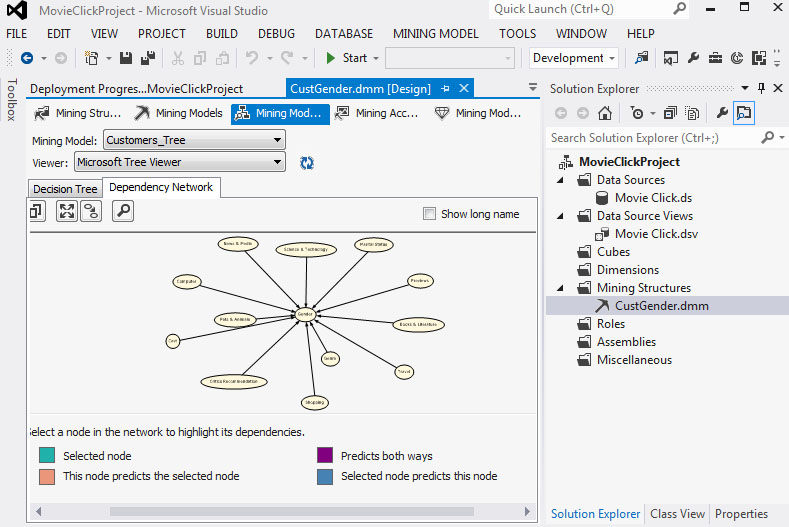
Εικόνα 7.62
4. Στο Lift Chart, όπως φαίνεται στην Εικόνα 7.63, με δείγμα 77% προβλέπουμε σωστά το φύλο σε ποστοστό 87,58% των ανδρών. Το ποσοστό είναι σχετικά καλό και το Score είναι στο 0,93. Οι τιμές είναι λίγο καλύτερες από το default δέντρο.
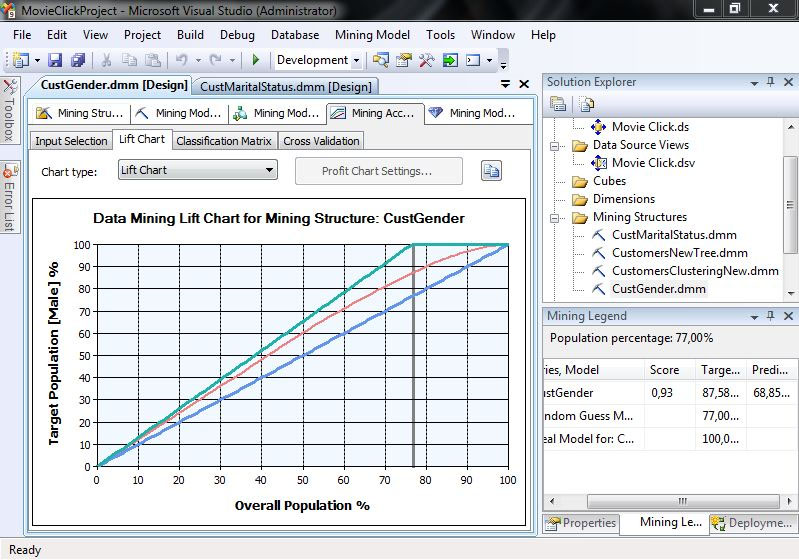
Εικόνα 7.63
5. Το ίδιο ισχύει και για τον Classification Matrix, όπως φαίνεται στην Εικόνα 7.64:
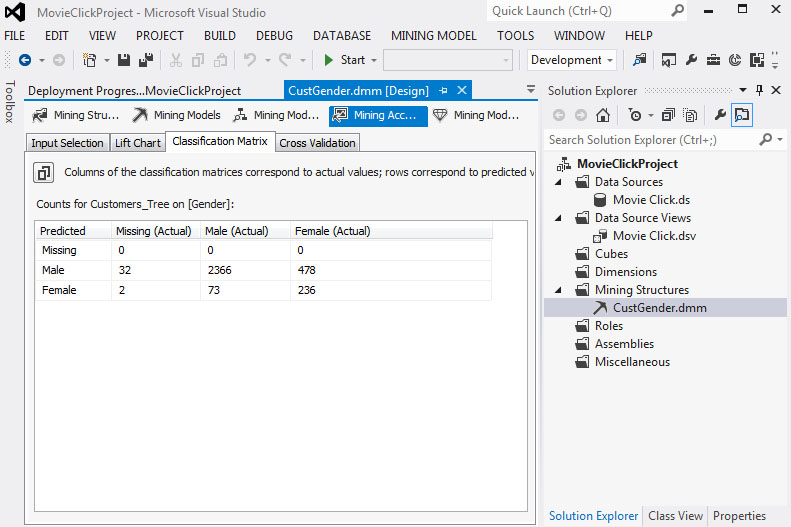
Εικόνα 7.64
6. Συμπερασματικά, αν χρησιμοποιήσουμε την εντροπία σε συνδυασμό με τις άλλες παραμέτρους (π.χ. minimum support), η ακρίβεια του δέντρου απόφασης μπορεί να μειώνεται αλλά, από την άλλη, το δέντρο που κατασκευάζεται είναι ευανάγνωστο, αφού η πολυπολοκότητά του έχει μειωθεί.
Πίνακας Περιεχομένων /
Περιεχόμενα Κεφαλαίου
7.6. Βιβλιογραφία/Αναφορές
Νανόπουλος, Α., & Μανωλόπουλος, Ι. (2008). Εισαγωγή στην Εξόρυξη και τις Αποθήκες Δεδομένων, Αθήνα, Εκδόσεις Νέων Τεχνολογιών.
Χαλκίδη, Μ., & Βεζυργιάννης, Μ. (2005). Εξόρυξη Γνώσης από Βάσεις Δεδομένων και τον Παγκόσμιο Ιστό, Αθήνα, Τυπωθήτω.
Πίνακας Περιεχομένων /
Περιεχόμενα Κεφαλαίου
Data Definition Language - DDL
Η γλώσσα ορισμού περιεχομένου χρησιμοποιείται για τον ορισμό των
πινάκων και των μεταξύ τους σχέσεων. Με τη γλώσσα αυτή δηλώνουμε τα
χαρακτηριστικά που έχει κάθε πίνακας και τους αντίστοιχους τύπους
δεδομένων του κάθε χαρακτηριστικού.
Data Manipulation Language - DML
Η γλώσσα χειρισμού δεδομένων χρησιμοποιείται για την επεξεργασία,
την ενημέρωση, την εισαγωγή και την διαγραφή δεδομένων.
Διάγραμμα οντοτήτων-συσχετίσεων (διάγραμμα E-R)
Τα Διάγραμματα οντοτήτων-συσχετίσεων παρέχουν ένα απλό και κατανοητό τρόπο περιγραφής της δομής των δεδομένων της Βάσης Δεδομένων
Ερώτημα SQL
Αποτελεί ένα δομημένο τρόπο σύνταξης ερωτοαποκρίσεων για την αναζήτηση περιεχομένου στη βάση δεδομένων μας.
create database
Ένας νέος πίνακας δημιουργείται με τη χρήση της εντολής CREATE TABLE ή σύνταξη της οποίας έχει ως εξής :
CREATE TABLE (
<όνομα πεδίου 1> <τύπος πεδίου 1>,
<όνομα πεδίου 2> <τύπος πεδίου 2>,
<όνομα πεδίου Ν> <τύπος πεδίου Ν>);
Drop Database
Μπορούμε να διαγράψουμε ολόκληρο πίνακα, μαζί με τα δεδομένα που τυχόν έχει χρησιμοποιώντας την εντολή DROP σύμφωνα με το ακόλουθο πρότυπο :
DROP TABLE <όνομα πίνακα>
ON UPDATE
H πρόταση ON UPDATE προσδιορίζει την ενέργεια που θα εκτελεστεί αν θέλουμε να αλλάξουμε την τιμή ενός πεδίου:
UPDATE <όνομα πίνακα> SET <όνομα πεδίου> <νέα τιμή πεδίου> WHERE <κριτήρια επιλογής εγγραφών>
ON DELETE
Ο σκοπός είναι πολύ απλός, διαγράφει εγγραφές από ένα πίνακα. Και πάλι έχομε την δυνατότητα να ορίσουμε ποιές εγγραφές θέλουμε να διαγραφούν (ή και όλες) π.χ.:
DELETE FROM product WHERE id=1
Καρτεσιανού γινομένου
To Καρτεσιανό γινόμενο αποτελεί την πράξη μεταξύ δύο πινάκων όπου η κάθε εγγραφή του ενός πίνακα συνδυάζεται με όλες τις εγγραφές του άλλου πίνακα
πράξη της επιλογής/selection
Η SQL εντολή μέσω της οποίας ανακτούμε πληροφορίες και συντάσσουμε ερωτήματα είναι η SELECT. Η γενική σύνταξη της SELECΤ είναι αρκετά σύνθετη, ωστόσο ένα απλό πρότυπο είναι το ακόλουθο:
SELECT <πεδίο που θέλουμε να φαίνονται>
FROM <πίνακες από τους οποίους θα αντληθούν τα δεδομένα>
WHERE <κριτήρια επιλογής των εγγραφών>
πράξης της σύνδεσης (join)
Η εντολή JOIN σημαίνει σύνδεση, δηλαδή συνδυασμός δεδομένων από δύο ή περισσότερους πίνακες.
left outer join
Περιλαμβάνει επιπρόσθετα και όλες τις εγγραφές του πίνακα που βρίσκεται στα αριστερά της πράξης της σύνδεσης (join) και δεν εμπεριέχονται στο αποτέλεσμα της πράξης της σύνδεσης.
πράξη του full outer join
Περιλαμβάνει επιπρόσθετα και όλες τις εγγραφές των πινάκων που βρίσκονται στα αριστερά και δεξιά της πράξης της σύνδεσης (join) και δεν εμπεριέχονται στο αποτέλεσμα της πράξης της σύνδεσης.
όρος distinct
Η λέξη DISTINCT αμέσως μετά την SELECT δηλώνει ότι κάθε εγγραφή του πίνακα του αποτελέσματος θα συμπεριληφθεί μία μόνο φορά. Επομένως χρησιμοποιείται όταν θέλουμε να εγγυηθούμε ότι στο αποτέλεσμα του ερωτήματος δεν θα υπάρχουν διπλοεγγραφές πρέπει να χρησιμοποιήσουμε το DISTINCT
όρος GROUP BY
H λέξη GROUP BY προσδιορίζει τις στήλες με τις οποίες θα πραγματοποιηθεί ομαδοποίηση (grouping) των δεδομένων.
όρος HAVING
Ο όρος HAVING χρησιμοποιείται για να ορίσει περιοσρισμούς που σχετίζονται με τα ήδη ομαδοποιημένα αποτελέσματα που έχουν δημιουργηθεί με την GROUP BY.
πράξη της ένωσης πινάκων/σχέσεων
H SQL παρέχει ειδικές εντολές για την υποστήριξη των πράξεων της σχεσιακής άλγεβρας που αναφέρονται στην ένωση, διαφορά και τομή πινάκων. Οι πράξη της ένωσης (UNION) συνενώνει τις εγγραφές δύο ή περισσότερων πινάκων.
Ένα παράδειγμα ένωσης δίνεται παρακάτω:
SELECT συνέδριο
FROM πρακτικά_συνεδρίου
UNION
SELECT τιτλος
FROM περιοδικό;
πράξη της τομής σχέσεων
H SQL παρέχει ειδικές εντολές για την υποστήριξη των πράξεων της σχεσιακής άλγεβρας που αναφέρονται στην ένωση, διαφορά και τομή πινάκων. Οι πράξεις αυτές υλοποιούνται στην SQL με τις εντολές UNION, EXCEPT και INTERSECΤ αντιστοίχως.
παράδειγμα τομής :
SELECT ονομα
FROM συνδρομητης
INTERSECT
SELECT ονομα
FROM συγγραφεας;
πράξη της διαφοράς σχέσεων
H SQL παρέχει ειδικές εντολές για την υποστήριξη των πράξεων της σχεσιακής άλγεβρας που αναφέρονται στην ένωση, διαφορά και τομή πινάκων. Οι πράξεις αυτές υλοποιούνται στην SQL με τις εντολές UNION, EXCEPT και INTERSECΤ αντιστοίχως.
παράδειγμα διαφοράς :
SELECT κωδικός,τίτλος
FROM άρθρο
EXCEPT
SELECT κωδικός,τίτλος
FROM άρθρο
WHERE κωδικός_περιοδικού IS NOT NULL;
Ο όρος ΙΝ
Σε περίπτωση που θέλουμε ένα πεδίο να λαμβάνει τιμές από ένα προκαθορισμένο σύνολο τιμών, τότε μπορούμε εναλλακτικά να χρησιμοποιήσουμε τον τελεστή ΙΝ.
Ο ορος Νot Ιn
Σε περίπτωση που θέλουμε ένα πεδίο να λαμβάνει τιμές από ένα προκαθορισμένο σύνολο τιμών, εξαιρώντας κάποιες τιμές τότε μπορούμε εναλλακτικά να χρησιμοποιήσουμε τον τελεστή ΝΟΤ ΙΝ.
Οι όροι all και some
H SQL προσφέρει τα κατηγορήματα SOME(ή ΑΝΥ) και ALL τα οποία αντιστοιχούν στον υπαρξιακό και καθολικό ποσοδείκτη που χρησιμοποιούμε στα μαθηματικά. Με τη χρήση των κατηγορημάτων αυτών μπορούμε να συντάξουμε πολύ χρήσιμα ερωτήματα με τη χρήση υποερωτημάτων. Πριν απο τα κατηγορήματα SOME και ALL, μπορεί να προηγείται οποιοσδήποτε τελεστής σύγκρισης (=, >, <, >=, <=, <>)
Οι όροι exists και not exists
Η τιμή που επιστρέφει το κατηγόρημα EXISTS είναι αληθής, αν το σύνολο που ακολουθεί δεν είναι κενό. Σε διαφορετική περίπτωση η τιμή που επιστρέφεται είναι ψευδής.
CREATE VIEW
Για τον ορισμό μιας όψης, η SQL παρέχει την εντολή CREATE VIEW που συντάσσεται ως εξής:
CREATE VIEW όνομα-όψης
AS
(υποερώτημα SQL);
DELETE FROM
Παρόμοια με την εντολή UPDATE λειτουργεί και η εντολή DELETE. Ο σκοπός της είναι πολύ απλός, διαγράφει εγγραφές από ένα πίνακα.
DROP TABLE
Η πλήρης διαγραφή ενός πίνακα γίνεται χρησιμοποιώντας την εντολή DROP σύμφωνα με τον ακόλουθο πρότυπο :
DROP TABLE <ονομα πίνακα>
Οι αποθηκευμένες διαδικασίες/stored procedures
O SQL Server δίνει την δυνατότητα υλοποίησης τμημάτων κώδικα τα οποία παραμένουν αποθηκευμένα μέσα στη Βάση Δεδομένων και καλούνται αποθηκευμένες διαδικασίες (stored procedures). Αυτά ενεργοποιούνται ανά τακτά χρονικά διαστήματα για την εκτέλεση μιας σημαντικής λειτουργίας.
Το εύναυσμα/trigger
Ένας σκανδαλισμός ή εύναυσμα (trigger) είναι ένα τμήμα κώδικα που εκτελείται όταν συμβεί ένα γεγονός. Τα γεγονότα που ενεργοποιούν σκανδαλισμούς είναι εισαγωγές, διαγραφές, και ενημερώσεις στα δεδομένα ενός πίνακα.
Ευρετήριο
Ένας κατάλογος (ευρετήριο) ορίζεται σε μία ή περισσότερες στήλες ενός πίνακα και στοχεύει στην αποδοτικότερη εκτέλεση των ερωτημάτων που χρησιμοποιούν τις στήλες αυτές στη συνθήκη WHERE. Η κατασκευή και κατάργηση καταλόγων πραγματοποιείται με τις εντολές CREATE INDEX και DROP INDEX αντίστοιχα.
ALTER TABLE
O ορισμός ενός πίνακα μπορεί να μεταβληθεί στην πορεία, αναλόγως με τις απαιτήσεις. H SQL προσφέρει την εντολή ALTER TABLE, με την οποία επιτρέπονται να γίνουν συγκεκριμένες αλλαγές στον πίνακα: (προσθήκη νέας στήλης, διαγραφή υπάρχουσας στήλης, αλλαγή πεδίου ορισμού μίας στήλης, εισαγωγή νέου περιορισμού, κατάργηση περιορισμού, αλλαγή της εξ ορισμού τιμής στήλης, κατάργηση αρχικής τιμής στήλης).
εντολή grant.
Με την εντολή GRANT δίνουμε δικαιώματα χρήσης της βάσης δεδομένων σε χρήστες.
εντολή revoke.
Με την εντολή REVOKE αφαιρούμε από τους χρήστες τα δικαιώματα χρήσης ενός στοιχείου (π.χ. πίνακα, όψη) μιας βάσης δεδομένων.
H παράμετρος Split method:
Αυτή η παράμετρος καθορίζει τη μέθοδο με την οποία διαχωρίζονται οι κόμβοι του δένδρου. Μπορεί να πάρει τις τιμές [1,3] όπου 1 είναι η τιμή για Binary δένδρο, 2 η τιμή για Complete (multi-way) δένδρο και 3 η τιμή και για τα δύο μαζί.
Κατηγοριοποίηση (classification)
Η κατηγοριοποίηση αποτελεί μια σημαντική λειτουργία εξόρυξης δεδομένων, όπου επιθυμούμε να προβλέψουμε σε πια κατηγορία εντάσσονται και ανήκουν κάθε φορά τα δεδομένα μας.
H παράμετρος Split method:
Αυτή η παράμετρος καθορίζει τη μέθοδο με την οποία διαχωρίζονται οι κόμβοι του δένδρου. Μπορεί να πάρει τις τιμές [1,3] όπου 1 είναι η τιμή για Binary δένδρο, 2 η τιμή για Complete (multi-way) δένδρο και 3 η τιμή και για τα δύο μαζί.
H παράμετρος Stopping Tolerance
Αυτή η παράμετρος καθορίζει τον αριθμό των περιπτώσεων που μετακινούνται μεταξύ των clusters σε κάθε πέρασμα του αλγορίθμου. Ο αλγόριθμος εφαρμόζεται επαναληπτικά στα δεδομένα και σχηματίζει τα cluster με την μορφή που εμείς τα βλέπουμε, ύστερα από ένα σύνολο επαναλήψεων. Επειδή σε κάθε επανάληψη προστίθενται διαρκώς και νέες περιπτώσεις, η τιμή της παραμέτρου μπορεί να θεωρηθεί ως ποσοστό και όχι ένας συγκεκριμένος αριθμός. Η προεπιλεγμένη τιμή της παραμέτρου είναι 10.
Η τάση (trend)
Η τάση μας δείχνει την γενική κατεύθυνση των δεδομένων μας. Για παράδειγμα, η τάση είναι αυξανόμενη στις πωλήσεις προϊόντων τις ημέρες των Χριστουγέννων.
Η περιοδικότητα (periodicity)
Η περιοδικότητα αφορά την επανεμφάνιση κάποιων τάσεων στα δεδομένα μας. Για παράδειγμα, οι πωλήσεις παγωτών αυξάνονται κάθε καλοκαίρι.
Οι ακραίες τιμές (outliers)
Κάποια δεδομένα ενδέχεται να μην είναι δυνατόν να συμπεριλφθούν σε κάποια ομάδα. Τα δεδομένα αυτά καλούνται απομακρυσμένα ή απομονωμένα (outliers) και συνήθως δημιουργούν πρόβλημα στις μεθόδους ομαδοποίησης.
ολοκληρωμένη (integrated)
Μια αποθήκη δεδομένων είναι ολοκληρωμένη διότι μπορεί και συνενώνει μέσα τις πολλές ανομοιογενείς βάσεις δεδομένων.
Μη ευμετάβλητη (non volatile)
Μια αποθήκη δεδομένων συνήθως δεν μεταβάλλεται ως προς το περιεχόμενο της. Αυτό που συμβαίνει είναι να προστίθεται μόνο καινούργιο περιεχόμενο.
Αφορά ιστορικά δεδομένα (time-variant)
Μια αποθήκη δεδομένων αφορά δεδομένα που μπορεί να έχουν βάθος δεκαετιών.
Ένα μέτρο ή αλλιώς μετρική (measure)
Είναι το μέγεθος ή τα μεγέθη που μας ενδιαφέρουν να συναθροίσουμε ή να αναλύσουμε κατά τις λειτουργίες OLAP.
διαστάσεις (dimensions)
Οι πληροφορίες που περιγράφουν τα γεγονότα, ονομάζονται διαστάσεις. Για ένα γεγονός πώλησης, διαστάσεις είναι, π.χ., το προϊόν που πωλήθηκε, το υποκατάστημα όπου έγινε η πώληση, η ημερομηνία πώλησης, κ.λπ.
Η ιεραρχία (hierarchy)
Η ιεραρχία (hierarchy) μιας διάστασης
Μια διάσταση μπορεί να αποτελείται από διαφορετικά επίπεδα ανάλυσης και να ενσωματώνει μια ιεραρχία. Για παράδειγμα, η διάσταση του χρόνου μπορεί να αναλυθεί σε μέρες, εβδομάδες, κτλ.
Το σχήμα Αστέρα (star schema)
Σύμφωνα με το μοντέλο αυτό η αποθήκη δεδομένων περιέχει ένα μεγάλο κεντρικό πίνακα που καλείται πίνακας γεγονότων (fact table) και ένα σύνολο μικρότερων πινάκων που καλούνται πίνακες διαστάσεων (fimension tables) και συνδέονται απευθείας στον fact table.
To σχήμα χιονονιφάδας (snowflake schema)
Το μοντέλο χιονιφάδας αποτελεί παραλλαγή του μοντέλου αστέρα. Διαφέρει κατά το ότι κάποιοι πίνακες διαστάσεων μπορούν να αναλυθούν περισσότερο χρησιμοποιώντας βοηθητικούς πίνακες. Η λειτουργία αυτή μοιάζει με τη διαδικασία της κανονικοποίησης στις σχεσιακές βάσεις δεδομένων.
Το σχήμα γαλαξία (galaxy schema),
Στο σχήμα γαλαξία έχουμε περισσότερους τους ενός fact tables, τους οποίους μπορούν να διαμοιράζονται περισσότερες διαστάσεις.
Η πράξη Roll-up
Η λειτουργία αυτή ομαδοποιεί τα δεδομένα του κύβου σε υψηλότερο επίπεδο ανάλυσης και μας οδηγεί σε ανώτερο επίπεδο της θεματικής ιεραρχίας, αθροίζοντας τα μετρικά στοιχεία.
Η πράξη Drill-down
Επιφέρει ακριβώς τα αντίθετα αποτελέσματα από τη λειτουργία ROLL-UP. Με τη λειτουργία DRILL-DOWN αυξάνουμε το επίπεδο λεπτομέρειας των δεδομένων μας.
Η πράξη Slice
Η λειτουργία SLICE επιλέγει τα δεδομένα του κύβου μας ως προς μία διάσταση.
Η πράξη Dice
H λειτουργία DICE επιλέγει τα δεδομένα ως προς πολλές διαστάσεις του κύβου μας, δημιουργώντας έναν μικρότερο κύβο.
Η πράξη Pivot
Η λειτουργία PIVOT πραγματοποιεί περιστροφή στις διαστάσεις του κύβου, με αποτέλεσμα τα δεδομένα να απεικονίζονται με διαφορετικό τρόπο κάθε φορά.
Συναθροιστικές συνάρτήσεις (aggregation function)
Οι συναρτήσεις συνάθροισης χρησιμοποιούνται για την εξαγωγή συγκεντρωτικών τιμών από τις τιμές μίας στήλης.
Προκειμένου να εξάγουμε έναν κανόνα συσχέτισης, πρέπει να ικανοποιούνται κάποια κατώτατα όρια τόσο για το support όσο και για τo confidence/probability. Ο κανόνας πρέπει να έχει support μεγαλύτερo από το όριο, που ονομάζεται ελάχιστη υποστήριξη (minimum_support), και η εμπιστοσύνη πρέπει να είναι μεγαλύτερη από το όριο, που ονομάζεται ελάχιστη εμπιστοσύνη (minimum_probability).
Προκειμένου να εξάγουμε έναν κανόνα συσχέτισης, πρέπει να ικανοποιούνται κάποια κατώτατα όρια τόσο για το support όσο και για τo confidence/probability. Ο κανόνας πρέπει να έχει support μεγαλύτερo από το όριο, που ονομάζεται ελάχιστη υποστήριξη (minimum_support), και η εμπιστοσύνη πρέπει να είναι μεγαλύτερη από το όριο, που ονομάζεται ελάχιστη εμπιστοσύνη (minimum_probability).
Slice
H λειτουργία Slice επιλέγει τα δεδομένα ως προς μία διάσταση του κύβου μας, δημιουργώντας μια φέτα ενός κύβου
Pivot
Η λειτουργία Pivot αλλάζει μόνο το τρόπο απεικόνισης των διαστάσεων του κύβου μα