Next: 9.4 Οι κανονικές γλώσσες Up: 9. Context free γραμματικές Previous: 9.2 Ορισμός context free Contents Index
Ας δούμε τώρα ένα παράδειγμα μιας CFG με παραπάνω από ένα
μη τερματικό σύμβολο.
Η γραμματική αυτή θα έχει ως γλώσσα της όλες τις λέξεις του
![]() που έχουν ίδιο πλήθος από
που έχουν ίδιο πλήθος από ![]() και
και ![]() . Θυμίζουμε
εδώ ότι αυτή η γλώσσα δεν είναι κανονική (αποδεικνύεται εύκολα
αυτό με χρήση του Λήμματος Άντλησης (Θεώρημα 7.6)).
. Θυμίζουμε
εδώ ότι αυτή η γλώσσα δεν είναι κανονική (αποδεικνύεται εύκολα
αυτό με χρήση του Λήμματος Άντλησης (Θεώρημα 7.6)).
Η γραμματική ![]() είναι η ακόλουθη:
είναι η ακόλουθη:
Ας συμβολίζουμε για μια λέξη ![]() του
του
![]() με
με ![]() και
και ![]() αντίστοιχα το πλήθος των
αντίστοιχα το πλήθος των ![]() και
και ![]() που περιέχει.
που περιέχει.
Πρέπει να δείξουμε ότι ισχύει
![]() αν και μόνο αν
αν και μόνο αν
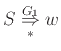 .
Αλλά αν προσπαθήσουμε να δείξουμε μόνο αυτό θα συναντήσουμε
δυσκολίες. Παρ' ότι δείχνει αντιφατικό μας διευκολύνει
το να δείξουμε παράλληλα και άλλες δύο προτάσεις.
Έτσι θα δείξουμε με επαγωγή ως προς το μήκος της λέξης
.
Αλλά αν προσπαθήσουμε να δείξουμε μόνο αυτό θα συναντήσουμε
δυσκολίες. Παρ' ότι δείχνει αντιφατικό μας διευκολύνει
το να δείξουμε παράλληλα και άλλες δύο προτάσεις.
Έτσι θα δείξουμε με επαγωγή ως προς το μήκος της λέξης ![]() τις εξής τρείς ισοδυναμίες.
τις εξής τρείς ισοδυναμίες.
Όπως είπαμε
συμβολίζουμε με ![]() το μήκος της λέξης
το μήκος της λέξης ![]() και κάνουμε επαγωγή
ως προς
και κάνουμε επαγωγή
ως προς ![]() .
Αν
.
Αν ![]() , τότε
, τότε
![]() και
και ![]() παράγεται από
το
παράγεται από
το ![]() με τον τελευταίο κανόνα παραγωγής του
με τον τελευταίο κανόνα παραγωγής του ![]() ενώ δεν παράγεται από τα
ενώ δεν παράγεται από τα ![]() ή
ή ![]() , αφού όλοι οι κανόνες παραγωγής
των
, αφού όλοι οι κανόνες παραγωγής
των ![]() και
και ![]() παράγουν μη κενές λέξεις.
Βλέπουμε έτσι ότι ισχύουν και οι τρεις ισοδυναμίες για τη λέξη
παράγουν μη κενές λέξεις.
Βλέπουμε έτσι ότι ισχύουν και οι τρεις ισοδυναμίες για τη λέξη
![]() ,
τη μοναδική λέξη με μήκος
,
τη μοναδική λέξη με μήκος ![]() .
.
Υποθέτουμε τώρα επαγωγικά
ότι ισχύουν και οι τρεις άνω ισοδυναμίες για κάθε λέξη
![]() με
με
![]() .
.
Έστω τώρα ![]() μια λέξη με μήκος
μια λέξη με μήκος ![]() .
Αποδεικνύουμε την πρώτη ισοδυναμία:
.
Αποδεικνύουμε την πρώτη ισοδυναμία:
![]() .
.
![]()
Αφού
![]() υπάρχει μια ακολουθία παραγωγών της
υπάρχει μια ακολουθία παραγωγών της ![]() που αρχίζει από το
που αρχίζει από το ![]() και καταλήγει στη
και καταλήγει στη ![]() .
Αν το πρώτο γράμμα της
.
Αν το πρώτο γράμμα της ![]() είναι
είναι ![]() τότε στην πρώτη
παραγωγή αναγκαστικά χρησιμοποιείται ο κανόνας
τότε στην πρώτη
παραγωγή αναγκαστικά χρησιμοποιείται ο κανόνας
![]() .
Αυτό συνεπάγεται ότι
.
Αυτό συνεπάγεται ότι ![]() όπου
όπου ![]() είναι μια λέξη για την οποία
ισχύει
είναι μια λέξη για την οποία
ισχύει
![]() , και
, και
![]() .
Από την επαγωγική υπόθεση έπεται ότι
.
Από την επαγωγική υπόθεση έπεται ότι
![]() και συνεπώς
και συνεπώς
![]() .
Ομοίως, αν το πρώτο γράμμα της
.
Ομοίως, αν το πρώτο γράμμα της ![]() είναι
είναι ![]() τότε ο πρώτος κανόνας
παραγωγής από το
τότε ο πρώτος κανόνας
παραγωγής από το ![]() στο
στο ![]() είναι αναγκαστικά ο
είναι αναγκαστικά ο ![]() , άρα
, άρα
![]() , με
, με
![]() και
και
![]() .
Από την επαγωγική υπόθεση
.
Από την επαγωγική υπόθεση
![]() από το οποίο προκύπτει
από το οποίο προκύπτει
![]() .
.
![]()
Αν το πρώτο γράμμα της ![]() είναι
είναι ![]() τότε
τότε ![]() με
με
![]() ,
και
,
και
![]() . Από την επαγωγική υπόθεση προκύπτει ότι
. Από την επαγωγική υπόθεση προκύπτει ότι
![]() , άρα υπάρχει τρόπος να παράγουμε το
, άρα υπάρχει τρόπος να παράγουμε το ![]() από το
μη τερματικό σύμβολο
από το
μη τερματικό σύμβολο ![]() . Αρχίζοντας τότε από το
. Αρχίζοντας τότε από το ![]() , εφαρμόζουμε
τον κανόνα παραγωγής
, εφαρμόζουμε
τον κανόνα παραγωγής ![]() και ακολούθως παράγουμε από το
και ακολούθως παράγουμε από το
![]() το
το ![]() . Συνολικά έχουμε παραγάγει έτσι το
. Συνολικά έχουμε παραγάγει έτσι το ![]() από το
από το ![]() δείχνοντας
σε αυτή την περίπτωση
δείχνοντας
σε αυτή την περίπτωση
![]() .
Ομοίως, αν το πρώτο γράμμα της
.
Ομοίως, αν το πρώτο γράμμα της ![]() είναι το
είναι το ![]() τότε γράφεται
τότε γράφεται
![]() με
με
![]() και
και
![]() , άρα, με την επαγωγική
υπόθεση, ισχύει
, άρα, με την επαγωγική
υπόθεση, ισχύει
![]() . Για να παραγάγουμε λοιπόν τη
. Για να παραγάγουμε λοιπόν τη ![]() από το
από το
![]() ξεκινούμε εφαρμόζοντας τον κανόνα
ξεκινούμε εφαρμόζοντας τον κανόνα ![]() , και ακολούθως παράγουμε
από το
, και ακολούθως παράγουμε
από το ![]() το
το ![]() , παίρνοντας έτσι τελικά το
, παίρνοντας έτσι τελικά το ![]() .
.
Εδώ έχουμε δείξει το επαγωγικό βήμα για την πρώτη ισοδυναμία.
Δείχνουμε τώρα το επαγωγγικό βήμα για
την ισοδυναμία
![]() .
Προσέξτε ότι εδώ υπάρχει ασυμμετρία στην απόδειξη όσον αφορά το ρόλο που
παίζει το
.
Προσέξτε ότι εδώ υπάρχει ασυμμετρία στην απόδειξη όσον αφορά το ρόλο που
παίζει το ![]() και το
και το ![]() ως πρώτο γράμμα της λέξης
ως πρώτο γράμμα της λέξης ![]() .
.
![]()
Έστω ότι το πρώτο γράμμα της λέξης ![]() είναι το
είναι το ![]() .
Τότε αναγκαστικά η πρώτη παραγαγωγή από το
.
Τότε αναγκαστικά η πρώτη παραγαγωγή από το ![]() στο
στο ![]() είναι
η
είναι
η ![]() , οπότε
, οπότε ![]() με
με
![]() και αναγκαστικά τότε
το
και αναγκαστικά τότε
το ![]() πρέπει να είναι παραγόμενο από το
πρέπει να είναι παραγόμενο από το ![]() , άρα
, άρα
![]() και από
την επαγωγική υπόθεση
και από
την επαγωγική υπόθεση
![]() , από το οποίο προκύπτει ότι
, από το οποίο προκύπτει ότι
![]() .
.
Αν το πρώτο γράμμα της ![]() είναι το
είναι το ![]() τότε ο πρώτος κανόνας που εφαρμόζεται
στην παραγωγή της
τότε ο πρώτος κανόνας που εφαρμόζεται
στην παραγωγή της ![]() από το
από το ![]() είναι αναγκαστικά ο
είναι αναγκαστικά ο
![]() ,
οπότε έχουμε
,
οπότε έχουμε
![]() όπου
όπου
![]() ,
και, φυσικά,
,
και, φυσικά,
![]() .
Από την επαγωγική υπόθεση τώρα προκύπτει ότι
.
Από την επαγωγική υπόθεση τώρα προκύπτει ότι
![]() και
και
![]() , από τα οποία προκύπτει
φυσικά ότι
, από τα οποία προκύπτει
φυσικά ότι
![]() .
.
![]()
Αν το πρώτο γράμμα της ![]() είναι το
είναι το ![]() τότε
τότε ![]() με
με
![]() ,
,
![]() , οπότε από την επαγωγική υπόθεση
προκύπτει
, οπότε από την επαγωγική υπόθεση
προκύπτει
![]() . Παράγοντας τώρα από το
. Παράγοντας τώρα από το ![]() με τον κανόνα
παραγωγής
με τον κανόνα
παραγωγής ![]() και συνεχίζοντας παράγοντας από το
και συνεχίζοντας παράγοντας από το ![]() το
το ![]() ,
καταλήγουμε σε μια ακολουθία παραγωγής του
,
καταλήγουμε σε μια ακολουθία παραγωγής του ![]() από το
από το ![]() , δηλ.
, δηλ.
![]() .
.
Αν το πρώτο γράμμα της ![]() είναι το
είναι το ![]() τότε
τότε ![]() με
με
![]() και
και
![]() .
Ισχύει όμως το παρακάτω Λήμμα.
.
Ισχύει όμως το παρακάτω Λήμμα.
Οπότε η λέξη
Παραλείπουμε την απόδειξη του επαγωγικού βήματος για την τρίτη ισοδυναμία
μια και αυτή είναι εντελώς παρόμοια με τη δεύτερη ισοδυναμία, με τους
ρόλους των ![]() .
.![]() και
και ![]() .
.![]() εναλλαγμένους.
εναλλαγμένους.
![]()
Mihalis Kolountzakis 2015-11-28